Nonlinear predictive control of dynamic systems represented by Wiener–Hammerstein models

Abstract

This paper is concerned with computationally efficient nonlinear model predictive control (MPC) of dynamic systems described by cascade Wiener–Hammerstein models. The Wiener–Hammerstein structure consists of a nonlinear steady-state block sandwiched by two linear dynamic ones. Two nonlinear MPC algorithms are discussed in details. In the first case the model is successively linearised on-line for the current operating conditions, whereas in the second case the predicted output trajectory of the system is linearised along the trajectory of the future control scenario. Linearisation makes it possible to obtain quadratic optimisation MPC problems. In order to illustrate efficiency of the discussed nonlinear MPC algorithms, a heat exchanger represented by the Wiener–Hammerstein model is considered in simulations. The process is nonlinear, and a classical MPC strategy with linear process description does not lead to good control result. The discussed MPC algorithms with on-line linearisation are compared in terms of control quality and computational efficiency with the fully fledged nonlinear MPC approach with on-line nonlinear optimisation.

1 Introduction

The dynamic model of the controlled process is used only during development of the classical controllers, e.g. linear quadratic regulator (LQR). A conceptually different approach is a model predictive control (MPC) algorithm, in which the model is used on-line in order to predict the future behaviour of the process and determine the optimal control policy [1]. Typically, the objective of MPC is to minimise the predicted deviations between the output (or state) trajectory and the set-point trajectory. The MPC algorithms have the unique ability to efficiently take into account constraints imposed on process inputs (manipulated variables) and outputs (controlled variables) or state variables. Furthermore, they may be applied not only to single-input single-output processes, but also to complex multiple-input multiple-output systems with strong cross-couplings. MPC algorithms make it possible to efficiently control nonminimum phase processes, e.g. with long time delays. As a result, the MPC algorithms are very frequently used in practice in different areas, primarily in chemical, petrochemical, food and paper industries [2]. Applications of MPC algorithms include: manipulators [3], active steering systems in cars [4], air conditioning systems [5], anti-lock brake systems in cars [6], chemical reactors [7], distillation columns [8], overhead cranes [9]. Examples of less typical applications of MPC are: active queue management in TCP/IP networks [10] and drinking water networks [11].

The classical formulations of MPC algorithms, e.g. dynamic matrix control (DMC) and generalised predictive control (GPC) [1], use for prediction linear models. Although they are successful in many applications, a large class of industrial processes are nonlinear and in such cases the classical MPC algorithms usually cannot give acceptable control quality. In nonlinear MPC the basic question is the choice of the model structure, which is next used on-line for prediction and optimisation of the future control policy. Although many implementations of MPC use black-box models, e.g. fuzzy structures [5] or neural networks [12], a viable alternative is to use block-oriented cascade models which are composed of linear dynamic parts and nonlinear steady-state parts [13, 14]. It is necessary to point out that the cascade model representation is a straightforward choice in case of many dynamic processes.

The simplest two-block cascade models are very frequently used for control, especially for MPC. MPC algorithms for the Hammerstein structure (a nonlinear steady-state block followed by a linear dynamic one) discussed in [15–17] use an inverse of the steady-state part of the model to compensate for process nonlinearity. It is also possible to find on-line a linear approximation of the model for current operating conditions and next use the linearised model in MPC [12, 18] or find directly a linear approximation of the predicted trajectory [12]. MPC algorithms for the Wiener structure (a linear dynamic block followed by a nonlinear steady-state one) with an inverse of the steady-state part are discussed in [19–21], MPC approaches with on-line model linearisation are discussed in [12, 22, 23], and MPC approaches with on-line trajectory linearisation are discussed in [12, 23]. In case of the three-block cascade models of the Hammerstein–Wiener type (a linear dynamic block sandwiched by two nonlinear steady-state ones), MPC algorithms with an inverse of the steady-state parts are detailed in [24, 25], and MPC with on-line trajectory linearisation is discussed in [26]. In all the cited MPC algorithms application of an inverse model or on-line linearisation makes it possible to obtain a computationally simple MPC quadratic optimisation problems. MPC with transformation of the nonlinearities into polytopic descriptions which results in a convex optimisation task subject to linear matrix inequalities is considered in [27].

The cascade Wiener–Hammerstein structure consists of a nonlinear steady-state block sandwiched by two linear dynamic ones. It may be used to describe different dynamic processes, e.g. a superheater–desuperheater [28], an RF amplifier [29], a paralysed muscle under electrical stimulation [13], a heat exchanger [30], a DC–DC converter [31], an equaliser for optical communication [32], an electronic circuit [33]. Although control of dynamic systems represented by Wiener–Hammerstein models is discussed in the literature, e.g. extremum seeking control is described in [34], MPC of such systems has not been considered so far. This paper details two computationally efficient nonlinear MPC algorithms based on Wiener–Hammerstein models. In the first case the model is successively linearised on-line for the current operating conditions, whereas in the second case the predicted output trajectory of the system is linearised along the trajectory of the future control scenario. In both MPC approaches on-line linearisation makes it possible to obtain quadratic optimisation problems, which may be efficiently solved using the available solvers [35]. In order to illustrate efficiency of the discussed nonlinear MPC algorithms, a heat exchanger represented by the Wiener–Hammerstein model is considered in simulations. The process is nonlinear, and a classical MPC strategy in which a linear process description is used does not lead to good control. The discussed MPC algorithms with on-line linearisation are compared in terms of control quality and computational efficiency with the fully fledged nonlinear MPC approach with on-line nonlinear optimisation. This work extends the algorithms developed for Hammerstein, Wiener and Hammerstein–Wiener systems discussed in [12, 23, 26].

This paper is structured as follows. Section 2 reminds the idea of MPC, and Sect. 3 defines the structure of the Wiener–Hammerstein–Wiener model. Section 4 details the nonlinear MPC algorithms for Wiener–Hammerstein systems. Section 5 presents simulation results and their comparisons for a benchmark heat exchanger system. Finally, Sect. 6 concludes the paper.

2 Model predictive control problem formulation

Let u denote the input (manipulated) variable of the process and y denote the output (controlled) variable. In contrast to the classical control schemes, e.g. PID, in MPC algorithms [1] at each consecutive sampling instant k not only the current value of the manipulated variable, u(k), but a control policy defined for a control horizon $N_{{\mathrm {u}}}$ is calculated. Typically, control increments

$$\begin{aligned} \triangle {\varvec{u}}(k)= & {} \left[ \triangle u(k|k) \ \triangle u(k+1|k)\ldots \triangle u(k+N_{{\mathrm {u}}}-1|k)\right] ^{{\mathrm {T}}}\nonumber \\ \end{aligned}$$

(1)

rather than values of the manipulated variable are determined, and the increments are defined as $\triangle u(k|k)=u(k|k)-u(k-1)$, $\triangle u(k+p|k)=u(k+p|k)-u(k+p-1|k)$ for $p=1,\ldots ,N_{{\mathrm {u}}}-1$. It is assumed that $\triangle u(k+p|k)=0$ for $p\ge N_{{\mathrm {u}}}$, i.e. $u(k+p|k)=u(k+N_{{\mathrm {u}}}-1|k)$ for $p\ge N_{{\mathrm {u}}}$. The decision variables (1) of the MPC algorithm are calculated at each sampling instant from an optimisation problem in which the predicted control errors are minimised. They are defined as the differences between the set-point trajectory $y^{\mathrm {sp}}(k+p|k)$ and the predicted values of the process output, i.e. $\hat{y}(k+p|k)$, over the prediction horizon $N\ge N_{{\mathrm {u}}}$, i.e. for $p=1,\ldots ,N$. A dynamic model of the controlled process is used for prediction on-line. The MPC cost function is usually

$$\begin{aligned} J(k)= & {} \sum _{p=1}^{N}\left( y^{\mathrm {sp}}(k+p|k)-\hat{y}(k+p|k)\right) ^{2}\\&+\,\lambda \sum _{p=0}^{N_{{\mathrm {u}}}-1}\left( \triangle u(k+p|k)\right) ^{2} \end{aligned}$$

where $\lambda >0$ is a weighting coefficient which makes it possible not only to influence the speed of the algorithm, but also to assure good computational properties for an optimisation solver (tuning of MPC is discussed elsewhere [1]). Additionally, the optimisation algorithm may take into account some constraints imposed on the manipulated variable, which result from the physical limits of actuators, and on the predicted values of the controlled variable, which are usually enforced by some technological reasons. Typically, the MPC optimisation problem has the following form

$$\begin{aligned}&\min \limits _{\triangle u(k|k),\ldots ,\triangle u(k+N_{{\mathrm {u}}}-1|k)} \left\{ J(k)\right\} \nonumber \\&\text {subject to}\nonumber \\&u^{\min } \le u(k+p|k)\le u^{\max },\ p=0,\ldots ,N_{{\mathrm {u}}}-1\nonumber \\&-\triangle u^{\max } \le \triangle u(k+p|k)\le \triangle u^{\max },\nonumber \\&\quad p=0,\ldots ,N_{{\mathrm {u}}}-1\nonumber \\&y^{\min } \le \hat{y}(k+p|k)\le y^{\max },\ p=1,\ldots ,N \end{aligned}$$

(2)

where $u^{\min }$, $u^{\max }$, $\triangle u^{\max }$, $y^{\min }$, $y^{\max }$ define constraints imposed on: the magnitude of the manipulated (input) variable, the increment of the input variable and the magnitude of the controlled (output) variable, respectively. If the output constraints are necessary, the MPC optimisation task (2) may be infeasible. A simple, but efficient method to solve the problem is to relax the output constraints by the so-called soft constraints, which may be temporarily relaxed [1]. Although in MPC at each sampling instant the whole sequence of control increments (1), of length $N_{{\mathrm {u}}}$, is calculated, only the first element of that sequence is actually applied to the process, i.e. $u(k)=\triangle u(k|k)+u(k-1)$. At the next sampling instant, $k+1$, the prediction is shifted one step forward and the whole procedure is repeated.

3 Hammerstein–Wiener model of the process

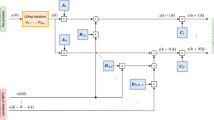
The structure of the Wiener–Hammerstein model is depicted in Fig. 1. It consists of three separate blocks: two linear dynamic ones and a nonlinear steady-state one, which are connected in series in such a way that the nonlinear block is between the linear ones. The auxiliary signal between the input linear dynamic part and the nonlinear steady-state one is denoted by v, and the auxiliary signal between the nonlinear steady-state part and the output linear dynamic one is denoted by x. The first (input) linear dynamic part of the model is described by

$$\begin{aligned} \varvec{A}^1(q^{-1})v(k)=\varvec{B}^1(q^{-1})u(k) \end{aligned}$$

(3)

where the polynomials in the backward shift operator ($q^{-1}$) are

$$\begin{aligned} \varvec{A}^1(q^{-1})&=1+a^1_1 q^{-1}+\ldots +a^1_{n_{\mathrm {A}^1}}q^{-n_{\mathrm {A}^1}} \end{aligned}$$

(4)

$$\begin{aligned} \varvec{B}^1(q^{-1})&=b^1_1q^{-1}+\ldots +b^1_{n_{\mathrm {B}^1}}q^{-n_{\mathrm {B}^1}} \end{aligned}$$

(5)

The order of dynamics of the first block is defined by the integers $n_{\mathrm {A}^1}$ and $n_{\mathrm {B}^1}$. The nonlinear steady-state block is characterised by

$$\begin{aligned} x(k)=f(v(k)) \end{aligned}$$

(6)

where it is assumed that the function $f:\mathbb {R}\rightarrow \mathbb {R}$ is differentiable. The second (output) linear dynamic part of the model is defined by

$$\begin{aligned} \varvec{A}^2(q^{-1})y(k)=\varvec{B}^2(q^{-1})x(k) \end{aligned}$$

(7)

where the polynomials are

$$\begin{aligned} \varvec{A}^2(q^{-1})&=1+a^2_1 q^{-1}+\ldots +a^2_{n_{\mathrm {A}^2}}q^{-n_{\mathrm {A}^2}} \end{aligned}$$

(8)

$$\begin{aligned} \varvec{B}^2(q^{-1})&=b^2_1q^{-1}+\ldots +b^2_{n_{\mathrm {B}^2}}q^{-n_{\mathrm {B}^2}} \end{aligned}$$

(9)

and the order of dynamics of the second dynamic block is defined by the integers $n_{\mathrm {A}^2}$ and $n_{\mathrm {B}^2}$.

Fig. 1

The structure of the Wiener–Hammerstein model

From Eqs. (7)–(9), the output of the model is

$$\begin{aligned} y(k)=\sum _{i=1}^{n_{\mathrm {B}^2}} b^2_i x(k-i)-\sum _{i=1}^{n_{\mathrm {A}^2}} a^2_i y(k-i) \end{aligned}$$

(10)

where from Eq. (6) the auxiliary signal x at the previous sampling instants is

$$\begin{aligned} x(k-i)=f(v(k-i)) \end{aligned}$$

(11)

for $i=1,\ldots ,n_{\mathrm {B}^2}$. From Eqs. (3)–(5), the auxiliary signal v for the current sampling instant k is

$$\begin{aligned} v(k)=\sum _{j=1}^{n_{\mathrm {B}^1}} b^1_j u(k-j)-\sum _{j=1}^{n_{\mathrm {A}^1}} a^1_j v(k-j) \end{aligned}$$

(12)

From Eqs. (10) and (11), one has

$$\begin{aligned} y(k)=\sum _{i=1}^{n_{\mathrm {B}^2}} b^2_i f(v(k-i))-\sum _{i=1}^{n_{\mathrm {A}^2}} a^2_i y(k-i) \end{aligned}$$

(13)

where from Eq. (12)

$$\begin{aligned} v(k-i)=\sum _{j=1}^{n_{\mathrm {B}^1}} b^1_j u(k-j-i)-\sum _{j=1}^{n_{\mathrm {A}^1}} a^1_j v(k-j-i) \end{aligned}$$

(14)

for $i=1,\ldots ,n_{\mathrm {B}^2}$. Taking into account Eqs. (11), (13) and (14), it is possible to express the output of the model for the current sampling instant k as a function of: the model input variable u, the auxiliary variable v and the output variable y at the same previous sampling instants

$$\begin{aligned} y(k)=&\sum _{i=1}^{n_{\mathrm {B}^2}} b^2_i f \left( \sum _{j=1}^{n_{\mathrm {B}^1}} b^1_j u(k-j-i)-\sum _{j=1}^{n_{\mathrm {A}^1}} a^1_j v(k-j-i)\right) \nonumber \\&-\sum _{i=1}^{n_{\mathrm {A}^2}} a^2_i y(k-i) \end{aligned}$$

(15)

4 Nonlinear MPC algorithms of Hammerstein–Wiener systems

The Wiener–Hammerstein model is used in MPC for prediction, i.e. to calculate the predicted values of the output variable for the consecutive sampling instants, i.e. $\hat{y}(k+1|k),\ldots ,\hat{y}(k+N|k)$. The prediction for a sampling instant $k+p$ is calculated at the current instant k as a sum of the model output supplemented by an estimation of the unmeasured disturbance, d(k), [1]. From Eq. (10), one obtains

$$\begin{aligned} \hat{y}(k+p|k)=&\sum _{i=1}^{I_{\mathrm {xf}}(p)} b^2_i x(k-i+p|k)\nonumber \\&+\sum _{i=I_{\mathrm {xf}}(p)+1}^{n_{\mathrm {B}^2}} b^2_i x(k-i+p)\nonumber \\&-\sum _{i=1}^{I_{\mathrm {yf}}(p)}a^2_i \hat{y}(k-i+p|k)\nonumber \\&-\sum _{i=I_{\mathrm {yf}}(p)+1}^{n_{\mathrm {A}^2}}a^2_i y(k-i+p)+{d}(k) \end{aligned}$$

(16)

for $p=1,\ldots ,N$, where $I_{\mathrm {xf}}(p)=\min (p,n_{\mathrm {B}^2})$, $I_{\mathrm {yf}}(p)=\min (p-1,n_{\mathrm {A}^2})$. The symbols $x(k-1),x(k-2),\ldots$ denote the past values of the auxiliary signal between the nonlinear steady-state part and the output linear dynamic part of the model, and their future predicted values are denoted by $x(k|k),x(k+1|k),\ldots$. Similarly, the symbols $y(k),y(k-1),\ldots$ denote the past values of the output signal (their measurements are available). Using the introduced notation, from Eq. (6) it is obvious that

$$\begin{aligned}&x(k-i+p|k)=f(v(k-i+p|k)) \ \mathrm {for} \ p-i\ge 0 \end{aligned}$$

(17a)

$$\begin{aligned}&x(k-i+p)=f(v(k-i+p)) \ \mathrm {for} \ p-i<0 \end{aligned}$$

(17b)

The prediction equation (16) introduces the integral action into the MPC algorithm which is necessary to compensate for disturbances which affects the process and for the mismatch between the process and its model [1]. It is possible because during prediction calculation not only the model, but also an estimate of the unmeasured disturbance d(k) acting on the process output is used. The disturbance is assessed as the difference between the real value of the process output variable measured at the current sampling instant, i.e. y(k), and the model output. From Eq. (15), one has

$$\begin{aligned} {d}(k)=&y(k)-\sum _{i=1}^{n_{\mathrm {B}^2}} b^2_i f \Bigg (\sum _{j=1}^{n_{\mathrm {B}^1}} b^1_j u(k-j-i)\nonumber \\&-\sum _{j=1}^{n_{\mathrm {A}^1}} a^1_j v(k-j-i)\Bigg )\nonumber \\&+\sum _{i=1}^{n_{\mathrm {A}^2}}a^2_i y(k-i) \end{aligned}$$

(18)

From Eq. (14) one may find the values of the predicted values of the auxiliary signal between the input linear dynamic part and the steady-state nonlinear part. If $p-i\ge 0$, one has

$$\begin{aligned} v(k-i+p|k)=&\sum _{j=1}^{I_{\mathrm {uf}}(i,p)} b^1_j u(k-j-i+p|k)\nonumber \\&+\sum _{j=I_{\mathrm {uf}}(i,p)+1}^{n_{\mathrm {B}^1}} b^1_j u(k-j-i+p)\nonumber \\&-\sum _{j=1}^{I_{{\mathrm {vf}}}(i,p)} a^1_j v(k-j-i+p|k)\nonumber \\&-\sum _{j=I_{{\mathrm {vf}}}(i,p)+1}^{n_{\mathrm {A}^1}} a^1_j v(k-j-i+p) \end{aligned}$$

(19)

where $I_{\mathrm {uf}}(i,p)=\min (p-i,n_{\mathrm {B}^1})$ and $I_{{\mathrm {vf}}}(i,p)=\min (p-i,n_{\mathrm {A}^1})$, while when $p-i<0$, one obtains

$$\begin{aligned} v(k-i+p)= & {} \sum _{j=1}^{n_{\mathrm {B}^1}} b^1_j u(k-j-i+p)\nonumber \\&-\sum _{j=1}^{n_{\mathrm {A}^1}} a^1_j v(k-j-i+p) \end{aligned}$$

(20)

The symbols $u(k-1),u(k-2),\ldots$ denote the past values of the manipulated variable (i.e. applied to the process), and their future predicted values (calculated on-line by the MPC algorithm) are denoted by $u(k|k),u(k+1|k),\ldots$. Similarly, the symbols $v(k-1),v(k-2),\ldots$ denote the past values of the auxiliary signal between the input linear dynamic part and the nonlinear steady-state one, and their predicted values are denoted by $v(k|k),v(k+1|k),\ldots$.

From the prediction equations (16)–(17a) and (19) it is clear that if the Wiener–Hammerstein model is directly used in MPC for prediction calculation, the obtained predicted values of the output variable over the prediction horizon, i.e. the signals $\hat{y}(k+1|k), \ldots ,\hat{y}(k+N|k)$, are nonlinear functions of the decision variables of MPC, i.e. the calculated on-line future control increments $\triangle u(k|k),\ldots ,\triangle u(k+N_{{\mathrm {u}}}|k)$. A direct consequence of this fact is that the MPC optimisation problem (2) becomes a constrained nonlinear task which must be solved on-line in real time. It means that a nonlinear solver must be used, and the optimisation problem is likely to be computationally demanding. Such a truly nonlinear MPC strategy is named the MPC algorithm with nonlinear optimisation (MPC-NO). In the following part of the article two nonlinear MPC algorithms with on-line linearisation (performed by means of different methods) are detailed which do not require solving nonlinear optimisation problems in real time, and relatively computationally not demanding quadratic optimisation is used. Provided that $\lambda >0$, the resulting quadratic optimisation tasks have only one global solution.

4.1 Nonlinear MPC algorithm with on-line simplified model linearisation

The simplest approach to nonlinear MPC of dynamic systems represented by the Wiener–Hammerstein model is to use for prediction a linear time-varying model obtained by linearisation of the nonlinear steady-state part of the model. For this purpose the specific serial structure of the model shown in Fig. 1 is exploited. Taking into account Eq. (6), the gain of the nonlinear block for the current operating point is

$$\begin{aligned} K(k)=\frac{{\mathrm {d}}x(k)}{{\mathrm {d}}v(k)}=\frac{{\mathrm {d}}f(v(k))}{{\mathrm {d}}v(k)} \end{aligned}$$

(21)

The output signal of the nonlinear steady-state part can be simply calculated for the current operating point from $x(k)=K(k)v(k)$. Hence, from Eq. (7), the nonlinear steady-state part and the output linear dynamic part of the model may be described by

$$\begin{aligned} \varvec{A}^2(q^{-1})y(k)=\varvec{B}^2(q^{-1})K(k)v(k) \end{aligned}$$

Next, taking into account the input linear dynamic part defined by Eq. (3), the linearised model becomes

$$\begin{aligned} \varvec{A}^1(q^{-1})\varvec{A}^2(q^{-1})y(k)=\varvec{B}^1(q^{-1})\varvec{B}^2(q^{-1})K(k)u(k) \end{aligned}$$

The linearised model may be compactly defined by

$$\begin{aligned} \varvec{A}(q^{-1})y(k)=K(k)\varvec{B}(q^{-1})u(k) \end{aligned}$$

(22)

where the polynomials in the backward shift operator are

$$\begin{aligned} \varvec{A}(q^{-1})&=\varvec{A}^1(q^{-1})\varvec{A}^2(q^{-1})\\&=1+a_1 q^{-1} +\ldots +a_{n_{\mathrm {A}^1}}q^{-n_{\mathrm {A}}}\\ \varvec{B}(q^{-1})&=\varvec{B}^1(q^{-1})\varvec{B}^2(q^{-1})\\&=b_1q^{-1}+\ldots +b_{n_{\mathrm {B}^1}}q^{-n_{\mathrm {B}}} \end{aligned}$$

the order of dynamics is defined by $n_{\mathrm {A}}=n_{\mathrm {A}^1}+n_{\mathrm {A}^2}$, $n_{\mathrm {B}}=n_{\mathrm {B}^1}+n_{\mathrm {B}^2}$ and the coefficients are

$$\begin{aligned} a_1&=a^2_1 + a^1_1\\ a_2&=a^2_2 + a^1_1 a^2_1 + a^1_2\\ a_3&=a^2_3 + a^1_1 a^2_2 + a^1_2 a^2_1 + a^1_3\\ a_4&=a^2_4 + a^1_1 a^2_3 + a^1_2 a^2_2 + a^1_3 a^2_1 + a^1_4\\ a_5&=a^2_5 + a^1_1 a^2_4 + a^1_2 a^2_3 + a^1_3 a^2_2 + a^1_4 a^2_1 + a^1_5\\&\quad \vdots \\ b_2&=b^1_1 b^2_1\\ b_3&=b^1_1 b^2_2 + b^1_2 b^2_1\\ b_4&=b^1_1 b^2_3 + b^1_2 b^2_2 + b^1_3 b^2_1\\ b_5&=b^1_1 b^2_4 + b^1_2 b^2_3 + b^1_3 b^2_2 + b^1_4 b^2_1\\&\quad \vdots \end{aligned}$$

which can be shortly expressed by

$$\begin{aligned} a_i&=a^1_i+a^2_i+\sum _{j=1}^{i-1}a^1_j a^2_{i-j}, \ i=1,\ldots ,n_{\mathrm {A}}\nonumber \\ b_i&=\sum _{j=1}^{i-1}b^1_j b^2_{i-j}, \ i=1,\ldots ,n_{\mathrm {B}} \end{aligned}$$

(23)

Because the nonlinear Wiener–Hammerstein system is approximated for the current sampling instant k by the linear time-varying model (22), the predicted trajectory of the output variable over the prediction horizon

$$\begin{aligned} \hat{\varvec{y}}(k)=\left[ \hat{y}(k+1|k)\ldots \hat{y}(k+N|k)\right] ^{{\mathrm {T}}} \end{aligned}$$

(24)

is a linear function of the decision variables of MPC, i.e. the calculated control increments (1), as derived in [12, 18]. The prediction equation in the vector-matrix notation is

$$\begin{aligned} \hat{\varvec{y}}(k)=\varvec{G}(k)\triangle {\varvec{u}}(k)+\varvec{y}^{0}(k) \end{aligned}$$

(25)

where the matrix $\varvec{G}(k)$, of dimensionality $N\times N_{{\mathrm {u}}}$, contains step-response coefficients of the local linear approximation of the nonlinear model. Using Eq. (22), it follows that

$$\begin{aligned} \varvec{G}(k)=K(k)\varvec{G} \end{aligned}$$

(26)

where the constant matrix

$$\begin{aligned} \varvec{G}=\left[ \begin{array}{cccc} s_{1} &{} 0 &{} \ldots &{} 0\\ s_{2} &{} s_{1} &{} \ldots &{} 0\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ s_{N} &{} s_{N-1} &{} \ldots &{} s_{N-N_{{\mathrm {u}}}+1} \end{array} \right] \end{aligned}$$

consists of step-response coefficients of two linear dynamic parts of the Wiener–Hammerstein model connected in series, i.e. the dynamic system described by $\varvec{A}(q^{-1})y(k)=\varvec{B}(q^{-1})u(k)$. Such step-response coefficients are calculated from the quantities defined by Eq. (23) in the following way

$$\begin{aligned} s_{p}=\sum _{i=1}^{\min (p,n_{\mathrm {B}})}b_{i}-\sum _{i=1}^{\min (j-1,n_{\mathrm {A}})}a_{i}s_{j-i} \end{aligned}$$

for $p=1,\ldots ,N$. Using Eq. (26), the prediction equation (25) becomes

$$\begin{aligned} \hat{\varvec{y}}(k)=K(k)\varvec{G}\triangle {\varvec{u}}(k)+\varvec{y}^{0}(k) \end{aligned}$$

(27)

In Eq. (27) the predicted output trajectory, $\hat{\varvec{y}}(k)$, is a sum of the forced trajectory $K(k)\varvec{G}\triangle {\varvec{u}}(k)$, which depends only on the future control increments (1), and the free trajectory vector $\varvec{y}^{0}(k)=[y^{0}(k+1|k)\ldots y^{0}(k+N|k)]^{T}$, which entirely depends on the past, i.e. on the values of the manipulated variable applied to the process before the instant k. The free trajectory is calculated from the nonlinear Wiener–Hammerstein model. From Eq. (16), one has

$$\begin{aligned} y^0(k+p|k)=&\sum _{i=1}^{I_{\mathrm {xf}}(p)} b^2_i x^0(k-i+p|k)\nonumber \\&+\sum _{i=I_{\mathrm {xf}}(p)+1}^{n_{\mathrm {B}^2}} b^2_i x(k-i+p)\nonumber \\&-\sum _{i=1}^{I_{\mathrm {yf}}(p)}a^2_i y^0(k-i+p|k)\nonumber \\&-\sum _{i=I_{\mathrm {yf}}(p)+1}^{n_{\mathrm {A}^2}}a^2_i y(k-i+p)+\text {d}(k) \end{aligned}$$

(28)

where $p=1,\ldots ,N$, $x^0(k+p|k)$ denotes the auxiliary signal between the nonlinear steady-state part and the output linear dynamic one predicted for the sampling instant $k+p$ calculated at the instant k. From Eq. (6)

$$\begin{aligned} x^0(k-i+p|k)=f(v^0(k-i+p|k)) \end{aligned}$$

(29)

where from Eq. (19) the auxiliary signal between the input linear dynamic part and the nonlinear steady-state one predicted for the sampling instant $k+p$ calculated at the instant k is

$$\begin{aligned} v^0(k-i+p|k)=&\sum _{j=1}^{I_{\mathrm {uf}}(i,p)} b^1_j u(k-1)\nonumber \\&+\sum _{j=I_{\mathrm {uf}}(i,p)+1}^{n_{\mathrm {B}^1}} b^1_j u(k-j-i+p)\nonumber \\&-\sum _{j=1}^{I_{{\mathrm {vf}}}(i,p)} a^1_j v^0(k-j-i+p|k)\nonumber \\&-\sum _{j=I_{{\mathrm {vf}}}(i,p)+1}^{n_{\mathrm {A}^1}} a^1_j v(k-j-i+p) \end{aligned}$$

(30)

and the past quantities $v(k-i+p)$ are found from Eq. (20). As the predicted output trajectory (27) is a linear function of the future control increments $\triangle {\varvec{u}}(k)$, the MPC optimisation problem (2) becomes the quadratic programming task

$$\begin{aligned}&\begin{array}{l} \min \limits _{\triangle {\varvec{u}}(k)} \Big \{ \left\| \varvec{y} ^{\mathrm {sp}}(k)-\varvec{y}^{0}(k)-K(k)\varvec{G}\triangle {\varvec{u}}(k)\right\| ^{2}+\left\| \triangle {\varvec{u}}(k)\right\| ^{2}_{\varvec{\Lambda }} \Big \}\nonumber \end{array}\\&\text {subject to}\nonumber \\&{\varvec{u}}^{\min }\le \varvec{J}\triangle {\varvec{u}}(k)+{\varvec{u}}(k-1) \le {\varvec{u}}^{\max }\nonumber \\&-\triangle {\varvec{u}}^{\max }\le \triangle {\varvec{u}}(k)\le \triangle {\varvec{u}}^{\max }\nonumber \\&\varvec{y}^{\min }\le \varvec{y}^{0}(k)+K(k)\varvec{G}\triangle {\varvec{u}}(k)\le \varvec{y}^{\max } \end{aligned}$$

(31)

where $\left\| \varvec{x}\right\| ^{2}=\varvec{x}^{{\mathrm {T}}}\varvec{x}$ and $\left\| \varvec{x}\right\| ^{2}_{\varvec{A}}=\varvec{x}^{{\mathrm {T}}}\varvec{A}\varvec{x}$, the set-point trajectory vector $\varvec{y}^{\mathrm {sp}}(k)=[y^{\mathrm {sp}}(k+1|k)\ldots y^{\mathrm {sp}}(k+N|k)]^{{\mathrm {T}}}$ and the vectors of output constraints, i.e. $\varvec{y}^{\min } =\left[ y^{\min }\ldots y^{\min }\right] ^{{\mathrm {T}}}$, $\varvec{y}^{\max }=\left[ y^{\max }\ldots y^{\max }\right] ^{{\mathrm {T}}}$, are of length N. The vectors of input constraints, i.e. ${\varvec{u}}^{\min }=\left[ u^{\min }\ldots u^{\min }\right] ^{{\mathrm {T}}}$, ${\varvec{u}}^{\max }=\left[ u^{\max }\ldots u^{\max }\right] ^{{\mathrm {T}}}$, $\triangle {\varvec{u}}^{\max }=[\triangle u^{\max }\ldots \triangle u^{\max }]^{{\mathrm {T}}}$ and the vector ${\varvec{u}}(k-1)=\left[ u(k-1)\ldots u(k-1)\right] ^{{\mathrm {T}}}$ are of length $N_{{\mathrm {u}}}$, the matrices $\varvec{\Lambda }=\mathrm {diag}(\lambda ,\ldots ,\lambda )$ and

$$\begin{aligned} \varvec{J}=\left[ \begin{array}{ccccc} 1 &{} 0 &{} 0 &{} \ldots &{} 0\\ 1 &{} 1 &{} 0 &{} \ldots &{} 0\\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ 1 &{} 1 &{} 1 &{} \ldots &{} 1 \end{array} \right] \end{aligned}$$

(32)

are of dimensionality $N_{{\mathrm {u}}}\times N_{{\mathrm {u}}}$.

The described MPC strategy is referred to as the MPC algorithm with nonlinear prediction and simplified linearisation (MPC-NPSL). It is because, at each sampling instant on-line, the nonlinear Wiener–Hammerstein model is used for prediction of the nonlinear free trajectory and the same model is used to find a linear approximation of the model for the current operating point. Linearisation is carried out in a simplified way, because the linear dynamic blocks are multiplied by the current gain of the nonlinear steady-state one. At each sampling instant k of the algorithm the gain K(k) of the steady-state part of the model for the current operating point is estimated from Eq. (21) and the nonlinear free trajectory $\varvec{y}^{0}(k)$ is found from Eqs. (28)–(30), (20), and the unmeasured disturbance is estimated from Eq. (18). The MPC-NPSL quadratic optimisation problem (31) is solved to find the future control increments $\triangle {\varvec{u}}(k)$, the first element of which is applied to the process, i.e. set $u(k)=\triangle u(k|k)+u(k-1)$. The MPC-NPSL quadratic optimisation problem has only one unique global solution provided that $\varvec{\Lambda }>0$ (i.e. $\lambda >0$).

The same approach may be also used for the Wiener model [23]. It is also possible to use the linearised model for calculation of the free trajectory [22]. It is necessary to stress the fact that the MPC-NPSL algorithm does not require an inverse model of the nonlinear steady-state part of the model, as it is necessary in the MPC algorithms with on-line model linearisation for cascade Wiener [19–21] and Hammerstein [15–17] systems, respectively.

4.2 Nonlinear MPC algorithm with on-line predicted trajectory linearisation

Although the time-varying linear approximation of the Wiener–Hammerstein system is calculated for the current operating conditions of the process, the same linearised model is used for the calculation of the output predictions for the whole prediction horizon. When the horizon is long and the operating point is changed significantly, such a linearised model is likely to describe properties of the real nonlinear process not precisely, i.e. the mismatch between the model prediction and behaviour of the real process may be significant. It may result in not acceptable quality of control. A conceptually better method is to calculate not a linear approximation of the model and next use it for finding the predicted trajectory, but to directly find a linear approximation of the nonlinear predicted trajectory defined on the prediction horizon, $\hat{\varvec{y}}(k)$, Eq. (24). It is important to stress the fact that linearisation is not carried out for the current operating point of the process, as in the MPC-NPSL algorithm, but along an assumed future sequence of the manipulated variable ${\varvec{u}}^{\mathrm {traj}}(k)=\left[ u^{\mathrm {traj}}(k|k) \ldots u^{\mathrm {traj}}(k+N_{{\mathrm {u}}}-1|k)\right] ^{{\mathrm {T}}}$. Using the Taylor’s series expansion method, a linear approximation of the nonlinear output trajectory $\hat{\varvec{y}}(k)$ along the input trajectory ${\varvec{u}}^{\mathrm {traj}}(k)$ is

$$\begin{aligned} \hat{\varvec{y}}(k)=\hat{\varvec{y}}^{\mathrm {traj}}(k)+\varvec{H}(k)\left( {\varvec{u}}(k)-{\varvec{u}}^{\mathrm {traj}}(k)\right) \end{aligned}$$

(33)

where the output trajectory $\hat{\varvec{y}}^{\mathrm {traj}}(k)$ describes the predictions for the input trajectory ${\varvec{u}}^{\mathrm {traj}}(k)$ and $\varvec{H}(k)$ is the matrix of the derivatives of the predicted output trajectory with respect to the future values of the control signal. The obtained approximation formula (33) is really a linear function of the future values of the control variable over the control horizon, i.e. ${\varvec{u}}(k)=\big [ u(k|k) \ldots u(k+N_{{\mathrm {u}}}-1|k)\big ]^{{\mathrm {T}}}$. The main issue is the choice of the future input trajectory ${\varvec{u}}^{\mathrm {traj}}(k)$, along which linearisation is performed. Ideally, it should be close to the trajectory corresponding to the optimal control increments (1), which is not known at the sampling instant k, because this is the decision variable vector in MPC, calculated at the same instant. A possible solution is to use for linearisation the trajectory determined by the most recent value of the manipulated variable, i.e. the value applied to the process at the previous sampling instant, ${\varvec{u}}^{\mathrm {traj}}(k)=\left[ u(k-1) \ldots u(k-1)\right] ^{{\mathrm {T}}}$. A better approach is to repeat trajectory linearisation and calculation of the future control policy a few times at each sampling instants in the internal iterations $t=1,\ldots ,t^{\max }$. In the current internal iteration t the predicted nonlinear output trajectory $\hat{\varvec{y}}^t(k)=\left[ \hat{y}^t(k+1|k) \ldots \hat{y}^t(k+N|k) \right] ^{{\mathrm {T}}}$ is linearised along the input trajectory found in the previous internal iteration ($t-1$), i.e. ${\varvec{u}}^{t-1}(k)=\left[ u^{t-1}(k|k) \ldots u^{t-1}(k+N_{{\mathrm {u}}}-1|k) \right] ^{{\mathrm {T}}}$. Analogously to the case when the trajectory is linearised along some assumed input trajectory ${\varvec{u}}^{\mathrm {traj}}(k)$, which results in the approximation (33), using the Taylor’s series expansion method, a linear approximation of the nonlinear output trajectory $\hat{\varvec{y}}^t(k)$ along the input trajectory ${\varvec{u}}^{t-1}(k)$ is

$$\begin{aligned} \hat{\varvec{y}}^t(k)=\hat{\varvec{y}}^{t-1}(k)+\varvec{H}^t(k)\left( {\varvec{u}}^t(k)-{\varvec{u}}^{t-1}(k)\right) \end{aligned}$$

(34)

where the output trajectory corresponding to the input trajectory calculated at the previous internal iteration, ${\varvec{u}}^{t-1}(k)$, is denoted by $\hat{\varvec{y}}^{t-1}(k)=\big [\hat{y}^{t-1}(k+1|k) \ldots \hat{y}^{t-1}(k+N|k) \big ]^{{\mathrm {T}}}$ and $\varvec{H}^t(k)$ is the matrix of the derivatives of the predicted output trajectory with respect to the future values of the control signal. The matrix is calculated for the input and output trajectories found in the previous internal iteration, $t-1$, because no new information is available. It is of dimensionality $N\times N_{{\mathrm {u}}}$ and has the structure

(35)

where $p=1,\ldots ,N$ and $r=0,\ldots ,N_{{\mathrm {u}}}-1$. Equation (34) is really a linear function of the future values of the control variable over the control horizon calculated at the current internal iteration t, i.e. ${\varvec{u}}^t(k)=\left[ u^t(k|k) \ldots u^t(k+N_{{\mathrm {u}}}-1|k)\right] ^{{\mathrm {T}}}$. It is possible to express the linear approximation of the nonlinear output trajectory as a function of the increments of the manipulated variable calculated for the current sampling instant k and in the current internal iteration t, i.e. the trajectory $\triangle {\varvec{u}}^t(k)=\left[ \triangle u^t(k|k) \ldots \triangle u^t(k+N_{{\mathrm {u}}}-1|k)\right] ^{{\mathrm {T}}}$ corresponding to the vector (1). It is necessary because future increments of the manipulated variable, not its future values, are minimised in the second part of the MPC cost function J(k). Taking into account that ${\varvec{u}}^t(k)=\varvec{J}\triangle {\varvec{u}}^t(k)+{\varvec{u}}(k-1)$, where the matrix $\varvec{J}$ of dimensionality $N_{{\mathrm {u}}}\times N_{{\mathrm {u}}}$ is defined by Eq. (32) and the vector ${\varvec{u}}(k-1)=\left[ u(k-1) \ldots u(k-1)\right] ^{{\mathrm {T}}}$ is of length $N_{{\mathrm {u}}}$, the linear approximation of the nonlinear predicted output trajectory (34) is

$$\begin{aligned} \hat{\varvec{y}}^t(k)=&\varvec{H}^t(k)\varvec{J}\triangle {\varvec{u}}^t(k)+\hat{\varvec{y}}^{t-1}(k)\nonumber \\&+\varvec{H}^t(k)\left( {\varvec{u}}(k-1)-{\varvec{u}}^{t-1}(k)\right) \end{aligned}$$

(36)

It is easy to note that the obtained approximation formula (36) is really a linear function of the future increments of the control variable over the control horizon, i.e. $\triangle {\varvec{u}}^t(k)$, which is calculated for the current sampling instant k and in the current internal iteration t. The vector ${\varvec{u}}^{t-1}(k)$ is known, the matrix $\varvec{J}$ is fixed, whereas the vector $\hat{\varvec{y}}^{t-1}(k)$ and the matrix $\varvec{H}^t(k)$ may be determined from the Wiener–Hammerstein model of the process. From Eq. (16), the predicted value of the output for the sampling instant $k+p$ calculated at the current instant k and at the current internal iteration t is

$$\begin{aligned} \hat{y}^t(k+p|k)=&\sum _{i=1}^{I_{\mathrm {xf}}(p)} b^2_i x^t(k-i+p|k)\nonumber \\&+\sum _{i=I_{\mathrm {xf}}(p)+1}^{n_{\mathrm {B}^2}} b^2_i x(k-i+p)\nonumber \\&-\sum _{i=1}^{I_{\mathrm {yf}}(p)}a^2_i \hat{y}^t(k-i+p|k)\nonumber \\&-\sum _{i=I_{\mathrm {yf}}(p)+1}^{n_{\mathrm {A}^2}}a^2_i y(k-i+p)+{d}(k) \end{aligned}$$

(37)

where from Eq. (6), one has

$$\begin{aligned} x^t(k-i+p|k)=f(v^t(k-i+p|k)) \end{aligned}$$

(38)

for $p-i\ge 0$. From Eq. (19), the predicted signals between the input linear dynamic part and the nonlinear steady-state one are

$$\begin{aligned} v^t(k-i+p|k)=&\sum _{j=1}^{I_{\mathrm {uf}}(i,p)} b^1_j u^t(k-j-i+p|k)\nonumber \\&+\sum _{j=I_{\mathrm {uf}}(i,p)+1}^{n_{\mathrm {B}^1}} b^1_j u(k-j-i+p)\nonumber \\&-\sum _{j=1}^{I_{{\mathrm {vf}}}(i,p)} a^1_j v^t(k-j-i+p|k)\nonumber \\&-\sum _{j=I_{{\mathrm {vf}}}(i,p)+1}^{n_{\mathrm {A}^1}} a^1_j v(k-j-i+p) \end{aligned}$$

(39)

and the past quantities $v(k-i+p)$ are calculated from Eq. (20). The entries of the matrix (35), i.e. the derivatives of the predicted trajectory $\hat{\varvec{y}}^{t-1}(k)$ for the previous internal iteration, $t-1$, with respect to the future control scenario $\triangle {\varvec{u}}^{t-1}(k)$ are found by differentiating Eq. (37), which gives

$$\begin{aligned} \frac{\partial y^{t-1}(k+p|k)}{\partial u^{t-1}(k+r|k)}=&\sum _{i=1}^{I_{\mathrm {xf}}(p)} b^2_i \frac{\partial x^{t-1}(k-i+p|k)}{\partial u^{t-1}(k+r|k)}\nonumber \\&-\sum _{i=1}^{I_{\mathrm {yf}}(p)}a^2_i \frac{\partial y^{t-1}(k\!-\!i\!+\!p)}{\partial u^{t-1}(k\!+\!r|k)} \end{aligned}$$

(40)

The first partial derivative in the right side of Eq. (40) depends on the specific type of the nonlinear steady-state block, described by the function f

$$\begin{aligned} \frac{\partial x^{t-1}(k-i+p|k)}{\partial u^{t-1}(k+r|k)}=&\frac{{\mathrm {d}}f(v^{t-1}(k-i+p|k))}{{\mathrm {d}}v^{t-1}(k-i+p)}\nonumber \\&\times \frac{\partial v^{t-1}(k-i+p|k)}{\partial u^{t-1}(k+r|k)} \end{aligned}$$

(41)

where from Eq. (39), the derivatives of the predicted signals between the input linear dynamic part and the nonlinear steady-state one are

$$\begin{aligned} \frac{\partial v^{t-1}(k-i+p|k)}{\partial u^{t-1}(k+r|k)}=&\sum _{j=1}^{I_{\mathrm {uf}}(i,p)} b^1_j \frac{\partial u^{t-1}(k-j-i+p|k)}{\partial u^{t-1}(k+r|k)}\nonumber \\&-\sum _{j=1}^{I_{{\mathrm {vf}}}(i,p)} a^1_j \frac{\partial v^{t-1}(k-j-i+p|k)}{\partial u^{t-1}(k+r|k)} \end{aligned}$$

(42)

Because $u(k+p|k)=u(k+N_{{\mathrm {u}}}-1|k)$ for $p\ge N_{{\mathrm {u}}}$, the first partial derivatives in the right side of Eq. (42) can only have two values

$$\begin{aligned}&\dfrac{\partial u^{t-1}(k+p|k)}{\partial u^{t-1}(k+r|k)}\nonumber \\&\quad = {\left\{ \begin{array}{ll} 1 &{} \text {if } p=r \text { or } (p>r \text { and } r=N_{{\mathrm {u}}}-1)\\ 0 &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

(43)

The second partial derivatives in Eqs. (40) and (42) must be calculated recursively. One may notice that

$$\begin{aligned} \frac{\partial \hat{y}^{t-1}(k+p|k)}{\partial u^{t-1}(k+r|k)}=0 \end{aligned}$$

(44)

for $r\ge p-1$ and

$$\begin{aligned} \frac{\partial v^{t-1}(k+p|k)}{\partial u^{t-1}(k+r|k)}=0 \end{aligned}$$

(45)

for $r\ge p$.

According to Eq. (36), linearisation makes it possible to express the predicted output trajectory $\hat{\varvec{y}}^t(k)$ as a linear function of the future control increments $\triangle {\varvec{u}}^t(k)$ calculated for the current sampling instant k and at the internal iteration t. Hence, the MPC optimisation problem (2) becomes the following quadratic programming task

$$\begin{aligned}&\begin{array}{l} \min \limits _{\triangle {\varvec{u}}^t(k)}\Big \{\big \Vert \varvec{y} ^{\mathrm {sp}}(k)-\varvec{H}^t(k)\varvec{J}\triangle {\varvec{u}}^t(k) -\hat{\varvec{y}}^{t-1}(k)\\ \qquad \quad \ \ \varvec{H}^t(k)({\varvec{u}}(k-1)-{\varvec{u}}^{t-1}(k))\big \Vert ^{2}+\left\| \triangle {\varvec{u}}^t(k)\right\| ^{2}_{\varvec{\Lambda }} \Big \} \end{array}\nonumber \\&\text {subject to}\nonumber \\&{\varvec{u}}^{\min }\le \varvec{J}\triangle {\varvec{u}}^t(k)+{\varvec{u}}(k-1) \le {\varvec{u}}^{\max }\nonumber \\&-\triangle {\varvec{u}}^{\max }\le \triangle {\varvec{u}}^t(k)\le \triangle {\varvec{u}}^{\max }\nonumber \\&\varvec{y}^{\min }\le \varvec{H}^t(k)\varvec{J}\triangle {\varvec{u}}^t(k) +\hat{\varvec{y}}^{t-1}(k)\nonumber \\&\qquad \quad +\varvec{H}^t(k)({\varvec{u}}(k-1)-{\varvec{u}}^{t-1}(k)) \le \varvec{y}^{\max } \end{aligned}$$

(46)

The obtained quadratic optimisation problem, analogously to that used in the MPC-NPSL algorithm [(Eq. (31)], has only one unique global solution provided that $\varvec{\Lambda }>0$ (i.e. $\lambda >0$).

The described MPC strategy is referred to as the MPC algorithm with nonlinear prediction and linearisation along the predicted trajectory (MPC-NPLPT). At each sampling instant k of the algorithm the unmeasured disturbance is estimated from Eq. (18) using the Wiener–Hammerstein model of the process. Next, the internal iteration is initialised ($t=1$): an initial guess of the future input trajectory is assumed, e.g. using the value of the manipulated variable calculated and applied to the process at the previous sampling instant, i.e. ${\varvec{u}}^0(k)=\left[ u(k-1) \ldots u(k-1)\right] ^{{\mathrm {T}}}$, or the last $N_{{\mathrm {u}}}-1$ elements of the optimal trajectory calculated at the previous instant and not applied to the process, i.e. the trajectory

$$\begin{aligned} {\varvec{u}}^{0}(k)= & {} \left[ \begin{array}{c} u^{0}(k|k)\\ \vdots \\ u^{0}(k+N_{{\mathrm {u}}}-3|k)\\ u^{0}(k+N_{{\mathrm {u}}}-2|k)\\ u^{0}(k+N_{{\mathrm {u}}}-1|k) \end{array} \right] \nonumber \\= & {} \left[ \begin{array}{c} u(k|k-1)\\ \vdots \\ u(k+N_{{\mathrm {u}}}-3|k-1)\\ u(k+N_{{\mathrm {u}}}-2|k-1)\\ u(k+N_{{\mathrm {u}}}-2|k-1) \end{array} \right] \end{aligned}$$

(47)

For the initial future input trajectory ${\varvec{u}}^0(k)$, the future output trajectory $\hat{\varvec{y}}^0(k)$ is calculated from Eqs. (17b), (19), (37), (38) and (39). The matrix $\varvec{H}^t(k)$, which consists of derivatives of the predicted output trajectory with respect to the future control policy, specified by Eq. (35), is calculated using Eqs. (40)–(42) and the conditions (43)–(44). The MPC-NPLPT quadratic optimisation problem (46) is solved to find the future control increments $\triangle {\varvec{u}}^1(k)$ in the first internal iteration. If the condition

$$\begin{aligned} \sum _{p=0}^{N_0}\left\| y^{\mathrm {sp}}(k-p)-y(k-p)\right\| ^2\ge \delta _{{\mathrm {y}}} \end{aligned}$$

(48)

is true, the internal iterations are continued ($t=2,\ldots ,t_{\max }$). The tuning parameters $N_0$ and $\delta _{{\mathrm {y}}}$ are chosen experimentally. In the internal iteration t the predicted output trajectory $\hat{\varvec{y}}^{t-1}(k)$ corresponding to the future input trajectory ${\varvec{u}}^{t-1}(k)=\varvec{J}\triangle {\varvec{u}}^{t-1}(k)+{\varvec{u}}(k-1)$ and the matrix $\varvec{H}^t(k)$ are calculated (in the same way it is done in the first internal iteration). The MPC-NPLPT quadratic optimisation problem (46) is solved to find the future control increments $\triangle {\varvec{u}}^t(k)$. If the difference between future control increments calculated in the consecutive internal iterations is small, it means when

$$\begin{aligned} \left\| \triangle {\varvec{u}}^t(k)-\triangle {\varvec{u}}^{t-1}(k)\right\| ^2<\delta _{{\mathrm {u}}} \end{aligned}$$

(49)

or $t>t_{\max }$, internal iterations are terminated. Otherwise, the next internal iteration is started ($t:=t+1$), the nonlinear output trajectory is linearised and the quadratic optimisation problem is solved. The tuning parameter $\delta _{{\mathrm {u}}}$ is chosen experimentally. Having completed the internal iterations, the first element of the obtained future control policy is applied to the process, i.e. set $u(k)=\triangle u^t(k|k)+u(k-1)$.

The MPC-NPLPT algorithm for Hammerstein and Wiener systems with a specific nonlinear part represented by a neural network is discussed in [12, 23], and the algorithm for a general Hammerstein–Wiener model is described in [26].

Fig. 2

The control system of the heat exchanger

5 Simulation results

The considered process is a heat exchanger [30], whose control system is depicted in Fig. 2. Cold water (the input stream) is heated by a hot steam, and the process produces hot water (the output stream). The objective of the temperature controller is to calculate the value of the manipulated variable (process input), u, which is typically a electric signal, in such a way that temperature of hot water, which is the controlled variable (process output), y, follows changes of its set point. The heat exchanger may be modelled as a Wiener–Hammerstein structure shown in Fig. 1. The first (input) linear dynamic part of the model represents the dynamic subsystem between the manipulated variable and the valve position, v, and it is defined by the second-order equation

$$\begin{aligned}&(1-1.5714 q^{-1}+0.6873 q^{-2})v(k)\nonumber \\&\quad =(0.0616 q^{-1}+0.0543 q^{-2})u(k) \end{aligned}$$

(50)

Fig. 3

The characteristics $x=f(v)$ of the nonlinear steady-state block and the characteristics $y=f(u)$ of the whole Wiener–Hammerstein system

i.e. $a^1_1=-1.5714$, $a^1_2=0.6873$, $b^1_1=0.0616$, $b^1_2=0.0543$, $n_{\mathrm {A}^1}=n_{\mathrm {B}^1}=2$. The nonlinear steady-state block represents the relation between the valve position and the flowrate of the input stream actually delivered to the heat exchanger, x, and it is defined by the nonlinear function

$$\begin{aligned} x(k)=f(v(k))=\frac{v(k)}{\sqrt{0.1+0.9v^2(k)}} \end{aligned}$$

(51)

Finally, the second (output) linear dynamic block represents the dynamic subsystem between the steam input stream and the temperature of the hot water and it is defined by the second-order equation

$$\begin{aligned}&(1-1.7608 q^{-1}+0.7661 q^{-2})v(k)\nonumber \\&\quad =(-5.7715 q^{-1}+5.673 q^{-2})u(k) \end{aligned}$$

(52)

i.e. $a^2_1=-1.7608$, $a^2_2=0.7661$, $b^2_1=-5.7715$, $b^2_2=5.673$, $n_{\mathrm {A}^2}=n_{\mathrm {B}^2}=2$. Figure 3 shows the characteristics $x=f(v)$ of the nonlinear steady-state block and the characteristics $y=f(u)$ of the whole Wiener–Hammerstein system.

In order to demonstrate advantages of the nonlinear MPC algorithms discussed in this work, the following MPC algorithms are compared:

• (a) The classical linear MPC algorithm (the generalised predictive control [1]). For prediction and optimisation of the future control increments, a linear model corresponding to the nominal operating point $u=v=x=y=0$ is used. The order of dynamics of the model is $n_{\mathrm {A}}=n_{\mathrm {A}^1}+n_{\mathrm {A}^2}=4$, $n_{\mathrm {B}}=n_{\mathrm {B}^1}+n_{\mathrm {B}^2}=4$, and from Eq. (22), it has the form

  $$\begin{aligned} \varvec{A}(q^{-1})y(k)=K\varvec{B}(q^{-1})u(k) \end{aligned}$$

  Model coefficients are calculated from Eqs. (23), (50) and (52), which gives

  $$\begin{aligned} \varvec{A}(q^{-1})=&1- 3.3322 q^{-1}+4.2203 q^{-2}-2.4140 q^{-3}\\&+0.5265 q^{-4}\\ \varvec{B}(q^{-1})=&-0.3555q^{-2}+0.0361q^{-3}+0.3080q^{-4} \end{aligned}$$

  From Eq. (51), the constant gain of the nonlinear steady-state part of the model is

  $$\begin{aligned} K= & {} \frac{{\mathrm {d}}x}{{\mathrm {d}}v} ={\left. \dfrac{{\mathrm {d}}x}{{\mathrm {d}}v}\right| _{x=0, \ v=0}}\\= & {} {\left. \dfrac{{\mathrm {d}}f(v)}{{\mathrm {d}}v}\right| _{v=0}}=0.1^{-0.5}=3.1623 \end{aligned}$$

• (b) The described MPC algorithm with on-line simplified linearisation (MPC-NPSL). The nonlinear Wiener–Hammerstein model is used to update the current gain of the parameter-varying linear model specified by Eq. (22). For the given steady-state nonlinear part of the model defined by Eq. (51), the gain of the nonlinear block for the current operating point, defined as the derivative of the auxiliary signal x of the model with respect to the auxiliary signal v (Eq. 21), is calculated as

  $$\begin{aligned} K(k)=&\frac{{\mathrm {d}}x(k)}{{\mathrm {d}}v(k)}=\frac{{\mathrm {d}}f(v(k))}{{\mathrm {d}}v(k)}=(0.1+0.9v^2(k))^{-0.5}\nonumber \\&-0.9v^2(k)(0.1+0.9v^2(k))^{-1.5} \end{aligned}$$

  (53)

  where the value v(k) defines the current operating point.

• (c) The MPC algorithm with on-line trajectory linearisation (MPC-NPLPT). For initialisation of linearisation $N_{{\mathrm {u}}}-1$ elements of the future control sequence calculated at the previous sampling instant are used, and the trajectory ${\varvec{u}}^{0}(k)$ is defined by Eq. (47). The derivative of the predicted auxiliary signal x of the model with respect to the auxiliary signal v, predicted for the sampling instant $k-i+p$ at the current instant k and in the internal iteration t (necessary for trajectory linearisation in Eq. (41)), using Eq. (51), is calculated from

  $$\begin{aligned}&\frac{{\mathrm {d}}f\left( v^{t-1}(k-i+p|k)\right) }{{\mathrm {d}}v^{t-1}(k-i+p)}\\&\quad =(0.1+0.9\left( v^{t-1}(k-i+p|k))^2\right) ^{-0.5}\\&\quad -0.9\left( v^{t-1}(k-i+p|k)\right) ^2\\&\quad \times \left( 0.1+0.9(v^{t-1}(k-i+p|k))^2\right) ^{-1.5} \end{aligned}$$

• (d) The “ideal” MPC algorithm with nonlinear optimisation (MPC-NO) in which the full nonlinear Wiener–Hammerstein model is used for prediction and optimisation of the future control policy [Eqs. (16)–(20)].

Fig. 4

Simulation results of the linear MPC algorithm; $\lambda =1$

In the nonlinear MPC algorithms, i.e. in MPC-NPSL, MPC-NPLPT and MPC-NO, the same nonlinear Hammerstein–Wiener model is used, although in a different way. At each sampling instant of the linear MPC strategy and in the MPC-NPSL algorithm a constrained quadratic optimisation problem is solved on-line, in the MPC-NPLPT maximally $t^{\max }$ such problems are necessary, whereas in the MPC-NO strategy a nonlinear optimisation task is solved. All algorithms are implemented in MATLAB. The active-set algorithm is used for quadratic optimisation, and the sequential quadratic programming (SQP) method is used for nonlinear optimisation [35]), both with their default parameters. The same dynamic model described by Eqs. (50)–(52) is used as the simulated system. Parameters of all compared MPC algorithms are the same: $N=10$, $N_{{\mathrm {u}}}=3$, typically $\lambda =1$, the constraints imposed on the value of the manipulated variable are: $u^{\min }=-1$, $u^{\max }=1$. If necessary, the additional constraints imposed on the rate of change of the manipulated variable are also taken into account, $\triangle u^{\max }=0.25$.

At first, the linear MPC algorithm is simulated. Figure 4 depicts the obtained simulation results. The set-point trajectory consists of four fast step changes. Because there is a significant mismatch between the nonlinear process and the linear model used for prediction, the linear MPC algorithm does not work, and it is unable to steer the process in such a way that the controlled variable follows the changes of the set-point trajectory with no steady-state error. Conversely, there is practically no steady-state, and the output variable of the process oscillates. In order to reduce the oscillations, the penalty factor $\lambda$ must be increased to the value 8000 (or more). Figure 5 shows simulation results. Increasing the value of $\lambda$ makes it possible to obtain stable control, but changes of the manipulated variable are very slow which leads to unacceptably slow trajectory tracking of the controlled output.

Fig. 5

Simulation results of the linear MPC algorithm; $\lambda =8000$

Fig. 6

Simulation results of the MPC-NPSL algorithm with simplified on-line model linearisation and quadratic optimisation; $\lambda =1$

Next, the MPC-NPSL algorithm with simplified linearisation is considered. The linear MPC algorithm uses for prediction the linear model, which is conceptually not a good idea whereas MPC-NPSL algorithm uses the nonlinear Wiener–Hammerstein model of the process, but in a simplified way, i.e. the transfer functions of the linear dynamic parts of the model are multiplied by the gain of the nonlinear steady-state block for the current operating point, defined by the value of the variable v(k) [Eq. (53)]. Figure 6 depicts the obtained simulation results when the penalty factor $\lambda$ has its default value 1. Unfortunately, although the obtained control quality is much better than in the case of the linear MPC algorithm, i.e. the output trajectory of the process is stable and there is no steady-state error, the MPC-NPSL algorithm gives big overshoot. It is because the changes of the set-point trajectory are fast and significant. It may be also noted that the input trajectory is characterised by big changes, even from the minimal to the maximal value of the manipulated variable. Similarly to the linear MPC algorithm, it is also possible to improve the MPC-NPSL algorithm by increasing the penalty $\lambda$. Figure 7 shows the trajectories obtained for $\lambda =250$. Because the MPC-NPSL algorithm uses more accurate approximation of the system than the linear MPC approach does, it requires much a lower value of $\lambda$ (250) in comparison with that necessary in the linear MPC algorithm (8000). In consequence, the MPC-NPSL (with increased $\lambda$) is faster than the linear MPC strategy, but it is still quite slow and its overshoot is unacceptable.

Fig. 7

Simulation results of the MPC-NPSL algorithm with simplified on-line model linearisation and quadratic optimisation; $\lambda =250$

Fig. 8

Simulation results: the MPC-NPLPT algorithm with on-line trajectory linearisation and quadratic optimisation with $t_{\max }=1$ (solid line), the MPC-NO algorithm with on-line nonlinear optimisation (dashed line); in both algorithms $\lambda =1$

Fig. 9

Simulation results: the MPC-NPLPT algorithm with on-line trajectory linearisation and quadratic optimisation with $t_{\max }=5$, $\delta _{{\mathrm {u}}}=\delta _{{\mathrm {y}}}=1$ (solid line), the MPC-NO algorithm with on-line nonlinear optimisation (dashed line); in both algorithms $\lambda =1$

Next, the MPC-NPLPT algorithm with on-line trajectory linearisation is considered. When compared with the MPC-NPSL strategy, it uses conceptually a more advanced approximation method of the predicted output trajectory. It is because the MPC-NPLPT scheme directly finds a linear approximation of the predicted output trajectory over the prediction horizon, linearisation is carried out for a future input trajectory defined over the control horizon, whereas in the MPC-NPSL algorithm only a linear approximation of the model is found for the current operating point of the process and the forced trajectory $\varvec{G}(k)\triangle {\varvec{u}}(k)$ in Eq. (25) is calculated from the same linearised model applied recurrently over the prediction horizon. Therefore, the MPC-NPLPT algorithm is likely to give more accurate approximation of the predicted output trajectory than the MPC-NPSL one and to result in better control quality. Figure 8 compares the trajectories of the MPC-NPLPT algorithm with those obtained in the MPC-NO in which the full nonlinear Wiener–Hammerstein model is used for prediction and optimisation of the future control policy, and no approximation of the model or the predicted output trajectory is used. In both algorithms the parameter $\lambda$ has its default value 1. Nevertheless, in contrast to the linear MPC algorithm and the NPC-NPSL one (Figs. 4, 6), the MPC-NPLPT algorithm gives very good, precise, steady-state error-free control, and overshoot is very small. Furthermore, it may be noticed that the trajectories of the MPC-NPLPT algorithm are very similar to those obtained in the truly nonlinear MPC-NO strategy. It is interesting to point out that very good control quality of the MPC-NPLPT algorithm is obtained even though only one internal iteration is performed at each sampling instant ($t_{\max }=1$), which means that the predicted output trajectory is linearised only once at each instant. In order to increase accuracy of the MPC-NPLPT algorithm, the maximal possible number of internal iterations is increased to 5, and the additional parameters are $\delta _{{\mathrm {u}}}=\delta _{{\mathrm {y}}}=1$. The obtained simulation results are shown in Fig. 9. In this case the trajectories of the MPC-NPLPT algorithm with on-line trajectory linearisation and quadratic optimisation are practically the same as those of the MPC-NO algorithm.

Table 1 Control accuracy (SSE), the relative accuracy criterion (D) and computational burden (MFLOPS) of compared MPC algorithms, for the MPC-NPLPT strategy the sum of internal iterations (NII) is also given; in all algorithms $\lambda =1$

Fig. 10

The number of internal iterations (NII) in the consecutive sampling instants of four versions of the MPC-NPLPT algorithm with on-line trajectory linearisation and quadratic optimisation; $\lambda =1$

Fig. 11

Simulation results: the MPC-NPLPT algorithm with on-line trajectory linearisation and quadratic optimisation with $t_{\max }=5$, $\delta _{{\mathrm {u}}}=\delta _{{\mathrm {y}}}=1$ (solid line), the MPC-NO algorithm with on-line nonlinear optimisation (dashed line); in both algorithms $\lambda =100$

Fig. 12

Simulation results: the MPC-NPLPT algorithm with on-line trajectory linearisation and quadratic optimisation with $t_{\max }=5$, $\delta _{{\mathrm {u}}}=\delta _{{\mathrm {y}}}=1$ (solid line), the MPC-NO algorithm with on-line nonlinear optimisation (dashed line); in both algorithms $\lambda =1000$

In order to conveniently compare effectiveness of the discussed MPC algorithms, two indices are defined. The first one is the sum of squared errors (SSE)

$$\begin{aligned} \mathrm {SSE}=\sum _{k=1}^{100} \left( y^{\mathrm {sp}}(k)-y(k)\right) ^{2} \end{aligned}$$

It is interesting to point out that the SSE index is not actually minimised in MPC. That is why the second, relative index takes into account the discrepancy between any MPC algorithm and theoretically the best MPC-NO strategy

$$\begin{aligned} D=\sum _{k=1}^{100}(y_{\mathrm {{MPC-NO}}}(k)-y(k))^2 \end{aligned}$$

(54)

where $y_{\mathrm {{MPC-NO}}}(k)$ denotes the output of the process when it is controlled by the MPC-NO algorithm, and y(k) is the output if a different MPC algorithm is used. Table 1 compares all evaluated MPC algorithms (linear MPC, MPC-NPSL, MPC-NPLPT) in terms of the indices SSE and D, as well as computational burden (MFLOPS). The linear MPC strategy is very bad, the MPC-NPSL is much better, but only the MPC-NPLPT strategy makes it possible to obtain control quality comparable with that typical of the MPC-NO strategy. As many as four versions of the MPC-NPLPT algorithms are compared: with one internal iteration and three versions with maximally 5 iterations, for different values of the tuning parameters $\delta _{{\mathrm {u}}}$ [(Eq. (49)] and $\delta _{{\mathrm {y}}}$ [(Eq. (48)]. Additionally, the total number of internal iterations is given in Table 1 for the MPC-NPLPT algorithm. In general, the smaller the values of $\delta _{{\mathrm {u}}}$ and $\delta _{{\mathrm {y}}}$, the smaller the discrepancy between the MPC-NPLPT algorithm and the MPC-NO one, and, at the same time, more internal iterations are necessary, which increases computational burden. The MPLPT algorithm with only one internal iteration is as many as 15.84 times more computationally efficient than the MPC-NO one. When 5 internal iterations are allowed, for $\delta _{{\mathrm {u}}}=\delta _{{\mathrm {y}}}=1$ this factor drops to 11, when $\delta _{{\mathrm {u}}}=\delta _{{\mathrm {y}}}=10^{-2}$, to 9.37 and when $\delta _{{\mathrm {u}}}=\delta _{{\mathrm {y}}}=10^{-4}$, to 7.69. Figure 10 shows the number of internal iterations in the consecutive sampling instants of four compared versions of the MPC-NPLPT algorithm. It is interesting to note that when $\delta _{{\mathrm {u}}}=\delta _{{\mathrm {y}}}=1$, which results in very good control quality, in the majority of sampling instants only one internal iteration is sufficient. More internal iterations are necessary when the set point changes.

In many practical control systems not only the range of the manipulated variable, but also its speed of change is constrained. It is possible to slower the MPC algorithms by increasing the penalty factor $\lambda$. Figures 11 and 12 depict simulation results of the MPC-NPLPT and MPC-NO algorithms for $\lambda =100$ and $\lambda =1000$, respectively. The bigger the penalty parameter, the slower the input and output trajectories of the process and the bigger the overshoot. Unfortunately, it is impossible to guarantee that all the increments of the manipulated variable for each sampling instant fulfil any fixed constraint. That is why the rate constraint is taken into account in the optimisation problems. The trajectories obtained in the MPC-NPLPT and MPC-NO algorithms with the additional constraint $\triangle u^{\max }=0.25$ are depicted in Fig. 13. The additional constraint is satisfied at each sampling instant. Also in this case there are no noticeable differences between the MPC-NPLPT and MPC-NO compared algorithms, although during the presented simulations the parameters are $\delta _{{\mathrm {u}}}=\delta _{{\mathrm {y}}}=1$, $t_{\max }=5$. Table 2 compares all discussed algorithms in terms of the indices SSE and D, computational burden (MFLOPS), and in the case of the MPC-NPLPT algorithm the number of internal iterations is given. The additional constraint increases computational burden of all MPC algorithms (when compared with Table 1), but still the MPC-NPLPT algorithm with trajectory linearisation and quadratic optimisation is many times more computationally efficient than the MPC-NO one.

An interesting issue is to verify effectiveness of the MPC algorithms when the process is affected by unmeasured output noise (with normal distribution with zero mean and standard deviation 0.1). The obtained simulation results of the MPC-NPLPT and MPC-NO algorithms are depicted in Fig. 14, and Table 3 compares all discussed algorithms in terms of the indices SSE and D, computational burden (MFLOPS) and the number of internal iterations (for the MPC-NPLPT algorithm). Finally, Fig. 15 compares the MPC-NPLPT and MPC-NO algorithms when the additional constraint $\triangle u^{\max }=0.25$ is taken into account and the process is affected by unmeasured noise, and the values of all criteria SSE, D, MFLOPS and NII are given in Table 4. It is necessary to point out that in all cases the MPC-NPLPT algorithm with trajectory linearisation and quadratic optimisation gives the trajectories practically the same as the MPC-NO approach with nonlinear on-line linearisation, whereas its computational burden is much lower.

Fig. 13

Simulation results: the MPC-NPLPT algorithm with on-line trajectory linearisation and quadratic optimisation with $t_{\max }=5$, $\delta _{{\mathrm {u}}}=\delta _{{\mathrm {y}}}=1$ (solid line), the MPC-NO algorithm with on-line nonlinear optimisation (dashed line); in both algorithms $\lambda =1$ and the additional constraint $\triangle u^{\max }=0.25$ imposed on the rate of change of the manipulated variable is taken into account

Table 2 Control accuracy (SSE), the relative accuracy criterion (D) and computational burden (MFLOPS) of compared MPC algorithms, for the MPC-NPLPT strategy the sum of internal iterations (NII) is also given; in all algorithms $\lambda =1$ and the additional constraint $\triangle u^{\max }=0.25$ imposed on the rate of change of the manipulated variable is taken into account

Fig. 14

Simulation results: the MPC-NPLPT algorithm with on-line trajectory linearisation and quadratic optimisation with $t_{\max }=5$, $\delta _{{\mathrm {u}}}=\delta _{{\mathrm {y}}}=1$ (solid line), the MPC-NO algorithm with on-line nonlinear optimisation (dashed line); in both algorithms $\lambda =1$ and the process is affected by unmeasured noise

Table 3 Control accuracy (SSE), the relative accuracy criterion (D) and computational burden (MFLOPS) of compared MPC algorithms, for the MPC-NPLPT strategy the sum of internal iterations (NII) is also given; in all algorithms $\lambda =1$ and the process is affected by unmeasured noise

Fig. 15

Simulation results: the MPC-NPLPT algorithm with on-line trajectory linearisation and quadratic optimisation with $t_{\max }=5$, $\delta _{{\mathrm {u}}}=\delta _{{\mathrm {y}}}=1$ (solid line), the MPC-NO algorithm with on-line nonlinear optimisation (dashed line); in both algorithms $\lambda =1$, the additional constraint $\triangle u^{\max }=0.25$ imposed on the rate of change of the manipulated variable is taken into account and the process is affected by unmeasured noise

Table 4 Control accuracy (SSE), the relative accuracy criterion (D) and computational burden (MFLOPS) of compared MPC algorithms, for the MPC-NPLPT strategy the sum of internal iterations (NII) is also given; in all algorithms $\lambda =1$, the additional constraint $\triangle u^{\max }=0.25$ imposed on the rate of change of the manipulated variable is taken into account and the process is affected by unmeasured noise

6 Conclusions

This work details two general nonlinear MPC algorithms for dynamic processes described by cascade Wiener–Hammerstein models, which consist of a nonlinear steady-state block sandwiched by two linear dynamic ones. The algorithms are computationally efficient, and since only quadratic optimisation problems are solved on-line, no nonlinear optimisation is necessary. In both cases the inverse steady-state block is not necessary, which is a very frequent approach to control based on cascade models.

The first algorithm (MPC-NPSL) is conceptually quite simple: at each sampling instant on-line the gain of the nonlinear block is found and used to update the parameters of the linear model. Such a linear approximation of the model is used to calculate the predicted output trajectory and the future control increments, and the influence of the past is determined from the nonlinear Wiener–Hammerstein model. A clear disadvantage of that approach is the fact that the model is linearised on-line in a simplified way and the same linearised model is used for the prediction over the whole prediction horizon. That is why the MPC algorithm with simplified model linearisation, although for the considered heat exchanger benchmark it works much better than the rudimentary MPC algorithms based on a linear model, gives big overshoot when the set point changes fast and significantly.

The second strategy (MPC-NPLPT) uses a more advanced linearisation method. At each sampling instant on-line a linear approximation of the predicted output trajectory is found over the whole prediction horizon. It is a conceptually better approach in comparison with the first one, in which the model itself is only linearised for the current operating point. Indeed, for the considered heat exchanger system the MPC algorithm with trajectory linearisation gives the same trajectory as the MPC-NO algorithm with nonlinear optimisation repeated at each sampling instant on-line. Furthermore, it is computationally efficient in two respects: qualitatively and quantitatively. Firstly, it needs only quadratic optimisation. Secondly, when compared with the MPC-NO algorithm it is many times less computationally demanding.

In contrast to the extended dynamic control (EDMC) algorithm [36] which extends the linear DMC algorithm by using a time-varying disturbance vector which captures the effect of nonlinearities, in the described MPC strategies the effect of the past is calculated directly from the full nonlinear model, the horizon of dynamics is not used (only prediction and control horizons are necessary), and it is not required that the process is stable and it does not contain integration.

A natural direction of future research is the incorporation of the Wiener–Hammerstein model in economic MPC [37, 38] or in set-point optimisation cooperating with MPC [1, 12]. The mentioned approaches tightly integrate economic optimisation and feedback MPC.