Abstract
This work describes a new model structure developed for prediction in Model Predictive Control (MPC). The model has a multi-model structure in which independent sub-models are employed for the consecutive sampling instants. The model lifts process states into a high-dimensional space in which a linear process description is applied. Depending on the influence of the manipulated variables on lifted states, three general model versions are described and model identification algorithms are derived. As a result of the multi-model structure, model parameters are found analytically from computationally uncomplicated least squares problems using the Extended Dynamic Mode Decomposition algorithm, but the evolution of states over the horizon used in MPC is taken into account. Next, the MPC algorithm for the described model is derived. It requires solving online simple quadratic optimisation tasks. The effectiveness of three considered model configurations and three versions of the lifting functions is examined for a nonlinear DC motor benchmark. Their impact on model accuracy, complexity, possible control accuracy and MPC calculation time is thoroughly discussed. Finally, a more complex polymerisation reactor process is considered to showcase the practical applicability of the presented approach to modelling and MPC.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Model Predictive Control (MPC) algorithms repeatedly use online a dynamical model of the controlled process to make predictions of its future trajectory and optimise the sequence of manipulated variables [1, 2]. They give good control quality and consider necessary constraints. The historical background of MPC and a comprehensive overview of recent theoretical developments are reviewed in [3]. Typically, MPC methods have been used for years in industrial process control; example processes are chemical reactors [4] and distillation columns [5]. Nowadays, MPC algorithms are used in embedded systems, e.g., in autonomous vehicles [6], aerial vehicles [7], quadrotors [8] and autonomous underwater vehicles [9]. Other applications include visual robot servoing systems [10], spacecrafts [11] as well as missile guidance and control systems [12]. Machine learning and neural networks are increasingly popular in MPC [13].
1.1 The problem
Using a linear model for prediction in MPC leads to easily solvable quadratic optimisation tasks with only one global minimum [1, 2]. Unfortunately, nonlinear models lead to nonlinear optimisation problems that must be solved online. Such problems are incomparably more difficult than quadratic tasks. It is not only because the calculation time may be longer but because the classical gradient-based optimisation algorithms may find shallow local solutions. A few methods are possible to simplify nonlinear MPC. A predominant practical solution is the utilisation of MPC schemes with the online linearisation, which lead to quadratic optimisation tasks [14, 15]. An inverse static model may compensate for static process nonlinearity and lead to quadratic optimisation tasks [15, 16]. Neural networks may approximate the explicit MPC control law or its coefficients [17,18,19]. Convex models [20] or some convexification techniques [21] lead to convex MPC optimisation tasks. Finally, some methods for selecting the initial solution for the nonlinear solver are possible [22, 23].
An interesting idea is to represent a nonlinear dynamical system using the Koopman operator. In this approach, the true states are replaced by the so-called lifted states and a nonlinear process may be described by a linear model but in the infinite-dimensional space [24, 25]. One of the methods to obtain a finite-dimensional approximation of the Koopman operator for dynamical systems with inputs is the Extended Dynamic Mode Decomposition (EDMD) algorithm [26]; possible alternatives are reviewed in [27]. Of note, the EDMD approach is purely data-driven; no fundamental knowledge of the process is necessary and computationally simple because the linear model in the lifted space is found analytically from simple least squares tasks. Because the choice of lifting functions is an issue, neural network-based approximations of the Koopman operator may be used [28, 29]. However, in such cases, training neural networks requires nonlinear optimisation, i.e., we cannot use the least squares problems. When an MPC algorithm uses Koopman operator-based models, we obtain simple to solve quadratic MPC optimisation tasks [30].
Let us highlight two essential limitations of the classical Koopman operator-based models determined using the classical EDMD algorithm. Firstly, the possibility of finding linear representations of nonlinear processes from least squares tasks is an advantage, but, on the other hand, such models are identified in the one-step-ahead configuration. Propagation of errors is inevitable when the MPC algorithm uses such models recurrently. Shi and Meng recently proposed a new Koopman operator-based model structure to solve the problem [29]. In their approach, the identification algorithm minimises model errors when the model is used recurrently, i.e., in the multiple-step-ahead mode over the horizon used in MPC. However, using least squares tasks is no longer possible and nonlinear optimisation is necessary for model identification. The second limitation of the classical Koopman operator-based models is that the input vector (i.e., the manipulated variables) is not lifted, which is likely to reduce the model’s ability to approximate properties of nonlinear processes. The state-dependent influence of the manipulated variables on the lifted states is very infrequently considered [29].
1.2 Contribution
This work has three objectives: it describes a new model structure developed for prediction in MPC, derives model identification algorithms and the resulting MPC algorithm. The discussed model aims to eliminate the abovementioned limitations of the classical models generated by the EDMD algorithm. Furthermore, the identification procedure of the model presented in this work is significantly computationally simpler compared to the model developed by Shi and Meng [29]. The model identification procedure uses simple least squares tasks solved analytically, but the evolution of states over a time horizon is taken into account. The model has a multi-model structure in which independent sub-models are used for the consecutive sampling instants to make it possible. Each sub-model is found independently in the one-step-ahead mode, which enables the formulation of easy-to-solve least squares problems. Depending on the influence of manipulated variables on the lifted states, three general model versions are described and model identification algorithms are derived. Namely, we consider a fixed linear influence and two time-varying approaches: one linear and one nonlinear, based on monomials. Next, the MPC algorithm for the described model is detailed. Although the model is nonlinear, MPC requires solving online simple quadratic optimisation tasks. Due to its multi-model structure, the model is not used recurrently in MPC.
This work is organised as follows. Section 2 describes three model versions while Sect. 3 derives least squares identification tasks. Section 4 derives the MPC quadratic optimisation task. Section 5 thoroughly investigates model selection issues and the efficiency of different model configurations utilised in MPC for a benchmark dynamical system. Next, a more complex polymerisation reactor process is considered to showcase the practical applicability of the presented approach to modelling and MPC. Finally, Sect. 6 summarises the whole work.
2 Koopman operator-based multi-model
2.1 Preliminaries
We consider a discrete-time nonlinear controlled dynamical system
where \(n_{\text {x}}\) and \(n_{\text {u}}\) stand for the number of states and inputs, respectively, i.e., \(x=\left[ x_1 \ \cdots \ x_{n_{\text {x}}}\right] ^{\text {T}}\) and \(u=\left[ u_1 \ \cdots \ u_{n_{\text {u}}}\right] ^{\text {T}}\), and \(f:{\mathbb R}^{n_{\text {x}}+n_{\text {u}}}\rightarrow {\mathbb R}^{n_{\text {x}}}\) is a nonlinear function. In the Koopman operator approach, we find a linear counterpart of the nonlinear system (1) in the lifted space [30, 31]
where \(z=\left[ z_1 \ \cdots \ z_{n_{\text {lift}}}\right] ^{\text {T}}\), \(n_{\text {lift}}> n_{\text {x}}\). The lifted state vector is
where \(\psi _n :{\mathbb R}^{n_{\text {x}}}\rightarrow {\mathbb R}\) are lifting functions, \(n=1,\ldots ,n_{\text {lift}}\). The manipulated variables, u, are not typically lifted in the state Eq. (2). It allows the imposition of linear constraints on manipulated variables easily. We express the original state as a linear function of the lifted state
Similarly, it allows using linear constraints on states. The EDMD algorithm [26] finds the matrices \(\varvec{A}\), \(\varvec{B}\) and \(\varvec{C}\) from simple least squares problems assuming \(n_{\text {lift}}\) is finite. The EDMD algorithm is entirely data-driven, so the nonlinear system representation (1) is not used. Instead, all calculations are based on measurements. We can use the discussed approach when the function f in Eq. (1) is unknown.
Exact lifting functions may be found analytically for some simple systems [27]. Since the Koopman operator is infinite-dimensional [24, 25], we use a finite number of lifting functions to obtain a computationally possible solution. It means the linear model in the lifted space (Eq. (2)) attempts to approximate the true nonlinear system (Eq. (1)).
2.2 Multi-models using Koopman operator
This work combines the Koopman operator method with the multi-model approach in which independent sub-models calculate at the current sampling instant, k, model states for the consecutive sampling instants over the prediction horizon N, i.e., the vectors \(x(k+1|k),\ldots ,x(k+N|k)\). Next, the MPC algorithm uses these model states for prediction. Previous research concentrated on input–output multi-models [14, 20]. A significant advantage of the multi-model approach is that the consecutive model outputs, and hence the predictions, are not found recurrently, i.e., they do not depend on model outputs or predictions found for the previous sampling instants. It is essential for two reasons. Firstly, identification is possible in the easy one-step-ahead non-recurrent configuration. It is much computationally easier than recurrent model identification. Secondly, when the MPC algorithm uses the multi-model for prediction, model errors are not propagated as necessary in classical recurrent models. Multi-models have two disadvantages: they usually have more parameters than the classical models and cannot be used for long horizons. The following part of this section describes three model versions, with the different influence of the manipulated variables on the lifted states.
The structure of model 1
2.2.1 Model 1: Koopman operator-based multi-model with constant matrices \(\varvec{B}_{p,i}\)
Combining the Koopman operator-based models defined by Eqs. (2) and (4) with the multi-model approach, we define the sub-model for the sampling instant \(k+p\)
for \(p=1,\ldots ,N\). Figure 1 presents the structure of model 1 comprised of N sub-models (5)–(6). Model matrices, i.e., \(\varvec{A}_p\) for \(p=1,\ldots ,N\), \(\varvec{B}_{p,i}\) for \(p=1,\ldots ,N\) and \(i=0,\ldots ,p-1\) and \(\varvec{C}_p\) for \(p=1,\ldots ,N\), are of dimensionality \(n_{\text {lift}} \times n_{\text {lift}}\), \(n_{\text {lift}} \times n_{\text {u}}\) and \(n_{\text {x}} \times n_{\text {lift}}\), respectively. According to Eq. (5), the lifted states, \(z(k+p|k)\), are linear functions of vectors of future manipulated variables optimised online by the MPC algorithm, i.e., \(u(k|k),\ldots ,u(k+N-1|k)\). Conversely, the lifted states are nonlinear functions of the current state, x(k), since \(z(k)=\varvec{\psi }(x(k))\) (Eq. (3)). Of note, we do not use the model recurrently, e.g., we do not apply model outputs for the previous sampling instants as inputs for the next sampling instants. The state vector, \(x(k+p|k)\), is finally calculated from Eq. (6) as a linear function of the lifted state; similarly, it is done in the case of the classical Koopman operator-based models (Eq. (4)).
Let us stress that we do not intend to find one model that aims to approximate the nonlinear system (1) by the model given by Eqs. (2) and (4) as done in the classical Koopman-operator approach. Instead, we intentionally use a set of sub-models. Each sub-model finds process state variables for only one sampling time and is not used recurrently. As a result, least squares can be used for identification, as shown in Sect. 3. Otherwise, considering a state trajectory over a time horizon and only one model will lead to nonlinear optimisation-based model identification [29].
Depending on lifting functions, we consider the following variants of model 1:
-
1.
Model 1a: monomials of the degree \(n_{\text {pol}}^{\text {A}}\) are used as lifting functions
$$\begin{aligned} \psi _{i+(j-1)n_{\text {x}}}(x(k))=x_i^j(k) \end{aligned}$$(7)for \(i=1,\ldots ,n_{\text {x}}\) and \(j=1,\ldots ,n_{\text {pol}}^{\text {A}}\). For example, for \(n_{\text {x}}=2\) and \(n_{\text {pol}}^{\text {A}}=3\), we have
$$\begin{aligned}&\psi _1(x(k))=x_1(k),\quad \psi _2(x(k))=x_2(k),\nonumber \\&\psi _3(x(k))=x_1^2(k), \quad \psi _4(x(k))=x_2^2(k),\nonumber \\&\psi _5(x(k))=x_1^3(k), \quad \psi _6(x(k))=x_2^3(k) \end{aligned}$$(8)The number of lifting functions is \(n_{\text {lift}}=n_{\text {x}}n_{\text {pol}}^{\text {A}}\).
-
2.
Model 1b: polynomials of the degree \(n_{\text {pol}}^ {\text {A}}\) (with mixed terms) are used as lifting functions
$$\begin{aligned} \psi _n(x(k))=x_1^{i_1}(k)\cdots x_{n_{\text {x}}}^{i_{n_{\text {x}}}}(k) \end{aligned}$$(9)where \(i_1=0,\ldots ,n_{\text {x}}\), ..., \(i_{n_{\text {x}}}=0,\ldots ,n_{\text {x}}\) and \(n=1,\ldots ,n_{\text {lift}}\). Because polynomials of high degree lead to numerical problems, we limit our consideration to polynomials that satisfy the condition \(\sum _{n=1}^{n_{\text {x}}}i_n \le n_{\text {pol}}^{\text {A}}\) which means that the maximal degree of each term is not greater than \(n_{\text {pol}}^{\text {A}}\). For example, for \(n_{\text {x}}=2\) and \(n_{\text {pol}}^{\text {A}}=3\), we have
$$\begin{aligned}&\psi _1(x(k))=x_1(k),\quad \psi _2(x(k))=x_2(k),\nonumber \\&\psi _3(x(k))=x_1^2(k), \quad \psi _4(x(k))=x_2^2(k),\nonumber \\&\psi _5(x(k))=x_1(k)x_2(k), \quad \psi _6(x(k))=x_1^3(k),\nonumber \\&\psi _7(x(k))=x_2^3(k), \quad \psi _8(x(k))=x_1(k)x_2^2(k),\nonumber \\&\psi _9(x(k))=x_1^2(k)x_2(k) \end{aligned}$$(10)The overall number of lifting functions is
$$\begin{aligned} \left( {\begin{array}{c}n_{\text {x}}+n_{\text {pol}}^{\text {A}}\\ n_{\text {pol}}^{\text {A}}\end{array}}\right) -1= \frac{(n_{\text {x}}+n_{\text {pol}}^{\text {A}})!}{n_{\text {pol}}^{\text {A}}!n_{\text {x}}!}-1 \end{aligned}$$(11) -
3.
Model 1c: \(n_{\text {RBF}}^{\text {A}}\) Radial Basis Functions (RBFs) are used as lifting functions. In this work, we use \(n_{\text {RBF}}^{\text {A}}\) Gaussian basis functions
$$\begin{aligned} \psi _i(x(k))=\exp \left( -\sigma ^2\left\Vert x(k)-c_i^{\text {A}}\right\Vert ^2 \right) \end{aligned}$$(12)where \(i=1,\ldots ,n_{\text {RBF}}^{\text {A}}\). The spread is denoted by \(\sigma \) and the vectors \(c_i^{\text {A}}\), of length \(n_{\text {x}}\), define centres. In the simplest approach, centres may be chosen randomly [30], but they may also be located at grid points of states or a clustering algorithm may be employed, e.g., the k-means approach. We also use original states as additional lifting functions [30], i.e., \(\psi _{n_{\text {RBF}}^{\text {A}}+i}(x(k))=x_i(k)\) for \(i=1,\ldots ,n_{\text {x}}\). Hence, \(n_{\text {lift}}=n_{\text {RBF}}^{\text {A}}+n_{\text {x}}\).
2.2.2 Model 2: Koopman operator-based multi-model with time-varying matrices \(\varvec{B}_{p,i}(k)\) using linear functions
The structure of models 2 and 3
Figure 2 shows the structure of models 2 and 3. Similarly to model 1 shown in Fig. 1, the matrices \(\varvec{A}_p\) and \(\varvec{C}_p\) for \(p=1,\ldots ,N\) are constant, but now the matrices \(\varvec{B}_{p,i}(k)\) for \(p=1,\ldots ,N\) and \(i=0,\ldots ,p-1\) are time-varying and defined by the functions \(\phi _{p,i}\)
The vector
defines the current operating point of the process. It is of length \(n_{\omega }=n_{\text {x}}+n_{\text {u}}\) and uses the most recent process information available at the current sampling instant, k. For this purpose, we use the current state vector and manipulated variables sent to the process at the previous sampling instant. At the current sampling instant, the vector u(k) is not available since it is computed by a control algorithm which means that the vector \(u(k-1)\) gives the most recent measurements of manipulated variables. Other choices of the vector \(\omega (k)\) are: \(\omega (k)=x(k)\) or \(\omega (k)=u(k-1)\). Using Eqs. (5)–(6), the following equations define models 2 and 3
for \(p=1,\ldots ,N\). The matrices \(\varvec{A}_p\) are not time-varying, which makes an easy determination of model stability. The state Eq. (15) is affine, i.e., linear in future values of manipulated variables, which means that constraints imposed on manipulated variables are linear.
Depending on the functions \(\phi _{p,i}:\mathbb {R}^{n_{\omega }}\rightarrow \mathbb {R}^{n_{\text {lift}}}\) that describe the dependence of the time-varying matrices \(\varvec{B}_{p,i}(k)\) on the current operating point, \(\omega (k)\), (Eq. (13)), we can distinguish a few model configurations. In this work, we name them models 2 and 3. In model 2, we assume the linear dependence
where matrices \(\varvec{w}_{p,i}^0\) are of dimensionality \(n_{\text {lift}} \times n_{\text {u}}\), matrices \(\varvec{w}_{p,i}^1\) are of dimensionality \(n_{\text {lift}} \times n_{\omega }\) and \(\varvec{\omega }_{n_{\text {u}}}(k)=\varvec{1}_{1\times n_{\text {u}}} \otimes \omega (k)\) are matrices of dimensionality \(n_{\omega } \times n_{\text {u}}\); the symbol \(\otimes \) stands for the Kronecker tensor product. The symbol \(\varvec{1}_{m\times n}\) stands for a matrix all entries of which equal 1.
Depending on the lifting functions, we distinguish model 2a (it uses monomials of the degree \(n_{\text {pol}}^{\text {A}}\) as in Eq. (7)), model 2b (it uses polynomials of the degree \(n_{\text {pol}}^{\text {A}}\) as in Eq. (9)) and model 2c (it uses \(n_{\text {RBF}}^{\text {A}}\) RBFs as in Eq. (12)).
2.2.3 Model 3: Koopman operator-based multi-model with time-varying matrices \(\varvec{B}_{p,i}(k)\) using monomials
In model 3, time-varying matrices \(\varvec{B}_{p,i}(k)\) for \(p=1,\ldots ,N\) and \(i=0,\ldots ,p-1\) depend on the current operating point defined by the vector \(\omega (k)\) as specified by Eq. (13). We use the general Eqs. (15)–(16) to compute the lifted state vector for the sampling instant \(k+p\) and the true state vector, respectively. The model matrices are monomial functions of the operating point
The monomial degree is denoted by \(n_{\text {pol}}^{\text {B}}\). Matrices \(\varvec{w}_{p,i}^0\) and \(\varvec{w}_{p,i}^j\) are of dimensionality \(n_{\text {lift}} \times n_{\text {u}}\) and \(n_{\text {lift}} \times n_{\omega }\), respectively. The symbol \(\circ \) stands for the Hadamard product. Depending on lifting functions, we distinguish models 3a, 3b and 3c (the lifting functions are specified by Eqs. (7), (9) and (12), respectively).
3 Identification of Koopman operator-based multi-models
We calculate all parameters from least squares problems whose solutions can be easily found analytically without numerical optimisation. Moreover, because model errors are quadratic functions of parameters, the calculated parameters are globally optimal, which means that they result in a minimal model error. We find model parameters using the EDMD algorithm [26], considering the specific model structures. For identification, we need a set of samples of input and state process variables (measured or observed).
Multi-model identification is performed independently for the consecutive sampling instants \(k+p\), where \(p=1,\ldots ,N\), i.e., we find parameters of consecutive sub-models separately. In all model configurations, matrices \(\varvec{C}_p\) are calculated in the same way as described in Sect. 3.1. Identification of model state equations depends on the model structure. Sections 3.2, 3.3 and 3.4 describe identification procedures of state equations for models 1, 2 and 3, respectively.
3.1 Calculation of matrices \(\varvec{C}_p\)
We define the model error when calculating the state vector, \(x(k+p|k)\), at the current sampling instant, k. The error takes into account the sum of squared differences between the data samples, \(x_i(k+p)\), and model outputs, \(x_i^{\text {mod}}(k+p|k)\), for all \(n_{\text {x}}\) state variables and all data samples
where the indices \(k_{\min }\) and \(k_{\max }\) define the range of considered samples. We can rewrite the error compactly
where \(||\varvec{A}||_{\text {F}}=\sqrt{\sum _i \sum _j a_{i,j}^2}\) is the Frobenius norm. Let \(n_{\text {s}}=k_{\max }-k_{\min }+1\) be the number of available data samples. The matrices of dimensionality \(n_{\text {x}}\times n_{\text {s}}\) are
For all model variants, the relations between the original state vector, \(x(k+p|k)\), and the lifted one, \(z(k+p|k)\), are the same, i.e., given by Eqs. (6) and (16); the choice of lifting functions does not impact this issue. Hence, we always calculate matrices \(\varvec{C}_p\) in the same way. We can rewrite Eqs. (6) or (16) compactly for all data samples
where the matrix
is of dimensionality \(n_{\text {nlift}} \times n_{\text {s}}\). The model matrices \(\varvec{C}_p\) are optimised in the one-step-ahead prediction mode. From Eqs. (20) and (23), the unconstrained optimisation problem is
Because process states are linear functions of lifted states (Eq. (23)), the optimisation problem (25) is of a least squares type. Its solution is determined analytically
where the symbol \((.)^{+}\) stands for the Moore–Penrose matrix pseudo-inverse. We compute matrices \(\varvec{C}_p\) for all sub-models, i.e., for \(p=1,\ldots ,N\).
3.2 Identification of Model 1
Let us rewrite the state Eq. (5) for all data samples in the following compact matrix form
where the matrix
is of dimensionality \(n_{\text {nlift}} \times (n_{\text {nlift}}+pn_{\text {u}})\) and the matrix
is of dimensionality \((n_{\text {nlift}}+pn_{\text {u}}) \times n_{\text {s}}\). The matrix
is of dimensionality \(n_{\text {nlift}} \times n_{\text {s}}\) and the vectors
are of dimensionality \(n_{\text {u}}\times n_{\text {s}}\), \(p=1,\ldots ,N\). We optimise the model matrix \(\overline{\varvec{AB}}_p\) in the one-step-ahead prediction mode. We define the model error for the lifted state vector
where the matrix \(\varvec{Z}_p\) is given by Eq. (24) and the matrix
is of dimensionality \(n_{\text {nlift}} \times n_{\text {s}}\). From Eqs. (27) and (32), we get the unconstrained optimisation problem
Because the future lifted state vectors are linear functions of the current lifted states and future manipulated variables (Eq. (27)), the optimisation problem (34) is of a least squares type. It is solved analytically
Next, the model matrices \(\varvec{A}_p\) and \(\varvec{B}_{p,0},\ldots ,\varvec{B}_{p,p-1}\) are formed from the calculated matrix \(\varvec{\overline{ AB}}_p\)
and
for \(i=0,\ldots ,p-1\). The symbol \(\varvec{I}_{m\times m}\) denotes an identity matrix, while the symbol \(\varvec{0}_{m\times n}\) stands for a matrix all entries of which equal 0. We compute matrices \(\varvec{A}_p\) and \(\varvec{B}_{p,i}\) for all sub-models, i.e., for \(p=1,\ldots ,N\).
Some models may have low training data errors and much larger validation data errors. We use regularisation to increase model generalisation. The optimisation task (34) becomes
where \(\alpha >0\) is a regularisation coefficient. Since the optimisation problem (38) is of a least squares type, its analytical solution is
where \(n_p^{\text {par}}\) stands for the number of model parameters. In this work, it is recommended not to use regularisation for the entries of the state matrices \(\varvec{A}_p\), but apply this technique only for the entries of matrices \(\varvec{B}_{p,i}\). Hence, we find the optimal model parameters from
where the matrix
is of dimensionality \(n_p^{\text {par}} \times n_p^{\text {par}}\).
3.3 Identification of Model 2
For model 2, we need to find constant matrices \(\varvec{A}_p\) and the matrices \(\varvec{w}_{p,i}^0\) and \(\varvec{w}_{p,i}^1\) that define the time-varying matrices \(\varvec{B}_{p,i}(k)\) as specified by Eq. (17). Let us rewrite the state Eq. (15) using the matrix Eq. (27), but now the matrix
is of dimensionality \(n_{\text {nlift}} \times (n_{\text {nlift}}+p(n_{\text {u}}+n_{\omega }))\) and the matrix
is of dimensionality \((n_{\text {nlift}}+p(n_{\text {u}}+n_{\omega })) \times n_{\text {s}}\). The matrix \(\varvec{Z}\) is defined by Eq. (30), the vectors \(\varvec{U}_p\) are characterised by Eq. (31) and the matrices
are of dimensionality \(n_{\omega } \times n_{\text {s}}\). Model parameters are calculated from the optimisation problem (34) or (38), the solution of which is given by Eqs. (35) or (39) or (40). Next, the model matrices \(\varvec{A}_p\), \(\varvec{w}_{p,i}^0\) and \(\varvec{w}_{p,i}^1\) are formed
and
and
for \(i=0,\ldots ,p-1\). We repeat calculations for \(p=1,\ldots ,N\).
3.4 Identification of Model 3
For model 3, we have to find constant matrices \(\varvec{A}_p\) as well as the matrices \(\varvec{w}_{p,i}^0\) and \(\varvec{w}_{p,i}^j\) that define the matrices \(\varvec{B}_{p,i}(k)\), as specified by Eq. (18). The state Eq. (15) may be expressed by the matrix Eq. (27), but now the matrix
is of dimensionality \(n_{\text {nlift}} \times (n_{\text {nlift}}+p(n_{\text {u}}+n_{\text {pol}}^{\text {B}}n_{\omega }))\) and the matrix
is of dimensionality \((n_{\text {nlift}}+p(n_{\text {u}}+n_{\text {pol}}^{\text {B}}n_{\omega })) \times n_{\text {s}}\). The matrix \(\varvec{Z}\) is defined by Eq. (30), the vectors \(\varvec{U}_p\) are characterised by Eq. (31) and the matrices
are of dimensionality \(n_{\omega } \times n_{\text {s}}\). The matrices
are of dimensionality \(n_{\omega } \times n_{\text {u}}\). The model parameters are calculated from the optimisation problem (34) or (38), the solution of which is given by Eqs. (35) or (39) or (40). Next, the model matrices \(\varvec{A}_p\), \(\varvec{w}_{p,i}^0\) and \(\varvec{w}_{p,i}^j\) are formed
and
for \(i=0,\ldots ,p-1\) and
for \(i=0,\ldots ,p-1\), \(j=1,\ldots ,n_{\text {pol}}^{\text {B}}\). We repeat calculations for \(p=1,\ldots ,N\).
4 MPC using Koopman operator-based multi-models
Typically, at each sampling instant of MPC, the increments of manipulated variables for the current and future sampling instants are calculated [1, 2]
where \(N_{\text {u}}\) stands for the control horizon; \(\triangle u(k+p|k)=0\) for \(p\ge N_{\text {u}}\). We compute the decision vector (55) as a result of solving the MPC optimisation task
where \(||x||_{\varvec{A}}^2=x^{\text {T}}\varvec{A}x\). The vector \(x^{\text {sp}}(k+p|k)\) defines the set-point values of state variables for the future sampling instant \(k+p\) known at the current instant, k. The vector \(\hat{x}(k+p|k)\) stands for state predictions for the sampling instant \(k+p\) calculated from the process model at the current instant. Both vectors are of length \(n_{\text {x}}\). Diagonal weighting matrices \(\varvec{M}_p\ge 0\) and \(\varvec{\varLambda }_p>0\) are of dimensionality \(n_{\text {x}}\times n_{\text {x}}\) and \(n_{\text {u}}\times n_{\text {u}}\), respectively. The constraints imposed on the manipulated variables and on the predicted states are defined by the vectors \(u^{\min }\), \(u^{\max }\), \(\triangle u^{\min }\) and \(\triangle u^{\max }\) of length \(n_{\text {u}}\) as well as the vectors \(x^{\min }\) and \(x^{\max }\) of length \(n_{\text {x}}\), respectively. The last constraint represents the prediction model used to find the predicted trajectory. Only the first \(n_{\text {u}}\) elements of the vector (55), i.e., the current increments \(\triangle u(k|k)\), are sent to the process at each sampling instant.
It is convenient for future derivations to compactly rewrite the problem (56). We define two vectors of length \(n_{\text {x}}N\): the set-point vector for the prediction horizon
and the corresponding vector of state predictions
We define the matrices \(\varvec{M}=\text {diag}(\varvec{M}_1,\ldots ,\varvec{M}_N)\) and
\(\varvec{\varLambda }=\text {diag}(\varvec{\varLambda }_0,\ldots ,\varvec{\varLambda }_{N_{\text {u}}-1})\) of dimensionality \(n_{\text {x}}N\times n_{\text {x}}N\) and \(n_{\text {u}}N_{\text {u}}\times n_{\text {u}}N_{\text {u}}\), respectively. We obtain
The vectors \(\varvec{u}(k-1)=\varvec{1}_{N_{\text {u}}\times 1} \otimes u(k-1)\), \(\varvec{u}^{\min }=\varvec{1}_{N_{\text {u}}\times 1} \otimes u^{\min }\), \(\varvec{u}^{\max }=\varvec{1}_{N_{\text {u}}\times 1} \otimes u^{\max }\), \(\triangle \varvec{u}^{\min }=\varvec{1}_{N_{\text {u}}\times 1} \otimes \triangle u^{\min }\) and
\(\triangle \varvec{u}^{\max }=\varvec{1}_{N_{\text {u}}\times 1} \otimes \triangle u^{\max }\) are of length \(n_{\text {u}}N_{\text {u}}\), the vectors
\(\varvec{x}^{\min }=\varvec{1}_{N\times 1} \otimes x^{\min }\) and \(\varvec{x}^{\max }=\varvec{1}_{N\times 1} \otimes x^{\max }\) are of length \(n_{\text {x}}N\). The \(n_{\text {u}}N_{\text {u}}\times n_{\text {u}}N_{\text {u}}\) matrix is
Let us explicitly embed the prediction model \(\varvec{\mathscr {M}}(\cdot )\) into the MPC cost function. We will derive predictions and the MPC optimisation task assuming variability of matrices \(\varvec{B}_{p,i}(k)\) used in models 2 and 3; the description for model 1 using constant matrices \(\varvec{B}_{p,i}\) can be easily obtained. Using Eqs. (15)–(16), the state vectors found from the model for the consecutive sampling instants over the prediction horizon, i.e., \(p=1,\ldots ,N\), are
Model errors and actual disturbances acting on the process are unavoidable. To obtain offset-free control, we use the prediction equation
In MPC, we name the vectors \(d(k+p|k)\), of length \(n_{\text {x}}\), predicted unmeasured disturbances. We find them as differences between measured or observed state variables and those found from the model [1, 2]. Using the model (61) for the current sampling instant, k, the disturbances are
for \(p=1,\ldots ,N\). Using Eq. (62), we find the predicted state trajectory (58) in the following compact vector–matrix form
where the matrix
is of dimensionality \(n_{\text {x}}N\times n_{\text {lift}}\), the matrix
is of dimensionality \(n_{\text {x}}N\times n_{\text {u}}N\), the vector
is of length \(n_{\text {u}}N\) and the vector
is of length \(n_{\text {x}}N\). We use the following relation between the vectors \(\varvec{u}_{\text {N}}(k)\) and \(\triangle \varvec{u}(k)\)
where \(\varvec{J}=\biggl [ \begin{array}{l} \varvec{J}_1\\ \varvec{J}_2 \end{array} \biggr ]\) is a matrix of dimensionality \(n_{\text {u}}N\times n_{\text {u}}N_{\text {u}}\). It is comprised of the matrix \(\varvec{J}_1\) defined by Eq. (60) and the following matrix of dimensionality \(n_{\text {u}}(N-N_{\text {u}})\times n_{\text {u}}N_{\text {u}}\)
The vector \(\varvec{u}_{\text {N}}(k-1)=\varvec{1}_{N\times 1} \otimes u(k-1)\) is of length \(n_{\text {u}}N\). We rewrite Eq. (64) using Eq. (69)
Finally, using Eq. (71), from the rudimentary MPC optimisation task (59), we derive the optimisation problem
We obtain a quadratic optimisation task since the cost function is quadratic in terms of the decision vector, \(\triangle \varvec{u}(k)\), and all constraints are linear.
The DC motor: the first 5000 samples of training and validation data sets
5 Simulations
At first, a DC motor benchmark is considered to thoroughly discuss the influence of three model configurations and three versions of the lifting functions on model accuracy and MPC control quality. Next, a more complex polymerisation reactor benchmark is considered to showcase the practical applicability of the presented approach to modelling and MPC.
5.1 DC motor
A Direct Current (DC) motor is an example of a nonlinear process. It is a frequent benchmark for assessing Koopman operator-based models, e.g., [30, 32, 33]. The process fundamental model is [34]
where \(x_1\) and \(x_2\) stand for the rotor current and the angular velocity, respectively. The manipulated variable u is the stator current. Process parameters are: \(L_{\text {a}}=0.314\), \(R_{\text {a}}=12.345\), \(k_{\text {m}}=0.253\), \(J=0.00441\), \(B=0.00732\), \(\tau _{\text {l}}=1.47\), \(u_{\text {a}}=60\). The manipulated variable is limited: \(-1\le u \le 1\).
The DC motor: the relationship between the validation data set vs outputs of the linear model
The DC motor, models 1: the influence of the complexity of the lifting functions (defined by the monomial or polynomial degree, \(n_{\text {pol}}^{\text {A}}\), and the number of basis functions, \(n_{\text {RBF}}^{\text {A}}\)) on training and validation errors
The fundamental model (73)–(75) is simulated open-loop for a series of random step changes of the manipulated variable, u; each change takes place every 100th sampling period, which equals 0.01 s. Differential model equations are solved using the Runge–Kutta method of order 45. As many as 200,000 samples of manipulated and state variables are collected. The available data set has been divided into training and validation sets, each with 100,000 samples. Figure 3 shows the first 5000 samples from training and validation data sets. The regularisation coefficient \(\alpha =10\) is used.
5.1.1 Modelling of DC motor
Linear multi-model. Taking into account Eqs. (5)–(6), we find the corresponding structure of the linear multi-model in which the state vector is not lifted
We can note that the linear multi-model can be obtained from model 1 (Eq. (5)) assuming that the lifted state vector equals the state vector, i.e., \(z(k)=x(k)\). Hence, the identification procedure detailed in Sect. 3.2 can also be used for the linear structure. Figure 4 shows the relationship between two state variables from the validation data set vs corresponding outputs (states) of the linear model for the consecutive sampling instants \(p=1,\ldots ,10\). The accuracy of the linear multi-model deteriorates as p grows. The sub-models are very inaccurate for \(p>2\) and \(p>5\) for the first and the second state variables, respectively. The cumulative error for all sub-models is
where \(E_p^{\text {X}}\) is given by Eq. (19). Since we will next compare different nonlinear models to the simplest linear structure (76), we scale the error for the linear model to 100%. The model has 150 parameters.
Koopman operator-based multi-model 1. Figure 5 shows the influence of the complexity of lifting functions on training and validation errors. We consider three model versions: 1a, 1b and 1c. Model 1a uses monomials of the degree \(n_{\text {pol}}^{\text {A}}\), model 1b uses polynomials of the degree \(n_{\text {pol}}^{\text {A}}\) and model 1c uses \(n_{\text {RBF}}^{\text {A}}\) radial basis functions (and two state variables). We consider the monomial and polynomial degrees: \(n_{\text {pol}}^{\text {A}}=2,3,4,5,6\) since numerical problems occur for higher degrees. To keep the number of model parameters on a relatively moderate level, we consider \(n_{\text {RBF}}^{\text {A}}=4,9,16,25,36\) radial basis functions. These numbers result from the fact that we have two state variables and centres of radial basis functions are located at \(2\times 2\), \(3\times 3\), \(4\times 4\), \(5\times 5\) and \(6\times 6\) grid points of states, respectively. All errors are expressed in relation to errors of the simple linear multi-model. In general, models 1 give much lower errors than the linear model and the more complex the lifting functions, the lower the errors. Monomials (model 1a) have the largest errors and the monomial degree’s impact on the error is insignificant. The polynomials (model 1b) give lower errors and the polynomial degree noticeably impacts the error. In general, radial basis functions (model 1c) lead to slightly lower errors than polynomials; we observe an exception for four basis functions that are insufficient.
Koopman operator-based multi-model 2. Figure 6 shows the influence of the complexity of the lifting functions on training and validation errors. Depending on the lifting functions, we consider three model versions: 2a, 2b and 2c, similarly to models 1a, 1b and 1c. In general, models 2 give at least two times lower errors than the corresponding models 1 (Fig. 5). Indeed, the more complex the lifting functions, the lower the errors. Monomials (model 2a) are the worst ones, while the polynomials (model 2b) improve modelling accuracy. Radial basis functions (model 2c) give the lowest errors.
The DC motor, models 2: the influence of the complexity of the lifting functions (defined by the monomial or polynomial degree, \(n_{\text {pol}}^{\text {A}}\), and the number of basis functions, \(n_{\text {RBF}}^{\text {A}}\)) on training and validation errors
Koopman operator-based multi-model 3. Figure 7 shows the influence of the complexity of the lifting functions (defined by the monomial or polynomial degree, \(n_{\text {pol}}^{\text {A}}\), and the number of basis functions, \(n_{\text {RBF}}^{\text {A}}\)) on training and validation errors. Additionally, model errors depend on the degree of the monomial that defines the complexity of the time-varying matrices \(\varvec{B}_{p,i}(k)\), i.e., \(n_{\text {pol}}^{\text {B}}\). We consider the following degrees: \(n_{\text {pol}}^{\text {A}}=2,3,4,5\) and \(n_{\text {pol}}^{\text {B}}=2,3,4,5\) as numerical problems occur for higher degrees. Regarding lifting functions, we consider three model versions: 3a, 3b and 3c. In general, in comparison with models 2 (Fig. 6), models 3 have some 20–30% lower errors. Similarly to models 1 and 2, lifting functions significantly impact model accuracy. The largest errors characterise monomials (model 3a), while radial basis functions (model 3c) give the best results.
The DC motor, models 3: the influence of the complexity of the lifting functions (defined by the monomial or polynomial degree, \(n_{\text {pol}}^{\text {A}}\), and the number of basis functions, \(n_{\text {RBF}}^{\text {A}}\)) and complexity of the time-varying matrices \(\varvec{B}_{p,i}(k)\) (defined by the monomial degree, \(n_{\text {pol}}^{\text {B}}\)) on training and validation errors
Comparison of Koopman operator-based multi-models 1, 2 and 3. Having analysed the influence of model configuration on errors in Figs. 5–7, we can select some models for thorough comparison. First, let us study Table 1, which details the number of lifting functions, training and validation errors and the number of parameters for minimal models. When it gives reasonable results, we accept the models with the minimal number of parameters, i.e., for \(n_{\text {pol}}^{\text {A}}=2\), \(n_{\text {pol}}^{\text {B}}=2\), \(n_{\text {RBF}}^{\text {A}}=4\), \(n_{\text {RBF}}^{\text {B}}=8\). In two cases, however, the most uncomplicated models give very poor results and we must use more complex alternatives. Namely, model 1c0 (\(n_{\text {RBF}}^{\text {A}}=4\), \(n_{\text {lift}}=6\)) has larger errors than potentially less advanced models 1a and 1b with the minimal number of parameters. Hence, model 1c (\(n_{\text {RBF}}^{\text {A}}=9\), \(n_{\text {lift}}=11\)) is chosen. Generally, the more complex the lifting functions and dependence of the matrices \(\varvec{B}_{p,i}(k)\) on the process operating point, the lower the errors, but also the higher the number of parameters.
Next, Table 2 reports the results for the best possible models, i.e., those that give minimal validation errors in each model category. The maximal working degrees of monomials and polynomials are used. In comparison with the minimal models listed in Table 1, we can see that all errors are reduced by some 10–20% in the case of models 1a, 1b, 1c, 2a, 2c, 3a, 3b, 3c, or even almost 40–50%, e.g., in the case of model 2b.
Since increasing the degree of monomials, polynomials and the number of basis functions leads to an unacceptable growth in the number of model parameters, we also select compromise models in each category. Table 3 shows the results. We select these models considering two conflicting objectives: minimising model errors and the number of parameters. The chosen compromise models have slightly greater errors than those for the best structures (Table 2), but the number of parameters is much lower.
All Koopman operator-based models are more precise than the linear model, whose error equals 100%. The error of the best Koopman operator-based model equals 11%, while the worst models have errors of about 60%.
It is interesting to discuss the influence of the lifting functions and the choice of the matrix \(\varvec{B}_{p,i}(k)\) on model accuracy. For the considered process, we observe that the type of the matrix \(\varvec{B}_{p,i}(k)\) has a very strong influence on model errors. For constant matrices \(\varvec{B}_{p,i}\) (models 1a, 1b and 1c), model errors are large, equal approx. 50–60%. Introduction of quite simple time-varying matrices \(\varvec{B}_{p,i}(k)\) that use linear functions (models 2a, 2b and 2c) leads to a significant reduction of errors at least three times. For more complex time-varying matrices \(\varvec{B}_{p,i}(k)\) that use monomials (models 3a, 3b and 3c), the errors are reduced at least four times in comparison with the rudimentary models 1a, 1b and 1c. Figure 8 presents the influence of the type of matrices \(\varvec{B}_{p,i}(k)\) on the accuracy of the model with polynomial lifting functions as the relationship between the validation data set vs outputs of the compromise models 1b and 2b. Model 1b is very inaccurate while model 2b is better, which means that variability of matrices \(\varvec{B}_{p,i}(k)\) leads to reducing model errors. Furthermore, from Table 3, it is interesting to note that more complex model 3b leads to some reduction of model errors, but it is bought by a dramatic increase in the number of parameters.
The DC motor: the influence of the type of the matrix \(\varvec{B}_{p,i}(k)\) on the accuracy of the model with polynomial lifting functions: the relationship between the validation data set vs outputs of the compromise models 1b (top) and 2b (bottom)
The type of the lifting functions also has an impact on model errors, but it is not as strong as the influence of matrices \(\varvec{B}_{p,i}(k)\). We observe the least gain of using complex lifting functions for models 1, which are generally bad. We observe quite a significant gain for models 2 and 3. The radial basis lifting functions are the best, but let us note that monomials and polynomials also give good results.
To sum up, we recommend using monomials or polynomials as lifting functions for the considered process; radial basis functions slightly improve accuracy but lead to a huge growth of model complexity. We also suggest that linear dependence of matrices \(\varvec{B}_{p,i}(k)\) on the process operating point should be used.
Classical Koopman operator-based model. Let us evaluate the efficiency of the classical Koopman operator-based model determined using the EDMD algorithm [26, 30]. It finds the model described by Eqs. (2) and (4); its objective is minimisation of model errors in the one-step-ahead mode. Different lifting functions are evaluated and, finally, the model utilising 100 Gaussian basis functions located at \(10\times 10\) grid points of states and the state vector itself are used. Figure 9 compares the first 2000 samples of the validation data set vs outputs, i.e., states, of the classical Koopman operator-based model used in the one-step-ahead mode and recurrently. The one-step-ahead mode gives good modelling accuracy. Unfortunately, model errors are significantly larger when the model is used recurrently.
The DC motor: the first 2000 samples of the validation data set vs outputs of the classical Koopman operator-based model used in the one-step-ahead mode and recurrently
To emphasise the bad prediction accuracy of the classical Koopman operator-based model used recurrently, let us consider predictions over the prediction horizon \(N=10\) that start from all consecutive available data samples. The cumulative scaled model error for the validation data set equals 730%. It means the classical Koopman-operator model used recurrently has lower accuracy than all discussed multi-models. It is because the considered Koopman-operator multi-models independently find state variables for all consecutive sampling instants over the prediction horizon; the model is not used recurrently. Figure 10 shows the relationship between the validation data set vs outputs of the classical Koopman operator-based model used recurrently for the chosen prediction horizon. Model accuracy is poor when it is used recurrently; it is much worse than the accuracy of the compromise model 2b (Fig. 8).
The DC motor: the relationship between the validation data set vs outputs of the classical Koopman operator-based model used recurrently
5.1.2 MPC of DC motor
The MPC horizons are: \(N=10\), \(N_{\text {u}}=3\). According to Eq. (75), the second state variable is the controlled output. Hence, the weighting matrix in the first part of the MPC cost function (Eq. (56)) is \(\varvec{M}_p=\biggl [ \begin{array}{ll} 0 &{} 0\\ 0 &{} 1 \end{array} \biggr ]\) for \(p=1,\ldots ,N\). Since we have only one manipulated variable, the weighting matrix in the second part of the MPC cost function, \(\varvec{\varLambda }_p\), is replaced by the scalar \(\lambda =0.1\) for \(p=0,\ldots ,N_{\text {u}}-1\).
First, let us verify the MPC’s efficacy using the linear model (76). Figure 11 presents the obtained results for a set-point trajectory with the same values as considered in [30], but faster changes. Additionally, from the sampling instant \(k=20\), the additive step disturbance 0.1 acts on the process output; it changes its value to \(-0.1\) starting from the sampling instant 60. Unfortunately, the default value \(\lambda =0.1\) gives very bad control quality when the MPC algorithm uses the linear model. We observe some oscillations in the first part of the simulation, while a large set-point error occurs in the second part. The linear model is imprecise, as shown in Fig. 4 and cannot make precise predictions in MPC. We must increase the penalty coefficient to obtain any set-point tracking and compensation of disturbances. Unfortunately, it leads to very slow process trajectories.
The DC motor: the MPC algorithm which uses the linear model
Let us compare numerically the efficiency of MPC algorithms based on all models listed in Tabs. 1, 2 and 3 using the classical sum of squared control errors
where \(k_{\min }\) and \(k_{\max }\) indicate the simulation horizon. The control error for the best model configuration is assumed to be 0% and all results are expressed in percentages. Table 4 presents the obtained relative control errors. The best results are possible for model 2c.
The control quality is poor when the MPC algorithm uses models 1 with constant matrices \(\varvec{B}_{p,i}\). Figure 12 depicts simulation results when we use the minimal models 1a, 1b and 1c. We do not obtain satisfying results as they are of very low quality. In the first two model cases, oscillations are observed for the first set-point change, while completely wrong trajectories are obtained for the second set-point step. The minimal model 1c results in better control quality, but much better results are possible for more complex models.
The DC motor: the comparison of control quality when the MPC algorithm uses minimal models 1a, 1b and 1c
The DC motor: the influence of the type of lifting functions on control quality when the MPC algorithm uses the compromise models 2a, 2b and 2c
The DC motor: the influence of the type of the matrix \(\varvec{B}_{p,i}(k)\) on control quality when the MPC algorithm uses the compromise models 1b, 2b and 3b
Figure 13 depicts the impact of the type of lifting functions on control quality when MPC uses compromise models 2a, 2b and 2c. These models have the same type of the matrix \(\varvec{B}_{p,i}(k)\) but different lifting functions, i.e., monomials, polynomials and RBFs. Because the accuracy of all these models is good, all obtained control trajectories are correct. The process output quickly follows all changes of the set-point trajectory and changes of the unmeasured disturbance are efficiently compensated. There is no steady-state error, which means that offset-free control is obtained. If the matrix \(\varvec{B}_{p,i}\) is time-varying, the choice of the lifting functions does not impact model accuracy and control quality.
Figure 14 presents the influence of the type of the matrix \(\varvec{B}_{p,i}(k)\) on control quality when we use compromise models 1b, 2b and 3b. These models use the same lifting functions (polynomials). The accuracy of these models is different since the compromise model 1b with the constant matrix \(\varvec{B}_{p,i}\) is much worse than the models 2b and 3b. The more complex the dependence of the time-varying matrix \(\varvec{B}_{p,i}(k)\) on the vector \(\omega (k)\), the more precise the model, but these differences are not very significant. The compromise model 2b with a linear dependence of the matrix \(\varvec{B}_{p,i}(k)\) on the vector \(\omega (k)\) gives very good control quality; it is not necessary to use more complex model configurations.
To sum up, for the considered process, we recommend model structure 2, which relies on time-varying matrices \(\varvec{B}_{p,i}(k)\). Even the simplest polynomial lifting functions give very good results in such a case. The negative feedback in MPC efficiently compensates for model inaccuracies and process disturbances. The more complicated structure 3, and more complex lifting functions do not significantly improve the control quality. Structure 1 gives the worst results; some configurations do not work in MPC.
Although the application of all models recommended in this work requires solving simple quadratic optimisation MPC problems, it is interesting to investigate the impact of model structure on the computational time. Table 5 specifies the relative calculation time for the minimal, the best and compromise models (Tables 1, 2 and 3); the time for the minimal model 1a is assumed to be 100%. In general, we can see that both the number of lifting functions and the complexity of the functions used to define the matrix \(\varvec{B}_{p,i}(k)\) have an impact on the computational burden. Namely, the more the lifting functions (as in models a, b and c, respectively), the longer the time. Similarly, the more complicated the matrix \(\varvec{B}_{p,i}(k)\) (as in models 1, 2 and 3, respectively), the longer the time. We also observe the shortest calculation time for the least complicated minimal models; compromise models require medium time, while the most complex best models need the longest time. We do not observe a significant increase in the calculation time of MPC as the model complexity increases. Namely, the recommended compromise model 2b, that leads to very good MPC control quality, needs the calculation time equal to approx. 130% of the time necessary when the simplest minimal model 1a is used.
5.2 Polymerisation reactor
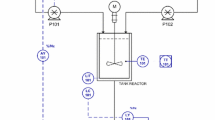
Next, we consider a polymerisation reactor [35]. Its manipulated and controlled variables are the inlet initiator flow rate \(F_{\textrm{I}}\) (m\(^3\) h\(^{-1}\)) and the Number Average Molecular Weight (\(\textrm{NAMW}\)) of the product (kg kmol\(^{-1}\)), respectively. The process fundamental model is [35]
where
and
The parameters of the fundamental model are given in Table 6. The manipulated variable is limited: \(0.003\le F_{\textrm{I}} \le 0.06\). The polymerisation reactor is a well-known benchmark for assessing model accuracy, e.g., [4, 14, 20, 36,37,38], and MPC performance, e.g., [4, 20, 38,39,40,41].
The polymerisation reactor: the first 1500 samples of training and validation data sets
5.2.1 Modelling of polymerisation reactor
The fundamental model (79)–(84) is simulated open-loop for a series of random step changes of the manipulated variable, \(F_{\textrm{I}}\); each change takes place every 30th sampling period, which equals 0.03 s. Differential model equations are solved using the Runge–Kutta method of order 45. 200,000 samples of manipulated and state variables are collected. The available data set has been divided into training and validation sets, each with 100,000 samples. Figure 15 shows the first 1500 samples from both sets.
Because process variables are of different range, they are scaled: \(u=100(F_{\textrm{I}}-\overline{F}_{\textrm{I}})\), \(x_1=3(C_{\textrm{m}}-\overline{C}_{\textrm{m}})\), \(x_2=4(C_{\textrm{I}}-\overline{C}_{\textrm{I}})\), \(x_3=400(D_0-\overline{D}_{0})\), \(x_4=0.025(D_{\textrm{I}}-\overline{D}_{\textrm{I}})\), where \(\overline{F}_{\textrm{I}}=0.028328\), \(\overline{C}_{\textrm{m}}=5.3745\), \(\overline{C}_{\textrm{I}}=2.2433\times 10^{-1}\), \(\overline{D}_{0}=3.1308\times 10^{-3}\), \(\overline{D}_{\textrm{I}}=6.2616\times 10^{-1}\) are process variables at the nominal operating point.
Table 7 reports the results for all considered models of the polymerisation process. To obtain relatively simple models, we limit our comparison to monomials used as lifting functions of degree \(n_{\text {pol}}^{\text {A}}=2,3,4\). We study all three versions of the matrix \(\varvec{B}_{p,i}(k)\) considered in this work, i.e., constant (models 1a), time-varying using linear functions (models 2a) and time-varying using monomials of degree \(n_{\text {pol}}^{\text {B}}=2,3,4,5\) (models 3a). The regularisation coefficient \(\alpha =10\). All model errors are scaled in relation to the error of the linear model which equals 100%. All Koopman operator-based multi-models are more precise than the linear multi-model. Similarly to the DC motor process, we observe that the models with a constant matrix \(\varvec{B}_{p,i}\) are the second worst. Moreover, depending on the degree of the monomials used as lifting functions, i.e., \(n_{\text {pol}}^{\text {A}}\), such models have validation errors equal to 44–50%. On the other hand, assuming time-varying matrix \(\varvec{B}_{p,i}(k)\) gives much lower errors, they equal to 10–18%. We see that increasing the degree of monomials used as lifting functions and to define the matrix \(\varvec{B}_{p,i}(k)\), i.e., the quantities \(n_{\text {pol}}^{\text {A}}\) and \(n_{\text {pol}}^{\text {B}}\), respectively, leads to reducing the model error. However, it is accompanied by significant growth in the number of model parameters. Hence, as a compromise between model accuracy and complexity, we choose the model 2a with \(n_{\text {pol}}^{\text {A}}=2\) and time-varying matrix \(\varvec{B}_{p,i}(k)\) using a linear function.
5.2.2 MPC of polymerisation reactor
All parameters of MPC are taken from previous study [20]. The MPC horizons are: \(N=10\), \(N_{\text {u}}=3\). The primary set-point trajectory is imposed on the process controlled output, i.e., the NAMW variable. Because in the MPC algorithm considered in this work, the set-points may be imposed only on state variables, considering the output Eq. (84), two corresponding set-point trajectories are utilised for the state variables \(x_3\) and \(x_4\). The weighting matrix in the first part of the MPC cost function (Eq. (56)) is \(\varvec{M}_p=\biggl [ \begin{array}{ll} 1 &{} 0\\ 0 &{} 1 \end{array} \biggr ] \) for \(p=1,\ldots ,N\). Since \(n_{\text {u}}=1\), the weighting matrix \(\varvec{\varLambda }_p\) is in fact the scalar \(\lambda =0.1\) for \(p=0,\ldots ,N_{\text {u}}-1\). Figure 16 depicts simulation results of the MPC algorithm based on the model 2a. We can see that the state variables \(x_3\) and \(x_4\) and the process output, NAMW, follow changes in the set-point trajectory.
The polymerisation reactor: simulation results of MPC based on model 2a with \(n_{\text {pol}}^{\text {A}}=2\) and time-varying matrix \(\varvec{B}_{p,i}(k)\) using a linear function
Let us emphasise that it is impossible to obtain good control quality without properly adjusting the regularisation coefficient. Figure 17 shows simulation results of the MPC algorithm that uses three versions of model 2a with \(n_{\text {pol}}^{\text {A}}=2\). These models have been found assuming the following values of \(\alpha \): 0, 0.001 and 100000. In the first case, the controller does not work, i.e., the signals NAMW, \(x_3\) and \(x_4\) do not follow changes in set-point trajectories. Next, the parameter \(\alpha =0.001\) is insufficiently small for the last two set-point changes. Finally, too large a regularisation coefficient, \(\alpha =100000\), leads to larger model errors and worsens the control quality.
The polymerisation reactor: the influence of the regularisation coefficient, \(\alpha \), on the MPC control quality utilising model 2a with \(n_{\text {pol}}^{\text {A}}=2\) and time-varying matrix \(\varvec{B}_{p,i}(k)\) using a linear function
6 Conclusions
This work presents a new model type for prediction in MPC. The model combines the Koopman operator modelling approach with the multi-model structure. Linear dynamics in the lifted space is used to approximate properties of nonlinear processes. We can represent the influence of the manipulated variables on the lifted states by constant or time-varying matrices that depend on the current operating point of the process. We consider linear functions or monomials in the latter case. As a result of the multi-model structure in which independent sub-models are used for the consecutive sampling instants, the parameters of each sub-model are easily calculated in the one-step-ahead mode; no recurrent model identification is necessary. It makes it possible to compute all model parameters analytically from computationally simple least squares problems. The use of the multi-model structure means that we do not use the model recurrently in MPC, but the model can find all predictions over a time horizon used in MPC. High one-step-ahead model accuracy of the classical Koopman operator-based model does not necessarily lead to high multiple-step-ahead accuracy, as shown for the first benchmark process considered in this work. Namely, the model gives excellent results in the one-step-ahead mode, but model errors are large when the model is used recurrently.
Since the Koopman operator-based multi-models rely on a time-varying but linear influence of future values of manipulated variables on the predicted process states, it is possible to derive a quadratic optimisation MPC task.
In this work, a set of models characterised by different lifting functions and types of matrices \(\varvec{B}_{p,i}(k)\) is found and compared. In the future, it will be of interest to develop a systematic method for automatically finding the model structure.
Data availability
The datasets generated during and/or analysed during the current study are available from the corresponding author upon reasonable request.
References
Maciejowski, J.M.: Predictive Control with Constraints. Prentice Hall, Harlow (2002)
Tatjewski, P.: Advanced Control of Industrial Processes, Structures and Algorithms. Springer, London (2007)
Schwenzer, M., Ay, M., Bergs, T., Abel, D.: Review on model predictive control: an engineering perspective. Int. J. Adv. Manuf. Technol. 117, 1327–1349 (2021)
Zarzycki, K., Ławryńczuk, M.: Advanced predictive control for GRU and LSTM networks. Inf. Sci. 616, 229–254 (2022)
Huyck, B., De Brabanter, J., De Moor, B., Van Impe, J.F., Logist, F.: Online model predictive control of industrial processes using low level control hardware: a pilot-scale distillation column case study. Control. Eng. Pract. 28, 34–48 (2014)
Ge, L., Zhao, Y., Shan, Z., Ma, F., Han, Z., Guo, K.: Efficient and integration stable nonlinear model predictive controller for autonomous vehicles based on the stabilized explicit integration method. Nonlinear Dyn. 111, 4325–4342 (2023)
Manzoor, T., Pei, H., Cheng, Z.: Composite observer-based robust model predictive control technique for ducted fan aerial vehicles. Nonlinear Dyn. 111, 3433–3450 (2023)
Eskandarpour, A., Sharf, I.: A constrained error-based MPC for path following of quadrotor with stability analysis. Nonlinear Dyn. 99, 899–918 (2020)
Pan, J., Li, H., Zhou, Z., Yu, J.: 3D path-following control of robotic penguin: an ETFLMPC approach. Nonlinear Dyn. 104, 1415–1427 (2021)
Nebeluk, R., Zarzycki, K., Seredyński, D., Chaber, P., Figat, M., Domański, P.D., Zieliński, C.: Predictive tracking of an object by a pan-tilt camera of a robot. Nonlinear Dyn. 111, 8383–8395 (2023)
Capannolo, A., Zanotti, G., Lavagna, M., Cataldo, G.: Model predictive control for formation reconfiguration exploiting quasi-periodic tori in the cislunar environment. Nonlinear Dyn. 111, 6941–6959 (2023)
Chai, R., Savvaris, A., Chai, S.: Integrated missile guidance and control using optimization-based predictive control. Nonlinear Dyn. 96, 997–1015 (2020)
Ren, Y.M., Alhajeri, M.S., Luo, J., Chen, S., Abdullah, F., Wu, Z., Christofides, P.D.: A tutorial review of neural network modeling approaches for model predictive control. Comput. Chem. Eng. 165, 107956 (2022)
Ławryńczuk, M.: Computationally efficient model predictive control algorithms: a neural network approach. In: Studies in Systems, Decision and Control, vol. 3. Springer, Cham (2014)
Ławryńczuk, M.: Nonlinear predictive control using wiener models: computationally efficient approaches for polynomial and neural structures. In: Studies in Systems, Decision and Control, vol. 389. Springer, Cham (2022)
Shafiee, G., Arefi, M.M., Jahed-Motlagh, M.R., Jalali, A.A.: Nonlinear predictive control of a polymerization reactor based on piecewise linear Wiener model. Chem. Eng. J. 143, 282–292 (2008)
Bonzanini, A.D., Paulson, J.A., Makrygiorgos, G., Mesbah, A.: Fast approximate learning-based multistage nonlinear model predictive control using Gaussian processes and deep neural networks. Comput. Chem. Eng. 145, 107174 (2021)
Ławryńczuk, M.: Explicit nonlinear predictive control algorithms with neural approximation. Neurocomputing 129, 570–584 (2014)
Maddalena, E. T., da S. Moraes, C. G., Waltrich, G., Jones, C. N.: A neural network architecture to learn explicit MPC controllers from data. IFAC-PapersOnLine 53, 11362–11367 (2020)
Ławryńczuk, M.: Input convex neural networks in nonlinear predictive control: a multi-model approach. Neurocomputing 513, 273–293 (2022)
Doncevic, D.T., Schweidtmann, A.M., Vaupel, Y., Schäfer, P., Caspari, A., Mitsos, A.: Deterministic global nonlinear model predictive control with recurrent neural networks embedded. IFAC-PapersOnLine 53, 5273–5278 (2020)
Stogiannos, M., Alexandridis, A., Sarimveis, H.: Model predictive control for systems with fast dynamics using inverse neural models. ISA Trans. 72, 161–177 (2018)
Wang, X., Mahalec, V., Qian, F.: Globally optimal nonlinear model predictive control based on multi-parametric disaggregation. J. Process Control 52, 1–13 (2017)
Koopman, B.: Hamiltonian systems and transformation in Hilbert space. Proc. Natl. Acad. Sci. USA 17, 315–318 (1931)
Koopman, B., von Neuman, J.: Dynamical systems of continuous spectra. Proc. Natl. Acad. Sci. USA 18, 255–263 (1932)
Williams, M.O., Kevrekidis, I.G., Rowley, C.W.: A data-driven approximation of the Koopman operator: extending dynamic mode decomposition. J. Nonlinear Sci. 25, 1307–1346 (2015)
Kutz, J.N., Brunton, S.L., Brunton, B.W., Proctor, J.L.: Dynamic Mode Decomposition: Data-Driven Modeling of Complex Systems. SIAM, Philadelphia (2016)
Lusch, B., Kutz, J.N., Brunton, S.L.: Deep learning for universal linear embeddings of nonlinear dynamics. Nat. Commun. 9, 1–10 (2018)
Shi, H., Meng, M.Q.-H.: Deep Koopman operator with control for nonlinear systems. IEEE Robot. Autom. Lett. 7, 7700–7707 (2022)
Korda, M., Mezić, I.: Linear predictors for nonlinear dynamical systems: Koopman operator meets model predictive control. Automatica 93, 149–160 (2018)
Williams, M.O., Hemati, M.S., Dawson, S.T.M., Kevrekidis, I.G., Rowley, C.W.: Extending data-driven Koopman analysis to actuated systems. IFAC-PapersOnLine 49, 704–709 (2016)
Lian, Y., Jones, C.N.: On Gaussian process based Koopman operators. IFAC-PapersOnLine 53, 449–455 (2020)
Liu, S., Zhang, X., Xu, L., Ding, F.: Expectation–maximization algorithm for bilinear systems by using the Rauch–Tung–Striebel smoother. Automatica 142, 110365 (2022)
Daniel-Berhe, S., Unbehauen, H.: Experimental physical parameter estimation of a thyristor driven DC-motor using the HMF-method. Control. Eng. Pract. 6, 615–626 (1998)
Doyle, F.J., Ogunnaike, B.A., Pearson, R.K.: Nonlinear model-based control using second-order Volterra models. Automatica 31, 697–714 (1995)
Madár, J., Abonyi, J., Szeifert, F.: Genetic programming for the identification of nonlinear input–output models. Ind. Eng. Chem. Res. 44, 3178–3186 (2005)
Ayala, H.V.H., Habineza, D., Rakotondrabe, M., Coelho, L.S.: Nonlinear black-box system identification through coevolutionary algorithms and radial basis function artificial neural networks. Appl. Soft Comput. 87, 105990 (2020)
Zarzycki, K., Ławryńczuk, M.: LSTM and GRU neural networks as models of dynamical processes used in predictive control: a comparison of models developed for two chemical reactors. Sensors 21, 5625 (2021)
Cheng, C., Chiu, M.S.: Adaptive IMC controller design for nonlinear process control. Chem. Eng. Res. Des. 85, 234–244 (2007)
Kansha, Y., Min-Sen, C.: Adaptive generalized predictive control based on JITL technique. J. Process Control 19, 1067–1072 (2009)
Tatjewski, P., Ławryńczuk, M.: Algorithms with state estimation in linear and nonlinear model predictive control. Comput. Chem. Eng. 143, 107065 (2020)
Funding
The authors have not disclosed any funding.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The author declares no Conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ławryńczuk, M. Koopman operator-based multi-model for predictive control. Nonlinear Dyn (2024). https://doi.org/10.1007/s11071-024-09615-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11071-024-09615-7