Bilinear forms and soliton interactions for two generalized KdV equations for nonlinear waves

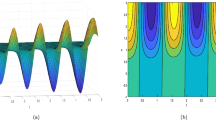
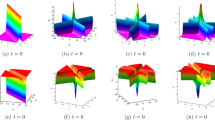
Abstract

Korteweg–de Vries (KdV)-type equations can describe the nonlinear waves in fluids, plasmas, etc. In this paper, two generalized KdV equations are under investigation. Bilinear forms of which are constructed with the Bell polynomials and an auxiliary variable. $N$-soliton solutions are given through the Hirota direct method. Via the asymptotic analysis, the soliton interactions of the first generalized KdV equation are analyzed, which turn out to be elastic. Singular breather solutions have been derived from the two-soliton solutions. The collision between soliton and singular breather appears to be elastic, and the bound states of soliton and singular breather are exhibited. Unlike the first one, the other generalized KdV equation can only support the bound states of solitons, for the regular and singular solitons alike.

Appendix

In the following, we give a brief introduction to the Bell polynomials, which are defined as [25]

$$\begin{aligned}&Y_{nx}\left( g\right) \equiv Y_n\left( g_{1x},g_{2x},\ldots ,g_{nx}\right) =e^{-g}\partial _x^n e^g,\nonumber \\&\quad n=1,2,\ldots , \end{aligned}$$

(44)

where $g$ is a $C^\infty$ function of $x$ and $g_{rx}\equiv \partial _x^r g\,(r=1,2,\ldots )$. The first three members of the Bell polynomials are

$$\begin{aligned} Y_1\left( g\right)&= g_{1x},\nonumber \\ Y_2\left( g\right)&= g_{2x}+g_x^2,\nonumber \\ Y_3\left( g\right)&= g_{3x}+3g_x g_{2x}+g_x^3 . \end{aligned}$$

(45)

If we take

$$\begin{aligned} g_{rx}= \left\{ \begin{array}{ll} p_{rx},&{}\quad \text {if r is odd}\\ q_{rx},&{}\quad \text {if r is even} \end{array}\right. , \end{aligned}$$

(46)

with $p$ and $q$ as both differentiable functions with respect to $x$, the binary Bell polynomials are obtained, which are also called the $\fancyscript{Y}$ polynomials. The first three members of the $\fancyscript{Y}$ polynomials are listed here

$$\begin{aligned} \fancyscript{Y}_{1x}\left( p\,,q\right)&= p_x,\nonumber \\ \fancyscript{Y}_{2x}\left( p\,,q\right)&= q_{2x}+p_{x}^2,\nonumber \\ \fancyscript{Y}_{3x}\left( p\,,q\right)&= p_{3x}+3p_x q_{2x}+p_x^3. \end{aligned}$$

(47)

Similarly, the two-dimensional Bell polynomials can be given as [27]

$$\begin{aligned} Y_{mx,nt}(g)\equiv Y_{m,n}\left( g_{\lambda x,\theta t}\right) = e^{-g}\partial _x^m \partial _t^n e^{g}, \end{aligned}$$

(48)

where $g$ is a $C^\infty$ function of $x$ and $t$, $m,\,\lambda$, and $\theta$ are all positive integers, while $g_{\lambda x,\theta t}=\partial _x^\lambda \partial _t^\theta g$. Two-dimensional binary Bell polynomials can be given as [27]

$$\begin{aligned}&\fancyscript{Y}_{mx,nt}(g)\equiv Y_{m,n}\left( g_{\lambda x,\theta t}\right) \Bigg | g_{\lambda x,\theta t}\nonumber \\&\ \ = \left\{ \begin{array}{ll} p_{\lambda x,\theta t},&{}\quad \text {if} \,\lambda +\theta \,\text { is odd}\\ q_{\lambda x,\theta t},&{}\quad \text {if} \,\lambda +\theta \,\text { is even} \end{array}\right. , \end{aligned}$$

(49)

with $p$ and $q$ as differentiable functions of $x$ and $t$, respectively.

When the D-operators act on a pair of the exponentials $F=e^U$ and $G=e^V$, they can be linked to the Bell polynomials [27], where $U$ and $V$ are the $C^\infty$ functions of $x$ and $t$, while the D-operators are defined as [21]

$$\begin{aligned} \begin{aligned}&D_x^mD_y^lD_t^n a\cdot b\\&\equiv \left( \frac{\partial }{\partial x}-\frac{\partial }{\partial x'}\right) ^m \left( \frac{\partial }{\partial y}-\frac{\partial }{\partial y'}\right) ^l \left( \frac{\partial }{\partial t}-\frac{\partial }{\partial t'}\right) ^n\\&a\left( x,y,t\right) b\left( x',y',t'\right) \bigg |_{x'=x,y'=y,t'=t}, \end{aligned} \end{aligned}$$

(50)

with $x',\,y'$, and $t'$ as the formal variables; $l$ as a positive integer; $a(x,y,t)$ as a $C^\infty$ function of $x,\,y$, and $t$; and $b(x',y',t')$ as a $C^\infty$ function of $x',\,y'$, and $t'$.

In the case for the one-dimension situation,

$$\begin{aligned} \left( FG\right) ^{-1}D_x^nF\cdot G\!\equiv \! \fancyscript{Y}_{nx}\left( p\!=\!\ln {F/G},q\!=\!\ln {FG}\right) .\nonumber \\ \end{aligned}$$

(51)

As for the two-dimension case,

$$\begin{aligned}&\left( FG\right) ^{-1}D_x^mD_t^n F\cdot G\equiv \fancyscript{Y}_{mx,nt}\nonumber \\&\quad \times \left( p=\ln {F/G},q=\ln {FG}\right) . \end{aligned}$$

(52)

Subsequently, the $\fancyscript{P}$ polynomials can be obtained from the $\fancyscript{Y}$ polynomials when we set $F=G$. Then from (51) and (52),

$$\begin{aligned}&\frac{D_x^nF\cdot F}{F^2}=\fancyscript{Y}_{nx}\left( p=0,q=2\ln {F}\right) \nonumber \\&\equiv \fancyscript{P}_{nx}\left( q\right) ,\end{aligned}$$

(53)

$$\begin{aligned}&\frac{D_x^m D_t^nF\cdot F}{F^2} = \fancyscript{Y}_{mx,nt}\left( p=0,q=2\ln {F}\right) \nonumber \\&\equiv \fancyscript{P}_{mx,nt}\left( q\right) . \end{aligned}$$

(54)