Landslide susceptibility mapping of the Sera River Basin using logistic regression model

Abstract

Of the natural hazards in Turkey, landslides are the second most devastating in terms of socio-economic losses, with the majority of landslides occurring in the Eastern Black Sea Region. The aim of this study is to use a statistical approach to carry out a landslide susceptibility assessment in one area at great risk from landslides: the Sera River Basin located in the Eastern Black Sea Region. This paper applies a multivariate statistical approach in the form of a logistics regression model to explore the probability distribution of future landslides in the region. The model attempts to find the best fitting function to describe the relationship between the dependent variable, here the presence or absence of landslides in a region and a set of independent parameters contributing to the occurrence of landslides. The dependent variable (0 for the absence of landslides and 1 for the presence of landslides) was generated using landslide data retrieved from an existing database and expert opinion. The database has information on a few landslides in the region, but is not extensive or complete, and thus unlike those normally used for research. Slope, angle, relief, the natural drainage network (including distance to rivers and the watershed index) and lithology were used as independent parameters in this study. The effect of each parameter was assessed using the corresponding coefficient in the logistic regression function. The results showed that the natural drainage network plays a significant role in determining landslide occurrence and distribution. Landslide susceptibility was evaluated using a predicted map of probability. Zones with high and medium susceptibility to landslides make up 38.8 % of the study area and are located mostly south of the Sera River Basin and along streams.

Introduction

Landslides are one of the most important geohazards, causing economic and social losses as well as damage to soil and water resources (Schlogel et al. 2015; Korup et al. 2012 Alimohammadlou et al. 2013). Worldwide, landslides account for 17 % of all deaths caused by natural hazards (Herath and Wang 2009; Kjekstad and Highland 2009). Rapid growth and urbanisation in the developing world as well as a changing climate are among the main reasons for the observed global increase in landslides. In Turkey, landslides triggered by both social and physical factors are the second most dangerous natural hazard in terms of socio-economic losses (Demir et al. 2015a, b). US$ 80 million of property is lost each year in Turkey due to landslides (Yalcin 2011, 2007). Moreover, a considerable amount of fertile land is carried away yearly by rivers as a result of soil erosion, which leaves the remaining fertile land exposed to increased erosion and landslides (Irvem et al. 2007; Aydin and Tecimen 2010). Such environmental hazards have been exacerbated by disorganised and traditional land use practices in rural areas, where planning and land management regulations are often disregarded (Demir et al. 2015b).

Landslides are a continuing problem in the Eastern Black Sea Region, especially in the Trabzon province where about 64 % of the region is at risk from landslides (Reis et al. 2009). From 2005 to 2008, 178 landslides occurred in areas with heavy rainfall and steep slopes (Bayrak and Ulukavak 2009). Several landslide-related studies have been conducted in the last decade for this region of the Black Sea (Demir et al. 2015b; Bayrak and Ulukavak 2009; Yalcin 2007; Nefeslioglu et al. 2008; Yalcin et al. 2011; Reis et al. 2009), with deforestation, population increase, extreme precipitation, topography, geology, river networks and land use being some of the observed factors that contribute to landslide activity. Widespread agriculture (hazelnuts and tea are cultivated) makes the Trabzon province an economically important region for Turkey. Also, the region, which is located on the legendary Silk Road, is an important hub for tourism and trade, registering an increase in ecotourism in the past decade (Reis et al. 2009; Cavus 2014).

Landslides occur regularly in the Sera River Basin, the designated study area of this paper. However, only a few relevant studies have been carried out in the area. The study area is located in the western part of the Eastern Black Sea region in the county of Akçaabat, southwest of the city of Trabzon, one of the most important harbour cities in Turkey. Landslides in this region are triggered both naturally and artificially. Natural triggers constitute heavy precipitation, stream erosion of slope toes and weathering of the bedrock. Artificial triggers include steep and improperly cut slopes, poorly controlled surface drainage, and uncontrolled settlement and agricultural activities. Landslide activity is currently concentrated in one area, north of Lake Sera. Nonetheless, it is believed that the spatial distribution of landslides is likely to increase as a result of extreme precipitation events in the Eastern Black Sea, and severe deforestation to accommodate more agriculture and infrastructure. For the purposes of disaster and risk management, an assessment of landslide susceptibility in the Sera River Basin is imperative.

Landslide susceptibility can be defined as the propensity of an area to generate landslides (Guzzetti et al. 2006). Several techniques can be employed for hazard modelling. These mainly fall into four categories: (1) expert evaluations, (2) statistical methods, (3) non-deterministic models and (4) mechanical approaches (deterministic or numerical models). While expert evaluation methods are the most common approach used to evaluate landslide hazards (Sarkar and Anbalagan 2008; Raghuvanshi et al. 2014; Kayastha et al. 2013), the subjectivity of decision making means there is a need for more sophisticated techniques to be integrated into the overall methodology. A way to reduce bias is to include statistical approaches (Fall et al. 2006). Since such methods are also relatively easy to implement in geographical information systems (GIS) (Kawasaki et al. 2001; Pradhan 2013), an increasing number of studies have adopted statistical approaches such as bivariate and multivariate analysis including logistic regression, for landslide susceptibility mapping (Zhuang et al. 2015; Nefeslioglu et al. 2008; Akgun et al. 2011; Mancini et al. 2010; Althuwaynee et al. 2014; Schicker and Moon 2012; Youssef et al. 2015; Bui et al. 2011; Hina et al. 2014). Many non-deterministic models are designed to overcome the complexity of landslide susceptibility mapping (matter-element model, fuzzy set methods, artificial neural network, fuzzy models) and have been employed in several studies concerning landslide hazard assessment (Wu et al. 2003; Bui et al. 2012; Pradhan 2011a, b; Shahabi et al. 2012; Zare et al. 2013; Wu et al. 2014). Mechanical approaches, on the other hand, use deterministic and/or numerical models that assess slope stability to evaluate landslide hazards (De Vita et al. 2013; Jia et al. 2012; Armas et al. 2013; Notti et al. 2015). Despite the effectiveness of non-deterministic and machine learning methods that consider complex classification problems, these methods have a steep learning curve. Furthermore, some of these methods can only be implemented using specific software.

The aim of this study was to carry out a landslide susceptibility assessment using a statistical approach for one of the regions in Turkey most at risk from landslides: the Sera River Basin. This area was chosen as it is at high risk of landslides and also shows high potential for tourism and recreation by local authorities (Cavus 2014; Bayrak and Ulukavak 2009). Tourist traffic to the Sera Lake and surrounding areas has led to more settlement in the region. In addition, quarrying operations are currently being carried out on land displaced by a landslide in 1950. The probability of landslide activity in the area has increased considerably as a result of vibrations from these operations. In identifying the areas sensitive to landslides, existing residential regions that are at risk and areas suitable for future settlement could be identified. Using data about past landslides, the study developed a tool to produce a landslide probability map. The binary logistic regression used in this study is one of the most popular statistical methods for determining landslide susceptibility and has often been applied for this purpose (Suzen and Doyuran 2004; Ercanoglu and Temiz 2011; Akgun 2012). The application of logistic regression requires the inclusion of landslide triggering and/or conditioning parameters as independent variables. In general, the more independent variables that are included, the more complete the model will be, given that the consideration of variables plays a major role in determining the dependent variable. According to Coe et al. (2000) and Fabbri et al. (2003), limited data, if of sufficiently high quality, can produce more accurate results as compared to more information of poorer quality. The main advantage of this method is therefore its ability to evaluate the significance of causative factors while eliminating those factors which are unrelated (Yesilnacar and Topal 2005; Chauhan et al. 2010; Ghosh et al. 2011). The study involved the derivation of a landslide probability equation which considers topographic, hydrological and geological parameters by applying logistic regression analysis to the modelling area. The equation was then validated by applying it to the whole of the Sera River Basin. Also, while most studies carried out in Trabzon province are on the regional scale (Yalcin et al. 2011; Reis et al. 2009), few focus on small-scale landslide hazard mapping (Akgun and Bulut 2007; Yalcinkaya and Bayrak 2005), which is helpful for those making administrative decisions in the region.

Study area

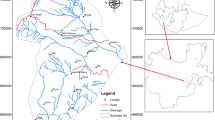
The Sera River Basin, with an area of 73.75 km², is located west of the Trabzon province, which is in the administrative boundaries of the county of Akçaabat. The basin is 2 km inland from the coast, between latitudes 40°52′0″–41°0′30″N and longitudes 39°31′0″–39°39′0″E (Fig. 1). It lies within the Eastern Black Sea Region Watershed, part of the Caucasus Ecologic Region, which is one of the five biologically diverse world regions as identified by the World Wildlife Fund (WWF) and thus is of international importance (WWF 2015).

Fig. 1

Location and topography of the Sera River Basin

Lake Sera, situated in the north of the basin, was formed as a result of a landslide in 1950 and is now a nature reserve and tourist destination in Turkey. The Sera Landslide occurred on 21 February 1950, about 2.5 km inland from the coast. It resulted in about 15 million m³ of land being displaced, making it one of the most significant landslides seen in the Eastern Black Sea Region. A week before the event, several signs of an impending landslide were observed, mainly in the form of long and deep cracks. The landslide was due to intensive chemical disintegration in the geomorphological structure of the region as a result of the presence of deep fissures in basaltic and andesitic lava formations from the Upper Cretaceous period (Fig. 2). This disintegration caused instability and susceptibility to moisture from higher-than-expected rainfall and the sudden melting of snow due to southern Foehn winds, which caused a significant amount of water to leak into the ground. The landslide, 220 m from foot to crown, is believed to have stemmed from the largest crack. The flow of land was complex, with three landslide types identified, namely single block slides, multiple rotational block slides and topple failures. The landslide created a wall from west to east that blocked the valley and the Sera River and led to the formation of a dam/lake. This endorheic basin is about 4 km long, 200 m wide and 50 m deep (Boztas 1986).

Fig. 2

Source: Sarıyılmaz (1972)

Cross section of the active landslide zone of the Sera River Basin

The topography of the basin has an average slope of 23°. The average precipitation in this region is 822 mm, considerably more than that for Turkey as a whole (643 mm). As in the rest of the Black Sea Region, subsistence/semi-subsistence farming is common, but there is little large-scale commercial farming as a result of the topography and land ownership issues (Inan et al. 2011; Demir et al. 2015b). Areas north and south of the lake have seen major infrastructure development with the construction of buildings and roads. This construction is believed to have been stimulated by tourism (Fig. 3). Ongoing soil erosion and conversion of land for agriculture and infrastructure has resulted in an increase in the frequency of landslides in the active landslide zone. Currently, this area is 0.12 km², but it might grow if current practices are not controlled. The last known landslide, along the site of a new road, is believed to have occurred in March–April 2015.

Fig. 3

Source: Images obtained from Google Earth

Aerial view of Lake Sera. Areas north and south of the Basin have seen considerable development leading to deforestation of the forest around thus increase landslide risks. The red line designates the extent of the Sera River Basin and yellow the presently active landslide zone

Input data sources

Landslide data

The application of logistic regression for the purpose of landslide susceptibility mapping requires a reliable inventory of the type, activity and spatial distribution of all landslides in the study area. However, in Turkey these inventories are not common (Akgun and Bulut 2007). The existing database of landslides in the region, obtained from national catalogues, includes only the 1950 landslide which led to the creation of Lake Sera. These data are in polygon form and may include debris runout zones, which would lead to an overestimation of the landslide source region. Post-1950, landslide activity in the Sera River Basin has been continuous, occurring regularly especially over the past 5 years as a result of the aforementioned reasons. In the absence of a complete landslide inventory, expert opinion was employed to map landslide activity (Fig. 4). This map shows that landslides of the slide type are the most common in the area. Because this study is based on limited data, this landslide susceptibility assessment should be considered preliminary until a landslide database is developed and a more advanced study is possible.

Fig. 4

Landslide and model area of the Sera River Basin

Landslide factors

Factors affecting slope stability are various and are in most cases interconnected. The main trigger factor for landslides in the study area and most of the Black Sea region is heavy precipitation due to the increase in precipitation extremes and intensity observed (Can et al. 2005; Yalcin and Kavurmaci 2013). The influence of precipitation on landslides differs depending on landslide type, dimension, kinematics and material involved. Shallow failures, often occurring in the Sera River Basin, are usually triggered by short intense storms (Guzzetti et al. 1992; Flentje et al. 2000; Can et al. 2005). Because precipitation is relatively uniform throughout the study area, it was not included in the regression analysis as its effect is negligible. Seismicity was not considered for the same reason. River incision and aggradation may occur as a result of tectonics and thus influence susceptibility to landslides leading to changes in the river courses and local topography (Dunning et al. 2007; Pirasteh et al. 2009). Roads were excluded because they are few. In the eastern part of the study area, there is a single road, running parallel to the Sera River. Land use is the main reason for anthropologically induced instability in the Sera River Basin. Land use pattern has been changing in this region in terms of agricultural needs and settlement area in order to cater for the increase in population. The deforestation of the native broadleaf forests has made this region more prone to landslides, especially in cleared and sparsely vegetated areas. However, the unavailability of current and accurate details of land use change in the region prevented the inclusion of this parameter. Similarly, no data were available on weathering of the bedrock and erosion of the slope toes and other soil properties. The spatial variation in slope stability and hydrological conditions, including soil moisture and groundwater flow, is controlled mainly by topographic conditions. As such, topographic indices such as the topographic wetness index (TWI) can be used to describe spatial soil moisture patterns (Yilmaz 2009). Subsequently, the analysis considered the following landslide-conditioning parameters: profile curvature, slope, aspect, relative relief, distance to rivers, topographic wetness index and lithology.

Supporting data for this study was obtained from 1:25,000-scale topographic maps and 1:100,000-scale geological maps prepared by the General Directorate of Mineral Research and Exploration of Turkey. Contour lines that contain elevation values were extracted from the topographic map, after which a digital elevation model (DEM) with cell size 25 m × 25 m was constructed. Slope, aspect, relief, profile curvature and topographic wetness index values were calculated using the DEM. Geologic maps were scanned and then digitised in ArcGIS to prepare the lithology. All the data layers mentioned below in the context of logistic regression analysis are shown in Fig. 5.

Fig. 5

Data layers used in the logistic regression analysis. a Slope, b aspect, c profile curvature, d relative relief, e lithology, f distance to river, g TWI

Profile curvature

Most slopes are not uniform but rather consist of a sequence of convex, concave and uniform areas, whose effect on sediment load and erosion is not properly reflected by overall average steepness (Di Stefano et al. 2000). The profile curvature refers to the curvature of the land surface in the direction of the steepest slope, with respect to the vertical plane of a flow line. The profile curvature affects the rate at which water drains from the surface and influences erosion and deposition. Erosion is more likely to be prominent in areas transitioning from convex (negative) and flat profile curvature to concave (positive) curvature while deposition occurs in places with convex surfaces (Alkhasawneh et al. 2013; Cavalli et al. 2016). Curvature was classified into three classes: concave (<0), flat (0) and convex (>0).

Slope and aspect

Slope and aspect are significant conditioning parameters of small-scale landslides (Lee and Min 2001; Dai and Lee 2002). Slope angle is used regularly in landslide susceptibility studies as it is one of the primary causes of landslides (Lee 2005; Yalcin 2008; Nefeslioglu et al. 2008), while aspect is also an important factor in assessing landslide hazard susceptibility (Yalcin and Bulut 2007; Galli et al. 2008). Aspect is associated with parameters such as exposure to sunlight, drying winds and rainfall, which may affect the location of landslides (Suzen and Doyuran 2004). The slope and aspect parameters for the model and validation area were extracted from the DEM. The overall slope was classified into five classes: <10°, 10°–20°, 20°–30°, 30°–40° and >40°. The aspect was also divided into five classes: flat (−1°), north (0°–45° and 315°–360°), east (45°–135°), south (135°–225°) and west (225°–315°).

Relative relief

Relative relief refers to the elevation range between the lowest and highest points of a region and is an important parameter in landslide hazard mapping. Landslide susceptibility increases as relief increases, but at different levels with different geology (Dai et al. 2001; Zhu et al. 2014). Bedrock incision caused by rivers can generate sufficient relief to predispose slopes to catastrophic land mass failures (Korup et al. 2007). The steepening of hillslopes by erosion leads to an increase in relief above a threshold value and landslides follow. Relief was divided into five classes: <50, 50–100, 100–150, 150–200 and >200 m.

Distance to river

The Sera River is a key feature of the Sera River Basin. Previous studies show that landslides tend to occur along the sides of valleys as a result of groundwater flowing towards streams and rivers, which in turn affects undercutting processes (Korup et al. 2007; Tang et al. 2011; Zaruba and Mencl 2014). In this study only first- and second-order rivers were considered as low-order streams are less important in the landslide process (Fan et al. 2013; Othman and Gloaguen 2013). Distance to river was calculated in ArcGIS and categorised into five classes: <250, 250–500, 500–1000, 1000–2000 and >2000 m.

Topographic wetness index (TWI)

Topographic indices, such as TWI, are used to describe soil moisture distribution and groundwater flow (Beven and Kirkby 1979; Moore et al. 1991). Therefore, it is important to account for TWI when considering landslide processes (Pourghasemi et al. 2012; Timilsina et al. 2014). TWI is defined as:

$${\text{TWI}} = \ln \left( {\frac{{A_{\rm s} }}{\tan \beta }} \right)$$

(1)

where A _s is the specific catchment area (the local upslope area draining through a certain point per unit contour length) and β is the slope. TWI is usually higher in flat, converging terrain and lower in regions of steep, diverging land (Timilsina et al. 2014). TWI values were normalised for a scale of 1–10 (1 the lowest, 10 the highest) and classified into six classes: <2, 2–4, 4–5, 5–6, 6–8 and >8.

Lithology

Rock permeability and strength are characterised by geological parameters such as lithology and structure. Therefore, determining rock boundaries and their overall distribution is important when considering landslide processes (Ayalew and Yamagishi 2005). Lithological data were grouped into five main domains (Table 1), and these were used for analysis.

Table 1 Lithology domains and rock formations of the study region

Materials and methods

The ArcGIS software was used to prepare data and represent modelling results, while the R statistical programme (R Development Core Team 2015) enabled logistic regression analysis (modelling and validation processes of the study area). The flowchart showing the different steps of the study is illustrated in Fig. 6.

Fig. 6

Flowchart of the study

Sample selection

Instead of using a single point to represent one landslide, this study considered the whole area of moved landslide masses from the previous landslides. This is because single points tend to not fully represent the characteristics of the landslide area (Timilsina et al. 2014). Previous studies also show that sampling patterns are best when “seed cells” or gridded points extracted from the landslide area are used to obtain attributes for landslide and random landslide-free points (Brenning et al. 2005; Meusburger and Alewell 2009; Van Den Eeckhaut et al. 2010). However, given the limited data considered in this study, the small sample may not fully cover the diversity of all the factors in the study area, on which the resulting model is dependent (Heckmann et al. 2014).

Addressing the issue of “rare events” when applying logistic regression, King and Zeng (2001) state that the number of non-events should typically be 2–5 times higher than that of events for the model area (Heckmann et al. 2014). In addition, they propose endogenous stratified sampling, that is, a sampling method that includes all events and a random sample of non-events. The sample selection of this study followed the reasoning of King and Zeng (2001): all the landslides events and a random sample of non-events around the current landslide active area were chosen. As shown in Fig. 4, of the 24,768 gridded points in the model area defined, 5992 were classified as landslide points (event points, 1) and 18,776 (non-event points, 0) as landslide-free points, giving a ratio of approximately 1:4.

The modelling strategy

Logistic regression allows the analysis of a problem where the result, measured with dichotomous variables such as 1 and 0 (or TRUE and FALSE), is determined from one or more independent factors (Menard 2002). Consideration of the influence of n independent variables (x ₁ to x _n ) on the dependent variable (Y) generates the model statistics and coefficients of a formula used to predict the probability of a logit transformation of the dependent variable. As such, logistic regression results do not define landslide susceptibility directly. Instead, an inference can be drawn using the probability values. In the case of landslide susceptibility mapping, logistic regression attempts to determine the model that best describes the relationship between the presence or absence of the dependent variable (landslides) and a set of independent variables. There are no universal criteria or guidelines for the selection of independent variables, although there is a general agreement that they should have a certain degree of affinity with the dependent variable, be fairly represented across the study area, vary spatially within the study area and be measurable (Ayalew and Yamagishi 2005). The independent variables employed in this study are slope, aspect, relief, lithology, distance to rivers and TWI, respectively. The independent variables can be continuous or categorical, but the latter was preferred here. With regard to the categorisation of the variables, the range of each class does not greatly affect the landslide hazard prediction capacity (Remondo et al. 2003), so both expert-based and landslide distribution-based classifications are applicable. Furthermore, due to the addition of an appropriate function to the usual linear regression model, the variables may either be continuous or discrete, or a combination of both types, and do not necessarily have normal distribution (Lee and Sambath 2006).

Logistic regression coefficients can be used in the model to estimate the effect of each of the independent variables on landslide occurrence (Pradhan and Lee 2010; Ayalew and Yamagishi 2005). While regression coefficients are not readily interpretable, standardised coefficients can be used to assess the relative importance of predictors (Mărgărint et al. 2013). In addition, the data firstly need to be normalised in order to generate an accurate model; combining data with different measuring scales can lead to problems in the interpretation of final results. The logistic regression model allows the integration of both continuous and discrete independent variables. In this study, all continuous variables were converted to discrete variables according to their classes. Categorical variables can be integrated into two ways: (1) by expressing the classes of each discrete parameter as dummy variables (Guzzetti et al. 1999; Dai and Lee 2002; Nefeslioglu et al. 2008) or (2) by computing landslide densities for discrete parameters and using these as the density predictors (Zhu and Huang 2006; Yilmaz 2009). This study used the latter approach to prevent the creation of an excessively high number of dummy variables. Use of landslide densities also allows for the representation of independent parameters on the same scale (Ayalew and Yamagishi 2005). Landslide densities for slope, aspect, relief, curvature, lithology, distance to rivers and TWI were computed using the following formulae (Bai et al. 2010):

$${\text{LD}}_{i} = \frac{{\left({\text{LA}}_{i} /A_{i} \right)}}{{\left({\text{LA}}/A \right)}}$$

(2)

where LD _i is the landslide density value for class i, LA _i and A _i are the landslide area in class i and the total area of class i, respectively, and LA and A are the total landslide area in the model region and the total area of the model region, respectively. A class with a high landslide density corresponds with a parameter having a higher coefficient in the logit function and hence is considered to play a greater role in landslide activity.

Therefore, the logit function that defines the probability of a landslide occurring (P) is expressed as:

$${\text{logit}} = \ln \left( {\frac{P}{1 - P}} \right) = b_{0} + b_{1} x_{1} + b_{2} x_{2} + \ldots + b_{n} x_{n}$$

(3)

and hence,

$$P = \frac{1}{{1 + e^{{ - \left( {b_{0} + b_{1} x_{1} + b_{2} x_{2} + \ldots + b_{n} x_{n} } \right)}} }}$$

(4)

where $b_{0} \ldots b_{n}$ are constants.

The regression coefficients are computed using the maximum likelihood estimation (Suzen and Doyuran 2004). Compared with linear regression, there is no unique solution for logistic regression coefficients, hence why the maximum likelihood estimation follows an iterative algorithm.

For the susceptibility model, 80 % of the landslide and non-landslide points were used as training samples. The remaining 20 %, randomly selected, were used as an independent data set for validation and for testing the predictive potential of the logistic regression model. Continuous susceptibility values, obtained from the model and ranging from 0 to 1, were classified into five classes. Several approaches can be taken in this regard including equal intervals, standard deviation-based separations, natural breaks method and quantiles. There is, however, no agreement on the best method. Ayalew and Yamagishi (2005) state that the use of equal intervals tends to emphasise one class over the other and recommend the standard deviation approach as the best choice for class separation. Conversely, Mărgărint et al. (2013) recommend the natural breaks algorithm (Jenks 1977) which groups similar values together thus maximising the differences between classes. This method was applied here and five landslide susceptibility classes were chosen, namely very low, low, medium, high and very high.

Evaluation

The goodness of fit for the susceptibility model was tested with the pseudo-R², the Nagelkerke $\bar{R}^{2}$, the Brier score and the area under the curve (AUC) of the receiver operating characteristic (ROC).

The Nagelkerke $\bar{R}^{2}$ can be interpreted as the proportion of explained variation in the regression model. Therefore, it can be used as a measure of success with regard to predicting the dependent variable from the independent variables (Nagelkerke 1991). Nagelkerke $\bar{R}^{2}$ is defined as:

$$\bar{R}^{2} = \frac{{R^{2} }}{{{ \hbox{max} }\left( {R^{2} } \right)}}$$

(5)

where

$$R^{2} = 1 - \left\{ {L\left( 0 \right)/L\left( {\hat{\beta }} \right)} \right\}^{{{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 n}}\right.\kern-0pt} \!\lower0.7ex\hbox{$n$}}}}$$

(6)

and

$$\hbox{max} \left( {R^{2} } \right) = 1 - L\left( 0 \right)^{{{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 n}}\right.\kern-0pt} \!\lower0.7ex\hbox{$n$}}}}$$

(7)

where $L\left( {\hat{\beta }} \right)$ and L(0) represent the fitted models with the independent variables and the “null” model fitted with only the intercept, respectively.

The Brier score provides a means of assessing relative accuracy and generates the “error rate” of the logistic regression model (Brier 1950). The formulation of the Brier score is as follows:

$${\text{BS}} = \frac{1}{N}\mathop \sum \limits_{t = 1}^{N} \left( {f_{t} - o_{t} } \right)^{2}$$

(8)

where f _t is the probability forecasted in Eq. 3, o _t is the observed outcome of the event at instance t and N is the number of forecasting instances. The Brier score ranges from 0 to 1 and measures the mean squared difference between the predicted probability and the observed outcome. Therefore, a completely accurate forecast would generate a value of 0.

Wald statistics, which evaluate the statistical significance of each coefficient b _j in the model, were calculated as follows:

$$W_{j} = \left( {\frac{b_{j}}{\text{SE}}_{b_{j}}} \right)^{2}$$

(9)

where W _j represents the Wald test and ${\text{SE}}_{{b_{j} }}$ represents the standard error of coefficient b _j for independent variable j.

Classification accuracy tables and the ROC methodology were used as validation for both the training and test samples. The ROC curve is a useful method for representing the quality of deterministic and probabilistic detections and forecast systems (Swets 1988). It analyses the relationship between sensitivity and specificity of a binary classifier, in this instance the occurrence of landslides. Sensitivity refers to the proportion of positives correctly classified, that is, the proportion of landslides correctly identified when comparing predicted probability to observed values. Specificity measures the proportion of negatives correctly classified, that is, the proportion of landslide-free regions correctly identified (Flach 2010; Yesilnacar and Topal 2005). Conventionally, the curve is a plot of the probability of a correctly predicted response to an event (true positive rate or sensitivity) versus the probability of a falsely predicted response to an event (false positive rate or 1-specificity), as the cut-off probability varies and in other words correctly predicting a landslide at a certain location, and incorrectly predicting a landslide at a certain location. The AUC evaluates the quality of the forecast system by describing the ability of the system to anticipate correctly the occurrence or non-occurrence of pre-defined “events”, in this case landslides. AUC is measured on a scale of 0 and 1. When AUC = 1, every positive has scored higher than every negative and the forecast is completely accurate—the model is ideal. Excellent models have AUC values greater than 0.9 and good models AUC values greater than 0.7 (Mărgărint et al. 2013).

Analysis and results

Landslide susceptibility model

Landslide densities were computed for each class of landslide-conditioning parameters (Table 2), and these values were used in the logistic regression analysis. With regard to slope angle, the highest landslide density values corresponded with angles of more than 40°. Higher landslide density values were also associated with eastern and western slopes, concave curvature, higher TWI values (2–8), areas within 500 m of rivers and, in terms of lithology, KTb and Tb.

Table 2 Landslide density (LD) for the classes of the landslide triggering parameters

The logistic regression coefficients and standardised coefficients obtained are given in Table 3. The slope aspect in the “West” class has the highest coefficient, indicating its strong influence, followed by distance to rivers (under 500 m) and slope angles (greater than 40°). With regard to slope aspect, the “north” class produced the second highest coefficient. This indicates that landslides in the Sera River Basin are first and foremost related to slope characteristics and proximity to rivers, then lithology.

Table 3 Performance results and logistic regression coefficients of the model

Landslide susceptibility mapping

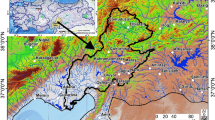
After the logistic regression modelling, the susceptibility values were classified from very low to very high according to the natural breaks method algorithm. The upper threshold values are presented in Table 4. This table shows that the very low and low susceptibility classes account for 43.5 and 17.7 % of the study area. Conversely, about 27 % of the study area is highly/very highly susceptible. Figure 7 shows the classified landslide susceptibility map. The map shows the area of the basin consisting of Tb, Tek and Pzm deposits and that steep slopes are the most hazardous. It is observed that the banks of the Sera River and its tributaries are the most susceptible to landslides. Similar results are observed for the area surrounding the basin.

Table 4 Upper threshold values (TV), derived by Jenks’ method, and percentages (%) of landslide susceptibility classes from the total area of the study region

Fig. 7

Landslide susceptibility map of the Sera River Basin

Evaluation

Previous studies include statements about evaluating the performance of logistic regression models: (1) the significant Wald statistic for independent variables should be less than 0.05 (Bai et al. 2010; Dahal et al. 2012); (2) the Nagelkerke $\bar{R}^{2}$ should be greater than 0.2 (Clark and Hosking 1986; Ayalew and Yamagishi 2005); (3) AUC should be greater than 0.7 (Hosmer and Lemeshow 2000; Song et al. 2008); and (4) the Brier score should be less than 0.25 (Steyerberg et al. 2010). Based on these criteria, the regression model generated in this study showing $\bar{R}^{2}$ of 0.545, Brier score of 0.133 and Wald statistics of <0.05 for most classes of predictors is considered satisfactory (Table 3). The percentages of correctly classified points were achieved for a cut-off value of 0.5 for the training and validation samples. Table 5 (classification accuracy results for the validation of the model) shows a good, stable logistic regression model with an overall accuracy of 80.1 and 81.9 % for the training and validation samples. Area under the ROC curves (Fig. 8) indicate that the logistic regression model is highly accurate, for both the training and validation samples generated high AUC values (89.3 and 83.0 %, respectively).

Table 5 Percentages of correctly classified points with respect to training and validation samples, using a cut-off value of 0.5

Fig. 8

ROC curves with associated AUC values computed from the training sample and the validation sample

Therefore, the computed logistic regression model is representative of landslide activity in the model area. The model can be used more widely to evaluate landslide susceptibility in the Sera River Basin as the basin has similar geomorphological and geological characteristics to the area under study.

Discussion

Areas with high susceptibility of landslides are found in close proximity to water courses. Toe erosion and steep slopes near river banks lead to slope instability and thus to landslides (Liu et al. 2004). Toe erosion, a main cause of landslides in river valleys refers to stream flows that undercut banks, resulting in sloughing and prompting slope failures (Tamrakar et al. 2014; Midgley et al. 2012). The Black Sea Region, including the Sera River Basin, is dominated by broadleaf forests. The root systems of broad-leaf trees are extensive, a factor that helps prevent landslides. However, along the rivers are settlements and arable land (hazelnut farms) (Demir et al. 2015b), which has led to an increase in landslide occurrences, particularly where land has been cleared on the steep banks (Fig. 7) and roots and other physical barriers have been removed (Pandey et al. 2007).

The steep slopes of the Sera River Basin may also be a factor in causing landslides. Highly susceptible regions in this regard are mostly south of Lake Sera, where strata dip uniformly in one direction and cause differential erosion. Similarly, the reason why the western and northern banks of the Sera River are more susceptible to landslides as compared to the eastern and southern banks may be due to the litho-structural characteristics of the region. Slope influences the susceptibility of an area to landslides as well as the magnitude of landslides (Grelle et al. 2011). The logistic regression model employed in this study emphasised the importance of aspect and lithology, which leads to the conclusion that slope is a major factor in determining landslide activity in the Sera River Basin. Rock lithologies such as sandstone, mudstone and claystone that have low shear strength properties and thin beds are the most landslide prone in the Black Sea region (Duman et al. 2005). In cataclinical slope areas where strata dip towards slope angle, such as on the western and southern banks of the Sera River, slope instability and translational slope failures and slumps are more likely (Liu et al. 2004; Grelle et al. 2011). Conversely, when the dip of the bed goes against the slope angle (anaclinal slope areas), strata tend to be more resistant to erosion and landslides.

Despite the positive results obtained, the landslide susceptibility model presented in this study, as is the case of any statistical method, has some inherent limitations. These are: (1) all landslides regardless of type were considered which resulted in a high degree of generalisation; (2) being small scaled, the model does not consider the large spatial variability of local conditions (especially geotechnical ones) which influence landslide occurrence; (3) the model assumes that landslides will occur under the influence of the same combination of predictors. For a more complete model, variables such as the dip of the bed/strata and vegetation cover could be included. The inclusion of more variables would not necessarily mean the model performs better, as this depends on the quality of data (Coe et al. 2000; Fabbri et al. 2003), but it would allow for testing and confirmation of how vegetation cover and dip of the bed relate to landslide activity. In this regard, lack of landslide records is a limiting factor. Despite the satisfactory results generated by the logistic regression model, the sample size was limited and concentrated on one area of the basin only. The expansion of the study area may allow for the inclusion of more landslide data from the surrounding areas, thus producing a richer landslide inventory that may be used for validation purposes. In addition, new methods are being developed for the preparation of landslide inventory maps, e.g. Santangelo et al. (2015) present a semi-automatic procedure using GIS for the digitalization of landslide obtained from aerial photographs, reducing the subjectivity from manual visual transfer to the digital database. Such methods may be used to improve the quality of the landslide inventory, although high-resolution aerial photographs of the study area, which are currently unavailable, are required for this purpose.

Landslide susceptibility values are not absolute but are relative (Fell et al. 2008). However, even with limited data, the landslide susceptibility map is significant to policy-makers as it allows the understanding of the increasing risk of landslide in the region. This can help to prioritise funding for landslide risk mitigation measures at the municipal levels, which is a preliminary stage for regional planning, and designing landslide risk mitigation plans (Pellicani et al. 2014).

Conclusion

This research attempted to follow different steps in order to produce the landslide susceptibility using logistic regression model in a GIS environment. This helps to understand the future landslide probability of the area and its spatial distribution, which is important in terms of infrastructure development and land use management.

Landslides are widespread geohazards caused by geology, geomorphology, hydrology, climate, land use and other factors. Most of the Trabzon province, in the Eastern Black Sea Region of Turkey, is currently at risk from landslides, mostly as a result of poor land use practice and deforestation. This includes the Sera River Basin. The Sera Lake, located in the north of the basin, was formed as a result of a landslide in 1950, and since then there have been further landslides in the region. Therefore, it is important to assess landslide susceptibility in the area. Hazard mapping allows us to understand past and present landslide activity and thus to determine the future risks. Landslide susceptibility refers to the spatial occurrence probability of landslides and can be modelled to a relatively high degree of accuracy by using a combination of statistical approaches and GIS.

Several approaches exist for modelling landslide susceptibility. A logistic regression model was employed in this study. The logistic regression model generated different probabilities for the occurrence of landslides by considering and assessing the conditions that led to past and present slope failures and landslides. The parameters selected included slope angle, aspect, lithology, TWI, proximity to rivers and relative relief. The model satisfied the criteria set for evaluating its performance and was therefore deemed to represent accurately the relationships between the selected parameters and potential landslide activity in the Sera River Basin. The landslide susceptibility maps showed that regions along streams and south of the Sera Lake are highly vulnerable to landslides. This is attributed to “soft” lithologies, which have low resistance to erosion and landslide processes, and slope instability as a result of toe erosion, which is shaped by the distance to water courses.

Other important causative factors of landslides include the dip of the bed, land use, and the type and extent of vegetation cover. However, these factors were not considered. Field investigations and the production of detailed geological maps (including strata dip angle and directions) were also beyond the scope of this study. The incomplete landslide inventory map of the region poses a problem for landslide susceptibility mapping as the current landslide activity is concentrated north of the lake, and the map reflects this. A means to improve model performance could be to expand the study area and consider a larger scale. However, this would require detailed landslide records, which are currently not available. Nevertheless, given the positive results obtained in this study, it can be concluded that logistic regression could be a significant means by which the landslide susceptibility in the Black Sea region can be assessed.