1 Introduction

Two-point nonlinear singular boundary value problems (TPN-SBVPs) has a diversity of domains and huge submissions in nuclear physics, reaction–diffusion mechanism, physiological responses, electro hydrodynamics, heat transfer, astrophysics, thermal-explosion theory, elasticity, shallow membrane and fluid mechanics [1,2,3,4,5,6,7,8,9,10]. Due to various challenges of these problems, there are some numerical or analytical approximation approaches have been applied. To mention a few notable numerical and analytic approaches, the perturbation technique [11] is an analytic method used to solve the nonlinear differential systems; even though, this technique cannot be used for the SBVPs due to the small/large values of the physical parameter. To overcome the constraint of the perturbation method, non-perturbation methods such as the homotopy method [12], variational iteration approach [13], Adomian decomposition method [14], and few more schemes have been developed in the literature [15,16,17,18,19]. Without guaranteeing approximation series convergence, the first three techniques are used to obtain the model’s approximation series outputs.

This research is presented to explore the stochastic strategy based on the Gudermannian neural networks (GNNs) for TPN-SBVPs that arise in thermal-explosion. Consequently, the stochastic techniques are famous to deal with the challenges of singularity as well as nonlinearity. In this study, GNNs along with the combination of global and local search schemes based genetic algorithm (GA) and sequential quadratic programming (SQP) is applied to solve the TPN-SBVPs. Differential systems in higher order [20], mosquito model [21], infection model [22, 23], and singular models [24,25,26] are a few such implementations of stochastic applications. The scholars are inspired to handle TPN-SBVPs arising within thermal-explosion theory by examining some good applications of stochastic solvers.

The fundamental form of TPN-SBVPs is shown as [27]:

$$ \left\{ {\begin{array}{*{20}c} {\frac{d}{dz}\left( {b(z)\frac{d\alpha }{{dz}}} \right) = b(z)q(z,\alpha ),} & {a > 0,\beta \ge 0} \\ {\alpha (0) = 0,} & {a\alpha (1) + \beta \frac{d\alpha (1)}{{dz}} = G} \\ \end{array} } \right. $$
(1)

where G is a positive constant. The following steps have been applied to both the functions b(z) and q(z,α) as:

  • The function q(z,α) is continuous ∀ q(z,α) ∈ ([0,1] × R).

  • \(\frac{\partial q(z,\alpha )}{{\partial y}}\) exists as well as continuous ∀ q(z,α) ∈ ([0,1] × R).

  • b(z) ≥ 0, b(z) = 0.

  • b(z) ∈ C1 (0,1].

  • b(z) ∈ L1 (0,1].

  • \(\int\limits_{0}^{1} {\frac{1}{b(z)}} \int\limits_{0}^{1} {b(x)dxdz < \infty .}\)

The distinctiveness and persistence of TPN-BVPs described in above Eq. (1) [28]. Because of the singular point at the origin, presenting solution for singular systems is usually intriguing and demanding. In literature, several approximate methods to solve the singular models have been proposed via b(z) = zR or zRq(z), R > 0 for boundary conditions (BCs) \(\alpha (0) = A\,\,\,\left( {or\,\,\,\,\frac{d\alpha (0)}{{dz}} = A_{1} } \right),\,\alpha (1) = B,\left( {a\alpha (1) + \beta \,\,\frac{d\alpha (1)}{{dz}} = D} \right)\).

For singular BVPs mentioned in Eq. (1), a direct technique B-spline is proposed via b(z) = zR,R ≥ 0 [29]. Iyengar et al. [30] described the finite difference spline approach for solving the singular models for b(z) = zR as well as \(\alpha (0) = A\,\,\,\left( {or\,\,\,\,\frac{d\alpha (0)}{{dz}} = 0} \right),\,\alpha (1) = D.\) Several research works employing cubic spline are presented to solve the singular BVPs with b(z) = zR,R ≥ 0 with BCs \(\frac{d\alpha (0)}{{dz}} = 0,\,\alpha (1) = D\) [31]. A novel strategy is provided that combines the B-spline collocation and a modified decomposition technique with b(z) = zR, R ≥ 0 as well as BCs w′(0) = 0,w(0) = E and (βw(1) + γw′(1) = E [32]. To analyze the singular BVPs provided in (1), Pandey et al. [33] proposed the finite difference approach b(z) = zRq(z), R ≥ 0. In addition, the model (1) was solved using the variational iteration approach employing b(z) = zR, R ≥ 0 as well as \(\alpha (0) = A\,\,\,\left( {or\,\,\,\,\frac{d\alpha (0)}{{dz}} = A_{1} } \right),\)\(\alpha (1) = B,\,\left( {or\,\,a\alpha (1) + \beta \,\,\frac{d\alpha (1)}{{dz}} = D} \right)\)[2]. The technique based GNNs enhanced by the optimization framework of GA and the SQP is used to solve the TPN-SBVPs are presented first time in this study. Few of the important aspects of this study are presented as:

  • A stochastic GNNs-GASQP is successfully presented for the numerical solutions of TPN-SBVPs.

  • The proposed stochastic computing procedure for solving the TPN-SBVPs is tested for reliability and validity by taking small and large neuron analysis.

  • The assessments of the numbers of neurons are not only provided the complexity cost and absolute error performance, but also in terms of weights, comparison, and statistical measures.

  • The accuracy, magnificence, and consistency of the stochastic methods are verified by solving the TPN-SBVPs with outcomes based on best and mean values.

  • The data for the TPN-SBVPs was examined using the statistical operators, such as mean, Theil inequality coefficient (TIC), mean square error (MSE), semi-interquartile range (SIR), as well as median (Med).

The remaining parts are as follows: The proposed GNNs-GASQP are shown in Sect. 2, the statistical measures are described in Sect. 3, the numerical outcomes are presented in Sect. 4. The concluding remarks are presented in the conclusion Sect. 4.

2 Methodology

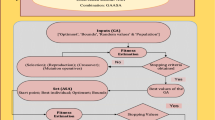
The proposed GNNs-GASQP are applied to solve the TPN-SBVPs in this section along with the mathematical modelling through GNNs, system performances via hybridization of GASQP and statistical performances.

2.1 Mathematical Modeling of GNNs

The suggested solutions in this modeling are \(\hat{\alpha }(z)\), whereas \(\frac{{d^{n} \hat{\alpha }(z)}}{{dz^{n} }}\) denotes the derivative of order n, which is given as:

$$ \begin{gathered} \hat{\alpha }(z) = \sum\limits_{s = 1}^{m} {\upsilon_{s} M(w_{s} z + q_{s} ),} \hfill \\ \frac{{d^{n} }}{{dz^{n} }}\hat{\alpha }(z) = \sum\limits_{s = 1}^{m} {\upsilon_{s} \frac{{d^{n} }}{{dz^{n} }}M(w_{s} z + q_{s} ).} \hfill \\ \end{gathered} $$
(2)

In Eq. (2), m denotes the number of neurons, M is fitness function, as well as [vs,ws,gs] are the weight vector forms. The Gudermannian function (GF) is represented as:

$$ M(z) = 2\tan^{ - 1} \left[ {\exp (z)} \right] - \frac{1}{2}\pi $$
(3)

This approximate mapping of differential operators can be described by using the GF in the above equation as:

$$ \hat{\alpha }(z) = \sum\limits_{s = 1}^{m} {\upsilon_{s} (2\tan^{ - 1} e^{{(w_{s} z + q_{s} )}} - \frac{1}{2}\pi ),} $$
(4)
$$ \frac{d}{dz}\hat{\alpha }(z) = \sum\limits_{s = 1}^{m} {2\upsilon_{s} w_{s} \left( {\frac{{e^{{(w_{s} z + q_{s} )}} }}{{1 + \left( {e^{{(w_{s} z + q_{s} )}} } \right)^{2} }}} \right),} $$
(5)
$$ \frac{{d^{2} }}{{dz^{2} }}\hat{\alpha }(z) = \sum\limits_{s = 1}^{m} {2\upsilon_{s} w_{s}^{2} \left( {\frac{{e^{{(w_{s} z + q_{s} )}} }}{{1 + \left( {e^{{(w_{s} z + q_{s} )}} } \right)^{2} }} - \frac{{2e^{{(w_{s} z + q_{s} )^{3} }} }}{{\left( {1 + \left( {e^{{(w_{s} z + q_{s} )}} } \right)^{2} } \right)^{2} }}} \right).} $$
(6)

The fitness function (EF ) in the mean squared error form is written as:

$$ E_{F} = E_{FI} + E_{FII} $$
(7)

where EFI and EFII are fitness functions associated with TPN-SBVPs and their BCs, expressed as:

$$ \begin{gathered} E_{F} = \frac{1}{N}\sum\limits_{s = 1}^{N} {\frac{d}{{dz_{s} }}\left( {b(z_{s} )\frac{d\alpha }{{dz_{s} }}} \right)} - b(z_{s} )c(z_{s} ,\alpha_{s} )^{2} + \hfill \\ \,\,\,\,\,\,\, + \frac{1}{2}\left( {\left( {\frac{d\alpha }{{dz_{0} }}} \right)^{2} + \left( {a\alpha_{N} + \beta \frac{d\alpha }{{dz_{N} }} - G} \right)^{2} } \right) \hfill \\ \end{gathered} $$
(8)

where Nh = 1, αs = α(z), b(α) = b(αs), and gs = sh.

2.2 Optimization: GASQP

The stochastic techniques rely on the GNNs-GASQP for solving the TPN-SBVPs are shown in this subsection.

Genetic algorithms (GAs) are a type of evolutionary computing strategy observed in natural evolutionary processes. In 1975, Holland was applied first time the GAs to simulate a relatively basic image of natural selection [34]. It is important in the optimization methods of both limited and unconstrained systems [35]. GA is a term that refers to the best heuristic, mutation, crossover, and selection performance. Signal processing, optical, robot, media announcing, Biotechnology, astronomy, electric grids, economic mathematics, chemical production, as well as economics are some of the domains, where it is commonly used. GA has been used to improve 2D industrial packing processes [36], pipe systems [37], wind power connections [38], integrated assessment-based circularity error [39], intrusion discovery prototype [40], food supply [41], management system of energy [42], heterogeneous modeling [43], as well as carrot dry processes in recent decades. These obvious ideas prompted to the authors for solving the TPN-SBVPs based on best outputs by employing GA optimization techniques. to provide the best GA values for initial input, a hybrid of the global/local search method involving rapid convergence. As for verify that parameters have stabilized, an efficient local search procedure called ’SQP’ is used. The SQP algorithm is a nonlinear programming technique for constrained optimization problems that have been applied by the research community. The scheme’s effectiveness has been demonstrated across many test issues in terms of effectiveness, precision, and percentage of successful solutions. The introduction and discussion of SQP algorithms by Nocedal and Wright [44] are outstanding. [45, 46] provides a comprehensive history, mathematical explanation, significance, and implementation of SQP approaches. From their inception to the present, SQP methods have been used in engineering and applied sciences domains.

2.3 Performance Evaluation

To examine the consistency and dependability of GNNs-GASQP for TPN-SBVPs. The statistics achievements using MSE, TIC, SIR as well as global visualizations of MSE, TIC, and SIR. These statistical operators’ mathematical forms are presented as:

$$ MSE = \sum\limits_{j = 1}^{k} {\left( {z_{j} - \hat{z}_{j} } \right)^{2} } $$
(9)
$$ TIC = \frac{{\sqrt {\frac{1}{n}\sum\limits_{j = 1}^{k} {\left( {z_{j} - \hat{z}_{j} } \right)^{2} } } }}{{\sqrt {\sum\limits_{j = 1}^{k} {z_{j}^{2} } } + \sqrt {\sum\limits_{j = 1}^{k} {\hat{z}_{j}^{2} } } }} $$
(10)
$$ \begin{gathered} SIR = - \frac{1}{2}\left( {Q_{1} - Q_{3} } \right), \hfill \\ Q_{1} \,and\,\,Q_{3} = 1^{st} and\,3^{rd} \,quartile \hfill \\ \end{gathered} $$
(11)

In the equations above, z denotes exact solutions, whereas zˆ denotes proposed solutions.

figure a

Algorithm 1 Proposed GNNs-GASQP optimization to solve TPN-SBVPs

3 Simulations and Results

The TPN-SBVPs are solved by using GNNs-GASQP in this part, which includes thorough explanations and simulations. To ensure that the GNNs-GASQP optimization towards tackling TPN-SBVPs is effective, a small and large neuron assessment is carried out. To solve TPN-SBVPs, each neuron is subjected to statistical analysis using several variables.

Problem I

Consider a TPN-SBVP is given as:

A merit function is as follows:

$$ \left\{ \begin{gathered} \frac{d}{dz}\left( {z\frac{d\alpha }{{dz}}} \right) + ze^{\alpha (z)} = 0, \hfill \\ \alpha (1) = 0,\,\frac{d\alpha (0)}{{dz}} = 0. \hfill \\ \end{gathered} \right. $$
(12)
$$ E_{F} = \frac{1}{N}\sum\limits_{s = 1}^{N} {\left( {\frac{d}{{dz_{s} }}\left( {(z_{s} )\frac{d\alpha }{{dz_{s} }} + z_{s} e^{{\alpha_{s} }} } \right)} \right)}^{2} + \frac{1}{2}\left( {\left( {\frac{d\alpha }{{dz_{0} }}} \right)^{2} + \left( {\frac{d\alpha }{{dz_{N} }}} \right)^{2} } \right) $$
(13)

The exact solution of the above equation is given as \(\alpha (z) = 2\log \left( {\frac{1 + U\beta }{{1 + Uz^{2} }}} \right),\,U = 3 - 2\sqrt 2\).

Problem II

Assume TPN-SBVP equilibrium of isothermal gas sphere is follows:

$$ \left\{ \begin{gathered} \frac{d}{dz}\left( {z^{2} \frac{d\alpha }{{dz}}} \right) + z^{2} \alpha^{5} (z) = 0, \hfill \\ \alpha (1) = \sqrt{\frac{3}{4}} ,\,\frac{d\alpha (0)}{{dz}} = 0. \hfill \\ \end{gathered} \right. $$
(14)

A merit function is as follows:

$$ E_{F} = \frac{1}{N}\sum\limits_{s = 1}^{N} {\left( {\frac{d}{{dz_{s} }}\left( {(z_{{_{s} }}^{2} )\frac{d\alpha }{{dz_{s} }} + z_{s}^{2} \alpha_{{_{s} }}^{5} } \right)} \right)}^{2} + \frac{1}{2}\left( {\left( {\frac{d\alpha }{{dz_{0} }}} \right)^{2} + \left( {\frac{d\alpha }{{dz_{N} - \sqrt{\frac{3}{4}} }}} \right)^{2} } \right). $$
(15)

The exact solution of the above equation is given as \(\alpha (z) = \sqrt {\frac{3}{{3 + z^{2} }}}\).

The optimization measurements depending on the GNNS-GASQP are shown for 40 iterations during solution of TPN-SBVPs. The proposed outputs have been used by taking 4, 12, and 20 numbers of neurons based on the best weight vectors. The following are the TPN-SBVPs solutions by taking 4 number of neurons.

$$ \begin{aligned} \hat{\alpha }_{1} (z) = & - 0.5010\left( {2*\arctan *\exp (3.4344z - 4.0366) - \frac{1}{2}\pi } \right) \\ & - 4.0890\left( {2*\arctan *\exp ( - 2.191z - 13.360) - \frac{1}{2}\pi } \right) \\ & - 17.760\left( {2*\arctan *\exp ( - 6.123z - 7.9571) - \frac{1}{2}\pi } \right) \\ & + 2.6948\left( {2*\arctan *\exp ( - 9.117z - 13.360) - \frac{1}{2}\pi } \right) \\ \end{aligned} $$
(16)
$$ \begin{aligned} \hat{\alpha }_{2} (z) = & 3.2310\left( {2*\arctan *\exp ( - 9.2659z - 19.427) - \frac{1}{2}\pi } \right) \\ & - 8.8719\left( {2*\arctan *\exp (1.0484z - 1.1174) - \frac{1}{2}\pi } \right) \\ & + 12.4081\left( {2*\arctan *\exp (0.734z - 1.0604) - \frac{1}{2}\pi } \right) \\ & - 4.2480\left( {2*\arctan *\exp (2.1602z - 6.5472) - \frac{1}{2}\pi } \right) \\ \end{aligned} $$
(17)

The following are the results obtained for 12 neurons:

$$ \begin{aligned} \hat{\alpha }_{1} (z) = & 1.7850\left( {2*\arctan *\exp ( - 8.5456z - 7.9720) - \frac{1}{2}\pi } \right) \\ & + 19.299\left( {2*\arctan *\exp ( - 2.4598z - 14.4221) - \frac{1}{2}\pi } \right) \\ & + 1.8894\left( {2*\arctan *\exp (0.2028z - 12.7546) - \frac{1}{2}\pi } \right) + ... + \\ & + 2.9571\left( {2*\arctan *\exp ( - 12.81z - 19.3876) - \frac{1}{2}\pi } \right) \\ \end{aligned} $$
(18)
$$ \begin{aligned} \hat{\alpha }_{2} (z) = & 1.5647\left( {2*\arctan *\exp (1.7946z + 1.1356) - \frac{1}{2}\pi } \right) \\ & - 1.5085\left( {2*\arctan *\exp (1.0014z + 1.0563) - \frac{1}{2}\pi } \right) \\ & + 1.1566\left( {2*\arctan *\exp ( - 0.6439z + 0.7848) - \frac{1}{2}\pi } \right) + ... + \\ & + 1.0505\left( {2*\arctan *\exp ( - 0.4261z - 0.1626) - \frac{1}{2}\pi } \right) \\ \end{aligned} $$
(19)

Likewise, the TPN-SBVPs solutions consisting of 20 neurons are as follows:

$$ \begin{aligned} \hat{\alpha }_{1} (z) = & - 0.8413\left( {2*\arctan *\exp (1.35976z - 0.7896) - \frac{1}{2}\pi } \right) \\ & + 0.2959\left( {2*\arctan *\exp (1.3175z - 0.2017) - \frac{1}{2}\pi } \right) \\ & + 0.3008\left( {2*\arctan *\exp ( - 0.3002z - 1.8950) - \frac{1}{2}\pi } \right) + ... + \\ & + 0.0775\left( {2*\arctan *\exp (1.4394z - 2.3935) - \frac{1}{2}\pi } \right) \\ \end{aligned} $$
(20)
$$ \begin{aligned} \hat{\alpha }_{2} (z) = & - 0.014\left( {2*\arctan *\exp (0.0637z + 0.3265) - \frac{1}{2}\pi } \right) \\ & + 0.0067\left( {2*\arctan *\exp ( - 3.3123z + 2.0382) - \frac{1}{2}\pi } \right) \\ & + 1.8994\left( {2*\arctan *\exp ( - 0.6135z + 0.1452) - \frac{1}{2}\pi } \right) + ... + \\ & - 0.5292\left( {2*\arctan *\exp ( - 0.2428z - 1.3927) - \frac{1}{2}\pi } \right) \\ \end{aligned} $$
(21)

Figure 1 displays the weights for solving the TPN-SBVPs by using GNNs-GASQP depending on the 4, 12, and 20 neurons. For such TPN-SBVPs, the weight vectors are shown in Eqs. (16–21) based on 4, 12, as well as 20 neurons. Figure 2 provides a comparative analysis of the outputs for solving the TPN-SBVPs using 4,12, and 20 neurons. The proposed results from the GNNs-GASQP were found to overlap with the true results for both problems. The accuracy of the GNNs-GASQP for the TPN-SBVPs is demonstrated by these comparisons of the outputs for the neurons 4, 12, and 20. Figure 3 shows the AE graphics for each problem. The AE values for 4, 12, and 20 neurons are seen in Fig. 3, respectively. Depending upon 4 neurons, the AE value is computed 10−05–10−07 regarding problem I, whereas the AE value is computed 10−04–10−06 for problem II. For corresponding problem, the TPN-SBVPs for 12 numbers of neurons, the AE value is computed about 10−07–10−08, whereas AE values for 2nd problem found as 10−07–10−09. Furthermore, the values of the AE for 20 neurons are conducted around 10−06–10−08 for problem I and II. The AE values for 4 neurons have been determined performed good; nevertheless, the AE is enhanced for 12 neurons, as well as perfect AE attained for 20 neurons. According to the AE results, which were displayed with 4, 12 and 20 neurons, one may conclude that the GNNs-GASQP works better with high neurons than with a small neuron.

Fig. 1
figure 1

Best weights vectors with 4, 12 as well as 20 neurons for solving problem I–II

Full size image
Fig. 2
figure 2

Best weights vectors with 4, 12 as well as 20 neurons for solving problem I–II

Full size image
Fig. 3
figure 3

AE values with 4, 12 as well as 20 neurons for solving problem I–II

Full size image

The outcomes of the FIT, MSC, and TIC operators for 4,12, and 20 neurons for TPN-BVSPs employing GNNs-GASQP are presented in Fig. 4a–c. The statistical measures for 4 neurons are shown in Fig. 4a. The FIT values for problem I and II are close to 10−09 and 10−10, respectively. The MSC measures for problem I and II lies 10−11 to 10−12 and 10−07 to 10−08. The TIC techniques for problems I and II lies around 10−09–10−10 and close to 10−08 for the singular model. The outcomes for 12 numbers of neurons are displayed in Fig. 4b. It is noted that the values of FIT are calculated close to 10−11 and 10−12–10−13 for problems I and II. The MSC measures for singular system’s problem lies 10−12–10−13 for problem I and close to 10−12 for problem II. The TIC techniques for the singular system’s respective problems are 10−10–10−11. The statistical associations for 20 neurons arising from the explosion and theory of isothermal gas spheres are given in Fig. 4c. It has been verified that FIT for problem I and II are calculated as 10−11–10−12 and 10−12–10−13. The MSC measurements for problem I and II lies around 10−14–10−15 and close to 10−13. For both singular model cases, the TIC procedures are computed around 10−11–10−12. Large neurons responded better than small neurons according to the performance measures.

Fig. 4
figure 4

Performance measures with 4, 12 as well as 20 neurons for solving problem I–II

Full size image

The 40 runs present a larger dataset in order to improve the scheme’s correctness and dependability. For 4, 12, and 20 neurons, the statistical FIT, MSC, and TIC operators are utilized, that are depicted in Figs. 5, 6 and 7. For both TPN-SBVP problems, the FIT values of 4, 12, as well as 20 numbers of neurons are about 10−03–10−10, 10−07–10−11, and 10−08–10−11, in Fig. 5a–c respectively. Figure 6a–c depicts MSE performance for 4, 12, and 20 neurons, corresponding to 10−02–10−10, 10−04–10−10, and 10−05–10−12, respectively, for TPN-SBVP I and II. For both TPN-SBVP problems, Fig. 7a, c shows the TIC values of 4,12, and 20 numbers of neurons, that range from 10−04 to 10−09, 10−04 to 10−11, and 10−08 to 10−11. It is also demonstrated by the FIT, MSE, and TIC outcomes that greater neurons produce better results than small neurons.

Fig. 5
figure 5

Fitness convergence with 4, 12 as well as 20 neurons for solving problem I–II

Full size image
Fig. 6
figure 6

MSE convergence with 4, 12 as well as 20 neurons for solving problem I–II

Full size image
Fig. 7
figure 7

TIC convergence with 4, 12 as well as 20 neurons for solving problem I–II

Full size image

To solve TPN-SBVPs, GNNs-GASQP is used to visualize the scheme performance through statistics. Tables 1, 2, 3, 4, 5, 6, 7, 8 and 9 show the statistical significance depending upon the Median, semi-Interquartile Ranges (SIR), Minimum, Mean, and standard deviation (STD) for 40 trials. Tables 1, 3 and 5 provide the global results depend upon G. FIT, G. MSE, as well as G. TIC operator. The G. FIT, G. MSE, and G. TIC operations outcomes are estimated as excellent ways to tackle both TPN-SBVPs issues using GNNs-GASQP. Tables 2, 4 and 6 show the complexity cost of research to tackle TPN-SBVPs utilizing the performed time, function designs, as well as generations for 4,12, and 20 neurons, respectively. To solve TPN-SBVPs,’function designs,’’performed time,’ and’generations’ were found to be tiny for 4 neurons, but raised with 12 neurons, as well as then rose even more by 20 neurons. Table. 7 shows that the Median, SIR, Minimum, Mean, STD values for 4 neurons for problem 1 are around 10−04–10−05, 10−01–10−02, 10−06–10−10, 10−01–10−02 and 10−01- 10−02. Following statistical measures are obtained for the problem II as 10−03–10−04, 10−02–10−03, 10−05–10−07, 10−02 and 10−01. For 12 neurons, Median, SIR, Minimum, Mean, STD values lies in Table 8 as 10−05–10−07, 10−05 10−07, 10−07–10−10, 10−04–10−07 and 10−03–10−06. For problem II, these values are 10−05–10−08, 10−05–10−08, 10−07–10−11, 10−02–10−05 and 10−01–10−05. For 20 neurons, Median, SIR, Minimum, Mean, STD values lies in Table 9 as 10−05–10−08, 10−05–10−08, 10−08–10−12, 10−02–10−07 and 10−01–10−06. For problem II, these values are 10−05–10−08, 10−04–10−07, 10−07–10−10, 10−01–10−06 and 10−01–10−05. When compared to small neurons, these operators output of 20 neurons is more effective.

Table 1 Global measures of Problem I–II using the GNNs-GASQP for 4 neurons
Full size table
Table 2 Complexity of Problem I–II using the GNNs-GASQP for 4 neurons
Full size table
Table 3 Global measures of Problem I–II using the GNNs-GASQP for 12 neurons
Full size table
Table 4 Complexity of Problem I–II using the GNNs-GASQP for 12 neurons
Full size table
Table 5 Global measures of Problem I–II using the GNNs-GASQP for 20 neurons
Full size table
Table 6 Complexity of Problem I–II using the GNNs-GASQP for 20 neurons
Full size table
Table 7 Statistical performances of Problem I–II using the GNNs-GASQP for 4 neurons
Full size table
Table 8 Statistical performances of Problem I–II using the GNNs-GASQP for 12 neurons
Full size table
Table 9 Statistical performances of Problem I–II using the GNNs-GASQP for 20 neurons
Full size table

4 Conclusions

The current research focuses on the construction of Gudermannian neural networks for the TPN-SBVPs by applying the optimization techniques based on global/ local search strategies. The numerical performances of the GNNs-GASQP are presented for the TPN-SBVPs that signify the theory of thermal-explosion as well as an isothermal gas sphere. The designed GNNS-GASQP is found to be efficient to solve the singular models, which have stiffer nature when other conventional techniques fail. The analysis with small and large neurons varying in size from 4, 12, and 20. The neuron analysis is performed by using a comparison of outcomes, AE, performance metrics, convergence analysis, as well as various statistical operators. These measurements show that precision of small neurons is low, but as number of neurons increases, authenticity improves. Small neurons, on the other hand, have a lower complexity cost than large neurons, which have been performed in the complexity analysis. The absolute average error for 4 neurons seems about 10−04–10−06, but the values of 20 neurons are about 10−06–10−08. The perfectly matched best as well as mean solutions with the true outcomes for tackle each TPN-SBVPs demonstrates the exactness of the GNNs-GASQP. The MSE, SIR, and TIC statistical best operator outcomes show the consistency of GNNs-GASQP for solving TPN-SBVPs. The Median, SIR, Minimum, Med and STD gages based on the statistical operator performances for the GNNs-GASQP using 40 trials are observed. Furthermore, the completeness, accurateness, and strength of GNNs-GASQP are applied to tackle the TPN-SBVPs.

The GNNS-GASQP approach is used in future to provide the numerical solutions of the biological, fluid dynamics and fractional-order systems [47,48,49,50,51,52,52].