Skip to main content
SpringerLink
Log in

A new numerical approach for solving a class of singular two-point boundary value problems

  • Original Paper
  • Published:
Numerical Algorithms Aims and scope Submit manuscript

Abstract

In this paper, we consider the following class of singular two-point boundary value problem posed on the interval x 𝜖 (0, 1]

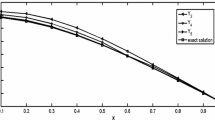
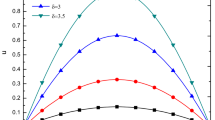
$$\begin{array}{@{}rcl@{}} (g(x)y^{\prime})^{\prime}=g(x)f(x,y),\\ y^{\prime}(0)=0,\mu y(1)+\sigma y^{\prime}(1)=B. \end{array} $$

A recursive scheme is developed, and its convergence properties are studied. Further, the error estimation of the method is discussed. The proposed scheme is based on the integral equation formalism and optimal homotopy analysis method in which a recursive scheme is established without any undetermined coefficients. The original differential equation is transformed into an equivalent integral equation to remove the singularity. The integral equation is then made free of undetermined coefficients by imposing the boundary conditions on it. Finally, the integral equation without any undetermined coefficients is efficiently treated by using optimal homotopy analysis method for finding the numerical solution. The optimal control-convergence parameter involved in the components of the series solution is obtained by minimizing the squared residual error equation. The present method is applied to obtain numerical solution of singular boundary value problems arising in various physical models, and numerical results show the advantages of our method over the existing methods.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Keller, J.B., Electrohydrodynamics, I.: The equilibrium of a charged gas in a container. J. Rational Mech. Anal. 5, 715–724 (1956)

    MathSciNet  Google Scholar 

  2. Chambre, P.L.: On the solution of the Poisson-Boltzmann equation with the application to the theory of thermal explosions. J. Chem. Phys. 20, 1795–1797 (1952)

    Article  Google Scholar 

  3. Parter, S.V.: Numerical methods for generalised axially symmetric potentials. SIAM J., Ser. B 2, 500–516 (1965)

    MATH  Google Scholar 

  4. Ames, W.F.: Nonlinear ordinary differential equations in transport process. Academia Press, New York (1968)

    MATH  Google Scholar 

  5. Thomas, L.: The calculation of atomic fields. In: Mathematical Proceedings of the Cambridge Philosophical Society, Cambridge University Press, vol. 23, pp 542–548 (1927)

  6. Fermi, E.: Un metodo statistio per la determinazione di alcune priorieta dell’atome. Rendicondi Accademia Nazionale de Lincei 32, 602–607 (1927)

    Google Scholar 

  7. McElwain, D.L.S.: A re-examination of oxygen diffusion in a spherical cell with Michaelis–Menten oxygen uptake kinetics. J. Theoret. Biol. 71, 255–263 (1978)

    Article  Google Scholar 

  8. Lin, H.S.: Oxygen diffusion in a spherical cell with nonlinear oxygen uptake kinetics. J. Theoretical. Biol. 60, 449–457 (1976)

    Article  Google Scholar 

  9. Flesch, U.: The distribution of heat sources in the human head: a theoretical consideration. J. Theoret. Biol. 54, 285–287 (1975)

    Article  Google Scholar 

  10. Gray, B.F.: The distribution of heat sources in the human head: a theoretical consideration. J. Theoret. Biol. 82, 473–476 (1980)

    Article  Google Scholar 

  11. Adam, J.A.: A simplified mathematical model of tumor growth. Math. Biosci. 81, 224–229 (1986)

    Article  MATH  Google Scholar 

  12. Adam, J.A.: A mathematical model of tumor growth II: effect of geometry and spatial nonuniformity on stability. Math. Biosci. 86, 183–211 (1987)

    Article  MATH  Google Scholar 

  13. Adam, J.A., Maggelakis, S.A.: Mathematical model of tumor growth IV: effect of necrotic core. Math. Biosci. 97, 121–136 (1989)

    Article  MATH  Google Scholar 

  14. Burton, A.C.: Rate of growth of solid tumor as a problem of diffusion. Growth 30, 157–176 (1966)

    Google Scholar 

  15. Greenspan, H.P.: Models for the growth of solid tumor as a problem by diffusion. Stud. Appl. Math. 52, 317–340 (1972)

    Article  MATH  Google Scholar 

  16. Nayfeh, A.H.: Perturbation methods. Wiley, New York (2000)

    Book  MATH  Google Scholar 

  17. He, J.H.: Variational iteration method: a kind of nonlinear analytic technique: some examples. Int. J. Nonlinear Mech. 34, 699–708 (1999)

    Article  MATH  Google Scholar 

  18. He, J.H.: Approximate analytical solution for seepage flow with fractional derivative with porous media. Comput. Meth. Appl Mech. 167, 57–68 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  19. Adomian, G.: Solving frontier problems of physics: the decomposition method. Kluwer Academic, Dordrecht (1994)

    Book  MATH  Google Scholar 

  20. Liao, S.J.: The proposed homotopy analysis technique for the solution of nonlinear problems, Ph.D. Thesis. Sanghai Jiao Tong University, Shangai (1992)

    Google Scholar 

  21. Liao, S.J.: A kind of approximate solution technique which does not depend upon small parameters: a special example. Int. J. Nonlinear Mech. 30, 371–380 (1995)

    Article  Google Scholar 

  22. Liao, S.J., Perturbation, Beyond: Introduction to the homotopy analysis method, Chapman and Hall. CRC Press, Boca Raton (2003)

    Google Scholar 

  23. Liao, S.J.: On the homotopy analysis method for nonlinear problems. Appl. Math. Comput. 147, 499–513 (2004)

    MathSciNet  MATH  Google Scholar 

  24. Liao, S.J., Tan, Y.: A general approach to obtain series solutions of nonlinear differential equations. Stud. Appl. Math. 119, 297–354 (2007)

    Article  MathSciNet  Google Scholar 

  25. Liao, S.J.: Notes on the homotopy analysis method: some definitions and theorems. Commun. Nonlinear Sci. Numer. Simulat. 14(4), 983–997 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  26. Liao, S.: An optimal homotopy anlysis approach for strongly nonlinear differential equations. Commun. Nonlinear Sci. Numer. Simulat. 15, 2003–2016 (2010)

    Article  MATH  Google Scholar 

  27. Marinca, V., Herisanu, N.: Application of optimal homotopy asymptotic method for solving nonlinear equations arising in heat transfer. Int. Commun. Heat Mass Transfer 35, 1216–1224 (2008)

    Article  Google Scholar 

  28. Pandey, R.K., Verma, A.K.: Existance-Uniqueness results for a class of singular boundary value problems arising in physiology. Nonlinear Anal. Real World Appl. 9, 40–52 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  29. Caglar, H., Caglar, N., Ozer, M.: B-Spline solution of non-linear singular boundary value problems arising in physiology. Chaos, Solitions and Fractals 39, 1232–1237 (2009)

    Article  MATH  Google Scholar 

  30. Iyengar, S.R.K., Jain, P.: Spline Finite Differnce Methods for singular two point Boundary Value problem. Numer. Math. 50, 363–376 (1987)

    Article  MathSciNet  MATH  Google Scholar 

  31. Ravi kant, A.S.V.: Cubic spline polynomial for non-linear singular two-point boundary value problem. Appl. Math. Comput. 189, 2017–2022 (2007)

    MathSciNet  MATH  Google Scholar 

  32. Khuri, S.A., Sayfy, A.: A novel approach for the solution of a class of singular boundary value problems arising in physiology. Math. Comput. Model. 52, 626–636 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  33. Pandey, R.K., Singh, A.K.: On the convergence of a finite difference method for a class of singular boundary value problems arising in physiology. J. Comp. Appl. Math 166, 553–564 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  34. Ravi Kanth, A., Aruna, K.: He’s varitional iteration method for treating nonlinear singular boundary value problem. Comput. Math. Appl. 60(3), 821–829 (2010)

    Article  MATH  Google Scholar 

  35. Roul, P., Warbhe, U.: New approach for solving a class of singular boundary value problem arising in various physical models. J. Math. Chem. 54, 1255–1285 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  36. Adomian, G.: Solution of the Thomas-Fermi Equation. Appl. Math. Lett. 11, 131 (1998)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgments

The authors thankfully acknowledge the financial support provided by the SERB, Department of science and Technology, New Delhi, India, in the form of project no. SB/S4/MS/877/2014. The authors are highly grateful to the referees for their constructive comments.

Author information

Authors and Affiliations

  1. VNIT, Nagpur, Maharashtra, India

    Pradip Roul & Dipak Biswal

Authors
  1. Pradip Roul
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Dipak Biswal
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Pradip Roul.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Roul, P., Biswal, D. A new numerical approach for solving a class of singular two-point boundary value problems. Numer Algor 75, 531–552 (2017). https://doi.org/10.1007/s11075-016-0210-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11075-016-0210-z

Keywords

Search

Navigation