Abstract
Dynamic light scattering (DLS) measures time-dependent fluctuations in the scattering intensity arising from particles undergoing random Brownian motion. Diffusion coefficient and particle size information can be obtained from the analysis of these fluctuations. This paper discusses the factors which will influence the lower size limit of DLS and reports the use of sucrose as a test sample to probe this lower limit of the technique. Hydrodynamic diameter values of less than 1 nm are obtained by the use of 173° backscatter detection that is applied to increase the sensitivity of DLS. The peak means (with standard deviations) obtained for the intensity and volume data from a series of sucrose concentrations, ranging from 5 to 35% w/v, were measured as DI,Mean = 0.82 nm (0.11 nm) and DV,Mean = 0.62 nm (0.05 nm), respectively. These sucrose results suggest that sub nanometer measurements are achievable with a precision of 0.1 nm. Evidence to support these size results for sucrose is discussed.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Measuring the size of small molecules is currently of great interest in many applications. For example, proteins are being utilized directly in the pharmaceutical industry as active agents in drugs (Akagi et al. 2007; Nam et al. 2002). The size of the molecules can be used as a quality control measure. Similarly during the production of nanoparticles, the size of the particles can be used as a measure in a quality control process (Hu et al. 2004; Zheng et al. 2002; Pascal et al. 1999). However, there are very few techniques available for the measurement of small molecules and particles in solution.
Dynamic light scattering (DLS) is a technique for characterizing the size of colloidal dispersions which utilizes the illumination of a suspension of particles or molecules undergoing Brownian motion by a laser beam (Dahneke 1983; Pecora 1985; ISO13321 1996; Peters 2000). The time-dependent fluctuations in the intensity of scattered light that occur are analyzed using an autocorrelator which determines the autocorrelation function of the signal. The correlation of the signal, G, decays at an exponential rate which is dependent upon the diffusion of the particles being measured (Dahneke 1983; Pecora 1985; ISO13321 1996).
where B = is the baseline, A is the amplitude, and D is the translational diffusion coefficient. The scattering vector (q) is defined by the equation below, where ñ is the solvent refractive index, λo is the vacuum wavelength of the laser, and θ is the scattering angle.
The speed of this Brownian motion is measured and provides the translational diffusion coefficient D. This diffusion coefficient can be converted into a hydrodynamic diameter (DH) using the Stokes-Einstein equation.
where k is the Boltzmann constant, T is the temperature and η is the dispersant viscosity.
The lower size limit of the dynamic light scattering technique depends on the amount of excess scattered light produced. This excess is the difference in scattering between the molecule or particle being studied and the dispersant it is prepared in. This in turn depends on a number of factors such as the refractive indices of the molecule and dispersant, the concentration of the sample, the power and wavelength of the laser used, the sensitivity of the detector and the optical configuration of the instrument. Inevitably, as the size of the molecule or particle becomes smaller, the amount of excess scattering produced reduces.
Conventional dynamic light scattering instruments use a detection angle of 90° and this optical configuration may not be sensitive enough for the successful measurement of small particles or molecules even with the incorporation of a powerful laser at low wavelength. An optical configuration that allows measurements of samples at lower concentrations of smaller sizes is backscatter detection. At 173° backscatter, the scattering volume observed at the detector is about 8 times the volume observed with classical 90° scattering optics. This results in an 8-fold increase in the detected count rate, which is directly correlated with instrument sensitivity, or the ability to measure small particles at lower concentrations. The use of fiber optics in combination with this optical arrangement ensures that the signal to background ratio, or more correctly, the intercept of the correlation function, is not degraded at high detection volumes as it would with ‘classical’ geometric optics (Peters 2000). Increasing the count rate while simultaneously reducing the intercept of the correlation function is of little value. This optical configuration provides the exceptional sensitivity that is required for measuring the size of nanoparticles and molecules at low concentrations.
Probing the ultimate capabilities of a DLS system in terms of both the size and concentration that can be measured poses some issues with regard to experimental technique and the samples that may be used as test materials. At sizes above 20 nm, monodisperse, traceable latex standards are available. For sizes below 10 nm, certain proteins such as lysozyme and bovine serum albumin are often used, although preparation of a sample of the monomer is not straightforward. For a sample close to or below 1 nm in size, something other than a protein must be considered. Suitable nanoparticle samples are difficult to obtain in a well dispersed state containing no aggregates. An ideal candidate as a test material to test the performance of a light scattering system is sucrose. It is easily obtained, available in a crystalline, pure form and readily dissolves in water. A sucrose molecule consists of a glucose and fructose molecule joined through an α-glycosidic linkage (Stryer 2002) (Fig. 1).
This paper explores the lower limits of size which are measurable by dynamic light scattering using sucrose as a test sample. The measurement of sucrose at a 173° detection angle is discussed and the advantages of using backscatter detection for characterizing sub nanometer sized samples is highlighted. Comparisons are made with size estimates using other techniques.
Experimental
Sucrose solutions of 5, 10, 15, 20, 25, 30 and 35% w/v, respectively were prepared in ultra pure water and filtered through Whatman Anotop 0.02 μm pore size filters (cat. no. 6809–3002). All chemicals used in this study were Analar grade or better.
Measurements of all sucrose concentrations were made on a Malvern Zetasizer Nano S (Malvern Instruments Ltd., UK) with a detection angle of 173°. All measurements in this study were taken at a temperature of 25 °C. At least 3 repeat measurements on each sample were taken to check for result repeatability. The Nano S uses a 4 mW He–Ne laser operating at a wavelength of 633 nm. The intensity size distributions were obtained from analysis of the correlation functions using the Multiple Narrow Modes algorithm in the instrument software. This algorithm is based upon a non-negative least squares fit (Twomey 1997; Lawson and Hanson 1995). These intensity particle size distributions were converted into volume using Mie theory (Mie 1908). The optical properties of the sucrose molecules were not considered important because their size is significantly lower than the incident laser wavelength used.
The technique of DLS measures the diffusion coefficients of molecules or particles undergoing Brownian motion. To convert the measured diffusion coefficient data into a hydrodynamic size, the viscosity of the sample must be entered into Stokes-Einstein’s equation as highlighted in the Introduction section of this paper. There are a number of ways in determining what the correct viscosity value for the samples that should be used. For example, the relative viscosity of known sucrose solutions with respect to water can be found in the literature (CRC Handbook 2006–2007) or the viscosities of the sucrose solutions can be determined with an appropriate viscometer. However, because the technique of dynamic light scattering measures the diffusion speed of molecules or particles undergoing Brownian motion, a useful method of determining the appropriate viscosity value is to dope each sucrose sample with a known size of polystyrene latex standard. In this study, 10 μl of a 150 nm polystyrene latex (cat. no. 3150 A) obtained from Duke Scientific (Palo Alto, US) was added to 990 μl of the appropriate sample. Comparison of the size obtained for the latex dispersed in sucrose (assuming the viscosity of water) with the size obtained for the same latex dispersed in 10 mM NaCl (the true hydrodynamic diameter), allows for the determination of the viscosities of the sucrose solutions. Measurements were made in 10 mM NaCl in order to suppress the electrical double layer according to the International Standard ISO13321 (1996). This method of adding latex to the sucrose solutions works well, as the scattering from the larger latex particles is much greater than that from the sucrose molecules.
Results and discussion
The viscosities of the sucrose solutions were determined by the method discussed above and the results obtained for the 150 nm polystyrene latex sample doped into 10 mM NaCl and the various sucrose concentrations are summarized in Table 1.
The table contains the intensity-averaged diameter in nanometers, the polydispersity index values and the calculated viscosities. The intensity-averaged particle diameter and the polydispersity index (PDI) values (an estimate of the distribution width) were calculated from the cumulants analysis as defined in ISO13321 (1996). The polydispersity index values are very sensitive to the presence of aggregates or dust. A monodisperse sample such as the polystyrene latex used in this study would be expected to give a PDI value of less than 0.05. All the PDI values reported in Table 1 are less than 0.05 indicating that the latex was not affected at any of the sucrose concentrations. The calculated viscosities for the various sucrose concentrations were determined by dividing the viscosity of 10 mM NaCl (0.8872 mPa s) by the ratio of the intensity-averaged diameter for the latex in 10 mM NaCl to the apparent intensity-averaged diameter for the latex in the appropriate sucrose concentration. The viscosity required for DLS measurements is the viscosity that the particle being studied experiences as it undergoes Brownian motion. This is the most appropriate way of obtaining this information and is a valid technique as long as the latex being used is not being affected by the dispersant it is doped into and as long as the introduction of latex does not significantly alter the sample viscosity. In this study, such a small aliquot addition to each sucrose concentration would not be expected to affect the viscosity of the solutions.
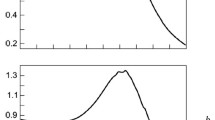
Figure 2 shows some typical correlation functions obtained from measurements performed on some of the sucrose solutions on a Zetasizer Nano S using backscatter detection. The figure shows the data obtained for three lowest sucrose concentrations (5, 10 and 15% w/v, respectively) as these would be expected to give the lowest excess scattering. The intercept of the correlation function (i.e. the intercept of the Y axis obtained by extrapolating the correlation coefficients to zero time) is the signal to noise ratio obtained for the measurement. Values of less than 0.1 indicate poor data quality. However, even the 5% sucrose concentration gave an intercept of around 0.5 and so the intercepts obtained for all samples in this study gave excellent values.
The correlation functions shown in Fig. 2 exhibit two visible decay rates. The rapid decay rates seen in delay times up to 10 μs are interpreted as arising from the diffusion of sucrose molecules. The slower decay rates seen near to the baseline of the correlation functions (at correlator delay times of between 10 and 1,000 μs, respectively) are probably due to collective diffusion of the sucrose molecules. This hypothesis is supported by the increase in amplitude of this slow decay rate with increasing sucrose concentration.
The intensity particle size distributions obtained from the analysis of these correlation functions are shown in Fig. 3. Each concentration gives a bimodal distribution with the main peak mode consistently around 1 nm diameter and a second peak mode around 200 nm. Conversions of the measured intensity size distributions into volume distributions were done using Mie theory (Mie 1908) and the volume size distributions obtained are shown in Fig. 4. These all consist of monomodal distributions with peak modes consistently less than 1 nm. Full peak analysis of both the intensity and volume size distributions are summarized in Table 2. This table shows the peak means and modes for the peak attributed to the sucrose molecule based on the intensity and volume size data.
The extrapolation of these intensity and volume peak mean and mode values to zero concentration enable infinite dilution values to be calculated (Fig. 5). This approach is recommended in the International Standard ISO13321 (1996) for samples which show a systematic concentration dependence in the particle size results obtained. This concentration dependence may be due to concentration-dependent conformational changes in the sucrose molecule. Water content has been reported to have an effect on the mobility and reorganization of sucrose molecules with the flexibility around the glycosidic bond increasing with sucrose concentration (Mathlouthi and Reiser 1995). This conformational change in the sucrose molecule would be expected to result in an increase in diffusion coefficient as the sample concentration increases. Another possible explanation for this concentration dependence in size is the interaction between the sucrose molecules which cannot be compensated by using the measured sample viscosity. Any interaction between molecules would be expected to increase with increasing sucrose concentration. In addition, a decrease in effective hydration at higher concentration would support the decreased hydrodynamic size (Schultz and Solomon 1961). The sizes obtained for the intensity and volume mean and mode data extrapolated to zero concentrations are 1.03, 0.97, 0.71 and 0.59 nm, respectively.
The results presented in this paper provide evidence that sub nanometer sizes can be measured using dynamic light scattering if an appropriate instrument optical configuration is used. However, are the sizes obtained from the measurements reported for the sucrose molecule realistic? Figure 6 shows space filling models of a sucrose molecule in its most extended conformation together with accurate dimensions along the 3 main axes of 1.06, 0.72 and 0.60 nm, respectively. The size obtained from a dynamic light scattering measurement is the hydrodynamic diameter of a sphere which has the same average diffusion coefficient as the molecule being measured. Therefore, the diameters obtained for the various sucrose concentrations reported in this paper fall within expected values. In addition, the translational diffusion coefficients of sucrose have been previously reported to be in the range of 5.0 to 5.5 × 10−6 cm2 s−1 at 298 K (CRC Handbook 2006–2007; Engelsen and Pérez 1997). If these values are converted into spherical hydrodynamic diameters using the Stokes-Einstein relationship, sizes in the range of 0.9–0.98 nm are obtained. These size values are very comparable to those obtained from the measurements reported in this study.
The results presented in this paper indicate that the measurement of sub nanometer sizes are now possible using dynamic light scattering if samples are carefully prepared and an appropriate optical configuration is used. The use of backscatter detection in combination with fiber optics provides exceptional sensitivity with retention in the signal to noise sufficient to be able to measure samples at these small sizes.
References
Akagi T, Wang X, Uto T, Baba M, Akashi M (2007) Protein direct delivery to dendritic cells using nanoparticles based on amphiphilic poly(amino acid) derivatives. Biomaterials 28:3427–3436
CRC Handbook of chemistry and physics: 87th edn. (2006–2007) CRC Press
Dahneke BE (1983) Measurement of suspended particles by quasi-elastic light scattering. Wiley, New York
Engelsen SB, Pérez S (1997) Internal motions and hydration of sucrose in a diluted water solution. J Mol Graph Model 15:122–131
Hu M, Chujo S, Nishikawa H, Yamaguchi Y, Okubo T (2004) Spontaneous formation of large-area monolayers of well-ordered nanoparticles via a wet-coating process. J Nanopart Res 6:479–487
International Standard ISO13321 (1996) Methods for determination of particle size distribution part 8: photon correlation spectroscopy. International Organization for Standardization (ISO)
Lawson CL, Hanson RJ (1995) Solving least squares problems. Society for industrial and applied mathematics (SIAM), Philadelphia
Mathlouthi M, Reiser P (eds) (1995) Sucrose: properties and applications. Blackie Academic and Professional, London
Mie G (1908) Beiträge zur optik trüber medien, speziell kolloidaler metallösungen. Ann Physik 4:377–445
Nam YS, Park JY, Han SH, Chang IS (2002) Intracellular drug delivery using poly(D,L-lactide-co-glycolide) nanoparticles derivatized with a peptide from a transcriptional activator protein of HIV-1. Biotechnol Lett 24:2093–2098
Pascal C, Pascal JL, Favier F, Moubtassim MLE, Payen C (1999) Electrochemical synthesis for the control of Fe2O3 nanoparticle size. Morphology, microstructure and magnetic behaviour. Chem Mater 11:141–147
Pecora R (1985) Dynamic light scattering: applications of photon correlation spectroscopy. Plenum Press, New York
Peters R (2000) Fibre optic device for detecting the scattered light of fluorescent light from a suspension. US Patent 6,016,195
Schultz SG, Solomon AK (1961) Determination of the effective hydrodynamic radii of small molecules by viscometry. J Gen Physiol 44:1189–1199
Stryer L (2002) Biochemistry. W.H. Freeman, New York
Twomey S (1997) Introduction to the mathematics of inversion of remote sensing and indirect measurements. Dover Publications, New York
Zhang F, Chan SW, Spanier JE, Apak E, Jin Q, Robinson RD, Herman IP (2002) Cerium oxide nanoparticles: size-selective formation and structure analysis. Appl Phys Lett 80:127–129
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License ( https://creativecommons.org/licenses/by-nc/2.0 ), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Kaszuba, M., McKnight, D., Connah, M.T. et al. Measuring sub nanometre sizes using dynamic light scattering. J Nanopart Res 10, 823–829 (2008). https://doi.org/10.1007/s11051-007-9317-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11051-007-9317-4