Abstract
Many real-world multi-objective optimization problems inherently have multiple multi-modal solutions and it is in fact very important to capture as many of these solutions as possible. Several crowding distance methods have been developed in the past few years to approximate the optimal solution in the search space. In this paper, we discuss some of the shortcomings of the crowding distance-based methods such as inaccurate estimates of the density of neighboring solutions in the search space. We propose a new classification for the selection operations of Pareto-based multi-modal multi-objective optimization algorithms. This classification is based on utilizing nearby solutions from other fronts to calculate the crowding values. Moreover, to address some of the drawbacks of existing crowding methods, we propose two algorithms whose selection mechanisms are based on each of the introduced types of selection operations. These algorithms are called NxEMMO and ES-EMMO. Our proposed algorithms are evaluated on 14 test problems of various complexity levels. According to our results, in most cases, the NxEMMO algorithm with the proposed selection mechanism produces more diverse solutions in the search space in comparison to other competitive algorithms.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
In many real-world applications, there are several conflicting objective functions to be optimized simultaneously. These types of optimization problem are called Multi-Objective Optimization Problems (MOP), described as follows:
where S represents a n-dimensional decision (search) space over real-valued variables. To compare two solution vectors \(\vec{z} \in S\) and \(\vec{y} \in S\), the dominance relation is used. \(\vec{z}\) is said to be dominated by \(\vec{y}\) (denoted by \(\vec{y} \prec \vec{z}\)) if and only if \(\forall j \in \{1,\cdots ,m\}\), \(f_{j}(\vec{y}) \le f_{j}(\vec{z})\), and \(\exists k \in \{1,\cdots ,m\}\), \(f_{k}(\vec{y}) < f_{k}(\vec{z})\). A solution is said to be non-dominated, if it is not dominated by any other solution. The Pareto set (PS) represents these optimal solutions in the search space, and the Pareto front (PF) represents their locations in the objective space.
There have been numerous Multi-Objective Evolutionary Algorithms (MOEAs), which are developed to deal with various kinds of MOPs. Three types of MOEAs can be distinguished as: decomposition-based algorithms [e.g. MOEA/D (Zhang and Li 2007)], Pareto-based algorithms [e.g. NSGA-II (Deb et al 2002)], and indicator-based algorithms [e.g. HypE (Bader and Zitzler 2011), and SMS-EMOA (Beume et al 2007)]. These algorithms are aimed to provide good coverage of the PF by expanding the search process towards previously unexplored regions of the objective space. Multi-objective evolutionary algorithms often converge prematurely, before the search space has been explored thoroughly (Osuna and Sudholt 2019). This is a result of diminishing diversity among the population in the search space.
When solving real-world problems, there is often more than one optimal solution set with the same or a bit inferior quality [e.g. route planing problems (Weise and Mostaghim 2021)]. Problems such as these are called Multi-modal Multi-objective Optimization Problems (MMOPs) (Liang et al 2016). These problems can be divided into two categories: either there are more than two Pareto-optimal solution sets (Type-1 MMOPs), or there is one Pareto-optimal solution set and several slightly less optimal solution set of acceptable quality (Type-2 MMOPs) (Tanabe and Ishibuchi 2019).
Identifying and maintaining these different optimal solutions is a challenging task, which is why it is necessary to boost the populations’ diversity in the search space, so the population could cover as many Pareto-optimal sets of solutions as possible. Over the last decade, a number of classic niche techniques were introduced to manipulate the solutions’ distribution in the search space for Multi-modal evolutionary optimization, including crowding (Thomsen 2004), clearing (Pétrowski 1996), speciation (Li et al 2002), and fitness sharing (Goldberg et al 1987). However, all of these methods deal with single-objective optimization algorithms. Since the environmental selection in MOEAs usually aims to handle the distribution of solutions in the objective space and approximate the PF more accurately, these algorithms are unsuitable for dealing with MMOPs. As a result, several algorithms have been developed to keep the decision space diverse when dealing with multi-modality in multi-objective optimization algorithms. They are known as Multi-modal Multi-Objective Evolutionary Algorithms (MMOEAs).
The two major types of algorithms are decomposition-based and Pareto dominance-based MMOEAs. The decomposition-based MMOEAs in (Hu and Ishibuchi 2018a) are an enhanced version of MOEA/D algorithm (Zhang and Li 2007). In (Hu and Ishibuchi 2018b) and (Tanabe and Ishibuchi 2018), two extended versions of MOEA/D are provided to solve MMOPs. Using weight vectors, the MOEA/D algorithm separates an optimization problem with M objectives into N single-objective problems, with each sub-problem assigned a single individual. N individuals are then simultaneously evolved using MOEA/D. In contrast to MOEA/D, its two variations in managing MMOPs assigns one or more individuals to handle equivalencies within each sub-problem (Tanabe and Ishibuchi 2019).
The MMOEAs from the second category are mainly extended versions of NSGA-II algorithms: the solutions are sorted according to the non-dominance sorting relationship into fronts which takes place in the environmental selection, then a secondary selection incorporates different niche techniques to maintain the distribution of the solutions in the search space. Examples of this method can be observed in (Kramer and Danielsiek 2010; Kramer and Koch 2009), where the diversity of solutions is preserved using clustering techniques to keep multiple optimal solutions by providing multiple stable subpopulations within a population. In more recent approaches, external archives are used to keep diverse non-dominated solutions in decision space (Sebag et al 2005; Hiroyasu et al 2005; Kim et al 2004). Some proposed MMOEAs implemented the crowding diversity measure in decision space to deal with MMOPs (Yue et al 2018; Deb and Tiwari 2005; Liang et al 2016; Javadi et al 2019; Javadi and Mostaghim 2021).
Moreover, it is noteworthy that there has been some discussion about implementing diversity or convergence indicators in set-oriented optimization, a technique that has shown considerable promise. These indicators have the potential to be incorporated into MMOEAs to preserve distributions of solutions in the search space and provide other interesting options (Grimme et al 2021). An example of this is the gap indicator (or the average of the distance to nearest neighbor) (Wang et al 2019), simple to implement and fast to compute, resulting in the maximization of diversity of obtained optimal solutions. Another example is the Rietze s-energy indicator (Falcón-Cardona et al 2019), which has the advantage of producing a uniform distribution of the points across a number of manifolds and its computation is scalable in regards to the number of decision variables (Grimme et al 2021).
As most MMOEAs measure search quality according to Pareto dominance, our paper primarily focuses on this type of MMOEAs. This paper analyzes the drawbacks of using the crowding distance method, including the illusion of the solution being in a sparser area when it is not, and calculating crowding value for solutions on the same front without accounting for neighbors on adjacent fronts. Moreover, considering the effects of solutions located on the same or other fronts within the selection process, we classify the environmental selection operations of Pareto dominance-based algorithms into two categories: (i) intra-front selection operations and (ii) inter-front selection operations. (i) The first type of density measurement entails finding each solution’s crowding distance based on the neighboring solutions that are located on the same front. The crowding value calculation can give the impression that the solution is far from other solutions in the decision space, although it could be located near many other solutions from previous fronts. As a result, the solution is more likely to survive and pass on to future generations.
(ii) To define the second type of diversity measurement, we count both the solutions in the same front of the search space and the solutions in the neighborhood of the prior fronts in the search space into the calculation of the diversity of the solutions. The crowding values of the solutions are more accurately calculated using this method of diversity measurement.
This paper additionally extends a previous paper in which we presented an algorithm called NxEMMO using a new selection operator (Javadi and Mostaghim 2021), which fits within the inter-front operation categories of our proposed selection operation types. Moreover, we propose another operator called ES-EMMO, which belongs to the category of intra-front operations.
The remainder of this paper is organized as follows: Sect. 2 presents our proposed intra-front operations and discusses other algorithms based intra-front selection operations and their performances. The following section is devoted to describing in detail the introduced inter-front selection operation. Analysis of the experiments and discussion of the results are presented in Sect. 3. An overview of our findings is provided in the last section of the paper, followed by a discussion of future research possibilities.
2 Pareto dominance-based algorithms
Most Pareto-dominance-based MMOEAs are based upon the NSGA-II algorithm (Deb et al. 2002), which is considered the most commonly used Pareto-dominance-based MOEA (Yusoff et al 2011). In the current population, Pareto dominance is used to evaluate fitness as the primary criterion. A non-dominated solution has a high fitness value than the dominated ones. Therefore, it is more likely to survive and be passed on to future generations. Following that, diversification is considered as a secondary criterion for selection.
2.1 Intra-front selection operations
The Pareto-dominance-based MMOEA calculates the crowding distance value of the solutions in the search space in order to maintain a good distribution of solutions. This value is calculated using a similar general structure as in NSGA-II in the objective space: For each solution in the \(\text {Front}_{i}\), the mean distance between two adjacent solutions on the left and right sides of the solution is calculated. Calculating the crowding distance for each solution is done by summation of these distances.
We call this type of method of calculating crowding value the intra-front selection operation, since it ignores the impact of solutions in the neighborhood of the solution from other fronts. Most existing MMOEAs use the crowding distance approach in the decision space to promote the population’s diversity, such as (Javadi et al. 2021; Liang et al. 2016; Deb and Tiwari. 2008).
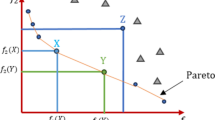
We present, in Fig. 1, an example of a visualized calculation of the crowding distance for the intra-front selection operations in order to better demonstrate the concept of an intra-front selection operation.
According to Fig. 1 , the crowding value of the solution A is calculated by taking into account the effects of the closest solutions on both sides of the solution in the same front, rather than other neighbouring solutions from other fronts, both in the search space and objective space. The volume of the orange highlighted regions indicates the crowding value of solution A in the search space as well as the objective space. This simple example clearly illustrates the concept of intra-front selection operation.
An example of an MMOEA utilizing the intra-front operation is the Omni-optimizer algorithm (Deb and Tiwari 2008). The difference between this algorithm and NSGA-II is that it takes both objective and decision space into consideration when calculating the crowding distance value.
For the \(\text {i}_{th}\) solution in each front, the crowding distance is computed the same manner as in the original NSGA-II. In the search space, the crowding value is calculated similarly to the objective space, with the exception that no infinity large value is given to the boundary individuals. This distance is calculated by summing the two-times products of the mean distance of a boundary solution from its adjacent solutions in each dimension.
After the crowding values of the solutions in decision space have been normalized by dividing the values by the number of decision variables, and the crowding values of the solutions in objective space have been divided by the number of objective functions, the average crowding value is obtained for all the solutions in both decision and objective spaces. In the situation where at least one of the crowding values for a solution in either search or objective space is greater than the average, the maximum value of the crowding distance for the solution in the decision or objective space is considered as the final crowding distance. Otherwise, the final crowding distance of the solutions is calculated by taking the minimum crowding distance value.
The Double Niched Evolutionary Algorithm (DNEA) (Liu et al 2018), along with Omni-optimizer, used two sharing functions in the search and objective spaces to calculate the crowding values of solutions. As follows, the crowding value \(f_{DS}(x_u)\) of each solution \(x_u\) in the \(\text {Front}_{i}\) is calculated using the double niche sharing function:
In this formulation, \(\hbox {Share}_{\mathrm {obj}} (u,v)\) and \(\hbox {Share}_{\mathrm {dec}} (u,v)\) are computed as follows:
Where \(\hbox {Euc}_{\mathrm {dec}}(u,v)\) and \(\hbox {Euc}_{\mathrm {obj}}(u,v)\) are euclidean distances between solutions \(x_{u}\) and \(x_v\) in the search and the objective spaces. \(\sigma _{obj}\) and \(\sigma _{dec}\) are the niche radius, in the search and objective spaces, respectively.
As another approach, DN-NSGA-II (Liang et al. 2016) is proposed to calculate crowding distances within the search space, instead of the objective space.
The Mo-Ring-PSO-SCD algorithm (Yue et al. 2018) calculates the crowding distance in the same fashion as Omni-optimizer, but uses a different method for computing the crowding value of boundary solutions in the objective space. With the minimization problem, when the \(i_{th}\) solution meets the minimum value for the \(m_{th}\) objective, the crowding value is 1, and when it meets the maximum value for the \(m_{th}\) objective, it is 0.
In another study, the so called Self-organizing MOPSO (SMPSO-MM) is introduced to conserve diverse solutions in decision space with the same objective function values by utilizing spatial crowding distances and self-organizing map networks (Liang et al. 2018).
In the \(\text {NSGA-II-CD}_{\text {ws}}\) algorithm which is proposed by (Javadi et al. 2021), the crowding distance value for each solution is calculated similar to the Omni-optimizer algorithm, but the final crowding value for \(x_u\) is determined using a weighted sum approach:
where \(\hbox {CD}_{\mathrm {obj}}(x_u)\) and \(\hbox {CD}_{\mathrm {dec}}(x_u)\) represent the crowding value of the solution \(x_u\) both in the decision and objective spaces. The weights associated with the crowding values in the search and objective spaces are \(w_1\) and \(w_1\).
To maintain the diversity in the decision space, (Javadi et al. 2020) presented a grid-based approach using the Manhattan distance in the search space. The obtained value is multiplied by its crowding distance value in the decision space for a more accurate calculation of densities. The following equation shows the assigned final crowding value for the solution \(x_u\):
where \(\hbox {NB}(x_u)\) is the list of solutions placed in the neighborhood of \(x_u\) in the decision space. n represents the number of decision variables. The grid-distance between \(x_u\) and \(x_v\) is called the \(\hbox {GD}(x_u,x_v)\).
Given all the above studies based on crowding distances, we have identified several limitations, as described below.
The first limitation is that there are more neighboring solutions in the decision space than in the objective space, making calculating the crowding distance in the decision space more challenging. Let’s consider there are two objectives and two decision variables in a problem. The crowding distance along a non-dominated front in the objective space can be calculated by using two neighboring solutions. In the search space, however, there can be up to four (i.e., \(2^n\)) neighboring solutions for the same non-dominated solution. An example of measuring the crowding distance in the search space is illustrated in Fig. 2. The crowding distance calculated for C is calculated using four solutions, F, B, D, and A, and the crowding distance for E is calculated using three solutions, F, D, and G. As we can see, C has a higher crowding distance value than E, even if the solution C is near to the solution B. The reason is that the crowding distance for C is heavily influenced by the solution A.
Another shortcoming of the crowding distance calculation in the decision space is that the overlap of distinct PSs in the search space creates the illusion that the solution is located in a dense area, so it is excluded from selection using crowding distance, even though it is essential to preserve solutions that enable us to explore uncovered areas in the decision space. Figure 3 shows the aforementioned drawback, when using the MMF4 test problem. Despite being located in a sparse space and the only solution covering \(\text {PS}_{\text {2}}\)’s left side, the solution A is still considered near the other solutions when crowding distances are calculated. This issue arises from the fact that the PSs are overlapped in both dimensions of the search space, making it appear crowded. As a consequence, if we use crowding distance as the secondary selection criterion, we eliminate these solutions from the search process and lose the opportunity to search for solutions that are optimal in the local area.
An alternative solution to the mentioned problems involves developing a selection methodology that uses euclidean distances among neighboring solutions on the same front to determine the best solution. The presented selection strategy is called Euclidean-based Selection Evolutionary Multi-modal Multi-objective (ES-EMMO) algorithm.
2.1.1 ES-EMMO algorithm
In this section, we propose the ES-EMMO algorithm which has a modified environmental selection from the original NSGA-II. The goal is to preserve solutions that cover different and several PSs. This is because in MMOEAs we aim to avoid removing solutions that are near each other in objective space but far away in search space, which can represent different PSs. Considering this concept and aiming to give higher chances to solutions located near one another in the objective space, but enough apart in the search space, we measure \(\text {Euc}_\text {{xy}}\) for each solution, which is used for the environmental selection procedure.
Figure 4, illustrates an example of the \(\text {Euc}_\text {{xy}}\) measurement for the solution A to make it easier to comprehend the concept. In the right figure, \(d_{AB}\) and \(d_{AD}\) represent the euclidean distances between solution A and its neighbor solution B and D, respectively. The left figure shows the distance between solution A and these solutions in the decision space with \(d'_{AB}\) and \(d'_{AD}\) representing the corresponding euclidean distances. A solution’s final crowding value is determined by multiplying its distance from its neighboring solution B in the search space and objective space, then by adding the distance between that solution and its neighboring solution D in the search and objective space.
In general, the \(\text {Euc}_\text {{xy}}\) for each solution \(x_u\) is calculated as follows:
where \(\text {NB}(\text {x}_\text {u})\) contains all the \(\text {x}_\text {u}\)’s adjacent solutions on both sides of its corresponding front based on each objective function, while \(\text {Euc}(\text {f}_\text {u}, \text {f}_\text {v})\) and \(\text {Euc}(\text {x}_\text {u}, \text {x}_\text {v})\) represent the euclidean distances between \(\text {x}_\text {u}\) and its neighbor solution \(\text {x}_\text {v}\) in the objective space and decision space.
2.2 Inter-front selection operations
Another disadvantage of crowding distance measurements, or any selection method that measures density by looking at neighboring solutions on the same front, is that density calculations do not consider the neighboring solutions on previous fronts and therefore are inaccurate.
We can see an example of this problem in Fig. 5. Crowding distance is calculated based on neighboring solutions located on the same front. According to the figure, solution A has a larger crowding distance value since it has a greater distance from the other solutions in the same front in the search space (i.e. B, C, and D), as the volume of the orange highlighted region denotes the crowding value of solution A. Using the crowding distance metric, therefore, increases the chance of selecting solutions A that will survive and transfer to the next population. In contrast, however, it does not improve the distribution of the solutions since the same area is already covered by some solutions from \(\text {Front}_1\) to \(\text {Front}_{i-1}\).
Therefore, we determine the density of the solutions in the search space by considering both solutions on the same front as well as neighboring solutions on previous fronts. In our study, we refer to these types of selection mechanisms as inter-front selection operations. Consequently, in the following section, we present an alternative environment selection method based on inter-front selection.
2.2.1 NxEMMO algorithm
The NxEMMO algorithm (Javadi and Mostaghim 2021) is developed based on the NSGA-II including several modifications. An overview of NxEMMO algorithm can be found in Algorithm 1.
The population P(t) is initialized at generation t with N random individuals (lines 1-2). The solutions are evaluated (line 3) and the parents are then determined using a mating selection operator (line 5). Offspring Q are generated using the Simulated Binary Crossover (SBX) operator and mutated by the Polynomial Mutation operator (Kumar and Deb 1995) (lines 6-7). On the basis of the max-min normalization techniques, the solutions are normalized in the search space and then the modified environmental selection mechanism is applied (line 10).
The proposed environmental selection mechanism (Algorithm 2) is performed on the combination of P and Q. The algorithm starts by applying non-dominated sorting as in NSGA-II, and then sorting the solutions into several fronts, each denoted by \(\text {Front}_i\) for its \(i_{th}\) front (line 1). As with NSGA-II, the solutions from \(\text {Front}_1\) to \(\text {Front}_{i-1}\) are passed onto the new population (\(P(t+1)\)) (lines 2 to 7). It is necessary to truncate the solutions in \(\text {Front}_i\) if they do not fit into the new population.
The major differences between the NxEMMO and NSGA-II is its truncation approach. NxEMMO has a new crowding distance mechanism which replaces the one from NSGA-II. There are two cases: 1) The Nearest Neighbor Distance (NND) mechanism is used if the front selected for truncation is itself \(\text {Front}_1\). This diversity estimated measurement was originally proposed by Zitzler et al. (Zitzler et al. 2001), which is designed to keep the size of a set of solutions to a predefined value. The operation is named Omission (line 10). 2) we perform the Harmonic Average Distance (HAD) for truncation but different from the crowding distance in NSGA-II, we compute HAD between every single solution in \(\text {Front}_i\) and all other solutions in \(\text {Front}_1\) to \(\text {Front}_{i-1}\). In other words, we set l in Equation 7 as the number of solutions in \(\text {Front}_1\) to \(\text {Front}_{i-1}\). Addition is referred to as this mechanism (line 8). Through this operator, the solution with the highest HAD value is transferred to the new population (\(P(t+1)\)). Once the HAD values for the remaining solutions in \(\text {Front}_i\) have been updated, the next individuals will be selected iteratively until \(R(t+1)\) has been filled up. Accordingly, HAD value is calculated as the distance between a solution i and its k-nearest neighbors:
Where the euclidean distance between a solution i and its nearest neighbor \(j_{th}\) is \(d_{ij}\). The neighborhood size (i.e. k) is calculated as follows:
Referring to Fig. 2, solution B and F are two nearest neighbors to solution C, while G and D are two neighbors to solution E. Let’s assume \(d_{BC}=1\), \(d_{CF}=3\), \(d_{EG}=2\) and \(d_{ED}=4\). As a result, the harmonic average distance is smaller for C than E, i.e. \(\text {HAD}(C)\) is smaller than \(\text {HAD}(E)\). Though, these solutions have an opposite relationship in the case of crowding value.
An example on the MMF1 test (Liang et al. 2016) in Fig. 6 (left) illustrates the influence of the Addition function on the diversity of solutions in the decision space. Solutions in \(\text {Front}_1\) to \(\text {Front}_{i-1}\) can be found as \(*\). A blue \(\Diamond \) is used to identify the solutions in \(\text {Front}_i\). Those solutions in the red circle are the results of the Addition function. In addition, the selected solutions are represented by purple \(\square \) based on the crowding distance method. The Addition function only selects those solutions that are located in sparse areas, considering all solutions, not just those in \(\text {Front}_i\), but also all other solutions from \(\text {Front}_1\) to \(\text {Front}_{i-1}\). Comparatively, the crowding distance method does not select the solutions evenly distributed across the decision space.


Using the test problem MMF1, an example of addition (left) and omission (right) functions (Javadi and Mostaghim 2021)
Figure 6 (right) depicts an example of the Omission function based on the NND mechanism. When only one front exists, this function is activated, which means the truncation occurs in \(Front_1\). We seek to omit two solutions in this example. With a blue \(*\), you can see non-dominated solutions, while a * shows the result of omission using NND function. As you can see in the figure, two solutions (duplicates) occupy the same position (marked by the red circle). One of the duplicate solutions and another solution in the crowded area are eliminated using NND function.
Taking HAD function as opposed to NND gives a better comparison of the result of the Omission function. HAD’s result is represented by red circles. HAD selected the above duplicates when selecting two solutions for omission. HAD results in elimination of both duplicates, so the empty position in that part of the decision space is left, whereas NND maintains one of the duplicates at the same position (the red circle) and eliminates the other in a crowded area. Because this is a non-dominated front, it has great significance.
3 Experimental setup
The performance of these two types of inter- and intra-front selection operations is evaluated and compared using experiments on 14 different multi-modal multi-objective test functions whose PFs and PSs have different shapes and the number of PSs differs. The size population is set to 100. To meet the termination criteria, all algorithms and testing problems are limited to a maximum of 10000 function evaluations each. Assuming n is the number of decision variables, \(P_{m} = 1/n\) and \(P_{c} = 1\) are the probability of polynomial mutation and simulated binary crossover (SBX), respectively. The distribution indices of these operators are set to \(\eta _{c}=20\) and \(\eta _{m}=20\).
In the \(\text {NSGA-II-CD}_{\text {ws}}\) the weights in the weighted sum approach have equal distribution in both the search and objective spaces as \(\text {w}_{\text {dec}}=0.5\) and \(\text {w}_{\text {obj}}=0.5\).
Implementation of algorithms was performed on PlatEmo Platform, version 2.8.0 (Tian et al. 2017), using Matlab R2020a running at 3 GHz and with 16 GB of RAM in a 64-bit environment using an Intel Core i7 processor.
In this study, we compare two of our proposed algorithms, NxEMMO [that is based on inter-front selection operations (Javadi and Mostaghim 2021)] and ES-EMMO (that is based on inter-front selection operations), with their competing algorithms that are based on inter-front operations. Moreover, the following algorithms were chosen for comparison: Omni-optimizer (Deb and Tiwari 2008), DN-NSGA-II (Liang et al. 2016), and \(\text {NSGA-II-CD}_{\text {ws}}\) and our proposed ES-EMMO algorithms.
3.1 Metrics for evaluating performance
The following performance indicators are employed for measuring the quality of the solutions obtained by the algorithms: Inverted Generational Distance Plus in the objective space \(\text {(IGD}^{+})\) (Ishibuchi 2015), Inverted Generational Distance in the decision space (IGDx) (Zhou et al. 2009), Pareto-Set Proximity (PSP) (Yue et al. 2018). IGDx and PSP performance indicators represent algorithms’ performances in the search space, whereas \(\text {(IGD}^{+})\) indicators display algorithms’ functionality in the objective space.
The IGDx value represents both the convergence and the diversity of the obtained optimized solutions:
Where \(P^{*}\) indicates the set of solutions which are uniformly distributed in the PS, and \(\vert P^{*}\vert \) is the cardinality of \(P^{*}\). R denoted as the obtained solution set in decision space. The euclidean distance \( \left\| R - v \right\| \) between a sampled point v and any point in R is determined as the minimum euclidean distance.
Moreover, the overlapping ratio between the bounding of the PS and the obtained results is demonstrated by the PSP value, which is calculated as the fraction of the cover-rate to its obtained IGDx values:
where CR (i.e. the cover rate), is a modified version of the Maximum Spread (MS) (Tang and Wang 2012) for search space:
Where in the search space, \(Q_i^{max}\) and \(Q_i^{min}\) are maximum and minimum values of the PS in dimension i, while \(q_i^{max}\) and \(q_i^{max}\) are maximum and minimum obtained values by the obtained optimal solutions in dimension i. The dimensionality of the decision space is represented by n.
To measure the similarity between optimal solutions in objective space and the PF, we applied the \(\text {IGD}^{+}\) performance metric, a weakly Pareto-compliant version of the IGD (Zhang et al. 2008) performance metric. Specifically, In both the decision and the objective spaces, low values of IGDx and \(\text {IGD}^{+}\), as well as a high PSP value, indicate that the solution set is distributed evenly in both spaces.
3.2 Benchmark problems
This study compares two types of optimization algorithms using state-of-the-art test cases for multi-modal and multi-objective optimization. We take 14 benchmark problems: MMF1z, MMF1 to MMF9, MMF14, and Omni-test, SYM-PART (simple and rotated) problems. We additionally take the test problems from the CEC2019 competition on Multi-modal Multi-Objective Optimization (Liang et al. 2019; Yue et al. 2019). Both the decision variables and the objective functions in the test problems are bi-dimensional. As it is discussed in (Yue et al. 2019), depending on the PS and PF geometries, the overlap between PSs on each dimension, the number of PSs, and the coexistence of local and global PSs, the level of difficulty of the test problems varies. The characteristics of the test cases presented in Table 1 represent important information about the difficulty of the test cases, as well as the reasons why certain algorithms perform better in certain test cases, and vice versa. For example, the number of PSs associated with MMOPs is an important indicator of their complexity, as problems with more PSs may become more difficult to solve. The shape of the PF determines how the MMOEAs will react to PFs of different shapes, such as linear/non-linear, convex or concave. In some cases, algorithms perform best in convex shapes, while others perform best in concave shapes. PF’s that are nonlinear are harder to find than those that are linear. In addition, the performance of the algorithms needs to be evaluated on different PS shapes, such as linear, nonlinear, symmetrical and asymmetric, and other complex ones. A nonsymmetric PS (e.g. MMF1z) is complex to solve and is more similar to real-life problems. Moreover, it is beneficial to examine the operation of the MMOEAs in the escaping of the trap of local PS by having test cases in which both the local and global PS coexist.
4 Analysis
Experimental results are based on 31 independent runs on each test problem for each algorithm. To examine the significance of differences between best-performing and the other algorithms, we present the median and interquartile range for each of the performance indicators. At the significance level of 5%, the null hypothesis of equal medians is rejected on each test problem using the Mann-Whitney-U statistic.
In Tables 2, 3, and 4 the best-performing algorithms are displayed in bold, whereas an asterisk (*) demonstrates significant statistical differences relative to the best-performing algorithms. The values in the tables show the algorithms regarding the selection categories. It is our intention to compare the performance of the proposed algorithms with the others, as well as to compare their performance of two selection operations with each other.
In Tables 2 and 3, we can see that the NxEMMO algorithm outperforms other algorithms in 11 out of 14 test instances. As expected, these results meet our expectations that modifications to the environmental selection and replacing the crowding distance in the NxEMMO algorithm lead to improved results. When NxEMMO is used, it is possible to detect the solutions in sparse areas in the decision space more effectively than the crowding distance method used in the algorithm that utilizes inter-front selection operations. Algorithm 2 describes how adding and omitting in subsequent steps leads to enhanced PS approximation. Moreover, as we see in Tables 2 and 3, ES-EMMO performs the best among others of the three algorithms on the MMF3 test case that involves local PS. It appears that DN-NSGA-II and Omni-optimizer algorithms are more prone to getting trapped into local PSs.
A closer look at the interquartile results for the IGDx values in Table 2 reveals that in 10 out of the 14 test cases, the NxEMMO has a lower score than its competition. It means that the results obtained with the NxEMMO algorithm are of better stability and robustness over several runs of the algorithm, since they did not show much variation when compared to the other state-of-the-art algorithms. Morover, when we compare the results for the NxEMMO algorithm and the proposed ES-EMMO algorithm, we can see that the NxEMMO algorithm does better in 10 out of 14 test cases based on statistical significance compared to ES-EMMO algorithms. In comparison to the results for the MMF3 test cases, ES-EMMO did not differ statistically from NxEMMO, regardless of the better IGDx value.
The performance indicator for PSP consists of the ratio of cover rate to IGDx, where cover rate (or overlap rate) indicates the percentage of the defined region between the optimal solution and the PS. The results in Tables 2 and 3 are nearly identical, since the overlap rate of the test results is one, which is ideal value.
Based on the results in terms of intra-front selection operations, ES-EMMO outperforms the \(\text {NSGA-II-CD}_{\text {ws}}\) algorithm in five cases. In addition, in most of the test cases, it also outperforms the Omni-optimizer and DN-NSGA-II algorithms, which use crowding distance metrics on the decision space. These results confirm that using other distance metric than the crowding distance metric can help to overcome the above-mentioned problem and boost the diversification over the PSs.
However, in Omni-test problem ES-EMMO, Omni-optimizer and DN-NSGA-II algorithms fail to deliver good performance; this could be attributed to a poor distribution of solutions within the search space, as they were unable to find all 27 PS. On the other hand, NxEMMO algorithm shows good results regarding preservation of a large number of PSs.
We additionally observe that \(\text {NSGA-II-CD}_{\text {ws}}\) shows superiority to all the other algorithms when it comes to IGD+ values (i.e. Table 4). We expect this algorithm to have a better approximation of PF in the objective space, since it considers the diversity of the solutions in the objective space in its density calculations. According to the analysis, NxEMMO is the second-best algorithm in the objective space, after \(\text {NSGA-II-CD}_{\text {ws}}\). Both Omni-optimizer and DN-NSGA-II algorithms perform not so well when compared to other algorithms in the category of intra-front selection. All in all, as we expected, considering the effects of neighboring solutions further improves the density estimation of the solutions within the search space. Therefore, inter-front selection operations generally outperform intra-front selection operations.
In order to provide better visualization of the result population and demonstrate the similarity between the obtained final solutions in both decision and objective spaces, Figs. 7, 8, and 9 show the results of the run with median IGDx performance indicator for the MMF6, MMF9, and \(\text {SYM-PART}_\text {simple}\) test cases. A solid blue line corresponds to the actual PF and PS of the test problems, while the red marker represents the solutions obtained using competitive algorithms. We compare the results for the NxEMMO algorithm, a representation of an inter-front selection operation, as well as ES-EMMO and \(\text {NSGA-II-CD}_{\text {ws}}\), a representation of an intra-front selection operation. On closer inspection of Figs. 7, 8, and 9 on the search space, the obtained results for the algorithm NxEMMO on the MMF6, MMF14 and \(\text {SYM-PART}_\text {simple}\) test cases, this algorithm has a better coverage area over the PS than the other two, and the results are distributed more evenly over the PS for those test problems. We can see, for instance, that in the \(\text {SYM-PART}_\text {simple}\) test case, the NxEMMO algorithm succeeds in finding and preserving all PSs, whereas other state-of-the-art algorithms are able to locate only some PSs. Furthermore, we can see that the NxEMMO algorithm is capable of providing reasonable coverage of the PF.
5 Conclusion and future works
This paper deals with multi-modal multi-objective optimization problems. It highlights some problems associated with crowding distance methods, and suggests two different methods to deal with these difficulties. Additionally, we classified the selection operations of Pareto-based MMOEAs into inter- and intra-front selection operations. In our comparisons, we include the proposed algorithms and other state-of-the-art algorithms, which also fall into the categories we introduced. the experiments demonstrate that the proposed inter-front selection method performs the best when compared to algorithms that use other selection methods. In the future, research will need to focus on developing algorithms to handle multiple PSs and PFs, and proposing performance indicators for measuring the density of solutions properly in their local area.
Code availability
The source code for the proposed NxEMMO algorithm can be found on our website: https://www.is.ovgu.de/Publications.html
References
Bader J, Zitzler E (2011) Hype: An algorithm for fast hypervolume-based many-objective optimization. Evol Comput 19(1):45–76
Beume N, Naujoks B, Emmerich M (2007) Sms-emoa: Multiobjective selection based on dominated hypervolume. Eur J Oper Res 181(3):1653–1669
Deb K, Tiwari S (2005) Omni-optimizer: a procedure for single and multi-objective optimization. In: International conference on evolutionary multi-criterion optimization, pp 47–61. Springer, Berlin
Deb K, Tiwari S (2008) Omni-optimizer: a generic evolutionary algorithm for single and multi-objective optimization. Eur J Oper Res 185(3):1062–1087
Deb K, Pratap A, Agarwal S et al (2002) A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans Evol Comput 6(2):182–197
Falcón-Cardona JG, Coello Coello CA, Emmerich M (2019) Cri-emoa: A pareto-front shape invariant evolutionary multi-objective algorithm. In: International conference on evolutionary multi-criterion optimization, pp 307–318. Springer
Goldberg DE, Richardson J, et al (1987) Genetic algorithms with sharing for multimodal function optimization. In: Genetic algorithms and their applications: proceedings of the second international conference on genetic algorithms, pp 41–49. Lawrence Erlbaum, Hillsdale
Grimme C, Kerschke P, Aspar P et al (2021) Peeking beyond peaks: challenges and research potentials of continuous multimodal multi-objective optimization. Comput Oper Res 136(105):489
Hiroyasu T, Nakayama S, Miki M (2005) Comparison study of SPEA2+, SPEA2, and NSGA-II in diesel engine emissions and fuel economy problem. In: 2005 IEEE congress on evolutionary computation, IEEE CEC 2005 Proceedings vol 1, pp 236–242
Hu C, Ishibuchi H (2018a) Incorporation of a decision space diversity maintenance mechanism into MOEA/D for multi-modal multi-objective optimization. In: GECCO 2018 Companion - proceedings of the 2018 genetic and evolutionary computation conference companion, pp 1898–1901
Hu C, Ishibuchi H (2018b) Incorporation of a decision space diversity maintenance mechanism into MOEA/D for multi-modal multi-objective optimization. In: Proceedings of the genetic and evolutionary computation conference companion, pp 1898–1901
Ishibuchi, (2015) Modified distance calculation in generational distance and inverted generational distance Hisao. Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics) 9019:110–125
Javadi M, Mostaghim S (2021) A neighborhood-based density measure for multimodal multi-objective optimization. In: Ishibuchi H et al (eds) Evolutionary multi-criterion optimization. EMO 2021. Lecture notes in computer science, vol 12654. pp 335–345. Springer, Cham
Javadi M, Zille H, Mostaghim S (2019) Modified crowding distance and mutation for multimodal multi-objective optimization. In: Proceedings of the genetic and evolutionary computation conference companion, pp 211–212
Javadi M, Ramirez-Atencia C, Mostaghim S (2020) A novel grid-based crowding distance for multimodal multi-objective optimization. In: 2020 IEEE congress on evolutionary computation (CEC), IEEE, pp 1–8
Javadi M, Zille H, Mostaghim S (2021) The effects of crowding distance and mutation in multimodal and multi-objective optimization problems. In: Advances in evolutionary and deterministic methods for design, optimization and control in engineering and sciences. pp 115–130. Springer
Kim M, Hiroyasu T, Miki M et al (2004) SPEA2+: Improving the performance of the strength pareto evolutionary algorithm 2. Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics) 3242:742–751
Kramer O, Danielsiek H (2010) Dbscan-based multi-objective niching to approximate equivalent pareto-subsets. In: Proceedings of the 12th annual conference on Genetic and evolutionary computation, pp 503–510
Kramer O, Koch P (2009) Rake selection: A novel evolutionary multi-objective optimization algorithm. In: Annual conference on artificial intelligence, pp 177–184. Springer
Kumar K, Deb K (1995) Real-coded genetic algorithms with simulated binary crossover: Studies on multimodal and multiobjective problems. Complex syst 9:431–454
Li JP, Balazs ME, Parks GT et al (2002) A species conserving genetic algorithm for multimodal function optimization. Evol Comput 10(3):207–234
Liang J, Yue C, Qu BY (2016) Multimodal multi-objective optimization: a preliminary study. In: 2016 IEEE congress on evolutionary computation (CEC), IEEE, pp 2454–2461
Liang J, Guo Q, Yue C, et al (2018) A self-organizing multi-objective particle swarm optimization algorithm for multimodal multi-objective problems. In: International conference on swarm intelligence, pp 550–560. Springer
Liang J, Qu B, Gong D, et al (2019) Problem definitions and evaluation criteria for the cec 2019 special session on multimodal multiobjective optimization. In: Computational intelligence laboratory, Zhengzhou University
Liu Y, Ishibuchi H, Nojima Y, et al (2018) A double-niched evolutionary algorithm and its behavior on polygon-based problems. In: International conference on parallel problem solving from nature, pp 262–273. Springer
Osuna EC, Sudholt D (2019) Runtime analysis of crowding mechanisms for multimodal optimization. IEEE Trans Evol Comput 24(3):581–592
Pétrowski A (1996) A clearing procedure as a niching method for genetic algorithms. In: Proceedings of IEEE international conference on evolutionary computation, IEEE, pp 798–803
Sebag M, Tarrisson N, Teytaud O et al (2005) A multi-objective multi-modal optimization approach for mining stable spatio-temporal patterns. IJCAI Int Joint Conf Artif Intell 2(1):859–864
Tanabe R, Ishibuchi H (2018) A decomposition-based evolutionary algorithm for multi-modal multi-objective optimization. In: International conference on parallel problem solving from nature, pp 249–261. Springer
Tanabe R, Ishibuchi H (2019) A review of evolutionary multimodal multiobjective optimization. IEEE Trans Evol Comput 24(1):193–200
Tang L, Wang X (2012) A hybrid multiobjective evolutionary algorithm for multiobjective optimization problems. IEEE Trans Evol Comput 17(1):20–45
Thomsen R (2004) Multimodal optimization using crowding-based differential evolution. Proc 2004 Cong Evol Comput, CEC2004 2:1382–1389
Tian Y, Cheng R, Zhang X et al (2017) Platemo: a matlab platform for evolutionary multi-objective optimization [educational forum]. IEEE Comput Intell Mag 12(4):73–87
Wang Y, Emmerich M, Deutz A, et al (2019) Diversity-indicator based multi-objective evolutionary algorithm: Di-moea. In: International conference on evolutionary multi-criterion optimization, pp 346–358. Springer
Weise J, Mostaghim S (2021) Many-objective pathfinding based on fréchet similarity metric. In: Evolutionary multi-criterion optimization: 11th international conference, EMO 2021, Shenzhen, China, March 28–31, 2021, Proceedings 11, pp 375–386. Springer International Publishing
Yue C, Qu B, Liang J (2018) A multiobjective particle swarm optimizer using ring topology for solving multimodal multiobjective problems. IEEE Trans Evol Comput 22(5):805–817
Yue C, Qu B, Yu K et al (2019) A novel scalable test problem suite for multimodal multiobjective optimization. Swarm Evol Comput 48:62–71
Yusoff Y, Ngadiman MS, Zain AM (2011) Overview of nsga-ii for optimizing machining process parameters. Proc Eng 15:3978–3983
Zhang Q, Li H (2007) MOEA/D: a multiobjective evolutionary algorithm based on decomposition. IEEE Trans Evol Comput 11(6):712–731
Zhang Q, Zhou A, Jin Y (2008) Rm-meda: a regularity model-based multiobjective estimation of distribution algorithm. IEEE Trans Evol Comput 12(1):41–63
Zhou A, Zhang Q, Jin Y (2009) Approximating the set of pareto-optimal solutions in both the decision and objective spaces by an estimation of distribution algorithm. IEEE Trans Evol Comput 13(5):1167–1189
Zitzler E, Laumanns M, Thiele L (2001) SPEA2: Improving the strength pareto evolutionary algorithm. Evolutionary methods for design optimization and control with applications to industrial problems. pp 95–100
Funding
Open Access funding enabled and organized by Projekt DEAL. No funding was received for conducting this study.
Author information
Authors and Affiliations
Contributions
MJ: Conception and design of the work; programming, acquisition, analysis, interpretation of data; writing SM: Conception, analysis, editing, supervision
Corresponding author
Ethics declarations
Conflict of interest
The authors Mahrokh Javadi and Sanaz Mostaghim declare that they have no conflict of interest.
Ethics approval
All procedures performed in studies were in accordance with the ethical standards of the institutional and/or national research committee and with the 1964 Helsinki declaration and its later amendments or comparable ethical standards.
Consent for publication
For this type of study, formal consent is not required.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Javadi, M., Mostaghim, S. Analysis of inter and intra-front operations in multi-modal multi-objective optimization problems. Nat Comput 22, 341–356 (2023). https://doi.org/10.1007/s11047-022-09921-2
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11047-022-09921-2