Angle-Based Crowding Degree Estimation for Many-Objective Optimization

Abstract

Many-objective optimization, which deals with an optimization problem with more than three objectives, poses a big challenge to various search techniques, including evolutionary algorithms. Recently, a meta-objective optimization approach (called bi-goal evolution, BiGE) which maps solutions from the original high-dimensional objective space into a bi-goal space of proximity and crowding degree has received increasing attention in the area. However, it has been found that BiGE tends to struggle on a class of many-objective problems where the search process involves dominance resistant solutions, namely, those solutions with an extremely poor value in at least one of the objectives but with (near) optimal values in some of the others. It is difficult for BiGE to get rid of dominance resistant solutions as they are Pareto nondominated and far away from the main population, thus always having a good crowding degree. In this paper, we propose an angle-based crowding degree estimation method for BiGE (denoted as aBiGE) to replace distance-based crowding degree estimation in BiGE. Experimental studies show the effectiveness of this replacement.

1 Introduction

Many-objective optimization problems (MaOPs) refer to the optimization of four or more conflicting criteria or objectives at the same time. MaOPs exist in many fields, such as environmental engineering, software engineering, control engineering, industry, and finance. For example, when assessing the performance of a machine learning algorithm, one may need to take into account not only accuracy but also some other criteria such as efficiency, misclassification cost, interpretability, and security.

There is often no one best solution for an MaOP since the performance increase in one objective will lead to a decrease in some other objectives. In the past three decades, multi-objective evolutionary algorithms (MOEAs) have been successfully applied in many real-world optimization problems with low-dimensional search space (two or three conflicting objectives) to search for a set of trade-off solutions.

The major purpose of MOEAs is to provide a population (a set of optimal individuals or solutions) that balance proximity (converging a population to the Pareto front) and diversity(diversifying a population over the whole Pareto front). By considering the two goals above, traditional MOEAs, such as SPEA2 [13] and NSGA-II [1] mainly focus on the use of Pareto dominance relations between solutions and the design of diversity control mechanisms.

However, compared with a low-dimensional optimization problem, well-known Pareto-based evolutionary algorithms lose their efficiency in solving MaOPs. In MaOPs, most solutions in a population become equally good solutions, since the Pareto dominance selection criterion fails to distinguish between solutions and drive the population towards the Pareto front. Then the density criterion is activated to guide the search, resulting in a substantial reduction of the convergence of the population and the slowdown of the evolution process. This is termed the active diversity promotion (ADP) phenomenon in [11].

Some studies [6] observed that the main reason for ADP phenomenon is the preference of dominance resistant solutions (DRSs). DRSs refer to those solutions that are extremely inferior to others in at least one objective but have near-optimal values in some others. They are considered as Pareto-optimal solutions despite having very poor performance in terms of proximity. As a result, Pareto-based evolutionary algorithms could search a population that is widely covered but far away from the true Pareto front.

To address the difficulties of MOEAs in high-dimensional search space, one approach is to modify the Pareto dominance relation. Some powerful algorithms in this category include: $\epsilon$-MOEA [2] and fuzzy Pareto dominance [5]. These methods work well under certain circumstances but they often involve extra parameters and the performance of these algorithms often depends on the setting of parameters. The other approach, without considering Pareto dominance relation, may be classified into two categories: aggregation-based algorithms [15] and indicator-based algorithms [14]. These algorithms have been successfully applied to some applications, however, the diversity performance of these aggregation-based algorithms depends on the distribution of weight vectors. The latter defines specific performance indicators to guide the search.

Recently, a meta-objective optimization algorithm, called Bi-Goal Evolution (BiGE) [8] for MaOPs is proposed and becomes the most cited paper published in the Artificial Intelligence journal over the past four years. BiGE was inspired by two observations in many-objective optimization: (1) the conflict between proximity and diversity requirement is aggravated when increasing the number of objectives and (2) the Pareto dominance relation is not effective in solving MaOPs. In BiGE, two indicators were used to estimate the proximity and crowding degree of solutions in the population, respectively. By doing so, BiGE maps solutions from the original objective space to a bi-goal objective space and deals with the two goals by the nondominated sorting. This is able to provide sufficient selection pressure towards the Pareto front, regardless of the number of objectives that the optimization problem has.

However, despite its attractive features, it has been found that BiGE tends to struggle on a class of many-objective problems where the search process involves DRSs. DRSs are far away from the main population and always ranked as good solutions by BiGE, thus hindering the evolutionary progress of the population. To address this issue, this paper proposes an angle-based crowding degree estimation method for BiGE (denoted as aBiGE). The rest of the paper is organized as follows. Section 2 gives some concepts and terminology about many-objective optimization. In Sect. 3, we present our angle-based crowding degree estimation method and its incorporation with BiGE. The experimental results are detailed in Sect. 4. Finally, the conclusions and future work are set out in Sect. 5.

2 Concepts and Terminology

When dealing with optimization problems in the real world, sometimes it may involve more than three performance criteria to determine how “good" a certain solution is. These criteria, termed as objectives (e.g., cost, safety, efficiency) need to be optimized simultaneously, but usually conflict with each other. This type of problem is called many-objective optimization problem (MaOP). A minimization MaOP can be mathematically defined as follows:

$$\begin{aligned} \begin{aligned}&\text {minimize} \quad \quad \;\; F(x) = (f_1(x), f_2(x), ..., f_N(x)) \\&\text {subject to} \quad \quad \; g_j(x) \le 0, \quad j = 1, 2, ..., J\\&\quad \quad \quad \quad \quad \quad \;\; h_k(x) = 0, \quad k = 1, 2, ..., K\\&\quad \quad \quad \quad \quad \quad \;\; x = (x_1, x_2, ..., x_M), \quad x \in \varOmega \end{aligned} \end{aligned}$$

(1)

where x denotes an M-dimensional decision variable vector from the feasible region in the decision space $\varOmega$, F(x) represents an N-dimensional objective vector (N is larger than three), $f_i(x)$ is the i-th objective to be minimized, objective functions $f_1, f_2, ..., f_N$ constitute N-dimensional space called the objective space, $g_j(x) \le 0$ and $h_k(x) = 0$ define J inequality and K equality constraints, respectively.

Definition 1 (Pareto Dominance)

Given two decision vectors $x, y \in \varOmega$ of a minimization problem, x is said to (Pareto) dominate y (denoted as $x \prec y$), or equivalently y is dominated by x, if and only if [4]

$$\begin{aligned} \begin{aligned} \forall \, i \in (1, 2, ..., N): f_i (x) \le f_i (y) \, \wedge \, \exists \, i \in (1, 2, ..., N): f_i (x) < f_i (y). \end{aligned} \end{aligned}$$

(2)

Namely, given two solutions, one solution is said to dominate the other solution if it is at least as good as the other solution in any objective and is strictly better in at least one objective.

Definition 2 (Pareto Optimality)

A solution $x \in \varOmega$ is said to be Pareto optimal if and only if there is no solution $y \in \varOmega$ dominates it. Those solutions that are not dominated by any other solutions is said to be Pareto-optimal (or non-dominated).

Definition 3 (Pareto Set)

All Pareto-optimal (or non-dominated) solutions in the decision space constitute the Pareto set (PS).

Definition 4 (Pareto Front)

The Pareto front (PF) is referred to corresponding objective vectors to a Pareto set.

Definition 5 (Dominance Resistant Solution)

Given a solution set, dominance resistant solution (DRS) is referred to the solution with an extremely poor value in at least one objective, but with near-optimal value in some other objective.

3 The Proposed Algorithm: aBiGE

3.1 A Brief Review of BiGE

Algorithm 1 shows the basic framework of BiGE. First, a parent population with M solutions is randomly initialized. Second, proximity and crowding degree for each solution is estimated, respectively. Third, in the mating selection, individuals that have better quality with regards to the proximity and crowding degree tend to become parents of the next generation. Afterward, variation operators (e.g., crossover and mutation) are applied to these parents to produce an offspring population. Finally, the environmental selection is applied to reduce the expanded population of parents and offspring to M individuals as the new parent population of the next generation.

In particular, a simple aggregation function is adopted to estimate the proximity of an individual. For an individual x in a population, denoted as $f_{p}(x)$, its aggregation value is calculated by the sum of each normalized objective value in the range [0, 1] (lines 3 in Algorithm 1), formulated as [8]:

$$\begin{aligned} f_{p}(x) = \sum _{j=1}^N \widetilde{f}_j(x). \end{aligned}$$

(3)

where $\widetilde{f}_j(x)$ denotes the normalized objective value of individual x in the j-th objective, and N is the number of objectives. A smaller $f_{p}$ value of an individual usually indicates a good performance on proximity. In particular, for a DRS, it is more likely to obtain a significantly large $f_{p}$ value in comparison with other individuals in a population.

In addition, the crowding degree of an individual x (lines 4 in Algorithm 1) is defined as follows [8]:

$$\begin{aligned} f_{c}(x)= (\sum _{y \in \varOmega ,x\ne y} sh(x,y))^{1/2}. \end{aligned}$$

(4)

where $sh(x,y))^{1/2}$ denotes a sharing function. It is a penalized Euclidean distance between two individuals x and y by using a weight parameter, defined as follows:

(5)

where r is the radius of a niche, adaptively calculated by $r = {1}/{\root N \of {M}}$ (M is the population size and N is the number of objectives). The function rand() means to assign either $sh(x,y)=(0.5(1- [{d(x,y)}/{r}]))^2$ and $sh(y,x)\!=\!(1.5(1-[{d(x,y)}/{r}]))^2$ or sh(x, y) $=\!(1.5(1-[{d(x,y)}/{r}]))^2$ and $sh(y,x)\!=\!(0.5(1- [{d(x,y)}/{r}]))^2$ randomly. Individuals with lower crowding degree imply better performance on diversity.

It is observed that BiGE tends to struggle on a class of MaOPs where the search process involves DRSs, such as DTLZ1 and DTLZ3 (in a well-known benchmark test suite DTLZ [3]). Figure 1 shows the true Pareto front of the eight-objective DTLZ1 and the final solution set of BiGE in one typical run on the eight-objective DTLZ1 by parallel coordinates. The parallel coordinates map the original many-objective solution set to a 2D parallel coordinates plane. Particularly, Li et al. in [9] systematically explained how to read many-objective solution sets in parallel coordinates, and indicates that parallel coordinates can partly reflect the quality of a solution set in terms of convergence, coverage, and uniformity.

Fig. 1.

The true Pareto front and the final solution set of BiGE on the eight-objective DTLZ1, shown by parallel coordinates.

Clearly, there are some solutions that are far away from the Pareto front in BiGE, with the solution set of eight-objective DTLZ1 ranging from 0 to around 450 compared to the Pareto front ranging from 0 to 0.5 on each objective. Such solutions always have a poor proximity degree and a good crowding degree (estimated by Euclidean distance)in bi-goal objective space (i.e., convergence and diversity), and will be preferred since there is no solution in the population that dominates them in BiGE. These solutions are detrimental for BiGE to converge the population to the Pareto front considering their poor performance in terms of convergence. A straightforward method to remove DRSs is to change the crowding degree estimation method.

3.2 Basic Idea

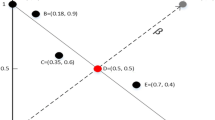
The basic idea of the proposed method is based on some observations of DRSs. Figure 2 shows one typical situation of a non-dominated set with five individuals including two DRSs (i.e, A and E) in a two-dimensional objective minimization scenario.

Fig. 2.

An illustration of a population of five solutions with two DRSs - A and E. They have good crowding degrees estimated by the Euclidean distance, but poor crowding degrees calculated by the vector angle between two neighbors.

As seen, it is difficult to find a solution that could dominate DRSs by estimating the crowding degree using Euclidean distance. Take individual A as an example, it performs well on objective $f_1$ (slightly better than B with a near-optimal value 0) but inferior to all the other solutions on objective $f_2$. It is difficult to find a solution with better value than A on objective $f_1$, same as individual E on objective $f_2$. A and E (with poor proximity degree and good crowding degree) are considered as good solutions and have a high possibility to survive in the next generation in BiGE. However, the results would be different if the distance-based crowding degree estimation is replaced by a vector angle. It can be observed that (1) an individual in a crowded area would have a smaller vector angle to its neighbor compared to the individual in a sparse area, e.g., C and D, (2) a DRS would have an extremely small value of vector angle to its neighbor, e.g., the angle between A and B or the angle between E and D. Namely, these DRSs would be assigned both poor proximity and crowding degrees, and have a high possibility to be deleted during the evolutionary process. Therefore, vector angles have the advantage to distinguish DRSs in the population and could be considered into crowding degree estimation.

3.3 Angle-Based Crowding Degree Estimation

Inspired by the work in [12], we propose a novel angle-based crowding degree estimation method, and integrate it into the BiGE framework (line 4 in Algorithm 1), called aBiGE. Before estimating the diversity of an individual in a population in aBiGE, we first introduce some basic definitions.

Norm. For individual $x_i$, its norm, denoted as $norm(x_i)$ in the normalzied objective space defined as [12]:

$$\begin{aligned} norm(x_i)=\sqrt{\sum _{j=1}^N \widetilde{f}_j(x_i)^2}. \end{aligned}$$

(6)

Vector Angles. The vector angle between two individuals $x_i$ and $x_k$ is defined as follows [12]:

$$\begin{aligned} angle_{\,x_i\rightarrow x_k}=arccos\left| \frac{F'(x_i)\bullet F'(x_k)}{norm(x_i)\cdot norm(x_k)}\right| . \end{aligned}$$

(7)

where $F'(x_i)\bullet F'(x_k)$ is the inner product between $F'(x_i)$ and $F'(x_k)$ defined as:

$$\begin{aligned} F'(x_i)\bullet F'(x_k) = \sum _{j=1}^N \widetilde{f}_j(x_i) \cdot \widetilde{f}_j(x_k). \end{aligned}$$

(8)

Note that angle$_{\,x_i\rightarrow x_k}\in [0,\pi /2]$.

The vector angle from an individual $x_i \in \varOmega$ to the population is defined as the minimum vector angle between $x_i$ and another individual in a population P: $\theta (x_i) = angle_{\,x_i\rightarrow P}$

When an individual x is selected into archive in the environmental selection, respectively, $\theta (x)$ value will be punished. There are several factors need to be considered in order to achieve a good balance between proximity and diversity.

• A severe penalty should be imposed on individuals that have more adjacent individuals in a niche. Inspired by the punishment method of crowding degree estimation, a punishment to an individual x is based on the number of individuals that have a lower proximity degree compared to x is counted (denote as c). The punishment is aggravated with an increase of c.

• In order to avoid the situation that some individuals have the same vector angle value to the population, individuals should be further punished. Therefore, the penalty is implemented according to the proportion value of $\theta (x)$ to all the individuals in the niche, denoted as p.

Keep the above factors in mind, in aBiGE, the diversity estimation of individual $x \in \varOmega$ based on vector angles is defined as

$$\begin{aligned} f_{a}(x)= \dfrac{c+1}{\theta (x)\cdot (p+1)+\dfrac{\pi }{90}}. \end{aligned}$$

(9)

By applying the angle-based crowding degree estimation method to BiGE framework in minimizing many-objective optimization problems, we aim to enhance the selection pressure on those non-dominated solutions in the population of each generation and avoid the negative influence of DRSs in the optimization process. Note that, a smaller value of $f_{a}(x)$ is preferred.

4 Experiments

4.1 Experimental Design

To test the performance of the proposed aBiGE on those MaOPs where the search process involves DRSs, the experiments are conducted on nine DTLZ test problems. For each test problem (i.e., DTLZ1, DTLZ3, and DTLZ7), five, eight, and ten objectives will be considered, respectively.

To make a fair comparison with the state-of-the-art BiGE for MaOPs, we kept the same settings as [8]. Settings for both BiGE and aBiGE are:

• The population size of both algorithms is set to 100 for all test problems.

• 30 runs for each algorithm per test problem to decrease the impact of their stochastic nature.

• The termination criterion of a run is a predefined maximum of 30, 000 evaluations, namely 300 generations for test problems.

• For crossover and mutation operators, crossover and mutation probability are set to 1.0 and 1/M (where M represents the number of decision variables) respectively. In particular, uniform crossover and polynomial mutation are used.

Algorithms performance is assessed by performance indicators that consider both proximity and diversity. In this paper, a modified version of the original inverted generational distance indicator (IGD) [15], called (IGD+) [7] is chosen as the performance indicator. Although IGD has been widely used to evaluate the performance of MOEAs on MaOPs, it has been shown [10] that IGD needs to be replaced by IGD+ to make it compatible with Pareto dominance. IGD+ evaluates a solution set in terms of both convergence and diversity, and a smaller value indicates better quality.

4.2 Performance Comparison

Test Problems with DRSs. Table 1 shows the mean and standard deviation of IGD+ metric results on nine DTLZ test problems with DRSs. For each test problem, among different algorithms, the algorithm that has the best result based on the IGD+ metric is shown in bold. As can be seen from the table, for MaOPs with DRSs, the proposed aBiGE performs significantly better than BiGE on all test problems in terms of convergence and diversity.

Table 1. Mean and standard deviation of IGD+ metric on nine DTLZ test problems. The best result for each test problem is highlighted in boldface.

To visualize the experimental results, Figs. 3 and 4 plot, by parallel coordinate, the final solutions of one run with respect to five-objective DTLZ1 and five-objective DTLZ7, respectively. This run is associated with the particular run with the closest results to the mean value of IGD+. As shown in Fig. 3(a), the approximation set obtained by BiGE has an inferior convergence on the five-objective DTLZ1, with the range of its solution set is between 0 and about 400 in contrast to the Pareto front ranging from 0 to 0.5 on each objective. From Fig. 3 (b), it can be observed that the obtained solution set of the proposed aBiGE converge to the Pareto front and only a few individuals do not converge.

Fig. 3.

The final solution sets of the two algorithms on the five-objective DTLZ1, shown by parallel coordinates.

Fig. 4.

The final solution sets of the two algorithms on the five-objective DTLZ7, shown by parallel coordinates.

For the solutions of the five-objective DTLZ7, the boundary of the first four objectives is in the range [0, 1], and the boundary of the last objective is in the range [3.49, 10] according to the formula of DTLZ7. As can be seen from (Fig. 4), all solutions of the proposed aBiGE appear to converge into the Pareto front. In contrast, some solutions (with objective value beyond the upper boundary in 5th objective) of BiGE fail to reach the Pareto front. In addition, the solution set of the proposed aBiGE has better extensity than BiGE on the boundaries. In particular, the solution set of BiGE fails to cover the region from 3.49 to 6 of the last objective and the solution set of the proposed aBiGE does not cover the range of Pareto front below 4 on 5th objective.

Test Problem Without DRSs. Figure 5 gives the final solution set of both algorithms on the ten-objective DTLZ2 in order to visualize their distribution on the MaOPs without DRSs. As can be seen, the final solution sets of both algorithms could coverage the Pareto front with lower and upper boundary within [0,1] of each objective. Moreover, refer to [9], parallel coordinates in Fig. 5 partly reflect the diversity of solutions obtained by aBiGE is sightly worse than BiGE. This observation can be assessed by the IGD+ performance indicator where BiGE obtained a slightly lower (better) than the proposed aBiGE.

Fig. 5.

The final solution sets of BiGE and aBiGE on the ten-objective DTLZ2 and evaluated by IGD+ indicator, shown by parallel coordinates. (a) BiGE (IGD+ = 2.4319E−01) (b) aBiGE (IGD+ = 2.5021E−01).

5 Conclusion

In this paper, we have addressed an issue of a well-established evolutionary many-objective optimization algorithm BiGE on the problems with high probability to produce dominance resistant solutions during the search process. We have proposed an angle-based crowding distance estimation method to replace distance-based estimation in BiGE, thus significantly reducing the effect of dominance resistant solutions to the algorithm. The effectiveness of the proposed method has been well evaluated on three representative problems with dominance resistant solutions. It is worth mentioning that for problems without dominance resistant solutions the proposed method performs slightly worse than the original BiGE. In the near future, we would like to focus on the problems without dominance resistant solutions, aiming at a comprehensive improvement of the algorithm on both types of problems.