Enhancement of light field disparity maps by reducing the silhouette effect and plane noise

Abstract

During the last decade, there has been an increasing number of applications dealing with multidimensional visual information, either for 3D object representation or feature extraction purposes. In this context, recent advances in light field technology, have been driving research efforts in disparity estimation methods. Among the existing ones, those based on the structure tensor have emerged as very promising to estimate disparity maps from Epipolar Plane Images. However, this approach is known to have two intrinsic limitations: (i) silhouette enlargement and (ii) irregularity of surface normal maps as computed from the estimated disparity. To address these problems, this work proposes a new method for improving disparity maps obtained from the structure-tensor approach by enhancing the silhouette and reducing the noise of planar surfaces in light fields. An edge-based approach is initially used for silhouette improvement through refinement of the estimated disparity values around object edges. Then, a plane detection algorithm, based on a seed growth strategy, is used to estimate planar regions, which in turn are used to guide correction of erroneous disparity values detected in object boundaries. The proposed algorithm shows an average improvement of 98.3% in terms of median angle error for plane surfaces, when compared to regular structure-tensor-based methods, outperforming state-of-the-art methods. The proposed framework also presents very competitive results, in terms of mean square error between disparity maps and their ground truth, when compared with their counterparts.

1 Introduction

While conventional video cameras only capture the light intensity, light field (LF) cameras are able to capture not only the intensity of light emanating from a scene, but also the direction of the light rays traveling in space towards the sensor. Therefore, with a single acquisition it is possible to capture rich scenic information, which can be used to render images with different focal planes or multiple points of view (Levoy and Hanrahan 1996). LF acquisition relies on the plenoptic principles defined by Adelson and Bergen (1991), as a plenoptic function that fully characterises the radiance information for every point in space and time and arriving from every direction. Ren Ng further cemented LF photography as a valuable solution for acquiring depth maps by designing a hand-held plenoptic camera, which greatly contributed to advance methods of computational photography (Ng 2006).

Fig. 1

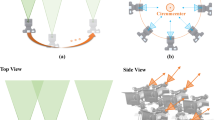
The Lytro light field camera and a high density camera array (image from Wilburn et al. (2005))

LFs may be obtained using single-tier lenslet LF cameras, i.e., with narrow baseline, such as those provided by Lytro$^{\mathrm{TM}}$ and Raytrix$^{\mathrm{TM}}$ or a high-density camera array (HDCA), i.e., with a wider baseline. Examples of these cameras are shown in Fig. 1. The versatility of LF technology enables many types of applications that require refocusing or 3D scenic features such as computer vision in industry, 3D television (Arai et al. 2013), medical imaging (de Faria et al. 2019) and many different applications requiring 3D information, where having multiple viewpoints of the same scene (views) allows disparity and depth map estimation (Wu et al. 2017).

In the past, several different disparity estimation methods have been investigated and described in the literature. Some of the most relevant are based on the so called focus stack, such as (Tao et al. 2013; Lin et al. 2015; Williem et al. 2018), and on multiview stereo correspondence (Jeon et al. 2015). More recently, a different approach based on a spinning parallelogram operator has been proposed by Zhang et al. (2016), while others have been pursuing learning approaches based on neural networks, such as Shin et al. (2018) and (Zhou et al. 2018). Neural networks can achieve interesting results, if a large enough amount of ground truth data is used for training. However, since ground truth light field data is scarce, in general, it is difficult to obtain convincing generalisation. Additionally, comparison of results with other methods cannot use a great portion of available data, because it was previously used for training.

This paper proposes a complete disparity estimation algorithmic pipeline, capable of achieving state-of-the-art results. The proposed method is based on the structure tensor method, originally presented by Bigun (1987). Previous methods for LF disparity estimation based on the structure tensor (Li and Li 2013; Wanner and Goldluecke 2012) suffer from known limitations, which consist in: (i) the enlargement of object boundaries where occlusions appear in transitions between distinct depths in the scene—this is known as the silhouette enlargement effect; (ii) low amplitude local noise affecting planar regions of the scene—this can be characterised as an irregularity of surface normal maps. This work specifically addresses these two limitations of structure tensor-based methods by proposing methods to improve the accuracy of object silhouettes in disparity maps and to reduce the low amplitude local noise in planar regions of depth maps. This is a novel unified framework capable of minimising the inaccuracies of LF estimated disparity, thus improving the quality of the resulting depth maps. The result is a method that is competitive with the state of the art in terms of MSE but superior in terms of the regularity of surface normals in planar regions, with the median angle error for those regions being improved up to 98.6%.

The remainder of this article is structured as follows: in Sect. 3, the structure tensor method is presented and the two main limitations of the method (discussed above) are characterised. In Sect. 4, the proposed algorithmic pipeline is presented along with its specific modules. Section 5, presents the results and discusses them in the light of the current state-of-the-art, and, finally, Sect. 6 draws the main conclusions and final remarks.

2 Background on disparity estimation

In a stereo image acquisition setup, the distance of an object to the camera (i.e., the depth) is inversely proportional to the difference between the position of the pixels representing the object in each image (i.e., disparity). Thus, the main problem in traditional stereo-based disparity estimation algorithms is to find accurate and reliable correspondences between the pixels in both images.

The concept of Epipolar Plane Images (EPI) was described by Bolles et al. (1987), stacking horizontal lines of each view of a sequence of images acquired with a moving camera on a straight rail. These images are formed by uniform stripes whose slope is proportional to the depth of the points included in those stripes. To obtain EPI images it is necessary to capture different views of the same scene, with small displacement between adjacent views, as shown in Fig. 2 for a matrix of views taken from a light field. A line or column of the view matrix is equivalent to the temporal sequence of images obtained by Bolles et al. (1987) with a camera moving in a straight rail.

Fig. 2

Light field cotton image from Johannsen et al. (2017)

This characteristic of EPI images reduces the problem of disparity estimation from the difficult case of matching interest points to the simpler problem of estimating the orientation of linearly symmetric structures in an image, which is potentially less complex from a computational point of view.

Due to their acquisition geometry, light fields typically show very low displacement between the same points in adjacent views, thus exploiting the EPIs is an efficient approach to estimate disparity. Mathematically, EPIs are equivalent to a cut of the 4D plenoptic function, where corresponding angular (s, t) and position (x, y) variables are fixed. For example, in Fig. 2b the horizontal EPI is obtained by fixing $t=3$ and $y=254$, and varying the x and s dimensions.

2.1 Disparity from light fields

Estimating disparity from Light Fields has been an important focus of study in the past decade. Tao et al. (2013) achieved a good disparity estimation by combining defocus and correspondence cues and then propagating the results using Markov Random Fields. However, objects far away from the camera and pixels near occlusion boundaries are prone to error. In Lin et al. 2015, the same principles of combining depth from defocus with stereo methods are associated with an analysis by synthesis method that ensures data consistency. Nonetheless, this method does not achieve angle consistency, producing a relatively large median angle error. In Williem et al. (2018), the problem of normal map regularisation is addressed directly by adding a novel optimisation step to the initial estimation introduced by Tao et al., achieving disparity maps that produce smooth surface normal maps. Yet, the optimisation approach still allows some normal map regularity errors in planar regions which can be addressed by the proposed method.

While these methods all focus on similar defocus and correspondence cues, other methods have been proposed. In Zhang et al. (2016), the orientation of lines in EPIs is detected using a spinning parallelogram operator by choosing the rotation angle that maximises the difference between a weighted sum of the texture of the pixels on either side of a parallelogram centred on a given pixel. This approach achieves good results in terms of MSE, especially near occlusion regions, but normal maps generated from the estimated disparity are less than ideal. Schilling et al. (2018) achieves excellent results by using a simple method based on Ransac line-fittings of the zero-crossings of the second order derivative of the EPIs to initialise a local optimisation method that directly enforces occlusion constraints. This method proves to be one of the best non-supervised methods at achieving good disparity in occlusion regions, however, it falls behind (Williem et al. 2018) when it comes to the accuracy of normal maps produced from the resulting disparity estimation.

Learning based methods have seen a greater focus in recent years. In Shin et al. (2018), LF specific data-augmentation techniques are used to train a neural network capable of fast disparity estimation. This technique achieves better results than most non-learning-based algorithms. However, it shows some limitations, as new training of the network is often necessary for different light fields. In Tsai et al. (2020), an attention-based network is proposed. By taking advantage of the symmetries and structural repetitions in the 4D LF, this method achieves the best results in the state-of-the-art in terms of badpix and mean squared error.

While learning based methods appear to be a viable alternative, it is still worthwhile to explore other options due to the opaque nature of such algorithms. Furthermore, neither of these algorithms prove more accurate than traditional methods when it comes to the accuracy of the surface normals obtained from the estimated disparity maps.

3 Background on the structure tensor method

The structure tensor was first used for disparity estimation in LF by Wanner and Goldluecke (2012). While the results achieved by this early paper do not stand up to the current state-of-the-art, the structure tensor is extremely fast, and unlike most other methods for initial estimation, most of its errors occur in a predictable manner and thus can be corrected explicitly. This section first presents an introduction on the technical concepts of the structure tensor, and then goes in depth into these predictable errors: Silhouette Enlargement and low amplitude local noise.

3.1 Technical concepts

The structure tensor was proposed by Bigun (1987) as a method for estimating the orientation of linear symmetry in images. Applying the tensor to overlapping windows of an EPI centered around each pixel is, thus, a good way of estimating the orientation of the linearly symmetric structures in the EPI and thus obtain an estimation of the disparity of the points represented in the EPI. For an horizontal EPI $I_h^{(y)}(s,x)$ the structure tensor computed for each pixel ${\mathbf {T}}(x,s)$ is represented by a 2$\times$2 matrix such that:

$$\begin{aligned} {\mathbf {T}}(x,s) = \begin{bmatrix} I_x^2 * G_\sigma &{} I_xI_s*G_\sigma \\ I_xI_s*G_\sigma &{} I_s^2*G_\sigma \end{bmatrix} = \begin{bmatrix} J_{xx} &{} J_{xs}\\ J_{xs} &{} J_{ss} \end{bmatrix}, \end{aligned}$$

(1)

where $I_x = \frac{\partial I}{\partial x}$, $I_s = \frac{\partial I}{\partial s}$, $G_\sigma$ represents a Gaussian kernel with scale $\sigma$, and $*$ represents the convolution operator.

The structure tensor has two orthogonal eigenvectors that indicate the direction of linear symmetry, as demonstrated by Bigun (1987). The eigenvalues relating to each of the eigenvectors can be calculated by solving

$$\begin{aligned} |{\mathbf {T}}(x,s)-\lambda {\mathbf {I}}_2| = 0, \end{aligned}$$

(2)

where $\lambda$ is an eigenvalue, ${\mathbf {I}}_2$ is a $2\times 2$ identity matrix and $|\cdot |$ symbolises the determinant of a matrix. This results in the second degree equation:

$$\begin{aligned}&\lambda ^2 - (J_{xx}+J_{ss})\lambda + (J_{xx} J_{ss}-J_{xs}^2) = 0 \Leftrightarrow \end{aligned}$$

(3)

$$\begin{aligned} \Leftrightarrow&\lambda = \frac{1}{2}\left( J_{ss}+J_{xx}\pm \sqrt{(J_{ss}-J_{xx})^2+4J^2_{xs}}\right) . \end{aligned}$$

(4)

From the definition of eigenvector, any eigenvector ${\mathbf {e}} = (e_0,e_1)$ of ${\mathbf {T}}(x,s)$ will respect the following:

$$\begin{aligned} ({\mathbf {T}(x,s)}-\lambda {\mathbf {I}}_2){\mathbf {e}}= 0, \end{aligned}$$

(5)

by substituting the previously calculated eigenvalues and solving the linear system of equations one can calculate the relation between the coordinates of the eigenvectors:

$$\begin{aligned} \Leftrightarrow e_0 = \frac{J_{ss}-J_{xx}\pm \sqrt{(J_{ss}-J_{xx}){}^{2}+4J^2_{xs}}}{2J_{xs}} e_1. \end{aligned}$$

(6)

As the direction of linear symmetry corresponds to the orientation of EPI structures, one of the eigenvectors will be co-linear with the lines in the EPI, while the other will be orthogonal. With the disparity, d at the point (x, s) being given by $\frac{e_1}{e_0}$ of the co-linear eigenvector:

$$\begin{aligned} d=\frac{J_{ss}-J_{xx}+\sqrt{(J_{ss}-J_{xx}){}^{2}+4J^2_{xs}}}{2J_{xs}}. \end{aligned}$$

(7)

This calculation allows for an expedited algorithm as the analytical computation of the direction of the eigenvector is much less computationally expensive than automatic numerical algorithms for calculating the eigenvectors of any matrix.

Furthermore, Bigun also describes a coherence measure for the structure tensor. The coherence is a value bounded between 0 and 1 that measures the linear symmetry of each patch of an image. In this way, a low coherence implies low linear symmetry, and therefore a less reliable direction and consequently disparity value. A reliability metric for the disparity can thus be calculated from the structure tensor, as given by Bigun:

$$\begin{aligned} r=\frac{(J_{ss}-J_{xx})^{2}+4J^2_{xs}}{(J_{xx}+J_{ss})^{2}}. \end{aligned}$$

(8)

Despite the good performance achieved by the structure tensor-based methods to estimate disparity maps (Wanner and Goldluecke 2012; Li and Li 2013), these algorithms often fail to accurately represent the objects’ silhouettes and planar regions, as described in Sects. 3.2 and 3.3, respectively.

3.2 Silhouette enlargement

Silhouette enlargement is one of the most noticeable artefacts created by disparity estimation methods using the structure tensor. This effect mostly affects the occlusion regions of the light field, where objects in a given scene, captured from a certain viewpoint, occlude other objects further away from the camera. The foreground object is an occluding object while the object in the background is an occluded object. The region located around the boundary between an occluding object and the occluded one is defined as an occlusion region.

In the EPI representation of a light field, an occlusion region is a region containing a single edge with a slope that is inversely proportional to the disparity of the occluding object. Figure 3 shows a cropped EPI from the Cotton light field, from the HCI dataset presented by Johannsen et al. (2017), and a zoomed $9\times 9$ detail of an occlusion region. Two surfaces (surface A and surface B) are represented in any occlusion region. The white arrow represents the direction of linear symmetry calculated for the center pixel of the $9\times 9$ window, which is orthogonal to the occlusion edge.

By definition, the structure tensor ${\mathbf {T}}(x,s)$ includes convolutions with a Gaussian kernel $G_\sigma$, as shown in (1). These convolutions can be understood as calculating ${\mathbf {T}}(x_0,s_0)$ in the small window around a pixel where the value of $G_\sigma$ at $(x_0,s_0)$ is different than zero, for each pixel in an EPI. This results in the structure tensor evaluated for a window centered around $(x_0,s_0)$ being assigned to the center pixel itself.

In an occlusion region, the small window will be similar to Fig. 3. Assuming surface A is occluding surface B, the pixel $(x_0,s_0)$, corresponding to the central pixel of the window, is a part of the occluded object. Nevertheless, this pixel is attributed a tensor ${\mathbf {T}}(x_0,s_0)$ that indicates the linear symmetry of the occlusion window, where the only edge belongs to the occluding surface A. Therefore, the disparity d of the occluding object, estimated from the tensor ${\mathbf {T}}(x_0,s_0)$ using (7), is incorrectly attributed to the central pixel $(x_0,s_0)$, which belongs to the occluded object.

Fig. 3

The image shows a detail from an EPI image from the cotton light field. The arrow shows the direction of linear symmetry calculated with the structure tensor for the window, but attributed to point $(x_0,y_0)$

Considering the disparity map for any view of the light field, this results in an enlargement of the occluding objects, as their disparity is spread into the surrounding occluded regions. This problem is exacerbated by the smoothing step necessary to obtain accurate derivative information from a discrete image. It can be observed in Fig. 4 where the difference between the estimated disparity map (top left) and the ground truth (top right) shows that the foreground object is larger in the former than in the latter.

Fig. 4

The difference image between the base disparity estimation and the ground truth shows the enlarged silhouettes

Some methods in the literature try to mitigate the silhouette enlargement issue. In Li and Li (2013), a penalty measure for the reliability r of the structure tensor was proposed as an attempt to overcome this type of artifact. However, it proved to be highly sensitive to texture in the background regions of the neighboring object edges, providing only a minimal penalty when the algorithm fails in regions of uniform texture. In Lourenco et al. (2018), the authors of this paper proposed an edge detection based method to detect erroneous areas and inpaint them with values from the nearest background region. Despite achieving good results, the inpainting method presents some limitations as it is based only on the nearest pixels of the background region. To overcome this issue, a new method is proposed to more accurately correct these erroneous regions.

3.3 Low amplitude local noise

The structure tensor does not enforce local smoothness in disparity maps. Therefore, the error in each adjacent sample is dissociated, resembling low-amplitude noise as can be seen in Fig. 5, where the disparity along a single horizontal line in the Cotton light field image is shown.

Fig. 5

Disparity along one horizontal line (Cotton dataset). Structure tensor disparity estimation (bottom). Ground truth disparity (top)

When comparing the ground truth disparity (top in Fig. 5) with the disparity estimated from the structure tensor (bottom in Fig. 5), it is possible to observe some amplitude errors in the latter, especially in the background region, i.e., the left and right sides where disparity is small. This mostly corresponds to low amplitude local noise, which mainly affects planar regions. Therefore the estimated disparity $d_i$ of pixel i can be defined as the sum between the actual value $d'_i$ and a local error $\epsilon _i$:

$$\begin{aligned} d_i = d'_i + \epsilon _i. \end{aligned}$$

(9)

Conversely, if the disparity $d_i$ is converted to depth $z_i$, then:

$$\begin{aligned} z_i = z'_i + e_i, \end{aligned}$$

(10)

where $z'_i$ is the true depth value and $e_i$ refers to the estimation error. Thus, to estimate the depth gradient of a surface in the horizontal or vertical directions by directly comparing two adjacent pixels i and $i-1$, it results in:

$$\begin{aligned} \begin{aligned} {\varDelta } z_i&= z_i - z_{i-1}\\&= (z'_i - z'_{i-1}) + (e_i - e_{i-1})\\&= {\varDelta } z'_i + {\varDelta } e_i, \end{aligned} \end{aligned}$$

(11)

where ${\varDelta } z'_i$ is the true difference between the depth of both pixels and ${\varDelta } e_i$ is the difference of their errors. It is then clear, that as long as ${\varDelta } e_i$ is significant, the estimate ${\varDelta } z_i$ will be inaccurate. Furthermore, this error will be more significant for smaller ${\varDelta } z'_i$, so the worst estimates are obtained for regions with constant disparity in the chosen direction (e.g., surfaces parallel to the image plane).

In this framework, a Laplacian Matting optimisation is performed as described in Sect. 4.2, to efficiently reduce per-pixel disparity error $e_i$. Nevertheless, while it has a smoothing component that enforces similarity between the disparity of adjacent pixels, it does not sufficiently enforce similarity in the depth gradient ${\varDelta } z'_i$.

A normal map $N: {\mathbb {R}}^2\rightarrow {\mathbb {R}}^3$ is a map that for each pixel of a given image provides the normal vector of the surface at the pixel. It is possible to calculate a normal map using an estimated depth map and camera parameters. These maps can be useful for 3D modeling and provide a good visualisation of the three dimensional structure of a scene. Nevertheless, normal maps obtained from the optimised disparity map are still highly inaccurate, as shown in Fig. 6.¹ As expected from (11), the noise is mostly visible in the background surface, which is parallel to the camera plane. It is possible to observe that, in the regions where the ground truth normal map (c) has constant values, the normal vectors obtained from the structure tensor estimation appear as random (a).

Fig. 6

Comparison between a normal map obtained from the structure tensor depth estimation, the matting optimised disparity estimation and the ground truth disparity

The most common methods to solve this limitation of disparity estimation algorithms are global optimisation steps, such as graph cuts (Boykov et al. 2001) and belief propagation (Sun et al. 2003). These methods are mostly focused on reducing the error ${\varDelta } e_i$ by assigning a higher cost as ${\varDelta } e_i$ differs from zero. In this way they enforce similarity between neighbors at the cost of some possible over-smoothing. However, other methods explicitly designed to enforce regularity of normal maps, such as Strecke et al. (2017), achieve better results in terms of low-amplitude local noise and on estimated normal maps, but require higher computational complexity. To overcome low amplitude local noise and create a local map that enables the estimation of coherent three-dimensional structure, a new method based on plane-fitting is proposed in Sect. 4.3.

4 Proposed method

The proposed method for enhanced disparity map (DM) estimation is presented in the processing pipeline represented in Fig. 7, which includes the methods specifically devised for improving the previously described issues, namely the silhouette enlargement and low amplitude local noise.

Fig. 7

Block diagram of the proposed framework for disparity map estimation

After estimating disparity using the structure tensor, an object boundary detection algorithm is used to estimate the regions affected by silhouette enlargement. A provisional correction of this effect is performed, as explained in Sect. 4.1. Then, a matting-based optimisation step is applied, as this smoothing operation is required to achieve optimal results. The description of this method and its output is addressed in Sect. 4.2. Finally, a plane fitting-based algorithm is applied in order to reduce the effects of local noise based on the orientation of planar surfaces in a light field image. The estimated orientations of these planar surfaces are used to correct the erroneous regions found after object boundary detection, as described in Sect. 4.3.

4.1 Disparity estimation and initial silhouette enhancement

The aim of the method proposed in this section is to find the location of object boundaries in the central view of the light field, which are used in a provisional correction of the silhouette enlargement problem described in Sect. 3.2. To achieve this goal, the algorithm follows the steps described in Fig. 8.

Fig. 8

Algorithmic structure of the disparity estimation and silhouette enhancement algorithm

The first step is to convert the light field L(s, t, x, y) into a collection of horizontal $I_h^{(y)}(s,x)$ and vertical $I_h^{(x)}(t,y)$ EPIs, so that:

$$\begin{aligned} I_v^{(x)}(t,y)&= L(s_{mid},t,x_i,y), \end{aligned}$$

(12)

$$\begin{aligned} I_h^{(y)}(s,x)&= L(s,t_{mid},x,y_j), \end{aligned}$$

(13)

where $t_{mid}=\mathrm{round}(\frac{t_{max}}{2})$ and $s_{mid} = \mathrm{round}(\frac{s_{max}}{2})$, with $t_{max}$ and $s_{max}$ being the number of views in the vertical and horizontal directions, respectively. The remainder of this section describes the method for the horizontal EPIs $I_h^{(y)}(s,x)$, as the method for the vertical EPIs $I_v^{(x)}(t,y)$ is equal.

The second step involves estimating a disparity map $d^{(y)}(s,x)$, for each EPI, using the structure tensor. Reliability maps $r^{(y)}(s,x)$ of these estimations are also calculated.

Thirdly, two edge estimation steps are necessary. Edge estimation is applied directly to $I_h^{(y)}(s,x)$ and to the corresponding disparity map $d^{(y)}(s,x)$. This is further described in Sect. 4.1.1.

The fourth step consists in the estimation of an object boundary map from both edge maps. This map should include only edges that represent object boundaries, excluding texture-only edges. The method for estimating this map is detailed in Sect. 4.1.2.

The object edge map has incomplete edges, therefore, the fifth step intends to improve the object boundary map by implementing an edge-connection algorithm. This is further explained in Sect. 4.1.3.

Finally, the sixth step is a provisional correction of the disparity map applied by comparing the improved object edge map with edges in the disparity map. This is detailed in Sect. 4.1.4.

4.1.1 Edge detection

The process of locating the object boundaries requires edge detection on both the horizontal EPI ($I_h^{(y)}(s,x)$) and the disparity map ($d^{(y)}(s,x)$). Since $I_h^{(y)}(s,x)$, is a gray scale image, common edge detection algorithms perform adequately, therefore the Canny edge detector was used to obtain a binary edge map $e_{EPI}^{(y)}(s,x)$. When it is applied to $I_h^{(y)}(s,x)$ (Fig. 9 (Top)) the result is an edge map, as can be seen in Fig. 9 (Bottom).

Fig. 9

EPI representation (top) and result of the Canny edge detector (bottom)

For the disparity map $d^{(y)}(s,x)$, gradient-based methods like the Canny edge detector, provide false-positive results in surfaces approximately orthogonal to the camera plane, due to the presence of high disparity gradient. In this case, the Laplacian $\nabla ^2 d^{(y)}(s,x)$ proves to be a better tool to compute the disparity edge maps of $d^{(y)}(s,x)$, so a binary map $e_d^{(y)}(s,x)$ is created such that

$$\begin{aligned} e_d^{(y)}(s,x) = {\left\{ \begin{array}{ll} 0\, \mathrm {if}\, \nabla ^2 d^{(y)}(s,x) &{}\le th\\ 1\, \mathrm {if}\, \nabla ^2 d^{(y)}(s,x) &{}> th \end{array}\right. }, \end{aligned}$$

(14)

where th is a predefined threshold. As the purpose of this method is to correct the disparity map for the central view, only the central lines of the edge maps $e_{EPI}^{(y)}(s,x)$ and $e_d^{(y)}(s,x)$ are necessary, as they correspond to the position of edges in the central view. These lines are defined as $l_{EPI}^{(y)}(x) = e_{EPI}^{(y)}(s_{mid},x)$ and $l_d^{(y)}(x)=e_d^{(y)}(s_{mid},x)$.

4.1.2 Initial object boundary estimation

Not all texture edges represented in $l_{EPI}^{(y)}(x)$ correspond to an object boundary because some of them merely describe a change in the colour of a surface. Therefore, these are texture edges which do not have a matching disparity edge in $l_d^{(y)}(x)$. In order to obtain an initial map of object boundaries $m_{init}(x,y)$, it is necessary to match all edges described in $l_{EPI}^{(y)}(x)$ with a matching disparity edge in $l_d^{(y)}(x)$ and to exclude from $m_{init}(x,y)$ edges without match. However, as edges in $l_d^{(y)}(x)$ do not have the same coordinates as those in $l_{EPI}^{(y)}(x)$, a matching algorithm is applied. This process is described as shown in pseudo-code in Algorithm 1.

To provide a visual intuition for the algorithm, a schematic representation is depicted in Fig. 10. The figure shows a schematic of an EPI where four different regions are visible. The dashed lines refer to texture edges (E1, E2), while the lighter shaded regions refer to same region in the disparity map, and the outside edges (D1, D2, D3) are the disparity edges. The point $P_2$ shows the position of $E_2$ in the centre view, while point $P_2'$ shows the position in the centre view of its associated edge in the disparity map. Similarly, $P_3'$ shows the position of the edge $D_3$ in the centre view. The region ${\varDelta } s$, between $E_2$ and $D_2$ is the region where the disparity does not match the texture information. Working out the position of this region involves starting from an EPI edge (P$_2$) and searching over a region of size a to determine the position of P$'_2$.

Fig. 10

Silhouette enlargement: the original EPI lines ($E_1$; $E_2$) and the corresponding lines on the disparity map ($D_1; D_2$)

First, a search region a is defined for all points ${\mathbf {P}}_2 (P_2^x,s_{mid})$, such that, $l_{EPI}^{(y)}(P_2^x) = 1$:

$$\begin{aligned} a = \{x: |x - P_2| < w\},\ \forall x\in {\mathbb {N}}, \end{aligned}$$

(15)

where w is a constant defined with base on the size of the Gaussian kernel $G_\sigma$ used to construct $\mathbf {T_{x,y}}$. Then a disparity edge can be considered as a matching candidate if:

$$\begin{aligned} \exists \, P_2' \in a \,|\, l_d^{(y)}(P_2') = 1. \end{aligned}$$

(16)

Matching candidates are only considered valid object boundaries if they respect the following disparity constraint:

$$\begin{aligned} d^{(y)}\left( s_{mid},P_2' + \frac{(P_2 - P_2')}{|P_2 - P_2'|}\right) < d^{(y)}(s_{mid},P_2), \end{aligned}$$

(17)

which imposes that the disparity on the occluding regions is larger than the disparity in the occluded region. If this constraint is satisfied, then the map of object boundaries $m_{init}(P_2,y_j) = 1$, in all other cases $m_{init}(P_2,y_j) = 0$.

Fig. 11

Edge map (left) and resulting object boundary map (right)

Figure 11 compares the edge map (on the left), obtained from concatenating all texture edge lines $l_{EPI}^{(y)}(x)$ with $1<j<j_{max}$ with the object boundary map $m_{init}(x,y)$ (on the right), obtained after excluding texture-only edges.

Additionally, to be used in the provisional improvement step, a map of the edges of the center view disparity, $m_d(x,y)$ is created by concatenating all disparity edge lines $l_d^{(y)}(x)$ with $1<j<j_{max}$.

4.1.3 Boundary map improvement

Due to limitations of both edge detectors, $m_{init}(x,y)$ still has broken edge segments. This leads to visible artifacts in the disparity, when such edge map is used to enhance the silhouettes of objects in disparity maps, as can be seen in Fig. 12.

Fig. 12

Silhouette enhancement artifacts on the disparity map (Cotton image)

In order to create the final disparity map m(x, y) with more accurate object boundaries, the following methodology was devised:

• 1. Very short edges are eliminated (i.e., shorter than 4 pixels);

• 2. The edges of the centre view of the light field $L(s_{mid},t_{mid},x,y)$ are computed using the Canny detector and compared to $m_{init}(x,y)$;

• 3. When an edge in $m_{init}(x,y)$ is coincident with an edge in the centre view, all connected points in the texture edge map are included in $m_{init}(x,y)$;

• 4. Finally, the remaining broken edges segments are reconstructed.

To reconstruct these broken edges, the spatial position of the end points for each line is determined and the euclidean distance between all pairs of endpoints is stored in a symmetric matrix M. Additionally, a directional estimate $\alpha$ is assigned to each endpoint, based on the four closest points.

The objective is to draw a straight line, using the Bresenham line-drawing algorithm, connecting endpoints that should constitute a single, complete boundary of an object. The challenge lies in estimating which endpoint pairs should be connected. Since closer unconnected endpoints are more likely to belong to the same edge, an iterative algorithm is used to choose the unconnected endpoint pair with the smallest euclidean distance, which is equivalent to find the smallest values in M (excluding its principal diagonal). For each endpoint pair, a decision must be made before connecting a pair with a straight line.

Fig. 13

Example of a broken edge with connected endpoints

As shown in Fig. 13, the black dashed lines represent the estimated direction associated to the endpoint (angles $\alpha$ and $\alpha '$ with the horizontal) and the colored dashed line represents the straight line connecting the endpoints (angle $\beta$). If the difference between $\alpha$ and $\alpha '$ is larger than $90^o$ the endpoint pair is ignored and no line is drawn. Similarly, if either $|\alpha - \beta |$ or $|\alpha ' - \beta |$ are larger than a predefined threshold ($50^o$ is used), the endpoints are considered unconnected, because this indicates that the respective directions are significantly different from the straight line that would be drawn by the Bresenham algorithm. In all other cases a connecting line is drawn in m(x, y) between the two endpoints, connecting them through the colored dashed line. After reconstructing all possible broken edges throughout the entire disparity map, an improved map with more accurate object boundaries is obtained.

Fig. 14

Edge reconstruction detail on the cotton image

The resulting m(x, y) is depicted in Fig. 14, where a detailed zoom shows the difference before and after edge improvement for the Cotton light field. As can be seen, there is an accurate reconstruction of incomplete edges around the shoulder area of the statue. As real object boundaries constitute closed forms and do not include discontinuities, it is valid to consider that any discontinuity in m(x, y) corresponds to some sort of error in the edge detection process, which is confirmed by the results presented in Sect. 5.

4.1.4 Provisional correction

Following the previous reconstruction process, the spatial position of the object boundary edges in m(x, y) is compared to the corresponding position of the disparity edges in $m_d(x,y)$. The region between these corresponding edges is corrected by using the median of the values in the background region closest to the matching disparity edge.

As $m(x,y_j)$ contains new edges and excludes others, it is necessary to repeat the process used to find matching candidates, defined in Sect. 4.1.2, for the lines $m(x,y_j)$ and $m_d(x,y_j)$. In this case, for every $P_2$, such that $m(P_2,y_j) = 1$, a neighborhood a is defined as in (15). Then a disparity edge can be considered a matching candidate if:

$$\begin{aligned} \exists \, P_2' \in a \,|\, m_d(P_2',y_j) = 1. \end{aligned}$$

(18)

Additionally, the following disparity constraint must hold for any two matching edges:

$$\begin{aligned} d\left( P_2' + \frac{(P_2' - P_2)}{|P_2' - P_2|},y_j\right) < d(P_2,y_j), \end{aligned}$$

(19)

where d(x, y) is the disparity map obtained by concatenating all lines $d^{(y)}(s_{mid},x)$ with $1<j<j_{max}$. Like previously discussed, if this constraint is not fulfilled, this would allow occluded objects to exhibit higher disparities. Therefore, in such case the disparity edge for $x=P_2'$ is discarded. If the constraint is fulfilled, then the edges are considered to match and the region E is defined:

$$\begin{aligned} E = {\left\{ \begin{array}{ll} \{x: P_2< x\le P_2'\},\ \mathrm {if}\ P_2'\ge P_2\\ \{x: P_2 > x\ge P_2'\},\ \mathrm {if}\ P_2'< P_2\\ \end{array}\right. }. \end{aligned}$$

(20)

After this step, the disparity values to be corrected are defined as the vector $d(e,y_j)\ \forall e \in E$, which contains the disparities of the occluding object, rather than those of the background region. Thus the corrected disparity map is obtained as,

$$\begin{aligned} d(e,y_j) = \mathrm {median}(d(b,y_j)), \end{aligned}$$

(21)

where $d(b,y_j)\ \forall b\in B$ contains only the pixels with reliable disparity values out of the first ${\varPsi }$ pixels (from the disparity edge position) of the background region:

$$\begin{aligned} B = x \in \{P_2',\ldots ,P_2'+({\varPsi }-1)\} \cap \{x:r(x,y_j) < {\mathcal {V}}\}, {\varPsi } \in {\mathbb {N}}, \end{aligned}$$

(22)

where r(x, y) is the reliability map obtained by concatenating all lines $r^{(y)}(s_{mid},x)$ with $1<j<j_{max}$ and ${\mathcal {V}}$ is a constant chosen via empirical testing.

4.1.5 Analysis of vertical and horizontal disparity estimations

Following the above steps for horizontal and vertical EPIs, two object boundary maps $m_{hor}(x,y)$ and $m_{ver}(x,y)$ are obtained. Similarly, two disparity maps for the central view of the light field $d_{hor}(x,y)$ and $d_{ver}(x,y)$ are obtained, as well as two reliability maps $r_{hor}(x,y)$ and $r_{ver}(x,y)$. To build a single disparity map $d_f(x,y)$, for each point (x, y) the disparity estimation associated with a higher degree of reliability is chosen. The reliability of the chosen pixels is stored in $r_f(x,y)$.

4.2 Optimisation step

As described in Sect. 3.3, there is a high level of noise in structure tensor based estimations. Such noise makes it difficult to estimate the orientation of surfaces from the disparity results. This would pose serious constraints to the plane noise reduction algorithm presented in Sect. 4.3, therefore an optimisation step is applied by considering a Laplacian-based image matting correction (Levin et al. 2008). Starting from an initial disparity map estimation $\widetilde{{\varvec{d}}}$, an optimal solution ${\varvec{d}}$ is achieved by minimizing the energy function:

$$\begin{aligned} J({\varvec{d}})={\varvec{d}}^{T}L{\varvec{d}}+\lambda ({\varvec{d}}-\varvec{{\widetilde{d}}})^{T}C({\varvec{d}}-\varvec{{\widetilde{d}}}), \end{aligned}$$

(23)

where the optimised disparity values ${\varvec{d}}$ and the estimated disparity $\widetilde{{\varvec{d}}}$ are $N\times 1$ vectors. N represents the number of pixels in each view (i.e. $N=\mathrm{Height}\times \mathrm{Width}$) and L represents the so called affinity matrix, whose $N\times N$ elements can be understood as a measure of the affinity between each pixel and the rest of the pixels in the image. Furthermore, $\lambda$ is a global weight of the data term determining the strength of the smoothing operation (in Levin et al. (2008) $\lambda =5$) and C is a diagonal $N\times N$ matrix with reliability values from $r_f(x,y)$).

The energy function can be understood as a weighted sum of two terms. An edge-aware smoothing term (${\varvec{d}}^{T}L{\varvec{d}}$), that provides a smoother response to low variance portions of the image while keeping sharp results in transition areas, and a data term weighted by the reliability of the structure tensor $\lambda ({\varvec{d}}-\varvec{{\widetilde{d}}})^{T}C({\varvec{d}}-\varvec{{\widetilde{d}}})$).

While the smoothing optimisation is edge-aware, some over-smoothing of object edges still occurs. Thus, a mean-shift segmentation is used to separate the image into different segments based on color similarity, which are optimised separately. It aims to keep different objects in different segments, in order to avoid over-smoothing of edges. Since the mean-shift segmentation algorithm is not totally accurate, over-smoothing still occurs in some cases.

4.3 Plane noise reduction

As pointed out in Sect. 3.3, structure tensor-based disparity maps do not enforce local smoothness. In this section, a novel approach based on a seed growing strategy is presented to minimise this effect for planar regions of the light field.

Fig. 15

Structure of the plane noise reduction algorithm

As shown in the diagram of Fig. 15, the proposed framework starts by changing from image coordinates to real-world coordinates before dividing the image into a number of regions, which act as initial seeds. A plane is estimated for each of these seeds and they grow by including neighboring points close to the estimated plane, in terms of perpendicular distance. These results are further refined and used to establish a better in-painting option for the silhouette enhancement framework. Finally, the planes are used to reconstruct the depth map with more accurate values.

4.3.1 From pixels to scene coordinates

Images captured from a light field camera do not usually reflect an orthographic projection. This leads to distances not changing linearly across the whole image. Therefore, a surface that is planar in the real-world, with axis x, y, and z will not be represented by a plane in pixel coordinates, where m and n give the pixel position in the horizontal and vertical directions, respectively. Thus, it is necessary to convert the center view of the light field images to scene coordinates before plane estimation.

Conversion from disparity to depth depends on the scene and camera geometry. This work uses the same representation as the evaluation toolkit for the HCI dataset (Johannsen et al. 2017):

$$\begin{aligned} z = \frac{d}{s \cdot f \cdot b \cdot \max (w,h)} + \frac{1}{D}, \end{aligned}$$

(24)

where s represents the sensor size, f represents the camera focus distance, w and h represent, respectively, the width and height of the image, and D represents the focal length. Here, $\max (\cdot ,\cdot )$ represents the larger value between the two entries.

To estimate the (x, y) coordinates for each pixel with coordinates (m, n), the position of the upper left corner of the image is treated as the origin, with coordinates $(0,0,z_0)$. Then, the x and y coordinates for each pixel are estimated as:

$$\begin{aligned} {\left\{ \begin{array}{ll} x = 0.5 \frac{m\cdot s}{w-1}\cdot \frac{z}{f} \\ y = 0.5 \frac{n\cdot s}{h-1}\cdot \frac{z}{f} \end{array}\right. }. \end{aligned}$$

(25)

Thus, each pixel (m, n) in the image corresponds to a point (x, y, z) in three dimensional euclidean space, representing the relative metric position of the object represented in the pixel. Having completed this necessary step, it is now possible to detect planes using a seed growing approach.

4.3.2 Initial plane estimation

After obtaining the position of each pixel in real-world coordinates, it is possible to divide this set of positions into seeds $s_{m,n}$ and estimate the plane equation that best describes each seed. Traditional seed growth methods, such as the one described by Jin et al. (2014), assume a locally smooth disparity and, therefore, utilise small windows of $3\times 3$ samples. However, as previously mentioned, the presence of noise in the depth maps obtained from a structure tensor-based estimation means a sufficiently large amount of points is necessary to obtain a good plane estimate. To this end, all possible overlapping regions with size $w\times w$ are considered ($w=20$ was adopted in the scope of this work).

A plane estimate, of the form $z = Ax + By + C$, is found for each seed using RANSAC (Fischler and Bolles 1981) algorithm. The algorithm randomly chooses three points and calculates the plane formed by them. The euclidean distance of all other points to this plane is used as the error metric. Points with a distance of less than $\epsilon$ are considered inliers. The plane with the most inliers after N iterations is considered an inlier. N and $\epsilon$ are chosen empirically as is common practice with the algorithm.

However, not all seeds represent planar surfaces. To ensure the best results and computational swiftness it is appropriate to rank the fitness of the estimated plane. The number of inliers performs poorly as a metric in this regard for the reasons stated in Sect. 3.3. Jin et al. (2014) suggest the variance of the perpendicular distance but once again this fitness metric provides mixed results. Instead, the fact that seeds with poor fitness show clustered inlier points, while seeds with high fitness have more scattered inlier points is used.

A closeness metric is here introduced. For each RANSAC inlier point P let there be a set ${\varOmega }$ consisting of all other inlier points $P_i$ in a circular region with a radius of three pixels. The average distance to each pixel is given by:

$$\begin{aligned} \chi = \frac{\sum _{{\varOmega }} ||P - P_i||}{|{\varOmega }|}, \end{aligned}$$

(26)

where $|{\varOmega }|$ represents the cardinality of the set. If there are no pixels in the vicinity, the average distance $\chi = 3$. The closeness metric ${\bar{\chi }}$ is then given as the inverse of the mean of the $\chi$ distance, for all inliers.

In this way, seeds with a low closeness value present the best fitness. The order of seed growth is thus chosen by increasing order of closeness. Seeds with too high closeness are discarded. This use of inlier closeness to rank the fitness of each seed proved to be a working solution. Figure 16 shows a map of the non discarded surfaces for the Cotton light field compared with the map of planar surfaces provided by the dataset. One can see an effective separation between planar and smooth regions.

Fig. 16

Seed selection using the closeness metric

4.3.3 Seed growth

Each well fitted seed $s_{m,n}$ must grow until it includes all points in a scene plane. For that purpose, the seed is represented as a binary image with the same size as a view from the light field.

A morphological dilation operation (Soille 2004) on this binary image is used to find all adjacent points to this seed. All adjacent points are considered candidate points that might belong to the same scenic plane as the seed.

An adapted RANSAC algorithm is used to estimate a plane based on three random candidate points. The same threshold used in Sect. 4.3.2 is used to select inliers. The plane estimated from the three random candidates is compared with the current estimate for the given plane. Regardless of the number of inliers, a given estimate is only considered if the planes are considered similar.

To measure similarity between planes two metrics are used: the dot product of the planes measures similarity in orientation and the distance between parallel planes. To measure the distance between planes with similar orientation the following formula is used:

$$\begin{aligned} \mathrm{plane\ distance} = \frac{|D_1 - D_2|}{A_1^2 + B_1^2 + C_1^2}, \end{aligned}$$

(27)

where the current global plane estimate is in the form $A_1x+B_1y+C_1z = D_1$ and the current ransac plane estimate is given by $A_2x+B_2y+C_2z = D_2$.

The inliers of the estimate with the most inliers that is sufficiently similar to the current plane are selected as belonging to the same plane. A pseudo-code version of this adapted ransac algorithm is described in Algorithm 2.

To improve the robustness of the algorithm, the distance between the selected candidate points and the current plane is calculated. Those points with a distance above the ninety ninth percentile are not considered as part of the scene plane.

The process is repeated iteratively. Every 10 iterations the same adapted RANSAC algorithm is run for all points currently considered as belonging to the plane, with the obtained plane estimate being considered as the new current estimate. Just as before, points with a distance to the estimated plane above the ninety ninth percentile are excluded from the plane.

The above exclusion process is robust against noise, however, might allow the growth of seeds in nearly planar smooth surfaces. To address that a new measure is calculated based on the inlier points obtained from the RANSAC estimate.

Planar regions will have outlier points spread evenly across the region of the seed. Non-planar regions will have outliers concentrated where the smooth region becomes distant from the estimated plane. To distinguish between these two situations, for every outlier point,j, the geodesic distance, in pixels, to the closest inlier $g_j$ is calculated. The metric is then considered as,

$$\begin{aligned} \mathrm {coherence} = \sum _{j}\frac{(g_j)}{J}, \end{aligned}$$

(28)

where J is the total number of outliers.

The plane is considered grown when the distance to a plane of the current points is sufficiently larger than the average distance to the planes for all points. The process proves insensitive to this choice of threshold, so long as it isn’t excessively small, as the previous steps ensure the elimination of points that differ too much from the initial plane estimate. Choosing an excessively large threshold simply leads to larger computation times for similar results.

To further guarantee robustness, a final RANSAC is run on all current points of the plane. Only inliers below the ninetieth percentile in terms of distance to the estimated plane are considered part of the final grown plane. The coherence metric is re-calcualted for this RANSAC estimate. The entire Seed Growth algorithm is described in pseudo code in Algorithm 3.

4.3.4 Merging planes

Seed growth might be halted prematurely due to excessive noise or due to random chance in the RANSAC algorithm. Similarly, the same surface might be disconnected in the image due to occlusions. In both circumstances it’s beneficial to the final result to find and merge planes that are similar so that the final result shows a plane with the exact same direction.

In order to perform this merging, we iteratively compare all planes with each other considering the same criteria used in the Adapted RANSAC algorithm described in Algorithm 2 with similar thresholds. Whenever two planes are considered similar, the plane area is merged by us of a logical ’or’ operation on the binary map and RANSAC is run on all points to find a new estimate that better fits all points.

4.3.5 Filling holes in fully grown seeds

Since the method requires accurate border delineation, the thresholds k and $k_p$ are set in such way that the seed growth becomes highly sensitive to noise. This leads to the seeds having an incomplete description of the scene plane, which areas coincide with those where the initial depth map has a larger error. Therefore, reconstructing these incomplete areas should significantly improve the impact of the algorithm on depth map quality.

In this context, a map ${\mathbf {M}}$ is created associating each pixel of the image with the index i of a plane $s'_i$. This map is binarised and morphological operations are used to create binary images of the position of each holes in this map. To ensure that no important details are erased from the improved depth map, only holes occupying an area inferior to a predefined number of pixels are included in the binary map of the region described by the seed. This predefined value can be easily adjusted for different light fields to ensure the best possible results, nevertheless the threshold has been kept at 400 (the area in pixels of a $20\times 20$ pixel window) for all results presented in this paper.

Fig. 17

Map of the different planar regions estimated for the Dino light field, before and after hole filling (black pixels represent regions identified as non-planar)

As can be seen in Fig. 17, for the map ${\mathbf {M}}$ before and after the hole filling process, the binary map on the left contains holes where some noise exist in the original depth map, but some of these are fixed in the final map (on the right).

4.3.6 Silhouette improvement

In Sect. 4.1, two binary maps representing the boundaries of object silhouettes in the disparity map and in the central view of the light field image were generated. Due to failures in the provisional silhouette enlargement correction method presented in Sect. 4.1.4 and the over-smoothing effect of the matting-based optimisation presented in Sect. 4.2, the boundaries of fully grown seeds do not accurately match the silhouette map of the image.

To overcome such issues, a new approach is proposed. Firstly, a map ${\mathbf {A}}$ with the size of the central view of the light field image is created, providing an index for the corresponding seed, for each pixel of the original disparity map. The value of ${\mathbf {A}}$ is set to zero for pixels where no corresponding seed was estimated.

Fig. 18

Details of the difference to a ground truth before and after silhouette enhancement (normalised between 0 and 0.1)

Secondly, for every point where the object boundary map $m_{horiz}(x,y) = 1$, the horizontal neighbourhood of the corresponding disparity edge is checked for a seed in ${\mathbf {A}}$, a search distance must be defined (in this case 10 pixels). If a seed is found, the area between the first position of that seed and the object boundary edge is considered part of the seed, if it was not previously considered part of another seed. This procedure is repeated in the vertical direction using the respective object boundary map $m_{vert}(x,y)$.

The improvement in the reconstructed disparity map can be observed in Fig. 18, after the silhouette improvement for the Cotton light field. This image shows the difference between the ground truth and the disparity map (0 being black and values above 0.7 in white). It is also possible to notice a significant difference in the accuracy of the border of the detected plane, especially on the right of the image, in the edge of the statue’s head.

4.3.7 Depth map reconstruction

Having attributed a seed with a corresponding estimated plane equation of the form $z = Ax + By+ C$ for each pixel (n, m) of the image, it is now necessary to compute a new z for each pixel that is coherent with the plane equation. The relationship between a pixel (m, n) and its (x, y) coordinates is given by (25). Thus, the dependency between z and the pixel (n, m) can be obtained from the following system of three equations:

$$\begin{aligned} {\left\{ \begin{array}{ll} z = Ax + By + C \\ x = \frac{(\frac{m}{w-1}\times 0.5)s\cdot z_i}{f} \\ y = \frac{(\frac{n}{h-1}\times 0.5)s\cdot z_i}{f} \end{array}\right. } \Leftrightarrow {\left\{ \begin{array}{ll} z = Ax + By + c \\ x = k_h(m) \cdot z_i \\ y = k_v(n) \cdot z_i \end{array}\right. } \Leftrightarrow {\left\{ \begin{array}{ll} z = \frac{C}{1-Ak_h(m) - Bk`_v(n)} \\ x = \frac{k_h(m)C}{1-Ak_h(m) - Bk_v(n)} \\ y = \frac{k_v(n)C}{1-Ak_h(m) - Bk_v(n)} \end{array}\right. }. \end{aligned}$$

(29)

The system is solved in relation to z, for every pixel of the image using the plane estimated for the corresponding seed and the parameters of the camera. The values of the input depth map are updated with the z values given by the system. In order to better compare results with other algorithms and benchmarks the depth results are converted back to disparity values.

5 Results and discussion

The experimental results are presented in this section. The algorithm was implemented in MATLAB$^{\text{\textregistered} }$ and not optimised for computing efficiency, nevertheless a breakdown of the running time for each section of the code is presented. Secondly, subjective observation and objective metrics are used to compare the different stages of the algorithm. Finally, the algorithm is compared with the state-of-the-art, where it proves slightly behind other methods in terms of the Mean Square Error metric, but mostly ahead in terms of median angle error in planar regions. The comparisons are performed using the artificial HCI Training dataset provided by Johannsen et al. (2017), and the real world Lytro light field Concrete Cubes from the EPFL dataset (Řeřábek and Ebrahimi 2016).

5.1 Run-time breakdown

A MATLAB$^{\text{\textregistered} }$ implementation of the algorithm was run for the Test images of the HCI dataset. The tests were run on a computer with a Intel$^{\text{\textregistered} }$ Core$^{\mathrm{TM}}$ i7-10750H CPU with 2.60 GHz clock speed and 16 GB of RAM.

The running time, for each image was, on average, 9:26 min. Of this total time, 25.45% is related to the Disparity Estimation and Initial Enhancement, described in Sect. 4.1, 10.4% relates to the Matting Optimisation step, described in Sect. 4.1, and the remaining 64.15% are related to the Plane Noise Reduction improvement, described in Sect. 4.3.

The run-time of the structure tensor-based disparity estimation, and the optimisation step depends only on the size of the light-field, but most other steps are reliant on the structure of the captured scene. The time-complexity of all initial enhancement steps depending on the number of detected image edges, with most computations occurring only where an edge is found. Meanwhile, the Plane Noise Reduction algorithm has an increased run-time for images with several non-contiguous planar regions. This results in a varying run-time for equal-sized images. For example, the Cotton dataset achieves a run-time of only 2 min and 51 s, well below the average. As the image represents a single non-planar object (a statue) over a contiguous planar background, the low run-time is expected.

5.2 Algorithm performance

The different stages of the algorithm provide different but significant benefits to the disparity maps. Figure 19 shows the difference between the ground truth disparity and the estimated disparity map (DM) obtained after various steps of improvement. For better visibility, a darker colour implies a larger error.

Fig. 19

Absolute difference between the ground truth disparity map and estimated disparity maps

The silhouette enlargement effect is visible for the optimised base DM, shown in the error images as a large black region. To make the comparison fairer, the structure tensor-based initial estimation is shown with a matting optimisation. This is compared with the proposed matting optimised DM and finally with the full proposed method, after plane-noise reduction. The provisional silhouette enhancement, combined with matting optimisation, provides the biggest improvements to the silhouette of the disparity map. The improvements from plane noise reduction and the final silhouette improvement, described in Sect. 4.3.6, are focused on removing small amplitude noise and the over-smoothing of borders. These phenomena are poorly captured in the depiction of the absolute error.

Table 1 compares the Mean Square Error (MSE) obtained from the same disparity maps as Fig. 19, with the addition of the base DM with no optimisation. The MSE results confirm that the initial enhancement is very effective at increasing the accuracy of the disparity estimation, with the MSE for the matting optimised Cotton DM being 78% lower than the MSE for the opt. base DM. However, the improvements relating to the final step of the Proposed method are, once again, poorly captured by the MSE metric. Matting-based optimisation results in DMs with smooth border boundaries and thus the mitigation of small errors in the locality of edges resultant from the initial improvement. The final silhouette improvement step trades this mitigation for sharper borders. DMs obtained from the Proposed method therefore have a slightly larger MSE which does not accurately reflect a reduction in the accuracy of the disparity estimation.

Table 1 MSE $\times 100$ for the disparity estimated at different algorithm stages

In Fig. 20, the estimated normal maps are shown. In this case the unoptimised base structure tensor initial estimation (Structure Tensor) is compared with the matting optimised disparity map after provisional silhouette enhancement (Opt-Structure Tensor) and the results of the proposed method (Proposed) (see the diagram in Fig. 7). One can see that the normal maps from the initial estimation are entirely irregular, with larger errors in planar surfaces parallel to the camera plane. This is visible in the background of the Cotton and Sideboard normal maps. The matting-based optimisation does little to correct this problem in these regions while making smoother curved regions much more regular. However, it is possible to observe a much bigger improvement when using the proposed method. It is, however, important to note that the proposed algorithm does not accurately detect all planar regions and therefore does not provide any improvements to some scene planes. This is done to ensure smooth regions of the image are not misidentified as planes, which would introduce unnecessary error.

Fig. 20

Normal Maps obtained with the structure tensor-based estimation with and without the optimisation step

These results are backed by Table 2. In this table the median angle error of the surface normals calculated from the disparity map is shown for planar and non-planar regions. The used planar region map is the one provided by the dataset. One can see outstanding improvements for planar regions, with the median angle error falling below 1$^{\circ }$ for all but the Boxes dataset. Specifically, the estimated surface normal map for the Cotton light field shows a decrease of about 76$^{\circ }$ in median angle error in planar regions, accounting for a 99.76% reduction in this metric. Meanwhile, both the lack of a large increase in mean square error and a decrease in median angle error in non-planar regions shows that the algorithm is not detrimental in other regions.

Table 2 Median angle error, in degrees, for the surface normals obtained from different algorithm stages

The effect of noise on the full algorithm is addressed by using the algorithm for an image with excessive noise, as is the case of the artificial light field Dots, from the HCI dataset. The extreme amounts of noise make edge and plane detection untenable, resulting in a disparity map wholly unaffected by Plane Noise Reduction, but slightly altered by the initial enhancement process. However, this sensibility to noise does not extend to real-world images.

Fig. 21

Disparity and Normal Map performance for a non-synthetic light field image

Figure 21 shows the disparity and normal maps between different stages for the non-synthetic light field Concrete Cubes from the EPFL Light-field dataset. As can be seen, the added noise makes it non-trivial to recognise surfaces as planar, nevertheless, some regions of the image are still recognised as planes and enhanced.

5.3 Comparisons with state-of-the-art

The proposed method is compared, in terms of mean square error (MSE) and median angle error in planar regions (MAE), to the Multi-Resolution (RM3DE) method by Neri et al. (2015), the Spinning Parallelogram Operator (SPO) method (Zhang et al. 2016), the OFSY method (Strecke et al. 2017), a robust optimisation method (OBER), presented by Schilling et al. (2018), and the attention-based neural network (AttNet) (Tsai et al. 2020).

Those methods were selected for comparison, as the RM3DE, SPO and OBER methods are the non-neural network methods that provide the best results in terms of MSE in the literature, while the OFSY method is an optimization method that minimises the angle difference of a focus stack-based disparity estimation, which achieves the best results in terms of MAE. The attention-based neural network was chosen as it achieves the best results in the literature. It is, however, important to mention that the dataset is used in the validation process of the training of the neural network and, therefore, the results are not fully comparable.

Table 3 shows that the proposed method (Prop) achieves a similar performance in terms of MSE to both the SPO and RM3DE algorithms. The algorithm proves inferior to the OBER algorithm for all but the Cotton light field. This can be explained by this light field consisting of a single large object with well-defined borders, which greatly aids the silhouette enhancement algorithm, which relies on the quality of the edge detection. Meanwhile, the robust model introduced in the OBER method provides better performance in terms of MSE for light fields consisting of smaller objects or containing ill-defined borders. The AttNet algorithm includes these training images in the supervised learning framework and thus the MSE values could be misleading as they show an MSE value extremely close to zero for the Cotton and Dino light fields.

Table 4 shows that the proposed algorithm is superior to all others in terms of MAE in planar regions, with a relative difference to the next best algorithm (OFSY) reaching 88.3% for the Sideboard light field.

Table 3 MSE ($\times 100$) comparison of state-of-the-art algorithms

Table 4 MAE in planar regions comparison of state-of-the-art algorithms

6 Final remarks

A novel algorithm for disparity estimation was proposed to address known limitations of the traditional structure-tensor approach, namely silhouette enlargement and low amplitude local noise. The proposed method is based on edge map comparison as well as plane fitting. Erroneous regions were detected and corrected by juxtaposing the estimated edges in the luminance images with those in their respective disparity maps with good accuracy, thus significantly minimising silhouette enlargement in the resulting disparity maps. A noise resilient seed growth algorithm managed to accurately estimate the position and orientation of planar surfaces in a light field, resulting in a significant reduction of low amplitude local noise in the resulting disparity maps, enabling the estimation of accurate normal maps.

In the performed experiments, the resulting disparity maps prove competitive in terms of MSE. In terms of MAE in planar regions, the plane noise reduction algorithm achieves improvements of up to 99.76% in planar regions, resulting in a sate-of-the-art performance, beating the next best method by an average of 1.878$^{\circ }$, thus obtaining an average relative difference of 64.2%.

In conclusion, the proposed algorithm is well suited for light fields with strong edges and large planar surfaces, and is especially effective in cases where the orientation of surface normals is important, for instance, when the end-goal is to render an accurate 3D model of the scene.

Future avenues of research could include other applications where the structure tensor might prove promising, such as image quality assessment techniques, which have seen success when using gradient based approaches such as the Difference of Gaussian filter (Pei and Chen 2015). As for direct improvements to the method, replacing the matting-based optimisation method with an optimisation framework that takes into account the 4D structure of the light field may lead to more accurate results. Similarly, extending this method for multiple orientations, and not just the cross-hair views, would take advantage of the full light field volume and possibly achieve more accurate disparity results.