Abstract
The floating frame of reference formulation is an established method for the description of linear elastic bodies within multibody dynamics. An exact derivation leads to rather complex equations of motion. In order to reduce the computational burden, it is common to neglect certain terms. In the literature this is done by strict application of the small deformation assumption to the kinetic energy. This leads to a remarkably simplified set of equations. In this work, the significance of all terms is investigated at the level of the equations of motion. It is shown that for a large number of applications the previously mentioned set of simple equations is sufficient. Furthermore, scenarios are described in which this simple set is no longer accurate enough. Finally, guidelines are provided, so that engineers can decide which terms should be considered or not. The theoretical conclusions drawn in this work are underlined by qualitative numerical investigations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The floating frame of reference formulation (FFRF) is a widely used strategy for the inclusion of a flexible body into multibody system dynamics. The key idea is the separation of the overall motion into nonlinear rigid body motion superimposed by a small elastic deformation. The latter one is described by the superposition of weighted shape functions which are expressed in a body attached coordinate system which translates and rotates with the body. The final equations of motion for each flexible body contain both simple and complex terms. Hence, the numerical evaluation of some terms is cheap, yet expensive for the others. The numerical costly terms are associated with the body’s flexibility, where the numerical effort increases with the number of considered shape functions. For many practical applications it has been observed that the flexibility related terms are of minor significance. Those terms are the inertia of the deformed body, inertia coupling and parts in the centrifugal and the Coriolis forces, which are related to elastic deformations. In the literature two approaches can be found that deal with the question of which terms need to be considered and which need not. The first one is the strict application of a small deformation assumption at the level of the kinetic energy; see, for example, [12] or [21]. With this assumption, a remarkably simple set of equations is obtained. This work demonstrates why the latter description is probably sufficient for many applications, but not for all. The second approach, examples of which can be found in the software package MSC.ADAMS [11], gives the user the possibility to activate or deactivate certain terms in the equations of motion. The final decision is up to the user, but the guidance is not very clear. However, for both approaches there is a final uncertainty which is addressed in this work.
All inertia related terms of a flexible body in the FFRF are investigated on the level of the equations of motion with respect to their relevance. It is shown why the simplest possible formulation, stemming from the strict application of the small deformation assumption at the level of the kinetic energy, is sufficient for many applications. Beyond that, a clear guidance will be given when, in addition, the deformation dependent inertia tensor, inertia coupling, or elastic deformation related parts of the centrifugal and Coriolis forces should be considered. This will be finally summarized in a “set of guidelines”.
The paper is organized as follows: The first section briefly recaps the equations of motion of a free flexible body considering the FFRF. The assumptions, on which this paper is based, together with the resulting implications for the equations of motion, are documented in the next section. The Finite Element structures which are used for the sake of numerical illustration of the theoretical conclusions are introduced in the subsequent section. Following this, the small deformation assumption and its implications for the magnitude of the modal coordinates are discussed. In the next section, the maximum entries of significant matrices are estimated. The latter two estimations will be important for the determination of the significance of certain terms. The subsequent section is the key section of this contribution. All terms will be investigated with respect to their significance. It starts with the inertia of the deformable body followed by the inertia coupling of the rotational and flexible degrees of freedom. Finally, the terms of the quadratic velocity vector will be discussed. All the theoretical considerations in this chapter are accompanied by qualitative numerical investigations. In the subsequent chapter, a set of guidelines is presented in order to simplify the decision when and which term has to be considered or not. The paper will be concluded by summarizing the benefits when certain terms of the equations of motion can be neglected.
2 Brief review of the equations of motion
In order to avoid redundancy, an extensive derivation of the equations of motion is omitted and only relevant equations are reviewed. Details can be found in Shabana [1] and the work of Sherif and Nachbagauer [2]. For better readability with respect to the mentioned publications, the same notation is used in this work. In contrast to [1], a superscript referring to the number of the flexible body will be omitted.
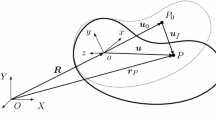
For the description of the position vector \(\boldsymbol{r}\), pointing to an arbitrary point P on a deformable body, two coordinate systems are used (see Fig. 1). One is a space-fixed coordinate system, which is called the inertial frame (IF), and the second is a so-called floating frame (FF), which is a body attached coordinate system.
The vector \(\boldsymbol{r}\) can be given as
where \(\boldsymbol{R}\) is the (\(3 \times 1\)) position vector from the origin of the IF to the origin of the FF. The matrix \(\boldsymbol{A}\) is the orthogonal rotation matrix transferring vectors expressed in the FF to their counterparts expressed in the IF. The vector from the origin of the FF to the point P is represented by \(\bar{\boldsymbol{u}}\). The overbar denotes that the quantity is expressed with respect to the FF. The vector \(\bar{\boldsymbol{u}}\) can be subdivided into \(\bar{\boldsymbol{u}}_{0}\) and \(\bar{\boldsymbol{u}}_{f}\) where \(\bar{\boldsymbol{u}}_{0}\) holds the time invariant vector from the origin of the FF to the particle’s position in the undeformed configuration. The \((3 \times 1)\) vector \(\bar{\boldsymbol{u}}_{f}\) represents the elastic deformations and is expressed by a superposition of weighted shape functions in the form \(\bar{\boldsymbol{u}}_{f} = \boldsymbol{Sq}_{f}\). The (\(3 \times n _{f}\)) matrix \(\boldsymbol{S}\) contains in its columns the time invariant shape functions, and the (\(n _{f}\times 1\)) vector \(\boldsymbol{q} _{f}\) holds the time variant weighting factors. In the context of the Finite Element Method, shape vectors are used instead of shape functions. Those shape vectors are commonly called “modes”. The expressions “shape functions, “shape vectors” and “modes” are used in this work synonymously. The kinetic energy \(T\) of the deformable body is given as
with the generalized coordinates
The (\(n_{\varTheta}\times 1\)) vector \(\boldsymbol{\varTheta}\) contains the generalized rotational coordinates where the number \(n_{\varTheta}\) depends on the particular choice (Euler parameters, Euler angles, …). All coordinates are collected in the (\(n \times 1\)) vector \(\boldsymbol{q}\) with \(n=3 + n_{\varTheta} + n _{f}\). According to [1, Chaps. 5.1 and 5.2], the submatrices can be computed using
where the matrix \(\boldsymbol{I}\) holds a (\(3 \times 3\)) identity matrix and \(\tilde{\bar{\boldsymbol{u}}}\) holds the (\(3 \times 3\)) skew symmetric matrix representation of the vector \(\bar{\boldsymbol{u}}\). The (\(3 \times n_{\varTheta}\)) matrix \(\bar{\boldsymbol{G}}\) transforms the generalized velocities into the (\(3 \times 1\)) angular velocity vector \(\bar{\boldsymbol{\omega}} \),
The parameters \(m\) and \(\rho \) represent the body’s mass and density, respectively, and \(V\) is the volume of the body. The application of the Lagrange formalism, together with the consideration of the body’s elastic forces, leads to the equations of motion in the form of
where the (\(n \times n\)) time invariant matrix \(\boldsymbol{K}\) can be given as
(see [1, Eq. (5.145)]). In contrast to the referenced equation, the constraints for a non-minimal set of rotational coordinates (e.g., Euler parameters) are omitted here, since they are not relevant for the considerations in this work. According to [2, Eqs. (25), (54) and (66)], the so-called (\(n\times 1\)) quadratic velocity vector \(\boldsymbol{Q} _{v}\) can be written as
Note that the different formulas for the quadratic velocity vector given in [2] and [1] are equal. This is discussed in detail in [2].
3 Assumptions and simplifications
In this section, some very common assumptions are discussed, since they lead to significant simplifications in the mass and stiffness matrix, as well as in the quadratic velocity vector.
3.1 Euler parameters
Euler parameters are used in this work for the parametrization of the rotation, see [1, Chap. 2.1]. Therefore, \(n _{\varTheta}=4\) and the constraint \(\boldsymbol{\varTheta} ^{\mathrm{T}} \boldsymbol{\varTheta} =1\) has to be considered in the final set of equations. An interesting discussion on Euler parameters can be found in [3]. However, due to its irrelevance for the subject of this paper, the constraint equation and its effect on the equations of motion are not considered. A consequence of the use of Euler parameters is the identity
(see [1, Eqs. (2.69) and (2.87)]). This leads to simplifications in (8) since terms containing the product \(\dot{\bar{\boldsymbol{G}}}\dot{\boldsymbol{\varTheta}}\) evaluate to zero.
3.2 Linearized mean-axis conditions
As mention before, the position of a mass particle is described with respect to an FF attached to the body. A distinct definition of the FF requires the determination of its origin and orientation. The most relevant suggestions, together with interesting discussions on this issue, can be found, among other references, in [4,5,6] and [7]. However, in this work a linearized mean axis frame, which is sometimes referred to as Buckens or linearized Tisserand frame, is considered. The constraint equations for the origin and the orientation of the FF are
In the next subsection, an advantageous choice of the shape functions in \(\boldsymbol{S}\) is discussed. Those shape functions automatically fulfill the constraints (10), and hence they need not be considered explicitly in the final set of equations.
3.3 Use of (pseudo) free surface modes together with an FF origin fixed to the center of gravity of the undeformed body
Again, just a brief review is given on the implications of the choice of free surface modes and an FF origin which is initially attached to the center of gravity of the undeformed body. More details can be found in [5] and [8].
Attaching the origin of the FF to the center of gravity of the undeformed body implies
Free surface modes are the eigenvectors of the unconstraint body with nonzero eigenvalues. The zero eigenvalue modes belong to the rigid body modes, see [8]. The properties of free surface modes can be given as
which is explained in detail in [8]. Due to the fact that \(\bar{\boldsymbol{u}}_{f} = \boldsymbol{Sq}_{f}\), and therefore \(\dot{\bar{\boldsymbol{u}}}_{f} = \boldsymbol{S}\dot{\boldsymbol{q}}_{f}\), the constraints (10) are fulfilled automatically, when free surface modes are used. The application of (12) to the equations of motion leads to significant simplifications of the equations of motion. Details on all resulting simplifications can be found in [5] and [8].
3.4 Use of mass normalized modes
Free surface modes are stiffness and mass orthogonal. Mass normalized modes are characterized by a scaling so that
where \(\boldsymbol{I} _{nf}\) is an (\(n _{f} \times n _{f}\)) identity matrix. The use of mass normalized modes leads to a diagonal stiffness matrix \(\boldsymbol{K} _{ff}\), which is hereafter denoted as \(\boldsymbol{\varOmega} ^{2}\). Its \(i\)th main diagonal entry \(\varOmega _{i} ^{2}\) holds the eigenvalue of mode number \(i\), which is equal to the squared eigenfrequency of the mode. From now on, it is assumed that the mode numbering correlates with increasing eigenfrequencies.
3.5 Use of central principal axis of inertia
It is assumed that the initial orientation of the axis of the FF matches the principal axis of inertia of the undeformed body.
3.6 Final equations of motion
The application of the former assumptions to the mass matrix (2) and the quadratic velocity vector (8) lead to much simpler equations of motions of the free flexible body in the form of
(see [1, Eqs. (8.15) and (8.23)] and [2, Eqs. (54) and (66), together with the subsequent discussion]). The slight difference to the referenced equations (\(\tilde{\bar{\boldsymbol{u}}}_{f}\) instead of \(\tilde{\bar{\boldsymbol{u}}}\)) in the third term of \((\boldsymbol{Q}_{v} )_{\varTheta} \) stems from a simplification due to (12). The same simplification leads to \(\tilde{\bar{\boldsymbol{u}}}_{f}\) instead of \(\tilde{\bar{\boldsymbol{u}}}\) in \(\boldsymbol{m}_{\varTheta f}\), which is well documented in [5] and [8].
In Shabana [1], so-called ”inertia shape“ integrals
can be found (see [1, Eqs. (5.70), (5.155), (5.156) and (5.158)]). The scalar \(\bar{u}_{0k}\) holds the \(k\)th component of the vector \(\bar{\boldsymbol{u}}_{0}\) (\(\bar{\boldsymbol{u}}_{0}^{\mathrm{T}} = \left[ \begin{array}{c@{\ }c@{\ }c} \bar{u}_{01} & \bar{u}_{02} & \bar{u}_{03} \end{array} \right]\)). The (\(1 \times n _{f}\)) row vector \(\boldsymbol{S} _{k}\) holds the \(k\)th row of \(\boldsymbol{S}\). In case free surface modes are used, it can be easily shown by the right equation of (12) that \(\bar{\boldsymbol{I}}_{kl}\) is equal to \(\bar{\boldsymbol{I}}_{lk}\). This interesting relationship has been found in unpublished records of Sherif ([2, 3, 8, 18] and [19]). By the use of (15), the integrals in Eq. (14) can be evaluated, and the equations of motion can be given in the form
where the (\(3 \times 3\)) matrix \(\boldsymbol{I} _{0}\), the (\(3 \times 3n _{f}\)) matrix \(\boldsymbol{W} _{1}\), the (\(3 n _{f} \times 3n _{f}\)) matrix \(\boldsymbol{W} _{2}\) and the (\(3n _{f} \times n _{f}\)) matrix \(\boldsymbol{W} _{3}\) hold invariant quantities and are defined as
and the (\(3n _{f} \times 3\)) matrix \(\boldsymbol{Q} _{f}\) holds the modal coordinates in the form of
This convenient nomenclature for the matrix \(\boldsymbol{W} _{1}\) and \(\boldsymbol{W} _{2}\) was introduced by Sherif, see [18] and [19]. The matrix \(\boldsymbol{W} _{3}\) can be found in the work of Shabana [1, Eqs. (5.74) to (5.76)] but is not denoted as \(\boldsymbol{W} _{3}\) there. It is worth mentioning that the (\(3 \times 3\)) matrix \(\boldsymbol{I} _{0}\) represents the inertia tensor of the undeformed body. Note that (14) and (16) contain the same equations of motion, the notation is merely different. Both equations are used in the following investigations.
3.7 Comment on the use of different mode basis
The literature offers several possibilities for the particular choice of shape vectors. The most famous mode base is probably the one of Craig [23]. Comparative studies of other possibilities can be found, among other references, in [24] and [25]. However, at this point of this work it is interesting to note that arbitrary mode shapes can be transformed into a mode base possessing the properties given before, see [8].
3.8 Comments on the complexity of the equations of motion and goal of this work
An obvious disadvantage of the equations of motion (16) are the necessary matrix vector operations related to the invariant matrices \(\boldsymbol{W} _{1}\), \(\boldsymbol{W} _{2}\) and \(\boldsymbol{W} _{3}\) stemming from the body’s flexibility. This increased numerical effort affects the residuum of (16) and the computation of the Jacobian matrix. In order to minimize this computational burden, some suggestions for the negligence of certain terms can be found in the literature and multibody dynamic software packages. As an example, [12] can be cited. This paper refers to the classical paper [13] where the hypothesis of small elastic deformations around the undeformed configuration is applied on the level of kinetic energy. As a consequence, the coupling between the rotational and flexible degrees of freedom in the mass matrix and in the quadratic velocity vector vanishes in the final equations of motion. Another example is the commercially available software package MSC.ADAMS [14], which offers the user a possibility to deactivate certain terms of the mass matrix. The explanation of the terms is quite vague and, hence, the decision is difficult to make for a user without extensive knowledge of the theory of flexible multibody systems.
The goal of this work is a systematic investigation on the relevance of all the terms related to the invariant matrices on the level of the equations of motion. As far as we know, this kind of in depth analysis of the FFRF is a new contribution to the existing literature. Beside the theoretical insights a set of guidelines is provided as practical benefit. Thereby engineers can decide which terms should be considered or not.
4 Illustrative examples used in the paper
In the practical use of multibody simulation, the flexible bodies are mostly modeled via the Finite Element Method. In that context, the displacements are evaluated at certain grid points and instead of shape functions, shape vectors are used to describe the elastic deformation. More comments on the transition from a “continuous formulation” to a formulation based on Finite Element models can be found in [1, Chap. 5.2, Sect. “Lumped mass”]. Although the details for the computation of the invariant matrices \(\boldsymbol{I} _{0}\), \(\boldsymbol{W} _{1}\), \(\boldsymbol{W} _{2}\) and \(\boldsymbol{W} _{3}\) may change, the final equations of motion (16) remain the same. Those matrices are computed based on the result of the Finite Element analysis and are part of the procedure when a flexible body is imported into the multibody simulation software. In MSC.ADAMS [14], for example, those matrices can be found in the so-called *.mtx file.
In this work several theoretical considerations are presented. The drawn conclusions are of fundamental character for all flexible bodies independent of the overall multibody system where the flexible bodies are embedded. Therefore, it is not necessary to present results of time integrations of particular multibody systems. Instead, the presented examples deal with estimations of effects based on the former mentioned invariant matrices, which are flexible body data only.
The Finite Element (FE) structures used to this end are introduced in this section. Six very different FE structures have been selected in order to cover a broad band of applications. All the assumptions mentioned in the former subsection are valid for the following FE structures. For all the Finite Element models given below, the consistent set of units, ton, millimeter and Newton, have been used. The necessary matrices \(\boldsymbol{I} _{0}\), \(\boldsymbol{W} _{1}\), \(\boldsymbol{W} _{2}\) and \(\boldsymbol{W} _{3}\) have been computed using the flexible body interface of MSC.ADAMS [14]. Consequently, the mode base of Craig [23] is used, which consists of constraint normal modes (CNM) and constraint interface modes (CIM). Screenshots of the FE models can be seen in Fig. 2 and additional information is collected in Table 1.
For reasons of confidentially, the picture of the car body can only be shown in low-resolution. The generic structure GenStruct1 has been created in order to underline the effect of a particular structural compliance with respect to centrifugal forces. The second generic structure GenStruct2 is similar as GenStruct1 without having this special sensitivity to centrifugal forces.
The eigenvalues of the final modes are later used to estimate an upper limit of the modal coordinates. Therefore, the eigenfrequencies of the first ten modes are given in Fig. 3.
5 Assumption of small deformations
All investigated terms are related to effects caused by the flexibility of the body. These effects are increasing with the elastic deformation of the body. Therefore, it is important to specify a realistic upper bound of expectable deformations, and hence an upper bound of the modal coordinates.
5.1 Small elastic deformations with respect to the body’s dimension
Commonly, the mode shapes are obtained by a linear Finite Element analysis. Consequently, the attribute “linear” defines the range of validity. The deformations have to be small enough, so that no geometric nonlinearities and no material nonlinearities take place. In the simple case of a tensile bar, the longitudinal deformation is given as \(\Delta l = \frac{\sigma l_{0}}{E}\), where \(\sigma \) is the stress, \(l _{0}\) the length of the bar and \(E\) the Young modulus. The use of an unrealistic high yield stress limit \(\sigma = 10^{3}~\mbox{N}/\mbox{mm}^{2}\) and \(E = 2\times 10^{5}~\mbox{N}/\mbox{mm}^{2}\) (steel) leads to a maximum displacement of 0.5% of the original length. In cases where slender structures like beams or plates are loaded by bending, geometric nonlinearities are the limiting criterion for the validity of a linear computation. In the case of a two-sided clamped beam or a four-sided clamped plate, geometric nonlinearities significantly influence the result even if the deflection of the center point is very small. The regime of validity is larger when just a one-sided clamped beam or plate is considered. However, in the literature it is often stated that for linear analysis, the maximum deflection should be in the range of the cross-section dimensions. To give an example, for the Finite Element solver in SolidWorks [9], it is suggested to use nonlinear techniques in case of deformations larger than 1/20 times the largest dimension of the body [10]. However, in this paper it is supposed that the elastic deformations are at least one to two magnitudes smaller than the body’s largest extension.
5.2 Magnitude of modes and modal coordinates
Two very frequently used sets of consistent units are kilogram/meter and ton/millimeter, respectively. When those units are used, experience shows that the requirement of small deformations (no material and no geometric nonlinearity) leads to modal scaling factors (so-called “modal coordinates”) typically much less than one. The following considerations show why this assumption mostly holds true.
A consequence of the mentioned mass normalization (Eq. (13)) is the relationship
where the symbol \(S_{i} ^{p}\) holds the component \(i\) of the \(p\)th mode \(\boldsymbol{S} ^{p}\). Using the mean value theorem, Eq. (19) can be modified into
where \(m _{t}\) holds the total mass of the structure and \(\bar{S}_{i}^{p}\) represents a kind of averaged modal deflection of component \(i\). It can be seen that the averaged modal deflection increases when the mass is decreasing, and vice versa. In the following, two extreme cases are investigated. For the first case, it is assumed that the modal deflections are uniformly distributed to all degrees of freedom. The averaged deflection \(\bar{S}_{a1}^{p}\) can then be given as
For the second case, it is assumed that the modal deflection is dominated by one component, like the first bending mode of a plate having only deflections normal to the plate plane. In that case the averaged deflection \(\bar{S}_{a2}^{p}\) can be approximated as
In Fig. 4 the averaged modal deflection is plotted vs total mass.
In case when kilogram and meter are used as units, a mass of 1 kilogram leads to an averaged modal deflection of 1 meter. A structure of 100 kilograms still leads to an averaged deflection of around 0.1 meter. When ton and millimeter are in use, a mass of 0.001 tons (=1 kg) would lead to an averaged modal deflection of around 40 millimeters. A mass of 0.1 tons (=100 kg) implies an averaged deflection of 4 millimeters. Note once again that these are averaged deflections, the maximum deflection is probably at least a factor of 2 higher. In order to fulfill the restriction of small deformations, modal coordinates smaller than one seem to be a valid assumption. However, heavy structures may not fulfill that assumption.
The former conclusion that the modal coordinates are normally smaller than one depends on the units employed; in this case, kilogram and meter and ton and millimeter, respectively. This conclusion may not be valid for all combinations of length and mass units. Nevertheless, the investigations on the relevance of certain terms in the equations of motion are of general nature since these terms describe mechanical effects like the change of inertia due to deformation, coupling between rotation and deformation, centrifugal and Coriolis forces. These phenomena are of a fundamental nature and their relevance does not depend on the units.
5.2.1 Numerical examples
In order to estimate the potential maximum modal amplitudes of the investigated FE structures the maximum von Mises stress for the first 16 modes is given in Fig. 5. A modal coordinate of one would imply that the stress contribution of this mode is of the same magnitude, as shown in Fig. 5.
It can be seen that for almost all structures a modal amplitude lower than one can be expected, because otherwise material nonlinearities take place. Only the car and plate require a more detailed investigation.
Car
The first mode of the car, scaled by 1, leads to a stress contribution of 258 N/mm2 (von Mises). This is already a high stress level, but one may argue that a very good material could handle that. Figure 6 shows the deflection due to this mode for scaling factors 1 and −1. It can be seen that a vibration with such an amplitude is an unrealistic scenario for a passenger car during operation.
Plate
The stresses inside the plate caused by the modes scaled with 1 are definitely in the linear range with respect to material nonlinearity. Figure 6 shows the deflection for the first mode when scaled with −1 and 1, together with the undeformed state (black). The maximum displacement of 42 mm is far beyond the plate thickness of 0.5 mm and occurs at the plates corners. It can be assumed that geometric nonlinear effects take place in case of such deformations. Therefore, the assumption that the modal coordinates remain smaller than 1 is probably a good estimate for that structure, too.
Based on the previous observations, the maximum modal coordinate for the first mode of the Finite Element structures given in this paper is 1 when the stress of the corresponding mode is lower than 500 N/mm2. Otherwise the maximum modal coordinate is chosen, so that the stress of the mode becomes 500 N/mm2. The maximum modal coordinate of all other modes is scaled by the ratio of the modes eigenvalue and the eigenvalue of the first mode. This is because the eigenvalue acts as stiffness (\({=}\boldsymbol{\varOmega} ^{2}\)) in Eq. (14). The maximum modal coordinates of the first ten modes for the examples in this paper are depicted in Fig. 7. The latter figure reveals a general tendency: The stiffer and compacter a structure, the smaller the expected modal amplitudes. For very stiff and very compact structures, like the connecting rod, modal amplitudes much smaller than 1 can be expected.
6 Magnitude of entries in invariants \(W_{1}\), \(W_{2}\) and \(W_{3}\)
In the key section of this paper, the significance of the terms holding the matrices \(\boldsymbol{W} _{1}\), \(\boldsymbol{W} _{2}\) and \(\boldsymbol{W} _{3}\) is investigated. This chapter is devoted to the magnitude of the entries of the latter matrices in order to estimate whether a certain effect may be negligible with respect to another one.
6.1 Magnitude of entries in matrix \(W_{1}\)
Matrix \(\boldsymbol{W} _{1}\) is constructed using submatrices \(\bar{\boldsymbol{I}}_{kl}\), see (17). The components of \(\bar{\boldsymbol{I}}_{kl}\) are computed along (15), which leads to the evaluation of an integral in the form of \(\int_{V} \bar{u}_{0k}S_{l}^{m}\rho \,\mathrm{d}V\). An application of the Cauchy–Schwarz inequality delivers
According to (15), the terms \(( \int_{V} ( \bar{u}_{0k} )^{2}\rho \,\mathrm{d}V )\) are defined as \(I _{kk}\), which are the main diagonal entries of \(\boldsymbol{I} _{0}\). Equation (19) shows that the maximum value of \(\int_{V} ( S_{l}^{m} )^{2}\rho \,\mathrm{d}V\) is 1. Due to inequality (23), it can be expected that the Euclidean norm of \(\boldsymbol{W} _{1}\) is normally significant less than the norm of \(\boldsymbol{I} _{0}\). This assumption is confirmed by the numerical examples in the next section.
6.1.1 Numerical examples
The following quantities are computed for matrix \(\boldsymbol{W} _{1}\) and summarized in Table 2:
-
Maximum absolute entry.
-
The average of the magnitude of all nonzero entries. This value gives an idea of whether most of the entries are around the maximum entry or much smaller.
-
Euclidean norms of \(\boldsymbol{W} _{1}\) and \(\boldsymbol{I}_{0}\).
It can be seen in Table 2 that the Euclidean norm of \(\boldsymbol{I} _{0}\) is always greater than that of \(\boldsymbol{W} _{1}\). Moreover, it is interesting to observe that the average value of the magnitude of all nonzero entries is always significantly less than the maximum entry. This leads to the conclusion that most of the entries in \(\boldsymbol{W} _{1}\) hold a magnitude which is significantly smaller than the maximum.
6.2 Magnitude of entries in matrices \(\boldsymbol{W}_{2}\) and \(\boldsymbol{W}_{3}\)
Matrices \(\boldsymbol{W} _{2}\) and \(\boldsymbol{W} _{3}\) are constructed using the submatrices \(\bar{\boldsymbol{S}}_{kl}\) (see (17)). The components of \(\bar{\boldsymbol{S}}_{kl}\) are computed as in (15), which leads to the evaluation of an integral in the form of \(\int_{V} S_{k}^{p}S_{l}^{m}\rho\, \mathrm{d}V\). An application of the Cauchy–Schwarz inequality delivers
Recalling Eq. (19), it is clear that the theoretical maximum value of \(\int_{V} ( S_{k}^{p} )^{2}\rho\, \mathrm{d}V\) is 1. Therefore, the entries of \(\bar{\boldsymbol{S}}_{kl}\) have to be between −1 and 1. Consequently, the entries of \(\boldsymbol{W} _{2}\) and \(\boldsymbol{W} _{3}\) have to be between −2 and 2 (see (17)). Based on the evaluated integrals it can be stated that the norms of \(\boldsymbol{W} _{2}\) and \(\boldsymbol{W} _{3}\) are typically much lower than the norms of \(\boldsymbol{I} _{0}\) and \(\boldsymbol{W} _{1}\). Due to the conservative assumption that the maximum value is 1, it can be expected that the magnitude of most of the entries is much smaller than 1. Both assumptions are confirmed by the numerical examples below.
6.2.1 Numerical examples
The following quantities are computed for matrices \(\boldsymbol{W} _{2}\) and \(\boldsymbol{W} _{3}\) and summarized in Table 3:
-
Maximum absolute entry.
-
The average of the magnitude of all nonzero entries. This value gives an idea whether most of the entries are around the maximum entry or much smaller.
-
Euclidean norm.
It can be seen that the maximum values are always below 2, which is in accordance with the theoretical considerations. In comparison to the entries in Table 2, it turns out that the norms of \(\boldsymbol{W} _{2}\) and \(\boldsymbol{W} _{3}\) are smaller than those of \(\boldsymbol{I} _{0}\) and \(\boldsymbol{W} _{1}\). It is notable that the average value of the magnitude of all nonzero entries is significant less than the maximum entry. This leads again to the conclusion that the entries of both matrices are mostly significantly smaller than the maximum entry. Finally, it can be stated that the entries of \(\boldsymbol{W} _{3}\) tend to be less than the entries of \(\boldsymbol{W} _{2}\).
7 Investigations on the relevance of the single terms in the equations of motion
The following considerations are based on the full set of equations of motion (14), or when expressed in matrix notation (16). By setting all the terms related to \(\boldsymbol{W} _{1}\), \(\boldsymbol{W} _{2}\) and \(\boldsymbol{W} _{3}\) to zero, the simplest possible representation of (16) is
An alternative way to obtain Eqs. (25) is by a strict application of the small deformation assumption to the kinetic energy (2). This means that in case of a sum of the body’s extension and its deformation, the deformation is always neglected, as reported in [12] (and the reference therein to [13]). The obvious advantage of (25) is its simplicity and the fact that for the free body all coordinates are decoupled. The intention of this key chapter is to clarify whether and when all terms have to be considered (like (16)) or just the simplest possible form (like (25)), or something in-between has to be used.
For the following investigations, a free floating flexible body is assumed as described by (14) and (16). If the body is connected to other bodies via constraining or imposed forces, the situation is somehow different and the resulting consequences are discussed as well.
7.1 Rotational inertia of the deformed body
7.1.1 Theoretical considerations
In this section the change of the inertia due to deformation is investigated. The corresponding term in the mass matrix is the (\(n _{\varTheta} \times n _{\varTheta}\)) matrix \(\mathbf{m}_{\varTheta \varTheta}\). According to (14) and (16), this matrix can be given as
The \((3 \times 3)\) matrix \(\boldsymbol{I}_{\varTheta \varTheta}\) holds the inertia of the deformed body. This matrix can be found in the first term of \((\boldsymbol{Q} _{v})_{\varTheta}\) in (14) as well. An evaluation of the integral in (26) gives
where \(I_{\varTheta \varTheta,kk}\) holds the \(k\)th main diagonal entry of \(\boldsymbol{I}_{\varTheta \varTheta}\), \(\bar{u}_{0l}\) holds the \(l\)th component of the vector \(\bar{\boldsymbol{u}}_{0}\), and \(\bar{u}_{fm}\) holds the \(m\)th component of the vector \(\bar{\boldsymbol{u}}_{f}\). The symbols \(k\), \(l\) and \(m\) represent the three directions in space. The first integrand contains the inertia of the undeformed body and can be found in the matrix \(\boldsymbol{I}_{0}\), which is a diagonal matrix due to the assumption of principal axis of inertia. The second integrand contains a linear change in inertia and is represented in matrix form by \(\boldsymbol{W} _{1} \boldsymbol{Q} _{f}\). The third integrand contains a quadratic change of inertia and is given by \(\boldsymbol{Q} _{f} ^{\mathrm{T}} \boldsymbol{W} _{2} \boldsymbol{Q} _{f}\). Under the assumption that the deformation is one or two magnitudes smaller than the largest dimension and within the linear range, just two special scenarios can occur, for which the inertia tensor changes significantly due to the body’s deformation:
-
The second and the third terms (\(\boldsymbol{W} _{1} \boldsymbol{Q} _{f}\) and \(\boldsymbol{Q} _{f} ^{\mathrm{T}} \boldsymbol{W} _{2} \boldsymbol{Q} _{f}\)) cannot be neglected if neither the body’s dimension in the direction \(l\) nor \(m\) in (27) is significantly greater than the flexible deformations in the same directions. A long beam with a small cross-section would be such a structure. In this case, the deformation may have a similar magnitude as the body’s dimension in that direction and the two state-dependent terms may be important for an accurate result. A close look at (27) gives no reason to assume that the quadratic term is less important than the linear part if such a beam-like structure is considered.
-
The state-dependent terms may also be non-negligible in case of structures being particularly soft with respect to centrifugal forces, like GenStruct1. For such structures, small displacements may have a considerable impact on the moment of inertia. If such a structure is considered, it can be assumed that the linear term will dominate the quadratic term since the product of the body’s extension and the elastic deformation will dominate the square of the elastic deformation, see Eq. (27).
Note that the former two considerations are just meaningful when the body’s state is dominated by its own inertia. Let us assume a body which fulfills one of the former two criteria for the consideration of the state-dependent terms. If such a body is stiffly connected to another body with remarkable inertia, it is sufficient to consider \(\boldsymbol{I} _{0}\) only. An example for such a situation is a rigid flywheel which is mounted on a flexible slender beam. As a general observation, it can be stated that the influence of \(\boldsymbol{W} _{1} \boldsymbol{Q} _{f}\) and \(\boldsymbol{Q} _{f} ^{\mathrm{T}} \boldsymbol{W} _{2} \boldsymbol{Q} _{f}\) decreases when other bodies are stiffly connected to the flexible body under consideration.
7.1.2 Numerical examples
In order to quantify the influence of the deformation on the inertia, the following two quantities are defined:
where \(I_{0,kk}\) holds the principle moment of inertia of the undeformed body around the axis \(k\); \(I_{L,kk,p}\) contains the result of \(\boldsymbol{W} _{1} \boldsymbol{Q} _{f}\) at the same position when the \(p\)th mode is scaled with a certain amplitude; \(I_{Q,kk,p}\) gives the corresponding quantity due to \(\boldsymbol{Q} _{f} ^{\mathrm{T}} \boldsymbol{W} _{2} \boldsymbol{Q} _{f}\). Therefore \(\Delta I_{L,kk,\max}\) and \(\Delta I_{Q,kk,\max}\) are measures of the change in the inertia around axis \(k\) due to the linear and the quadratic part of Eq. (27). In Fig. 8, \(\Delta I_{L,kk,\max}\) and \(\Delta I_{Q,kk,\max}\) are given for the first ten modes of the investigated structures. Thereby the maximum modal amplitudes have been chosen as depicted in Fig. 7. It can be seen that all changes are below 5% except in GenStruct1 and the beam. This is in good accordance with the former theoretical considerations. The beam structure is characterized by a mass distribution which is dominated by one dimension in space, namely direction ‘3’. Therefore, \(\Delta I_{Q,33,\max}\) comes into the range of \(I_{0,33}\). It is interesting to note that the linear change is negligible in comparison to the quadratic one. As it was already assumed in the theoretical part, it is wrong to argue that the quadratic part is less important than the linear one in case of a beam-like structure.
The structure GenStruct1 is very soft around axis 1. Its first bending mode is depicted in Fig. 9 together with the undeformed structure. Due to the special mass distribution and the particular softness, a remarkable effect on the inertia around axis 1 can be expected; even the deformation may remain in the linear range. Therefore \(\Delta I_{L,11,\max}\) and \(\Delta I_{Q,11,\max}\) come into the range of 10% of \(I_{0,11}\). A similar structure GenStruct2 does not show this effect because of its stiffer character.
7.1.3 Summary
The deformation-related change of a body’s rotational inertia can be mostly neglected. Exceptions are only possible if the body has either a dominant extension in one direction or a very particular mass distribution in combination with particular (soft) stiffness properties. If one of those two situations takes place, an additional requirement needs to be fulfilled, which is that the body is a free body or at least very softly connected to other bodies, so that its state is mainly determined by its own inertia. Consequently, in nearly all industrial applications the terms \(\boldsymbol{W} _{1} \boldsymbol{Q} _{f}\) and \(\boldsymbol{Q} _{f} ^{\mathrm{T}} \boldsymbol{W} _{2} \boldsymbol{Q} _{f}\) can be neglected, except when the previously mentioned criteria are fulfilled.
7.2 Inertia coupling
7.2.1 Theoretical considerations
In this section the coupling effect of \(\boldsymbol{m}_{\varTheta f}\ddot{\boldsymbol{q}}_{f}\) on \(\boldsymbol{\varTheta} \) (second line in equations of motion (14)) and \(\boldsymbol{m}_{\varTheta f}^{\mathrm{T}}\ddot{\boldsymbol{\varTheta}} \) on \(\ddot{\boldsymbol{q}}_{f}\) (third line in equations of motion (14)) is investigated. For the subsequent investigations, the second line in (14) and (16) is pre-multiplied with \(\bar{\boldsymbol{G}}\). This leads to
and
where the relations
[1, Eqs. (2.87), (2.69) and (2.84)] have been used. The same equations in matrix form, using the definition of the inertia integrals (15), can be given as
with
Note that the change of the inertia due to the body’s deformation has already been investigated in the preceding section and is therefore neglected in the mass matrix and in the quadratic velocity vector. Another obvious observation is that the inertia coupling depends on the modal deflection but not on velocity, like the quadratic velocity vector does. As a consequence, it is not necessary to distinguish between moderate and high angular velocities, which is the case when the terms of \(\bar{\boldsymbol{Q}}_{v}\) are investigated. In the next step, \(\ddot{\boldsymbol{q}}_{f}\) of the first line in (29) is expressed by the second line, which leads to
Expressing \(\bar{\boldsymbol{\alpha}} \) of the second line in (29) by the first line leads to
In (34) the modal coordinates’ inertia is reduced to the rotational coordinates while the rotational inertia is reduced to the flexible coordinates in (35). The reduced inertias can be given in integral and matrix form as
and
where \(\boldsymbol{I}_{f\to\varTheta}\) has dimension \((3 \times 3)\) and \(\boldsymbol{I}_{\varTheta\to f}\) has dimension (\(n _{f} \times n _{f}\)). The main diagonal entries of \(\boldsymbol{I}_{f\to \varTheta}\) and \(\boldsymbol{I}_{\varTheta\to f}\) can be given as
and
where the symbol \(S _{k} ^{p}\) holds the \(k\)th component of the \(p\)th shape function. A closer look at Eq. (38) reveals that the second integral is not dominated by the first integral when the deformations are in the range of the body’s extension in two directions. This may happen in cases of beam-like structures with one dominating spatial extension. This is basically the same observation as in the section before. For the inertia coupling from the rotational unto the flexible degrees of freedom, the same conclusion can be drawn when Eq. (39) is investigated. The part of the inertia which comes from the angular acceleration may have a reasonable magnitude with respect to 1 (=inertia of mass normalized modes) due to the same reason as mention before, considering Eq. (38). Although Eqs. (38) and (39) look different, the conclusion is the same for both. It can be expected that the inertia coupling is only relevant for those bodies for which the change of rotational inertia may be relevant. These are beam-like structures and structures with a particular mass and stiffness distribution, as in the previous section. This estimation is numerically confirmed in the following section.
Note again that the former considerations hold true for a body which is not stiffly connected to other bodies with remarkable inertia. In that case the coupling effect loses importance and can be neglected for all kinds of flexible body.
7.2.2 Numerical examples
In order to quantify the influence of the inertia coupling, the following two quantities are defined:
The scalar value \(I_{f \to \varTheta,kk,p}\) contains the result of \(\boldsymbol{Q}_{f}^{\mathrm{T}}\boldsymbol{W}_{3}\boldsymbol{W}_{3}^{\mathrm{T}}\boldsymbol{Q}_{f}\) at the main diagonal entry \(k\) due to a scaling of mode \(p\). The scalar value \(I_{\varTheta\to f,rr,p}\) contains the result of \(\boldsymbol{W}_{3}^{\mathrm{T}}\boldsymbol{Q}_{f}^{\mathrm{T}}\boldsymbol{I}_{0}^{ - 1}\boldsymbol{Q}_{f}\boldsymbol{W}_{3}\) at the main diagonal entry \(r\) due to a scaling of mode \(p\). A value of 1 indicates for both quantities an influence of the coupled inertia, which is of the same magnitude as the inertia of the corresponding degrees of freedom.
In Fig. 10, the quantities defined by (40) are given for the first ten modes of the investigated structures. Thereby the maximum modal amplitudes have been chosen as depicted in Fig. 7. It can be seen that only the structures GenStruct1 and “Beam” have the potential that the inertia coupling may significantly influence the equations of motion. The same two structures have been denoted as “critical” in the preceding subsection (see Fig. 8). This was predicted due to the theoretical considerations before. If we consider the conservative assumption for the maximum modal displacement, just the beam remains potentially sensitive to the inertia coupling.
7.2.3 Summary
The inertia coupling is relevant for the same type of structures, which are critical in terms of deformation induced inertia changes. The influence of the inertia coupling decreases with the number of stiff connections to other bodies. Similar to the preceding section, it can be concluded that inertia coupling is an effect of minor practical relevance.
7.3 Quadratic velocity vector
The quadratic velocity vector is formed by centrifugal, Coriolis and Euler forces. The latter evaluate to zero when Euler parameters are used. In such cases, along with the assumptions on which this paper is based, the quadratic velocity vector can be repeated as
(see (14) and (30)). The centrifugal forces are described by the first terms in each line, which contain the square of the angular velocity. The Coriolis forces are given by the terms where a product of the angular and modal velocities can be found. A subdivision of (41) into centrifugal and Coriolis forces gives
The quadratic velocity vector is responsible for the so-called rotordynamics effects, such as the gyroscopic effect and a meaningful coupling between rotational and elastic degrees of freedom. There is a lot of literature available on this subject (see Gasch [17]). From the literature it is known that rotor dynamic effects are of minor importance when the quotient of rotational speed and lowest eigenfrequencies of the assembled system is small enough. Note that the lowest eigenfrequencies of the assembled system are the relevant ones and not the first eigenfrequencies of a free single flexible body which is the square root of the first entries in the \(\boldsymbol{\varOmega} ^{2}\) matrix. An example would be a multibody system where a rigid disk is constrained to an elastic beam. In that case, the lowest eigenfrequencies of the entire system (beam plus disk), depend on the inertia data of the disk, the position where the disk is fixed to the beam, and on the mounting of the beam.
7.3.1 Theoretical considerations
Rotational part of quadratic velocity vector
The rotational part of the quadratic velocity vector can be given in integral form as
and in matrix form as
The subdivision into the centrifugal and Coriolis forces can be written as
The centrifugal force holds the inertia tensor of the deformed body and is responsible for the gyroscopic effects. The importance of the change in inertia due to the deformation of the body has already been discussed in the section “Rotational inertia of the deformed body”. In this chapter it has been shown that the terms \(\boldsymbol{W} _{1} \boldsymbol{Q} _{f}\) and \(\boldsymbol{Q} _{f} ^{\mathrm{T}} \boldsymbol{W} _{2} \boldsymbol{Q} _{f}\) are only important for beam-like structures and for structures which are soft with respect to centrifugal forces. Therefore, the terms \(\boldsymbol{W} _{1} \boldsymbol{Q} _{f}\) and \(\boldsymbol{Q} _{f} ^{\mathrm{T}} \boldsymbol{W} _{2} \boldsymbol{Q} _{f}\) can almost always be neglected and the inertia tensor of the undeformed body is sufficient. In this work it is suggested to always consider the gyroscopic effects based on \(\boldsymbol{I} _{0}\), since the angular velocity needs to be computed anyway and, hence, the computation of the centrifugal force is cheap. Furthermore, it is worth mentioning that such a consideration of the centrifugal force does not couple the rotational and flexible degrees of freedom of the free flexible body.
The Coriolis force couples the modal and the rotational degrees of freedom via a product of the angular and the modal velocities. It stems from the fact that the elastic body is characterized with respect to a co-rotating reference frame. It can be observed that all three terms of the Coriolis force consist of a matrix–matrix or a matrix–vector product of the angular and modal velocities together with a kind of inertia. One term holds a constant inertia (\(\boldsymbol{W} _{1}\)) while the other terms hold an inertia which is scaled by the modal coordinates (\(\boldsymbol{Q} _{f} ^{\mathrm{T}} \boldsymbol{W} _{2}\) and \(\boldsymbol{Q} _{f} ^{\mathrm{T}} \boldsymbol{W} _{3}\)). From a former section it is known that the entries of \(\boldsymbol{W} _{1}\) are typically significantly higher as those of \(\boldsymbol{W} _{2}\) and \(\boldsymbol{W} _{3}\). Moreover, the latter two matrices are scaled by modal coordinates smaller than 1, which leads to even smaller values. Based on the insights of the former sections, it can be expected that exceptions may occur in case of beam-like bodies and when a body is particularly soft with respect to the centrifugal force.
Flexible part of quadratic velocity vector
In the next subsection, the flexible part of the quadratic velocity vector is investigated in terms of its relevance for the overall solution. The (\(n _{f} \times 1\)) vector \(\bar{\boldsymbol{Q}}_{v,f}\) contains the effect of centrifugal and Coriolis forces on the modal coordinates. This vector evaluates to zero, when the small deformation assumption is applied to the kinetic energy; see (25). The flexible part of the quadratic velocity vector can be given as
or in matrix form
A subdivision into the centrifugal and Coriolis forces can be written as
A well-known effect of the centrifugal force is the elastic expansion (widening) of a flexible body when it rotates around one axis. The general question of considering or neglecting this kind of deformation cannot be answered in general and is application dependent. In case of compliant structure with respect to the centrifugal force, like GenStruct1, it seems obvious to consider the deformation induced by the centrifugal force. However, even small deformations of actually stiff structures can be important in some applications. Such an example would be the fatigue life prediction of a crankshaft based on modal stress recovery (see [15] and [16]). Although the crankshaft deformation due to the rotational speed is small, the thereby induced stress can have significant impact on the fatigue life prediction. This is because it acts as kind of mean stress which has considerable impact on fatigue lifetime. Elastic deformations caused by centrifugal forces are a fundamental effect of rotating elastic bodies. Their complete negligence only makes sense when either the rotational speed is low or the body is stiff and the neglected small deformations are non-critical. It can be seen that the centrifugal force consists of a part with constant inertia (\({=}\boldsymbol{W} _{1}\)) and a second one where the matrix \(\boldsymbol{W} _{2}\) is scaled by the modal coordinates. As in the section before, it can be stated that the entries of \(\boldsymbol{W} _{1}\) are much larger than those of \(\boldsymbol{W} _{2}\). Moreover, \(\boldsymbol{W} _{2}\) is multiplied with modal coordinates, which are typically smaller than one. Therefore, the constant term normally dominates the state-dependent one. The numerical examples below underline the latter considerations. Exceptions may be special structures, which are particularly soft in terms of centrifugal forces or beam-like bodies.
It may be interesting to note that the term holding \(\boldsymbol{W} _{2}\) represents a reduction of the structure’s effective stiffness since the centrifugal force leads to an expansion of the body, which leads to a higher centrifugal force. If the rotational speed exceeds a certain limit, the effective stiffness becomes negative and the system is instable. This is a more academic scenario, however, because under such conditions the structure will not fulfill the small deformation assumption.
Once again, it is emphasized that the former considerations do not contain the centrifugal and Coriolis forces due to other bodies which are somehow stiffly connected to the flexible body under consideration. Even if the body is just connected to ground the mounting forces may influence the body’s behavior much more than the latter discussed quadratic velocity vector. Again, a tendency can be assumed: The more the flexible body interacts with the ground or other bodies, the more the previously discussed terms become irrelevant for the overall solution.
7.3.2 Numerical examples
Rotational part of quadratic velocity vector
In the discussion of the Coriolis force, it has been assumed that the term holding \(\boldsymbol{W} _{1}\) is normally dominating. Exceptions are expected in cases of slender structures and structures with a special mass distribution and an extraordinary sensitivity to centrifugal forces.
In Table 4 the ratio of the Euclidian norm of the deformation-dependent terms with respect to the non-deformation-dependent term can be seen. For the construction of \(\boldsymbol{Q} _{f} ^{\mathrm{T}}\) the maximum modal deformation is used for the first ten modes, see Fig. 7. The modal coordinates of the remaining modes have been set to zero. For the construction of the modal velocities it has been assumed that those ten modes vibrate with the modes’ eigenfrequencies. The angular velocity has been set to \(\bar{\boldsymbol{\omega}}^{\mathrm{T}} = [ \begin{array}{c@{\ }c@{\ }c} 1 & 1 & 1 \end{array} ]\). Note that a scaling of the angular velocity does not change the ratio given in Table 4. It can be seen that the norm of the deformation-dependent terms is of two to three magnitudes smaller than that with the non-deformation-dependent term, except in the case of the Beam and GenStruct1. This is in accordance with the theoretical considerations mentioned before. It should be emphasized at this point that the assumptions made for the latter ratio are very conservative. Firstly, the maximum modal coordinates themselves are conservative (see the discussion around Fig. 7) and secondly, the fact that all maximum coordinates and velocities act (without phase shift) simultaneously is even more conservative. Therefore, it seems that in reality the ratio of the norms is expected to be even smaller.
Flexible part of quadratic velocity vector
It has been assumed that the state-dependent part of the centrifugal force can normally be neglected in comparison to the constant one. Table 5 contains the ratio of the Euclidean norm of the two parts of the centrifugal force when the maximum modal coordinates are applied for the first ten modes simultaneously. It can be seen that the contribution of the deformation-dependent term is at least of two magnitudes smaller than that with the constant term, excluding GenStruct1. This was expected because of the special characteristics of this structure.
7.3.3 Summary
Considering the gyroscopic forces due to the undeformed body is suggested in any case, since they do not couple the equations of motion and are cheap to evaluate. If the body’s widening due to centrifugal force has to be considered, it is necessary to add the term \([ \begin{array}{c@{\ }c@{\ }c} \bar{\omega}_{1}\boldsymbol{I} & \bar{\omega}_{2}\boldsymbol{I} & \bar{\omega}_{3}\boldsymbol{I} \end{array} ][ \frac{1}{2}\boldsymbol{W}_{1}^{\mathrm{T}} ]\bar{\boldsymbol{\omega}} \). For very special rotational soft structures (in the sense of GenStruct1) the term \([ \begin{array}{c@{\ }c@{\ }c} \bar{\omega}_{1}\boldsymbol{I} & \bar{\omega}_{2}\boldsymbol{I} & \bar{\omega}_{3}\boldsymbol{I} \end{array} ][ \boldsymbol{W}_{2}\boldsymbol{Q}_{f} ]\bar{\boldsymbol{\omega}} \) may be relevant as well.
From rotor dynamics it is known that the Coriolis force can be neglected when the ratio of the assembled systems’ first eigenfrequency and the rotational speed are considerable lower than 1. If this is not the case, the Coriolis forces should be taken into account, whereby, for the rotational degrees of freedom, the term \(\boldsymbol{W}_{1}\dot{\boldsymbol{Q}}_{f}\bar{\boldsymbol{\omega}} \) is sufficient. Exceptions are beam-like structures and, once again, rotational soft structures in the sense of GenStruct1, when the inertia forces of those structures are dominated by themselves and not by other bodies which are stiffly attached.
8 “Set of guidelines” for practical use
I. The simple and decoupled equations of motion
which are obtained by the strict application of the small deformation assumption on the level of the kinetic energy can be used in the following cases:
-
Moderate angular velocities when the body is neither a beam nor an extraordinary rotational soft structure (in the sense of GenStruct1). Examples are ground vehicles, housings, aircrafts, and so on.
-
In cases of flexible bodies which are stiffly connected to other bodies, so that the effective inertia or effective stiffness of the assembled system is different to that of the free body. Examples are crankshafts, connecting rods, or a beam with a mounted flywheel.
In industrial operations, the latter cases will probably cover most the applications.
II. If, in addition, the widening due to the centrifugal force is of interest, Eq. (50) should be considered. In this equation the centrifugal force acting on the flexible coordinates is additionally regarded.
III. In case of rotating structures, the following extraordinary situations can require additional terms:
-
If the body under consideration is very soft with respect to centrifugal forces (in the sense of GenStruct1) and this softness is not influenced by connections to other bodies (or ground), the linear change in inertia should be considered in the form of \(\boldsymbol{I}_{0} + \boldsymbol{W}_{1}\boldsymbol{Q}_{f}\). If, in addition, the widening of such structures due to centrifugal forces is of interest, the full centrifugal force acting on the flexible coordinates should be regarded in the form of \([\bar{\omega}_{1}\boldsymbol{I} \ \bar{\omega}_{2}\boldsymbol{I} \ \bar{\omega}_{3}\boldsymbol{I} ][ \frac{1}{2}\boldsymbol{W}_{1}^{\mathrm{T}} + \boldsymbol{W}_{2}\boldsymbol{Q}_{f} ]\bar{\boldsymbol{\omega}} \).
-
In cases where a long slender (beam-like) structure with an inertia which is not influenced by connections to other bodies (or ground) the full change of inertia \(\bar{\boldsymbol{G}}^{\mathrm{T}}[ \boldsymbol{I}_{0} + \boldsymbol{W}_{1}\boldsymbol{Q}_{f} + \boldsymbol{Q}_{f}^{\mathrm{T}}\boldsymbol{W}_{2}\boldsymbol{Q}_{f} ]\bar{\boldsymbol{G}}\) should be computed. In addition, the inertia coupling \(\bar{\boldsymbol{G}}^{\mathrm{T}}\boldsymbol{Q}_{f}^{\mathrm{T}}\boldsymbol{W}_{3}\) in mass matrix should be regarded as well.
IV. The Coriolis force should be considered when the ratio of the assembled system’s first eigenfrequency and the rotational speed is not considerably lower than 1 and when the inertia of the rotating body is determined by itself and not by other bodies which are stiffly connected. In such a case, the term \(-\bar{\boldsymbol{G}}^{\mathrm{T}}\boldsymbol{W}_{1}\dot{\boldsymbol{Q}}_{f}\bar{\boldsymbol{\omega}} \) is normally sufficient for the rotational degrees of freedom. The full expression (\(- \bar{\boldsymbol{G}}^{\mathrm{T}}[ \boldsymbol{W}_{1} + 2\boldsymbol{Q}_{f}^{\mathrm{T}}\boldsymbol{W}_{2} ]\dot{\boldsymbol{Q}}_{f}\bar{\boldsymbol{\omega}} - 2\dot{\bar{\boldsymbol{G}}}^{\mathrm{T}}\boldsymbol{Q}_{f}^{\mathrm{T}}\boldsymbol{W}_{3}\dot{\boldsymbol{q}}_{f}\)) needs to be regarded only in cases with beam like structures or rotational soft structures, like GenStruc1. For the flexible coordinates the Coriolis force is then covered by the term \(- 2\boldsymbol{W}_{3}^{\mathrm{T}}\dot{\boldsymbol{Q}}_{f}\bar{\boldsymbol{\omega}}\).
9 Benefit
The well-founded negligence of certain terms in the equations of motion leads to the following benefits:
The first benefit is obviously the reduction of the computational burden. The matrixes \(\boldsymbol{W} _{1}\), \(\boldsymbol{W} _{2}\) and \(\boldsymbol{W} _{3}\) are involved in matrix–matrix and matrix–vector products which need to be computed at each iteration during the numerical time integration. This has to be done for the equations of motions and also for the computation of the Jacobian matrix. When terms including \(\boldsymbol{W} _{1}\), \(\boldsymbol{W} _{2}\) and \(\boldsymbol{W} _{3}\) can be neglected, the simulation time decreases significantly in cases where models with a high number of flexible bodies and/or when flexible bodies with many modes are considered. Note that the latter becomes more and more relevant because there is a tendency to consider more and more local effects in flexible multibody dynamics (see, for example, [18,19,20,21] and [26]). In order to illustrate the potential, two examples are given. The first example deals with an elastic piston rod simulation where the mode base of Craig [23] is extended by so called “contact modes” so that in total 90 modes are in use. Those “contact modes” enable an efficient and accurate consideration of the nonlinear contact forces in the bearing cap, see Sect. 4.2. of [26] for more details. Two simulations are performed with MSC.ADAMS: one with the default setting “partial coupling” and another with “full coupling”. In the first case just the terms holding \(\boldsymbol{W} _{1}\) are considered, while in the second case all terms of the equations of motion are considered. Even though the results are almost identical, the difference with respect to the CPU time is almost 50%. For the second example, the freely available code FreeDyn [27] is used. A 6 cylinder V-engine as in Fig. 11 has been constructed with rigid bodies and 6 flexible piston rods. For the piston rod, a Craig mode base [23] is used with 12 constraint interface modes and 15 constraint normal modes. The crankshaft is mounted to ground by a revolute joint and a moment accelerates the entire mechanism up to 8000 rpm. The same two kinds of simulation are performed as in the former example. It can be reported that the difference in the CPU time is around 15%, while the modal coordinates of both computations are almost identical.
A second benefit is that the computation of \(\boldsymbol{W} _{1}\), \(\boldsymbol{W} _{2}\) and \(\boldsymbol{W} _{3}\) is not necessary at all when they are not needed. Consequently, the eigenvalues and mode shapes are enough for flexible multibody dynamics. This is standard output of many Finite Element codes, while \(\boldsymbol{W} _{1}\), \(\boldsymbol{W} _{2}\) and \(\boldsymbol{W} _{3}\) are not. This simplifies the numerical implementation of the equations of motion enormously.
The third benefit is that negligence of the terms including \(\boldsymbol{W} _{1}\), \(\boldsymbol{W} _{2}\) and \(\boldsymbol{W} _{3}\) leads to equations of motion where the mass matrix and the quadratic velocity vector are decoupled with respect to the translational, rotational and flexible degrees of freedom. This fact simplifies considerations with respect to separated time integration [19] or model reduction of multibody systems [22] tremendously.
Finally, the set of guidelines given above removes uncertainty concerning the question of which invariant needs to be considered and which not. In available software packages it is common to commit this decision to the user without clear guidance. The former suggestions can be used as such a guidance in order to activate or deactivate the proper invariants.
10 Conclusion
In this work the significance of all inertia related terms of a flexible body in the FFRF were investigated at the level of the equations of motion. It turned out that for a lot of applications a remarkably simple and decoupled set of equations are sufficient. This has already been suggested in the literature when the small deformation assumption is strictly applied at the level of the kinetic energy (see [12] or [21]). However, there are situations which require either the deformation-dependent inertia tensor, or the inertia coupling, or the centrifugal and Coriolis forces which are related to the elastic deformation. All of these terms were investigated with respect to their significance and, finally, these results were condensed in a set of guidelines which give simple advice about which term needs to be considered and which not. All theoretical considerations have been underlined by simple numerical investigations which have been applied to a couple of very different Finite Element structures.
References
Shabana, A.: Dynamics of Multibody Systems, 4th edn. Cambridge University Press, New York (2013)
Sherif, K., Nachbagauer, K.: A detailed derivation of the velocity-dependent inertia forces in the floating frame of reference formulation. J. Comput. Nonlinear Dyn. 9(4), 044501 (2013)
Sherif, K., Nachbagauer, K., Steiner, W.: On the rotational equations of motion in rigid body dynamics when using Euler parameters. Nonlinear Dyn. 81(1–2), 343–352 (2015)
Canavin, J.R.: Vibration of a flexible spacecraft with momentum exchange controllers. School of Engineering and Applied Science, University of California. https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19770004153.pdf (cited 23.02.2018)
Wielenga, T.J.: Simplifications in the simulation of mechanisms containing flexible members. Dissertation, Department of Mechanical Engineering, University of Michigan (1984)
Nikravesh, P.E.: Understanding mean-axis conditions as floating reference frame. In: Ambrósio, J.A. (ed.) Advances in Computational Multibody Systems. Computational Methods in Applied Sciences, vol. 2. Springer, Dordrecht (2005)
Nikravesh, P.E., Lin, Y.S.: Use of principal axes as the floating reference frame for a moving deformable body. Multibody Syst. Dyn. 13, 211–231 (2005)
Sherif, K., Irschik, H., Witteveen, W.: Transformation of arbitrary elastic mode shapes into pseudo-free-surface and rigid body modes for multibody dynamic systems. J. Comput. Nonlinear Dyn. 7(2), 021008 (2012)
https://www.solidline.de/wp-content/uploads/2017/10/Die-nicht-lineare-Analyse.pdf (cited 28.02.2018)
http://www.mscsoftware.com/. Files are named “full_beam.mnf” and “quarter_beam.mnf”
Geradin, M., Rixen, D.J.: Impulse-based substructuring in a floating frame to simulate high frequency dynamics in flexible multibody dynamics. Multibody Syst. Dyn. 42, 47–77 (2018)
de Veubeke, F.: The dynamics of flexible bodies. Int. J. Eng. Sci. 14(10), 895–913 (1976)
Schwertassek, R., Dombrowski, S.V., Wallrapp, O.: Modal representation of stress in flexible multibody simulation. Nonlinear Dyn. 20, 381–399 (1999)
Fischer, P., Witteveen, W., Schabasser, M.: Integrated MBS-FE-Durability Analysis of Truck Frame Components by Modal Stresses, ADAMS User Meeting Rome 2000 (2000). https://www.researchgate.net/profile/Wolfgang_Witteveen/publication/237305950_Integrated_MBS_-_FE_-_Durability_Analysis_of_Truck_Frame_Components_by_Modal_Stresses/links/00463529eda2ae996c000000/Integrated-MBS-FE-Durability-Analysis-of-Truck-Frame-Components-by-Modal-Stresses.pdf (cited April 2018)
Gasch, R., Nordmann, R., Pfützner, H.: Rotordynamik, 2nd edn. Springer, Berlin (2006). ISBN 3-540-41240-9
Sherif, K.: Novel computationally efficient formulations for the equations of motion of a modally reduced flexible member undergoing large rigid body motion. PhD Thesis, Johannes Kepler University, Institute of technical Mechanics (2012)
Sherif, K., Witteveen, W., Mayerhofer, K.: Quasi-static consideration of high-frequency modes for more efficient flexible multibody simulations. Acta Mech. 223(6), 1285–1305 (2012)
Pichler, F., Witteveen, W., Fischer, P.: A complete strategy for efficient and accurate multibody dynamics of flexible structures with large lap joints considering contact and friction. Multibody Syst. Dyn. 40, 407–436 (2017). https://doi.org/10.1007/s11044-016-9555-2
Geradin, M., Rixen, D.: A nodeless dual superelement formulation for structural and multibody dynamics application to reduction of contact problems. Int. J. Numer. Methods Eng. 106, 773–798 (2016). https://doi.org/10.1002/nme.5136
Stadlmayr, D., Witteveen, W., Steiner, W.: A generalized constraint reduction method for reduced order MBS models. Multibody Syst. Dyn. 41, 259–274 (2017). https://doi.org/10.1007/s11044-016-9557-0
Craig, R.R., Bampton, M.C.C.: Coupling of sub-structures for dynamic analysis. AIAA J. 6(7), 1313–1319 (1968). https://doi.org/10.2514/3.4741
Witteveen, W.: On the modal and non-modal model reduction of metallic structures with variable boundary conditions. World J. Mech. 2(6), 311–324 (2012). https://doi.org/10.4236/wjm.2012.26037
Koutsovasilis, P., Beitelschmidt, M.: Comparison of model reduction techniques for large mechanical systems. Multibody Syst. Dyn. 20(2), 111–128 (2008). https://doi.org/10.1007/s11044-008-9116-4
Pichler, F., Witteveen, W., Fischer, P.: Reduced order modeling of preloaded bolted structure in multibody systems by the use of trial vector derivatives. J. Comput. Nonlinear Dyn. 12(5) (2017). https://doi.org/10.1115/1.4036989
Acknowledgements
Open access funding provided by University of Applied Sciences Upper Austria.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Witteveen, W., Pichler, F. On the relevance of inertia related terms in the equations of motion of a flexible body in the floating frame of reference formulation. Multibody Syst Dyn 46, 77–105 (2019). https://doi.org/10.1007/s11044-018-09662-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11044-018-09662-0