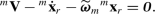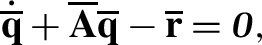A two-field approach to multibody dynamics of rotating flexible bodies

Abstract

A two-field version of the floating frame-of-reference approach is developed to describe the dynamics of a flexible body in the case of motion in a uniformly rotating frame. Full decoupling of the kinetic energy results from splitting of the motion into rigid-body modes of the floating center of mass and a velocity field orthogonal to them. The motion equations are developed from a canonical variational expression in which displacement and velocity fields play independent roles. They turn out to keep the same global structure as in the case of motion in an inertial frame. The discretization of all inertia terms is discussed in depth. It is also shown that, in the case of discretization of the continuum with 3D solid elements, all gyroscopic terms can be derived from a mass kernel and associated $\mathbf{S} _{i}$ matrices. Model reduction is proposed using the Herting–Martinez method in order to automatically satisfy orthogonality of the velocity field to rigid-body modes. Two application examples of high-speed rotating systems are developed at length to assess the efficiency of the proposed methodology.

1 Introduction

Rotor dynamics is an essential topic in mechanical engineering since it is of major importance for the analysis and design of a large variety of systems such as steam turbines, aircraft engines, wind turbines, helicopter rotors, crank and transmission shafts, gear boxes, car wheels, aircraft landing gears, etc. An important literature covers the subject through reference books, research articles and it has also its dedicated journal.¹

From a historical point of view, an early comprehensive description of the dynamic behavior of rotating machinery can be found in Den Hartog’s classical book on Mechanical vibrations [1], as the result of his industrial experience at Westinghouse starting in 1926. In the same period, Biezeno and Grammel devoted in their classical treaty on Technische Dynamik [2] two chapters to disks in rotation on the one hand, and critical velocities on the other hand. Worthwhile mentioning is also a short technical note by Fraeijs de Veubeke published in 1943 [3] addressing the topic of gyroscopic effects on bending critical speeds of shafts.

Following the pioneering theoretical work by Tondl [4] and Ziegler [5] during the 1960s, there has been an abundant literature addressing the fundamental concepts of critical speed and stability analysis of rotating machinery, e.g., [6–14].

The first applications of the finite-element method to rotor dynamics are probably the ones described by Dubigeon and Michon [15] in 1975 and by Nelson and Mac Vaugh in 1976 [16]. Like many subsequent authors, they built a linearized model of a rotor-bearing system based on the following hypotheses:

• both rotating and fixed parts of the structure have linear material and geometric behaviors;

• the rotating shaft is represented by linear beam finite elements (with shear deformation and rotary inertia of cross sections possibly included);

• the stiffness and damping properties of bearings and seals are linear functions of displacements and velocities;

• large disks are assumed to be rigid, their gyroscopic effect resulting from second-order linearization of inertia forces.

The book published in 1998 by Lalanne and Ferraris soon became a reference regarding finite-element modeling of rotating machinery [17].

In [18], a more general approach has been proposed that consisted of treating the structural components of a rotating system as a 3D continuum. Advantage was taken of the axisymmetric geometry of the system to develop the model with axisymmetric finite elements and apply to it model reduction [19]. A similar approach, using 3D finite elements, was described in [20]. An extensive review of reduction methods applied to rotor dynamics can be found in [21].

To our knowledge, treating a rotating machine as a nonlinear multibody system using a floating frame-of-reference approach was proposed for the first time in 2004 by Sopanen in his PhD thesis [22]. However, the model description was made in the inertial frame, and therefore rotation resulted from the external excitation on the system. The same approach has been followed in [23].

The fundamental specificity of the approach proposed hereafter consists in the fact that the kinematics of the flexible body is described in a noninertial frame rotating with uniform angular speed with respect to the inertial frame. Therefore, the two-field frame-of-reference method proposed in [24, 25] is generalized to describe the motion of an elastic body in a frame undergoing uniform rotation relatively to the inertial one. As will be shown in the examples, the proposed methodology presents over a classical FFRF approach, based on a single-field discretization and using the inertial frame as reference, at least three main advantages:

• A difficulty generally encountered in the development of a FFRF model is the computation of elastic inertia forces of gyroscopic origin. Formulating the problem as a first-order one, based on simultaneous discretization of motion and velocity fields, makes it easier to develop without any approximation the inertia terms of gyroscopic origin in a flexible body.

• Introducing the rotation speed of the reference frame as an additional parameter makes it possible to study the dynamic response of the system within a given speed range without the need to start the simulation from zero speed.

• It also allows treating stationary responses at fixed rotation speed, such as the response to mass unbalance, as static problems.

The paper is organized as follows.

Section 2 is devoted to the kinematic description of the flexible body in the rotating frame. The development of its kinetic energy in a floating frame of reference is performed in Sect. 3. It is shown that its full decoupling results from the definition of a compound elastic velocity field that includes a convective term due to angular rotation and the assumed orthogonal to rigid-body motion. In Sect. 4, a canonical expression of kinetic energy is introduced that allows us to treat displacement and velocity fields independently, thus allowing the generalization of the two-field floating frame-of-reference approach introduced in [24, 25] to elastic motion in a reference frame rotating at uniform speed. Finite-element discretization is discussed in Sect. 6. It is shown that in the case of discretization with 3D solid elements, all gyroscopic inertia terms can be efficiently computed using the concept of $\mathbf{S} _{i}$ matrices introduced in Sect. 6.3.3. The latter are obtained from a 1D kernel extracted from the isotropic 3D mass matrix. Superelement implementation following the Herting–Martinez method [26, 27] is described in Sect. 7.

The first example, presented in Sect. 8, is a simple benchmark taken from Reference [28] consisting of a simple rotor-disk system subjected to mass unbalance in a gravity field. The second example, in Sect. 9, is a more complex system consisting of a twin-disk elastic rotor on magnetic bearings subject to mass unbalance [23]. In both examples it is shown that being able to simulate the rotor either at a specified speed or within a given speed range gives a better insight into the system behavior. The ability provided by the formalism to describe as a stationary problem the rotor behavior at constant speed allows for a fast characterization of the system over its entire speed range to be also demonstrated. Finally, the effect of disk flexibility is investigated through superelement modeling following the methodology proposed in Sect. 7.

2 Kinematics of a flexible body undergoing uniform angular motion

In this section, we generalize the description of the general motion of a flexible body to the case when the frame of reference in which the elastic body is moving is no longer inertial, but a frame rotating at constant speed with respect to the inertial one.

2.1 Motion description

The general motion of a flexible body undergoing rotation with uniform angular velocity $\omega _{m}$ about a rotation axis $\mathbf{k}$ will be decomposed into three parts:

• the rotation motion at constant angular velocity relative to the inertial frame;

• the rigid motion of a reference frame $r$ on the body relative to the rotating frame $m$;

• the elastic motion relative to the reference frame $r$.

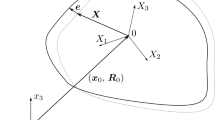
As a result, the current inertial position $\mathbf{x}$ of a given point of an elastic body undergoing overall rigid-body motion (Fig. 1) can be expressed in the form

$$ \mathbf{x} _{P} = \mathbf{R} ({\boldsymbol{\omega}} _{m}t) ({^{m}\mathbf{x} _{r}}+ {^{m} \mathbf{R} _{r}}({^{r} \mathbf {X}_{P}}+{^{r} {\mathbf{e}} _{P},})), $$

(1)

with the notations provided in Table 1.

Fig. 1

Kinematics of a flexible body undergoing uniform rotation

Table 1 Definitions involved in Equation (1) for describing the motion of an arbitrary point $P$ on the elastic body. Vector and matrix quantities are noted as follows: objects like $^{y}\mathbf {A}_{x}$ and $^{y}\mathbf {a}_{x}$ are, respectively, a matrix / a vector belonging to frame $x$ relative to frame $y$. The absence of a left superscript characterizes objects defined relative to the inertial frame

2.2 Velocities

The inertial-frame expression of the velocity vector of point $P$ is computed as

$$ \dot{\mathbf{x}} _{P} = \dot{\mathbf{R}} _{m}( {^{m}\mathbf{x} _{r}}+ {^{m} \mathbf{R} _{r}}({^{r} \mathbf {X}_{P}}+{^{r} {\mathbf{e}} _{P},})) + \mathbf{R} _{m}({^{m}{\dot{\mathbf{x}} }_{r}}+ {^{m} {\dot{\mathbf{R}} }_{r}}({^{r} \mathbf {X}_{P}}+{^{r} {\mathbf{e}} _{P},}) + {^{m} \mathbf{R} _{r}}{^{r} {\dot {\mathbf{e}} _{P}}}). $$

(2)

Multiplying (2) by $(\mathbf{R} _{m}{^{m} \mathbf{R} _{r}})^{T}$ provides its material-frame expression as

$$ \begin{aligned} {^{r}\mathbf {V}_{P}}& = {{^{m} {\mathbf{R} }_{r}^{T}}}( {^{m}{\dot{\mathbf{x}} }_{r}}+ \mathbf{R} _{m}^{T} \dot {\mathbf{R} _{m}}{^{m}\mathbf{x} _{r}}) + \\ & ({{^{m} {\mathbf{R} }_{r}^{T}}}\mathbf{R} _{m}^{T} \dot {\mathbf{R} _{m}}{^{m} \mathbf{R} _{r}}+ {{^{m} {\mathbf{R} }_{r}^{T}}}{^{m} {\dot{\mathbf{R}} }_{r}}) ({^{r} \mathbf {X}_{P}}+ {^{r} {\mathbf{e}} _{P},}) +{^{r} {\dot {\mathbf{e}} _{P}}} \\ & = {{^{m} {\mathbf{R} }_{r}^{T}}}( {^{m}{\dot{\mathbf{x}} }_{r}}+ { \widetilde {\boldsymbol{\omega}} _{m}}{^{m}\mathbf{x} _{r}}) + ({{^{m} {\mathbf{R} }_{r}^{T}}}{\widetilde {\boldsymbol{\omega}} _{m}}{^{m} \mathbf{R} _{r}}+ {{^{m} {\mathbf{R} }_{r}^{T}}}{^{m} {\dot{\mathbf{R}} }_{r}}) ({^{r} \mathbf {X}_{P}}+ {^{r} {\mathbf{e}} _{P},}) +{^{r} {\dot {\mathbf{e}} _{P}}}\; , \end{aligned} $$

(3)

where²

$$ {\widetilde {\boldsymbol{\omega}} _{m}}= \mathbf{R} _{m}^{T} \dot {\mathbf{R} _{m}}$$

(4)

is the skew-symmetric angular velocity matrix associated with the imposed driving motion.

In order to alleviate the notation we will define the skew-symmetric matrix “function” ${^{r} \widetilde{\mathbf {W}}_{r}}$ and the associated vector ${^{r} \mathbf {W}_{r}}$ ³ that expresses the relative angular velocity of the material frame with respect to the driving one by

$$ {^{r} \widetilde{\mathbf {W}}_{r}}= {^{r} \widetilde{\mathbf {W}}_{r}}({^{m} \mathbf{R} _{r}}) = {{^{m} {\mathbf{R} }_{r}^{T}}}{^{m} {\dot{\mathbf{R}} }_{r}} \quad \Leftrightarrow \quad {^{r} \mathbf {W}_{r}}= \text{vect}( {^{r} \widetilde{\mathbf {W}}_{r}}). $$

(5)

The material expression of translation velocity (3) is rewritten in the form

$$ {^{r}\mathbf {V}_{P}}= {^{r}\mathbf {V}_{r}}+ ^{r} \widetilde{{\boldsymbol {\varOmega}}}_{r}({^{r} \mathbf {X}_{P}}+ {^{r} {\mathbf{e}} _{P},}) +{^{r} {\dot {\mathbf{e}} _{P}}}\; , $$

(6)

with kinematic relationships between the velocities ${}^{m}\mathbf {V}$ and ${}^{r}\widetilde{{\boldsymbol {\varOmega}}}_{r}$ on the one hand, and the associated kinematic quantities ${^{m}\mathbf{x} _{r}}$ and ${^{m} \mathbf{R} _{r}}$ on the other hand:

• ${}^{m}\mathbf {V}$ and ${}^{r}\mathbf {V}_{r}$ are the rotating-frame and material-frame expressions of the translation velocity of the reference point $r$

  $$ \begin{aligned} {}^{m}\mathbf {V}& = {^{m}{\dot{\mathbf{x}} }_{r}}+ {\widetilde {\boldsymbol{\omega}} _{m}}{^{m} \mathbf{x} _{r}} \\ {^{r}\mathbf {V}_{r}}& = {{^{m} {\mathbf{R} }_{r}^{T}}}{^{m}\mathbf {V}}\end{aligned} . $$

  (7)

• The skew-symmetric matrix appearing in the second term of Equation (3) provides the material-frame expression of the angular-velocity matrix ${}^{r}\widetilde{{\boldsymbol {\varOmega}}}_{r}$

  $$ \begin{aligned} {}^{r}\widetilde{{\boldsymbol {\varOmega}}}_{r}& = {^{r} \widetilde{\mathbf {W}}_{r}}+ {{^{m}{\mathbf{R} }_{r}^{T}}}{\widetilde {\boldsymbol{\omega}} _{m}}{^{m} \mathbf{R} _{r}} \\ & = {^{r} \widetilde{\mathbf {W}}_{r}}+ {^{r} \widetilde {\boldsymbol{\omega}} _{m}}\end{aligned} $$

  (8)

  and the associated vector

  $$ {^{r} {\boldsymbol {\varOmega}}_{r}}= {^{r} \mathbf {W}_{r}}+ {^{r} {\boldsymbol{\omega}} _{m}}\; , $$

  (9)

  ${^{r}{\boldsymbol{\omega}} _{m}}$ being the driving velocity vector expressed in the material frame

  $$ {^{r} {\boldsymbol{\omega}} _{m}}= {{^{m} {\mathbf{R} }_{r}^{T}}}{\boldsymbol{\omega}} _{m}\, , $$

  (10)

  ${\boldsymbol{\omega}} _{m}$ being time dependent we compute the acceleration vector and matrix associated to (10) as

  $$ {^{r} \dot {\boldsymbol{\omega}} _{m}}= {^{r} \widetilde{\mathbf {W}}_{r}}^{T} {^{r} {\boldsymbol{\omega}} _{m}} {^{r} \dot{\widetilde {\boldsymbol{\omega}} }_{m}}= {{^{r} \widetilde{\mathbf {W}}_{r}}}^{T} {^{r} \widetilde {\boldsymbol{\omega}} _{m}}{^{r} \widetilde{\mathbf {W}}_{r}}\, . $$

  (11)

Equation (6) can also be split in the form

$$ {^{r}\mathbf {V}_{P}}= {^{r}\mathbf {V}_{P}}_{,rig}+ {^{r}\mathbf {V}_{P}}_{,e}, $$

(12)

where

$$ {^{r}\mathbf {V}_{P}}_{,rig}= {^{r}\mathbf {V}_{r}}+ ^{r} \widetilde{{\boldsymbol {\varOmega}}}_{r}{^{r} \mathbf {X}_{P}}$$

(13)

is the material-frame expression of the velocity due to rigid motion, and

$$ {^{r}\mathbf {V}_{P}}_{,e} = {^{r} {\dot {\mathbf{e}} _{P}}}+^{r} \widetilde{{\boldsymbol {\varOmega}}}_{r}{^{r} {\mathbf{e}} _{P},}$$

(14)

is the additional velocity due to elastic deformation.

Finally, the velocity field due to rigid motion (13) may also be written in the form

$$ {^{r}\mathbf {V}}_{rig}= \mathbf {U}({^{r} \mathbf {X}_{P}})^{T} \begin{bmatrix} {^{r}\mathbf {V}_{r}} \\ {^{r} {\boldsymbol {\varOmega}}_{r}}\end{bmatrix} , $$

(15)

the rigid-body modes being described in the material frame by the $6 \times 3$ matrix

$$ \mathbf {U}({^{r} \mathbf {X}_{P}}) = \begin{bmatrix} \mathbf {I}\\ {^{r} \widetilde{\mathbf {X}}_{P}}\end{bmatrix} \;. $$

(16)

2.3 Virtual displacements and velocities

Let us now introduce the angular variation ${\delta ^{r} \tilde{{\boldsymbol {\theta}}}_{r}}$ associated with rotation motion in the reference frame through

$$ \delta{^{m}{ \mathbf{R} }_{r}}= {^{m} \mathbf{R} _{r}}{\delta ^{r} \tilde{{\boldsymbol {\theta}}}_{r}}\, , $$

(17)

in order to compute the variation of angular velocity

$$ \delta{^{r}{\boldsymbol {\varOmega}}}_{r}= {\delta ^{r} \mathbf {W}_{r}}+ {\delta ^{r} {\boldsymbol{\omega}} _{m}}\, . $$

(18)

On the one hand, from (10) we compute

$$ {\delta ^{r} {\boldsymbol{\omega}} _{m}}= - {\delta ^{r} \tilde{{\boldsymbol {\theta}}}_{r}}{^{r} {\boldsymbol{\omega}} _{m}}= {^{r} \widetilde {\boldsymbol{\omega}} _{m}}{\delta ^{r} {\boldsymbol {\theta}}_{r}.}\, . $$

(19)

On the other hand, we compute the time derivative of (17) and the variation of (5)

$$\begin{aligned} {\delta ^{r} \dot{\tilde{{\boldsymbol {\theta}}}}_{r}}& = {{^{m} {\dot{\mathbf{R}} }_{r}^{T}}}\delta{^{m}{ \mathbf{R} }_{r}}+ {{^{m} {\mathbf{R} }_{r}^{T}}}\delta {^{m} {\dot{\mathbf{R}} }_{r}}= - {^{r} \widetilde{\mathbf {W}}_{r}}{\delta ^{r} \tilde{{\boldsymbol {\theta}}}_{r}}+ {{^{m} {\mathbf{R} }_{r}^{T}}}\delta {^{m} {\dot{\mathbf{R}} }_{r}} \end{aligned}$$

(20)

$$\begin{aligned} {\delta ^{r} \widetilde{\mathbf {W}}_{r}}& = \delta{^{m}{ \mathbf{R} }_{r}^{T}}{^{m} {\dot{\mathbf{R}} }_{r}}+ {{^{m} {\mathbf{R} }_{r}^{T}}}\delta {^{m} {\dot{\mathbf{R}} }_{r}}= - {\delta ^{r} \tilde{{\boldsymbol {\theta}}}_{r}}{^{r} \widetilde{\mathbf {W}}_{r}}+ {{^{m} {\mathbf{R} }_{r}^{T}}}\delta {^{m} {\dot{\mathbf{R}} }_{r}}\, . \end{aligned}$$

(21)

Combining (20) and (21) provides the matrix relationship

$$ {\delta ^{r} \widetilde{\mathbf {W}}_{r}}= {\delta ^{r} \dot{\tilde{{\boldsymbol {\theta}}}}_{r}}+ {^{r} \widetilde{\mathbf {W}}_{r}}{\delta ^{r} \tilde{{\boldsymbol {\theta}}}_{r}}- {\delta ^{r} \tilde{{\boldsymbol {\theta}}}_{r}}{^{r} \widetilde{\mathbf {W}}_{r}}$$

(22)

to which corresponds the vector equation

$$ {\delta ^{r} \mathbf {W}_{r}}= {\delta{^{r} \dot{{\boldsymbol {\theta}}}_{r}}}+ {^{r} \widetilde{\mathbf {W}}_{r}}{\delta ^{r} {\boldsymbol {\theta}}_{r}.}$$

(23)

Finally, substituting (19) and (23) into (18) provides a quite simple expression for the variation of the angular-velocity vector (9)

$$ \delta{^{r}{\boldsymbol {\varOmega}}}_{r}= {\delta{^{r} \dot{{\boldsymbol {\theta}}}_{r}}}+ ({^{r} \widetilde{\mathbf {W}}_{r}}+ {^{r} \widetilde {\boldsymbol{\omega}} _{m}}) {\delta ^{r} {\boldsymbol {\theta}}_{r}.} $$

(24)

The conclusion of this section is that the kinematic decomposition of the velocity field in the material frame is not fundamentally affected by the introduction of the driving motion. The only difference lies in adding to the material expression of the body-frame velocity field ${^{r} \widetilde{\mathbf {W}}_{r}}$, the material expression ${^{r} \widetilde {\boldsymbol{\omega}} _{m}}$ of the driving angular velocity. This thus makes it possible and easy to generalize the two-field formulation proposed in references [24, 25] to systems undergoing uniform rotation with respect to the inertial frame.

The development of the two-field formulation relies upon the relaxation of kinematic compatibility in time. Table 2 summarizes the duality that will be exploited between velocities and their counterpart resulting from time differentiation of the motion field.

Table 2 Duality between velocities and time derivatives of the motion field

3 Kinetic energy

The purpose of this section is two-fold: first, to provide an expression of kinetic energy in which rigid-body motion and elastic motion are fully uncoupled; secondly, to introduce the concept of duality that will allow us to assume an equal role in the formulation to the kinematic variables describing the general motion (displacements and rotations) and the associated velocities.

3.1 General expression

The instantaneous kinetic energy of the elastic body is computed from the relationships (12)–(14) as

$$ \begin{aligned} {\mathcal{K}} & = \frac{1}{2}\int _{V} {{^{r}\mathbf {V}_{P}}^{T}} \, {{^{r}\mathbf {V}_{P}}} \,\rho dV = {\mathcal{K}}_{1} + {\mathcal{K}}_{2} +{\mathcal{K}}_{3} \\ & = \frac{1}{2}\int _{V} ({^{r}\mathbf {V}_{r}}+ {^{r} {\boldsymbol {\varOmega}}_{r}}\, {^{r} \mathbf {X}_{P}})^{T} \, ({^{r}\mathbf {V}_{r}}+ {^{r} {\boldsymbol {\varOmega}}_{r}}\, {^{r} \mathbf {X}_{P}}) \ \rho dV \\ & + \frac{1}{2}\int _{V} {{^{r}\mathbf {V}}_{P,e}^{T}} \, {{^{r}\mathbf {V}}_{P,e}} \ \rho dV + \int _{V} {^{r}\mathbf {V}}_{P,e}^{T} ({^{r}\mathbf {V}_{r}}+ {^{r} {\boldsymbol {\varOmega}}_{r}}\, {^{r} \mathbf {X}_{P}}) \ \rho dV \; . \end{aligned} $$

(25)

The first term, ${\mathcal{K}}_{1}$, represents the kinetic energy resulting from rigid motion. Assuming that the center of mass of the undeformed body is taken as the origin of the material frame $r$

(26)

it can be decoupled in the form

$$ {\mathcal{K}}_{1} = \frac{1}{2}m_{B} \; {^{r}\mathbf {V}_{r}}^{T} \, {^{r} \mathbf {V}_{r}}+ \frac{1}{2}{^{r} {\boldsymbol {\varOmega}}_{r}}^{T} \mathbf {J}\, {^{r} {\boldsymbol {\varOmega}}_{r}}, $$

(27)

with $m_{B}$ and $\mathbf {J}$ being, respectively, the mass of the body and its tensor of inertia in rigid configuration

$$ m_{B} = \int _{V} \rho d V \quad \text{and} \quad \mathbf {J}= \int _{V} \widetilde{{^{r}\mathbf {X}_{P}}}\, \widetilde{{^{r}\mathbf {X}_{P}}}\ \rho d V \; . $$

(28)

The second term, ${\mathcal{K}}_{2}$, is the kinetic energy resulting from elastic deformation

$$ {\mathcal{K}}_{2} = \frac{1}{2}\int _{V} {{^{r}\mathbf {V}}_{P,e}^{T}} \, {{^{r} \mathbf {V}}_{P,e}} \ \rho dV \; . $$

(29)

This depends implicitly on the compound angular velocity (9) of the body frame.

3.2 Choice of body axes and decoupling

The third term, ${\mathcal{K}}_{3}$, is a coupling kinetic energy between rigid and elastic motions that can be canceled as follows.

The choice of body axes is not unique since the splitting (12) between rigid and elastic velocity is not unique. Indeed, the amplitudes of the rigid-motion velocities ${^{r}\mathbf {V}_{r}}$ and ${^{r} {\boldsymbol {\varOmega}}_{r}}$ are not uniquely determined but depend on the choice of the instantaneous reference axes for the deformed configuration. The choice can thus be made so as to cancel the coupling term ${\mathcal{K}}_{3}$ in (25) following a procedure already described in [24, 25].

Let us thus assume, as proposed [29], that the choice of the reference axes for the deformed configuration is made so that the kinetic energy associated with elastic motion ${{\mathcal{K}}}_{2}$ is minimum.

For that purpose, we develop (29) in the alternate form

$$ \begin{aligned} {\mathcal{K}}_{2} = & \frac{1}{2}\int _{V} ( {^{r}\mathbf {V}_{P}}- {^{r}\mathbf {V}}_{P,rig})^{T} ( {^{r}\mathbf {V}_{P}}- {^{r}\mathbf {V}}_{P,rig}) \ \rho dV \\ = & \frac{1}{2}\int _{V} ( {^{r}\mathbf {V}_{P}}- {^{r}\mathbf {V}_{r}}- {^{r} {\boldsymbol {\varOmega}}_{r}}\, {^{r} \mathbf {X}_{P}})^{T} ( {^{r}\mathbf {V}_{P}}- {^{r}\mathbf {V}_{r}}- {^{r} {\boldsymbol {\varOmega}}_{r}}\, {^{r} \mathbf {X}_{P}}) \ \rho dV \end{aligned} , $$

(30)

in which the material velocity ${^{r}\mathbf {V}_{r}}$ has to be regarded as invariant to a change of reference. Therefore, expressing the condition

$$ \min _{({^{r}\mathbf {V}_{r}},\ {^{r} {\boldsymbol {\varOmega}}_{r}})} \frac{1}{2}\int _{V} ( {^{r}\mathbf {V}_{P}}- {^{r}\mathbf {V}_{r}}- {^{r} {\boldsymbol {\varOmega}}_{r}}\, {^{r} \mathbf {X}_{P}})^{T} ( {^{r}\mathbf {V}_{P}}- {^{r}\mathbf {V}_{r}}- {^{r} {\boldsymbol {\varOmega}}_{r}}\, {^{r} \mathbf {X}_{P}}) \ \rho dV $$

(31)

yields

$$ \begin{aligned} -\delta {^{r}\mathbf {V}_{r}}^{T} \int _{V} ( {^{r}\mathbf {V}_{P}}& - {^{r}\mathbf {V}_{r}}- {^{r} {\boldsymbol {\varOmega}}_{r}}\, {^{r} \mathbf {X}_{P}}) \ \rho dV \\ & - \delta{^{r}{\boldsymbol {\varOmega}}}_{r}^{T} \int _{V} \widetilde {{^{r}\mathbf {X}_{P}}}^{T} ( {^{r}\mathbf {V}_{P}}- {^{r}\mathbf {V}_{r}}- {^{r} {\boldsymbol {\varOmega}}_{r}}\, {^{r} \mathbf {X}_{P}}) \ \rho dV =0 \end{aligned} $$

(32)

and we thus obtain the conditions

(33)

These mean that the translation and rotation momentums resulting from elastic motion around the rigid reference configuration vanish.

Owing to the definition (16) of the rigid-body modes, the conditions (33) also express the orthogonality of the elastic velocity field to rigid-body motion

(34)

Reorganizing the last term in (25) yields

$$ {\mathcal{K}}_{3} = \int _{V} {^{r}\mathbf {V}}_{P,e}^{T} \, ({^{r}\mathbf {V}_{r}}- \widetilde{{^{r}\mathbf {X}_{P}}}\, {^{r} {\boldsymbol {\varOmega}}_{r}}) \ \rho dV = \begin{bmatrix} {^{r}\mathbf {V}_{r}} \\ {^{r} {\boldsymbol {\varOmega}}_{r}}\end{bmatrix} ^{T} \int _{V} \mathbf {U}({^{r} \mathbf {X}_{P}}) \, {^{r}\mathbf {V}}_{P,e} \, \rho dV = 0 \; . $$

(35)

Under the assumption that the material axes and the principal axes of the undeformed body coincide and invoking the invariance property ${^{r}\mathbf {V}_{r}}^{T}{^{r}\mathbf {V}_{r}}= {^{m}\mathbf {V}}^{T}{^{m} \mathbf {V}}$, the system kinetic energy ${\mathcal{K}}$ can be expressed in either one of the fully uncoupled forms

$$\begin{aligned} {\mathcal{K}} & = \frac{1}{2}m_{B}{^{r}\mathbf {V}_{r}}^{T}{^{r}\mathbf {V}_{r}}+ \frac{1}{2}{^{r} {\boldsymbol {\varOmega}}_{r}}^{T} \mathbf {J}{^{r} {\boldsymbol {\varOmega}}_{r}}+ \frac{1}{2}\int _{V} {^{r}\mathbf {V}}_{P,e}^{T} {^{r} \mathbf {V}}_{P,e} \ \rho dV \end{aligned}$$

(36)

$$\begin{aligned} & = \frac{1}{2}m_{B}{^{m}\mathbf {V}}^{T}{^{m}\mathbf {V}}+\frac{1}{2}{^{r} {\boldsymbol {\varOmega}}_{r}}^{T} \mathbf {J}{^{r} {\boldsymbol {\varOmega}}_{r}}+ \frac{1}{2}\int _{V} {^{r}\mathbf {V}}_{P,e}^{T} {^{r} \mathbf {V}}_{P,e} \ \rho dV \; . \end{aligned}$$

(37)

3.3 Primal and dual forms of kinetic energy

The expression (37) of kinetic energy in terms of the velocities $({^{m}\mathbf {V}}, \, {^{r} {\boldsymbol {\varOmega}}_{r}}, {^{r}\mathbf {V}}_{P,e})$ can be regarded as the dual form of kinetic energy

$$ {\mathcal{K}}^{\star }({^{m}\mathbf {V}}, \, {^{r} {\boldsymbol {\varOmega}}_{r}}, {^{r}\mathbf {V}}_{P,e}) = \frac{1}{2}m_{B}{^{m}\mathbf {V}}^{T}{^{m} \mathbf {V}}+\frac{1}{2}{^{r} {\boldsymbol {\varOmega}}_{r}}^{T} \mathbf {J}\, {^{r} {\boldsymbol {\varOmega}}_{r}}+ \frac{1}{2}\int _{V} {^{r}\mathbf {V}}_{P,e}^{T} \, {^{r} \mathbf {V}}_{P,e} \ \rho dV \; . $$

(38)

This is indicated by the ⋆ superscript.

The primal form of kinetic energy results from the substitution of the kinematic relationships (7), (9), and (14) into (37). This has for expression

$$ \begin{aligned} {\mathcal{K}} ({^{m}\mathbf{x} _{r}}, & {^{m}{\dot{\mathbf{x}} }_{r}}, {^{m} \mathbf{R} _{r}}, {^{m} {\dot{\mathbf{R}} }_{r}},{^{r} {\mathbf{e}} _{P},}, {^{r} {\dot {\mathbf{e}} _{P}}}) = \frac{1}{2}m_{B} ({^{m}{\dot{\mathbf{x}} }_{r}}+ { \widetilde {\boldsymbol{\omega}} _{m}}{^{m}\mathbf{x} _{r}})^{T} ({^{m}{\dot{\mathbf{x}} }_{r}}+ {\widetilde {\boldsymbol{\omega}} _{m}}{^{m}\mathbf{x} _{r}}) \\ & + \frac{1}{2}({^{r} {\boldsymbol{\omega}} _{m}}+ {^{r} \mathbf {W}_{r}})^{T} \mathbf {J}\, ({^{r} {\boldsymbol{\omega}} _{m}}+ {^{r} \mathbf {W}_{r}}) \\ &+ \frac{1}{2}\int _{V} \left ({^{r} {\dot {\mathbf{e}} _{P}}}+ ({^{r} \widetilde {\boldsymbol{\omega}} _{m}}+ {^{r} \widetilde{\mathbf {W}}_{r}}) {^{r} {\mathbf{e}} _{P},}\right )^{T} \left ({^{r} {\dot {\mathbf{e}} _{P}}}+ ({^{r} \widetilde {\boldsymbol{\omega}} _{m}}+ {^{r} \widetilde{\mathbf {W}}_{r}}) {^{r} {\mathbf{e}} _{P},}\right ) \ \rho dV \; , \end{aligned} $$

(39)

with the definitions (5) and (10).

4 Canonical form of kinetic energy

The canonical form of kinetic energy is an expression of kinetic energy in which the motion and velocity fields play equal roles. Its variation will provide the inertia-force contribution to the system equations of the two-field formulation.

4.1 General expression

To develop the canonical form of kinetic energy, let us introduce a transformation between the primal and dual expressions of kinetic energy inspired from the classical concept of Legendre transformation [30, p. 114]. This is based on the fact that the following forms of kinetic energy are quantitatively equivalent:

$$ \begin{aligned} {\mathcal{K}} ({^{m}\mathbf{x} _{r}}, {^{m}{\dot{\mathbf{x}} }_{r}}, {^{m} \mathbf{R} _{r}}, & {^{m} {\dot{\mathbf{R}} }_{r}},{^{r} {\mathbf{e}} _{P},}, {^{r} {\dot {\mathbf{e}} _{P}}}) = {\mathcal{K}}^{\star }({^{m}\mathbf {V}}, \, {^{r} {\boldsymbol {\varOmega}}_{r}}, {^{r}\mathbf {V}_{P,e}}) \\ & = \frac{1}{2}\left ( m_{B} {^{m}\mathbf {V}}^{T} ({^{m}{\dot{\mathbf{x}} }_{r}}+ {\widetilde {\boldsymbol{\omega}} _{m}}{^{m}\mathbf{x} _{r}}) + {^{r} {\boldsymbol {\varOmega}}_{r}}^{T} \mathbf {J}\, ({^{r} {\boldsymbol{\omega}} _{m}}+ {^{r} \mathbf {W}_{r}}) \right ) \\ & \phantom{=} + \frac{1}{2}\int _{V} {^{r}\mathbf {V}_{P,e}}^{T} ({^{r} {\dot {\mathbf{e}} _{P}}}+ ({^{r} \widetilde {\boldsymbol{\omega}} _{m}}+ {^{r} \widetilde{\mathbf {W}}_{r}}) {^{r} {\mathbf{e}} _{P},}) \ \rho dV \; . \end{aligned} $$

(40)

Combining the relationships (40) and (38) allows construction of the canonical form of kinetic energy

$$ \begin{aligned} {\mathcal{K}}^{\star \star} & = m_{B} {^{m}\mathbf {V}}^{T} ({^{m}{ \dot{\mathbf{x}} }_{r}}+ {\widetilde {\boldsymbol{\omega}} _{m}}{^{m}\mathbf{x} _{r}}) + {^{r} {\boldsymbol {\varOmega}}_{r}}^{T} \mathbf {J}\, ({^{r} {\boldsymbol{\omega}} _{m}}+ {^{r} \mathbf {W}_{r}}) \\ & \phantom{=} + \int _{V} {^{r}\mathbf {V}_{P,e}}^{T} ({^{r} {\dot {\mathbf{e}} _{P}}}+ ({^{r} \widetilde {\boldsymbol{\omega}} _{m}}+ {^{r} \widetilde{\mathbf {W}}_{r}}) {^{r} {\mathbf{e}} _{P},}) \ \rho dV \; \\ & \phantom{=} - \frac{1}{2}m_{B} {^{m}\mathbf {V}}^{T} {^{m}\mathbf {V}}- \frac{1}{2}{^{r} {\boldsymbol {\varOmega}}_{r}}^{T} \mathbf {J}\, {^{r} {\boldsymbol {\varOmega}}_{r}}- \frac{1}{2}\int _{V} {^{r}\mathbf {V}_{P,e}}^{T} \, {^{r}\mathbf {V}_{P,e}}\ \rho dV \; . \end{aligned} $$

(41)

Equation (41) is a two-field expression of kinetic energy in which displacement / rotation and velocity fields play equal roles. As a result, second-order derivation in time will be avoided in the development of the motion equations.

In order to derive the latter via Hamilton’s principle, a variation of the integral of the kinetic energy over an interval $[t_{1},t_{2}]$ must be computed. Substituting into it the canonical form (41)

$$ \begin{aligned} \delta \int _{t_{1}}^{t_{2}} {\mathcal{K}}^{\star \star} \ dt & = \ \delta \int _{t_{1}}^{t_{2}} \left ( m_{B} {^{m}\mathbf {V}}^{T} ({^{m}{ \dot{\mathbf{x}} }_{r}}+ {\widetilde {\boldsymbol{\omega}} _{m}}{^{m}\mathbf{x} _{r}}) \right . \\ & + {^{r} {\boldsymbol {\varOmega}}_{r}}^{T} \mathbf {J}\, ({^{r} {\boldsymbol{\omega}} _{m}}+ {^{r} \mathbf {W}_{r}}) \\ & + \int _{V} {^{r}\mathbf {V}_{P,e}}^{T} ({^{r} {\dot {\mathbf{e}} _{P}}}+ ({^{r} \widetilde {\boldsymbol{\omega}} _{m}}+ {^{r} \widetilde{\mathbf {W}}_{r}}) {^{r} {\mathbf{e}} _{P},}) \ \rho dV \\ & \left . - \frac{1}{2}(m_{B} {^{m}\mathbf {V}}^{T} {^{m}\mathbf {V}}+ {^{r} {\boldsymbol {\varOmega}}_{r}}^{T} \mathbf {J}{^{r} {\boldsymbol {\varOmega}}_{r}}+ \int _{V} {^{r}\mathbf {V}_{P,e}}^{T} {^{r}\mathbf {V}_{P,e}}\ \rho dV) \right ) \ d t \; , \end{aligned} $$

(42)

allows development of the inertia contribution to the set of equations governing the motion of the rotating flexible body.

4.2 Compatibility in time

On the one hand, performing the velocity variations $\delta {^{m}\mathbf {V}}$, $\delta {^{r} {\boldsymbol {\varOmega}}_{r}}$ and $\delta {^{r}\mathbf {V}_{P,e}}$ restores the kinematic conditions in time

• Translation velocity of the reference frame

  

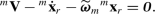  (43)

• Rotation velocity of the reference frame

  

  (44)

• Elastic velocity

  

  (45)

4.3 Equilibrium

On the other hand, extracting the inertia-force expressions from (42) requires integrating by parts in time whenever appropriate.

In order to compute the rotation contribution, we will make use of the relationships (17) and (24) relating the variation to the rotation operator ${^{m} \mathbf{R} _{r}}$ and its time derivative ${^{m} {\dot{\mathbf{R}} }_{r}}$ to the angular variation ${\delta ^{r} {\boldsymbol {\theta}}_{r}.}$ and its derivative ${\delta ^{r} \dot{{\boldsymbol {\theta}}}_{r}}$.

By performing the displacement variations $\delta {^{m}\mathbf{x} _{r}}$, ${\delta ^{r} {\boldsymbol {\theta}}_{r}.}$, and $\delta {^{r} {\mathbf{e}} _{P},}$ we calculate successively the inertia forces corresponding to:

• Equilibrium in translation:

  $$ -m_{B}(\dot{{^{m}\mathbf {V}}}+ {\widetilde {\boldsymbol{\omega}} _{m}}{^{m}\mathbf {V}}). $$

  (46)

• Equilibrium in rotation: both the rigid-body rotary inertia and the elastic inertia contribute, thus introducing coupling between rigid and elastic motion. The evaluation of the terms of elastic origin is performed as was done in [24]. The final result is

  $$ \begin{aligned} - \mathbf {J}{^{r} \dot{{\boldsymbol {\varOmega}}}_{r}}- ({^{r} \widetilde{\mathbf {W}}_{r}}+ {^{r} \widetilde {\boldsymbol{\omega}} _{m}}) (\mathbf {J}{^{r} {\boldsymbol {\varOmega}}_{r}}& +\int _{V} \tilde{{^{r}{\mathbf{e}} _{P},}}{^{r} \mathbf {V}_{P,e}}\; \rho dV ) \\ & - \int _{V} ({^{r} \tilde {\mathbf{e}} _{P}}{^{r}\dot{\mathbf {V}}_{P,e}}-{^{r}\tilde{\mathbf {V}}_{P,e}}{^{r} {\dot {\mathbf{e}} _{P}}}) \; \rho dV \; . \end{aligned} $$

  (47)

• Elastic equilibrium: Since the elastic virtual displacement occurs inside the volume integral, this last term has to be kept in variational form

  $$ - \int _{V} \delta {^{r} {\mathbf{e}} _{P},}^{T}( {^{r}\dot{\mathbf {V}}_{P,e}}+({^{r} \widetilde{\mathbf {W}}_{r}}+ {^{r} \widetilde {\boldsymbol{\omega}} _{m}}) {^{r}\mathbf {V}_{P,e}})\; \rho dV \; . $$

  (48)

In conclusion, we observe that the first-order set of equations governing the dynamics of a flexible body undergoing uniform rotation keeps globally the same structure in the rotating frame as in the case of motion from rest in an inertial reference. The only difference lies in the addition of a convection term involving the driving angular velocity ${^{r} {\boldsymbol{\omega}} _{m}}$ measured in the body frame. The kinematic conditions to be fulfilled are simply modified through the addition of the driving angular velocity.

The single-field, second-order form of the motion equations could a posteriori be obtained through substitution of the time-compatibility equations (43)–(45) into the equilibrium equations (46)–(48). It is needless to stress the fact that adopting a two-field description of the system dynamics clearly leads to considerable simplification in the problem formulation.

5 Strain energy

Elastic forces in the body are derived from the assumption of the existence of an internal potential energy ${\mathcal{V}}_{int}$. The latter results from the integration over the body of the strain-energy density $W$

$$ {\mathcal{V}}_{int} = \int _{V} W(\epsilon _{ij}) \ dV, $$

(49)

where the strain tensor $\epsilon _{ij}$ is derived from the elastic displacements. The strain–displacement relationship is assumed to be linear

$$ {\boldsymbol {\epsilon}}_{P} = \mathbf {D}\, {^{r} {\mathbf{e}} _{P},}$$

(50)

where $\mathbf {D}$ is the linear strain operator. Assuming also linear material behavior with $\mathbf {E}$ being a symmetric, positive-definite matrix of the elastic coefficients, the internal potential energy is described by the quadratic expression

$$ {\mathcal{V}}_{int} = \frac{1}{2} \int _{V} (\mathbf {D}\, {^{r} {\mathbf{e}} _{P}})^{T} \mathbf {E}(\mathbf {D}\, {^{r} {\mathbf{e}} _{P}}) dV \, . $$

(51)

The stiffness contribution to elastic equilibrium is thus

$$ \int _{S} \delta {^{r} {\mathbf{e}} _{P}}^{T} \mathbf {n}^{T} \mathbf {E}(\mathbf {D}\, {^{r} {\mathbf{e}} _{P}}) dS - \int _{V} \delta {^{r} {\mathbf{e}} _{P}}^{T} \mathbf {D}^{T} \left (\mathbf {E}(\mathbf {D}\, {^{r} {\mathbf{e}} _{P}})\right )) dV, $$

(52)

with $S$ being the undeformed body surface and $\mathbf {n}$ the outer normal to it.

6 Finite-element discretization

The finite-element discretization is achieved in the material frame and based on a simultaneous interpolation of the motion and velocity fields. Special attention is given to the discretization of inertia forces of gyroscopic origin. As will be seen, in the specific case of 3D solid modeling, obtaining the discretized expression of the gyroscopic forces is greatly simplified using the $\mathbf{S} _{i}$ matrices that can be derived from a mass kernel of the model.

6.1 Choice of shape functions

Let us make the natural choice to discretize the elastic displacement and velocity fields using the same set of shape functions in the form ^4,5

(53)

and

(54)

where $\mathbf {q}_{i},\, \mathbf {r}_{i}, \, \mathbf {N}_{i} (\mathbf {X}) \, i=1,2,3$ denote the generalized elastic displacement and velocity degrees of freedom and the matrix of shape functions in direction $i$, $\mathbf {N}(\mathbf {X})$ is the shape function matrix

(55)

and $\mathbf {L}$ is a Boolean operator that reorders the degrees of freedom into the node-by-node set $\mathbf {q}$

$$ \begin{bmatrix} \mathbf {q}_{1} \\ \mathbf {q}_{2} \\ \mathbf {q}_{3}\end{bmatrix} = \mathbf {L}\mathbf {q}, $$

(56)

which verifies the identity

$$ \mathbf {L}\mathbf {L}^{T} = \mathbf {I}\; . $$

(57)

6.2 Discretization of strain energy

Substituting the discretized form of elastic displacements (53) into the strain energy (51) provides the discrete form of strain energy

$$ {\mathcal{V}}_{int} = \frac{1}{2} \mathbf {q}^{T} \mathbf {K}\mathbf {q}, $$

(58)

with the linear stiffness matrix

$$ \mathbf {K}= \int _{V} \mathbf {L}^{T} (\mathbf {D}\, \mathbf {N}(\mathbf {X}))^{T} \mathbf {E}\, (\mathbf {D}\, \mathbf {N}(\mathbf {X})) \, \mathbf {L}\, dV \; . $$

(59)

This is by construction symmetric, and the elastic forces associated with rigid-body motion $\mathbf {U}$ vanish

(60)

Assuming in all generality a discretization in terms of elastic translations and rotations at nodes of the finite-element mesh, the generalized displacements at a given node $P$ can be computed in the following manner

$$ \mathbf {q}_{P} = \begin{bmatrix} \boldsymbol{\epsilon }_{P} \\ {\boldsymbol {\kappa}}_{P} \end{bmatrix} = \begin{bmatrix} {{^{m} {\mathbf{R} }_{r}^{T}}}({^{m}\mathbf{x} _{P}}-{^{m}\mathbf{x} _{r}}) -{^{r} \mathbf {X}_{P}} \\ p ({{^{m} {\mathbf{R} }_{r}^{T}}}{^{m} \mathbf{R} _{P}}) \end{bmatrix} , $$

(61)

where

• $\boldsymbol{\epsilon }_{P}$ is a discrete set of translation displacements computed from (1),

• ${ p} ({{^{m} {\mathbf{R} }_{r}^{T}}}{^{m} \mathbf{R} _{P}})$ is a set of 3 parameters (e.g., rotation parameters) measuring the relative rotation ${{^{m} {\mathbf{R} }_{r}^{T}}}{^{m} \mathbf{R} _{P}}$.

In the case of finite-element modeling using 3D solid elements, only the translation displacements $\boldsymbol{\epsilon }_{P}$ are generally defined at nodes. The angular dofs ${\boldsymbol {\kappa}}_{P}$ have to be used to build finite-element models for 2D media such as beams and shells.

6.3 Discretization of inertia forces

A key issue in developing the expression of the elastic contribution to inertia forces is to discretize the terms of gyroscopic origin appearing in equations (47) and (48). Their evaluation is greatly simplified by assuming that the same shape functions are adopted in all three directions in space

$$ \mathbf {N}_{1} (\mathbf {X}) = \mathbf {N}_{2} (\mathbf {X}) = \mathbf {N}_{3} (\mathbf {X}) = \mathbf {N}^{\star }(\mathbf {X}) $$

(62)

as is generally the case when building 3D solid-element models .⁶ If the shape functions adopted for the discretization of the strain energy do not fulfill that condition, it is still possible to discretize the inertia forces in a nonconsistent manner with shape functions fulfilling the condition (62). All the matrices resulting from the discretization of the elastic inertia terms in (41) can then be developed in terms of the one-dimensional mass kernel

$$ \mathbf {M}^{\star }= \int _{V} \mathbf {N}^{\star }(\mathbf {X})^{T} \mathbf {N}^{ \star}(\mathbf {X}) \rho dV \; . $$

(63)

The different matrices resulting from the discretization of the virtual work expression (48) associated with elastic inertia forces are developed next.

6.3.1 Elastic mass matrix $\mathbf {M}$

Discretizing the first part provides the expression of the elastic-mass matrix:

$$ \delta \mathbf {q}^{T} \mathbf {f}_{e,1} = - \int _{V} \delta {^{r} {\mathbf{e}} }^{T} {^{r}\dot{\mathbf {V}}_{e}}\; \rho dV = - \delta \mathbf {q}^{T} \mathbf {M}\dot{\mathbf {r}}, $$

(64)

with, owing to (63), the elastic-mass matrix

(65)

The essential condition (34) expressing orthogonality of elastic velocities to rigid-body modes is discretized in the form

(66)

Therefore, the shape functions (55) of the discretization must be selected so as to fulfill this condition. An efficient way to fulfill condition (66) is to apply to the set of equations Herting’s reduction method [26] as proposed in [24] and achieved in Sect. 7 since it makes use of a combined set of attachment and free-free elastic modes orthogonal to rigid-body motion to describe the elastic deformation.

6.3.2 Gyroscopic matrix $\mathbf {G}$

In order to discretize the second term of (48), let us first simplify the notation by defining the skew-symmetric matrix of “computed” angular velocities

$$ {\tilde{{\boldsymbol {\alpha}}}}= {^{r} \widetilde{\mathbf {W}}_{r}}+ {^{r} \widetilde {\boldsymbol{\omega}} _{m}}. $$

(67)

The gyroscopic contribution is computed in the form

$$ \begin{aligned} \delta \mathbf {q}^{T} \mathbf {f}_{e,2} & = - \int _{V} \delta \, {^{r} {\mathbf{e}} }^{T} \,\tilde{{\boldsymbol {\alpha}}}\, {^{r}\mathbf {V}_{e}}\, \rho dV \\ & = - \delta \mathbf {q}^{T} \mathbf {L}^{T} \int _{V} \mathbf {N}(\mathbf {X}) \tilde{{\boldsymbol {\alpha}}} \mathbf {N}(\mathbf {X}) \, \rho dV \; \mathbf {L}\dot{\mathbf {r}}\end{aligned} $$

(68)

and, assuming isotropy of the mass matrix (Equation (65))

(69)

Taking into account the identity (57), the result (68) can finally be reorganized in the form

$$ \delta \mathbf {q}^{T} \mathbf {f}_{e,2} = - \delta \mathbf {q}^{T} \mathbf {A}( {\boldsymbol {\alpha}}) \mathbf {M}\dot{\mathbf {r}}= - \delta \mathbf {q}^{T} \mathbf {G}( {\boldsymbol {\alpha}}) \dot{\mathbf {r}}, $$

(70)

where the gyroscopic matrix $\mathbf {G}({\boldsymbol {\alpha}})$ appears to result very simply from the product

$$ \mathbf {G}({\boldsymbol {\alpha}}) = \mathbf {A}({\boldsymbol {\alpha}}) \mathbf {M}, $$

(71)

with the skew-symmetric block-diagonal matrix

(72)

Let us note that the gyroscopic matrix can easily be precomputed when expressing it in the linear form

(73)

with being the unit vector along direction $i$.

We also note that matrices $\mathbf {M}$ and $\mathbf {A}(\tilde{{\boldsymbol {\alpha}}})$ commute due to the skew-symmetry of matrix $\mathbf {G}$ and the symmetry of matrix $\mathbf {M}$

$$ \begin{aligned} \mathbf {G}({\boldsymbol {\alpha}}) = \mathbf {A}({\boldsymbol {\alpha}}) \mathbf {M}& = - (\mathbf {A}( {\boldsymbol {\alpha}}) \mathbf {M})^{T} \\ & = - \mathbf {M}(\mathbf {A}({\boldsymbol {\alpha}}))^{T} \\ & = + \mathbf {M}\mathbf {A}({\boldsymbol {\alpha}}) \; . \end{aligned} $$

(74)

6.3.3 Gyroscopic coupling terms and $\mathbf{S} _{i}$ matrices

Developing the elastic contribution to the dynamic equilibrium of the center of mass (Equation (47)) requires computing the discrete form of the volume integral

$$ \mathbf {s}({^{r} {\mathbf{e}} }, {^{r}\mathbf {V}_{e}}) = \int _{V} {^{r} \tilde {\mathbf{e}} }\, {^{r}\mathbf {V}_{e}}\, \rho dV = \mathbf{S} (\mathbf {q}) \mathbf {r}\; . $$

(75)

Equation (75) is a 3-component vector that can be decomposed in the form

$$ \mathbf {s}({^{r} {\mathbf{e}} }, {^{r}\mathbf {V}_{e}}) = \int _{V} \begin{bmatrix} - e_{3}^{T} V_{2} + e_{2}^{T} V_{3} \\ - e_{1}^{T} V_{3} + e_{3}^{T} V_{1} \\ - e_{2}^{T} V_{1} + e_{1}^{T} V_{2} \end{bmatrix} \rho dV \; . $$

(76)

The vector components ${^{r} {\mathbf{e}} }_{i}$ and ${^{r}\mathbf {V}_{e}}_{i}$ are discretized in the form

$$ e_{i} = \mathbf {N}_{i} (\mathbf {X}) \mathbf {L}_{i} \mathbf {q}V_{i} = \mathbf {N}_{i} (\mathbf {X}) \mathbf {L}_{i} \mathbf {r}\quad i = 1,2,3, $$

(77)

where $\mathbf {L}_{i}$ is the submatrix of the Boolean operator $\mathbf {L}$ that extracts from vector $\mathbf {q}$ its components along direction $i$

$$ \mathbf {L}= \begin{bmatrix} \mathbf {L}_{1} \\ \mathbf {L}_{2} \\ \mathbf {L}_{3}\end{bmatrix} \; . $$

(78)

Assuming again isotropy of the shape functions, we obtain

$$ \mathbf {s}({^{r} {\mathbf{e}} }, {^{r}\mathbf {V}_{e}}) = \begin{bmatrix} \mathbf {q}^{T} ( - \mathbf {L}_{3}^{T} \mathbf {M}^{\star }\mathbf {L}_{2} + \mathbf {L}_{2}^{T} \mathbf {M}^{\star }\mathbf {L}_{3} )\mathbf {r}\\ \mathbf {q}^{T} ( - \mathbf {L}_{1}^{T} \mathbf {M}^{\star }\mathbf {L}_{3} + \mathbf {L}_{3}^{T} \mathbf {M}^{\star }\mathbf {L}_{1} )\mathbf {r}\\ \mathbf {q}^{T} ( - \mathbf {L}_{2}^{T} \mathbf {M}^{\star }\mathbf {L}_{1} + \mathbf {L}_{1}^{T} \mathbf {M}^{\star }\mathbf {L}_{2} )\mathbf {r}\end{bmatrix} , $$

(79)

a result that we write formally in the compact form

$$ \mathbf{S} (\mathbf {q}) \mathbf {r}= \begin{bmatrix} \mathbf {q}^{T} \mathbf{S} _{1} \mathbf {r}\\ \mathbf {q}^{T} \mathbf{S} _{2} \mathbf {r}\\ \mathbf {q}^{T} \mathbf{S} _{3} \mathbf {r}\end{bmatrix} = - \mathbf{S} (\mathbf {r}) \mathbf {q}, $$

(80)

with the skew-symmetric $\mathbf{S} _{i}$ matrices

$$ \mathbf{S} _{i} = \epsilon _{ijk} \mathbf {L}_{j}^{T} \mathbf {M}^{\star }\mathbf {L}_{k} \; . $$

(81)

The use of the $\mathbf{S} _{i}$ matrices makes easy the computation of gyroscopic forces of elastic origin, and also simplifies the computation of the gyroscopic matrix $\mathbf {G}$ as shown hereafter.

6.3.4 Alternative method to compute the gyroscopic matrix $\mathbf {G}$

From a practical point of view, it might be convenient to express the gyroscopic matrix $\mathbf {G}$ in terms of the same matrices (81). For that purpose, let us start again from the virtual work expression (68). It can be transformed as follows

$$ \begin{aligned} \delta \mathbf {q}^{T} \mathbf {f}_{e,2} & = - \int _{V} \delta {^{r} {\mathbf{e}} }^{T} \,{\tilde{{\boldsymbol {\alpha}}}}\, {^{r}\mathbf {V}_{e}}\, \rho dV \\ & = + {\boldsymbol {\alpha}}^{T} \int _{V}\delta {^{r} \tilde {\mathbf{e}} }\, {^{r}\mathbf {V}_{e}}\, \rho dV \end{aligned} , $$

(82)

or, owing to (75) and (80)

$$ \begin{aligned} \delta \mathbf {q}^{T} \mathbf {f}_{e,2}= - \delta \mathbf {q}^{T} \mathbf {G}( {\boldsymbol {\alpha}}) \mathbf {r}& = {\boldsymbol {\alpha}}^{T} \mathbf{S} (\delta \mathbf {q}) \mathbf {r}\\ & = \sum _{i} \alpha _{i} \delta \mathbf {q}^{T} \mathbf{S} _{i} \mathbf {r}\\ & = \delta \mathbf {q}^{T} (\sum _{i} \alpha _{i} \mathbf{S} _{i}) \mathbf {r}. \end{aligned} $$

(83)

According to its definition (70), the final expression of the gyroscopic matrix is thus

$$ \mathbf {G}({\boldsymbol {\alpha}}) = - \sum _{i} \alpha _{i} \mathbf{S} _{i}. $$

(84)

6.3.5 Discretized form of elastic inertia forces

The discretized form of elastic inertia forces results from Equation (48)

$$ - \int _{V} \left ( \delta { {^{r}\mathbf{e}} }^{T} {^{r}\dot{\mathbf {V}}_{e}}- (^{r}\mathbf {W}_{r} + {{^{m} {\mathbf{R} }_{r}^{T}}}{\boldsymbol{\omega}} _{m})^{T} \widetilde{\delta {^{r}{\mathbf{e}} }} {^{r}\mathbf {V}_{e}} \right )\rho dV \; . $$

(85)

We obtain immediately the discrete form

$$ - \mathbf {M}\dot{\mathbf {r}}- \mathbf {G}({^{r} {\boldsymbol{\omega}} _{m}}+ {^{r} \mathbf {W}_{r}}) \mathbf {r}, $$

(86)

where $\mathbf {G}({\boldsymbol {\alpha}})$ can be precomputed in the form (84).

6.3.6 Discretized form of inertia forces on the center of mass

Owing to Equations (79) and (80) the inertia forces (47) on the center of mass can be expressed in the form

$$ - \mathbf {J}{^{r} \dot{{\boldsymbol {\varOmega}}}_{r}}- ({^{r} \widetilde{\mathbf {W}}_{r}}+ {^{r} \widetilde {\boldsymbol{\omega}} _{m}}) (\mathbf {J}{^{r} {\boldsymbol {\varOmega}}_{r}}+\mathbf{S} (\mathbf {q}) \mathbf {r}) -\mathbf{S} (\mathbf {q}) \dot{\mathbf {r}}+ \mathbf{S} (\mathbf {r}) \dot{\mathbf {q}}, $$

(87)

with $\mathbf{S} (\mathbf {q}) \mathbf {r}$) and $\mathbf{S} (\mathbf {r}) \mathbf {q}$) computed from (80).

6.4 Discretized form of compatibility in time

The discretized form of the compatibility-in-time equation (45) results from the variational equation extracted from (42)

$$ \int _{V} \delta {^{r}\mathbf {V}_{e}}^{T} ({^{r} {\dot {\mathbf{e}} }}+ {\boldsymbol {\alpha}}) {^{r} {\mathbf{e}} }- {^{r}\mathbf {V}_{e}}) \ \rho dV =0 \quad \text{with} \quad {\boldsymbol {\alpha}}= {^{r} {\boldsymbol{\omega}} _{m}}+ {^{r} \mathbf {W}_{r}}, $$

(88)

or

$$ \int _{V} \delta {^{r}\mathbf {V}_{e}}^{T} \left ( ({^{r} {\dot {\mathbf{e}} }}- {^{r}\mathbf {V}_{e}}) - {\boldsymbol {\alpha}}^{T} \, \delta {^{r} \tilde{\mathbf {V}}_{e}}\, {^{r} {\mathbf{e}} }\right ) \rho dV =0 \; . $$

(89)

We thus obtain

$$ \delta \mathbf {r}^{T} \mathbf {M}( \dot{\mathbf {q}}- \mathbf {r}) - {\boldsymbol {\alpha}}^{T} \mathbf{S} (\delta \mathbf {r}) \mathbf {q}=0, $$

(90)

or, owing to (83)

(91)

Finally, multiplying by $\mathbf {M}^{-1}$ and making use of (74) provides the discretized time-compatibility relationship

(92)

where $\mathbf {A}({\boldsymbol {\alpha}})$ can be precomputed in the form

(93)

6.5 Summary

Table 3 summarizes the floating-frame equations obtained for the flexible body undergoing a uniform angular velocity ${\boldsymbol{\omega}} _{m}$. The equilibrium part represents the contribution of the body to the equilibrium equations of the assembled global system. The translation motion of the center of mass is expressed in the rotating frame, while its rotational motion is expressed in the material frame. Worthwhile noticing is the fact that the rotation equilibrium about the center of mass is modified by the elastic deformation of the body: the additional terms involving the $\mathbf{S} _{i}$ matrices (Equation (81)) represent in fact the change of inertia tensor due to elastic deformation.

Table 3 Floating-frame equations of a flexible body undergoing uniform rotation ${\boldsymbol{\omega}} _{m}$

The last column of Table 3 provides the steady equations of the system. They can be used to study the stationary response of the system in the rotating frame, as is the case for a rotating system subject to mass unbalance.

Application of the essential orthogonality condition will be discussed in Sect. 7.

7 Superelement implementation

The superelement implementation of the floating system of equations of Table 3 can be achieved by selecting a modal-reduction basis $\mathbf {Y}$ that equally applies to displacements and velocities⁷ [24, 25]

$$ \mathbf {q}= \mathbf {Y}\overline{\mathbf {q}} \mathbf {r}=\mathbf {Y}\overline{\mathbf {r}}, $$

(94)

$\overline{\mathbf {q}}$ and $\overline{\mathbf {r}}$ being the reduced sets of generalized displacements and velocities.

The choice of the modal basis $\mathbf {Y}$ is not arbitrary since it has to fulfill the following requirements:

• 1. The orthogonality condition (66) of the elastic velocity field $\mathbf {r}$ to rigid-body modes is an essential condition to be satisfied by the modal-reduction basis. The widely used Component Mode Synthesis (CMS) method [19] cannot be used in this case since it generates a modal-reduction basis composed of static boundary modes and vibration modes resulting from fixation conditions on the boundary. Indeed, by construction, the latter are not orthogonal to rigid-body modes. Therefore, the CMS method does not fulfill the essential condition (66) and is not applicable in the present case.

• 2. The modal-reduction method adopted should be able to provide a statically correct solution on the boundary $B$ of the reduced model to allow for a correct transmission of reaction forces resulting from interaction between bodies of global system. This can be achieved using a set of attachment modes, filtered from their rigid-body contribution in order to fulfill the essential condition (66).

• 3. The boundary displacements $\mathbf {q}_{B}$ should be a subset of the reduced set $\overline{\mathbf {q}}$ to facilitate kinematic connections on the boundary shared by adjacent bodies.

As demonstrated in [24, 25], conditions 1 and 2 are fulfilled by choosing a modal-reduction scheme of type

$$ \mathbf {q}= \mathbf {Y}\overline{\mathbf {q}} = \begin{bmatrix} \mathbf {F}_{B} & {\boldsymbol {\varPsi}}\end{bmatrix} \begin{bmatrix} \mathbf {p}_{B} \\ {\boldsymbol {\eta}}\end{bmatrix} , $$

(95)

where $\mathbf {F}_{B}$ is a set of free attachment modes defined on the boundary $B$, $\mathbf {p}_{B}$ the associated nodal intensities, ${\boldsymbol {\varPsi}}$ a set of free-free vibration modes, and ${\boldsymbol {\eta}}$ the associated modal intensities. The modal-reduction scheme (95) as initially proposed in [32] is, however, not appropriate as such due its hybrid nature, the $\mathbf {p}_{B}$ being unknowns of force type.

A displacement to displacement relationship can be constructed from (95) using a transformation proposed in [26, 27]. Equation (95) can then be recast in terms of the conjugated boundary nodal displacements $\mathbf {q}_{B}$ in the form

(96)

The matrices $\mathbf {F}_{BB}$, $\mathbf {F}_{IB}$, ${\boldsymbol {\varPsi}}_{B}$, and ${\boldsymbol {\varPsi}}_{I}$ involved in the transformation result from a splitting of the matrices $\mathbf {F}_{B}$ and ${\boldsymbol {\varPsi}}$ into boundary and internal contributions.

Not all discrete canonical equations are affected by the modal reduction. The modified ones are:

• Equation (87) describing the contribution to rotational equilibrium of the center of mass, rewritten in the form:

  $$ - \mathbf {J}{^{r} \dot{{\boldsymbol {\varOmega}}}_{r}}- ({^{r} \widetilde{\mathbf {W}}_{r}}+ {^{r} \widetilde {\boldsymbol{\omega}} _{m}}) (\mathbf {J}{^{r} {\boldsymbol {\varOmega}}_{r}}+\mathbf{S} (\mathbf {Y}{\overline{\mathbf {q}}})\mathbf {Y}{ \overline{\mathbf {r}} }) + \frac{d}{dt}\left (\mathbf{S} (\mathbf {Y}\overline{\mathbf {q}})\mathbf {Y}{\overline{\mathbf {r}} }\right ). $$

  (97)

  Owing to Equation (80) the third term of (97) can be expressed as follows:

  $$ \mathbf{S} (\mathbf {Y}\overline{\mathbf {q}}) \mathbf {Y}\overline{\mathbf {r}} = \begin{bmatrix} \overline{\mathbf {q}} ^{T} \mathbf {Y}^{T} \mathbf{S} _{1} \mathbf {Y}\overline{\mathbf {r}} \\ \overline{\mathbf {q}} ^{T} \mathbf {Y}^{T}\mathbf{S} _{2} \mathbf {Y}\overline{\mathbf {r}} \\ \overline{\mathbf {q}} ^{T} \mathbf {Y}^{T} \mathbf{S} _{3} \mathbf {Y}\overline{\mathbf {r}} \end{bmatrix} = \begin{bmatrix} \overline{\mathbf {q}} ^{T} \overline{\mathbf{S}} _{1} \overline{\mathbf {r}} \\ \overline{\mathbf {q}} ^{T} \overline{\mathbf{S}} _{2} \overline{\mathbf {r}} \\ \overline{\mathbf {q}} ^{T} \overline{\mathbf{S}} _{3} \overline{\mathbf {r}} \end{bmatrix} = \overline{\mathbf{S}} (\overline{\mathbf {q}})\overline{\mathbf {r},} $$

  (98)

  with the reduced skew-symmetric matrices

  $$ \overline{\mathbf{S}} _{i} = \mathbf {Y}^{T} \mathbf{S} _{i} \mathbf {Y}\, . $$

  (99)

  The final form of the reduced contribution to rotational equilibrium of the floating center of mass is thus

  $$ - \mathbf {J}{^{r} \dot{{\boldsymbol {\varOmega}}}_{r}}- ({^{r} \widetilde{\mathbf {W}}_{r}}+ {^{r} \widetilde {\boldsymbol{\omega}} _{m}}) (\mathbf {J}{^{r} {\boldsymbol {\varOmega}}_{r}}+\overline{\mathbf{S}} ({\overline{\mathbf {q}}}){\overline{\mathbf {r}} }) + \frac{d}{dt}\left (\overline{\mathbf{S}} ( \overline{\mathbf {q}}){ \overline{\mathbf {r}} }\right ). $$

  (100)

• The elastic momentum equation (91) that we first reduce in the form

  

  (101)

  The first and last terms are expressed in terms of the reduced-mass matrix

  $$ \overline{\mathbf {M}}= \mathbf {Y}^{T} \mathbf {M}\mathbf {Y}, $$

  (102)

  while, by making use of Equation (84), the reduced gyroscopic matrix of the second term becomes

  $$ \begin{aligned} \mathbf {Y}^{T} \mathbf {G}({^{r} {\boldsymbol{\omega}} _{m}}+ {^{r} \mathbf {W}_{r}}) \mathbf {Y}\overline{\mathbf {q}} & = -\sum _{i} ({^{r} {\boldsymbol{\omega}} _{m}}+ {^{r} \mathbf {W}_{r}})_{i} \mathbf {Y}^{T} \mathbf{S} _{i} \mathbf {Y}\\ & = -\sum _{i} ({^{r} {\boldsymbol{\omega}} _{m}}+ {^{r} \mathbf {W}_{r}})_{i} \overline{\mathbf{S}} _{i} = \overline{\mathbf {G}}({^{r} {\boldsymbol{\omega}} _{m}}+ {^{r} \mathbf {W}_{r}}) \end{aligned} $$

  (103)

  and therefore we can write (101) in the final form

  

  (104)

  with the reduced gyroscopic matrix

  $$ \overline{\mathbf {G}} ({^{r} {\boldsymbol{\omega}} _{m}}+ {^{r} \mathbf {W}_{r}}) = -\sum _{i} ({^{r} {\boldsymbol{\omega}} _{m}}+ {^{r} \mathbf {W}_{r}})_{i} \overline{\mathbf{S}} _{i}. $$

  (105)

  From a computational standpoint it can be more efficient to rewrite it as a velocity equation

  

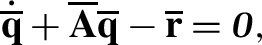  (106)

  with

  $$ {\overline{\mathbf {A}}} = {\overline{\mathbf {M}}}^{-1}\overline{\mathbf {G}} ({^{r} {\boldsymbol{\omega}} _{m}}+ {^{r} \mathbf {W}_{r}})\; , $$

  (107)

  since the velocity dofs can then be eliminated at the superelement level, thus reducing the number of unknowns of the global equation system.

• Finally, the contribution of the elastic continuum to dynamic equilibrium is reduced as

  $$ - \mathbf {Y}^{T} \mathbf {K}\mathbf {Y}\overline{\mathbf {q}} - \mathbf {Y}^{T} \mathbf {M}\mathbf {Y}\dot{\overline{\mathbf {r}}} - - \mathbf {Y}^{T} \mathbf {G}({^{r} {\boldsymbol{\omega}} _{m}}+ {^{r} \mathbf {W}_{r}}) \mathbf {Y}\mathbf {r}$$

  (108)

  and can obviously expressed as

  $$ - \overline{\mathbf {K}}\overline{\mathbf {q}} - \overline{\mathbf {M}} \dot{\overline{\mathbf {r}}} - \overline{\mathbf {G}} ({^{r} {\boldsymbol{\omega}} _{m}}+ {^{r} \mathbf {W}_{r}}) \overline{\mathbf {r}} , $$

  (109)

  with the reduced stiffness matrix

  $$ \overline{\mathbf {K}}= \mathbf {Y}^{T} \mathbf {K}\mathbf {Y}\; . $$

  (110)

8 Vibration and stability of a single-disk rotating shaft

The first example is taken from reference [28]. It consists of a flexible shaft of length $L$ supported at its ends by bearings, as depicted in Fig. 2.

Fig. 2

Single-disk rotating shaft: system layout [28]

The shaft is connected to the ground at point $R$ by means of a revolute joint and at point $T$ via a cylindrical joint. The angular speed of the shaft is a prescribed function of time, $\Omega (t)$. A rigid disk is attached to the shaft at its midlength point $M$. The disk center of mass is located a distance $d$ above the reference axis of the shaft, thus creating an unbalance of the system.

At $t=0$, the shaft is at rest and deformed under the effect of the gravity acceleration acting in the vertical direction. It is set in motion by prescribing its rotation at the revolute joint, and lateral oscillations occur due to mass unbalance. As the shaft accelerates, it passes through the first critical speed of the system (close to the first natural bending frequency) and the operation goes from sub- to supercritical. As predicted by linear rotor dynamics theory, the shaft becomes unstable when operating at the critical speed, and therefore the magnitudes of lateral oscillations and corresponding internal forces rise as the shaft is accelerated through the critical speed.

The shaft has a length $L = 6$ m and is made of steel (density $\rho = 7800$ kg/m³, Young’s modulus $E= 210$ GPa, and Poisson’s ratio $\nu = 0.3$). The cross section is annular with inner and outer radii $r_{i} = 0.045$ and $r_{o}= 0.05$ m, respectively. The shaft’s sectional stiffness properties are summarized in Table 4.

Table 4 Single-disk rotating shaft: shaft sectional properties

The mass per unit length is $m= 11.64$ kg/m, the moments of inertia per unit length are $m_{22} = m_{33}=13.17$ g m²/m and the resulting polar moment of inertia per unit length is $m_{11}=26.34$ g m²/m. The circular disk at midlength is of mass $m_{d} = 70.573$ kg, radius $r_{d}=0.24$ m, and thickness $t_{d} = 0.05$ m. Its inertial tensor computed with respect to the center of mass is diagonal, diag(2.0325, 1.0163, 1.0163) g m². Its center of mass is located a distance $d =0.05$ m above the shaft reference axis, thus generating a mass unbalance. The gravity acceleration is $g=9.81$ m/s².

As in reference [28], the shaft rotation speed at the revolute joint is prescribed to be

$$ \Omega (t) = \textstyle\begin{cases} \frac{1}{2} A_{1} \omega [ 1 - cos (\frac{\pi t}{T_{1}})], & 0 \leq t \leq T_{1} , \\ A_{1} \omega , & T_{1} \leq t \leq T_{2} , \\ A_{1} \omega + \frac{1}{2}(A_{2} - A_{1}) \omega [ 1 - cos ( \frac{\pi (t-T_{2})}{T_{3} - T_{2}})] , & T_{2} \leq t \leq T_{3} , \\ A_{2} \omega , & t > T_{3}, \end{cases} $$

(111)

with the following parameter values: $\omega= 60$ rad/s, $A_{1} = 0.8$, $A_{2}=1.2$, $T_{1}=0.5$ s, $T_{2} = 1$ s, and $T_{3}=1.25$ s.

The shaft has been modeled with 20 geometrically exact nonlinear beam elements with independent linear interpolation of the displacement and velocity fields. Their inertia terms of gyroscopic origin are developed according the procedure described in Sect. 7.

As in [28], the system response has been first computed over a time interval of 2.5 s with a constant time step $h=1.0$ ms. The generalized-$\alpha$ time integration scheme for first-order systems as described in [33] has been used with a spectral radius $\rho _{\infty }= 0.8$. As in [28], the shaft dynamic response is illustrated by the trajectory of its midspan point as viewed by inertial and rotating observers. The plots of Figs. 3 and 4 are in complete agreement with those of the reference.

Fig. 3

Single-disk rotating shaft: trajectory of the shaft center at midlength as seen by an inertial observer

Fig. 4

Single-disk rotating shaft: trajectory of the shaft center at midlength as seen by a rotating observer

The first eigenfrequency of the system at rest is $\omega _{1}=9.08$ Hz (57.05 rad/s) and therefore the velocity profile (111) is such that the system crosses its first critical velocity during run-up. As a result, the average position of the shaft center at midlength as seen by the rotating observer is moving from positive to negative position along the $z$-axis. Figure 5 displays the first natural frequency of the system as observed by a rotating observer, computed as

$$ \omega _{rot} = \omega _{iner} - \Omega . $$

(112)

It decreases linearly from $\omega _{1}=9.08$ Hz (green dot on the figure) to 0 at the critical speed $\Omega _{cr}= 56.3$ rad/s. It is observed that the first critical speed remains close to the first natural frequency. This could be expected since the first vibration mode is perfectly symmetric with respect to the shaft midnode. As a result, there is no gyroscopic stiffening effect due to a change of orientation of the polar component of the disk moment of momentum.

Fig. 5

Single-disk rotating shaft: fundamental vibration frequency $\omega _{1}$ versus rotation speed $\Omega$ as measured by a rotating observer. (Color figure online)

Describing the system in the rotating frame gives deeper insight into its physical behavior. In that case, however, one has to take into account the time-varying character of the gravity force.

All dynamic simulations presented below were done at constant speed starting from homogeneous initial conditions. They thus include a transient part of the response due to sudden application of both gravity and unbalance forces.

Gravity is responsible for a forcing vibration at frequency $\Omega$, as seen by the rotation observer, which means that resonance would occur at the rotating velocities

$$ \Omega _{i} = 0.5 \, \omega _{iner,i}. $$

(113)

In the present case, the first resonance due to gravity occurs at $\Omega _{1} \simeq 4.54$ rad/s. Figure 6 displays the vertical displacement at the midnode at $\Omega = 4.54$ rad/s as seen by a rotating observer. The response is computed over a period of 1.5 s with a time step of 1.E-04 s. and with spectral radius $\rho _{\infty }= 0.8$. It can be interpreted as a beating between two signals (the free-vibration response and the forced response due to gravity) with neighboring frequencies.

Fig. 6

Single-disk rotating shaft: vertical displacement at the midnode as seen by a rotating observer at $\Omega =4.54$ Hz, exhibiting beating between two signals close to 9.0 Hz

The system behavior has also been investigated by computing the rotatory motion at different speeds below and above the critical speed $\Omega _{cr} = 56.3$ rad/s. Figure 7 displays the trajectories in the rotating frame of the disk center of mass at 30, 50, 70, and 90 rad/s. All simulations were made with the same parameters as before. Two main observations can be made:

• In all cases, the disk center of mass (CM) trajectory is confined in a circle of increasing amplitude when approaching the critical speed.

• The average position of the CM moves from positive to negative $z$ when passing the critical speed, and tends to move back to the rotation axis at sufficiently high speed.

Fig. 7

Single-disk rotating shaft: disk CM trajectories as seen by a rotating observer at $\Omega =30$, 50, 70, and 90 rad/s. (Color figure online)

Finally, the steady-state behavior of the system in the rotating frame can also be investigated as long as the gravity effect is omitted. This results, as stated before, from the assumption that the only inertia forces in the system are those generated by steady rotation motion. The main advantage of the steady-state analysis is that it provides much information on system behavior at negligible computation cost since it consists of a series of static analyses.

The steady-state response of the system to unbalance has been investigated from 0.0 to 400.0 rad/s. Figure 8 displays the steady deflections along the material axis $z$ of the disk CM node and the shaft midnode as seen by a rotating observer. Only one critical velocity is appearing in that velocity range. As already observed, beyond the first critical speed, the CM disk node tends to stay in the vicinity of the rotation axis. Finally, Fig. 9 displays the frequency spectrum as computed at each speed step included in the steady-state analysis. It shows the occurrence of a second critical speed around 300 rad/s that did not appear on the $u_{z}$ steady response to unbalance as displayed by Fig. 8. Indeed, this second critical speed corresponds to an antisymmetrical vibration mode that could not be excited by the specific unbalance introduced in the system.

Fig. 8

Single-disk rotating shaft: steady vertical displacements of the disk CM node and shaft midnode as seen by a rotating observer. (Color figure online)

Fig. 9

Single-disk rotating shaft: eigenfrequency spectrum of the system over the speed rotation range 0.0 to 400.0 rad/s as measured by a rotating observer. (Color figure online)

9 Dynamic response of a twin-disk rotor system

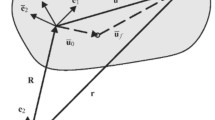
The second example is the twin-disk rotor system described in [23]. It is an electromagnetically levitated rotor consisting of an elastic shaft equipped with two relatively thick elastic disks, as shown in Fig. 10. In reference [23], a floating-frame model of the system was built starting from the finite-element mesh with 3D solid elements, as shown in Fig. 10.

Fig. 10

Twin-disk rotor system: finite-element model [23]

The rotor axle is 0.2 m long and has a diameter of 0.008 m. Two discs of radius 0.016 m and 0.02 m are attached at lengths $l_{1}=0.036$ m and $l_{2}=$ 0.172 m, respectively. Both discs are of thickness 0.004 m. The smaller disc, depicted in green, and the rotor axle are made of steel with a density $\rho = 7850$ kg/m³, a Young’s modulus $E = \mbox{2.1E11}$ N/m² and a Poisson ratio $\nu =0.3$. The larger disc is made of aluminum, with a density $\rho = 2700$ kg/m³, a Young’s modulus $E = 7.2$ E10 N/m² and a Poisson ratio $\nu =0.3$. A point mass of 10.0 E-5 kg is attached to the larger disc, as visualized in Fig. 2. Due to this unbalance mass, an eccentric motion of the rotor can be observed, which will be compared in the different analyses. The total mass of the rotor is approximately 0.116 kg. The active and passive parts of the electromagnetic bearings are modeled by spring-dampers with spring stiffness $k= 1000$ N/m and damping coefficient $c = 2$ N/(m/s).

Due to the slenderness of the rotor axle, we have chosen to model it with geometrically exact nonlinear beam elements of first order, with a description of the gyroscopic forces due to overall motion included. Independent interpolation of displacements and velocities has been performed as described in Sect. 6, but using position and rotation degrees of freedom. The beam model of the rotor shaft numbers 20 elements.

The first vibration frequencies of both disks are estimated to 14 663.0 Hz and 9238.40 Hz in a clamped configuration at their center, and 17 446.0 Hz and 11 697.0 in a free-free configuration. They are clearly out of the range of investigation of rotor speed, and therefore disk elasticity will be neglected in a first step. The effect of disk elasticity will be examined later, and for that purpose the effect of a change in disk properties will also be investigated.

Table 5 provides a comparison of the vibration eigenspectra obtained from the solid-element model of [23] and the current beam model. Two sets of values are provided in each case, corresponding to free-free and on-bearing configurations. The frequency range obtained for the whole system confirms that the effect of disk elasticity remains negligible with regards to the rotation speed range in which the rotor behavior has to be investigated.

Table 5 Twin-disk rotor system: comparison of free-free and on-bearing eigenspectra computed from solid and beam finite-element models

Finally, it is observed that the beam model provides systematically lower estimates of eigenfrequencies than the solid one. A possible explanation could be that the solid model needs to be further refined to properly capture the bending and shear properties of the shaft as given by the beam model.

9.1 Linear vibration properties of the rotor system

In order to obtain a preliminary insight into the change in dynamic behavior of the system with rotor speed, let us consider the linear eigenvalue problem that can be formulated in the rotation frame. Without giving too much detail, owing to the fact that the stiffness and damping properties of the bearings are isotropic, it can easily be established that the homogeneous equation governing the system dynamics in the absence of perturbation obeys the general form

$$ \left ( \mathbf {K}+ \mathbf {K}_{c}(\omega _{m}^{2}) + \mathbf {K}_{d}(\omega _{m}) \right )\mathbf {q}+ \left ( \mathbf {C}+ \mathbf {G}(\omega _{m}) \right ) \dot{\mathbf {q}}+ \mathbf {M}\ddot{\mathbf {q}}= 0, $$

(114)

with the following definitions:

• $\mathbf {K}$ and $\mathbf {M}$ are the linear stiffness and mass matrices of the system at rest, resulting from beam elasticity and inertia, and bearing elasticity.

• $\mathbf {K}_{c}(\omega _{m}^{2})$ and $\mathbf {G}(\omega _{m})$ are the centrifugal stiffness and gyroscopic matrices, resulting from beam and disk inertia in rotation. The latter are developed in Appendix A.

• $\mathbf {C}$ is the linear damping matrix from the bearings at rest. This is developed in Appendix B.

• $\mathbf {K}_{d}(\omega _{m})$ is a “damping stiffness matrix”, resulting from the expression of the damping forces in the bearings as seen by a rotating observer. This is also developed in Appendix B.

The second-order eigenvalue problem (114) can be recast in the first-order form

(115)

and its eigenvalues obey the general form

$$ \lambda _{i} = \alpha _{i} \pm \omega _{i}, $$

(116)

where $\omega _{i}$ is the frequency of the vibration motion observed in the rotating frame, and $\alpha _{i}$ is a damping constant resulting from dissipation in the bearings. The damping constants vanish when .

Figure 11 displays a Campbell plot of the system. It shows the existence of four critical speeds over the rotation speed range 0–3500 Hz: two critical speeds at 19.6 and 36.4 Hz due to rigid translation and tilting of the shaft over its bearings, and two critical speeds at 918.8 and 2664.9 Hz corresponding to bending deformation of the shaft. The latter result from the existence of bending vibration frequencies at 853 and 2274 Hz. They are shifted upward due to the stiffening effect generated by the centrifugal torque on the disks.

Fig. 11

Twin-disk rotor system: vibration frequencies observed in a rotating frame versus rotation speed: critical speeds occur at 19.6, 36.4, 918.8, and 2664.9 Hz. (Color figure online)

9.2 Steady-state motion

Provided that the rotor bearings have symmetric properties in the rotor transverse plane, the system response at constant rotor speed to mass unbalance is a steady one. Therefore, it is characterized by the fact that the elastic velocities $\dot{\mathbf {q}}$ and the global accelerations $\dot{\mathbf {r}}$ observed in the rotating frame vanish

(117)

The kinematic compatibility equations in time (43), (44), and (92) then reduce to the form

$$ \mathbf {r}= \mathbf {h}(\mathbf {q}, {\boldsymbol{\omega}} _{m}) \; . $$

(118)

Likewise, the set of equilibrium equations describes a nonlinear static equilibrium problem

(119)

where $\mathbf {f}_{iner}(\mathbf {q}, \mathbf {r}, {\boldsymbol{\omega}} _{m})$ is a distribution of inertia forces that depends on a steady global velocity and elastic deformation. In the case of purely symmetric mass distribution, Equation (119) reduces to , meaning that the inertia forces are in self-equilibrium and do not produce elastic deformation. In the case of mass unbalance, however, additional centrifugal and gyroscopic forces occur that induce steady elastic deformation $\mathbf {q}$ solutions of the stationary equation (119).

Sweeping over a specified speed range and computing the steady response from Equations (118) and (119) at each velocity step provides a fast characterization of system response to unbalance, as shown in Fig. 12. As expected, the largest displacement amplitudes occur on the bearings at the main critical frequency (918.8 Hz). Beyond the main critical speed, stabilization of the system occurs. Therefore, the geometric center of the steel disk tends to stay on the rotation axis since it coincides with the center of mass. Conversely, the geometric center of the aluminum disk moves away from the rotation axis so that the disk center of mass remains on the axis.

Fig. 12

Twin-disk rotor system: displacement amplitudes induced by mass unbalance at midlength, bearings, and disk centers. (Color figure online)

The system eigenfrequencies have been recomputed from the nonlinear steady model during the sweep over the velocity range, as displayed in Fig. 13. One can observe that they match exactly the frequencies obtained before from the linear model (Fig. 11) since, the mass unbalance being small, the system deflections remain small.

Fig. 13

Twin-disk rotor system: system eigenfrequencies computed from steady responses during velocity sweep. (Color figure online)

9.3 Dynamic response at fixed rotation velocity

Another way to investigate the system behavior is to observe in the rotating frame the dynamic response of the system under mass unbalance at different rotation speeds. The principle of the analysis is thus to compute the dynamic response at given ${\boldsymbol{\omega}} _{m}$ starting from homogeneous initial conditions, and select a time-integration window wide enough to observe stabilization of the response. In practice, the time window has been set to 0.1 s. Figure 14 displays the responses in the rotating frame observed at 318 Hz and 923 hz. In the first case, the response observed remains small and oscillatory after extinction of the transients. It can be verified that the oscillation frequency matches the frequency predicted by the Campbell plot of Fig. 13. In the second case, the driving velocity being close to the fundamental speed, the oscillation frequency is close to 0. After extinction of the transients, one thus observes in the rotating frame a quasisteady response. The mass unbalance being attached to the aluminum disk, the latter thus undergoes a significantly larger displacement than the disk of steel.

Fig. 14

Twin-disk rotor system: dynamic response in the rotating frame due to unbalance at constant speeds (318 and 923 Hz). (Color figure online)

Still another way to exploit the results provided by the successive dynamic responses at constant speed consists in computing the Fast Fourier Transforms of the successive responses. Figure 15 displays the FFTs corresponding to the dynamic responses of $u_{Z}$ displacements at both disks. Their maximum value occurs at zero frequency, which corresponds to the steady response in the rotation frame. They exhibit a much lower contribution around the rotation speed at which the response is evaluated.

Fig. 15

Twin-disk rotor system: FFT of dynamic responses in the rotating frame due to unbalance at 318 Hz (left) and 923 Hz (right). (Color figure online)

It is interesting to make a plot of these amplitudes versus rotation speed and compare them to the amplitudes resulting from the computation of steady responses, as is done in Fig. 16. As could be expected, there is a perfect agreement between both methods of investigation of system behavior. The main advantage of the steady-response approach is that it provides an extremely fast characterization of the response with regards to the higher computational cost of dynamic responses.

Fig. 16

Twin-disk rotor system: comparison between steady response amplitudes and FFT amplitudes at zero frequency for $u_{Z}$ displacement at both disks. (Color figure online)

9.4 Dynamic response over a specified velocity range

A nice feature of the proposed formalism to simulate the solution in a rotating frame at constant velocity is that it allows investigation of the dynamic response over a specified velocity range, as shown in Fig. 17. It is thus not needed to simulate a run-up from zero velocity to examine the system properties in a given speed range. This has a double advantage: not only is there significant saving of computational effort, but isolating the specified speed range facilitates result interpretation.

Fig. 17

Velocity profile on specified speed range

In order to investigate a given speed range $\Omega (t) \in [\Omega _{1}, \Omega _{2}]$ on a time interval $[0,T]$, the effective excitation on the system is defined as an angular rotation-imposed motion in the form

$$ \phi (t) = \int _{0}^{T} ( \Omega (t)- \omega _{m} ) dt, $$

(120)

with $\omega _{m} = \Omega _{1}$. Figure 18 displays the dynamic response observed in the rotating frame at both disk geometric centers during a run-up from 0 to 1000 rad/s in 1.0 s followed by a rotation at constant speed during 0.5 s. The parameters of the generalized-$\alpha$ time-integration method are $h =$ 3.e-3 s and $\rho _{\infty}=0.5$. One observes a very fast stabilization of the response after 1.0 s since the velocity is then kept constant to 1000 rad/s. Likewise, Fig. 19 displays the response observed at both disk geometric centers during a run-up from 5000 to 6500 rad/s in 1.5 s. The rotation speed is maintained at 5000 rad/s for 0.2 s in order to start the run-up period with correct initial conditions. A second constant-velocity period starts at 1.7 s during which stabilization of the response takes place. The parameters of the generalized-$\alpha$ time-integration method for this second simulation are $h =$ 8.e-5 s and $\rho _{\infty}= 0.5$. The speed range has been chosen so as to include the main critical speed of the system at 918 Hz. Due to the speed change over time, the maximum of the response occurs after crossing of the critical speed at 0.95 s. Again, very rapid stabilization of the response is observed in the zero-acceleration zone starting at 1.7 s.

Fig. 18

Twin-disk rotor system: dynamic response during run-up form 0 to 1000 rad/s in 1.0 s. (Color figure online)

Fig. 19

Twin-disk rotor system: dynamic response on the run-up speed interval 5000–6500 rad/s. (Color figure online)

9.5 Taking account of disk elastic behavior

Despite the high vibration frequency range of the disks ($f_{1}=14\ 663.0$ Hz for the steel disk, $f_{1} = 9238.40$ Hz for the aluminum disk in the clamped configuration), it has been decided to represent the elastic disks by elastic superelement models developed according to the methodology developed in Sect. 7. For that purpose, 3D finite-element models have been defined as displayed in Fig. 20. The number of nodes of the initial model for both disks is 2915.

Fig. 20

3D finite-element modeling of the disks. (Color figure online)

In order to exploit the model obtained from a standard finite-element analysis, different transformations have to be performed on the $(\mathbf {K}, \, \mathbf {M})$ matrices obtained.

• First, a central node has to be defined to express the connection between the 3D disk models and the shaft-beam model. For that purpose, it is assumed that the central inner ring of both disks is rigid. In both disks, 265 nodes of the inner-ring region are assumed to participate in the connection. Therefore, 795 linear constraints are expressed to link these nodes to a fictitious 6-dof node located at the center of the inner ring.

• Secondly, this constrained model is transformed into a superelement model following the procedure described in Sect. 7. This includes the reference node defined at the floating center of mass, the boundary node defined on the central ring for connection with the beam model, a second boundary node at which the unbalance mass can be attached and 5 free-free vibration modes that enrich the vibration content of the model. The superelement being constructed with independent interpolation of displacement and velocity fields, also numbers 20 velocity degrees of freedom.

• Finally, the gyroscopic matrices $\mathbf{S}$ of the superelement are constructed and reduced consistently to $\mathbf {K}$ and $\mathbf {M}$ as described in Sect. 7.

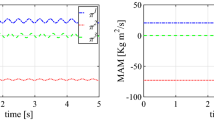
Figure 21 displays a comparison of the quasisteady responses obtained for both disks over the rotating speed range (0, 3000) Hz. The blue lines represent the rigid response while the red dots show the elastic ones. As was expected, taking into account the elastic behavior of the disks has no effect on the system response. It has been verified that the dynamic responses over different speed ranges match each other in the same manner.

Fig. 21

Twin-disk rotor system: comparison of rigid and elastic steady responses at disk steel (left) and aluminum (right). (Color figure online)

9.6 Modified shaft exhibiting elastic deformation

In order to investigate the effect of disk elasticity on the system behavior and also validate the superelement methodology developed for that purpose, the initial shaft model has been modified to increase disk elasticity. In order to keep the system modification realistic it has been assumed that both disks keep the same mass, but have their radius doubled and thickness thus reduced by a 0.25 factor in order to lower their vibration frequency range.

In the rigid configuration it is expected that the main critical velocities will increase compared to the nominal case since the polar moment of inertia of both disks is increased, thus generating higher gyroscopic torques at the disk-attachment points.

The size of the 3D finite-element models had to be increased (16 530 nodes for the steel disk, 25 530 for the aluminum disk) in order to generate models with elements having an appropriate aspect ratio. The disk fundamental vibration frequencies in the free-free configuration are now 1217 Hz (steel disk) and 1279 Hz (aluminum disk), so that strong interaction between shaft and disk deformation is now expected.

Figure 22 displays the first vibration mode of the steel disk occurring at 1217 Hz. The reduction procedure to construct the disk superelement models is similar to the nominal case, the only difference being that the number of nodes participating in the constraint sets that define the fictitious central nodes are now obtained from 570 nodes.

Fig. 22

First vibration mode of the 2R radius steel disk at 1217 Hz. (Color figure online)

A detailed comparison has been made, as in the nominal case, between the rigid and elastic models with disks of 2R size.

A very interesting piece of information results from the comparison of the steady responses to mass unbalance. As before, Campbell diagrams showing vibration frequencies in the rotating frame versus rotation speed have been obtained. Figure 23 displays the vibration spectra obtained successively with rigid and elastic disks of 2R radius.

Fig. 23

Twin-disk rotor system with disks of 2R radius: comparison of vibration frequencies between the rigid model (left) and the elastic one (right). (Color figure online)

On the one hand, it can be observed for the rigid case (left figure) that increasing the disk inertias (masses being constant) shifts to the right both critical speeds due to shaft bending. The first one now occurs at 1019 Hz (instead of 918 Hz) and the second one occurs above 3000 Hz (instead of ≃ 2600 Hz before). This frequency increase results from the larger disk inertias that generate higher stabilizing gyroscopic torques at disk-attachment nodes.

On the other hand, the elastic response (right figure) shows that there is now interaction between shaft and disk deformation since vibration shaft and disk frequencies are now within the same range. Therefore, one observes a significant decrease in critical velocities associated with bending: the first one decreases from 1019 to 931 Hz and the second one occurs now at 2530 Hz.

A significant change in dynamic behavior resulting form disk elastic deformation can be observed from the comparison of the steady responses to mass unbalance on Figure 24. On the one hand, the shift in amplitude responses is consistent with the results of the eigenvalue analysis. On the other hand, it is observed that disk elastic deformation has a beneficial effect on amplitude response: there is not only a reduction of amplitude response at the critical speeds, but also a drastic change of response amplitude between critical speeds.

Fig. 24

Twin-disk rotor system with disks of 2R radius: comparison of steady responses to unbalance between the rigid model (left) and the elastic one (right). (Color figure online)

10 Conclusion

The two-field, floating frame-of-reference approach to the dynamics of a flexible body has been extended to the case of motion in a noninertial frame rotating at fixed angular velocity. Independent finite-element discretization of displacements and velocities leads to a system of second-order equations. It has been shown that in the case of 3D solid modeling in particular, all inertia terms can be easily and exactly evaluated using the concept of $\mathbf{S} _{i}$ matrices obtained from a 1D mass kernel. In the case of model reduction, the $\mathbf{S} _{i}$ matrices of the initial model obey the same reduction scheme as the stiffness and mass matrices. The size of the resulting mixed FE model can always be drastically reduced through elimination of the velocity dofs at the element (superelement) level.

The proposed approach has been implemented in the JUDYN prototype code written in the JULIA^© language. Both examples presented have been selected and developed to emphasize the main features of the proposed methodology, namely:

• the ability to develop easily and without any approximation the inertia terms of gyroscopic origin of a flexible body thanks to the independent discretization of displacements/rotations and velocities on the one hand, and on the use of the concept of $\mathbf{S} _{i}$ matrices on the other hand;

• the possibility to study the dynamic response of the system within a given speed range without the need to start the simulation from zero speed;

• the capability to provide stationary responses in the rotating frame such as response to mass unbalance as solutions of a static problem.

Appendices

Appendix A: Linearization of rigid-body inertia forces

The case of the rigid body is directly deduced from Equations (43), (44), (46), and (47) governing the motion of the center of mass in the absence of elastic deformation.

Kinematic compatibility in time is thus described by the set of equations

(A.1)

(A.2)

while inertia behavior is described by the forces and torques

$$\begin{aligned} \mathbf {f}_{tr} & = -m_{B}\; (\dot{{^{m}\mathbf {V}}}+ { \widetilde {\boldsymbol{\omega}} _{m}}{^{m}\mathbf {V}}) \end{aligned}$$

(A.3)

$$\begin{aligned} \mathbf {f}_{rot} & = - \mathbf {J}\, {^{r} \dot{{\boldsymbol {\varOmega}}}_{r}}- ({^{r} \widetilde{\mathbf {W}}_{r}}+ {^{r} \widetilde {\boldsymbol{\omega}} _{m}}) \mathbf {J}\, {^{r} {\boldsymbol {\varOmega}}_{r}} . \end{aligned}$$

(A.4)

In order to understand how the gyroscopic forces generated by a fast rotating rigid disk influence the behavior of their support, it is of interest to perform the linearization of the rotation field and express the inertia forces in second-order form.

For the translation part (A.3) we obtain

$$ \mathbf {f}_{tr} = -m_{B}(\dot{{^{m}\mathbf {V}}}+ 2{\widetilde {\boldsymbol{\omega}} _{m}} \dot {{^{m}\mathbf{x} _{r}}}+ {\widetilde {\boldsymbol{\omega}} _{m}}{ \widetilde {\boldsymbol{\omega}} _{m}}{^{m}\mathbf{x} _{r}}) \, . $$

(A.5)

For the rotation part (A.4), assuming small rotations from the rotating frame to the body frame

$$ {^{m} \mathbf{R} _{r}}\simeq \mathbf {I}+ \begin{bmatrix} 0 & -\psi _{3} &\psi _{2} \\ \psi _{3} & 0 & -\psi _{1} \\ -\psi _{2} &\psi _{1} & 0 \end{bmatrix} = \mathbf {I}+ \tilde{\boldsymbol {\psi }}\quad \text{with} \quad \boldsymbol {\psi }= \begin{bmatrix} \psi _{1} \\ \psi _{2} \\ \psi _{3} \end{bmatrix} \, , $$

(A.6)

we obtain

$$ {^{r} {\boldsymbol{\omega}} _{m}}\simeq {\boldsymbol{\omega}} _{m}+ {\widetilde {\boldsymbol{\omega}} _{m}} \boldsymbol {\psi }\, . $$

(A.7)

The angular-velocity vector from body to rotation frame is likewise linearized in the form

$$ \widetilde{^{r}\mathbf {W}}= {{^{m} {\mathbf{R} }_{r}^{T}}}{^{m} {\dot{\mathbf{R}} }_{r}}\simeq \begin{bmatrix} 0 & -\dot{\psi}_{3} & \dot{\psi}_{2} \\ \dot{\psi _{3}} & 0 & -\dot{\psi _{1} } \\ -\dot{\psi _{2} } & \dot{\psi _{1}} & 0 \end{bmatrix} \quad \leftrightarrow \quad {\boldsymbol {\varPsi}}\simeq \dot{\boldsymbol {\psi }} \, . $$

(A.8)

Substituting (A.7) and (A.8) into (A.2) provides the linearized expression of the kinematic compatibility relationship as

$$ {^{r} {\boldsymbol {\varOmega}}_{r}}- {\boldsymbol{\omega}} _{m}- {\widetilde {\boldsymbol{\omega}} _{m}} \boldsymbol {\psi }- \dot{\boldsymbol {\psi }} = 0 \, . $$

(A.9)

Likewise, if the equations governing the rigid body are formulated in second-order form, the angular acceleration is linearized as

$$ {^{r} \dot{{\boldsymbol {\varOmega}}}_{r}}\simeq \ddot{\boldsymbol {\psi }}+ {\widetilde {\boldsymbol{\omega}} _{m}} \dot{\boldsymbol {\psi }} \; . $$

(A.10)

Finally, substituting (A.7), (A.8), and (A.10) into (A.4) provides the linearized form of the rotation inertia torque

$$ \begin{aligned} \mathbf {f}_{rot} & = - \mathbf {J}\ddot{\boldsymbol {\psi }}- (\mathbf {J}{ \widetilde {\boldsymbol{\omega}} _{m}}+ {\widetilde {\boldsymbol{\omega}} _{m}}\mathbf {J}- \widetilde{\mathbf {J}{\boldsymbol{\omega}} _{m}}) \dot{\boldsymbol {\psi }} - ( { \widetilde {\boldsymbol{\omega}} _{m}}\mathbf {J}{\widetilde {\boldsymbol{\omega}} _{m}}- \widetilde{\mathbf {J}{\boldsymbol{\omega}} _{m}} {\widetilde {\boldsymbol{\omega}} _{m}}) \boldsymbol {\psi }+ O(\boldsymbol {\psi }^{2}) \\ & = - \mathbf {J}\ddot{\boldsymbol {\psi }}- \mathbf {G}({\boldsymbol{\omega}} _{m}) \dot{\boldsymbol {\psi }} - \mathbf {K}({\boldsymbol{\omega}} _{m}^{2})\boldsymbol {\psi }\; . \end{aligned} $$

(A.11)

The matrices

$$\begin{aligned} \mathbf {G}({\boldsymbol{\omega}} _{m}) & \mathbf {J}{\widetilde {\boldsymbol{\omega}} _{m}}+ { \widetilde {\boldsymbol{\omega}} _{m}}\mathbf {J}- \widetilde{\mathbf {J}{\boldsymbol{\omega}} _{m}} \end{aligned}$$

(A.12)

$$\begin{aligned} \mathbf {K}({\boldsymbol{\omega}} _{m}^{2}) & = ( {\widetilde {\boldsymbol{\omega}} _{m}} \mathbf {J}{\widetilde {\boldsymbol{\omega}} _{m}}- \widetilde{\mathbf {J}{\boldsymbol{\omega}} _{m}} {\widetilde {\boldsymbol{\omega}} _{m}}) \end{aligned}$$

(A.13)

are, respectively, the gyroscopic matrix and the centrifugal stiffness matrices of the rigid body. Their explicit form can easily be obtained when the body axes are the principal axes of inertia:

$$ \mathbf {J}= \begin{bmatrix} J_{x} & 0 & 0 \\ 0 & J_{y} & 0 \\ 0 & 0 & J_{z} \end{bmatrix} . $$

(A.14)

We obtain the matrices

$$ \mathbf {G}({\boldsymbol{\omega}} _{m}) = \begin{bmatrix} 0 & -\omega _{3} (J_{x} + J_{y}-J_{z}) & \omega _{2} (J_{x} + J_{z} -J_{y}) \\ \omega _{3} (J_{x} + J_{y}-J_{z}) & 0 & - \omega _{1} (J_{y} + J_{z} -J_{x}) \\ - \omega _{2} (J_{x} + J_{z} -J_{y}) & \omega _{1} (J_{y} + J_{z} -J_{x}) & 0 \end{bmatrix} $$

(A.15)

and

$$ \mathbf {K}({\boldsymbol{\omega}} _{m}^{2}) = \begin{bmatrix} (\omega _{3}^{2} -\omega _{2}^{2} ) ( J_{z} - J_{y} ) & \omega _{1} \omega _{2} (J_{z} - J_{y}) & \omega _{1}\omega _{3} (J_{y} - J_{z}) \\ \omega _{1}\omega _{2} (J_{z} - J_{x}) & (\omega _{1}^{2} -\omega _{3}^{2} ) ( J_{x} - J_{z} ) & \omega _{2}\omega _{3} (J_{x} - J_{z}) \\ \omega _{1}\omega _{3} (J_{y} - J_{x}) & \omega _{2}\omega _{3} (J_{x} - J_{y}) & (\omega _{1}^{2} -\omega _{2}^{2} ) ( J_{x} - J_{y} ) \end{bmatrix} . $$

(A.16)

In the common case of a rigid body rotating at the uniform velocity $\omega _{m}$ around the body axis $X$

$$ {\boldsymbol{\omega}} _{m}^{T} = \omega _{m} \begin{bmatrix} 1 & 0 & 0 \end{bmatrix} \; , $$

(A.17)

they are further simplified as

$$ \mathbf {G}(\omega _{m}) = \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & - \omega _{m} (J_{y} + J_{z} -J_{x}) \\ 0 & \omega _{m} (J_{y} + J_{z} -J_{x}) & 0 \end{bmatrix} $$

(A.18)

and

$$ \mathbf {K}(\omega _{m}^{2}) = \begin{bmatrix} 0 & 0 & 0 \\ 0 &\omega _{m}^{2} ( J_{x} - J_{z} ) & 0 \\ 0 & 0 & \omega _{m}^{2}( J_{x} - J_{y} ) \end{bmatrix} \; . $$

(A.19)

It is immediately observed from (A.19) that the centrifugal forces on a rigid disk exert a stiffening effect when its inertia properties are such that $J_{x} \, > \, J_{z}$ and $J_{x} \, > \, J_{y}$.

Appendix B: Bearing modeling

Assuming that there is no crosscoupling between directions, a simple bearing model with linear stiffness $k_{i}$ and viscous damping $c_{i}$ properties can be described in the inertial frame by a constitutive law in the form

$$ \mathbf {f}_{bearing} = \text{diag} (k_{1}, \, k_{2}, \, k_{3} ) \mathbf{x} _{b} + \text{diag} (c_{1}, \, c_{2}, \, c_{3} ) \dot{\mathbf{x}} _{b} \; , $$

(B.20)

where $\mathbf{x} _{b}$ is the position vector of the bearing central point. Its expression into the rotation frame ${^{m} \mathbf{R} _{r}}$ with angular velocity ${\boldsymbol{\omega}} _{m}$ becomes

$$ \begin{aligned} ^{m}\mathbf {f}_{bearing} & = {{^{m} {\mathbf{R} }_{r}^{T}}}\mathbf {f}_{bearing} \\ & = {{^{m} {\mathbf{R} }_{r}^{T}}}( \text{diag} (k_{1}, \, k_{2}, \, k_{3} ) {^{m} \mathbf{R} _{r}}{^{m}\mathbf{x} _{b}} \\ & + {{^{m} {\mathbf{R} }_{r}^{T}}}\text{diag} (c_{1}, \, c_{2}, \, c_{3} ) {^{m} \mathbf{R} _{r}}{^{m}{\dot{\mathbf{x}}}_{b}} + {{^{m} {\mathbf{R} }_{r}^{T}}}\text{diag} (c_{1}, \, c_{2}, \, c_{3} ) {^{m} \mathbf{R} _{r}}{\widetilde {\boldsymbol{\omega}} _{m}}{^{m}\mathbf{x} _{b}}. \end{aligned} $$

(B.21)

It is immediately apparent that, in the absence of isotropic stiffness and damping properties, the bearing will be characterized in the rotating frame by time-varying stiffness and damping matrices

$$ \begin{aligned} \mathbf {K}_{bearing} (t) & = {{^{m} {\mathbf{R} }_{r}^{T}}}\left ( \text{diag} (k_{1}, \, k_{2}, \, k_{3} ) {^{m} \mathbf{R} _{r}}+ \text{diag} (c_{1}, \, c_{2}, \, c_{3} ) {^{m} \mathbf{R} _{r}}{\widetilde {\boldsymbol{\omega}} _{m}}\right ) \\ \mathbf {C}_{bearing} (t) & = {{^{m} {\mathbf{R} }_{r}^{T}}}\text{diag} (c_{1}, \, c_{2}, \, c_{3} ) {^{m} \mathbf{R} _{r}}\; . \end{aligned} $$

(B.22)

Therefore, in the general case, there is no possible steady motion of the system.

The special case of bearings with transverse isotropic properties for a system rotating about the $O_{x}$-axis (with angular velocity thus of the form ${\boldsymbol{\omega}} _{m}^{T} = [\omega _{m} \; 0 \; 0]$) can be described by assuming stiffness and damping matrices of the system at rest as

$$ \mathbf {K}_{0} = k \mathbf {I}_{0}, \quad \mathbf {C}_{0} = c \mathbf {I}_{0} \quad \text{with} \quad \mathbf {I}_{0} = \text{diag} (1, \, 1, \, 0 ) \; . $$

(B.23)

The bearing is then characterized in the rotating frame by the constant stiffness and damping matrices

$$\begin{aligned} \mathbf {K}_{bearing} & = k \mathbf {I}_{0} + c \mathbf {I}_{0} \,{ \widetilde {\boldsymbol{\omega}} _{m}}= \begin{bmatrix} 0 & 0& 0 \\ 0 & k & -\omega _{m} c \\ 0 &\omega _{m} c & k \end{bmatrix} \end{aligned}$$

(B.24)

$$\begin{aligned} \mathbf {C}_{bearing} & = c \mathbf {I}_{0} = \begin{bmatrix} 0 &0 & 0 \\ 0 & c & 0 \\ 0 & 0 & c \end{bmatrix}. \end{aligned}$$

(B.25)

Equation (B.24) shows that, in the rotating frame, there is a skew-symmetric contribution of the bearing viscous damping to the stiffness matrix.