Abstract
This paper deals with the dynamics of jointed flexible structures in multibody simulations. Joints are areas where the surfaces of substructures come into contact, for example, screwed or bolted joints. Depending on the spatial distribution of the joint, the overall dynamic behavior can be influenced significantly. Therefore, it is essential to consider the nonlinear contact and friction phenomena over the entire joint. In multibody dynamics, flexible bodies are often treated by the use of reduction methods, such as component mode synthesis (CMS). For jointed flexible structures, it is important to accurately compute the local deformations inside the joint in order to get a realistic representation of the nonlinear contact and friction forces. CMS alone is not suitable for the capture of these local nonlinearities and therefore is extended in this paper with problem-oriented trial vectors. The computation of these trial vectors is based on trial vector derivatives of the CMS reduction base. This paper describes the application of this extended reduction method to general multibody systems, under consideration of the contact and friction forces in the vector of generalized forces and the Jacobian. To ensure accuracy and numerical efficiency, different contact and friction models are investigated and evaluated. The complete strategy is applied to a multibody system containing a multilayered flexible structure. The numerical results confirm that the method leads to accurate results with low computational effort.
Similar content being viewed by others
1 Introduction
Complex mechanical structures commonly consist of different substructures connected by joints. In this article, the term “joint” is used for the region where two substructures interact with each other. Inside the joint area, nonlinear contact and friction forces occur, which can strongly influence the overall dynamic behavior of such structures. This is especially true for structures that include joints with a large spacial distribution. In this work, only joints where the relative displacement of the two involved surfaces with respect to each other remains small are of interest. Such joints, for example, bolted joints, spot welded seams, and joints, are of technical relevance.
In engineering practice, structures that include nonlinear contact and friction forces are commonly analyzed with the direct finite element method (FEM). If the jointed structure needs to be considered in a multibody simulation where it can be connected to other rigid or flexible bodies and undergo a large rigid body motion, then a different strategy must be applied. Linear flexible bodies are often considered using component mode synthesis (CMS) [1–5] in combination with the floating frame of reference formulation (FFRF) [6, 7] in the multibody simulation (MBS). For local nonlinearities, like in jointed structures, the trial vectors provided by CMS are not suitable to capture small local deformations and, consequently, the local contact pressure inside the joints. Therefore, in [8] a problem-oriented extension of the common reduction base is presented using special joint trial vectors (JTVs) that are based on trial vector derivatives (TVDs). These JTVs add local flexibility to the joint area to ensure an accurate computation of the gapping or penetrating areas inside the joint. TVDs have already been used in [9–12] to extend the common reduction base in order to capture nonlinear effects. In [12] TVDs are also used in the context of MBS for an efficient reduction of structures showing geometric nonlinearities.
In addition to the JTVs, the contact and friction models are also of high importance for the efficient consideration of structures with lap joints in the MBS. In order to produce realistic results within acceptable computational time, the models must combine the properties of accuracy and numerical efficiency. Systematic research on jointed structures has been carried out by Gaul and his associates [13–15]. Their contributions are based on an experiment with an isolated generic joint, which has been systematically investigated. The tangential stiffness and damping properties of the joint were studied with respect to normal pressure, excitation frequency, and excitation amplitude. Based on the experimental results, proper mathematical models were deduced from literature and applied to certain problems. The conclusions drawn from these investigations are summarized in the review paper [16]. It was revealed that a Coulomb-type friction model is able to describe the main characteristics of a lap joint with dry friction. This observation has been shared by other authors as well, and examples of variations of the Coulomb fiction models (e.g., Iwan model) are given [17, 18]. In [18] a jointed beam is compared to a monolithic structure with the same geometric dimensions, and the results underline the importance of the proper consideration of joints in dynamic simulations. For the local energy dissipation, the local contact pressure is of significant importance. Consequently, a varying normal pressure distribution throughout the joint due to varying deformations must be regarded for accurate dynamics [19].
The required flexibility inside the joint area of the reduced structure is achieved by extending the reduction base with special JTVs. Furthermore, an investigation into contact and friction models with a focus on numerical efficiency is performed to ensure a low overall computational time.
After a general problem description and introduction in Sect. 1, the paper continues in Sect. 2 with a short review of the properties of dry friction joints. Out of this review, the physical requirements on the friction model are defined. In Sect. 3 the theory of JTVs in the context of multibody simulation and the FFRF will be given. Section 4 discusses how nonlinear contact and friction forces inside a joint are considered in the vector of generalized forces together with their contribution to the Jacobian. Following that, a comparison of different contact models (Sect. 5.1) and friction models (Sect. 5.2) in terms of numerical efficiency and accuracy is given. Nonpenalty methods, for example, the Lagrange method or the augmented Lagrange method [20] are not included in this investigation. This section ends with a numerical investigation of the friction models on a simple multimass oscillator. A numerical example of a multibody system (car pendulum model with multilayer sheet metal structure) is presented in Sect. 6, where the suggested JTVs and contact models are investigated in more detail. Finally, a discussion and some conclusions are given in Sect. 7 and Sect. 8.
2 Brief review of lap joints with dry friction
A detailed investigation of dry friction inside joints has been performed by Gaul and his associates [13–15]. These latter contributions are based on an interesting experiment, in which a generic joint was isolated and systematically investigated. The tangential stiffness and damping properties of the joint were studied with respect to normal pressure, excitation frequency, and amplitude. The literature points out that the fundamental characteristics of experimental results can be analytically or numerically reproduced when the friction model of an arbitrary point inside the joint can capture three different states, namely:
-
Gaping: The involved surfaces are not in contact at the considered point. Consequently, there is no friction stress.
-
Sticking: The involved surfaces at the considered point are in contact, and the local friction stress is lower than a certain sticking stress limit. The sticking stress limit typically depends on the contact pressure and a friction coefficient. During sticking, no energy is dissipated, and the relative displacement of the two surfaces is zero or elastic (reversible).
-
Slipping: The involved surfaces at the considered point are in contact, and the local friction stress is higher than the sticking stress limit. Slipping leads to energy dissipation because the relative displacement of the involved surfaces is irreversible. The frequency dependency of the energy dissipation is very small and can be neglected. Note that also in the case of local sliding, the small displacement assumption still holds due to the construction of the joint.
Furthermore, the cited literature mentions that the described behavior can be captured with a three-parameter Coulomb-type friction model, as shown in Fig. 1, where \(\tau_{F}\) denotes the friction stress, \(s\) is the relative tangential displacement, \((c_{1}+c_{2})\) is the slope of the stick motion, \(c_{2}\) is the slope of slip motion, and \(R_{G}\) is the sticking stress limit. For the investigated metallic joints, the stick motion slope \(( c_{1} + c _{2} ) \) and the slip motion slope \(c_{2}\) are nonzero.
The mathematical formulation of this model [14, 15] can be given as
where \(\tau_{F,1}\), \(\tau_{F,2}\) denote the friction stresses according to the springs, \(s_{G}\) is the displacement at the switching point between sticking and slipping, and \(\operatorname{sgn} \left( \right) \) is the signum function. In [15], it is mentioned that the common approach \(R_{G}= \mu p_{N}\), where \(\mu \) is the friction coefficient and \(p_{N}\) is the contact pressure, is valid for the friction model defined by Eq. (1). Furthermore, the friction coefficient \(\mu \) has been computed based on the measured data. This reveals that the computed values are similar to those known from the literature. Furthermore, it has been confirmed by experiments that \(\mu \) does not depend on contact pressure.
The resulting frictional characteristic of a distributed joint and its effect on the entire structure is given as the sum of all gapping, sticking, and slipping areas inside the joint. Consequently, the local description of Eq. (1) has to be applied to the relevant degrees of freedom (DOFs) over the entire joint in case of a discrete approach like the FEM. Considering the entire joint, three different states can occur:
-
The sticking condition is satisfied at each location throughout the joint.
-
The joint is partially slipping and sticking. In the literature, this state often constitutes microslip.
-
There is no sticking subarea, and the entire joint is slipping. This state is commonly referred to macroslip. Note that in such a case, the former restriction of small relative displacement of the joint surfaces with respect to each other no longer holds. For many types of joints, the appearance of macroslip indicates joint failure. Therefore, the macroslip state lies outside the scope of this paper.
3 Joint trial vectors based on trial vector derivatives
The computation of contact and friction forces is based on the deformation of the joint area. Classical trial vectors for model reduction, for example, CMS, do not describe the deformation inside the joint accurately enough. In this section a problem-oriented extension of classical reduction bases with the purpose of getting sufficient accuracy in the joint deformation is discussed. Based on an accurate deformation of the joint, the contact and friction forces can be precisely computed.
Such an extension was introduced by Witteveen and the author [8] for the FEM and is based on the computation of TVDs. This approach is extended to the MBS in this and the following sections.
For FE-modeled jointed flexible structures, the equation of motion can be written in the form
if a penalty formulation of the contact and friction phenomenon [20, 21] is used. In this equation, the \(( n_{\mathrm{FE}} \times 1 ) \) vector \(\mathbf{x}\) denotes the nodal DOFs, \(\mathbf{M}\) and \(\mathbf{K}\) denote the structures \(( n_{\mathrm{FE}} \times n _{\mathrm{FE}} ) \) mass matrix and stiffness matrix, respectively. The external forces are collected in the \(( n_{\mathrm{FE}} \times 1 ) \) vector \(\mathbf{f}_{(t)}\), and the nonlinear contact and friction forces are combined in the \(( n_{\mathrm{FE}} \times 1 ) \) vector \(\mathbf{f} _{(\mathbf{x})}^{\,\mathrm{NL}}\). One possible strategy to reduce the number of DOFs in Eq. (2) for dynamic simulations is model order reduction via projection. Therefore, \(r\) time-invariant \(( n_{\mathrm{FE}} \times 1 ) \) trial vectors \(\boldsymbol{\varphi }_{i}\), together with the time-varying scaling factors \(q_{f,i}\), are used to approximate the displacements
The \(r\) trial vectors are collected in the \(( n_{\mathrm{FE}} \times r ) \) matrix \(\boldsymbol{\Phi }\), and the scaling factors in the \(( r \times 1 ) \) vector \(\mathbf{q}_{f}\). In the context of multibody simulation, the scaling factors are also called flexible coordinates. In order to get a reduced equation of motion, Eq. (3) is inserted into Eq. (2) and premultiplied with \(\boldsymbol{\Phi }^{ \mathsf{T}}\). This leads to
with the \(( r \times r ) \) reduced mass matrix and stiffness matrix \(\widetilde{\mathbf{M}} = \boldsymbol{\Phi }^{\mathsf{T}} \mathbf{M} \boldsymbol{\Phi }\), \(\widetilde{\mathbf{K}} = \boldsymbol{\Phi }^{\mathsf{T}} \mathbf{K} \boldsymbol{\Phi }\).
For linear flexible structures, CMS has become an established reduction method (see [1–5]). In this case, the reduction base \(\boldsymbol{\Phi }\) is a combination of \(v\) vibration mode shapes \(\boldsymbol{\Phi }_{\mathrm{V}}\) (also called normal modes (NMs)) and \(s\) trial vectors, which are basically deformation shapes due to static loads \(\boldsymbol{\Phi }_{ \mathrm{S}}\),
Both types of trial vectors are functions of the mass and stiffness matrix of the structure. In the nonlinear case, the stiffness matrix becomes state dependent. Consequently, a certain trial vector should be state dependent as well. Due to model order reduction (Eq. (3)), this state dependency leads to a dependency on the trial vector weighting factors. This dependency can be expressed by a Taylor series expansion as
The principal idea of JTVs is to use the first order TVDs \(\frac{\partial \boldsymbol{\varphi}_{i}}{\partial q_{f,j}}\) to approximate the change of a certain trial vector due to the deformation state. A general derivation for TVDs can be found in [9–11]. In [8] also a practical computation algorithm for contact problems is given.
For both types of trial vectors, vibration mode shapes and static deformation mode shapes, the first-order TVDs can be computed along
as long as inertia-related terms are neglected.
Using the first-order TVDs to approximate the state dependency provides far too high a number \((2 ( v+s ) ^{2}) \) of potential new trial vectors for an efficient model order reduction. Furthermore, investigations showed that TVDs contain redundant information. Therefore, a weighted proper orthogonal decomposition (POD) [22, 23] is used in [8] to determine the important directions of the space spanned by all TVDs. The thereby computed trial vectors are finally used for the extension of the reduction base
with the \(( n_{\mathrm{FE}} \times t ) \) matrix \(\boldsymbol{\Phi }_{ \mathrm{T}}\) containing the \(t\) chosen JTVs based on TVDs. The number of additionally used JTVs depends on the actual problem. In [8] a possible estimator for this number is given, and also the advantages of JTVs based on TVDs compared to other “joint modes” like the one suggested in [24] are discussed in detail.
The practical computation of the \(( n_{\mathrm{FE}} \times 1 ) \) additional JTVs \(\boldsymbol{\varphi}_{\mathrm{T},i}\) is done by solving the eigenvalue problem
with the \(( n_{\mathrm{FE}} \times 2 ( v+s ) ^{2} ) \) matrix \(\boldsymbol{\Phi }_{\mathrm{TVD}}\) containing all TVDs. To use the reduction base defined in Eq. (8) in the MBS, it must be ensured that the trail vectors do not contain any rigid body content. Therefore, most commonly mode shape orthogonalization [25] is used. Thereby an additional generalized eigenvalue problem using the reduced mass and stiffness matrix
is solved to obtain a new set of trial vectors
The \(( n_{\mathrm{FE}} \times r ) \) matrix \(\boldsymbol{\Phi }_{\mathrm{free}}\) contains the so-called free–free modes, and the \(( r \times r ) \) matrix \(\mathbf{Y}\) contains the \(r\) eigenvectors computed from Eq. (10). By rejecting the columns of \(\boldsymbol{\Phi } _{\mathrm{free}}\), which correspond to zero eigenvalues, the rigid body content is removed.
A different strategy, which also leads to a set of new trial vectors that do not contain rigid body content, is proposed in [26]. This strategy separates a set of arbitrary trial vectors into pseudo-free-surface modes and rigid body modes.
It should be mentioned that the computation of TVDs and JTVs is not restricted to fixed interface trial vectors. In [8] a remark on the computation of TVDs for free interface methods (e.g., the Rubin method [2, 27]) can be found.
4 Contact and friction forces in the framework of MBS
Considering an FFRF for jointed flexible structure, the equations of motion for a multibody system in combination with the constraint equations can be written as
where \(\mathbf{q}\) denotes the \(( n \times 1 ) \) vector of generalized coordinates, and the \(( n \times n ) \) matrix \(\hat{\mathbf{M}}(\mathbf{q})\) represents the mass matrix of the system. The \(( n \times 1 ) \) vector \(\mathbf{Q}(\dot{\mathbf{q}},\mathbf{q},\mathbf{t})\) includes the generalized forces, \(\mathbf{C}(\mathbf{q})\) and \(\mathbf{C}_{\mathbf{q}}\) denote the \(( m \times 1 ) \) constraint equations and the \(( m \times n ) \) constraint Jacobian, and \(\boldsymbol{\lambda }\) is the \(( m \times 1 ) \) vector of Lagrange multipliers. For more details, the interested reader is referred to [6, 28].
The vector of generalized forces can be partitioned in
with \(\mathbf{Q}_{v}\) being the quadratic velocity vector, also known as the velocity inertia vector [29], \(\mathbf{Q}_{e}\) including the generalized external forces, and \(\mathbf{Q}_{\mathrm{nl},f}\) containing the generalized contact and friction forces and the generalized flexible forces.
For body \(i\) in the multibody system, the equation of motion can be written in a partitioned matrix form as
where the vector of generalized coordinates is partitioned into the translational DOFs \(\mathbf{R}\), the rotational DOFs \(\mathbf{\theta }\), and the flexible coordinates \(\mathbf{q}_{f}\). A detailed insight into the separate submatrices of \(\mathbf{M}^{i}\) can be found in [6, 26, 28]. In Eq. (15), \(\mathbf{f}_{\mathrm{nl}}^{i}\) denotes the \(( n_{\mathrm{FE}} \times 1 ) \) vector of nonlinear forces of the flexible structure. Note that \(\mathbf{f}_{\mathrm{nl}}^{i} \) is a self-equilibrated force, which has no contribution to the rigid body motion. The vector \(\mathbf{f}_{\mathrm{nl}}^{i}\) can be partitioned into the \(( n_{\mathrm{FE}} \times 1 ) \) vectors of contact \(\mathbf{f}_{N}^{i}\) and friction forces \(\mathbf{f}_{F}^{i} \):
The system of second-order differential equations defined in Eq. (15) still has to satisfy the constraint equations \(\mathbf{C(q)} = \mathbf{0}\). One possibility for the numerical implementation is to apply a time integration algorithm to the full system of differential algebraic equations. An example for such a time integration algorithm is the HHT integrator as presented in [30, 31]. Therefore, the system’s Jacobian must be computed, and the following system of equations must be solved:
where \(h\) denotes the time step size, and \(\alpha \), \(\beta \), \(\gamma \) are parameters of the time integration algorithm. In Eq. (17) the subscripts \(( \; ) _{\mathbf{q}}\) and \(( \; ) _{ \dot{\mathbf{q}}}\) denote the derivatives with respect to the vector of generalized coordinates and the vector of generalized velocities. The vectors \(\mathbf{e}_{1}\), \(\mathbf{e}_{1}\) are the residual vectors for the equation of motion and the constraint equations.
Because the vector of nonlinear forces contributes to the vector of generalized forces \(\mathbf{Q} \), the derivatives \(( \boldsymbol{\Phi } ^{i\,\mathsf{T}} \mathbf{f}_{\mathrm{nl}}^{i} ) _{\mathbf{q}}\), \(( \boldsymbol{\Phi } ^{i\,\mathsf{T}} \mathbf{f}_{\mathrm{nl}}^{i} ) _{\dot{\mathbf{q}}}\) need to be computed for the Jacobian. Note that the superscript \(i \) marking the body index in the MBS is omitted from now on. As a consequence of the penalty formulation for contact forces and the claimed velocity independence of the friction model, the derivation with respect to the generalized velocities, \(( \boldsymbol{\Phi }^{\mathsf{T}} \mathbf{f}_{\mathrm{nl}} ) _{\dot{\mathbf{q}}} \) can be set to zero.
The nonlinear forces are only functions of the flexible coordinates \(\mathbf{q}_{f} \) and not of the other components of the generalized coordinates. Therefore, only the derivation \(( \boldsymbol{\Phi }^{ \mathsf{T}} \mathbf{f}_{\mathrm{nl}} ) _{\mathbf{q}_{f}} \) must be computed. By introducing the \(( r \times 1 ) \) vector of modal nonlinear forces \(\mathbf{f}_{\mathrm{nl}}^{m} = \boldsymbol{\Phi }^{\mathsf{T}} \mathbf{f}_{\mathrm{nl}} \) and the vectors of modal contact and friction forces \(\mathbf{f}_{N}^{m} = \boldsymbol{\Phi }^{\mathsf{T}} \mathbf{f}_{N}, \mathbf{f}_{F}^{m} = \boldsymbol{\Phi } ^{\mathsf{T}} \mathbf{f}_{F} \) the required derivative can be written as
The contact and friction force vectors \(\mathbf{f}_{N}\), \(\mathbf{f}_{F}\) can be directly calculated from the contact pressure vector \(\mathbf{p}_{N} \) and the friction stress vector \(\boldsymbol{\tau }_{F} \):
where \(\mathbf{P} \) denotes a time- and state-independent mapping matrix defined by the FE shape functions.
Because of the time-invariant matrices \(\boldsymbol{\Phi }\) and \(\mathbf{P}\), the derivatives \(\frac{\partial \mathbf{p}_{N}}{\partial \mathbf{q}_{f}}\), \(\frac{ \partial \boldsymbol{\tau }_{F}}{\partial \mathbf{q}_{f}}\) can be computed for the derivatives needed in Eq. (18). The computation of these derivatives will be further discussed in the following subsections.
For simpler reading, only a node-to-node contact is considered, and the derivatives are only computed for a single contact pair. A general extension to the vector containing all contact pairs is quite straightforward.
4.1 Computation of the contact pressure
In the penalty formulation, the \(( 3 \times 1 ) \) contact pressure vector \(\mathbf{p}_{N,i}\) for the \(i\)th contact pair is given by
with the \(( 3 \times 1 ) \) normal vector \(\mathbf{n}_{i}\) of the contact pair. For all penalty formulations, the contact pressure \({p}_{N,i}\) is a function of the normal gap \(g_{N,i} \) defined as
with \(\mathbf{x}_{i}^{2}\), \(\mathbf{x}_{i}^{1}\) representing \(( 3 \times 1 ) \) vectors containing the translational DOFs of the corresponding FE nodes of the master and slave surfaces.
In general, the normal vector is a function of the deformation state and consequently a function of the flexible coordinates \(( \mathbf{n} _{i} = {\mathbf{n}_{i}}(\mathbf{q}_{f}) ) \). For the derivation of Eq. (20) with respect to the flexible coordinates, this dependency leads to the \(( 3 \times r ) \) matrix
In terms of trial-vector-based model order reduction, Eq. (21) becomes a function of the flexible coordinates leading to
With \(\boldsymbol{\Phi }_{i}^{2}\), \(\boldsymbol{\Phi }_{i}^{1}\) being \(( 3 \times r ) \) matrices containing the translational DOFs for the \(i\)th master–slave contact pair of all trial vectors. Performing a derivation of Eq. (23) with respect to the flexible coordinates leads to the \(( 1 \times r ) \) row vector
For the application of jointed structures with small sliding and the use of an FFRF, it can be assumed that the normal vector does not change significantly with respect to the reference configuration. Therefore, the term \(\frac{\partial \mathbf{n}_{i}}{\partial \mathbf{q}_{f}} \) vanishes, and Eq. (24) simplifies to
and accordingly Eq. (22) can be written as
In Sect. 5 the derivative \(\frac{\partial p _{N,i}}{\partial g_{N,i}}\) for some selected penalty models is computed.
4.2 Computation of the friction stress
Depending on the friction model used, the relative tangential displacement \(s_{i} \) and the sticking stress limit \(R_{G,i} \) of the contact pair are used to describe the magnitude of the friction stress \(\tau_{F,i} \). With the \(( 3 \times 1 ) \) tangential vector \(\mathbf{t}_{i} \), the \(( 3 \times 1 ) \) friction stress vector \(\boldsymbol{\tau }_{F,i} \) can be written as
with the quantities \(\mathbf{t}_{i} = \mathbf{t}_{i} ( \mathbf{q}_{f} ) \), \(s_{i} = s_{i} ( \mathbf{q}_{f} ) \), \(R_{G,i} = R_{G,i} ( \mathbf{q}_{f} ) \) depending on the flexible coordinates. Therefore, the required derivative \(\frac{\partial \boldsymbol{\tau }_{F,i}}{\partial \mathbf{q}_{f}} \) can be computed along
Similarly to the normal gap \(g_{N,i} \) (Eq. (23)), the tangential displacement can be computed with
in the case of trial-vector-based model order reduction. For each contact pair, there exist two constant \(( 3 \times 1 ) \) tangential vectors \(\mathbf{t}_{1,i}\), \(\mathbf{t}_{2,i}\). With the tangential displacements in these principal directions
the total tangential displacement can also be computed along
and the tangential vector with
The derivatives \(\frac{\partial \tau_{F,i}}{\partial s_{i}}\), \(\frac{ \partial \tau_{F,i}}{\partial R_{G,i}}\) in Eq. (28) depend on the friction model, whereas the other terms can be evaluated in general along
with
5 Selection of contact and friction models based on efficiency criteria
The reduction base presented in Sect. 3 shows an efficient way of getting an accurate representation of the deformation inside a joint during dynamic simulations. To ensure low computational effort for the entire computation process, it is also important that the contact and friction models are numerically efficient. In addition to the numerical efficiency, it is also important that the models capture the physical characteristics of the joint. Based on these requirements, in the following sections, different contact and friction models are evaluated, and a recommendation is given.
5.1 Investigation of contact models
Contact models have to ensure that the contacting surfaces do not penetrate (or at least not perceptibly). Furthermore, the model should give a realistic representation of the contact mechanics and the contact pressure with (few) physically meaningful parameters. In [32] a review and comparison of different contact force models for contact and impact in multibody dynamics can be found, but these do not consider lap joints inside flexible structures or numerical efficiency. In the following subsections, different penalty contact models are investigated. For readability reasons, the derivative \(\frac{\partial p_{N,i}}{\partial g_{N,i}}\) for different models is given in Appendix A.
5.1.1 Linear penalty model
The linear penalty model [20, 21] is a very widely used approach for the computation of contact problems. For this model, the pressure-gap relationship is given by
where \(\varepsilon_{N} > 0\) is the penalty parameter. The linear penalty model needs only one parameter \(\varepsilon_{N}\), which can be physically interpreted as a linear spring stiffness. The pressure-gap relationship for this model is plotted in Fig. 2.
5.1.2 Multistage linear penalty model
The multistage linear penalty model is a simple extension of the classic linear penalty model. The idea is that the pressure-gap relationship is divided into \(k\) sections with different penalty parameters \(\varepsilon_{N,k}\). Therefore, this model requires \(2 k\) parameters. The model is often used by Gaul and his associates [33–36]. In [33, 35] a two-stage version of this model is used, and the contact parameters for a best match between simulation and experiment are given. For the two-stage linear penalty model, the pressure-gap relationship is plotted in Fig. 3. Mathematically, this relationship can be written for \(g_{0}>g_{1}\) and \(\varepsilon_{N,1} > \varepsilon_{N,0} > 0\) as
For the two-stage linear penalty model, the parameters \(( \varepsilon_{N,0}, \varepsilon_{N,1}, g_{0}, g_{1} ) \) are required. A physical interpretation of the parameters similar to the linear penalty model is easily possible.
5.1.3 Power-function-based nonlinear penalty model
This version of a pressure gap relationship can be found in [37, 38] and uses the power function. The pressure-gap relationship is plotted in Fig. 4 and mathematically described by
The relationship was developed based on statistical models. For most metallic materials, the parameter \(\varepsilon_{N}\) is proportional to the modulus of elasticity, and the parameter \(m \approx 2\) [37].
5.1.4 Combined quadratic-linear penalty model
This model has been used in [39, 40] and combines quadratic and linear penalty models in order to get a smoother transition between gapping and penetration. The pressure-gap relationship plotted in Fig. 5 is mathematically formulated as
This model has a continuous slope of the pressure-gap relationship at the points \(g_{0}\), \(g_{1}\) and requires three parameters \(( \varepsilon_{N}, g_{0}, g_{1})\).
5.1.5 Exponential penalty model
An exponential penalty model can be found in [41] and is implemented in the commercially available FEM software Abaqus. For this model, the pressure-gap relationship is plotted in Fig. 6 and mathematically defined as
where \(p_{0}\) is the contact pressure at \(g_{N,i}=0\), and \(g_{0}>0\) is the gap at which \(p_{N,i} = 0\). For this penalty model, only two parameters \(p_{0}\), \(g_{0}\) are needed. One disadvantage of this exponential model is that a lot of floating point operations are required.
5.1.6 Joint-adapted exponential penalty model
This section describes a joint-adapted exponential penalty model, which is based on statistical approaches for describing the height distribution of the asperity summits, as in [42, 43]. Due to the roughness of metallic surfaces, contact only takes place on the summits of the asperities of the surface. The Hertzian normal contact of two elastic spheres is applied to model the contact of one single asperity of the surfaces. Furthermore, it is assumed that the height distribution of the asperity summits can be described by an exponential distribution [42, 43]. The statistical approach leads to a penalty model with physically meaningful contact parameters [38]. The mathematical formulation of the pressure-gap relationship is given by
where \(\lambda_{N}\) is a statistical parameter, \(g_{0}>0\) is the initial distance between the highest peak of the rough surface and the reference plane, and \(p_{0}>0\) is the pressure at \(g_{N,i} = g_{N,0}\). The parameter \(\lambda_{N}\) is defined as \(\lambda_{N} = \frac{1}{\sigma } > 0\), where \(\sigma \) is the standard deviation of the height profile of the rough surface. Therefore, a relationship between the profile roughness parameters \(R_{a}\), \(R_{z}\) and the parameter \(\lambda_{N}\) can be derived.
The main disadvantage of the numerical computation of Eq. (40) is that the contact pressure is never exactly zero and needs to be evaluated for all values of \(g_{N,i}\). Therefore, a modified exponential pressure-gap relationship is defined by
and plotted in Fig. 7. For this joint-adapted exponential penalty model, three parameters \(g_{0}\), \(\lambda_{N}\), \(\varepsilon_{N}\) are needed. The parameter \(g_{0}\) can in most cases be set to zero. For some investigations, it may be a numerical advantage to have a small negative value for \(g_{0}\).
5.1.7 Comparison of contact models
In Fig. 8 the pressure-gap relationship for all discussed contact models is plotted. The parameters for the different models have been chosen in a way that they lead to the same contact pressure for a defined penetration (\(g = -2.5~\upmu\mbox{m} \)). It can be seen that for the linear and multistage linear models, a step in the slope of the pressure-gap relationship at \(g = 0 \) occurs. Besides these two models, all other penalty models show a continuous transition in the pressure-gap relationship between gaping and penetration.
In Table 1 the properties of all discussed contact models are summarized and rated. The linear penalty model is clearly the simplest. The multistage penalty model is also rather simple but requires additional distinction in the pressure-gap relationship. This additional distinction is also needed for the quadratic-linear model. The power-function-based and exponential models do not include additional case distinction but have a more complicated (time consuming) mathematical description with a higher number of floating point operations.
The exponential and the power function based pressure-gap relationship can be associated with the Hertzian contact theory by using statistical models for the roughness of the surfaces. For all other models, such a contact mechanical interpretation is not possible.
A study investigating the numerical efficiency of the different models follows in Sect. 6.2.
5.2 Investigation of friction models
In the sections that follow, different models for calculating the magnitude of the friction stress \(\tau_{F,i}\) found in the literature are reviewed and compared to the characteristics of dry fiction mentioned in Sect. 2. A good starting point for a literature review on friction models is given by [16, 44, 45]. An investigation of alternatives to the Coulomb friction model can also be found in [46], where especially the continuity of the models is investigated. The focus in this paper is on friction models for dry friction inside joints that can capture the microslip range mentioned in Sect. 2. Therefore, friction models describing sliding friction (LuGre friction model [47], signum-friction models, Karnopp model, etc.) are not further discussed here. The interested reader is referred to [44, 45, 48, 49].
Based on the insights in Sect. 2, the requirements for a friction model characterizing dry fiction are:
-
Two different nonzero slopes for the stick and slip regime.
-
No energy dissipation in case of sticking.
-
Frequency-independent energy dissipation.
-
Physically reasonable parameters (as few as possible).
In the following sections different friction models are briefly reviewed, whereby the mathematical descriptions are given in Appendix B. The friction models are investigated on a multimass oscillator and rated based on the defined criteria together with a special focus on numerical efficiency. Finally, a decision matrix with a comprehensive evaluation of the investigated friction models is presented.
5.2.1 Three-parameter Coulomb-type friction model
The three-parameter Coulomb-type friction model mentioned in Sect. 2 is used as a reference model for the computation of dry friction inside joints. The parameters of this model are the sticking stress limit \(R_{G} \) and two stiffness parameters \(c_{1}\), \(c_{2}\) for the slope of the sticking and slipping motion.
The reference model is implemented using a trial frictional stress \(\tau_{F}^{\mathrm{tr}} \) and decomposing the tangential displacement into elastic (reversible) and plastic (irreversible) components \(s = s ^{e} + s^{p} \) as discussed in [50].
5.2.2 Adapted Dahl friction model
The Dahl friction model [51] is a simple friction model, which was developed in 1968. This model implies that the friction stress is only a function of the tangential displacement. The displacement dependency of the friction stress \(\frac{d \tau_{D}}{d s}\) was described in further studies [52] by Eq. (B.1), where \(\sigma_{0}\) is a stiffness parameter, and \(\alpha \) is a model parameter.
In this form the Dahl friction model is well documented, for example, in [44, 45]. In order to get the two required stiffness regimes for sticking and slipping, it is necessary to extend the Dahl friction model by a parallel linear spring in the form of Eq. (B.3).
The Dahl friction model has three parameters \(\left( \sigma_{0}, c _{2},\alpha \right) \) in the discussed form. The two stiffness parameters can be easily related to the reference model as \(\sigma_{0} = c_{1}; c_{2} = c_{2}\). It must be mentioned that, for \(R_{G} \rightarrow 0\), numerical problems and a division by zero can occur. Therefore, precautions must be applied to capture this case.
5.2.3 Valanis friction model
The Valanis model, originally known from plasticity theory, is used as a friction model in [13, 15, 16]. In [15] a detailed derivation of the original plasticity model to the Valanis friction model can be found. The final equation for the friction stress is given by the differential equation (B.4) with four model parameters \(E_{0}\), \(E_{t}\), \(\kappa \), \(\lambda \).
A physical interpretation of the parameters for joints is possible. A detailed investigation of the parameters in [15] results in the conclusion that \(E_{0} = c_{1} + c_{2}\) represents the sticking stiffness and \(E_{t} = c_{2}\) the sliding stiffness analogous with the reference model. The parameter \(\kappa \) influences the transition between sticking and sliding and therefore the shape of the hysteresis curve. For a physical meaningful hysteresis \(( E_{0}>E_{t} ) \), the parameter has to be chosen between \(0<\kappa <1\). The best fit of the hysteresis curve compared to the reference model can be achieved with high values of \(\kappa \). The parameter \(\lambda \) can be set into context to the other parameters by Eq. (B.6).
5.2.4 Bouc–Wen friction model
A further possibility for describing the hysteresis curve is the Bouc–Wen friction model [15]. The Bouc–Wen friction model is mathematically given by the differential equation (B.7). Applying an implicit Euler scheme to discretize Eq. (B.7) leads to an equation that cannot be solved explicitly. Similarly to the Dahl friction model, it is necessary to extend the Bouc–Wen friction model with a parallel linear spring, and the final friction stress is given by Eq. (B.8). In [15] a detailed investigation of the Bouc–Wen model can be found, and the model parameters \(A\), \(B\), \(\gamma \), \(n\) are identified with respect to the reference model as
where \(n\) is a model parameter that determines the shape of the hysteresis.
5.2.5 Viscous damping models
A widely used method for the introduction of local joint damping in a jointed system is the application of viscous dampers inside a joint; see [53]. Figure 9 contains three common spring damper elements. Note that there exist different models with a different number of serial and/or parallel springs and/or dampers. The advantage of this modeling approach is its simplicity and the fact that the final system remains linear.
5.2.6 Comparison of the friction models
In this section the hysteresis curves of the afore-mentioned friction models are compared. For these curves, the different friction models are excited with a prescribed relative tangential displacement \(s \) and tangential slip velocity \(\dot{s} \). Figure 10(a) shows that the reference model, the Valanis model, and the Bouc–Wen model are able to give a good representation of two different slopes for sticking and sliding. For the Dahl friction model with \(\alpha =1 \), the two slopes are not clearly separated, and for viscous damping, the sticking and slipping slopes cannot be seen at all. In Fig. 10(b) the curves for pure sticking are plotted. Only the reference model shows real zero energy dissipation during sticking. For the Valanis model and the Bouc–Wen model, the hysteresis for this case is very small and seems to give a good representation of the real physical behavior. The Dahl friction model and the viscous damping clearly show a hysteresis and therefore energy dissipation during sticking. Comparing the parameters of the friction models in Table 2 shows that for all parameters of the reference model, a physical interpretation can be found. All other models have at least one parameter that has no clear physical meaning but is necessary for the mathematical description.
In Table 3 the characteristics of the investigated friction models with respect to the defined criteria are summarized. Drawing a conclusion from Table 3, it can be stated that viscous damping is not able to fulfill any of the criteria to model dry friction inside joints. Therefore, viscous damping is not included in the numerical study in Sect. 5.2.7.
5.2.7 Evaluation of friction models on a multimass oscillator
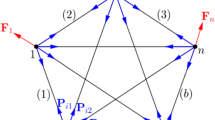
The four friction models (three-parameter Coulomb type model (reference model), Dahl, Valanis, Bouc–Wen), which fulfill (most of) the defined criteria, are investigated in terms of numerical efficiency in this section. Therefore, a multimass oscillator, as shown in Fig. 11, is used, where each mass is connected to the ground with a friction element. For the investigations, the multimass oscillator was simulated with \(n=100 \) masses, and the parameters were set to \(k=100~\mbox{N}/\mbox{m}, m =0.1~\mbox{kg}, f _{\mathrm{ext}}(t) = 0.2 \sin ( 2 \pi t )~\mbox{N}\). The friction parameters for different friction models are represented by the vector \(\mathbf{c} \), and the particular parameters are defined in Table 2. In order to achieve approximately the same behavior as in a real joint, different cases are simulated. As one major influencing factor in all friction models, the sticking limit \(R_{G} \) is varied as shown in Table 4. For the case where gaping is simulated, a negative value \(R_{G}\) is interpreted as gaping. Besides the variation of \(R_{G}\), also the number of excited masses and the sticking stiffness (\(c_{1}+c_{2} \)) in the friction models is varied. The system was simulated with all masses or only ten masses (\(m_{i}\), \(i=1, 10, 15, 25, 50, 65, 80, 85, 90, 99\)) being excited. This leads to the behavior of some masses changing between sticking and slipping, whereas other masses show pure sticking.
Exemplary for the different variations in the model parameters, the displacement curve of mass \(m_{25} \) for varying \(R_{G}\) and ten masses excited is plotted in Fig. 12. It can be seen that the reference model, the Valanis model, and the Bouc–Wen model produce nearly the same displacement curve. The Dahl friction model matches the curves quite well in the time periods of sliding, whereas in the periods of sticking, a deviation from the other friction models can be seen.
In order to evaluate the numerical efficiency of the four friction models, the computational time, the number of time steps, and the number of Jacobian updates during the time integration are used as criteria. Averaged over all parameter variations, the results are shown in Fig. 13. The results show that the reference model and the Dahl friction model share the same computational time, whereas the computational time for the Valanis and Bouc–Wen models is much higher. The reason for this is probably the higher number of floating point operations for the computation of the friction force and the Jacobian. The required time steps for all models are a little lower than for the reference model, whereas the number of the Jacobian updates is higher.
None of the investigated cases shows a qualitatively different result in terms of numerical efficiency than the averaged results shown in Fig. 13. As a result of the findings summarized in Table 3 and the numerical investigations on the multimass oscillator, the three-parameter Coloumb-type friction model (reference model) seems to be the best choice for the modeling of dry friction inside jointed structures although it is not continuous.
6 Numerical example—putting it all together
A 2D car pendulum model including an additional point mass at one end of the pendulum as shown in Fig. 14 is used to demonstrate the method described in Sect. 3 and Sect. 4. The pendulum is designed as a flexible multilayer sheet structure with three metal sheets rotationally fixed to the car. The two outer metal sheets (\(300~\mbox{mm} \times 20~\mbox{mm} \times 1~\mbox{mm}\)) are connected via beams at two locations. The central metal sheet (\(400~\mbox{mm} \times 20~\mbox{mm} \times 1~\mbox{mm}\)) is not directly connected to the outer sheets but connected through contact and friction forces. The flexible structure has been modeled out of steel in the FE software Abaqus [41], and the resulting mass and stiffness matrices have been imported into Scilab [54] for all following computations. The entire model of the structure has \(n_{\mathrm{FE}} = 3009\) DOFs, whereof 2709 DOFs are involved in the joint. The system is excited either by an external force at the point mass (see Fig. 15 and Table 5) or by gravity (see Table 6).
The differential algebraic equations describing the multibody system as defined by Eq. (12) and Eq. (13) are solved with a modified HHT solver [30, 31] written in Scilab [54]. The algorithm is very similar to the solver presented in [31].
6.1 Evaluation of the reduction base
Before the contact models are investigated on the car pendulum model, the convergence in terms of additional JTVs is analyzed. For that reason, the system is computed with the parameters defined in Table 5 and an increasing number of JTVs. In Fig. 16 the first 18 trial vectors of the reduction base, computed with mode shape orthogonalization out of five vibration modes, six static deformation modes, and 20 JTVs are shown. The first five trial vectors in this figure correspond to the vibration modes, whereas the other trial vectors are JTVs. The figure shows the increased flexibility of the JTVs between the metal sheets in the joint area. The external force \(f_{\mathrm{ext}} \) in this investigation is applied as a smoothed step function (FORCE 0) using a half-wave cosine with a short period of \(T= 0.05~\mbox{s} \) as shown in Fig. 15. As a convergence criterion, the Euclidean norm of the contact force vector \(\mathbf{f}_{c} \) is used and plotted for different number of JTVs in Fig. 17. For this convergence study, the linear penalty model is used, but the use of the contact model does not influence the convergence in terms of JTVs.
Without the use of additional JTVs, the contact forces are distinctly overestimated. The contact forces computed with 60 JTVs are very close to the converged solution, and, therefore, all further computations are executed with 60 JTVs. For the practical application, also 20 JTVs would suffice, as the results in Sect. 6.3 show. Comparing the convergence of JTVs to the use of additional normal modes shows that with 20 JTVs the results are much closer to the converged solution than the results with 20 additional NMs. These results are in agreement with [8], where also a comparison to a full nonlinear computation is given.
In terms of computational time, it can be reported that the simulation with 60 JTVs needs only 0.2 % of the CPU time required for the simulation where all 903 contact pairs are considered separately.
6.2 Numerical investigation on contact models
For the numerical investigation on the contact models, the 2D car pendulum model was simulated for the three described cases over a period of \(T_{\mathrm{sim}} = 2.5~\mbox{s}\). To compare the different penalty models, the contact parameters have been chosen in a way that the maximal penetration is approximately equal. The parameters given in Table 7 lead to a maximal penetration of \(g_{\mathrm{max}} \approx -3~\upmu\mbox{m} \). Clearly, for penalty models with more than one parameter, different combinations of the parameters are possible to achieve this maximal penetration. The parameters in Table 7 lead to a similar pressure-gap relationship as shown in Fig. 8. With the parameters in Table 7, all contact models lead to a comparable contact force for all excitations (external force or gravity). In order to benchmark the numerical efficiency of the different contact models, the required computational time, the number of time steps, and the number of Jacobian updates are used as criteria. The results in Fig. 18(b) show that for the excitation with force0, the simple linear penalty model leads to the lowest computational effort. The number of time steps and Jacobian updates is at the same level for all models. For the excitation with force1 (Fig. 18(c)) or with gravity (Fig. 18(d)), the numerical investigations show quite different results. For these two cases, the linear penalty model shows clearly the highest computational effort. The reason for the difference between the results might be in the different bending of the flexible structure for the different cases. Whereas the excitation with force0 only leads to varying bending in one direction, the bending direction changes for the other two cases. Therefore, it seems that contact models with a quite smooth transition in the pressure-gap relationship between gapping and penetration have numerical advantages when it comes to qualitative changes in the deformation state during the dynamic simulation. Apart from the linear model, all other penalty models show a numerical performance that is approximately at one level for the cases force0 and gravity.
Considering the averaged results (Fig. 18a) of the numerical investigations, it seems that all models that have a smooth transition in the pressure-gap relationship tend to have lower computational effort. Together with the comparison of Table 1, the joint-adapted exponential model seems to be the best choice for computing the contact pressure inside jointed structures.
6.3 Car pendulum with friction
In order to bring together the results of the previous sections, the multibody system is computed with friction forces inside the joint. As a result of the findings in Sect. 5.2.7, the three-parameter Coulomb model is used. For the computation of the contact forces, the joint-adapted exponential model is applied. The friction coefficient is set to \(\mu = 0.15 \) for these simulations. In Fig. 19(a) the displacement of the car and in Fig. 19(b) relative displacement between the point mass and the car for the excitation with force1 are shown.
The figures clearly show the damping influence of the dry friction. In both figures, the results for using additional 20 NMs, 20 JTVs, and a converged solution with 60 JTVs are compared. It can be seen that the overestimation of the contact forces by the use of additional NMs leads to a different dynamic behavior of the flexible structure and the car. The solution with 20 NMs deviates from the converged solution in the amplitude and in the phase of the motion. Even in this configuration, where the point mass is directly excited by the external force, the accurate consideration of the nonlinear joint forces influences the displacement significantly. Note that this effect might be even more observable in the three-dimensional case.
In Fig. 20 the errors normalized by the mean of the reference solution
for the relative displacement for 20 NMs and 20 JTVs are shown. The figure shows that, with an equal number of additional JTVs and NMs, the error is up to three times higher when using NMs instead of JTVs.
7 Discussion
This paper describes the use of JTVs based on TVDs to extend the classical reduction base for model reduction. In context with FEM, this method is compared to other possibilities for model reduction of nonlinear mechanical systems in [8], whereas the focus of this discussion is on flexible multibody dynamics. An alternative approach for an extension of the reduction base for jointed structures is given in [24]. The advantages of JTVs based on TVDs compared to the trial vectors found in [24] are faster convergence in terms of additional trial vectors (especially for multilayered complex structures) and easier implementation of the algorithm. TVDs are also used in [12] for the model reduction of flexible multibody systems with geometric nonlinearities. In [12] the TVDs are directly used for the extension of the reduction base, which is a major difference to the JTVs, which are computed via POD out of all TVDs. Furthermore, the TVDs for geometric nonlinearities are symmetric, whereas for contact problems, they are not \((\frac{\partial \boldsymbol{\varphi}_{i}}{\partial q_{f,j}} \neq \frac{\partial \boldsymbol{\varphi}_{j}}{\partial q_{f,i}} ) \).
Different contact models can be found in the literature as mentioned in Sect. 5.1. The contact model preferred in this paper is an adaption of an exponential model and based on the usage of the exponential distribution describing the asperity of a metallic surface. In [38] a normal distribution is supposed for the height distribution of the summits a rough surface. This leads to a pressure-gap relationship, which is similar to the power function based model in Sect. 5.1.3. The idea of using statistical models for describing asperity heights is also used in [55]. In this paper it is also mentioned that the height distribution of the asperity summits tends to be rather a normal distribution than an exponential distribution, but the latter is sufficient to describe the uppermost 25 % of the asperities of most surfaces.
The work of Gaul and his associates [13, 15] has focused on the investigation of dry friction and finding alternatives to the Coulomb friction model. In their contributions, however, the continuity and numerical efficiency of the models was not investigated. In [46] the continuity of different models is studied in detail, but the computational effort of the different model was not considered. The difficulties with the discontinuity of the Coulomb model in dynamic simulations are discussed in [56]. Nevertheless, the results of the numerical investigations showed that the continuity of the used friction model is of minor importance when the overall numerical efficiency is evaluated.
For preloaded structures (e.g., clamped joints), the deformation and stress state can be dominated by the preload force even through a dynamic simulation. For such structures, it seems to be a promising strategy to consider the preload state for the computation of the reduction base to achieve further decrease of the number of trial vectors. The Taylor series expansion of state-dependent trail vectors leads in an intuitive way to the consideration of the preload state in the TVDs. Therefore, the use of JTVs based on TVDs for considering preloaded structures will be investigated in future work.
8 Conclusions
The strategy presented in this paper for considering contact and friction inside lap joints of flexible structures within multibody simulation focuses on three main points:
-
Accurate representation of the joint deformation with JTVs
-
Efficient computation of the contact forces
-
Efficient modeling of the dry friction characteristics
The numerical example in Sect. 6 confirms that the extension of the reduction base with JTVs based on TVDs leads to an accurate description of the joint deformation. Furthermore, the study shows that the computational time for a simulation with the number of additional JTVs required for a converged solution is significantly lower than for a simulation considering all contact pairs in the joint area.
The joint adapted exponential contact model presented in Sect. 5.1.6 is recommended for computing contact forces. The model turned out to be numerically efficient, and it has the advantage that it can be derived from some contact physical background.
Different friction models that capture the characteristics of dry friction were evaluated. Although the three-parameter Coulomb-type friction model is not continuous, it turned out to be numerically very efficient and also fulfills all other defined criteria for a dry friction model.
References
Craig, R.R., Bampton, M.C.C.: Coupling of substructures for dynamic analysis. AIAA J. 6(7), 1313–1319 (1968). doi:10.2514/3.4741
Craig, R.R.: Coupling of substructures for dynamic analyses—an overview. In: 41st Structures, Structural Dynamics, and Materials Conference and Exhibit. AIAA, Washington (2000). doi:10.2514/6.2000-1573
Craig, R.R., Kurdila, A.J.: Fundamentals of Structural Dynamics, 2nd edn. Wiley, Hoboken (2006)
Koutsovasilis, P., Beitelschmidt, M.: Comparison of model reduction techniques for large mechanical systems. Multibody Syst. Dyn. 20(2), 111–128 (2008). doi:10.1007/s11044-008-9116-4
Qu, Z.Q.: Model Order Reduction Techniques with Applications in Finite Element Analysis. Springer, New York (2004). doi:10.1007/978-1-4471-3827-3
Shabana, A.A.: Flexible multibody dynamics: review of past and recent developments. Multibody Syst. Dyn. 1(2), 189–222 (1997). doi:10.1023/A:1009773505418
Wasfy, T.M., Noor, A.K.: Computational strategies for flexible multibody systems. Appl. Mech. Rev. 56(6), 553–613 (2003). doi:10.1115/1.1590354
Witteveen, W., Pichler, F.: Efficient model order reduction for the dynamics of nonlinear multilayer sheet structures with trial vector derivatives. Shock Vib. 2014, 913136 (2014). doi:10.1155/2014/913136
Idelsohn, S.R., Cardona, A.: A load-dependent basis for reduced nonlinear structural dynamics. Comput. Struct. 20(1–3), 203–210 (1985). doi:10.1016/0045-7949(85)90069-0
Idelsohn, S.R., Cardona, A.: A reduction method for nonlinear structural dynamic analysis. Comput. Methods Appl. Mech. Eng. 49(3), 253–279 (1985). doi:10.1016/0045-7825(85)90125-2
Slaats, P., de Jongh, J., Sauren, A.: Model reduction tools for nonlinear structural dynamics. Comput. Struct. 54(6), 1155–1171 (1995). doi:10.1016/0045-7949(94)00389-K
Wu, L., Tiso, P.: Nonlinear model order reduction for flexible multibody dynamics: a modal derivatives approach. Multibody Syst. Dyn. 36, 405–425 (2015). doi:10.1007/s11044-015-9476-5
Gaul, L., Lenz, J.: Nonlinear dynamics of structures assembled by bolted joints. Acta Mech. 125(1–4), 169–181 (1997). doi:10.1007/BF01177306
Lenz, J., Gaul, L.: The influence of microslip on the dynamic behavior of bolted joints. In: Proceedings of the IMAC XIII, pp. 248–254. SEM, Bethel (1995)
Lenz, J.: Strukturdynamik unter dem Einfluß von Mikro- und Makroschlupf in Fügestellen. Ph.D. thesis, Universität der Bundeswehr, Hamburg (1997)
Gaul, L., Nitsche, R.: The role of friction in mechanical joints. Appl. Mech. Rev. 54(2), 93–106 (2001). doi:10.1115/1.3097294
Segalman, D.J.: Modelling joint friction in structural dynamics. Struct. Control Health Monit. 13(1), 430–453 (2006). doi:10.1002/stc.119
Song, Y., Hartwigsen, C., McFarland, D., Vakakis, A., Bergman, L.: Simulation of dynamics of beam structures with bolted joints using adjusted Iwan beam elements. J. Sound Vib. 273(1–2), 249–276 (2004). doi:10.1016/S0022-460X(03)00499-1
Song, Y., McFarland, D.M., Bergman, L.A., Vakakis, A.F.: Effect of pressure distribution on energy dissipation in a mechanical lap joint. AIAA J. 43(2), 420–425 (2005). doi:10.2514/1.10139
Wriggers, P.: Computational Contact Mechanics, 2nd edn. Springer, Berlin (2006)
Laursen, T.A.: Computational Contact and Impact Mechanics: Fundamentals of Modeling Interfacial Phenomena in Nonlinear Finite Element Analysis. Springer, Berlin (2002). doi:10.1007/978-3-662-04864-1
Chatterjee, A.: An introduction to the proper orthogonal decomposition. Curr. Sci. 78(7), 808–817 (2000)
Volkwein, S.: Model reduction using proper orthogonal decomposition (2014)
Witteveen, W., Irschik, H.: Efficient mode-based computational approach for jointed structures: joint interface modes. AIAA J. 47(1), 252–263 (2009). doi:10.2514/1.38436
Friberg, O., Karhu, V.: Use of mode orthogonalization and modal damping in flexible multibody dynamics. Finite Elem. Anal. Des. 7(1), 51–59 (1990). doi:10.1016/0168-874X(90)90014-6
Sherif, K., Irschik, H., Witteveen, W.: Transformation of arbitrary elastic mode shapes into pseudo-free-surface and rigid body modes for multibody dynamic systems. J. Comput. Nonlinear Dyn. 7(2), 021008 (2012). doi:10.1115/1.4005237
Junge, M., Brunner, D., Becker, J., Gaul, L.: Interface-reduction for the Craig–Bampton and Rubin method applied to FE–BE coupling with a large fluid-structure interface. Int. J. Numer. Methods Eng. 77(12), 1731–1752 (2009). doi:10.1002/nme.2474
Shabana, A.A.: Dynamics of Multibody Systems. Cambridge Univ. Press, Cambridge (2005). doi:10.1017/CBO9780511610523
Sherif, K., Nachbagauer, K.: A detailed derivation of the velocity-dependent inertia forces in the floating frame of reference formulation. J. Comput. Nonlinear Dyn. 9(4), 044501 (2014). doi:10.1115/1.4026083
Hilber, H.M., Hughes, T.J.R., Taylor, R.L.: Improved numerical dissipation for time integration algorithms in structural dynamics. Earthq. Eng. Struct. Dyn. 5(3), 283–292 (1977). doi:10.1002/eqe.4290050306
Negrut, D., Rampalli, R., Ottarsson, G., Sajdak, A.: On an Implementation of the Hilber–Hughes–Taylor method in the context of index 3 differential-algebraic equations of multibody dynamics (DETC2005-85096). J. Comput. Nonlinear Dyn. 2(1), 73–85 (2006). doi:10.1115/1.2389231
Machado, M., Moreira, P., Flores, P., Lankarani, H.M.: Compliant contact force models in multibody dynamics: evolution of the Hertz contact theory. Mech. Mach. Theory 53, 99–121 (2012). doi:10.1016/j.mechmachtheory.2012.02.010
Becker, J., Gaul, L.: CMS Methods for efficient damping prediction for structures with friction. In: Proceedings of the IMAC XXVI (2008)
Bograd, S., Reuss, P., Schmidt, A., Gaul, L., Mayer, M.: Modeling the dynamics of mechanical joints. Mech. Syst. Signal Process. 25(8), 2801–2826 (2011). doi:10.1016/j.ymssp.2011.01.010
Gaul, L., Becker, J.: Damping prediction of structures with bolted joints. Shock Vib. 17(4–5), 359–371 (2010). doi:10.3233/SAV-2010-0532
Mayer, M., Gaul, L.: Modeling of contact interfaces using segment-to-segment-elements for FE vibration analysis. In: Proceedings of the IMAC XXIII (2005)
Wriggers, P., Van Vu, T., Stein, E.: Finite element formulation of large deformation impact-contact problems with friction. Comput. Struct. 37(3), 319–331 (1990). doi:10.1016/0045-7949(90)90324-U
Willner, K.: Ein statistisches Modell für den Kontakt metallischer Körper. Ph.D. thesis, Universität der Bundeswehr, Hamburg (1995)
Pichler, F.: Effizientes Verfahren zur Berechnung mehrfach geschichteter Blechstrukturen auf Basis modaler Ableitungen. Master thesis. University of Applied Sciences Upper Austria, Campus Wels (2013)
Prechtl, G.: Efficient consideration of non-linear friction in the joints of modal reduced structures. Master thesis. University of Applied Sciences Upper Austria, Campus Wels (2011)
Dassault Systèmes: Abaqus Theory Manual 6.12 (2012)
Gaul, L., Mayer, M.: Modeling of contact interfaces in built-up structures by zero-thickness elements. In: Proceedings of the IMAC XXVI (2008)
Willner, K., Gaul, L.: A penalty approach for contact description by FEM based on interface physics. In: Aliabadi, M.H., Allesandri, C. (eds.) Proceedings of Contact Mechanics II. Computational Mechanics Publications, vol. 7, pp. 257–264 (1995)
Armstrong-Hélouvry, B., Dupont, P., De Wit, C.C.: A survey of models, analysis tools and compensation methods for the control of machines with friction. Automatica 30(7), 1083–1138 (1994). doi:10.1016/0005-1098(94)90209-7
Olsson, H., Aström, K., Canudas de Wit, C., Gäfvert, M., Lischinsky, P.: Friction models and friction compensation. Eur. J. Control 4(3), 176–195 (1998). doi:10.1016/S0947-3580(98)70113-X
Padthe, A., Drincic, B., Oh, J., Rizos, D., Fassois, S., Bernstein, D.S.: Duhem modeling of friction-induced hysteresis. IEEE Control Syst. 28(5), 90–107 (2008). doi:10.1109/MCS.2008.927331
De Canudas, W.C., Olsson, H., Astrom, K.J., Lischinsky, P.: A new model for control of systems with friction. IEEE Trans. Autom. Control 40(3), 419–425 (1995). doi:10.1109/9.376053
Marques, F., Flores, P., Lankarani, H.M.: On the frictional contacts in multibody system dynamics. In: Font-Llagunes, M.J. (ed.) Multibody Dynamics: Computational Methods and Applications, pp. 67–91. Springer, Cham (2016). doi:10.1007/978-3-319-30614-8_4
Pennestrì, E., Rossi, V., Salvini, P., Valentini, P.P.: Review and comparison of dry friction force models. Nonlinear Dyn. 83(4), 1785–1801 (2016). doi:10.1007/s11071-015-2485-3
Garino, C.G., Ponthot, J.P.: A quasi-Coulomb model for frictional contact interfaces: application to metal forming simulations. Lat. Am. Appl. Res. 38(2), 95–104 (2008)
Dahl, P.R.: A solid friction model. Tech. rep. TOR-0158(3107-18)-1, Aerospace Corporation, El Segundo, CA (1968)
Dahl, P.R.: Solid friction damping of mechanical vibrations. AIAA J. 14(12), 1675–1682 (1976). doi:10.2514/3.61511
Fischer, P., Engelbrechtsmüller, M.: Local damping effects in acoustic analysis of large FE engine structures. In: Proceedings of ISMA 25th, pp. 1293–1299 (2000)
Scilab: vol. 5.5.0. http://www.scilab.org
Greenwood, J.A., Williamson, J.B.P.: Contact of nominally flat surfaces. Proceedings of the Royal Society 295(1442), 300–319 (1966). doi:10.1098/rspa.1966.0242
Pennestrì, E., Valentini, P.P., Vita, L.: Multibody dynamics simulation of planar linkages with Dahl friction. Multibody Syst. Dyn. 17(4), 321–347 (2007). doi:10.1007/s11044-007-9047-5
Acknowledgements
Open access funding provided by University of Applied Sciences Upper Austria. The author was supported by a researcher development program financed by the government of Upper Austria.
Furthermore, this project was supported by the program “Regionale Wettbewerbsfähigkeit OÖ 2010–2013”, which is financed by the European Regional Development Fund and the government of Upper Austria.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: Contact models
For completeness, the derivations of the contact pressure \(p_{N,i} \) with respect to \(g_{N,i}\) for the contact models described in Sect. 5.1 are given in this appendix.
1.1 A.1 Linear penalty model
1.2 A.2 Multistage linear penalty model
1.3 A.3 Power-function-based nonlinear penalty model
1.4 A.4 Combined quadratic-linear penalty model
1.5 A.5 Exponential penalty model
1.6 A.6 Joint-adapted exponential penalty model
Appendix B: Friction models
The mathematical description of the friction models considered in Sect. 5.2 is given in the following.
2.1 B.7 Dahl friction model
The parameter \(\alpha \) determines the shape of the hysteresis curve and is commonly set to \(\alpha = 1\). This assumption simplifies Eq. (B.1) to
2.2 B.8 Valanis friction model
2.3 B.9 Bouc–Wen friction model
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Pichler, F., Witteveen, W. & Fischer, P. A complete strategy for efficient and accurate multibody dynamics of flexible structures with large lap joints considering contact and friction. Multibody Syst Dyn 40, 407–436 (2017). https://doi.org/10.1007/s11044-016-9555-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11044-016-9555-2