Temperature-dependent thermal buckling and free vibration behavior of smart sandwich nanoplates with auxetic core and magneto-electro-elastic face layers

Abstract

This article addresses the thermomechanical thermal buckling and free vibration response of a novel smart sandwich nanoplate based on a sinusoidal higher-order shear deformation theory (SHSDT) with a stretching effect. In the proposed sandwich nanoplate, an auxetic core layer with a negative Poisson’s ratio made of Ti-6Al-4V is sandwiched between Ti-6Al-4V rim layers and magneto-electro-elastic (MEE) face layers. The MEE face layers are homogenous volumetric mixtures of cobalt ferrite (CoFe₂O₄) and barium titanate (BaTiO₃). The mechanical and thermal material properties of the auxetic core and MEE face layers are temperature-dependent. Using Hamilton’s principle, governing equations are constructed. To characterize the size-dependent behavior of the nanoplate, governing equations are adapted with the nonlocal strain gradient theory (NSGT). By applying the principles of Navier’s technique, closed-form solutions are obtained. Parametric simulations are carried out to examine the effects of auxetic core parameters, temperature-dependent material properties, nonlocal parameters, electric, magnetic, and thermal loads on the free vibration and thermal buckling behavior of the nanoplate. According to the simulation results, it is determined that the auxetic core parameters, temperature-dependent material properties, and nonlocal factors significantly affect the thermomechanical behavior of the nanoplate. The outcomes of this investigation are expected to contribute to the advancement of smart nano-electromechanical systems, transducers, and nanosensors characterized by lightweight, exceptional structural integrity and temperature sensitivity. Also, the auxetic core with a negative Poisson’s ratio provides a metamaterial feature, and thanks to this feature, the proposed model has the potential to be used as an invisibility technology in sonar and radar-hiding applications.

1 Introduction

Auxetic structures characterized by a negative Poisson’s ratio, a type of metamaterial, have found widespread use in structural applications due to their distinctive mechanical attributes such as ultra-lightweight, high strength-to-weight ratio, acoustic dampening, and enhanced energy absorption capacities (Nouraei and Zamani 2023). Under uniaxial compression conditions, auxetic structures undergo transverse contraction, while under uniaxial tension, they undergo transverse expansion (Ren et al. 2018). These unique characteristics of auxetic metamaterials make them suitable for potential uses including smart sensors, nano-electromechanical systems (NEMs), sonar systems, smart dampers, and acoustic isolators. The auxetic structures are lightweight and have a high shear modulus, but their mechanical performance is constrained by their low stiffness. In order to enhance the mechanical properties of auxetic structures, it has become essential to sandwich lightweight auxetic core layer between face layers that are more stiff. As face layers, piezoelectric plates, magneto-electro-elastic plates, and composite plates reinforced with carbon nanotubes (CNTs) or graphene platelets (GPLs) are frequently used (Fatih Pehlivan and Aktas 2024; Mahapatra et al. 2024; Nouraei and Zamani 2023). The integration of auxetic, honeycomb, and foam structures has been a subject of interest in various studies, shedding light on different aspects of their mechanical behavior and performance (Guo and Zhang 2023; Tian 2023; Xia et al. 2023; Zhang et al. 2022). Pawlus (2022) investigated the static stability of composite annular plates with auxetic properties, highlighting the composition of three-layered plates with auxetic facings and a soft foam core. This study provides insights into the structural behavior of plates with auxetic cores, offering valuable information for understanding the static performance of such composite structures. Janus-Michalska and Jasinska (2017) conducted a comparative study of the bending stiffness of sandwich plates with cellular cores, including those with cellular auxetic cores. By considering the bending behavior of plates with different core types, this study contributes to understanding the mechanical response of sandwich plates with auxetic cores, providing valuable insights into their structural performance. Furthermore, Mahesh (2023) delved into the integrated effects of auxetic and pyro-coupling on the nonlinear static behavior of MEE sandwich plates subjected to multifield interactive loads. Zhang et al. (2023b) presented an experimental investigation on the application of a carbon fiber-reinforced plastic plate to externally attach an advanced composite beam. While this study focused on MEE plates, it underscores the impact of blast loads on the dynamic behavior of plates with auxetic cores, offering valuable insights into the potential applications and performance of auxetic cores in sandwich structures under dynamic loading conditions.

Sandwich structures, a class of composite materials, have gained significant attention due to their versatile application in various engineering fields. These structures typically consist of two thin, stiff face sheets separated by a lightweight core material, forming a high-strength and lightweight configuration. The design of sandwich structures presents a unique challenge in load introduction, as highlighted by Janus-Michalska and Jasinska (2017), emphasizing the need for innovative concepts to efficiently distribute and manage loads within the structure. The mechanical behavior and stability of sandwich structures have been the focus of extensive research, with studies such as (Arefi et al. 2020) providing insights into the size-dependent free vibration analysis and stability of these structures. Additionally, the introduction of novel core materials, as demonstrated by Iftimiciuc et al. (2023), has further expanded the design possibilities and performance capabilities of sandwich structures. The unique properties of sandwich structures have led to diverse applications, ranging from flexible energy harvesters (Fu et al. 2020) to aerospace components (Joubaneh et al. 2018). Furthermore, the introduction of advanced materials and manufacturing techniques, as explored by Wang et al. (2022) and Khan et al. (2017), has significantly enhanced the performance and functionality of sandwich structures. The introduction of innovative materials, such as graphene oxide and bismuth ferrite, has further expanded the capabilities of sandwich structures, as evidenced by studies from Yin et al. (2020) and Wu et al. (2011). In summary, sandwich structures represent a crucial area of research and development, with ongoing efforts focused on enhancing their mechanical properties, introducing novel materials, and exploring diverse applications across engineering disciplines (Sayyad and Avhad 2022; Shokravi and Jalili 2019; Tran et al. 2023; Wang et al. 2021).

MEE materials have gained significant attention due to their ability to convert one form of energy to another, their simple geometry, and their economic design, making them useful in smart or intelligent structure applications (Yildirim and Simsek 2022). These materials are composed of piezoelectric and piezomagnetic phases, and they have found vast applications in different industries owing to their predictable and controllable ability to couple different phases (Moshtagh et al. 2019). The mechanics of MEE composites have been extensively studied over the past few decades, with research focusing on various aspects such as wave propagation, vibration control, and free vibration analysis (Li et al. 2021; Vinyas et al. 2018; Zhang et al. 2020b; Zhou et al. 2020). Additionally, the development of new models, such as the microstructure-dependent anisotropic magneto-electro-elastic Mindlin plate model, has contributed to a deeper understanding of the behavior of MEE materials (Qu et al. 2020). Furthermore, MEE materials have been investigated for their potential applications in nanotechnology, with studies focusing on the vibration performance evaluation of smart magneto-electro-elastic nanobeams and the buckling analysis of magneto-electro-thermo-elastic cylindrical nanoshells (Gui and Li 2023; Liu and Lv 2019). The unique properties of MEE materials have also led to the development of new models, such as the transversely isotropic magneto-electro-elastic Timoshenko beam model, which incorporates microstructure and foundation effects, providing valuable insights for the design of MEE nanodevices (Wang and Jin 2022; Zhang et al. 2020a).

MEE materials at the microscale and nanoscale have gained significant attention due to their unique properties and potential applications. MEE materials exhibit coupling of mechanical, electrical, and magnetic fields, providing excellent magneto-electrical coupling at smaller scales (Ebrahimi and Barati 2017a). The smaller size and larger surface-to-volume ratio of MEE nanoscale structures have been noted to offer enhanced magneto-electrical coupling, making them suitable for applications in nano-electromechanical systems (NEMs) (Ebrahimi and Barati 2017a). Additionally, the material surface has been shown to have a marked effect on the mechanical behavior of MEE structures at the nanoscale (Wu et al. 2015). Classical theories are scale-free and fail to account for small scales. Moreover, these methods cannot accurately estimate the mechanical properties of nanostructures. The investigation of small-scale nonlocal impacts and size effects has been a key area of study for almost half a century, primarily through the nonlocal elasticity theory (NET) (Eringen and Wegner 2003; Eringen 1983a, 1972a,b; Eringen and Edelen 1972; Eringen and Suhubi 1964). Within this theory, the nonlocal parameter e₀a is precisely described. Both practical and theoretical research has demonstrated that the structure experiences a softening effect that is contingent upon the magnitude of this parameter. Subsequently, the impact of material size on microbeams was investigated using the strain gradient elasticity theory (SGT) (Kong et al. 2009; Wang et al. 2010). SGT (Kong et al. 2009, 2008a; Mindlin 1964), designed for small-scale systems, indicates the presence of a nonlocal characteristic that results in the substance becoming stiffer rather than softer. The property of being nonlocal is commonly known as the material size parameter. The modified coupled stress theory (MCST) was introduced with the advancement of the SGT (Kong et al. 2008b; Ma et al. 2008). MCST (Şimşek and Reddy 2013; Yang et al. 2002) is explained by variables similar to the size parameter with an equivalent hardening influence. Due to scaling inconsistencies between nonlocal elasticity and strain gradient theories, a novel approach capable of capturing the two softening and hardening stiffness size impacts is required (Alghanmi 2023). Finally NSGT, which combines Eringen’s nonlocal theory with the strain gradient elasticity theory, was developed (Alghanmi 2022; Ebrahimi and Barati 2017b; Li et al. 2015; Lim et al. 2015). In recent years, this theory has grown increasingly popular. Research has delved into various aspects of MEE materials at the micro and nanoscales, including wave propagation analysis, bending behavior, buckling analysis, and the development of exact solutions for different configurations (Hong et al. 2022; Pan 2001; Pan and Han 2005). Zhang et al. (2023a) showed unprecedented mechanical and microstructural features of advanced composites that include nanoparticles. Furthermore, the effective properties of MEE composites and the impact of interfacial cracks on their properties were investigated (Bhangale and Ganesan 2006; Huang et al. 2009). The potential applications of MEE materials in transducers, sensors, and actuators were highlighted, emphasizing their significance in various technological domains (Huang et al. 2009). Ferroelectric artificial application for high-performance neuromorphic computing was presented by Zhao et al. (2024), and tunable conductivity and ferromagnetism was studied by Guo et al. (2024). The interdisciplinary nature of this research, spanning physics, materials science, and engineering, underscores the significance of MEE materials in advancing technological innovation and addressing diverse engineering challenges. The development of novel formulations and exact solutions has enabled the analysis of MEE materials at the micro and nanoscales, contributing to the understanding of their mechanical behavior and potential applications (Pan and Han 2005; Yakhno 2018). In conclusion, extensive research on micro and nanoscale MEE materials has provided valuable insights into their behavior, properties, and potential applications. The unique coupling of mechanical, electrical, and magnetic fields in these materials has opened new avenues for technological advancements and the development of tailor-made materials with promising applications (Tiwari et al. 2021).

Extensive research has been conducted on functionally graded structures and functionally graded reinforced composite structures. These studies have particularly focused on the application of higher-order shear deformation theories, as evidenced by the literature (Alghanmi and Zenkour 2021; Daikh et al. 2023a,b, 2022; Koç et al. 2023; Melaibari et al. 2022; Özmen 2023; Saini and Pradyumna 2022; Yıldız and Esen 2023).

When employed at high temperature, MEE materials exhibit enhanced pyroelectric and pyromagnetic interactions. In addition, the mechanical, electrical, and magnetic characteristics of composite structures can change significantly with temperature. For this reason, it is essential to consider the temperature-dependent material attributes for the mechanical analysis of systems operated at high temperatures. The static reaction of a multilayer FG-MEE plate in a thermal environment was investigated by Vinyas and Kattimani (2017) for various temperature variations and boundary conditions utilizing the FEM. Additionally, Vinyas and Kattimani performed static deflection analysis of an FG-MEE structure using FEM under hygrothermal effects. Ebrahimi and Barati (2016a) used the HSDT to assess the impacts of distinct temperature distributions on the frequency performance of magneto-electro-thermo-elastic functionally graded (METE-FG) nanostructures. Ebrahimi and Barati (2016b) investigated the thermo-electro-mechanical buckling behavior of functionally graded piezoelectric (FGP) nanobeams with HSDT. Wang et al. (2023) conducted an investigation on the thermal properties of high-entropy RE-disilicates, which were regulated through high throughput composition design and optimization.

Having conducted an extensive review of the existing literature, it was concluded that the five-layer smart sandwich nanoplate with an auxetic core and MEE face layers is a novel nanostructure that has not been previously investigated, particularly in relation to the temperature-dependent properties of the MEE face layers (BaTiO3 and CoFe2O4) and auxetic core layer. Thus, the temperature dependent free vibration and thermal buckling analysis of the presented sandwich smart nanoplate with a metamaterial property will be presented for the first time. Models developed by neglecting the auxetic core and MEE face layers’s actual temperature behavior will produce inaccurate findings in practice because they do not accurately represent the physical behavior of the presented sandwich structure. Therefore, with this study, a model in which the thermomechanical properties of these materials are obtained through rigorous simulation studies has been created and presented to the reader. Auxetic core has a negative Poisson’s ratio, and it can be adjusted with auxetic core parameters. This feature gives smart nanoplates additional metamaterial properties, and thanks to this feature, they provide potential for use in hiding applications from sonar and radar waves. Additionally, nano electromechanical systems that will operate in high noise environments have the potential to be used in sound or noise insulation applications. Moreover, they can be used in military applications such as impact dampening, target confusion, and personal protective equipment. This research aims to help understand the effect of auxetic core parameters (inclination angle, length of the horizontal wall, length of the inclined cell wall, and thickness of the cell wall), temperature-dependent material properties, nonlocal parameters, electric, magnetic, and thermal loads on the thermal buckling and free vibration characteristics of sandwich plate systems and to gain more insight into their possible applications in nanotechnology.

2 Theory and formulation

2.1 Summary of the suggested sandwich nanoplate

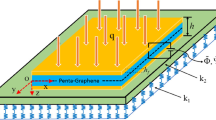
With this study, we consider a smart sandwich nanoplate with two MEE layers, an auxetic core layer, and two rim layers, which has length $a$, width $b$, and thickness $h$ as illustrated in Fig. 1. $x$ and $y$ are in-plane axes located at the middle layer of the auxetic core, and z is the direction that extends along the thickness of the plate. $h_{s}$, $h_{r}$, and $h_{p}$ are the thicknesses of the core layer, rim layer, and MEE layer, respectively.

Fig. 1

An auxetic core sandwich nanoplate composed of thermo-magneto-electro-elastic face layers

The auxetic core layer with a negative Poisson’s ratio is sandwiched between two MEE nanoplate layers and two metal rim layers. The materials used for the auxetic core and rim layers are biocompatible material Ti-6Al-4V. In addition, $\mathrm{Co} \mathrm{Fe}_{2} \mathrm{O}_{4}$ and $\mathrm{BaTi} \mathrm{O}_{3}$ are considered to be homogeneously distributed in the MEE lower and upper face plates. Also, an external electrical voltage and magnetic field are applied through the thickness of the MEE layers, causing these layers to expand and contract along the z-axis.

2.2 Auxetic core

The core layer of the proposed sandwich plate is made of an auxetic material with a negative Poisson’s ratio. The auxetic core layer consists of honeycomb cells placed in a systematic way, where $\theta$, $d$, $l$, and $t$ represent the angle of inclination, the length of the horizontal wall, the length of the inclined cell wall, and the thickness of the cell wall, respectively. The material properties such as Young modulus ($E$), shear modulus ($G$), and density ($\rho$) of the auxetic core can be expressed using the following equations (Li and Yuan 2022; Nouraei and Zamani 2023):

$$ E_{11}^{C} = E_{Ti} \left [ \frac{\left ( \beta _{1} - \sin \theta \right ) \beta _{3}^{3}}{\left [ \left ( \beta _{1} sec^{2} \left ( \theta \right ) + tan^{2} \left ( \theta \right ) \right ) \beta _{3}^{2} +1 \right ] cos^{3} \left ( \theta \right )} \right ] $$

(1)

$$ E_{22}^{C} = E_{Ti} \left [ \frac{\beta _{3}^{3}}{\left ( \beta _{3}^{2} + tan^{2} \left ( \theta \right ) \right ) \left ( \cos \left ( \theta \right ) \beta _{1} - \cos \left ( \theta \right ) \sin \left ( \theta \right ) \right )} \right ] $$

(2)

$$ G_{12}^{C} = G_{Ti} \left [ \frac{\beta _{3}^{3}}{\left ( 2 \beta _{1}^{2} + \beta _{1} \right ) \cos \theta} \right ] $$

(3)

$$ G_{13}^{C} = G_{Ti} \left [ \frac{2 sin^{2} \left ( \theta \right ) + \beta _{1}}{2 \left ( \beta _{1} - \sin \left ( \theta \right ) \right )} + \frac{- \sin \left ( \theta \right ) + \beta _{1}}{2 \beta _{1} +1} \right ] \frac{\beta _{3}}{2 \cos \left ( \theta \right )} $$

(4)

$$ G_{23}^{C} = G_{Ti} \left [ \frac{\beta _{3} \cos \left ( \theta \right )}{\beta _{1} - \sin \left ( \theta \right )} \right ] $$

(5)

$$ \rho ^{C} = \rho _{Ti} \left [ \frac{\left ( 2+ \beta _{1} \right ) \beta _{3}}{2 \left ( \beta _{1} - \sin \left ( \theta \right ) \right ) \cos \left ( \theta \right )} \right ], $$

(6)

in which $\beta _{1} \ =\ d/l$ and $\beta _{3} \ =\ t/l$. Also, the superscript $c$ and subscript $Ti$ represent the core layer and titanium, respectively. Furthermore, Poisson’s ratio ($v$) can be derived from the geometric parameters in the form that follows (Li and Yuan 2022):

$$ v_{12}^{C} = \frac{\left ( \sin \left ( \theta \right ) - \beta _{1} \right ) \left ( \sin \left ( \theta \right ) \right ) \left ( 1 - \beta _{3}^{2} \right )}{\cos ^{2} \left ( \theta \right ) \left [ \beta _{3}^{2} \left ( \beta _{1} sec^{2} \left ( \theta \right ) + tan^{2} \left ( \theta \right ) \right ) +1 \right ]} $$

(7)

$$ v_{21}^{C} = \frac{\left ( \beta _{3}^{2} -1 \right ) \sin \left ( \theta \right )}{\left ( \beta _{1} - \sin \left ( \theta \right ) \right ) \left ( \beta _{3}^{2} + tan^{2} \left ( \theta \right ) \right )}. $$

(8)

For the thermal expansion coefficients of the auxetic core, $\alpha _{11}^{C}$ and $\alpha _{22}^{C}$ can be described by (Hoang et al. 2023)

$$ \alpha _{11}^{C} = \alpha _{Ti} \frac{\beta _{3} \cos \left ( \theta \right )}{\beta _{1} + \sin \left ( \theta \right )}, $$

(9)

$$ \alpha _{22}^{C} = \alpha _{Ti} \frac{\beta _{3} \left ( \beta _{1} + \sin \left ( \theta \right ) \right )}{\left ( 2\beta _{1} + 1 \right ) \cos \left ( \theta \right )}. $$

(10)

2.3 Magneto-electro-elastic face layers

The mechanical, electrical, thermal, and magnetic properties of the face plates vary uniformly with volumetric ratio of $\mathrm{Co} \mathrm{Fe}_{2} \mathrm{O}_{4}$ and $\mathrm{BaTi} \mathrm{O}_{3}$ along the $z$-axis. Using the rule of mixture, the effective material parameters of MEE face layers can be defined as follows (Amini et al. 2015):

$$\begin{gathered} \begin{gathered} P_{eff}^{lp} \left ( z \right ) = C_{f} P_{C} + B_{f} P_{B},\quad h_{1} \underline{< } z \underline{< } h_{2},\\ P_{eff}^{up} \left ( z \right ) = C_{f} P_{C} + B_{f} P_{B},\quad h_{5} \underline{< } z \underline{< } h_{6},\\ C_{f} + B_{f} =1, \end{gathered} \end{gathered}$$

(11)

where $P_{eff} \left ( z \right )$ defines the effective material parameters, including the modulus of elasticity $E$, mass density $\rho$, Poisson’s ratio $v$, piezoelectric stress coefficient $e$, and dielectric constant $\varepsilon$. The length from the neutral plane is represented by $z$; $C_{f}$ and $B_{f}$ are the volumetric ratios of $\mathrm{Co} \mathrm{Fe}_{2} \mathrm{O}_{4}$ and $\mathrm{BaTi} \mathrm{O}_{3}$, respectively; $P_{C}$ and $P_{B}$ define the properties of $\mathrm{Co} \mathrm{Fe}_{2} \mathrm{O}_{4}$ and $\mathrm{BaTi} \mathrm{O}_{3}$ for the upper and lower face layers, respectively; and superscripts $up$ and $lp$ are the upper MEE plate and lower MEE plate, respectively.

Both the host structure and the face layers have temperature-dependent material characteristics that can be described by a nonlinear temperature equation, involving the modulus of elasticity $E$, Poisson’s ratio $\nu$, thermal conductivity $\psi$, and thermal expansion $\kappa$ (Reddy and Chin 1998; Touloukian 1967, 1966):

$$ P= P_{0} \left ( P_{-1} T^{-1} +1+ P_{1} T+ P_{2} T^{2} + P_{3} T^{3} \right ). $$

(12)

Here, $P$ represents any temperature-dependent material coefficient. Table 1 lists the properties of CoFe₂O₄ and BaTiO₃ as a function of temperature, whereas Table 2 lists the properties of Ti-6Al-4V as a function of temperature. The temperature-dependent thermomechanical coefficients given in Table 1 for CoFe₂O₄ and BaTiO₃ were obtained as a result of partial experimental studies in the literature (Reddy and Chin 1998; Touloukian 1967), and from the analysis and simulations conducted and developed in this study.

Table 1 Temperature-dependent material coefficients for CoFe₂O₄ and BaTiO₃ (Koç et al. 2023)

Table 2 Temperature-dependent material coefficients of Ti-6Al-4V (Reddy and Chin 1998)

2.4 Temperature increment on the sandwich nanoplate

In this subsection, we present the relevant formulations for three different types of temperature rises throughout the nanoplate: uniform (UTR), linear (LTR), and nonlinear (NLTR). A nanoplate with an initial temperature of $T_{0}=300 K$ is consistently increased to its peak temperature $T$ with a uniform temperature rise (UTR) using the following equation (Özmen and Esen 2023):

$$ \Delta T=T- T_{0}. $$

(13)

The temperature of a horizontal surface that extends in the z-axis with the temperatures of its lower and upper surfaces $T_{b}$ and $T_{t}$, respectively, can be calculated as follows, assuming that the temperature rises linearly (LTR) from $T_{b}$ to $T_{t}$ through the thicknesses (Kiani and Eslami 2013):

$$ T \left ( z \right ) = T_{b} + \left ( T_{t} - T_{b} \right ) \left ( \frac{h+2z}{2 h} \right ). $$

(14)

In the presence of a nonlinear temperature increase (NLTR) across the thickness direction of the nanoplates, the one-dimensional heat transfer problem given below can be addressed with specific temperature boundary limits to figure out the upper and lower surface temperatures ($T_{t}$ and $T_{b}$) of the plate (Zhang 2014).

$$ - \frac{d}{dz} \left ( \kappa \left ( z \right ) \frac{dT}{dz} \right ) =0,\qquad T \left ( \frac{h}{2} \right ) = T_{t},\qquad T \left ( - \frac{h}{2} \right ) = T_{b}. $$

(15a)

Here, $\kappa \left ( z \right )$ denotes the thermal conductivity coefficient. For a given boundary condition, the temperature of any point through the thickness $z$-axis can be calculated as follows (Esen and Özmen 2022a):

$$ T \left ( z \right ) = T_{b} + \frac{\left ( T_{t} - T_{b} \right )}{\int _{- \frac{h}{2}}^{\frac{h}{2}} \frac{1}{\kappa \left ( z \right )} d \left ( z \right )} \int _{- \frac{h}{2}}^{z} \kappa \left ( z \right ) dz. $$

(15b)

2.5 Application of nonlocal strain gradient theory to MEE sandwich nanoplates

According to Eringe’s work (Eringen 1983b), the stress at any place on the structure is a function of the stresses at all points in the body. In this theory, the stiffness of the body depends on the strength of the nonlocal and material scale effects. In proportion to the strength of the nonlocal effect, the structure acts in a manner that is less rigid than traditional forms. On the other hand, the SGT presumes that just the material scale effect, which contributes to an increase in the object’s stiffness, is taken into consideration. In conclusion, Eringen’s NETs and SGTs illustrate two separate material properties. The NSGT models nonlocal effects by combining these two distinct effects into a single effect (Li et al. 2016; Lim et al. 2015). In the NSGT, the stress can be calculated as (Lim et al. 2015)

$$ \sigma = \int _{V} \alpha _{0} ( \boldsymbol{x}^{\boldsymbol{'}}, \boldsymbol{x}, e_{0} a ) \boldsymbol{C}: \varepsilon ' \left ( \boldsymbol{x}^{\boldsymbol{'}} \right ) dV ', $$

(16)

$$ \sigma ^{(h)} = l_{m}^{2} \int _{V} \alpha _{1} ( \boldsymbol{x}^{\boldsymbol{'}}, \boldsymbol{x}, e_{1} a) \boldsymbol{C}: \nabla \varepsilon ' ( \boldsymbol{x}^{\boldsymbol{'}} ) dV ', $$

(17)

where $e_{0} a$ and $e_{1} a$ represent the nonlocality constants with $e_{1}$ and $e_{0}$ material coefficients, and $\alpha _{0}$ and $\alpha _{1}$ are the kernel and higher-order nonlocal functions, respectively. $\boldsymbol{C}$ and $\nabla$ represent the fourth-order material coefficient and Laplacian operator $\left ( \nabla =\partial /\partial x\ +\partial /\partial y) \right .$, respectively. $\nabla \varepsilon$ and $\varepsilon$ are the strain tensor and the strain gradient, respectively. $l_{m}$ is the material length size factor. The stress tensor can be expressed as follows based on the NSGT (Farajpour and Rastgoo 2017; Lim et al. 2015):

$$ \sigma ^{t} =\sigma - \nabla ^{2} \sigma ^{\left (1\right )}. $$

(18)

By using the notations given in Ref. (Eringen 1983a) for $\alpha _{1} ( \boldsymbol{x}^{\boldsymbol{'}}, \boldsymbol{x}, e_{1} a)$ and $\alpha _{0} ( \boldsymbol{x}^{\boldsymbol{'}}, \boldsymbol{x}, e_{0} a)$, and assuming $e_{0} = e_{1} =e_{0} a$, utilizing the linear differentiation operator to Eq. (18) gives

$$ \left [ 1 - ( e_{0} a )^{2} \nabla ^{2} \right ] \sigma = \mathrm{C}: \varepsilon , $$

(19)

$$ \left [ 1 - ( e_{0} a )^{2} \nabla ^{2} \right ] \sigma ^{(1)} = l_{m}^{2} \mathrm{C}: \nabla \varepsilon . $$

(20)

Using Eqs. (18)–(20), the total stress can be obtained as follows:

$$ \left [ 1 - ( e_{0} a )^{2} \nabla ^{2} \right ] \sigma = \mathrm{C}: \varepsilon - l_{m}^{2} \nabla \mathrm{C}: \nabla \varepsilon . $$

(21)

The stress–strain relations of the plate structure are defined by (Li et al. 2016; Lim et al. 2015)

$$ \begin{gathered} \left [ 1 - ( e_{0} a )^{2} \nabla ^{2} \right ] \sigma _{xx} = \left [ 1- l_{m}^{2} \nabla ^{2} \right ] E ( z ) \varepsilon _{xx}\\ \left [ 1 - ( e_{0} a )^{2} \nabla ^{2} \right ] \sigma _{yy} = \left [ 1- l_{m}^{2} \nabla ^{2} \right ] E ( z ) \varepsilon _{yy} \\ \left [ 1 - ( e_{0} a )^{2} \nabla ^{2} \right ] \sigma _{xz} = \left [ 1- l_{m}^{2} \nabla ^{2} \right ] G ( z ) \gamma _{xz} \\ \left [ 1 - ( e_{0} a )^{2} \nabla ^{2} \right ] \sigma _{yz} = \left [ 1- l_{m}^{2} \nabla ^{2} \right ] G ( z ) \gamma _{yz} \end{gathered} $$

(22)

where $\sigma _{xx}$, $\sigma _{yy}$ and $\varepsilon _{xx}$, $\varepsilon _{yy}$, represent the stresses and strains, respectively. Additionally, $\sigma _{xz}$, $\sigma _{yz}$, $\gamma _{xz}$, and $\gamma _{yz}$ represent the shear stresses and strains, respectively. $E$ ($z$) is the Young modulus, while $G$ ($z$) is the shear modulus. As a result, taking into account the MEE characteristics of the NGST nanostructure under thermal effects may be expressed as follows (Eringen 1983a):

$$\begin{aligned} \boldsymbol{\sigma} \left ( x,y,z \right ) \left ( 1- e_{0} a^{2} \nabla ^{2} \right ) & = \left ( 1- l_{m}^{2} \nabla ^{2} \right ) \left [ \overline{\boldsymbol{C}} \left ( z \right ) \boldsymbol{\varepsilon} - \overline{\boldsymbol{e}} \left ( z \right ) \boldsymbol{E}- \overline{\boldsymbol{q}} \left ( z \right ) \boldsymbol{H} \right ] - \overline{\boldsymbol{C}} \left ( z \right ) \alpha \left ( z \right ) \Delta T \\ \boldsymbol{D} \left ( x,y,z \right ) \left ( 1- e_{0} a^{2} \nabla ^{2} \right )& = \left ( 1- l_{m}^{2} \nabla ^{2} \right ) \left [ \overline{\boldsymbol{e}}^{\mathrm{T}} \left ( z \right ) \boldsymbol{\varepsilon} - \overline{\boldsymbol{\varepsilon}} \left ( z \right ) \boldsymbol{E}+ \overline{\mathbf{g}} \left ( z \right ) \boldsymbol{H} \right ] \\ \boldsymbol{B} \left ( x,y,z \right ) \left ( 1- e_{0} a^{2} \nabla ^{2} \right ) & = \left ( 1- l_{m}^{2} \nabla ^{2} \right ) \left [ \overline{\boldsymbol{q}}^{\mathrm{T}} \left ( z \right ) \boldsymbol{\varepsilon} + \overline{\mathbf{g}} \left ( z \right ) \boldsymbol{E}+ \overline{\boldsymbol{\mu}} \left ( z \right ) \boldsymbol{H} \right ], \end{aligned}$$

(23)

where $e$, $q$, $\varepsilon$, $\mathrm{g}$, and $\mu$ represent the piezoelectric, magneto strictive, dielectric, magneto-electric, and magnetic permeability constants, respectively; $E$, $H$, $D$, and $B$ denote the electrical field, magnetic field, electrical displacement, and magnetic induction, respectively. The mechanical, electrical, magnetic, and thermal material properties of CoFe₂O₄ and BaTiO₃ are presented in Table 3.

Table 3 Electromechanical material properties of CoFe₂O₄ and BaTiO₃ (Esen and Özmen 2022b)

2.6 Displacement fields and strains

The sinusoidal high-order shear deformation theory was applied to the five-layer sandwich nanoplate presented in this study under the following assumptions (Żur et al. 2020):

• 1. Because the displacements are small compared to the thickness of the plate, the strains involved are also very small.

• 2. The in-plane displacements $u$ and $v$ comprise extension $u_{0}$, bending $w_{b}$, and shear $w_{s}$ components, respectively.

• 3. The transverse strains ($\varepsilon _{xz}$, $\varepsilon _{yz}$, $\varepsilon _{zz}$) and stresses ($\sigma _{xz}$, $\sigma _{yz}$, $\sigma _{zz}$) are considered as a result of the transverse displacement $w$, which includes components of bending $w_{b}$, shear $w_{s}$, and stretching $w_{st}$.

• 4. Including the shear components ($w$ transverse displacements and $w_{st}$ in $v$, $u$ in-plane) leads to a rise in the trigonometric variation of the shear stresses ($\sigma _{xz}$, $\sigma _{yz}$) and strains ($\varepsilon _{xz}$, $\varepsilon _{yz}$) throughout the thickness of the plate. Consequently, the plate’s top and bottom faces experience no shear stresses ($\sigma _{xz}$, $\sigma _{yz}$).

By using SHSDT, the nanoplate’s displacement field is described as follows (Żur et al. 2020):

$$ u \left ( x,y,z,t \right ) = u_{0} \left ( x,y,t \right ) -z \frac{\partial w_{b} \left ( x,y,t \right )}{\partial x} -f \left ( z \right ) \frac{\partial w_{s} \left ( x,y,t \right )}{\partial x}, $$

(24a)

$$ v \left ( x, y, z, t \right ) = v_{0} \left ( x, y, t \right ) - z \frac{\partial w_{b} \left ( x, y, t \right )}{\partial y} - f \left ( z \right ) \frac{\partial w_{s} \left ( x, y, t \right )}{\partial y}, $$

(24b)

$$ w \left ( x,y,z,t \right ) = w_{b} \left ( x,y,t \right ) + w_{s} \left ( x,y,t \right ) + w_{st} \left ( x,y,z,t \right ), $$

(24c)

where $u$, $v$, and $w$ are the movements of any point in the $x$, $y$, and $z$ axes, respectively. $w_{b}$, $w_{s}$, and $w_{st}$ represent bending, shear, and stretching, respectively. Additionally, $u_{0}$, $v_{0}$, and $w_{b}$ are the displacements of the mid-plane. Here, $f \left ( z \right )$, $w_{st}$, and $g \left ( z \right )$ are defined as (Tahir et al. 2021)

$$ f \left ( z \right ) = z- \frac{2z \sin \left ( \frac{z^{2}}{h^{2}} \right )}{2 \sinh \left ( \frac{1}{4} \right ) + \cosh \left ( \frac{1}{4} \right )}, $$

(25)

$$ w_{st} \left ( x,y,z,t \right ) =g \left ( z \right ) \emptyset \left ( x,y,t \right ), $$

(26)

$$ g \left ( z \right ) = \frac{df \left ( z \right )}{dz}. $$

(27)

The displacement field in Eq. (24a)–(24c) is related to the strain-displacement interactions, which have the following general form (Żur et al. 2020):

$$ \left \{ \textstyle\begin{array}{c} \varepsilon _{xx}\\ \varepsilon _{yy}\\ 2\varepsilon _{xy} \end{array}\displaystyle \right \} = \left \{ \textstyle\begin{array}{c} \varepsilon _{xx}^{(0)}\\ \varepsilon _{yy}^{(o)}\\ \gamma _{xy}^{(0)} \end{array}\displaystyle \right \} + z \left \{ \textstyle\begin{array}{c} \varepsilon _{xx}^{(b)}\\ \varepsilon _{yy}^{(b)}\\ \gamma _{xy}^{(s)} \end{array}\displaystyle \right \} +f(z) \left \{ \textstyle\begin{array}{c} \varepsilon _{xx}^{(s)}\\ \varepsilon _{yy}^{(s)}\\ \gamma _{xy}^{(s)} \end{array}\displaystyle \right \} $$

(28a)

$$ \left \{ \textstyle\begin{array}{c} 2\varepsilon _{xz}\\ 2\varepsilon _{yz} \end{array}\displaystyle \right \} =g(z) \left \{ \textstyle\begin{array}{c} \gamma _{xz}^{(0)}\\ \gamma _{yz}^{(0)} \end{array}\displaystyle \right \} $$

(28b)

$$ \varepsilon _{zz} = g' (z) \varepsilon _{zz}^{(0)}. $$

(28c)

The spatial derivative of $g(z)$ with respect to z is represented here by $g' (z)$. The specific strain elements can be written as follows:

$$ \left \{ \textstyle\begin{array}{c} \varepsilon _{xx}^{(0)}\\ \varepsilon _{yy}^{(0)}\\ \gamma _{xy}^{(0)} \end{array}\displaystyle \right \} = \left \{ \textstyle\begin{array}{c} \displaystyle \frac{\partial u_{0}}{\partial x}\\ \displaystyle \frac{\partial v_{0}}{\partial y}\\ \displaystyle \frac{\partial u_{0}}{\partial y} + \frac{\partial v_{o}}{\partial x} \end{array}\displaystyle \right \},\qquad \left \{ \textstyle\begin{array}{c} \varepsilon _{xx}^{(b)}\\ \varepsilon _{yy}^{(b)}\\ \gamma _{xy}^{(b)} \end{array}\displaystyle \right \} = \left \{ \textstyle\begin{array}{c} \displaystyle {-} \frac{\partial ^{2} w_{b}}{\partial x^{2}}\\ \displaystyle {-} \frac{\partial ^{2} w_{b}}{\partial y^{2}}\\ \displaystyle {-}2 \frac{\partial ^{2} w_{b}}{\partial x\partial y} \end{array}\displaystyle \right \} $$

(29a)

$$\begin{aligned} \begin{gathered} \left \{ \textstyle\begin{array}{c} \varepsilon _{xx}^{(s)}\\ \varepsilon _{yy}^{(s)}\\ \gamma _{xy}^{(s)} \end{array}\displaystyle \right \} = \left \{ \textstyle\begin{array}{c} \displaystyle {-} \frac{\partial ^{2} w_{s}}{\partial x^{2}}\\ \displaystyle {-} \frac{\partial ^{2} w_{s}}{\partial y^{2}}\\ \displaystyle {-}2 \frac{\partial ^{2} w_{s}}{\partial x\partial y} \end{array}\displaystyle \right \}\\ \left \{ \textstyle\begin{array}{c} \gamma _{xz}^{(0)}\\ \gamma _{yz}^{(o)} \end{array}\displaystyle \right \} = \left \{ \textstyle\begin{array}{c} \displaystyle \left ( 1- f' \left ( z \right ) \right ) \frac{\partial w_{s}}{\partial x} +g(z) \frac{\partial \emptyset}{\partial x}\\ \displaystyle \left ( 1- f ' \left ( z \right ) \right ) \frac{\partial w_{s}}{\partial y} +g(z) \frac{\partial \emptyset}{\partial y} \end{array}\displaystyle \right \} = \left \{ \textstyle\begin{array}{c} \displaystyle g(z) \left ( \frac{\partial w_{s}}{\partial x} + \frac{\partial \emptyset}{\partial x} \right )\\ \displaystyle g(z) \left ( \frac{\partial w_{s}}{\partial y} + \frac{\partial \emptyset}{\partial y} \right ) \end{array}\displaystyle \right \}. \end{gathered} \end{aligned}$$

(29b)

2.7 Constitutive equations

In this study, an auxetic core is considered to be sandwiched between orthotropic piezomagnetic face layers and isotropic rim layers. Using the differential form of Eringen’s constitutive relations, we can formulate the following definitions of the auxetic core ($s$) and rim layer ($r$) (Żur et al. 2020):

$$ \left \{ \textstyle\begin{array}{l} \textstyle\begin{array}{c} \mathcal{L} \left ( \sigma _{xx} \right )\\ \mathcal{L} \left ( \sigma _{yy} \right )\\ \mathcal{L} \left ( \sigma _{zz} \right ) \end{array}\displaystyle \\ \mathcal{L} \left ( \sigma _{yz} \right )\\ \mathcal{L} \left ( \sigma _{xz} \right )\\ \mathcal{L} \left ( \sigma _{xy} \right ) \end{array}\displaystyle \right \}^{s,r} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} C_{11} & C_{12} & C_{13} & 0 & 0 & 0\\ C_{12} & C_{22} & C_{23} & 0 & 0 & 0\\ C_{13} & C_{23} & C_{33} & 0 & 0 & 0\\ 0 & 0 & 0 & C_{44} & 0 & 0\\ 0 & 0 & 0 & 0 & C_{55} & 0\\ 0 & 0 & 0 & 0 & 0 & C_{66} \end{array}\displaystyle \right ]^{s,r} \left \{ \textstyle\begin{array}{l} \varepsilon _{xx}\\ \varepsilon _{yy}\\ \varepsilon _{zz}\\ 2\varepsilon _{yz}\\ 2\varepsilon _{xz}\\ 2\varepsilon _{xy} \end{array}\displaystyle \right \}. $$

(30)

Here, $C_{ij}^{n}$ represents the elastic constant and can be calculated as follows:

$$ C_{11}^{s,r} = \frac{1-v}{v} \lambda (z) $$

(31a)

$$ C_{12}^{s,r} =\lambda (z) $$

(31b)

$$ C_{66}^{s,r} =\mu (z) $$

(31c)

$$ C_{11}^{s,r} = C_{22}^{s,r} = C_{33}^{s,r} $$

(31d)

$$ C_{12}^{s,r} = C_{13}^{s,r} = C_{23}^{s,r} $$

(31e)

$$ C_{44}^{s,r} = C_{55}^{s,r} = C_{66}^{s,r}, $$

(31f)

where $\lambda (z)$ and $\mu (z)$ are the Lamé constants $\left ( \lambda \left ( z \right ) = \frac{vE(z)}{(1+v)(1-2v)},\ \mu \left ( z \right ) = \frac{E(z)}{2(1+v)} \ \right )$.

The MEE face layer ($p$) constitutive relations are provided by Pan and Heyliger (2002) using nonlocal and strain-gradient differential operators. $\mathcal{L} \left ( * \right ) \equiv 1- (e_{0} a)^{2} \nabla ^{2}$ and $\Gamma \left ( * \right ) \equiv 1- (l_{m} )^{2} \nabla ^{2}$.

$$\begin{aligned} \begin{aligned} \left \{ \textstyle\begin{array}{c} \mathcal{L}( \sigma _{xx}^{p} )\\ \mathcal{L}( \sigma _{yy}^{p} )\\ \mathcal{L}( \sigma _{zz}^{p} ) \\ \mathcal{L}( \sigma _{yz}^{p} )\\ \mathcal{L}( \sigma _{xz}^{p} )\\ \mathcal{L} ( \sigma _{xy}^{p} ) \end{array}\displaystyle \right \} ={}& \Gamma \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} C_{11}^{p} & C_{12}^{p} & C_{13}^{p} & 0 & 0 & 0\\ C_{12}^{p} & C_{22}^{p} & C_{23}^{p} & 0 & 0 & 0\\ C_{13}^{p} & C_{23}^{p} & C_{33}^{p} & 0 & 0 & 0\\ 0 & 0 & 0 & C_{44}^{p} & 0 & 0\\ 0 & 0 & 0 & 0 & C_{55}^{p} & 0\\ 0 & 0 & 0 & 0 & 0 & C_{66}^{p} \end{array}\displaystyle \right ] \left \{ \textstyle\begin{array}{l} \varepsilon _{xx}\\ \varepsilon _{yy}\\ \varepsilon _{zz}\\ 2\varepsilon _{yz}\\ 2\varepsilon _{xz}\\ 2\varepsilon _{xy} \end{array}\displaystyle \right \} \\ &{}- \Gamma \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} 0&0& e_{31}\\ 0&0& e_{32}\\ 0&0& e_{33}\\ 0&e_{24}& 0\\ e_{15}&0& 0\\ 0 & 0 & 0 \end{array}\displaystyle \right ] \left \{ \textstyle\begin{array}{c} E_{x}\\ E_{y}\\ E_{z} \end{array}\displaystyle \right \} - \Gamma \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} 0& 0& q_{31}\\ 0& 0& q_{32}\\ 0& 0& q_{33}\\ 0& q_{24}& 0\\ q_{15}& 0& 0\\ 0 0 & 0 \end{array}\displaystyle \right ] \left \{ \textstyle\begin{array}{c} H_{x}\\ H_{y}\\ H_{z} \end{array}\displaystyle \right \} \end{aligned} \end{aligned}$$

(32a)

$$\begin{aligned} \begin{aligned} \left \{ \textstyle\begin{array}{c} \mathcal{L}( D_{x} )\\ \mathcal{L}( D_{y} )\\ \mathcal{L}( D_{z} ) \end{array}\displaystyle \right \} ={}& \Gamma \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} 0 & 0 & 0 & 0 & e_{15} & 0\\ 0 & 0 & 0 & e_{24} & 0 & 0\\ e_{31} & e_{32} & e_{33} & 0 & 0 & 0 \end{array}\displaystyle \right ] \left \{ \textstyle\begin{array}{c} \varepsilon _{xx}\\ \varepsilon _{yy}\\ \varepsilon _{zz}\\ 2\varepsilon _{yz}\\ 2\varepsilon _{xz}\\ 2\varepsilon _{xy} \end{array}\displaystyle \right \} \\ &{}+ \Gamma \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \varepsilon _{11} & 0 & 0\\ 0 & \varepsilon _{22} & 0\\ 0 & 0 & \varepsilon _{33} \end{array}\displaystyle \right ] \left \{ \textstyle\begin{array}{c} E_{x}\\ E_{y}\\ E_{z} \end{array}\displaystyle \right \}+ \Gamma \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \mathrm{g}_{11} & 0 & 0\\ 0 & \mathrm{g}_{22} & 0\\ 0 & 0 & \mathrm{g}_{33} \end{array}\displaystyle \right ] \left \{ \textstyle\begin{array}{c} H_{x}\\ H_{y}\\ H_{z} \end{array}\displaystyle \right \} \end{aligned} \end{aligned}$$

(32b)

$$\begin{aligned} \begin{aligned} \left \{ \textstyle\begin{array}{c} \mathcal{L}( B_{x} )\\ \mathcal{L}( B_{y} )\\ \mathcal{L}( B_{z} ) \end{array}\displaystyle \right \} = {}&\Gamma \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} 0 & 0 & 0 & 0 & q_{15} & 0\\ 0 & 0 & 0 & q_{24} & 0 & 0\\ q_{31} & q_{32} & q_{33} & 0 & 0 & 0 \end{array}\displaystyle \right ] \left \{ \textstyle\begin{array}{c} \varepsilon _{xx}\\ \varepsilon _{yy}\\ \varepsilon _{zz}\\ 2\varepsilon _{yz}\\ 2\varepsilon _{xz}\\ 2\varepsilon _{xy} \end{array}\displaystyle \right \} \\ &{} + \Gamma \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \varepsilon _{11} & 0 & 0\\ 0 & \varepsilon _{22} & 0\\ 0 & 0 & \varepsilon _{33} \end{array}\displaystyle \right ] \left \{ \textstyle\begin{array}{c} E_{x}\\ E_{y}\\ E_{z} \end{array}\displaystyle \right \}+ \Gamma \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \mu _{11} & 0 & 0\\ 0 & \mu _{22} & 0\\ 0 & 0 & \mu _{33} \end{array}\displaystyle \right ] \left \{ \textstyle\begin{array}{c} H_{x}\\ H_{y}\\ H_{z} \end{array}\displaystyle \right \}. \end{aligned} \end{aligned}$$

(32c)

The elements of electric $E_{i}$ and magnetic loads $H_{i}$ are defined with three-dimensional electric $\breve{\varphi}$ and magnetic potentials $\breve{\psi}$ as follows (Żur et al. 2020):

$$ E_{i} = \left \{ - \breve{\varphi}_{i} \right \}, H_{i} = \left \{ - \breve{\psi}_{,i} \right \},\quad i=x,y,z. $$

(33)

The electric and magnetic potentials in three dimensions satisfying Maxwell’s equations are defined with a cosine function, as given below (Arefi and Zenkour 2018, 2016):

$$ \left \{ \textstyle\begin{array}{c} \breve{\varphi} (x,y,z,t)\\ \breve{\psi} (x,y,z,t) \end{array}\displaystyle \right \} = \left \{ \textstyle\begin{array}{c} \varphi _{0}\\ \psi _{0} \end{array}\displaystyle \right \} \frac{2 \hat{z}}{H_{t}} - \left \{ \textstyle\begin{array}{c} \varphi \left ( x,y,t \right )\\ \psi \left ( x,y,t \right ) \end{array}\displaystyle \right \} cos \left ( \frac{\pi \hat{z}}{H_{t}} \right ), $$

(34)

where $\varphi _{0}$ and $\psi _{0}$ represent the initial conditions for electric and magnetic charges, respectively; $\varphi (x,y,t)$ and $\psi (x,y,t)$ are the time-dependent electric and magnetic potential distributions, respectively; $\hat{z}$ variable is defined for the upper and lower MEE face layers. $\hat{z}$ is denoted as $\hat{z} =z+ h_{s} /2+ h_{r} + h_{p} /2$ for the upper face layer and $\hat{z} =z- h_{s} /2- h_{r} - h_{p} /2$ for the lower face layer.

2.8 Equations of motion

To get the differential equations of the MEE nanoplate, the virtual displacement approach (Reddy 2020), a variant of the Hamilton method, is applied:

$$ \int _{0}^{T} \left ( \delta \mathcal{U}- \delta \mathcal{E}- \delta \mathcal{M}- \delta \mathcal{K}+ \delta \mathcal{V} \right ) dt=0. $$

(35)

Here, $\delta \mathcal{U}$, $\delta \mathcal{K}$, and $\delta \mathcal{V}$ represent the virtual strain energy, kinetic energy, and virtual work obtained by applied external forces, respectively. Also, $\delta \mathcal{E}$ and $\delta \mathcal{M}$ define the electric and magnetic energy, respectively. The strain energy, denoted by $\delta \mathcal{U}$, is obtained by

$$\begin{aligned} \begin{aligned} \delta \mathcal{U}={}& \int _{\Omega} \left [ \int _{h_{1}}^{h_{2}} \left ( \sigma _{xx}^{lp} \delta \varepsilon _{xx} + \sigma _{yy}^{lp} \delta \varepsilon _{yy} + \sigma _{zz}^{lp} \delta \varepsilon _{zz} + 2\sigma _{yz}^{lp} \delta \varepsilon _{yz} + 2\sigma _{xz}^{lp} \delta \varepsilon _{xz} + 2\sigma _{xy}^{lp} \delta \varepsilon _{xy} \right ) dz \right .\\ &{}+ \int _{h_{2}}^{h_{3}} \left ( \sigma _{xx}^{lr} \delta \varepsilon _{xx} + \sigma _{yy}^{lr} \delta \varepsilon _{yy} + \sigma _{zz}^{lr} \delta \varepsilon _{zz} + 2\sigma _{yz}^{lr} \delta \varepsilon _{yz} + 2\sigma _{xz}^{lr} \delta \varepsilon _{xz} + 2\sigma _{xy}^{lr} \delta \varepsilon _{xy} \right ) dz\\ &{} + \int _{h_{3}}^{h_{4}} \left ( \sigma _{xx}^{s} \delta \varepsilon _{xx} + \sigma _{yy}^{s} \delta \varepsilon _{yy} + \sigma _{zz}^{s} \delta \varepsilon _{zz} + 2\sigma _{yz}^{s} \delta \varepsilon _{yz} + 2\sigma _{xz}^{s} \delta \varepsilon _{xz} + 2\sigma _{xy}^{s} \delta \varepsilon _{xy} \right ) dz \\ &{}+ \int _{h_{4}}^{h_{5}} \left ( \sigma _{xx}^{ur} \delta \varepsilon _{xx} + \sigma _{yy}^{ur} \delta \varepsilon _{yy} + \sigma _{zz}^{ur} \delta \varepsilon _{zz} + 2\sigma _{yz}^{ur} \delta \varepsilon _{yz} + 2\sigma _{xz}^{ur} \delta \varepsilon _{xz} + 2\sigma _{xy}^{ur} \delta \varepsilon _{xy} \right ) dz\\ &{} + \int _{h_{5}}^{h_{6}} \left ( \left ( \sigma _{xx}^{up} \delta \varepsilon _{xx} + \sigma _{yy}^{up} \delta \varepsilon _{yy} + \sigma _{zz}^{up} \delta \varepsilon _{zz} + 2\sigma _{yz}^{up} \delta \varepsilon _{yz}\right .\right .\\ & \left .\left .\left .{} + 2\sigma _{xz}^{up} \delta \varepsilon _{xz} + 2\sigma _{xy}^{up} \delta \varepsilon _{xy} \right ) dz \right ) \right ] dxdy. \end{aligned} \end{aligned}$$

(36)

The electric $\delta \mathcal{E}$ and magnetic $\delta \mathcal{M}$ energy contributions can be defined by

$$ \begin{aligned} \delta \mathcal{E}= {}&\int _{\Omega} \left [ \int _{h_{1}}^{h_{2}} \left ( D_{x} \delta E_{x} + D_{y} \delta E_{y+} D_{z} \delta E_{z} \right ) dz\right.\\ &\left.{}+ \int _{h_{5}}^{h_{6}} \left ( D_{x} \delta E_{x} + D_{y} \delta E_{y+} D_{z} \delta E_{z} \right ) dz \right ] dxdy, \end{aligned} $$

(37)

$$ \begin{aligned} \delta \mathcal{M}={}& \int _{\Omega} \left [ \int _{h_{1}}^{h_{2}} \left ( B_{x} \delta H_{x} + B_{y} \delta H_{y+} B_{z} \delta H_{z} \right ) dz\right.\\ &\left. {}+ \int _{h_{5}}^{h_{6}} \left ( B_{x} \delta H_{x} + B_{y} \delta H_{y+} B_{z} \delta H_{z} \right ) dz \right ] dxdy. \end{aligned} $$

(38)

Additionally, the kinetic energy is given by

$$ \begin{aligned} \delta \mathcal{K}= {}&\int _{\Omega} \left [ \int _{h_{1}}^{h_{2}} \rho ^{lp} \left ( \dot{u} \delta \dot{u} + \dot{v} \delta \dot{v} + \dot{w} \delta \dot{w} \right ) dz+ \int _{h_{2}}^{h_{3}} \rho ^{lr} \left ( z \right ) \left ( \dot{u} \delta \dot{u} + \dot{v} \delta \dot{v} + \dot{w} \delta \dot{w} \right ) dz \right.\\ &{}+ \int _{h_{3}}^{h_{4}} \rho ^{s} \left ( z \right ) \left ( \dot{u} \delta \dot{u} + \dot{v} \delta \dot{v} + \dot{w} \delta \dot{w} \right ) dz + \int _{h_{4}}^{h_{5}} \rho ^{ur} \left ( z \right ) \left ( \dot{u} \delta \dot{u} + \dot{v} \delta \dot{v} + \dot{w} \delta \dot{w} \right ) dz\\ &\left.{} + \int _{h_{5}}^{h_{6}} \rho ^{up} \left ( \dot{u} \delta \dot{u} + \dot{v} \delta \dot{v} + \dot{w} \delta \dot{w} \right ) \right ] dxdy, \end{aligned} $$

(39)

where $\rho ^{p} (z)$, $\rho ^{s} \left ( z \right )$, and $\rho ^{r} (z)$ are the densities of the piezomagnetic face layers, auxetic core layer, and rim layers, respectively. The virtual work can be calculated by

$$ \begin{aligned} \delta \mathcal{V}={}&{-} \int _{\Omega} \left [ \left ( N_{xx0} + N_{xx \mathcal{E}} + N_{xx \mathcal{M}} \right ) \frac{\partial w_{b}}{\partial x} \frac{\partial \delta w_{b}}{\partial x} \right. \\ &\left.{}+ \left ( N_{yy0+} N_{yy \mathcal{E}} + N_{xx \mathcal{M}} \right ) \frac{\partial w_{b}}{\partial y} \frac{\partial \delta w_{b}}{\partial y} + \right ] dxdy, \end{aligned} $$

(40)

where, the 0, ℰ, and ℳ subscripts define the compressive mechanical, electrical, and magnetic forces, respectively. The following equation represents the thickness-integrated resultant forces and moments:

$$ \begin{aligned} &\left \{ \textstyle\begin{array}{c@{\quad}c@{\quad}c} N_{xx} & N_{yy} & N_{xy}\\ M_{xx}^{\left ( b \right )} & M_{yy}^{\left ( b \right )} & M_{xy}^{\left ( b \right )}\\ M_{xx}^{\left ( s \right )} & M_{yy}^{\left ( s \right )} & M_{xy}^{\left ( s \right )} \end{array}\displaystyle \right \}\\ &\quad = \int _{h_{1}}^{h_{2}} \left ( \sigma _{xx}^{lp}, \sigma _{yy}^{lp}, \sigma _{xy}^{lp} \right ) \left \{ \textstyle\begin{array}{c} 1\\ z\\ f \left ( z \right ) \end{array}\displaystyle \right \} dz + \int _{h_{2}}^{h_{3}} \left ( \sigma _{xx}^{lr}, \sigma _{yy}^{lr}, \sigma _{xy}^{lr} \right ) \left \{ \textstyle\begin{array}{c} 1\\ z\\ f \left ( z \right ) \end{array}\displaystyle \right \} dz \\ &\qquad {}+ \int _{h_{3}}^{h_{4}} \left ( \sigma _{xx}^{s}, \sigma _{yy}^{s}, \sigma _{xy}^{s} \right ) \left \{ \textstyle\begin{array}{c} 1\\ z\\ f \left ( z \right ) \end{array}\displaystyle \right \} dz + \int _{h_{4}}^{h_{5}} \left ( \sigma _{xx}^{ur}, \sigma _{yy}^{ur}, \sigma _{xy}^{ur} \right ) \left \{ \textstyle\begin{array}{c} 1\\ z\\ f \left ( z \right ) \end{array}\displaystyle \right \} dz \\ &\qquad {}+ \int _{h_{5}}^{h_{6}} \left ( \sigma _{xx}^{up}, \sigma _{yy}^{up}, \sigma _{xy}^{up} \right ) \left \{ \textstyle\begin{array}{c} 1\\ z\\ f \left ( z \right ) \end{array}\displaystyle \right \} dz, \end{aligned} $$

(41a)

$$ \begin{aligned} N_{zz} ={}& \int _{h_{1}}^{h_{2}} \sigma _{zz}^{lp} g' (z) dz+ \int _{h_{2}}^{h_{3}} \sigma _{zz}^{lr} g' (z) dz+ \int _{h_{3}}^{h_{4}} \sigma _{zz}^{s} g' (z) dz\\ &{}+ \int _{h_{4}}^{h_{5}} \sigma _{zz}^{ur} g' (z) dz+ \int _{h_{5}}^{h_{6}} \sigma _{zz}^{up} g' \left ( z \right ) dz, \end{aligned} $$

(41b)

$$ \begin{aligned} \left \{ S_{xz}, S_{yz} \right \} ={}& \int _{h_{1}}^{h_{2}} \left \{ \sigma _{xz}^{lp}, \sigma _{yz}^{lp} \right \} \mathrm{g} \left ( z \right ) dz+ \int _{h_{2}}^{h_{3}} \left \{ \sigma _{xz}^{lr}, \sigma _{yz}^{lr} \right \} \mathrm{g} \left ( z \right ) dz\\ &{}+ \int _{h_{3}}^{h_{4}} \left \{ \sigma _{xz}^{s}, \sigma _{yz}^{s} \right \} \mathrm{g} \left ( z \right ) dz+ \int _{h_{4}}^{h_{5}} \left \{ \sigma _{xz}^{ur}, \sigma _{yz}^{ur} \right \} \mathrm{g} \left ( z \right ) dz\\ &{}+ \int _{h_{5}}^{h_{6}} \left \{ \sigma _{xz}^{up}, \sigma _{yz}^{up} \right \} \mathrm{g} \left ( z \right ) dz. \end{aligned} $$

(41c)

Additionally, the strain energy can be rearranged as follows:

$$ \begin{aligned} \delta \mathcal{U}= {}&\int _{\Omega} \left ( N_{xx} \delta \varepsilon _{xx}^{(0)} + N_{yy} \delta \varepsilon _{yy}^{(0)} + N_{zz} \delta \varepsilon _{zz}^{(0)} + N_{xy} \delta \varepsilon _{xy}^{(0)} + N_{xz} \delta \varepsilon _{xz}^{(0)}\right. \\ & {} + N_{yz} \delta \varepsilon _{yz}^{(0)}+ M_{xx} \delta \varepsilon _{xx}^{(b)}+ M_{yy} \delta \varepsilon _{yy}^{(b)} + M_{xy} \delta \varepsilon _{xy}^{(b)} + M_{xx} \delta \varepsilon _{xx}^{(b)}\\ &\left.{} + M_{yy} \delta \varepsilon _{yy}^{(b)} + M_{xy} \delta \varepsilon _{xy}^{(b)} \right ) dxdy. \end{aligned} $$

(42)

The thickness-related electric and magnetic constants are defined as follows:

$$ \begin{aligned} \left \{ \overline{D}_{x}, \overline{D}_{y}, \overline{D}_{z} \right \} ={}& \int _{h_{1}}^{h_{2}} \left ( D_{x}, D_{y}, D_{z} \right ) \left \{ \textstyle\begin{array}{c} cos \left ( \frac{\pi z_{2}}{h_{lp}} \right )\\ cos \left ( \frac{\pi z_{2}}{h_{lp}} \right )\\ \frac{\pi}{h_{lp}} sin \left ( \frac{\pi z_{2}}{h_{lp}} \right ) \end{array}\displaystyle \right \} dz\\ &{}+ \int _{h_{5}}^{h_{6}} \left ( D_{x}, D_{y}, D_{z} \right ) \left \{ \textstyle\begin{array}{c} cos \left ( \frac{\pi z_{1}}{h_{up}} \right )\\ cos \left ( \frac{\pi z_{1}}{h_{up}} \right )\\ \frac{\pi}{h_{up}} sin \left ( \frac{\pi z_{1}}{h_{up}} \right ) \end{array}\displaystyle \right \} dz, \end{aligned} $$

(43a)

$$ \begin{aligned} \left \{ \overline{B}_{x}, \overline{B}_{y}, \overline{B}_{z} \right \} ={}& \int _{h_{1}}^{h_{2}} \left ( B_{x}, B_{y}, B_{z} \right ) \left \{ \textstyle\begin{array}{c} cos \left ( \frac{\pi z_{2}}{h_{lp}} \right )\\ cos \left ( \frac{\pi z_{2}}{h_{lp}} \right )\\ \frac{\pi}{h_{lp}} sin \left ( \frac{\pi z_{2}}{h_{lp}} \right ) \end{array}\displaystyle \right \} dz\\ &{}+ \int _{h_{5}}^{h_{6}} \left ( B_{x}, B_{y}, B_{z} \right ) \left \{ \textstyle\begin{array}{c} cos \left ( \frac{\pi z_{1}}{h_{up}} \right )\\ cos \left ( \frac{\pi z_{1}}{h_{up}} \right )\\ \frac{\pi}{h_{up}} sin \left ( \frac{\pi z_{1}}{h_{up}} \right ) \end{array}\displaystyle \right \} dz. \end{aligned} $$

(43b)

The virtual form of electric and magnetic loads may be rearranged as follows:

$$ \delta \mathcal{E}= \int _{\Omega} \left ( \overline{D}_{x} \frac{\partial \delta \varphi}{\partial x} + \overline{D}_{y} \frac{\partial \delta \varphi}{\partial y} - \overline{D}_{z} \delta \varphi \right ) dxdy, $$

(44)

$$ \delta \mathcal{M}= \int _{\Omega} \left ( \overline{B}_{x} \frac{\partial \delta \psi}{\partial x} + \overline{B}_{y} \frac{\partial \delta \psi}{\partial y} - \overline{B}_{z} \delta \psi \right ) dxdy. $$

(45)

The virtual kinetic energy mass inertia can be defined as

$$\begin{aligned} \delta \mathcal{K}={}& \int _{\Omega} \left [ m_{0} \left ( \dot{u}_{0} \delta \dot{u}_{0} + \dot{v}_{0} \delta \dot{v}_{0} + \dot{w}_{b} \delta \dot{w}_{b} + \dot{w}_{b} \delta \dot{w}_{s} + \dot{w}_{s} \delta \dot{w}_{0} + \dot{w}_{s} \delta \dot{w}_{s} \right )\right. \\ & {}- m_{1} \left ( \dot{u}_{0} \frac{\partial \delta \dot{w}_{b}}{dx} + \frac{\partial \dot{w}_{b}}{dx} \delta \dot{u}_{0} + \dot{v}_{0} \frac{\partial \delta \dot{w}_{b}}{dy} + \frac{\partial \dot{w}_{b}}{dy} \delta \dot{v}_{0} \right ) \\ & {}- m_{2} \left ( \frac{\partial \dot{w}_{b}}{dx} \frac{\partial \dot{\delta w}_{b}}{dx} + \frac{\partial \dot{w}_{b}}{dy} \frac{\partial \dot{\delta w}_{b}}{dy} \right ) \\ & {}- m_{3} \left ( \dot{u}_{0} \frac{\partial \delta \dot{w}_{b}}{dx} + \frac{\partial \dot{w}_{b}}{dx} \delta \dot{u}_{0} + \dot{v}_{0} \frac{\partial \delta \dot{w}_{b}}{dy} + \frac{\partial \dot{w}_{b}}{dy} \delta \dot{v}_{0} \right ) \\ & {} + m_{4} \left ( \frac{\partial \dot{w}_{b}}{dx} \frac{\partial \dot{\delta w}_{b}}{dx} + \frac{\partial \dot{w}_{b}}{dx} \frac{\partial \dot{\delta w}_{b}}{dx} + \frac{\partial \dot{w}_{b}}{dy} \frac{\partial \dot{\delta w}_{b}}{dy} + \frac{\partial \dot{w}_{b}}{dy} \frac{\partial \dot{\delta w}_{b}}{dy} \right ) \\ & {}+ m_{5} \left ( \frac{\partial \dot{w}_{s}}{dx} \frac{\partial \dot{\delta w}_{s}}{dx} + \frac{\partial \dot{w}_{s}}{dy} \frac{\partial \dot{\delta w}_{s}}{dy} \right ) + m_{6} \left ( \dot{w}_{b} \delta \dot{\phi} + \dot{w}_{s} \delta \dot{\phi} + \dot{\phi} \delta \dot{w}_{b} + \dot{\phi} \delta \dot{w}_{s} \right ) \\ &\left.{} + m_{7} \dot{\phi} \delta \dot{\phi} \right ] dxdy, \end{aligned}$$

(46)

in which

$$ \begin{aligned} m_{i} = {}&\int _{h_{1}}^{h_{2}} \rho ^{lp} z^{i} dz+ \int _{h_{2}}^{h_{3}} p^{lr} \left ( z \right ) z^{i} dz + \int _{h_{3}}^{h_{4}} p^{s} \left ( z \right ) z^{i} dz\\ &{}+ \int _{h_{4}}^{h_{5}} p^{ur} \left ( z \right ) z^{i} dz + \int _{h_{5}}^{h_{6}} \rho ^{up} z^{i} dz, \end{aligned} $$

(47a)

$$ \begin{aligned} m_{i+3} = {}&\int _{h_{1}}^{h_{2}} \rho ^{lp} f(z) z^{i} dz+ \int _{h_{2}}^{h_{3}} p^{lr} \left ( z \right ) f(z)z^{i} dz \\ &{}+ \int _{h_{3}}^{h_{4}} p^{s} \left ( z \right ) f(z)z^{i} dz+ \int _{h_{4}}^{h_{5}} p^{ur} \left ( z \right ) f(z)z^{i} dz + \int _{h_{5}}^{h_{6}} \rho ^{up} f(z)z^{i} dz, \end{aligned} $$

(47b)

$$ \begin{aligned} m_{6} ={}& \int _{h_{1}}^{h_{2}} \rho ^{lp} \mathrm{g} \left ( z \right ) dz+ \int _{h_{2}}^{h_{3}} p^{lr} \left ( z \right ) \mathrm{g} \left ( z \right ) dz \\ &{}+ \int _{h_{3}}^{h_{4}} p^{s} \left ( z \right ) \mathrm{g} \left ( z \right ) dz+ \int _{h_{4}}^{h_{5}} p^{ur} \left ( z \right ) \mathrm{g} \left ( z \right ) dz + \int _{h_{5}}^{h_{6}} \rho ^{up} \mathrm{g} \left ( z \right ) dz, \end{aligned} $$

(47c)

$$ \begin{aligned} m_{7} ={}& \int _{h_{1}}^{h_{2}} \rho ^{lp} \mathrm{g}^{2} \left ( z \right ) dz+ \int _{h_{2}}^{h_{3}} p^{lr} \left ( z \right ) \mathrm{g}^{2} \left ( z \right ) dz \\ &{}+ \int _{h_{3}}^{h_{4}} p^{s} \left ( z \right ) \mathrm{g}^{2} \left ( z \right ) dz+ \int _{h_{4}}^{h_{5}} p^{ur} \left ( z \right ) \mathrm{g}^{2} \left ( z \right ) dz+ + \int _{h_{5}}^{h_{6}} \rho ^{up} \mathrm{g}^{2} \left ( z \right ) dz, \end{aligned} $$

(47d)

where $i=0, 1, 2$. In its final form, the virtual information resulting from applied external forces is presented by

$$ \delta \mathcal{V}= \int _{\Omega} \left [ \left ( p_{x0} + p_{e31} + p_{q31} \right ) \frac{\partial w_{b}}{\partial x} \frac{\partial \delta w_{b}}{\partial x} + \left ( p_{y0} \right ) + p_{e32} + p_{q32} ) \frac{\partial w_{b}}{\partial x} \frac{\partial \delta w_{b}}{\partial x} \right ] dxdy. $$

(48)

The mechanical compression forces are assumed to be equal to $p_{x0} = N_{0}$ and $p_{y0} \ =\ \gamma N_{0}$. The electric force $p_{e3i}$ and the magnetic force $p_{q3i}$ are expressed as

$$ p_{e3i} =- \left [ \int _{h_{1}}^{h_{2}} e_{3i} \left ( \frac{2 V_{0}}{h_{lp}} \right ) dz+ \int _{h_{2}}^{h_{3}} e_{3i} \left ( z \right ) \left ( \frac{2 V_{0}}{h_{s}} \right ) dz + \int _{h_{3}}^{h_{4}} e_{3i} \frac{2 V_{0}}{h_{up}} dz \right ], $$

(49a)

$$ p_{q3i} =- \left [ \int _{h_{1}}^{h_{2}} q_{3i} \left ( \frac{2 H_{0}}{h_{lp}} \right ) dz+ \int _{h_{2}}^{h_{3}} q_{3i} \left ( z \right ) \left ( \frac{2 H_{0}}{h_{s}} \right ) dz + \int _{h_{3}}^{h_{4}} q_{3i} \left ( \frac{2 H_{0}}{h_{up}} \right ) dz \right ], $$

(49b)

where $i=1,\ 2$. Due to the temperature rise, the thermomechanical loads $N_{x}^{T}$ and $N_{y}^{T}$ in the $x$-$y$ directions are given by

$$ \begin{aligned} N_{x}^{T} ={}&b \left [ \int _{h_{1}}^{h_{2}} C_{11}^{p} \alpha _{lp} \Delta Tdz + \int _{h_{2}}^{h_{3}} C_{11}^{lr} \alpha _{lr} \Delta Tdz + \int _{h_{3}}^{h_{4}} C_{11}^{s} \alpha _{s} \Delta Tdz \right.\\ &\left.{}+ \int _{h_{4}}^{h_{5}} C_{11}^{ur} \alpha _{ur} \Delta Tdz + \int _{h_{5}}^{h_{6}} C_{11}^{p} \alpha _{up} \Delta Tdz \right ], \end{aligned} $$

(50a)

$$ \begin{aligned} N_{y}^{T} ={}&a \left [ \int _{h_{1}}^{h_{2}} C_{11}^{p} \alpha _{lp} \Delta Tdz + \int _{h_{2}}^{h_{3}} C_{11}^{lr} \alpha _{lr} \Delta Tdz + \int _{h_{3}}^{h_{4}} C_{11}^{s} \alpha _{s} \Delta Tdz \right.\\ &\left.{}+ \int _{h_{4}}^{h_{5}} C_{11}^{ur} \alpha _{ur} \Delta Tdz + \int _{h_{5}}^{h_{6}} C_{11}^{p} \alpha _{up} \Delta Tdz \right ]. \end{aligned} $$

(50b)

Differential equations representing the motion of the sandwich nanoplate can be obtained by substituting the virtual energy contributions $\delta \mathcal{U}$, $\delta \mathcal{E}$, $\delta \mathcal{M}$, $\delta \mathcal{K}$, and $\delta \mathcal{V}$ from Eqs. (42), (44–46), and (48) into Eq. (35).

$$ \delta u_{0}: \frac{\partial N_{xx}}{\partial x} + \frac{\partial N_{xy}}{\partial x} = m_{0} \ddot{u}_{0} - m_{1} \frac{\partial \ddot{w}_{b}}{\partial x} - m_{1} \frac{\partial \ddot{w}_{s}}{\partial x} $$

(51a)

$$ \delta v_{0}: \frac{\partial N_{yy}}{\partial y} + \frac{\partial N_{xy}}{\partial x} = m_{0} \ddot{v}_{0} - m_{1} \frac{\partial \ddot{w}_{b}}{\partial y} - m_{3} \frac{\partial \ddot{w}_{s}}{\partial y} $$

(51b)

$$ \begin{aligned} &\delta w_{b}: \frac{\partial ^{2} M_{xx}^{(b)}}{\partial x^{2}} +2 \frac{\partial ^{2} M_{xy}^{(b)}}{dxdy} + \frac{\partial ^{2} M_{yy}^{(b)}}{d y^{2}}- \left ( N_{x}^{T} + p_{x0} + p_{e31} + p_{q31} \right ) \frac{\partial ^{2} w_{b}}{\partial x^{2}}\\ &\qquad {} - \left ( N_{y}^{T} + p_{x0} + p_{e31} + p_{q31} \right ) \frac{\partial ^{2} w_{b}}{\partial y^{2}} \\ &\quad = m_{0} \left ( \ddot{w}_{b} + \ddot{w}_{s} \right ) + m_{1} \left ( \frac{\partial \ddot{u}_{0}}{\partial x} + \frac{\partial \ddot{v}_{0}}{\partial y} \right ) - m_{2} \left ( \frac{\partial \ddot{w}_{b}}{\partial x^{2}} + \frac{\partial \ddot{w}_{b}}{\partial y^{2}} \right )\\ &\qquad {} - m_{4} \left ( \frac{\partial ^{2} \ddot{w}_{s}}{d x^{2}} + \frac{\partial ^{2} \ddot{w}_{s}}{d y^{2}} \right ) + m_{6} \ddot{\phi} \end{aligned} $$

(51c)

$$ \begin{aligned} &\delta w_{s}: \frac{\partial ^{2} M_{xx}^{(s)}}{\partial x^{2}} +2 \frac{\partial ^{2} M_{xy}^{(s)}}{dxdy} + \frac{\partial ^{2} M_{yy}^{(s)}}{d y^{2}} + \frac{\partial S_{xz}}{\partial x} + \frac{\partial S_{yz}}{\partial y} \\ &\quad = m_{0} \left ( \ddot{w}_{b} + \ddot{w}_{s} \right ) + m_{3} \left ( \frac{\partial \ddot{u}_{0}}{\partial x} + \frac{\partial \ddot{v}_{0}}{\partial y} \right ) - m_{4} \left ( \frac{\partial ^{2} \ddot{w}_{b}}{d x^{2}} + \frac{\partial ^{2} \ddot{w}_{b}}{d y^{2}} \right )\\ &\qquad {} - m_{5} \left ( \frac{\partial ^{2} \ddot{w}_{s}}{d x^{2}} + \frac{\partial ^{2} \ddot{w}_{s}}{d y^{2}} \right ) + m_{6} \ddot{\phi} \end{aligned} $$

(51d)

$$ \delta \phi : \frac{\partial S_{xz}}{\partial x} + \frac{\partial S_{yz}}{\partial y} - N_{zz} = m_{6} \left ( \ddot{w}_{b} + \ddot{w}_{s} \right ) + m_{7} \ddot{\phi} $$

(51e)

$$ \delta \varphi : \frac{\partial \overline{D}_{x}}{\partial x} + \frac{\partial \overline{D}_{YZ}}{\partial y} + \overline{D}_{z} =0 $$

(51f)

$$ \delta \psi : \frac{\partial \overline{B}_{x}}{\partial x} + \frac{\partial \overline{B}_{yz}}{\partial y} + \overline{B}_{z} =0. $$

(51g)

The boundary conditions of the sandwich nanoplate are given as

$$ \delta u_{0}:0= N_{xx} n_{x} + N_{xy} n_{y} - m_{1} \ddot{w}_{b} n_{x} - m_{3} \ddot{w}_{s} n_{x} $$

(52a)

$$ \delta v_{0}:0= N_{yy} n_{y} + N_{xy} n_{x} - m_{1} \ddot{w}_{b} n_{y} - m_{3} \ddot{w}_{s} n_{y} $$

(52b)

$$ \begin{aligned} \delta w_{b}:0= {}&\left [ \frac{\partial M_{xx}^{(b)}}{\partial x} + \frac{\partial M_{xy}^{(b)}}{\partial y} - \left ( N_{x}^{T} + p_{x0} + p_{e31} + p_{q31} \right ) \frac{\partial w_{b}}{\partial x} \right ] n_{x}\\ &{}+ \left [ \frac{\partial M_{yy}^{(b)}}{\partial y} + \frac{\partial M_{xy}^{(b)}}{\partial x} \frac{\partial M_{xy}^{(b)}}{\partial y} - \left ( N_{y}^{T} + p_{y0} + p_{e32} + p_{q32} \right ) \frac{\partial w_{b}}{\partial y} \right ] n_{y} \\ &{}+ \left ( m_{1} \ddot{u}_{0} - m_{2} \frac{\partial \ddot{w}_{b}}{\partial x} - m_{4} \frac{\partial \ddot{w}_{s}}{\partial x} \right ) n_{x} + \left ( m_{1} \ddot{v}_{0} - m_{2} \frac{\partial \ddot{w}_{b}}{\partial y} - m_{4} \frac{\partial \ddot{w}_{s}}{\partial y} \right ) n_{y} \end{aligned} $$

(52c)

$$ \delta \frac{\partial w_{b}}{\partial n}:0= M_{nn}^{(b)} $$

(52d)

$$ \delta \frac{\partial w_{s}}{\partial n}:0= M_{nn}^{(s)} $$

(52e)

$$ \delta \phi :0= S_{xz} n_{x} + S_{yz} n_{y} $$

(52f)

$$ \delta \varphi :0= \overline{D}_{x} n_{x} + \overline{D}_{y} n_{y}, $$

(52g)

where

$$ M_{nn}^{(b)} = M_{xx}^{(b)} n_{x}^{2} + 2M_{xy}^{(b)} n_{x} n_{y} + M_{yy}^{(b)} n_{y}^{2}, M_{nn}^{(s)} = M_{xx}^{(s)} n_{x}^{2} + 2M_{xy}^{(s)} n_{x} n_{y} + M_{yy}^{(s)} n_{x}^{2}. $$

(53)

The equilibrium equations for the displacements and MEE coefficients of a nanostructure may be calculated as follows by combining the nonlocal and strain-gradient differential operators $\mathcal{L} \left ( * \right ) \equiv 1- (e_{0} a)^{2} \nabla ^{2}$ and $\Gamma \left ( * \right ) \equiv 1- (l_{m} )^{2} \nabla ^{2}$:

$$ \begin{aligned} &\Gamma \left [ A_{11}^{(0)} \frac{\partial ^{2} u_{0}}{\partial x^{2}} - A_{11}^{\left (1\right )} \frac{\partial ^{3} w_{b}}{\partial x^{3}} - A_{11}^{-\left (0\right )} \frac{\partial ^{3} w_{s}}{\partial x^{3}}+ \left ( A_{12}^{\left (0\right )} + A_{66}^{\left (0\right )} \right ) \frac{\partial v_{0}}{\partial x\partial y}\right.\\ &\qquad {}- \left ( A_{12}^{\left (1\right )} +2 A_{66}^{\left (1\right )} \right ) \frac{\partial ^{3} w_{s}}{\partial x\partial y^{2}} - \left ( A_{12}^{-\left (0\right )} +2 A_{66}^{-\left (0\right )} \right ) \frac{\partial ^{3} w_{s}}{\partial x\partial y^{2}} + A_{66}^{\left (0\right )} \frac{\partial ^{2} u_{0}}{\partial y^{2}} \\ &\qquad \left.{}+ \tilde{A}_{13}^{\left (0\right )} \frac{\partial \phi}{\partial x} + \overline{B}_{e31}^{\left (0\right )} \frac{\partial \varphi}{\partial x} + \overline{B}_{q31}^{\left (0\right )} \frac{\partial \psi}{\partial x} \right ] \\ &\quad =\mathcal{L} \left [ m_{0} \ddot{u}_{0} - m_{1} \frac{\partial \ddot{w}_{b}}{\partial x} -m_{3} \frac{\partial \ddot{w}_{s}}{\partial x} \right ] \end{aligned} $$

(54a)

$$ \begin{aligned} &\Gamma \left [ A_{22}^{(0)} \frac{\partial ^{2} v_{0}}{\partial y^{2}} - A_{22}^{\left (1\right )} \frac{\partial ^{3} w_{b}}{\partial y^{3}} - A_{22}^{-\left (0\right )} \frac{\partial ^{3} w_{s}}{\partial y^{3}} + \left ( A_{12}^{\left (0\right )} + A_{66}^{\left (0\right )} \right ) \frac{\partial u_{0}}{\partial x\partial y}\right.\\ & \qquad {} - \left ( A_{12}^{\left (1\right )} +2 A_{66}^{\left (1\right )} \right ) \frac{\partial ^{3} w_{b}}{\partial x^{2} \partial y} - \left ( A_{12}^{-\left (0\right )} +2 A_{66}^{-\left (0\right )} \right ) \frac{\partial ^{3} w_{s}}{\partial x^{2} \partial y} + A_{66}^{\left (0\right )} \frac{\partial ^{2} v_{0}}{\partial x^{2}} \\ &\left. \qquad {} + \tilde{A}_{13}^{\left (0\right )} \frac{\partial \phi}{\partial y} + \overline{B}_{e32}^{\left (0\right )} \frac{\partial \varphi}{\partial y} + \overline{B}_{e32}^{\left (0\right )} \frac{\partial \psi}{\partial y} \right ] =\mathcal{L} \left [ m_{0} \ddot{v}_{0} - m_{1} \frac{\partial \ddot{w}_{b}}{\partial y} -m_{3} \frac{\partial \ddot{w}_{s}}{\partial y} \right ] \end{aligned} $$

(54b)

$$ \begin{aligned} &\Gamma \left [ A_{11}^{(1)} \frac{\partial ^{3} u_{0}}{\partial x^{3}} - A_{22}^{\left (2\right )} \frac{\partial ^{4} w_{b}}{\partial y^{4}} - A_{11}^{-\left (1\right )} \frac{\partial ^{4} w_{s}}{\partial y^{4}} + \left ( A_{12}^{\left (1\right )} +2 A_{66}^{\left (1\right )} \right ) \left ( \frac{\partial ^{3} u_{0}}{\partial x\partial y^{2}} + \frac{\partial ^{3} v_{0}}{\partial x^{2} \partial y} \right )\right.\\ & \qquad {} -2 \left ( A_{12}^{\left (2\right )} +2 A_{66}^{\left (2\right )} \right ) \frac{\partial ^{4} w_{b}}{\partial x^{2} \partial y^{2}} -2 \left ( A_{12}^{-\left (1\right )} +2 A_{66}^{-\left (1\right )} \right ) \frac{\partial ^{4} w_{s}}{\partial x^{2} \partial y^{4}}\\ & \qquad {} + A_{22}^{\left (1\right )} \frac{\partial ^{3} v_{0}}{\partial x^{3}} - A_{22}^{\left (2\right )} \frac{\partial ^{4} w_{b}}{\partial y^{4}} - \overline{A}_{22}^{\left (1\right )} \frac{\partial ^{4} w_{s}}{\partial y^{4}} + \tilde{A}_{13}^{\left (1\right )} \frac{\partial ^{2} \phi}{\partial x^{2}} + A_{23}^{\left (1\right )} \frac{\partial ^{2} \phi}{\partial y^{2}} \\ &\left.\qquad {} + \overline{B}_{e31}^{\left (1\right )} \frac{\partial ^{2} \varphi}{\partial x^{2}} + \overline{B}_{e32}^{\left (1\right )} \frac{\partial ^{2} \varphi}{\partial y^{2}}+ \overline{B}_{q31}^{\left (1\right )} \frac{\partial ^{2} \psi}{\partial x^{2}} + \overline{B}_{q32}^{\left (1\right )} \frac{\partial ^{2} \psi}{\partial y^{2}} \right ] \\ &\quad =\mathcal{L} \left [ \left ( N_{x}^{T} + P_{x0} + P_{e31} + P_{q31} \right ) \frac{\partial ^{2} w_{b}}{\partial x^{2}} + \left ( N_{y}^{T} + P_{y0} + P_{e32} + P_{q32} \right ) \frac{\partial ^{2} w_{b}}{\partial y^{2}} \right.\\ & \qquad {} + m_{0} \left ( \ddot{w}_{b} + \ddot{w}_{s} \right ) + m_{1} \left ( \frac{\partial \ddot{u}_{0}}{\partial x} + \frac{\partial \ddot{u}_{0}}{\partial y} \right ) - m_{2} \left ( \frac{\partial ^{2} \ddot{w}_{b}}{\partial x^{2}} + \frac{\partial ^{2} \ddot{w}_{b}}{\partial y^{2}} \right )\\ &\left.\qquad {} - m_{4} \left ( \frac{\partial ^{2} \ddot{w}_{b}}{\partial x^{2}} + \frac{\partial ^{2} \ddot{w}_{b}}{\partial y^{2}} \right ) + m_{6} \ddot{\phi} \right ] \end{aligned} $$

(54c)

$$ \begin{aligned} &\Gamma \left [ \overline{A}_{11}^{(0)} \frac{\partial ^{3} u_{0}}{\partial x^{3}} - \overline{A}_{11}^{\left (1\right )} \frac{\partial ^{4} w_{b}}{\partial x^{4}} - \overline{A}_{11}^{\left ( f \right )} \frac{\partial ^{4} w_{s}}{\partial x^{4}} + \left ( \overline{A}_{12}^{\left (0\right )} +2 \overline{A}_{66}^{\left (0\right )} \right ) \left ( \frac{\partial ^{3} u_{0}}{\partial x\partial y^{2}} + \frac{\partial ^{3} v_{0}}{\partial x^{2} \partial y} \right )\right.\\ & \qquad {}-2 \left ( \overline{A}_{12}^{\left (1\right )} +2 \overline{A}_{66}^{\left (1\right )} \right ) \frac{\partial ^{4} w_{b}}{\partial x^{2} \partial y^{2}} -2 \left ( \overline{A}_{12}^{\left ( f \right )} +2 \overline{A}_{66}^{\left ( f \right )} \right ) \frac{\partial ^{4} w_{s}}{\partial x^{2} \partial y^{2}} + \overline{A}_{22}^{\left (0\right )} \frac{\partial ^{3} v_{0}}{\partial y^{3}} \\ & \qquad {}- \overline{A}_{22}^{\left (1\right )} \frac{\partial ^{4} w_{b}}{\partial y^{4}} - \overline{A}_{22}^{\left ( f \right )} \frac{\partial ^{4} w_{s}}{\partial y^{4}} + \hat{A}_{44}^{\left (0\right )} \frac{\partial ^{2} w_{s}}{\partial y^{2}} + \hat{A}_{55}^{\left (0\right )} \frac{\partial ^{2} w_{s}}{\partial x^{2}} + \left ( \tilde{A}_{13}^{\left ( f \right )} + \hat{A}_{55}^{\left (0\right )} \right ) \frac{\partial ^{2} \phi}{\partial x^{2}}\\ & \qquad {} + \left ( \tilde{A}_{23}^{\left ( f \right )} + \hat{A}_{44}^{\left (0\right )} \right ) \frac{\partial ^{2} \phi}{\partial y^{2}} + \left ( B_{e31}^{\left ( f \right )} - B_{e15}^{\left ( \mathrm{g} \right )} \right ) \frac{\partial ^{2} \varphi}{\partial x^{2}} + + \ddot{w}_{s} )+ m_{3} \left ( \frac{\partial \ddot{u}_{0}}{\partial x} + \frac{\partial \ddot{v}_{0}}{\partial y} \right )\\ & \left.\qquad {} - m_{4} ( \frac{\partial ^{2} \ddot{w}_{0}}{\partial x^{2}} \left ( \overline{B}_{e32}^{\left ( f \right )} - B_{e24}^{\left ( \mathrm{g} \right )} \right ) \frac{\partial ^{2} \varphi}{\partial y^{2}} + \left ( \overline{B}_{q31}^{\left ( f \right )} - B_{q15}^{\left ( \mathrm{g} \right )} \right ) \frac{\partial ^{2} \psi}{\partial x^{2}} \right ]\\ &\quad =\mathcal{L} \left [ \left ( N_{x}^{T} + P_{x0} + P_{e31} + P_{q31} \right ) \frac{\partial ^{2} w_{b}}{\partial x^{2}} + \left ( N_{y}^{T} + P_{y0} + P_{e32} + P_{q32} \right ) \frac{\partial ^{2} w_{b}}{\partial y^{2}} \right.\\ &\left.\qquad {}+ \left ( m_{0} \left ( \ddot{w}_{0} + \frac{\partial ^{2} \ddot{w}_{b}}{\partial y^{2}} \right ) \right ) - m_{5} \left ( \frac{\partial ^{2} \ddot{w}_{s}}{\partial x^{2}} + \frac{\partial ^{2} \ddot{w}_{s}}{\partial y^{2}} \right ) + m_{6} \ddot{\phi} \right ] \end{aligned} $$

(54d)

$$\begin{aligned} &\Gamma \left [ - \tilde{A}_{13}^{\left (0\right )} \frac{\partial u_{0}}{\partial x} + \tilde{A}_{13}^{\left (1\right )} \frac{\partial ^{2} w_{b}}{\partial x^{2}} + \left ( - \tilde{A}_{13}^{\left ( f \right )} + \hat{A}_{55}^{\left (0\right )} \right ) \frac{\partial ^{2} w_{s}}{\partial x^{2}} - \tilde{A}_{23}^{\left (0\right )} \frac{\partial v_{0}}{\partial y} + \tilde{A}_{23}^{\left (1\right )} \frac{\partial ^{2} w_{b}}{\partial y^{2}}\right. \\ & \qquad {} + \left ( - \tilde{A}_{23}^{\left ( f \right )} + \hat{A}_{44}^{\left (0\right )} \right ) \frac{\partial ^{2} w_{s}}{\partial y^{2}} - \tilde{A}_{33}^{\left ( \mathrm{g} \right )} \phi + \hat{A}_{44}^{\left (0\right )} \frac{\partial ^{2} \phi}{\partial y^{2}} + \hat{A}_{55}^{\left (0\right )} \frac{\partial ^{2} \phi}{\partial x^{2}} - B_{e15}^{\left ( \mathrm{g} \right )} \frac{\partial ^{2} \varphi}{\partial x^{2}} \\ &\left.\qquad {} - B_{e24}^{\left ( \mathrm{g} \right )} \frac{\partial ^{2} \varphi}{\partial y^{2}}- B_{q15}^{\left ( \mathrm{g} \right )} \frac{\partial ^{2} \psi}{\partial x^{2}}- B_{q24}^{\left ( \mathrm{g} \right )} \frac{\partial ^{2} \psi}{\partial y^{2}} - \overline{B}_{e33}^{\left ( \mathrm{g} \right )} \varphi - \overline{B}_{q33}^{\left ( \mathrm{g} \right )} \psi + \overline{B}_{e33}^{\left ( \mathrm{g} \right )} + \overline{B}_{q33}^{\left ( \mathrm{g} \right )} \right ] \\ &\quad =\mathcal{L} \left [ m_{6} \left ( \ddot{w}_{b} + \ddot{w}_{s} \right ) + m_{7} \ddot{\phi} \right ] - \tilde{A}_{13}^{\left (0\right )} \frac{\partial u_{0}}{\partial x} + \tilde{A}_{13}^{\left (1\right )} \frac{\partial ^{2} w_{b}}{\partial x^{2}} + \left ( \tilde{A}_{13}^{\left ( f \right )} + \hat{A}_{55}^{\left (0\right )} \right ) \frac{\partial ^{2} w_{b}}{\partial x^{2}} \\ &\qquad {} - \tilde{A}_{23}^{\left (0\right )} \frac{\partial v_{0}}{\partial y} + \tilde{A}_{23}^{\left (1\right )} \frac{\partial ^{2} w_{b}}{\partial y^{2}} + \left ( \tilde{A}_{23}^{\left ( f \right )} + \hat{A}_{44}^{\left (0\right )} \right ) \frac{\partial ^{2} w_{s}}{\partial y^{2}} - \left ( - \tilde{A}_{23}^{\left ( f \right )} + \hat{A}_{44}^{\left (0\right )} \right ) \frac{\partial ^{2} w_{s}}{\partial y^{2}} \\ &\qquad {}- \tilde{A}_{23}^{\left ( \mathrm{g} \right )} \phi + \hat{A}_{44}^{\left (0\right )} \frac{\partial ^{2} \phi}{\partial y^{2}} + \hat{A}_{55}^{\left (0\right )} \frac{\partial ^{2} \phi}{\partial x^{2}} - B_{e15}^{\left ( \mathrm{g} \right )} \frac{\partial ^{2} \varphi}{\partial x^{2}} - B_{e24}^{\left ( \mathrm{g} \right )} \frac{\partial ^{2} \varphi}{\partial y^{2}} - B_{q15}^{\left ( \mathrm{g} \right )} \frac{\partial ^{2} \psi}{\partial x^{2}} \\ &\qquad {}- B_{q24}^{\left ( \mathrm{g} \right )} \frac{\partial ^{2} \psi}{\partial y^{2}} - \overline{B}_{e33}^{\left ( \mathrm{g} \right )} \varphi - \overline{B}_{q33}^{\left ( \mathrm{g} \right )} \psi + B_{e33}^{\left (1\right )} + B_{q33}^{\left (1\right )} =\mathcal{L} \left [ m_{6} \left ( \ddot{w}_{b} + \ddot{w}_{s} \right ) + m_{7} \ddot{\phi} \right ] \end{aligned}$$

(54e)

$$ \begin{aligned} &\overline{B}_{e31}^{(0)} \frac{\partial u_{0}}{\partial x} + \overline{B}_{e32}^{(0)} \frac{\partial v_{0}}{\partial y} - \overline{B}_{e31}^{\left (1\right )} \frac{\partial ^{2} w_{b}}{\partial x^{2}} - \overline{B}_{e32}^{\left (1\right )} \frac{\partial ^{2} w_{b}}{\partial y^{2}} + \left ( B_{e15}^{\left ( \mathrm{g} \right )} - \overline{B}_{e31}^{\left ( f \right )} \right ) \frac{\partial ^{2} w_{s}}{\partial y^{2}} \\ & \qquad {} + \overline{B}_{e32}^{\left ( \mathrm{g} \right )} \phi + B_{e15}^{\left ( \mathrm{g} \right )} \frac{\partial ^{2} \phi}{\partial x^{2}} + B_{e24}^{\left ( \mathrm{g} \right )} \frac{\partial ^{2} \phi}{\partial y^{2}} - P_{\varepsilon 33}^{\left ( s2 \right )} \varphi - P_{\mathrm{g} 33}^{\left ( c2 \right )} \psi + P_{\varepsilon 11}^{\left ( c2 \right )} \frac{\partial ^{2} \varphi}{\partial x^{2}} \\ & \qquad {} + P_{\varepsilon 22}^{\left ( c2 \right )} \frac{\partial ^{2} \varphi}{\partial y^{2}} + P_{\mathrm{g}11}^{\left ( c2 \right )} \frac{\partial ^{2} \psi}{\partial x^{2}} + P_{\mathrm{g}22}^{\left ( c2 \right )} \frac{\partial ^{2} \psi}{\partial y^{2}} - P_{\mathrm{g}33}^{\left ( s \right )} - P_{\varepsilon 33}^{\left ( s \right )} =0 \end{aligned} $$

(54f)

$$ \begin{aligned} &\overline{B}_{q31}^{(0)} \frac{\partial u_{0}}{\partial x} + \overline{B}_{q32}^{(0)} \frac{\partial v_{0}}{\partial y} - \overline{B}_{q31}^{\left (1\right )} \frac{\partial ^{2} w_{b}}{\partial x^{2}} - \overline{B}_{q32}^{\left (1\right )} \frac{\partial ^{2} w_{b}}{\partial y^{2}} + \left ( B_{q15}^{\left ( \mathrm{g} \right )} - \overline{B}_{q31}^{\left ( f \right )} \right ) \frac{\partial ^{2} w_{s}}{\partial x^{2}} \\ & \qquad {} + \left ( B_{q24}^{\left ( g \right )} - \overline{B}_{q32}^{\left ( f \right )} \right ) \frac{\partial ^{2} w_{s}}{\partial y^{2}} + \overline{B}_{q33}^{\left ( \mathrm{g} \right )} \phi + B_{q15}^{\left ( \mathrm{g} \right )} \frac{\partial ^{2} \phi}{\partial x^{2}} + B_{q24}^{\left ( \mathrm{g} \right )} \frac{\partial ^{2} \phi}{\partial y^{2}} - P_{\mathrm{g} 33}^{\left ( s2 \right )} \varphi - P_{\mu 33}^{\left ( c2 \right )} \psi \\ & \qquad {} + P_{\mathrm{g} 11}^{\left ( c2 \right )} \frac{\partial ^{2} \varphi}{\partial x^{2}} + P_{\mathrm{g} 22}^{\left ( c2 \right )} \frac{\partial ^{2} \varphi}{\partial y^{2}} + P_{\mu 11}^{\left ( c2 \right )} \frac{\partial ^{2} \psi}{\partial x^{2}} + P_{\mu 22}^{\left ( c2 \right )} \frac{\partial ^{2} \psi}{\partial y^{2}} - P_{\mathrm{g}33}^{\left ( s \right )} - P_{\mu 33}^{\left ( s \right )} =0. \end{aligned} $$

(54g)

2.9 Solution procedure

The Navier approach is applied to obtain the response of the MEE nanoplate under simple supported boundary conditions. A double trigonometric series is used for expanding the seven unknowns as follows (Żur et al. 2020):

$$ \begin{pmatrix} u_{0}\\ v_{0}\\ w_{b}\\ w_{s}\\ \phi \\ \varphi \\ \psi \end{pmatrix} = \sum _{m=1}^{\infty} \sum _{n=1}^{\infty} \begin{pmatrix} \overline{u} cos \left ( \alpha x \right ) sin \left ( \beta y \right ) e^{i\omega t}\\ \overline{v} sin \left ( \alpha x \right ) cos \left ( \beta y \right ) e^{i\omega t}\\ \overline{w}_{b} sin \left ( \alpha x \right ) sin \left ( \beta y \right ) e^{i\omega t}\\ \overline{w}_{s} sin \left ( \alpha x \right ) sin \left ( \beta y \right ) e^{i\omega t}\\ \overline{\phi} sin \left ( \alpha x \right ) sin \left ( \beta y \right ) e^{i\omega t}\\ \overline{\varphi} sin \left ( \alpha x \right ) sin \left ( \beta y \right ) e^{i\omega t}\\ \psi sin \left ( \alpha x \right ) sin \left ( \beta y \right ) e^{i\omega t} \end{pmatrix},\qquad \alpha = \frac{m\pi}{a}, \beta = \frac{n\pi}{b}, $$

(55)

where $\overline{u}$, $\overline{v}$, $\overline{w}_{b}$, $\overline{w}_{s}$, $\overline{\phi}$, $\overline{\varphi}$, and $\overline{\psi}$ define the maximum displacement, the electric potential, and the magnetic potential, respectively. Additionally, $w$ is the natural frequency. The variables can be written as follows:

$$ \left \{ \Delta \right \} = \begin{bmatrix} \overline{u} & \overline{v} & \overline{w}_{b} & \overline{w}_{s} & \overline{\phi} & \overline{\varphi} & \overline{\psi} \end{bmatrix} ^{T}. $$

(56)

The governing equations for the sandwich structure are derived as given below:

$$ \left \{ \left [ K \right ] - \omega _{mn}^{2} \left [ M \right ] \right \} \left \{ \Delta \right \} = \left \{ F \right \}, $$

(57)

where $\left [ K \right ]$, $\left [ M \right ]$, and $\left \{ F \right \}$ define the stiffness, the mass matrix, and the force vector, respectively. Here, the force vector can be written as (Żur et al. 2020)

$$ \left \{ F \right \} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} 0 & 0 & \textstyle\begin{array}{c@{\quad}c@{\quad}c} 0 & 0 & \textstyle\begin{array}{c@{\quad}c@{\quad}c} - \left ( B_{e33}^{( \mathrm{g} )} + B_{q33}^{( \mathrm{g} )} \right ) & - \left ( P_{g33}^{( \mathrm{g} )} + P_{e33}^{( \mathrm{g} )} \right ) & - \left ( P_{g33}^{( \mathrm{g} )} + P_{e33}^{( \mathrm{g} )} \right ) \end{array}\displaystyle \end{array}\displaystyle \end{array}\displaystyle \right ]^{T}. $$

(58)

For free vibration, Eq. (57) may be rearranged as shown below:

$$ \left \{ \left [ K \right ] - \omega _{mn}^{2} \left [ M \right ] \right \} \left \{ \Delta \right \} = \left \{ 0 \right \}. $$

(59)

A mathematical description of the MEE coefficients is given in Appendices (A1)–(A3). The elements of the stiffness and mass matrices are presented in Appendices (A4)–(A5).

Additionally, for buckling analysis, Eq. (57) can be modified as follows:

$$ \left [ K \right ] \left \{ \Delta \right \} = \left \{ 0 \right \}. $$

(60)

3 Numerical results and discussion

In this section, first, a validation study is performed for the proposed method. Then, the proven approach is applied to analyze the temperature-dependent effective material coefficients and free vibration response of the MEE nanoplate under electric, magnetic, and thermal loads. The structural dimensions of the auxetic core structure and MEE plate layers used in the numerical analysis are given by $a = b =1$, $h=a/25$, $h_{\mathrm{s}} =0.4 h$, $h_{\mathrm{r}} =0.1 h$,and $h_{\mathrm{p}} =0.2 h$.

3.1 Model verification

To assess the reliability of the current method, a comparison is made with two examples of published scientific research. The initial investigation compares the first five natural frequencies of a composite plate, which are simulated using the CUF method under thermal loads, with the results obtained in the present study (Azzara et al. 2023a). The dimensions of the plate are $a =1\ \mathrm{m}$, $h =0.01\ \mathrm{m}$, and ${a} / {h} =100$. The material properties of the plate structure are: $E_{1} =144.8$ GPa, $E_{2} = E_{3} =9.65$ GPa, $v_{12} =0.3$, $G_{12} = G_{13} =4.14$ GPa, $G_{23} =3.45$ GPa, $\rho =1450$ kg/m³, $\alpha _{11} =-2.6279 \times 10^{-7} {}^{\mathrm{o}}$C⁻¹, and $\alpha _{12} =30.535 \times 10^{-6} {}^{\mathrm{o}}$C⁻¹. Table 4 shows the assessment of the dimensionless frequency values gained from the present study with the findings obtained from (Azzara et al. 2023b). In accordance with the data presented in this table, the results obtained from the CUF model and the current model are completely compatible with one another.

Table 4 Comparison of the first five natural frequencies for CUF and SHSDT

In the second verification work, the nondimensional frequency values of the rectangular and square plates for various $a/b$ and $a/h$ ratios and nonlocal parameter $ea$ are examined under simply supported boundary conditions and compared with the results obtained by Aghababaei and Reddy (2009). In the analyses, the material properties and dimensions of the plates were set to $a=10$, $v=0.3$, and $E=300\times10^{6}$ Pa. The following equation is used to compare the natural frequencies:

$$ \overline{\omega} = \omega h \sqrt{\frac{\rho}{G}}. $$

(61)

Table 5 depicts the variations in the first three nondimensional frequencies $\overline{\omega}_{11}$, $\overline{\omega}_{22}$, and $\overline{\omega}_{33}$ of the plate according to the three different plate theories and the proposed method. According to this table, there is a high degree of agreement between the numerical results derived from the present investigation and those from the reference study.

Table 5 Comparison of the dimensionless natural frequencies $\overline{\omega}_{11}$, $\overline{\omega}_{22}$, and $\overline{\omega}_{33}$ of the plate structure

3.2 Effective material properties of the auxetic core

In this section, the effects of the geometrical parameters $\beta _{3}$ and $\theta$ of the auxetic core cell on the effective material properties, such as the modulus of elasticity $E$, shear modulus $G$, Poisson’s ratio $v$, density $\rho$, and thermal expansion coefficient $\alpha$, are investigated through Figs. 2–5 for $\Delta T=0$, the material size parameter $l_{m} =0$, the nonlocal parameter $e_{0} a=0$, $\beta _{1} =1.5$ and $\beta _{3} =0.1,\ 0.15,\ 0.20$ and 0.25.

Fig. 2

Evaluation of the effective modulus of elasticity and density of the auxetic core layer depending on the inclined angle $\theta$ for $\beta _{3} =0.1, 0.15, 0.20$, and 0.25

In Fig. 2, the variation in the effective modulus of elasticity and density in the $xx$ and $yy$ directions according to $\beta _{3}$ and the cell inclination angle $\theta$ is discussed. An examination of Fig. 2a shows that the modulus of elasticity increases nonlinearly with increasing $\theta$. A slight increase in $E_{11}$ is observed by increasing $\theta$ to approximately $70^{\circ}$. However, this increase is quite high at $\theta$ values greater than $70^{\circ}$, especially for high values of $\beta _{3}$. For $\beta _{3} =0.25$, the modulus of elasticity in the $xx$ plane $\left ( E_{11} \right )$ is obtained as $0.02963\times 10^{11} \ \mathrm{Pa}$ for $\theta = 45^{\circ}$, while this value is obtained as $0.1017\times 10^{11} \ \mathrm{Pa}$ for $\theta = 70^{\circ}$ and $3.0240\times 10^{11} \ \mathrm{Pa}$ for $\theta = 89^{\circ}$. When Fig. 2b is examined, it is determined that the modulus of elasticity in the $yy$ direction $\left ( E_{22} \ \right )$ increases with increasing $\beta _{3}$ and decreases with increasing $\theta$. While $E_{22}$ decreases rapidly between $\theta = 0^{\circ}$ and $\theta = 30^{\circ}$, it decreases more slowly between $\theta = 30^{\circ}$ and $\theta = 90^{\circ}$. For $\beta _{3} =0.25$, $E_{22}$ is obtained as $0.11\times 10^{11} \ \mathrm{Pa}$ for $\theta = 15^{\circ}$, while this value is obtained as $0.009098\times 10^{11} \ \mathrm{Pa}$ for $\theta = 75^{\circ}$. In Fig. 2c, it is determined that the auxetic core density $\rho$ increases nonlinearly with both $\beta _{3}$ and $\theta$. This increase is quite high, especially for high values of $\beta _{3}$.

Figure 3 displays the variation in the shear modulus values of the auxetic core in the $xy$, $xz$, and $yz$ planes according to $\beta _{3}$ and $\theta$. An examination of Fig. 3a and Fig. 3b reveals that for a constant $\beta _{1} =1.5$, $G_{12}$ and $G_{13}$ increase nonlinearly with increasing $\theta$ and $\beta _{3}$. In both figures, high shear modulus values are obtained for high values of $\beta _{3}$. In Fig. 3c, the highest shear modulus values are similarly obtained for $\beta _{3} =0.25$. When the shear modulus increases between $\theta = 0^{\circ}$ and $\theta = 43^{\circ}$, a decrease is observed after approximately $\theta = 43^{\circ}$.

Fig. 3

Evaluation of the effective shear modulus of the auxetic core layer versus the inclined angle $\theta$ for $\beta _{3} =0.1, 0.15, 0.20$, and 0.25

Figure 4 provides an evaluation of the change in Poisson’s ratio in the $xy$ and $yx$ planes according to $\beta _{3}$ and $\theta$. Here, a negative Poisson’s ratio can be observed for the auxetic core layer. Figure 4a demonstrates that higher values of Poisson’s ratios are obtained as $\beta _{3}$ decreases. Additionally, this figure shows that higher f Poisson’s ratios are obtained as $\theta$ increases. Increasing $\theta$ up to approximately $50^{0}$ causes Poisson’s ratio to increase slightly, regardless of the $\beta _{3}$ value. However, this increasing trend becomes more pronounced, especially after $\theta = 60^{\circ}$. Similarly, in Fig. 4b, a rise in $\beta _{3}$ leads to a drop in Poisson’s ratio. In Fig. 4a, as $\theta$ approaches $90^{\circ}$, Poisson’s ratio $v_{12}$ exhibits an increasing trend. Conversely, in Fig. 4b, as $\theta$ approaches $90^{\circ}$, Poisson’s ratio $v_{21}$ demonstrates a decreasing pattern.

Fig. 4

Evaluation of effective Poisson’s ratio of the auxetic core layer depending on the inclined angle $\theta$ for $\beta _{3} =0.1, 0.15, 0.20$, and 0.25

Figure 5 assesses the variation in the thermal expansion coefficient according to $\beta _{3}$ and $\theta$ in the $xx$ and $yy$ planes. The figures illustrate that as $\theta$ grows, $\alpha _{11}$ exhibits a linear drop, while $\alpha _{22}$ demonstrates a nonlinear increase. As $\beta _{3}$ increases, both $\alpha _{11}$ and $\alpha _{22}$ also increase.

Fig. 5

Evaluation of the effective thermal expansion coefficient of the auxetic core layer versus the inclined angle $\theta$ for $\beta _{3} =0.1, 0.15, 0.20$, and 0.25

3.3 Free vibration analysis of the FGM sandwich nanoplate

In this subsection, the frequency response analysis of the sandwich nanoplate with an auxetic core is examined with respect to the parameters of temperature rise, electrical load, magnetic load, nonlocal parameter, and material size factor. The input magnetic field is defined by Eq. (62), and the electric field is defined by Eq. (63).

$$ H_{m} = \frac{H_{0}}{D},\quad D= \frac{E H^{3}}{12 \left ( 1- \nu ^{2} \right )}. $$

(62)

$$ V_{m} = \frac{V_{0}}{D},\quad D= \frac{E H^{3}}{12 \left ( 1- \nu ^{2} \right )}. $$

(63)

Figure 6 exhibits the effects of the temperature difference $\Delta T$, cell inclination angle $\theta$, and $\beta _{3}$ on the nondimensional frequency $\lambda _{1}$ of the sandwich nanoplate. As shown in Fig. 6a-b, the first dimensionless frequency of the sandwich nanoplate decreases as both $\beta _{3}$ and $\Delta T$ increase. The reason for this decrease in the dimensionless frequency is the decrease in the modulus of elasticity of all the materials in the sandwich plate with increasing temperature and, accordingly, the drop in the stiffness of the structure. Another reason for the decrease in the dimensionless frequency is that the stiffness of the auxetic core increases as $\beta _{3}$ increases, but the mass increases more than the stiffness. For $\beta _{3}$ values of 0.10, 0.15, 0.20, and 0.25, the buckling temperature of the sandwich plate is calculated as 267 K, 264 K, 258.50 K, and 250.50 K for Fig. 6a, 262.40 K, 256 K, 246 K, and 236 K for Fig. 6b, and 249 K, 231 K, 226 K, and 254.50 K for Fig. 6c, respectively. As can be seen, the buckling temperature decreases with increasing $\beta _{3}$. An examination of Fig. 6d reveals that the natural frequency and buckling temperature decrease with increasing $\theta$.

Fig. 6

Variation in the dimensionless frequency $\lambda _{1}$ depending on the $\beta _{3}$ and $\theta$ values of the auxetic core and temperature rise $\Delta T$; applied electric load $V_{m} =0$; and applied magnetic load $H_{m} =0$

Figure 7 evaluates the influence of $\Delta T$, $\theta$, and $\beta _{1}$ on the nondimensional frequency of the MEE sandwich nanoplate. As shown in Figure, the first dimensionless frequency and buckling temperature of the sandwich nanoplate increase as $\beta _{1}$ increases. For $\beta _{1}$ values of 1, 1.5, 2, and 2.5, the buckling temperature of the sandwich plate is calculated as 253.5 K, 265 K, 267 K, and 269 K for Fig. 7a, 195.5 K, 256 K, 265.5 K, and 267.5 K for Fig. 7b, and 188 K, 231.5 K, 259.5 K, and 265 K for Fig. 7c, respectively. When Fig. 7d is examined, it is concluded that the natural frequency and buckling temperature decrease with increasing $\theta$.

Fig. 7

Variation of the dimensionless frequencies $\lambda _{1}$ depending on the $\beta _{1}$ and $\theta$ values of the auxetic core and temperature rise $\Delta T$; applied electric load $V_{m} =0$; applied magnetic load $H_{m} =0$

The variation in the dimensionless frequency of the sandwich nanoplate with respect to the thermal and electrical load is shown in Fig. 8 for three different BaTiO₃ and CoFe₂O₄ mixing ratios. In the analysis, four different voltage values are applied ($V_{m}=0$, 0.1, 0.2, and 0.3). Figure 8a exhibits the effect of the four different voltage parameters upon the first nondimensional natural frequency. As shown in Fig. 8a-c, the dimensionless first frequency values decline as the temperature difference increases. It is also seen from the figure that increasing voltage has a decreasing effect on the natural frequency and buckling temperature. For example, in Fig. 8a, when no voltage is applied, the dimensionless natural frequency is obtained as 1.25 for $\Delta T=$150, while this value is 1.24 for $V_{m}=0.1$, 1.02 for $V_{m}=0.2$, and 0.88 for $V_{m}=0.3$. In addition, the buckling temperatures for $V_{m}=0$, 0.1, 0.2, and 0.3 are obtained as 222 K, 210 K, 199 K, and 187 K, respectively. In Fig. 8b, the material composition ratio of the MEE plate is BaTiO$_{3}=0.3$ and CoFeO$_{4}=0.7$. As can be seen, the natural frequency and buckling temperatures increased with increasing CoFeO₄ ratio. When the $V_{m}=0$ curves in Fig. 8a-b are examined, it is understood that the increase in the natural frequency is attributed to the higher stiffness property of CoFe₂O₄ compared to BaTiO₃. Again, when Fig. 8b is examined, the natural frequency decreases with increasing electrical load. However, according to Fig. 8a, with decreasing BaTiO₃ concentration, the rate of drop in the natural frequency decreased. This is due to the piezoelectric behavior of BaTiO₃. When no voltage is applied for the BaTiO$_{3}=0.3$ and CoFe₂O$_{4}=0.7$ ratios, the dimensionless natural frequency is 1.28 for a $\Delta T\ =$150, while this value is 1.23 for $V_{m}=0.1$, 1.16 for $V_{m}=0.2$, and 1.10 for $V_{m}=0.3$. In addition, the buckling temperatures for $V_{m}=0$, $V_{m}=0.1$, $V_{m}=0.2$, and $V_{m}=0.3$ are obtained as 229 K, 223 K, 216 K, and 210 K, respectively. The variation in the nondimensional fundamental frequency of the sandwich nanoplate with respect to temperature and electrical charge for BaTiO$_{3}=0.7$ and CoFe₂O$_{4}=0.3$ is shown in Fig. 8c. As shown in the figure, with increasing BaTiO₃ ratio in the MEE plate, the dimensionless natural frequency decreased due to the stiffness of BaTiO₃ and CoFe₂O₄. In addition, the piezoelectric property of the MEE plate increased with increasing BaTiO₃ ratio, thus a significant decrease in the natural frequency and buckling temperature occurred.

Fig. 8

Variation in the dimensionless frequency $\lambda _{1}$ depending on the temperature rise and electrical load; for the face plate material mixture BaTiO₃ 70%, 50%, and 30% and CoFe₂O₃ %30, 50%, and 70%; applied magnetic load $H_{m} =0$

The fluctuations in the dimensionless frequency of the sandwich nanoplate with respect to thermal and magnetic loads are shown in Fig. 9 for three different BaTiO₃ and CoFe₂O₄ mixing ratios. In the analysis, four different magnetic field loads are applied ($H_{m}=0$, 0.001, 0.002, 0.003). Figure 9a shows the effect of four different magnetic load parameters on the first dimensionless natural frequency for BaTiO$_{3}=0.5$ and CoFe₂O$_{4}=0.5$. As depicted in the figure, increasing temperature has a decreasing effect on the dimensionless natural frequency, while increasing magnetic field load has an increasing effect on the natural frequency. In addition, increasing magnetic field load also increases the buckling temperature of the plate. For example, in Fig. 9a, for $H_{m}=0$, the dimensionless natural frequency is 1.62 for $\Delta T\ =$150, while this value is 1.50 for $H_{m}=0.001$, 1.38 for $H_{m}=0.002$, and 1.25 for $H_{m}=0.003$. In addition, the buckling temperatures for $H_{m}=0$, 0.001, 0.002, and 0.003 are 222 K, 236 K, 249 K, and 263 K, respectively. The effect of the magnetic field load on the dimensionless natural frequency of the sandwich plate for BaTiO$_{3}=0.3$ and CoFe₂O$_{4}=0.7$ is investigated with Fig. 9b. As illustrated in the figure, the natural frequency and buckling temperature increase with the increasing CoFe₂O₄ ratio in the MEE face plate. Increasing CoFe₂O₄ ratio has two effects on the natural frequency and buckling. First, the natural frequency and buckling temperature of the plate directly increase due to the high stiffness of CoFe₂O₄. Second, the magnetic behavior of the MEE face plates increases with increasing CoFe₂O₄ concentration, which increases the natural frequency of the plate and the buckling temperature. The effects of BaTiO$_{3}=0.7$ and CoFe₂O$_{4}=0.3$ on the natural frequency and buckling temperature are depicted in Fig. 9c. With the dominance of the BaTiO₃ ratio in the MEE face plate, the natural frequency of the plate decreased due to the low Young’s modulus of BaTiO₃ compared to that of CoFe₂O₄. However, the natural frequency increased with the effect of the applied magnetic field. It can be concluded from Fig. 9 that the magnetic field has a stiffness increasing effect on the plate.

Fig. 9

Variation in the dimensionless frequency $\lambda _{1}$ depending on the temperature rise and magnetic load; for the face plate material mixture BaTiO₃ 70%, 50%, and 30% and CoFe₂O₃ %30, 50%, and 70%; applied electric load $V_{m} =0$

Figure 10a presents the variation in the nondimensional natural frequency and buckling temperature of the nanoplate depending on the nonlocal parameters $e_{0} a$ and $\Delta T$. An evaluation of the figure demonstrates that the natural frequency decreases with increasing $e_{0} a$ and $\Delta T$. When the buckling temperature is 265 K for $e_{0} a=0$, it drops to 58 K for $e_{0} a=0.5\text{ nm}^{2}$. In Fig. 10b, the variation in the natural frequency of the sandwich nanoplate with respect to the temperature difference is shown for material size factors $l_{m} =0$, 1, 1.41, and 2 nm². As shown in the figure, the dimensionless natural frequency of the plate increases as the material size factor increases. When the buckling temperature is 265 K for $l_{m} =0$, it increases to 372 K for $l_{m} =2 \text{ nm}^{2}$. A general evaluation of Fig. 10 shows that while the nonlocal parameter and temperature difference have similar effects on decreasing the natural frequency, the material size factor has an effect on increasing the natural frequency.

Fig. 10

Variation in the dimensionless frequency $\lambda _{1}$ depending on the nonlocal parameter $e_{0} a$ and material size parameter $_{l m}$; applied electric load $V_{m} =0$; applied magnetic load $H_{m} =0$

4 Conclusions

In this study, the thermomechanical free vibration and buckling behavior of smart sandwich nanostructures with auxetic cores and MEE face layers were investigated using SHSDT and NSGT. While the material properties of the face plates are determined by the rule of mixture, the material properties of the auxetic core layer vary according to the $\beta _{1}$, $\beta _{3}$, and $\theta$ parameters. First, the influence of various $\beta _{3}$ and $\theta$ parameters with respect to nonlinear temperature fluctuations was examined to determine the effective material properties (modulus of elasticity, shear modulus, Poisson’s ratio, thermal expansion, and density). As a consequence, the findings that have been gained from performing these computational models are expressed as follows:

The elastic modulus of the auxetic core layer in the $xx$ direction ($E_{11}$) exhibits a nonlinear increase with increasing $\theta$ and $\beta _{3}$. On the other hand, the modulus of elasticity in the $yy$ direction ($E_{22}$) exhibits an increase with increasing $\beta _{3}$ and a reduction with rising $\theta$. Therefore, the elastic modulus of the auxetic core layer in the $x$ and $y$ directions can be adjusted using the $\theta$, thickness and aspect ratio parameters of the auxetic core. This feature offers the possibility to adjust the elastic modulus in the sandwich nanoplate depending on the directions.

Higher values of $v_{12}$ are obtained as $\beta _{3}$ decreases. Additionally, higher values of $v_{12}$ are obtained as $\theta$ increases. A rise in $\beta _{3}$ leads to a decrease in $v_{21}$. Depending on $\theta$, $v_{12}$ increases negatively close to linear between $\theta =1$° and $\theta =50$°. In the range of $\theta =50$° and $\theta =89$°, it shows a nonlinear parabolic trend. For $\beta _{1}=1.5$ and $\theta =80$°, $v_{12}$ increases negatively to −2.1178 at $\beta _{3}=0.25$ and −9.2511 at $\beta _{3}=0.1$. For $\beta _{1}=1.5$ and $\theta =6$°, $v_{21}$ increases negatively to −0.9548 at $\beta _{3}=0.25$ and −3.5233 at $\beta _{3}=0.1$. Therefore, the negative Poisson’s ratios can be tuned in the $xy$ and $yx$ directions and thus the metamaterial properties can be adjusted.

When weight control and lightweight design are required, the mass density $\rho$ of the auxetic core can be adjusted with the auxetic core parameters. The auxetic core layer density increases nonlinearly with both $\beta _{3}$ and $\theta$. This increase is quite high, especially for high values of $\beta _{3}$.

The variation of the shear modulus also varies significantly in auxetic core in a nonlinear manner depending on the parameters. The shear modulus values $G_{12}$ and $G_{13}$ increase nonlinearly with increasing $\theta$ and $\beta _{3}$. High shear modulus values are obtained for high values of $\beta _{3}$.

The coefficient of thermal expansion of the auxetic core can also be tuned. When $\theta$ increases, $\alpha _{11}$ exhibits a linear drop, while $\alpha _{22}$ demonstrates a nonlinear increase. As $\beta _{3}$ increases, both $\alpha _{11}$ and $\alpha _{22}$ also increase.

Second, the frequency response and buckling analysis of the sandwich nanoplate were examined with respect to the parameters of temperature rise, electrical load, magnetic load, nonlocal parameter, and material size factor. As a consequence, the findings that have been gained from performing these computational models are expressed as follows:

Besides the thermal effect, the properties of the auxetic core also affect the thermomechanical vibration behaviour of the smart nanoplate. When inclination angle $\theta$ and length ratio $\beta _{1}$ of the auxetic core are kept constant, the dimensionless frequency of the MEE nanoplate decreases as both $\Delta T$ and $\beta _{3}$ increase.

The increase in the natural frequency and buckling temperature is physically a result of the stiffness and therefore the modulus of elasticity in the smart sandwich nanoplate. In addition, a low coefficient of thermal expansion results in a high buckling temperature and natural frequency. When $\beta _{1}$ and $\theta$ are constant, a decrease in the buckling temperature of the MEE nanoplate is observed as the values of $\beta _{3}$ and $\theta$ increase. When $\beta _{3}$ is constant, with the increase in $\beta _{1}$, the MEE nanoplate experiences an increase in both the dimensionless frequency and buckling temperature. Increasing $\theta$ causes a decrease in both the dimensionless frequency and the buckling temperature.

Due to the electro-elastic property of the face layers, increasing the electrical load has a decreasing effect on the nondimensional natural frequency and buckling temperature of the sandwich plate. In other words, the electric charge reduces the stiffness of the structure. This property becomes more effective with the increase of BaTiO₃ ratio in the surface layers.

Because of the magnetostrictive property of CoFe₂O₄ in the face layers, increasing magnetic field load has an increasing impact on the nondimensional natural frequency. Additionally, increasing the magnetic field load increases the buckling temperature of the sandwich plate.

The effect of the size factor creates a strength enhancement effect in the smart nanoplate with the strain gradient elasticity effect. Thus, the dimensionless first natural frequency of the sandwich plate increases as the material size factor increases.

On the contrary, due to the effect of nonlocal integral elasticity, softening effect occurs in the smart nanoplate depending on the nonlocal parameter and, therefore, the nonlocal parameter has a decreasing effect on the natural frequency. In other words, while the material size factor stiffens the plate, the nonlocal parameter softens the plate.

With this study, important inferences were obtained about the thermal buckling and free vibration behavior of sandwich MEE plates with auxetic cores. It is considered that a reference will be provided to the gap in the literature with the analyzes made by considering the temperature-dependent material properties of BaTiO₃ and CoFe₂O₄.

Appendix

$$\begin{gathered} \begin{gathered} A_{ij}^{\left ( n \right )} = \int _{-h/2- h_{s}}^{-h/2} C_{ij}^{s} \left \{ 1,z, z^{2} \right \} dz + \int _{-h/2}^{h/2} C_{ij}^{c} \left \{ 1,z, z^{2} \right \} dz\\ + \int _{h/2}^{{h} / {2} + h_{s}} C_{ij}^{s} \left \{ 1,z, z^{2} \right \} dz\quad n=0,1,2 \\ \overline{A}_{ij}^{\left ( \overline{n} \right )} = \int _{-h/2- h_{s}}^{-h/2} C_{ij}^{s} f \left ( z \right ) \left \{ 1,z,f \left ( z \right ) \right \} dz + \int _{-h/2}^{h/2} C_{ij}^{c} f \left ( z \right ) \left \{ 1,z,f \left ( z \right ) \right \} dz\\ + \int _{h/2}^{{h} / {2} + h_{s}} C_{ij}^{s} f \left ( z \right ) \left \{ 1,z,f \left ( z \right ) \right \} dz,\quad \overline{n} =0,1,f\\ \tilde{A}_{ij}^{( \tilde{n} )} = \int _{-h/2- h_{s}}^{-h/2} C_{ij}^{s} g^{,} (z) \left \{ 1,z, g ' \left ( z \right ),f(z) \right \} dz\\ + \int _{-h/2}^{h/2} C_{ij}^{c} g^{,} (z) \left \{ 1,z, g ' \left ( z \right ),f(z) \right \} dz\\ + \int _{h/2}^{{h} / {2} + h_{s}} C_{ij}^{s} g ' (z) \left \{ 1,z, g^{,} \left ( z \right ),f(z) \right \} dz, \overline{n} =0,1, g^{,},f \\ \tilde{A}_{ij}^{( \tilde{n} )} = \int _{-h/2- h_{s}}^{-h/2} C_{ij}^{s} g^{2} (z)dz + \int _{-h/2}^{h/2} C_{ij}^{c} g^{2} (z)dz + \int _{h/2}^{{h} / {2} + h_{s}} C_{ij}^{s} g^{2} (z)dz \end{gathered} \end{gathered}$$

(A1)

$$\begin{gathered} \begin{gathered} B_{e_{ij}}^{(k)} =- \left [ \int _{-h/2- h_{s}}^{-h/2} e_{ij} \left ( \frac{2\varphi _{0}}{h_{s}} \right ) \left \{ z,f \left ( z \right ), g ' \left ( z \right ), \left ( \frac{h_{s}}{2\varphi _{0}} \right ) cos \left ( \frac{\pi z_{2}}{h_{s}} \right ) \right \} dz \right.\\ {}+ \int _{-h/2}^{h/2} e_{ij} \left ( \frac{2\varphi _{0}}{h} \right ) \left \{ z,f \left ( z \right ), g ' \left ( z \right ), \left ( \frac{h_{s}}{2\varphi _{0}} \right ) cos \left ( \frac{\pi z}{h_{s}} \right ) \right \} dz \\ \left.{}+ \int _{h/2}^{h/2+ h_{s}} e_{ij} \left ( \frac{2\varphi _{0}}{h_{s}} \right ) \left \{ z,f \left ( z \right ), g ' \left ( z \right ), \left ( \frac{h_{s}}{2\varphi _{0}} \right ) cos \left ( \frac{\pi z_{2}}{h_{s}} \right ) \right \} dz \right ],\quad k=1,f, g ',g \\ \overline{B}_{e_{ij}}^{(k)} =- \left [ \int _{-h/2- h_{s}}^{-h/2} e_{ij} \left [ \frac{\pi}{h_{s}} sin \left ( \frac{\pi z_{1}}{h_{s}} \right ) \right ] \left \{ 1,z,f \left ( z \right ), g ' \left ( z \right ) \right \} dz\right. \\ {}+ \int _{-h/2}^{h/2} e_{ij} \left [ \frac{\pi}{h} sin \left ( \frac{\pi z}{h} \right ) \right ] \left \{ 1,z,f \left ( z \right ), g ' \left ( z \right ) \right \} dz \\ \left.{}+ \int _{h/2}^{h/2+ h_{s}} e_{ij} \left [ \frac{\pi}{h_{s}} sin \left ( \frac{\pi z_{2}}{h_{s}} \right ) \right ] \left \{ 1,z,f \left ( z \right ), g ' \left ( z \right ) \right \} dz \right ],\quad k=0,1,f, g '\\ B_{q_{ij}}^{(k)} =- \left [ \int _{-h/2- h_{s}}^{-h/2} q_{ij} \left ( \frac{2\varphi _{0}}{h_{s}} \right ) \left \{ z,f \left ( z \right ), g ' \left ( z \right ), \left ( \frac{h_{f}}{2\varphi _{0}} \right ) cos \left ( \frac{\pi z_{1}}{h_{s}} \right ) \right \} dz \right.\\ {}+ \int _{-h/2}^{h/2} q_{ij} \left ( \frac{2\varphi _{0}}{h} \right ) \left \{ z,f \left ( z \right ), g ' \left ( z \right ), \left ( \frac{h}{2\varphi _{0}} \right ) cos \left ( \frac{\pi z}{h} \right ) \right \} dz \\ \left.{}+ \int _{h/2}^{h/2+ h_{s}} q_{ij} \left ( \frac{2\varphi _{0}}{h_{s}} \right ) \left \{ z,f \left ( z \right ), g ' \left ( z \right ), \left ( \frac{h_{f}}{2\varphi _{0}} \right ) cos \left ( \frac{\pi z_{2}}{h_{s}} \right ) \right \} dz \right ], \quad k=1,f, g ',g\\ \overline{B}_{q_{ij}}^{(k)} =- \left [ \int _{-h/2- h_{s}}^{-h/2} q_{ij} \left [ \frac{\pi}{h_{s}} sin \left ( \frac{\pi z_{1}}{h_{s}} \right ) \right ] \left \{ 1,z,f \left ( z \right ), g ' \left ( z \right ) \right \} dz \right.\\ {}+ \int _{-h/2}^{h/2} q_{ij} \left [ \frac{\pi}{h} sin \left ( \frac{\pi z}{h} \right ) \right ] \left \{ 1,z,f \left ( z \right ), g ' \left ( z \right ) \right \} dz \\ \left.{}+ \int _{h/2}^{h/2+ h_{s}} q_{ij} \left [ \frac{\pi}{h_{s}} sin \left ( \frac{\pi z_{2}}{h_{s}} \right ) \right ] \left \{ 1,z,f \left ( z \right ), g ' \left ( z \right ) \right \} dz \right ],\quad k=0,1,f, g ' \end{gathered} \end{gathered}$$

(A2)

$$\begin{gathered} P_{\varepsilon _{ij}}^{(n)} =- \left [ \int _{-h/2- h_{s}}^{-h/2} \varepsilon _{ij} \left \{ \left ( \frac{2\varphi _{0}}{h_{s}} \right ) \left [ \frac{\pi}{h_{s}} sin \left ( \frac{\pi z_{1}}{h_{s}} \right ) \right ],\right.\right. \\ \qquad \qquad \left. \left [ \frac{\pi}{h_{s}} sin \left ( \frac{\pi z_{1}}{h_{s}} \right ) \right ]^{2}, \left [ cos \left ( \frac{\pi z_{1}}{h_{s}} \right ) \right ]^{2} \right \} dz \\ {}+ \int _{-h/2}^{h/2} \varepsilon _{ij} \left \{ \left ( \frac{2\varphi _{0}}{h} \right ) \left [ \frac{\pi}{h} sin \left ( \frac{\pi z}{h} \right ) \right ], \left [ \frac{\pi}{h} sin \left ( \frac{\pi z}{h} \right ) \right ]^{2}, \left [ cos \left ( \frac{\pi z}{h} \right ) \right ]^{2} \right \} dz \\ {}+ \int _{h/2}^{h/2+ h_{s}} \varepsilon _{ij} \left \{ \left ( \frac{2\varphi _{0}}{h_{s}} \right ) \left [ \frac{\pi}{h_{s}} sin \left ( \frac{\pi z_{2}}{h_{s}} \right ) \right ], \right. \\ \qquad \qquad \left.\left.\left [ \frac{\pi}{h_{s}} sin \left ( \frac{\pi z_{2}}{h_{s}} \right ) \right ]^{2}, \left [ cos \left ( \frac{\pi z_{2}}{h_{s}} \right ) \right ]^{2} \right \} dz \right ], \\ \quad n=1,s2,c2 \\ \begin{gathered} P_{g_{ij}}^{(n)} =- \left [ \int _{-h/2- h_{s}}^{-h/2} g_{ij} \left \{ \left ( \frac{2\varphi _{0}}{h_{s}} \right ) \left [ \frac{\pi}{h_{s}} sin \left ( \frac{\pi z_{1}}{h_{s}} \right ) \right ], \right.\right.\\ \qquad \qquad \left.\left [ \frac{\pi}{h_{s}} sin \left ( \frac{\pi z_{1}}{h_{s}} \right ) \right ]^{2}, \left [ cos \left ( \frac{\pi z_{1}}{h_{s}} \right ) \right ]^{2} \right \} dz \\ {} + \int _{-h/2}^{h/2} g_{ij} \left \{ \left ( \frac{2\varphi _{0}}{h} \right ) \left [ \frac{\pi}{h} sin \left ( \frac{\pi z}{h} \right ) \right ], \left [ \frac{\pi}{h} sin \left ( \frac{\pi z}{h} \right ) \right ]^{2}, \left [ cos \left ( \frac{\pi z}{h} \right ) \right ]^{2} \right \} dz \\ {}+ \int _{h/2}^{h/2+ h} g_{ij} \left \{ \left ( \frac{2\varphi _{0}}{h_{s}} \right ) \left [ \frac{\pi}{h_{s}} sin \left ( \frac{\pi z_{2}}{h_{s}} \right ) \right ],\right.\\ \qquad \qquad \left.\left. \left [ \frac{\pi}{h_{s}} sin \left ( \frac{\pi z_{2}}{h_{s}} \right ) \right ]^{2}, \left [ cos \left ( \frac{\pi z_{2}}{h_{s}} \right ) \right ]^{2} \right \} dz \right ],\\ \quad n=1,s2,c2 \end{gathered} \end{gathered}$$

(A3)

$$\begin{gathered} P_{\mu _{ij}}^{(n)} =- \left [ \int _{-h/2- h_{s}}^{-h/2} \mu _{ij} \left \{ \left ( \frac{2\varphi _{0}}{h_{s}} \right ) \left [ \frac{\pi}{h_{s}} sin \left ( \frac{\pi z_{1}}{h_{s}} \right ) \right ],\right.\right. \\ \qquad \qquad \left.\left [ \frac{\pi}{h_{s}} sin \left ( \frac{\pi z_{1}}{h_{s}} \right ) \right ]^{2}, \left [ cos \left ( \frac{\pi z_{1}}{h_{s}} \right ) \right ]^{2} \right \} dz \\ {} + \int _{-h/2}^{h/2} \mu _{ij} \left \{ \left ( \frac{2\varphi _{0}}{h} \right ) \left [ \frac{\pi}{h} sin \left ( \frac{\pi z}{h} \right ) \right ], \left [ \frac{\pi}{h} sin \left ( \frac{\pi z}{h} \right ) \right ]^{2}, \left [ cos \left ( \frac{\pi z}{h} \right ) \right ]^{2} \right \} dz \\ {} + \int _{h/2}^{h/2+ h_{s}} \mu _{ij} \left \{ \left ( \frac{2\varphi _{0}}{h_{s}} \right ) \left [ \frac{\pi}{h_{s}} sin \left ( \frac{\pi z_{2}}{h_{s}} \right ) \right ], \right. \\ \qquad \qquad \left.\left.\left [ \frac{\pi}{h_{s}} sin \left ( \frac{\pi z_{2}}{h_{s}} \right ) \right ]^{2}, \left [ cos \left ( \frac{\pi z_{2}}{h_{s}} \right ) \right ]^{2} \right \} dz \right ], \\ \quad n=1,s2,c2 \\ K_{11} =- c_{2} \left ( \alpha ^{2} A_{11}^{\left (0\right )} + \beta ^{2} A_{66}^{\left (0\right )} \right ) \\ K_{12} =- c_{2} \alpha \beta \left ( A_{12}^{(0)} + A_{66}^{(0)} \right ) \\ K_{13} = c_{2} \left ( \alpha ^{3} A_{11}^{(1)} +\alpha \beta ^{2} \left ( A_{12}^{(1)} +2 A_{66}^{(1)} \right ) \right ) \\ K_{14} = c_{2} \left ( \alpha ^{3} \overline{A}_{11}^{(0)} +\alpha \beta ^{2} \left ( \overline{A}_{12}^{(0)} +2 \overline{A}_{66}^{(0)} \right ) \right ) \\ K_{15} = c_{2} \alpha \tilde{A}_{13}^{(0)} \\ K_{16} = c_{2} \alpha \overline{B}_{e31}^{(0)} \\ K_{17} = c_{2} \alpha \overline{B}_{q31}^{(0)} \\ K_{22} =- c_{2} \left ( \left ( \beta ^{2} A_{22}^{(0)} + \alpha ^{2} A_{66}^{(0)} \right ) \right ) \\ K_{23} =- c_{2} \left ( \beta ^{3} A_{22}^{\left (1\right )} +\beta \alpha ^{2} \left ( A_{12}^{(1)} +2 A_{66}^{(1)} \right ) \right ) \\ K_{24} = c_{2} \left ( \beta ^{3} \overline{A}_{22}^{\left (0\right )} +\beta \alpha ^{2} \left ( \overline{A}_{12}^{(0)} +2 \overline{A}_{66}^{(0)} \right ) \right ) \\ K_{25} = c_{2} \beta \tilde{A}_{23}^{(0)} \\ K_{26} = c_{2} \beta \overline{B}_{e32}^{(0)} \\ K_{27} = c_{2} \beta \overline{B}_{q32}^{(0)} \\ K_{33} = \alpha ^{2} \left [ 1+ \mathcal{B} \left ( \alpha ^{2} + \beta ^{2} \right ) \right ] \left ( N_{0} + p_{e31} + p_{q31} \right ) \\ + \beta ^{2} \left [ 1+ \mathcal{B} \left ( \alpha ^{2} + \beta ^{2} \right ) \right ] \left ( \gamma N_{0} + p_{e32} + p_{q32} \right ) \\- c_{2} \left ( \alpha ^{4} A_{11}^{\left (2\right )} - \beta ^{4} A_{22}^{\left (2\right )} -2 \alpha ^{2} \beta ^{2} \left ( A_{12}^{\left (2\right )} + 2A_{66}^{\left (2\right )} \right ) \right ) \end{gathered}$$

(A4)

$$\begin{gathered} K_{34} = -c_{2} \left ( \alpha ^{4} \overline{A}_{11}^{(1)} +\beta ^{4} \overline{A}_{22}^{(1)} +2 \alpha ^{2} \beta ^{2} \left ( \overline{A}_{12}^{(1)} + 2 \overline{A}_{66}^{(1)} \right ) \right ) \\ K_{35} = -c_{2} \left ( \alpha ^{2} \tilde{A}_{13}^{(1)} +\beta ^{2} A_{23}^{\left (1\right )} \right) \\ K_{36} = -c_{2} \left ( \alpha ^{2} \overline{B}_{e31}^{(1)} +\beta ^{2} \overline{B}_{e32}^{(1)} \right ) \\K_{37} = -c_{2} \left ( \alpha ^{2} \overline{B}_{q31}^{(1)} +\beta ^{2} \overline{B}_{q32}^{(1)} \right ) \\ K_{44} = -c_{2} \left ( \alpha ^{2} \hat{A}_{55}^{(0)} +\beta ^{2} \hat{A}_{44}^{(0)} +\alpha ^{4} \overline{A}_{11}^{(f)} +\beta ^{4} \overline{A}_{22}^{(f)} +2 \alpha ^{2} \beta ^{2} \left ( \overline{A}_{12}^{(f)} +2 \overline{A}_{66}^{(f)} \right ) \right ) \\ K_{45} = -c_{2} \left ( \alpha ^{2} \left ( \tilde{A}_{13}^{(f)} + \hat{A}_{55}^{(0)} \right ) +\beta ^{2} \left ( \tilde{A}_{23}^{(f)} + \hat{A}_{44}^{(0)} \right ) \right ) \\ K_{46} = c_{2} \left ( \alpha ^{2} \left ( B_{e15}^{(g)} - \overline{B}_{e31}^{(f)} \right ) +\beta ^{2} \left ( B_{e24}^{(g)} - \overline{B}_{e32}^{(f)} \right ) \right ) \\ K_{47} = c_{2} \left ( \alpha ^{2} \left ( B_{q15}^{(g)} - \overline{B}_{q31}^{(f)} \right ) +\beta ^{2} \left ( B_{q24}^{(g)} - \overline{B}_{q32}^{(f)} \right ) \right ) \\ K_{55} = -c_{2} \left ( \tilde{A}_{33}^{(g)} +\alpha ^{2} \hat{A}_{55}^{(0)} + \beta ^{2} \hat{A}_{44}^{(0)} \right ) \\ K_{56} = c_{2} \left ( \alpha ^{2} B_{e15}^{(g)} +\beta ^{2} B_{e24}^{(g)} - \overline{B}_{e33}^{(g)} \right ) \\ K_{57} = c_{2} \left ( \alpha ^{2} B_{q15}^{(g)} +\beta ^{2} B_{q24}^{(g)} - \overline{B}_{q33}^{(g)} \right ) \\ K_{66} = c_{2} \left ( \alpha ^{2} p_{\varepsilon 11}^{(c2)} +\beta ^{2} p_{\varepsilon 22}^{(c2)} + p_{\varepsilon 33}^{(s2)} \right ) \\ K_{66} = c_{2} \left ( \alpha ^{2} p_{g11}^{(c2)} +\beta ^{2} p_{g22}^{(c2)} + p_{g33}^{(s2)} \right ) \\ K_{77} = c_{2} \left ( \alpha ^{2} p_{\mu 11}^{(c2)} +\beta ^{2} p_{\mu 22}^{(c2)} + p_{\mu 33}^{(s2)} \right ) \\ c_{2} =(1+ l_{m} ( \alpha ^{2} +\beta ^{2} ) \\ M_{11} =- \left [ 1+ \mathcal{B} \left ( \alpha ^{2} +\beta ^{2} \right ) \right ] m_{0} \\ M_{13} =\alpha \left [ 1+ \mathcal{B} \left ( \alpha ^{2} +\beta ^{2} \right ) \right ] m_{1} \\ M_{14} =\alpha \left [ 1+ \mathcal{B} \left ( \alpha ^{2} +\beta ^{2} \right ) \right ] m_{3} \\ \begin{gathered} M_{12} = M_{15} = M_{16} = M_{17} =0 \\ M_{22} =- \left [ 1+ \mathcal{B} \left ( \alpha ^{2} +\beta ^{2} \right ) \right ] m_{0} \\ M_{23} =\beta \left [ 1+ \mathcal{B} \left ( \alpha ^{2} +\beta ^{2} \right ) \right ] m_{1} \\ M_{24} =\beta \left [ 1+ \mathcal{B} \left ( \alpha ^{2} +\beta ^{2} \right ) \right ] m_{3} \\ M_{25} = M_{26} = M_{27} =0 \\ M_{33} =- \left [ 1+ \mathcal{B} \left ( \alpha ^{2} +\beta ^{2} \right ) \right ] m_{0} - \left ( \alpha ^{2} +\beta ^{2} \right ) \left [ 1+ \mathcal{B} \left ( \alpha ^{2} +\beta ^{2} \right ) \right ] m_{2} \\ M_{34} =- \left [ 1+ \mathcal{B} \left ( \alpha ^{2} +\beta ^{2} \right ) \right ] m_{0} - \left ( \alpha ^{2} +\beta ^{2} \right ) \left [ 1+ \mathcal{B} \left ( \alpha ^{2} +\beta ^{2} \right ) \right ] m_{4} \\ M_{35} =- \left [ 1+ \mathcal{B} \left ( \alpha ^{2} +\beta ^{2} \right ) \right ] m_{6} \\ M_{36} = M_{37} =0 \\ M_{44} =- \left [ 1+ \mathcal{B} \left ( \alpha ^{2} +\beta ^{2} \right ) \right ] m_{0} - \left ( \alpha ^{2} +\beta ^{2} \right ) \left [ 1+ \mathcal{B} \left ( \alpha ^{2} +\beta ^{2} \right ) \right ] m_{5} \end{gathered}\\ M_{45} =- \left [ 1+ \mathcal{B} \left ( \alpha ^{2} +\beta ^{2} \right ) \right ] m_{6} \\ M_{46} = M_{47} =0 \\ M_{55} =- \left [ 1+ \mathcal{B} \left ( \alpha ^{2} +\beta ^{2} \right ) \right ] m_{7} \end{gathered}$$

(A5)