1 Introduction

Nowadays nonlinear waves have received considerable interest in plasma physics because of their importance in the environment of space and in laboratory. Among the nonlinear wave structures, solitons are of particular interest for researchers as the solitons offer a rich physical insight underlying the nonlinear phenomena. During the last several decades, the propagation of ion acoustic solitary waves in plasma with unbounded planar geometry has been extensively studied theoretically and also in laboratory (Ikeji et al. 1970; Cairns et al. 1996; Yoshimura and Watanabe 1991; Konotop 1996; Hashimoto and Ono 1972; Duan et al. 1997; Mahmood and Saleem 2002). Solitary wave propagation in unmagnetized plasmas without the dissipation can be described by the Korteweg-de Vries (KdV) equation or Kadomtsev-Petviashvili (KP) equation. Ghosh and Bharuthram (2008) investigated the propagation of small but finite amplitude ion acoustic solitons and double layers in electronpositronion plasmas in presence of highly negatively charged impurities or dust. However, most of the studies done so far on ion acoustic waves were confined to the unbounded planer geometry, though recently some works have been published in which cylindrical and spherical ion acoustic and dust-ion acoustic waves have been discussed (Mamun and Shukla 2001, 2002; Xue 2003a, b; Sahu and Roychoudhury 2003). Eslami et al. (2011) studied the propagation of cylindrical and spherical electron-acoustic solitary waves in unmagnetized dusty plasma with superthermal ions and electrons. Misra et al. (2007) investigated the nonlinear propagation of electron acoustic solitary waves in an electron-ion quantum plasma in nonplanar geometry. Shah et al. (2010) studied nonplanar converging and diverging shock waves in the presence of thermal ions in electron-positron plasma. Tian and Gao (2005) have derived a spherical KP equation with symbolic computation for the dust ion acoustic waves with zenith-angle perturbation. They discussed the spherical strustures of the expanding dark and nebulon, shrinking dark and nebulon. Xue (2005) has investigated the dust-ion acoustic or dust acoustic waves with the combined effects of bounded cylindrical/spherical geometry and the transverse perturbation deriving the cylindrical/spherical KP equation (CKPE/SKPE). Recently, Wang and Zhang (2008) have investigated the dust acoustic waves in a three component ultra-cold Fermi dusty plasma by considering the two dimensional quantum hydrodynamic model in nonplanar geometry. However, in these studies electrons were assumed to be isothermal. But in a number of heliospheric environments the plasma contains the nonthermally distributed ions or electrons (Verheest 2000; Shukla and Mamun 2002; Verheest and Pillay 2008; Verheest 2009; Mamun et al. 1996; Mendoza-Briceno et al. 2000; Maharaj et al. 2004, 2006). Nonthermal ions have been observed in and around the Earth’s bowshock and foreshock (Asbridge et al. 1968; Feldman et al. 1983). Therefore nonthermality plays an important role in determining the nature of nonlinear waves. Following Cairns et al. (1995), we take the electrons to be nonthermally distributed. The motivation for this came from the observations of solitary structures with density depletions made by the Freja and Viking satellites (Boström 1992; Dovner et al. 1994). It was noticed by Cairns et al. (1995) that if the solitary electrostatic structures, observed by the Freja Satellite, are interpreted as ion sound solitons the difficulty arises that the standard Korteweg-de Vries (KdV) description predicts structures with enhanced rather than depleted density of the solitons. However, the presence of non-thermal electrons may allow existence of structures similar to those observed. Mamun (1997) and later Tang and Xue (2004), Pakzad (2009), Das et al. (2009) also considered the nonthermal electrons to study ion acoustic waves. Das and Chatterjee (2009) investigated large amplitude double layers in dusty plasma with non-thermal electrons and two temperature isothermal ions. Saha and Chatterjee (2009) studied obliquely propagating ion acoustic solitary waves in magnetized dusty plasma in the presence of nonthermal electrons. Alinejad (2010) studied dust ion-acoustic solitary and shock waves in a dusty plasma with non-thermal electrons. In the present paper, we studied the propagation of IAWs in an unmagnetized plasma with nonthermally distributed electrons in bounded nonplanar geometry. In fact it has been shown here that for certain values of β, the non isothermal parameter, cylindrical and spherical KP equations are not valid and one has to consider modified KP equation. For the special case, when the coefficient of nonlinearity vanishes, modified cylindrical and spherical KP equations are derived. The organization of the paper is as follows. In Sect. 2 the basic set of equations are given and cylindrical and spherical KP equations are derived. In Sect. 3 solitonic solutions of cylindrical and spherical KP equations and modified CKPE/SKPE are given. The numerical results are discussed in Sect. 4, while Sect. 5 is kept for conclusion.

2 Basic Equations and Derivation of the Nonplanar KP Equations

We consider a homogeneous, collisionless, unmagnetized plasma consisting of warm ions, and electrons obeying nonthermal velocity distribution. The basic system of normalized equations in cylindrical and spherical geometry in such a plasma model is governed by Tian and Gao (2005) Xue (2004, 2005), Wang and Zhang (2008) the following equations.

$$ \frac{\partial n_i}{\partial t}+\frac{1}{r^\nu}\frac{\partial}{\partial r}(r^\nu n_i u_i)+\frac{1}{r}\frac{\partial}{\partial \theta}(n_i v_i) +\frac{(\nu-1)\cot \theta}{r}n_i v_i=0 $$
(1)
$$ \frac{\partial u_i}{\partial t}+ u_i\frac{\partial u_i}{\partial r}+\frac{v_i}{r}\frac{\partial u_i}{\partial \theta} -\frac{v_i^2}{r}=-\frac{\partial \phi}{\partial r}-\frac{\sigma}{n_i}\frac{\partial p_i}{\partial r} $$
(2)
$$ \frac{\partial v_i}{\partial t}+ u_i\frac{\partial v_i}{\partial r}+\frac{v_i}{r}\frac{\partial v_i}{\partial \theta} +\frac{u_i v_i}{r}=-\frac{1}{r}\frac{\partial \phi}{\partial \theta}-\frac{1}{r}\frac{\sigma}{n_i}\frac{\partial p_i}{\partial \theta} $$
(3)
$$ \frac{\partial p_i}{\partial t}+ u_i\frac{\partial p_i}{\partial r}+\frac{v_i}{r}\frac{\partial p_i}{\partial \theta}+3p_i\left[\frac{1}{r^\nu}\frac{\partial}{\partial r}(r^\nu u_i)+\frac{1}{r}\frac{\partial v_i}{\partial \theta}+\frac{(\nu-1)\cot \theta}{r} v_i\right]=0 $$
(4)
$$ \frac{1}{r^\nu}\frac{\partial}{\partial r} \left(r^\nu \frac{\partial \phi}{\partial r}\right)+\frac{1}{r^2}\frac{\partial^2 \phi}{\partial \theta^2} +\frac{(\nu-1)\cot \theta}{r^2}\frac{\partial \phi}{\partial \theta}=n_e-n_i $$
(5)

where ν = 0, for one dimensional geometry and ν = 1, 2 for cylindrical and spherical geometry respectively. In the above equations, the subscripts i and e refer to ion and electron respectively. r, θ are the radial and angle coordinates and u i , v i are the ion fluid speed in r and θ directions respectively. n i is the ion number density normalized to its unperturbed equilibrium plasma density n i0, (u i , v i ) are the ion fluid speeds normalized to the ion acoustic velocity \(v_s=(k_BT_e/m_i)^{\frac{1}{2}}, p_i\) and ϕ are normalized to n i0 T i and k B T e /e respectively. The time and space variables are in units of the ion plasma period \({\omega_{Pi}}^{-1}=(m_i/4 \pi n_{i0} e^2)^{\frac{1}{2}}\) and the Debye radius \(\lambda_{Dm}=(k_BT_e/4 \pi n_{i0} e^2)^{\frac{1}{2}}\), respectively. σ = T i /T e is the ion to electron temperature ratio.

The electrons are assumed to be nonthermally distributed and their distribution function is taken as (Cairns et al. 1995)

$$ f(E)=n_{i0}(1+\alpha E^2)\exp(-E)/(1+3 \alpha) $$
(6)

where E is the nonthermalized electron energy. Consequently the electron number density is given by Cairns et al. (1995)

$$ n_e=(1-\beta\phi+\beta \phi^2)\exp(\phi) $$
(7)

where

$$ \beta=\frac{4\alpha}{1+3\alpha} $$
(8)

Here β denotes the ratio of the high energy electrons to the Boltzmann distributed electrons. It is clear that Eq. (7) expresses the isothermally distributed electrons when β = 0 (i.e. α = 0). The parameter α represents the nonthermality of electrons distribution, i.e. determining the fast particles presented in our plasma model. Also it is assumed that v thi  <  < v s  <  < v the , so that Landau damping can be neglected, where v thi is the ion thermal velocity and v the is the electron thermal velocity.

To derive the cylindrical and spherical KP equations we use the stretched coordinates (Johnson 1980; Huang et al. 1998)

$$ \xi={\epsilon}^{1/2}(r-v_0 t),\quad \eta={\epsilon}^{-1/2}\theta \quad {and} \quad \tau={\epsilon}^{3/2}t $$
(9)

Furthermore, the plasma parameters \(\Uppsi\equiv[n_i,u_i,p_i,\phi]\) are expanded as power series in \(\epsilon\) about their equilibrium values as

$$ \Uppsi=\sum_{s=0}^{\infty}\epsilon^s\Uppsi^{(s)}, $$
(10)

with the conditions

$$ n^{(0)}_i=p^{(0)}_i=1, \quad u^{(0)}_i=\phi^{(0)}=0, $$
(11)

while v i is expanded as

$$ v_i={\epsilon}^{3/2} {v}^{(1)}_i+{\epsilon}^{5/2} {v}^{(2)}_i+ \cdot\cdot\cdot, $$
(12)

Substituting (10–12) into (1–5), we obtain from the lowest order in \(\epsilon\),

$$ \begin{aligned} & n^{(1)}_i=\frac{1}{v^2_0-3\sigma}\phi^{(1)}, \quad u^{(1)}_i=\frac{v_0}{v^2_0-3\sigma}\phi^{(1)},\quad p^{(1)}_i=\frac{3}{v^2_0-3\sigma}\phi^{(1)},\\ & {\quad \quad \,v_0 =\sqrt{{\frac{1}{1-\beta}}+3\sigma},\quad \frac{\partial v^{(1)}_i}{\partial \xi}=\frac{1}{(v^2_0-3\sigma)\tau}\frac{\partial \phi^{(1)}}{\partial \tau}.} \end{aligned} $$
(13)

To next higher order in \(\epsilon\), we obtain the following set of equations,

$$ \frac{\partial n^{(1)}_i}{\partial \tau}-v_0 \frac{\partial n^{(2)}_i}{\partial \xi}+\frac{\partial}{\partial \xi}(n^{(1)}_i u^{(1)}_i)+\frac{\partial u^{(2)}_i}{\partial \xi}+\frac{1}{v_0\tau}\left(\nu u^{(1)}_i+\frac{\partial v^{(1)}_i}{\partial \eta}+\frac{\nu-1}{\eta}v^{(1)}_i\right)=0 $$
(14)
$$ \frac{\partial u^{(1)}_i}{\partial \tau}-v_0 \frac{\partial u^{(2)}_i}{\partial \xi}+u^{(1)}_i\frac{\partial u^{(1)}_i}{\partial \xi}=-\frac{\partial \phi^{(2)}}{\partial \xi}-\sigma \frac{\partial p^{(2)}_i}{\partial \xi}+\sigma n^{(1)}_i\frac{\partial p^{(1)}_i}{\partial \xi} $$
(15)
$$ \frac{\partial p^{(1)}_i}{\partial \tau}-v_0 \frac{\partial p^{(2)}_i}{\partial \xi}+u^{(1)}_i\frac{\partial p^{(1)}_i}{\partial \xi}+3\frac{\partial u^{(2)}_i}{\partial \xi}+3p^{(1)}_i \frac{\partial u^{(1)}_i}{\partial \xi}+\frac{3}{v_0\tau}\left(\nu u^{(1)}_i+\frac{\partial v^{(1)}_i}{\partial \eta}+\frac{\nu-1}{\eta}v^{(1)}_i\right)=0 $$
(16)
$$ \frac{\partial^2 \phi^{(1)}}{\partial \xi^2}=(1-\beta)\phi^{(2)}+\frac{{\phi^{(1)}}^2}{2}-n^{(2)}_i $$
(17)

Combining Eqs. (14–17), we get a modified cylindrical or spherical KP-equation

$$ \frac{\partial }{\partial \xi}\left[\frac{\partial \phi^{(1)}}{\partial \tau}+\frac{\nu}{2\tau}\phi^{(1)} +A\phi^{(1)}\frac{\partial \phi^{(1)}}{\partial \xi} +B\frac{\partial^3 \phi^{(1)}}{\partial \xi^3}\right]+\frac{1}{2v_0\tau^2}\left(\frac{\partial^2 \phi^{(1)}}{\partial \eta^2}+\frac{\nu-1}{\eta}\frac{\partial \phi^{(1)}}{\partial \eta} \right)=0 $$
(18)

where

$$ A=\frac{v_0\{3(1-\beta)^2+12(1-\beta)^3\sigma-1\}}{2\{(1-\beta)+3(1-\beta)^2\sigma\}} \quad \hbox{and}\quad B=\frac{v_0}{2\{(1-\beta)+3(1-\beta)^2\sigma\}} $$
(19)

Thus the CKPE (ν = 1) and the SKPE (ν = 2) of the ion acoustic solitary waves (IASWs) are obtained as, respectively

$$ \frac{\partial }{\partial \xi}\left[\frac{\partial \phi^{(1)}}{\partial \tau}+\frac{\phi^{(1)}}{2\tau} +A\phi^{(1)}\frac{\partial \phi^{(1)}}{\partial \xi} +B\frac{\partial^3 \phi^{(1)}}{\partial \xi^3}\right]+\frac{1}{2v_0\tau^2}\frac{\partial^2 \phi^{(1)}}{\partial \eta^2}=0 $$
(20)
$$ \frac{\partial }{\partial \xi}\left[\frac{\partial \phi^{(1)}}{\partial \tau}+\frac{\phi^{(1)}}{\tau} +A\phi^{(1)}\frac{\partial \phi^{(1)}}{\partial \xi} +B\frac{\partial^3 \phi^{(1)}}{\partial \xi^3}\right]+\frac{1}{2v_0\tau^2}\left(\frac{\partial^2 \phi^{(1)}}{\partial \eta^2}+\frac{1}{\eta}\frac{\partial \phi^{(1)}}{\partial \eta} \right)=0 $$
(21)

It is seen that for \(\sigma=\frac{1-3(1-\beta)^2}{12(1-\beta)^3}, A=0\), whence the coefficient of nonlinearity vanishes. Then one has to consider the modified KP (MKP) equation. For example if σ = 1/6 and β = 1/2(α = 1/5), then A = 0.

When A = 0, we introduce the following stretched coordinates, \(\xi=\epsilon(r-v_0 t),\quad\eta={\epsilon}^{-1}\theta,\quad \tau=\epsilon^3t\) and expand n i , u i , p i and ϕ in a power series of \(\epsilon\) as given by (10–12) and develop equations in various powers of \(\epsilon\).

To lowest order in \(\epsilon\), Eqs. (1–5) give

$$ n^{(1)}_i=\frac{1}{v^2_0-3\sigma}\phi^{(1)}, u^{(1)}_i=\frac{v_0}{v^2_0-3\sigma}\phi^{(1)}, p^{(1)}_i=\frac{3}{v^2_0-3\sigma}\phi^{(1)} , v_0=\sqrt{\frac{3\sigma(1-\beta)+1}{1-\beta}},\hbox{ and} $$

\(\frac{\partial v^{(1)}_i}{\partial \xi}=\frac{1}{(v^2_0-3\sigma)\tau}\frac{\partial \phi^{(1)}}{\partial \tau}\).

To next higher order in \(\epsilon\), we obtain

$$ \begin{aligned} (1-\beta)v_0u^{(2)}_i-\frac{1-\beta}{2}(u^{(1)}_i)^2- \frac{(1-\beta)\sigma}{v_0}\left(\frac{6}{v_0}(u^{(1)}_i)^2+3u^{(2)}_i\right)&\\ +\frac{3(1-\beta)\sigma}{2}(n^{(1)}_i)^2+\frac{1}{2}(\phi^{(1)})^2- \frac{1}{v_0}u^{(2)}_i-\frac{1}{v_0}n^{(1)}_iu^{(1)}_i=0&\\ \end{aligned} $$
(22)

If \(v_0=\sqrt{\frac{1}{1-\beta}+3\sigma}\) and \(\sigma=\frac{1-3(1-\beta)^2}{12(1-\beta)^3}\), then Eq. (22) becomes an identity. But we have already found that \(v_0=\sqrt{\frac{1}{1-\beta}+3\sigma}\) and \(\sigma=\frac{1-3(1-\beta)^2}{12(1-\beta)^3}\), when A = 0. So Eq. (22) does not give us any new information.

To next higher order in \(\epsilon\), we obtain the following set of equations

$$ \frac{\partial n^{(1)}_i}{\partial \tau}-v_0 \frac{\partial n^{(3)}_i}{\partial \xi}+\frac{\partial}{\partial \xi}\left(u^{(3)}_i+n^{(1)}_i u^{(2)}_i+n^{(2)}_i u^{(1)}_i\right) +\frac{\nu u^{(1)}_i}{v_0 \tau}+\frac{1}{v_0 \tau}\left(\frac{\partial v^{(1)}_i}{\partial \eta}+\frac{\nu-1}{\eta}v^{(1)}_i\right)=0 $$
(23)
$$ \frac{\partial u^{(1)}_i}{\partial \tau}-v_0 \frac{\partial u^{(3)}_i}{\partial \xi}+u^{(1)}_i \frac{\partial u^{(2)}_i}{\partial \xi}+u^{(2)}_i \frac{\partial u^{(1)}_i}{\partial \xi}+\sigma \frac{\partial p^{(3)}_i}{\partial \xi} -\sigma n^{(1)}_i \frac{\partial p^{(2)}_i}{\partial \xi} -\sigma n^{(2)}_i \frac{\partial p^{(1)}_i}{\partial \xi} +\sigma (n^{(1)}_i)^2 \frac{\partial p^{(1)}_i}{\partial \xi} =-\frac{\partial \phi^{(3)}}{\partial \xi} $$
(24)
$$ \begin{array}{c} \frac{\partial p^{(1)}_i}{\partial \tau}-v_0 \frac{\partial p^{(3)}_i}{\partial \xi}+u^{(1)}_i \frac{\partial p^{(2)}_i}{\partial \xi}+u^{(2)}_i \frac{\partial p^{(1)}_i}{\partial \xi}+3\frac{\partial u^{(3)}_i}{\partial \xi} +3 p^{(1)}_i \frac{\partial u^{(2)}_i}{\partial \xi} +3p^{(2)}_i \frac{\partial u^{(1)}_i}{\partial \xi} \\ +\frac{3 \nu u^{(1)}_i}{v_0 \tau}+\frac{3}{v_0 \tau}\left(\frac{\partial v^{(1)}_i}{\partial \eta}+\frac{\nu-1}{\eta}v^{(1)}_i\right) =0 \end{array} $$
(25)
$$ \frac{\partial^2 \phi^{(1)}}{\partial \xi^2}-(1-\beta) \phi^{(3)}-\phi^{(1)}\phi^{(2)}-\frac{1+3\beta}{6}(\phi^{(1)})^3+n^{(3)}_i=0 $$
(26)

Combining Eqs. (23–26), a modified KP equation is obtained

$$ \frac{\partial }{\partial \xi}\left[\frac{\partial \phi^{(1)}}{\partial \tau}+\frac{\nu}{2\tau}\phi^{(1)} +A_1(\phi^{(1)})^2\frac{\partial \phi^{(1)}}{\partial \xi} +B_1\frac{\partial^3 \phi^{(1)}}{\partial \xi^3}\right]+\frac{1}{2v_0\tau^2}\left(\frac{\partial^2 \phi^{(1)}}{\partial \eta^2}+\frac{\nu-1}{\eta}\frac{\partial \phi^{(1)}}{\partial \eta} \right)=0 $$
(27)

where

$$ \begin{array}{c} A_1=\frac{(1-\beta)+12(1-\beta)^2 \sigma-3(1-\beta)^4\sigma-\frac{1+3\beta}{2}+\frac{1}{2(1-\beta)}}{2 v_0 (1-\beta)^2}\\ \hbox{and}\quad B_1=\frac{1}{2 v_0 (1-\beta)^2}. \end{array} $$
(28)

3 Solitonic Solutions of the CKPE and SKPE

It is possible to find a special solitary wave solution for the Eq. (18) by using a suitable transformation (Johnson 1980; Huang et al. 1998). Equation (18) can be reduced to the standard KdV equation using the following coordinate transformations

$$ \zeta=\xi-\frac{v_0}{2}\eta^2\tau, \quad \widetilde{\phi}^{(1)}(\zeta,\tau)=\phi^{(1)}(\xi,\eta,\tau), \quad \tau'=\tau $$
(29)

Using this transformations, Eq. (18) reduces to the following standard KdV equation,

$$ \frac{\partial \widetilde{\phi}^{(1)}}{\partial \tau'} +A\widetilde{\phi}^{(1)}\frac{\partial \widetilde{\phi}^{(1)}}{\partial \zeta} +B\frac{\partial^3 \widetilde{\phi}^{(1)}}{\partial \zeta^3}=0. $$
(30)

In deriving Eq. (30) we have used the boundary conditions \(\widetilde{\phi}^{(1)}\rightarrow 0, d^2 \widetilde{\phi}^{(1)}/d\xi^2\rightarrow 0\) as \(\xi\rightarrow \infty\). Using Eqs. (29) and (30), we find that Eq. (18) has the travelling wave solution of the form,

$$ \phi^{(1)}=\frac{3U}{A}\sec h^2\left[\sqrt{\frac{U}{4B}}\left\{\xi-\left(U+\frac{v_0}{2}\eta^2\right) \tau\right\}\right]. $$
(31)

where U is the soliton velocity. The amplitude and width of the solitary waves are \(\frac{3U}{A}\) and \(\sqrt{\frac{4B}{U}}\), respectively. For the existence of soliton, \(\frac{U}{B}\) must be positive, otherwise soliton solution (31) would be destroyed. Equation (31) is a special solution which is independent of ν. However, one can not get back the planar geometry solution because there does not exist any value of ν which will simultaneously remove the terms associated with 1/τ and 1/η in Eq. (18).

Using the same set of transformations, given in Eqs. (29, 27) reduces to the modified KdV equation,

$$ \frac{\partial \widetilde{\phi}^{(1)}}{\partial \tau} +A_1(\widetilde{\phi}^{(1)})^2\frac{\partial \widetilde{\phi}^{(1)}}{\partial \zeta} +B_1\frac{\partial^3 \widetilde{\phi}^{(1)}}{\partial \zeta^3}=0. $$
(32)

Using Eqs. (29) and (32) it is found that Eq. (27) has the following stationary solution,

$$ \phi^{(1)}=\sqrt{\frac{6 U}{A_1}}\sec h\left[\sqrt{\frac{U}{B_1}}\left\{\xi-\left(U+\frac{v_0}{2}\eta^2\right) \tau\right\}\right]. $$
(33)

Conditions for existence of solitonic solution (31) is U/B > 0. For Eq. (33) to be valid we must have U/B 1 > 0 and U/A 1 > 0. It may be mentioned that A 1 does not vanish for any real positive values of β if σ < 0.49. This has been checked numerically. Analytically one can see that when σ = 0, A 1 = 0 only for imaginary values of β. However, as mentioned earlier, there is a critical value of β, say β c (which will depend on the temperature ratio parameter σ) for which A = 0, and beyond which A will change sign. Thus for β > β c , Eq. (31) will represent a dip soliton instead of a hump soliton (assuming U > 0). This is the reason for considering nonthermal electrons to explain the Freja satellite data.

Again there are many methods to solve Eq. (18), such as the F-expansion method (Wang et al. 2005), the extended Jacobian elliptic function expansion method (Yan 2002), the generalized projected Ricatti equation expansion method (Dai et al. 2006) and so on. Of the three methods, discussed in references Wang et al. (2005), Yan (2002), and Dai et al. (2006), respectively we found that the generalized projected Ricatti equation expansion method used in reference Dai et al. (2006) is the most suitable one for our purpose. Using this method the solutions for CKPE and SKPE of IASWs are respectively given by Misra et al. (2007), Tian and Gao (2005),

$$ \begin{aligned} \phi^{(1)}=&-\frac{4C^2BR}{A}+\frac{\eta\alpha_1(\tau)}{CA\tau} -\frac{\alpha_1^2(\tau)}{2C^2Av_0\tau^2}-\frac{1}{CA} \frac{d\alpha_1(\tau)}{d\tau}\eta-\frac{1}{CA}\frac{d\alpha_2(\tau)}{d\tau}\\ &+\frac{12BC^2R}{A}\sec h^2\left[\sqrt{R}\left(C\xi- \frac{Cv_0\tau}{2}\eta^2+\alpha_1(\tau)\eta+\alpha_2(\tau)\right)\right], \end{aligned} $$
(34)
$$ \phi^{(1)}=-\frac{4C^2B}{A}-\frac{1}{CA}\frac{d\alpha_1(\tau)}{d\tau} +\frac{12BC^2}{A}\sec h^2\left[C\xi-\frac{Cv_0\tau}{2}\eta^2+\alpha_1(\tau)\right], $$
(35)

where C and R are positive arbitrary constant and α1(τ), α2(τ) are arbitrary function of τ. It can be seen that Eq. (31) is a special case of the solution given in (34) if one takes \(C=\sqrt{U/4B}, \alpha_1(\tau)=0, \alpha_2(\tau)=-CU\tau, R=1\). Again solution (35) reduces to the solution (31), if one takes \(C=\sqrt{U/B}, \alpha_1(\tau)=-CU\tau\). Here it should be noted that solutions (34) and (35) can be converted to nebulonic solutions as given in Eq. (25) by Tian and Gao (2005) (replacing C by β1 and α = 0). However, in our solution the effect of nonthermal parameter lies in the expression of A and B.

4 Results and discussion

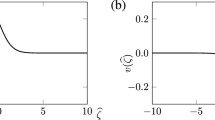
In this section we numerically investigate the parametric dependence of IASWs, given by (31), (33), (34) and (35). In Figs. 1a, b and 2 we plot the special solution (31) for different values of α and σ respectively. It is important to note that compressive and rarefactive solitons can exist in our present plasma model. We can see that the electrostatic potential will change from positive to negative when α increases and σ is fixed. Whether the electrostatic potential is positive or negative depends on the sign of the ratio of coefficient of nonlinear term to dispersive term (A/B). It is also seen that the amplitude of the solitary waves increases for hump soliton and decreases for dip soliton with the increase of α, if the other parameters are kept fixed. This is owing to the fact that the increasing number of nonthermal electrons decreases the nonlinearity and increase the dispersion. This shows that the properties of soliton are affected by the presence of nonthermally distributed electrons. This is in good agreement with the result of Mamun (1997) that the presence of nonthermal electrons changes the properties of the solitary waves and that for a suitable nonthermal electron distribution it is possible to obtain both positive (compressive) and negative (rarefactive) solitary waves. Also, it is found that the amplitude of the solitary waves decreases with the increase of σ when α is kept fixed. Actually, the increase in ion temperature can be depicted as increase in ion thermal velocities as a result of which the convection thrives and at the same time dispersion debilitates in the system, consequently the soliton amplitude is decreased. The behavior is similar to the results obtained by Mamun (1997) in a plasma system consisting of warm adiabatic ions and nonthermally distributed electrons. In Fig. 3 the coefficient of nonlinear term A against β and σ for the solution (31) is plotted. It is seen that the nonlinear term decreases with the increase of β and becomes zero when β satisfies the relation \(\beta=\beta_c=\frac{1-3(1-\beta)^2}{12(1-\beta)^3}=\sigma\). When β becomes greater than β c , the soliton becomes a dip soliton. So the presence of nonthermal electrons may completely change the nature of solitons. Figure 4 shows the evolution of solitary wave structures for several values of η for the solution (33). In Fig. 5a and b we present the cylindrical soliton solutions (34) for small and large values of η. It is interesting to note that the transverse co-ordinate η will significantly affect the structure of solitons. It is seen that the solitary waves propagate along a route of sinusoid as time goes on depending upon the choice of arbitrary functions α1 and α2 as sinusoid. Figure 6 shows the effect of α on the propagation of IASWs given by (34). It is found that the amplitude of the cylindrical solitons increases with the nonthermal parameter α. In Fig. 7 we plot the solutions of cylindrical and spherical solitons for different values of α. It is seen that the spherical and cylindrical solitons attend their respective peaks at different values of ξ, when the transverse co-ordinate η is fixed. This figure reveals that the amplitude of the spherical solitons is larger than that of the cylindrical one. It is also found that spherical solitary waves travel faster than cylindrical solitary waves. Figure 8 shows an interesting phenomena viz. the soliton changes its position due to the transverse co-ordinate η as time goes on. It forms part of a loop soliton. It is to be noted that this kind of phenomena has been observed in coronal plasma.

Fig. 1
figure 1

a Plot of ϕ(1) against ξ for different values of α = 0.01 (solid line), α = 0.05 (dotted line), α = 0.1 (dashed line), for the solution (31), where σ = 0.1, τ = 2, η = 0.1, U = 0.03. b Plot of ϕ(1) against ξ for different values of α = 0.2 (solid line), α = 0.22 (dotted line), α = 0.25 (dashed line), for the solution (31), where σ = 0.1, τ = 2, η = 0.1, U = 0.03

Full size image
Fig. 2
figure 2

Plot of ϕ(1) against ξ for different values of σ = 0.01 (solid line), σ = 0.1 (dotted line), σ = 0.2 (dashed line), for the solution (31), where α = 0.05 and the other parameters are same as Fig. 1

Full size image
Fig. 3
figure 3

(color online) Three dimensional plot of A against β and σ for the expression of A in (19)

Full size image
Fig. 4
figure 4

Plot of ϕ(1) against ξ for different values of η = 0.1 (solid line), η = 1 (dotted line), η = 2 (dashed line), η = 3 (dot-dashed line), for the solution (33) where α = 1/5 i.e. (β = 1/2), σ = 1/6, η = 0.1, τ = 2, U = 0.05

Full size image
Fig. 5
figure 5

(color online) Plot of the solitary wave solution of cylindrical KP equation (Eq. 34) a for η = 0.02 and b for η = 2, where the other parameters are \(C=4, R=0.03, \alpha=0.01, \sigma=0.5, \alpha_1(\tau)=\sin(3\tau), \alpha_2(\tau)=\cos(3\tau)\)

Full size image
Fig. 6
figure 6

(color online) Plot of the solitary wave solution of cylindrical KP equation (Eq. 34) against ξ and α, where C = 0.7, R = 1.5, σ = 0.2, η = 0.1 and τ = 4

Full size image
Fig. 7
figure 7

Plot of the solitary wave solution of cylindrical and spherical KP equation (Eqs. 34, 35) against ξ for several values of α = 0.01 (solid line), α = 0.03 (dotted line), α = 0.05 (dashed line), where η = 0.1, C = 1, R = 0.03, σ = 0.01 and τ = 2

Full size image
Fig. 8
figure 8

(color online) Plot of the solitary wave solution of cylindrical KP equation (Eq. 34) against ξ and η, where the other parameters are C = 3, R = 0.05, α = 0.01, σ = 0.5 and τ = 4

Full size image

5 Conclusion

In the present study we have investigated the nature of nonlinear propagation of IASWs in an unmagnetized collisionless plasma with nonthermally distributed electrons and warm ions in nonplanar geometries. We have derived the CKPE/SKPE and modified CKPE/SKPE (when the coefficients of the nonlinear terms in CKPE and SKPE vanish) using the standard reductive perturbation technique. It is seen that nonthermally distributed electrons have a very significant role in the formation of the propagation of IASWs in an unmagnetized plasma in nonplanar geometries. When β, the nonthermal distribution parameter becomes large the nature of solitons completely changes. It is also seen that the nature of propagation of solitary structures changes with the transverse perturbation in nonplanar geometry. We hope that the present investigation on the properties of solitary waves would be helpful for better understanding of the nonlinear features of solitary waves in astrophysical as well as in laboratory plasmas in a nonplanar geometry frame work.