Skip to main content
SpringerLink
Log in

Nonlinear vibration of initially stressed hybrid composite plates on elastic foundations

  • Published:
Mechanics of Composite Materials Aims and scope

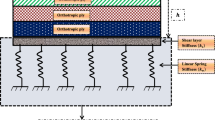
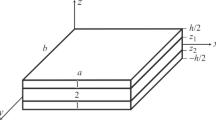
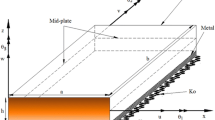
Nonlinear vibration equations of motion based on the Mindlin plate theory are derived for a hybrid composite plate with an initial stress on elastic foundations. Using the governing equations derived, the nonlinear vibration behavior of an initially stressed hybrid composite plate on Pasternak and Winkler elastic foundations is studied. The initial stress is taken to be a combination of a pure bending stress and a tensile stress in the plane of the plate. The Galerkin method is employed to reduce the governing nonlinear partial differential equations to ordinary nonlinear differential equations, and the Runge–Kutta method is used to obtain the nonlinear frequencies. The linear frequency can be calculated by neglecting the nonlinear terms in the ordinary nonlinear differential equations. The results obtained reveal that the foundation stiffness and initial stresses lead to a drastic change in the nonlinear vibration behavior of the plate. The effects of various parameters on the nonlinear vibration of hybrid composite plates are investigated and discussed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

References

  1. M. Amabili, “Nonlinear vibrations of rectangular plates with different boundary conditions: Theory and experiments,” Comput. Struct., 82, 2587–2605 (2004).

    Article  Google Scholar 

  2. A. K. Onkar and D. Yadav, “Forced nonlinear vibration of laminated composite plates with random material properties,” Comp. Struct., 70, 334–342 (2005).

    Article  Google Scholar 

  3. M. Ye, Y. Sun, W. Zhang, X. Zhan, and Q. Ding, “Nonlinear oscillations and chaotic dynamics of an antisymmetric cross-ply laminated composite rectangular thin plate under parametric excitation,” J. Sound Vibr., 287, 723–758 (2005).

    Article  Google Scholar 

  4. Z. Kazanci and Z. Mecitoglu, “Nonlinear damped vibrations of a laminated composite plate subjected to blast load,” AIAA J., 44, 2002–2008 (2006).

    Article  Google Scholar 

  5. M. K. Singha and R. Daripa, “Nonlinear vibration of symmetrically laminated composite skew plates by finite element method,” Int. J. Non-Linear Mech., 42, 1144–1152 (2007).

    Article  Google Scholar 

  6. X. Huang, X. L. Jia , J. Yang, and Y. Wu, “Nonlinear vibration and dynamic response of three-dimensional braided composite plates,” Mech. Adv. Mat. Struct., 15, 53–63 (2008).

    Article  Google Scholar 

  7. M. Amabili and S. Farhadi, “Shear deformable versus classical theories for nonlinear vibrations of rectangular isotropic and laminated composite plates,” J. Sound Vibr., 320, 649–667 (2009).

    Article  Google Scholar 

  8. H. S. Shen, J. Yang and L. Zhang, “Free and forced vibration of Reissner-Mindlin plates with free edges resting on elastic foundations,” J. Sound Vibr., 244, 299–320 (2001).

    Article  Google Scholar 

  9. X. L. Huang and J. J. Zheng, “Nonlinear vibration and dynamic response of simply supported shear deformable laminated plates on elastic foundations,” Engng. Struct., 25, 1107–1119 (2003).

    Article  Google Scholar 

  10. P. Malekzadeh and G. Karami, “Vibration of non-uniform thick plates on elastic foundation by differential quadrature method,” Engng. Struct., 26, 1473–1482 (2004).

    Article  Google Scholar 

  11. D. Zhou, S. H. Lo, F. T. K. Au, and Y. K. Cheung, “Three-dimensional free vibration of thick circular plates on Pasternak foundation,” J. Sound Vibr., 292, 726–741 (2006).

    Article  Google Scholar 

  12. Z. Celep and K. Culer, “Axisymmetric forced vibrations of an elastic free circular plate on a tensionless two parameter foundation,” J. Sound Vibr., 301, 495–509 (2007).

    Article  Google Scholar 

  13. P. Y. Tovstik, “The vibrations and stability of a prestressed plate on an elastic foundation,” J. Appl. Math. Mech., 73, 77–87 (2009).

    Article  Google Scholar 

  14. F. Pellicano and F. Mastroddi, “Nonlinear dynamics of a beam on elastic foundation,” Non. Dyn., 14, 335–355 (1997).

    Article  Google Scholar 

  15. B. P. Patel, M. Ganapathi and M. Touratier, “Nonlinear free flexural vibrations/post-buckling analysis of laminated orthotropic beams/columns on a two parameter elastic foundation,” Comp. Struct., 46, 189–196 (1999).

    Article  Google Scholar 

  16. A. Lal, B. N. Singh, and R. Kumar, “Nonlinear free vibration of laminated composite plates on an elastic foundation with random system properties,” Int. J. Mech. Sci., 50, 1203–1212 (2008).

    Article  Google Scholar 

  17. A. Lal and B. N. Singh, “Stochastic nonlinear free vibration of laminated composite plates resting on an elastic foundation in thermal environments,” Comput. Mech., 44, 15–29 (2009).

    Article  Google Scholar 

  18. R. D. Chien and C. S. Chen, “Nonlinear vibration of laminated plates on an elastic foundation,” Thin-Walled Struct., 44, 852–860 (2006).

    Article  Google Scholar 

  19. C. M. Wang, C. Wang, and K. K. Ang, “Vibration of initially stressed Reddy plates on a Winkler–Pasternak foundation,” J. Sound Vibr., 204, 203–212 (1997).

    Article  Google Scholar 

  20. K. G. Muthurajan, K. Sankaranarayanasamy, S. B. Tiwari and B. N. Rao, “Nonlinear vibration analysis of initially stressed thin laminated rectangular plates on elastic foundations,” J. Sound Vibr., 282, 949–969 (2005).

    Article  Google Scholar 

  21. A. Benjeddou, J. F. Deu, and S. Letombe, “Free vibrations of simply supported piezoelectric adaptive plates: An exact sandwich formulation,” Thin-Walled Struct., 40, 573–593 (2002).

    Article  Google Scholar 

  22. C. Ossadzow and M. Touratier, “Multilayered piezoelectric refined plate theory,” AIAA J., 41, 90–99 (2003).

    Article  Google Scholar 

  23. S. Kapuria and G. G. S. Achary, “Exact 3D piezoelasticity solution of hybrid cross-ply plates with damping under harmonic electromechanical loads,” J. Sound Vibr., 282, 617–634 (2005).

    Article  Google Scholar 

  24. Y. Chen, K. Lu, T. Zhou, T. Liu, and C. Lu, “Study of a mini-ultrasonic motor with square metal bar and piezoelectric plate hybrid,” Jap. J. Appl. Phy., 45, 4780–4781 (2006).

    Article  CAS  Google Scholar 

  25. P. Dash and B. N. Singh, “Nonlinear free vibration of a piezoelectric laminated composite plate,” Finite Ele. Anal. Des., 45, 686–694 (2009).

    Article  Google Scholar 

  26. B. P. Patel, M. Ganapathi, and D. P. Makhecha, “Hygrothermal effects on the structural behaviour of thick composite laminates using higher-order theory,” Comp. Struct., 56, 25–34 (2002).

    Article  Google Scholar 

  27. Y. S. Lee and Y. W. Kim, “Analysis of nonlinear vibration of hybrid composite plates,” Comput. Struct., 61, 573–578 (1996).

    Article  Google Scholar 

  28. B. Harras, R. Benamar, and R. G. White, “Experimental and theoretical investigation of the linear and non-linear dynamic behaviour of a glare 3 hybrid composite panel,” J. Sound Vibr., 252, 281–315 (2002).

    Article  Google Scholar 

  29. C. S. Chen and C. P. Fung, “Nonlinear vibration of an initially stressed hybrid composite plate,” J. Sound Vibr., 274, 1013–1029 (2004).

    Article  Google Scholar 

  30. C. S. Chen, W. S. Cheng, and A. H. Tan, “Nonlinear vibration of initially stresses plates with initial imperfections,” Thin-Walled Struct., 43, 33–45 (2005).

    Article  Google Scholar 

  31. C. S. Chen, C. P. Fung, and J. G. Yang, “Assessment of plate theories for initially stressed hybrid laminated plates,” Comp. Struct., 88, 195–201 (2009).

    Article  Google Scholar 

  32. C. S. Chen, W. R. Chen, and R. D. Chien, “Stability of parametric vibrations of hybrid laminated plates,” Eur. J. Mech. A/Solids, 28, 329–337 (2009).

    Article  Google Scholar 

  33. E. J. Brunell and S. R. Robertson, “Vibrations of an initially stressed thick plate,” J. Sound Vibr., 45, 405–416 (1976).

    Article  Google Scholar 

  34. C. S. Chen, J. R. Hwang, and J. L. Doong, “Large-amplitude vibration of plates according to a modified higher-order deformation theory,” Int. J. Solids Struct., 38, 8563–8583 (2001).

    Article  Google Scholar 

  35. C. S. Chen and C. P. Fung, “Nonlinear vibration of an initially stressed hybrid composite plate,” J. Sound Vibr., 274, 1013–029 (2004).

    Article  Google Scholar 

  36. C. S. Chen, “Analysis of nonlinear vibration of a composite laminated plate,” Comp. Part B: Engng., 38, 437–447 (2007).

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Lunghwa University of Science and Technology, Guishan Shiang, 33306, Taiwan

    Ching-Long Wei & Chun-Sheng Chen

  2. Department of Mechanical Engineering, Hwa Hsia Institute of Technology, New Taipei City, 23568, Taiwan

    Chia-Sheng Shih

  3. Department of Civil Engineering, National Taipei University of Technology, Taipei, 10608, Taiwan

    Yi-Chen Chang

Authors
  1. Ching-Long Wei
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Chun-Sheng Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Chia-Sheng Shih
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Yi-Chen Chang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Chia-Sheng Shih.

Additional information

Russian translation published in Mekhanika Kompozitnykh Materialov, Vol. 48, No. 4, pp. 679-700, July-August, 2012.

Appendix

Appendix

$$ \begin{array}{*{20}{c}} {\left( {{u_{x,y}} + {u_{y,x}}} \right) + {B_{11}}{\varphi_{x,x}} + {B_{12}}\;{\varphi_{y,y}} + {B_{16}}\left( {{\varphi_{x,y}} + {\varphi_{y,x}}} \right),} \\ {{L_2} = {A_{12}}{u_{x,x}} + {A_{22}}\;{u_{y,y}} + {A_{26}}\left( {{u_{x,y}} + {u_{y,x}}} \right) + {B_{12}}{\varphi_{x,x}} + {B_{22}}\;{\varphi_{y,y}} + {B_{26}}\left( {{\varphi_{x,y}} + {\varphi_{y,x}}} \right),} \\ {{L_3} = {B_{11}}{u_{x,x}} + {B_{12}}\;{u_{y,y}} + {B_{16}}\left( {{u_{x,y}} + {u_{y,x}}} \right) + {D_{11}}{\varphi_{x,x}} + {D_{12}}\;{\varphi_{y,y}} + {D_{16}}\left( {{\varphi_{x,y}} + {\varphi_{y,x}}} \right),} \\ {{L_4} = {B_{12}}{u_{x,x}} + {B_{22}}\;{u_{y,y}} + {B_{26}}\left( {{u_{x,y}} + {u_{y,x}}} \right) + {D_{12}}{\varphi_{x,x}} + {D_{22}}\;{\varphi_{y,y}} + {D_{26}}\left( {{\varphi_{x,y}} + {\varphi_{y,x}}} \right),} \\ {{L_5} = {A_{16}}{u_{x,x}} + {A_{26}}{u_{y,y}} + {A_{66}}\left( {{u_{x,y}} + {u_{y,x}}} \right) + {B_{16}}{\varphi_{x,x}} + {B_{26}}{\varphi_{y,y}} + {B_{66}}\left( {{\varphi_{x,y}} + {\varphi_{y,x}}} \right),} \\ {{L_6} = {A_{45}}\left( {{w_{,y}} + {\varphi_y}} \right) + {A_{55}}\left( {{w_{,x}} + {\varphi_x}} \right),\;{L_7} = {A_{44}}\left( {{w_{,y}} + {\varphi_y}} \right) + {A_{45}}\left( {{w_{,x}} + {\varphi_x}} \right),} \\ {{L_8} = {B_{16}}{u_{x,x}} + {B_{26}}{u_{y,y}} + {B_{66}}\left( {{u_{x,y}} + {u_{y,x}}} \right) + {D_{16}}{\varphi_{x,x}} + {D_{26}}{\varphi_{y,y}} + {D_{66}}\left( {{\varphi_{x,y}} + {\varphi_{y,x}}} \right),} \\ \end{array} $$
$$ \begin{array}{*{20}{c}} {{N_1} = {A_{11}}{{{w_{,x}^2}} \left/ {{2 + {A_{12}}{{{w_{,y}^2}} \left/ {2} \right.} + {A_{16}}{w_{,x}}{w_{,y}},}} \right.}} \hfill \\ {{N_2} = {A_{12}}{{{w_{,x}^2}} \left/ {{2 + {A_{22}}{{{w_{,y}^2}} \left/ {2} \right.} + {A_{26}}{w_{,x}}{w_{,y}},}} \right.}} \hfill \\ {{N_3} = {A_{16}}{{{w_{,x}^2}} \left/ {{2 + {{{{A_{26}}w_{,y}^2}} \left/ {{2 + {A_{66}}{w_{,x}}{w_{,y}},\;{N_4} = \left( {{Q_1} + {L_1}} \right){w_{,x}},}} \right.}}} \right.}} \hfill \\ {{N_5} = \left( {{Q_5} + {L_3}} \right){w_{,x}},\;{N_6} = \left( {{Q_2} + {L_2}} \right){w_{,y}},\;{N_7} = \left( {{Q_5} + {L_3}} \right){w_{,y}},} \hfill \\ {{N_8} = {{{{B_{11}}w_{,x}^2}} \left/ {{2 + {B_{12}}{{{w_{,y}^2}} \left/ {{2 + {B_{16}}{w_{,x}}{w_{,y}},}} \right.}}} \right.}} \hfill \\ {{N_9} = {B_{12}}{{{w_{,x}^2}} \left/ {{2 + {{{{B_{22}}w_{,y}^2}} \left/ {{2 + {B_{26}}{w_{,x}}{w_{,y}},}} \right.}}} \right.}} \hfill \\ {{N_{10}} = {B_{16}}{{{w_{,x}^2}} \left/ {{2 + {{{{B_{26}}w_{,y}^2}} \left/ {{2 + {B_{66}}{w_{,x}}{w_{,y}},}} \right.}}} \right.}} \hfill \\ \end{array} $$
$$ \begin{array}{*{20}{c}} {{R_1} = {N_{xx}}{u_{x,x}} + {M_{xx}}{\varphi_{x,x}},\;{R_2} = {N_{xy}}{u_{x,y}} + {M_{xy}}{\varphi_{x,y}} + {N_{xz}}{u_{z,x}},} \hfill \\ {{R_3} = {N_{xx}}{u_{y,x}} + {M_{xx}}{\varphi_{y,x}} + {N_{xy}}{u_{y,y}} + {M_{xy}}{\varphi_{y,y}} + {N_{xz}}{u_{z,y}},\;{R_4} = {N_{xx}}{w_{,x}} + {N_{xy}}{w_{,y}},} \hfill \\ {{R_5} = {M_{xx}}{u_{x,x}},\;{R_6} = {M_{xy}}{u_{x,y}} + {M_{xz}}{\varphi_{z,x}},\;{R_7} = {M_{xx}}{u_{y,x}} + {M_{xy}}{u_{y,y}} + {M_{xz}}{u_{z,y}},} \hfill \\ {{R_8} = {N_{xz}}{u_{x,x}} + {M_{xz}}{\varphi_{x,x}} + {N_{zz}}{\varphi_x} + {N_{zy}}{u_{x,y}} + {M_{zy}}{\varphi_{x,y}},} \hfill \\ {{R_9} = {N_{xz}}{u_{y,x}} + {M_{xz}}{\varphi_{y,x}} + {N_{zz}}{\varphi_{yx}} + {N_{zy}}{u_{y,y}} + {M_{zy}}{\varphi_{y,y}},} \hfill \\ \end{array} $$
$$ \begin{array}{*{20}{c}} {{S_1} = {N_{yy}}{u_{x,y}} + {M_{yy}}{\varphi_{x,y}},\;{S_2} = {N_{xy}}{u_{x,x}} + {M_{xy}}{\varphi_{x,x}} + {N_{yz}}{u_{z,x}},} \\ {{S_3} = {N_{yy}}{u_{y,y}} + {M_{yy}}{\varphi_{y,y}} + {N_{xy}}{u_{y,x}} + {M_{xy}}{\varphi_{y,x}} + {N_{xz}}{u_{z,y}},\;{S_4} = {N_{xy}}{w_{,x}} + {N_{yy}}{w_{,y}},} \\ {{S_5} = {M_{yy}}{u_{x,y}},\;{S_6} = {M_{xy}}{u_{x,x}} + {M_{yz}}{u_{z,x}},\;{S_7} = {M_{yy}}{u_{y,y}} + {M_{xy}}{u_{y,x}} + {M_{xz}}{u_{z,y}},} \\ \end{array} $$
$$ \begin{array}{*{20}{c}} {{B_1} = {L_5} + {N_3} + {S_1},\;{B_2} = {L_2} + {N_2} + {S_2},\;{B_3} = {L_7} + {N_5} + {S_3},\quad {B_4} = {L_8} + {S_4},} \\ {{B_5} = {L_8} + {R_5},\;{B_6} = {L_1} + {N_1} + {R_1},\;{B_7} = {L_5} + {N_3} + {R_2},\;{B_8} = {L_6} + {N_4} + {R_3},} \\ {{B_9} = {L_8} + {S_4},\;{B_{10}} = {L_8} + {R_5},} \\ \end{array} $$
$$ \begin{array}{*{20}{c}} {{f_x} = \int\limits_{ - {{h} \left/ {2} \right.}}^{{{h} \left/ {2} \right.}} {\left( {{{\bar{X}}_x} + \varDelta {X_x}} \right)dz + \sigma_{zx}^{+} - \sigma_{zx}^{-}, } } \\ {{f_y} = \int\limits_{ - {{h} \left/ {2} \right.}}^{{{h} \left/ {2} \right.}} {\left( {{{\bar{X}}_y} + \varDelta {X_y}} \right)dz + \sigma_{zy}^{+} - \sigma_{zy}^{-}, } } \\ {{f_z} = \int\limits_{{{{ - h}} \left/ {2} \right.}}^{{{h} \left/ {2} \right.}} {\left( {{{\bar{X}}_z} + \varDelta {X_z}} \right)dz + \left( {\sigma_{zx}^{+} - \sigma_{zx}^{-} } \right){w_{,x}} + \left( {\sigma_{zy}^{+} - \sigma_{zy}^{-} } \right){w_{,y}} + \sigma_{zz}^{+} - \sigma_{zz}^{-}, } } \\ \end{array} $$
$$ \begin{array}{*{20}{c}} {{m_x} = \int\limits_{{{{ - h}} \left/ {2} \right.}}^{{{h} \left/ {2} \right.}} {\left( {{{\bar{X}}_x} + \varDelta {X_x}} \right)zdz + h{{{\left( {\sigma_{zx}^{+} - \sigma_{zx}^{-} } \right)}} \left/ {2} \right.},} } \\ {{m_y} = \int\limits_{{{{ - h}} \left/ {2} \right.}}^{{{h} \left/ {2} \right.}} {\left( {{{\bar{X}}_y} + \varDelta {X_y}} \right)zdz + h{{{\left( {\sigma_{zy}^{+} - \sigma_{zy}^{-} } \right)}} \left/ {2} \right.}.} } \\ \end{array} $$

Rights and permissions

Reprints and permissions

About this article

Cite this article

Wei, CL., Chen, CS., Shih, CS. et al. Nonlinear vibration of initially stressed hybrid composite plates on elastic foundations. Mech Compos Mater 48, 467–482 (2012). https://doi.org/10.1007/s11029-012-9291-5

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11029-012-9291-5

Keywords

Search

Navigation