A study on the stress and vibration characteristics of laminated composite plates resting on elastic foundations using analytical and finite element solutions

Abstract

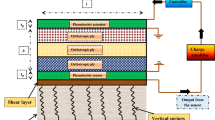
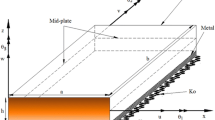
This paper presents the stress and vibration analysis of advanced composites and sandwich plates supported by elastic foundations. An inter-laminar transverse shear stress continuous plate theory is used to model the deformation responses of the multilayered plates. This plate theory is a refinement of the classical plate theory and utilizes a trigonometric function to define the nonlinear behavior of the transverse shear strains across the thickness of the plates. Additionally, unit step functions are assumed along with some auxiliary variables to satisfy the piecewise continuity requirements of displacements. The deformation behavior of the elastic foundations is modeled using a two-parameter foundation model known as the Pasternak’s foundation. The equations of motion are derived using Hamilton’s principle for the dynamic problem which can also be reduced to a static problem by ignoring the effects of inertia. Two solution schemes are proposed: the Navier-based analytical method, and the finite element method for the spatial solutions of the displacement variables. Further, the solutions in time are obtained using Newmark’s time integration technique. Detailed parametric studies on static, free vibration and forced-vibration analysis of laminated composite plates are carried out to show the effects of the elastic foundations on the structural responses. It is concluded from the results that both analytical and finite element solutions are capable of accurately predicting the responses of composite plates supported by elastic foundations.

Appendices

Appendix 1

Rigidity sub-matrices of bending

$$ \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\left[ A \right]_{{\left( {3 \times 3} \right)}} } & {\left[ B \right]_{{\left( {3 \times 3} \right)}} } \\ \end{array} } \\ {\begin{array}{*{20}c} {\left[ C \right]_{{\left( {3 \times 3} \right)}} } & {\left[ D \right]_{{\left( {3 \times 3} \right)}} } \\ \end{array} } \\ \end{array} } \\ {\begin{array}{*{20}c} {\left[ G \right]_{{\left( {3 \times 3} \right)}} } & {\left[ H \right]_{{\left( {3 \times 3} \right)}} } \\ \end{array} } \\ {\begin{array}{*{20}c} {\left[ I \right]_{{\left( {3 \times 3} \right)}} } & {\left[ L \right]_{{\left( {3 \times 3} \right)}} } \\ \end{array} } \\ {\begin{array}{*{20}c} {\left[ M \right]_{{\left( {3 \times 3} \right)}} } & {\left[ P \right]_{{\left( {3 \times 3} \right)}} } \\ \end{array} } \\ \end{array} } \right] = \mathop \sum \limits_{k = 1}^{{{\text{NL}}}} \left\{ {\mathop \smallint \limits_{{z^{k} }}^{{z^{k + 1} }} \left( {\left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\left[ {\overline{Q}_{ij} } \right]^{k} } & {z\left[ {\overline{Q}_{ij} } \right]^{k} } \\ \end{array} } \\ {\begin{array}{*{20}c} {p_{1} \left[ {\overline{Q}_{ij} } \right]^{k} } & {p_{2} } \\ \end{array} \left[ {\overline{Q}_{ij} } \right]^{k} } \\ {\begin{array}{*{20}c} {z^{2} \left[ {\overline{Q}_{ij} } \right]^{k} } & {zp_{1} } \\ \end{array} \left[ {\overline{Q}_{ij} } \right]^{k} } \\ {\begin{array}{*{20}c} {zp_{2} \left[ {\overline{Q}_{ij} } \right]^{k} } & {p_{1}^{2} } \\ \end{array} \left[ {\overline{Q}_{ij} } \right]^{k} } \\ {\begin{array}{*{20}c} {p_{1} p_{2} \left[ {\overline{Q}_{ij} } \right]^{k} } & {p_{2}^{2} } \\ \end{array} \left[ {\overline{Q}_{ij} } \right]^{k} } \\ \end{array} } \right]{\text{d}}z} \right)} \right\}\quad (i,j = 1,2,3) $$

Rigidity sub-matrices of shear

$$ \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\left[ {AA} \right]_{{\left( {2 \times 2} \right)}} } & {\left[ {EE} \right]_{{\left( {2 \times 2} \right)}} } & {\left[ {FF} \right]_{{\left( {2 \times 2} \right)}} } \\ \end{array} } \\ {\begin{array}{*{20}c} {\left[ {SS} \right]_{{\left( {2 \times 2} \right)}} } & {\left[ {TT} \right]_{{\left( {2 \times 2} \right)}} } & {\left[ {UU} \right]_{{\left( {2 \times 2} \right)}} } \\ \end{array} } \\ \end{array} } \right] = \mathop \sum \nolimits_{k = 1}^{{{\text{NL}}}} \left\{ {\mathop \int \nolimits_{{z^{k} }}^{{z^{k + 1} }} \left( {\left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\left[ {\overline{Q}_{ij} } \right]^{k} } & {q_{1} \left[ {\overline{Q}_{ij} } \right]^{k} } & {q_{2} \left[ {\overline{Q}_{ij} } \right]^{k} } \\ \end{array} } \\ {\begin{array}{*{20}c} {q_{1}^{2} \left[ {\overline{Q}_{ij} } \right]^{k} } & {q_{1} q_{2} \left[ {\overline{Q}_{ij} } \right]^{k} } & {q_{2}^{2} \left[ {\overline{Q}_{ij} } \right]^{k} } \\ \end{array} } \\ \end{array} } \right]{\text{d}}z} \right)} \right\}\quad (i,j = 4,5) $$

Appendix 2

Partial differential equation terms of the primary variables

${{\varvec{\delta}}{\varvec{u}}}_{0}$:

$$ \begin{aligned} & A_{11} \frac{{\partial^{2} u_{0} }}{{\partial x^{2} }} + A_{12} \frac{{\partial^{2} v_{0} }}{\partial x\partial y} + B_{11} \left( { - \frac{{\partial^{3} w_{0} }}{{\partial x^{3} }} + {\Omega }_{x} \frac{{\partial^{2} \beta_{x} }}{{\partial x^{2} }}} \right) + B_{12} \left( { - \frac{{\partial^{3} w_{0} }}{{\partial x\partial y^{2} }} + {\Omega }_{y} \frac{{\partial^{2} \beta_{y} }}{\partial x\partial y}} \right) \hfill \\ &\quad + C_{11} \frac{{\partial^{2} \beta_{x} }}{{\partial x^{2} }}D_{12} \frac{{\partial^{2} \beta_{y} }}{\partial x\partial y} + A_{66} \left( {\frac{{\partial^{2} u_{0} }}{{\partial y^{2} }} + \frac{{\partial^{2} v_{0} }}{\partial x\partial y}} \right) + B_{66} \left( { - 2\frac{{\partial^{3} w_{0} }}{{\partial x\partial y^{2} }} + {\Omega }_{x} \frac{{\partial^{2} \beta_{x} }}{{\partial y^{2} }} + {\Omega }_{y} \frac{{\partial^{2} \beta_{y} }}{\partial x\partial y}} \right) \hfill \\ &\quad + C_{66} \frac{{\partial^{2} \beta_{x} }}{{\partial y^{2} }} + D_{66} \frac{{\partial^{2} \beta_{y} }}{\partial x\partial y} - \overline{I}_{0} \ddot{u}_{0} + \overline{I}_{1} \frac{{\partial \ddot{w}_{o} }}{\partial x} - \overline{I}_{3} \ddot{\beta }_{x} = 0 \hfill \\ \end{aligned} $$

${{\varvec{\delta}}{\varvec{v}}}_{0}$:

$$ \begin{aligned} & A_{12} \frac{{\partial^{2} u_{0} }}{\partial x\partial y} + A_{22} \frac{{\partial^{2} v_{0} }}{{\partial y^{2} }} + B_{12} \left( { - \frac{{\partial^{3} w_{0} }}{{\partial x^{2} \partial y}} + {\Omega }_{x} \frac{{\partial^{2} \beta_{x} }}{\partial x\partial y}} \right) + B_{22} \left( { - \frac{{\partial^{3} w_{0} }}{{\partial y^{3} }} + {\Omega }_{y} \frac{{\partial^{2} \beta_{y} }}{{\partial y^{2} }}} \right) \hfill \\ &\quad + C_{12} \frac{{\partial^{2} \beta_{x} }}{\partial x\partial y}+D_{22} \frac{{\partial^{2} \beta_{y} }}{{\partial y^{2} }} + A_{66} \left( {\frac{{\partial^{2} u_{0} }}{\partial x\partial y} + \frac{{\partial^{2} v_{0} }}{{\partial x^{2} }}} \right) + B_{66} \left( { - 2\frac{{\partial^{3} w_{0} }}{{\partial x^{2} \partial y}} + {\Omega }_{x} \frac{{\partial^{2} \beta_{x} }}{\partial x\partial y} + {\Omega }_{y} \frac{{\partial^{2} \beta_{y} }}{{\partial x^{2} }}} \right) \hfill \\ &\quad + C_{66} \frac{{\partial^{2} \beta_{x} }}{\partial x\partial y} + D_{66} \frac{{\partial^{2} \beta_{y} }}{{\partial x^{2} }} - \overline{I}_{0} \ddot{v}_{0} + \overline{I}_{1} \frac{{\partial \ddot{w}_{o} }}{\partial y} - \overline{I}_{6} \ddot{\beta }_{y} = 0 \hfill \\ \end{aligned} $$

${{\varvec{\delta}}{\varvec{w}}}_{0}$:

$$ \begin{aligned} & B_{11} \frac{{\partial^{3} u_{0} }}{{\partial x^{3} }} + B_{12} \frac{{\partial^{3} v_{0} }}{{\partial x^{2} \partial y}} + G_{11} \left( { - \frac{{\partial^{4} w_{o} }}{{\partial x^{4} }} + {\Omega }_{x} \frac{{\partial^{3} \beta_{x} }}{{\partial x^{3} }}} \right) + G_{12} \left( { - \frac{{\partial^{4} w_{o} }}{{\partial x^{2} \partial y^{2} }} + {\Omega }_{y} \frac{{\partial^{3} \beta_{y} }}{{\partial x^{2} \partial y}}} \right) \hfill \\ &\quad + H_{11} \frac{{\partial^{3} \beta_{x} }}{{\partial x^{3} }} + I_{12} \frac{{\partial^{3} \beta_{y} }}{{\partial x^{2} \partial y}} + 2B_{66} \left( {\frac{{\partial^{3} u_{0} }}{{\partial x\partial y^{2} }} + \frac{{\partial^{3} v_{0} }}{{\partial x^{2} \partial y}}} \right) + 2G_{66} \left( { - 2\frac{{\partial^{4} w_{o} }}{{\partial x^{2} \partial y^{2} }} + {\Omega }_{x} \frac{{\partial^{3} \beta_{x} }}{{\partial x\partial y^{2} }} + {\Omega }_{y} \frac{{\partial^{3} \beta_{y} }}{{\partial x^{2} \partial y}}} \right) \hfill \\ &\quad + 2H_{66} \frac{{\partial^{3} \beta_{x} }}{{\partial x\partial y^{2} }} + 2I_{66} \frac{{\partial^{3} \beta_{y} }}{{\partial x^{2} \partial y}} + B_{12} \frac{{\partial^{3} u_{0} }}{{\partial x\partial y^{2} }} + B_{22} \frac{{\partial^{3} v_{0} }}{{\partial y^{3} }} + G_{12} \left( { - \frac{{\partial^{4} w_{o} }}{{\partial x^{2} \partial y^{2} }} + {\Omega }_{x} \frac{{\partial^{3} \beta_{x} }}{{\partial x\partial y^{2} }}} \right) \hfill \\ &\quad + G_{22} \left( { - \frac{{\partial^{4} w_{o} }}{{\partial y^{4} }} + {\Omega }_{y} \frac{{\partial^{3} \beta_{y} }}{{\partial y^{3} }}} \right) + H_{12} \frac{{\partial^{3} \beta_{x} }}{{\partial x\partial y^{2} }} + I_{22} \frac{{\partial^{3} \beta_{y} }}{{\partial y^{3} }} - \overline{I}_{1} \left( {\frac{{\partial \ddot{u}_{o} }}{\partial x} + \frac{{\partial \ddot{v}_{o} }}{\partial y}} \right) + \overline{I}_{2} \left( {\frac{{\partial^{2} \ddot{w}_{0} }}{{\partial x^{2} }} + \frac{{\partial^{2} \ddot{w}_{0} }}{{\partial y^{2} }}} \right) \hfill \\ &\quad - \overline{I}_{4} \frac{{\partial \ddot{\beta }_{x} }}{\partial x} - \overline{I}_{7} \frac{{\partial \ddot{\beta }_{y} }}{\partial y} - \overline{I}_{0} \ddot{w}_{0} + q(t) - k_{w} w_{0} + k_{s} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} + k_{s} \frac{{\partial^{2} w_{0} }}{{\partial y^{2} }} = 0 \hfill \\ \end{aligned} $$

${\varvec{\delta}}{{\varvec{\beta}}}_{{\varvec{x}}}$:

$$ \begin{aligned} & {\Omega }_{x} B_{11} \frac{{\partial^{2} u_{0} }}{{\partial x^{2} }} + {\Omega }_{x} B_{12} \frac{{\partial^{2} v_{0} }}{\partial x\partial y} + {\Omega }_{x} G_{11} \left( { - \frac{{\partial^{3} w_{0} }}{{\partial x^{3} }} + {\Omega }_{x} \frac{{\partial^{2} \beta_{x} }}{{\partial x^{2} }}} \right) + {\Omega }_{x} G_{12} \left( { - \frac{{\partial^{3} w_{0} }}{{\partial x\partial y^{2} }} + {\Omega }_{y} \frac{{\partial^{2} \beta_{x} }}{\partial x\partial y}} \right) \hfill \\ &\quad + {\Omega }_{x} H_{11} \frac{{\partial^{2} \beta_{x} }}{{\partial x^{2} }} + {\Omega }_{x} I_{12} \frac{{\partial^{2} \beta_{y} }}{\partial x\partial y} + C_{11} \frac{{\partial^{2} u_{0} }}{{\partial x^{2} }} + C_{12} \frac{{\partial^{2} v_{0} }}{\partial x\partial y} + H_{11} \left( { - \frac{{\partial^{3} w_{o} }}{{\partial x^{3} }} + {\Omega }_{x} \frac{{\partial^{2} \beta_{x} }}{{\partial x^{2} }}} \right) \hfill \\ &\quad + H_{12} \left( { - \frac{{\partial^{3} w_{o} }}{{\partial x\partial y^{2} }} + {\Omega }_{y} \frac{{\partial^{2} \beta_{y} }}{\partial x\partial y}} \right) + L_{11} \frac{{\partial^{2} \beta_{x} }}{{\partial x^{2} }} + M_{12} \frac{{\partial^{2} \beta_{y} }}{\partial x\partial y} + {\Omega }_{x} B_{66} \left( {\frac{{\partial^{2} u_{0} }}{{\partial y^{2} }} + \frac{{\partial^{2} v_{0} }}{\partial x\partial y}} \right) \hfill \\ &\quad + {\Omega }_{x} G_{66} \left( { - 2\frac{{\partial^{3} w_{o} }}{{\partial x\partial y^{2} }} + {\Omega }_{x} \frac{{\partial^{2} \beta_{x} }}{{\partial y^{2} }} + {\Omega }_{y} \frac{{\partial^{2} \beta_{y} }}{\partial x\partial y}} \right) + {\Omega }_{x} H_{66} \frac{{\partial^{2} \beta_{x} }}{{\partial y^{2} }} + {\Omega }_{x} I_{66} \frac{{\partial^{2} \beta_{y} }}{\partial x\partial y} \hfill \\ &\quad + C_{66} \left( {\frac{{\partial^{2} u_{0} }}{{\partial y^{2} }} + \frac{{\partial^{2} v_{0} }}{\partial x\partial y}} \right) + H_{66} \left( { - 2\frac{{\partial^{3} w_{o} }}{{\partial x\partial y^{2} }} + {\Omega }_{x} \frac{{\partial^{2} \beta_{x} }}{{\partial y^{2} }} + {\Omega }_{y} \frac{{\partial^{2} \beta_{y} }}{\partial x\partial y}} \right) + L_{66} \frac{{\partial^{2} \beta_{x} }}{{\partial y^{2} }} \hfill \\ &\quad + M_{66} \frac{{\partial^{2} \beta_{y} }}{\partial x\partial y} - {\Omega }_{x}^{2} AA_{22} \beta_{x} - 2{\Omega }_{x} FF_{22} \beta_{x} - UU_{22} \beta_{x} - \overline{I}_{3} \ddot{u}_{0} + \overline{I}_{4} \frac{{\partial \ddot{w}_{0} }}{\partial x} - \overline{I}_{5} \ddot{\beta }_{x} = 0 \hfill \\ \end{aligned} $$

${\varvec{\delta}}{{\varvec{\beta}}}_{{\varvec{y}}}$:

$$ \begin{aligned} & {\Omega }_{y} B_{12} \frac{{\partial^{2} u_{0} }}{\partial x\partial y} \\ &\quad + {\Omega }_{y} B_{22} \frac{{\partial^{2} v_{0} }}{{\partial y^{2} }} + {\Omega }_{y} G_{12} \left( { - \frac{{\partial^{3} w_{0} }}{{\partial x^{2} \partial y}} + {\Omega }_{x} \frac{{\partial^{2} \beta_{x} }}{\partial x\partial y}} \right) + {\Omega }_{y} G_{22} \left( { - \frac{{\partial^{3} w_{0} }}{{\partial y^{3} }} + {\Omega }_{y} \frac{{\partial^{2} \beta_{y} }}{{\partial y^{2} }}} \right) \hfill \\ &\quad + {\Omega }_{y} H_{12} \frac{{\partial^{2} \beta_{x} }}{\partial x\partial y} + {\Omega }_{y} I_{22} \frac{{\partial^{2} \beta_{y} }}{{\partial y^{2} }} + D_{12} \frac{{\partial^{2} u_{0} }}{\partial x\partial y} + D_{22} \frac{{\partial^{2} v_{0} }}{{\partial y^{2} }} + I_{12} \left( { - \frac{{\partial^{3} w_{o} }}{{\partial x^{2} \partial y}} + {\Omega }_{x} \frac{{\partial^{2} \beta_{x} }}{\partial x\partial y}} \right) \hfill \\ &\quad + I_{22} \left( { - \frac{{\partial^{3} w_{o} }}{{\partial y^{3} }} + {\Omega }_{y} \frac{{\partial^{2} \beta_{y} }}{{\partial y^{2} }}} \right) + M_{12} \frac{{\partial^{2} \beta_{x} }}{\partial x\partial y} + P_{22} \frac{{\partial^{2} \beta_{y} }}{{\partial y^{2} }} + {\Omega }_{y} B_{66} \left( {\frac{{\partial^{2} u_{0} }}{\partial x\partial y} + \frac{{\partial^{2} v_{0} }}{{\partial x^{2} }}} \right) \hfill \\ &\quad + {\Omega }_{y} G_{66} \left( { - 2\frac{{\partial^{3} w_{o} }}{{\partial x^{2} \partial y}} + {\Omega }_{x} \frac{{\partial^{2} \beta_{x} }}{\partial x\partial y} + {\Omega }_{y} \frac{{\partial^{2} \beta_{y} }}{{\partial x^{2} }}} \right) + {\Omega }_{y} H_{66} \frac{{\partial^{2} \beta_{x} }}{\partial x\partial y} + {\Omega }_{y} I_{66} \frac{{\partial^{2} \beta_{y} }}{{\partial x^{2} }} \hfill \\ &\quad + D_{66} \left( {\frac{{\partial^{2} u_{0} }}{\partial x\partial y} + \frac{{\partial^{2} v_{0} }}{{\partial x^{2} }}} \right) + I_{66} \left( { - 2\frac{{\partial^{3} w_{o} }}{{\partial x^{2} \partial y}} + {\Omega }_{x} \frac{{\partial^{2} \beta_{x} }}{\partial x\partial y} + {\Omega }_{y} \frac{{\partial^{2} \beta_{y} }}{{\partial x^{2} }}} \right) + M_{66} \frac{{\partial^{2} \beta_{x} }}{\partial x\partial y} \hfill \\ &\quad + P_{66} \frac{{\partial^{2} \beta_{y} }}{{\partial x^{2} }} - {\Omega }_{y}^{2} AA_{11} \beta_{y} - 2{\Omega }_{y} EE_{11} \beta_{y} - SS_{11} \beta_{y} - \overline{I}_{6} \ddot{v}_{0} + \overline{I}_{7} \frac{{\partial \ddot{w}_{0} }}{\partial y} - \overline{I}_{8} \ddot{\beta }_{y} = 0 \hfill \\ \end{aligned} $$

Appendix 3

The elements of matrix ‘$\left[{\varvec{H}}\right]$’

$$ \left[ H \right] = \left[ {\begin{array}{*{20}l} 1 \hfill & 0 \hfill & 0 \hfill & z \hfill & 0 \hfill & 0 \hfill & {p_{1} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & z \hfill & 0 \hfill & 0 \hfill & {p_{2} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & z \hfill & 0 \hfill & 0 \hfill & {p_{1} } \hfill & {p_{2} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & {q_{1} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & {q_{2} } \hfill \\ \end{array} } \right] $$

The nonzero elements of matrix ‘$\left[{\varvec{B}}\right]$’ for the ith node are written as

$$ \begin{gathered} \overline{B}_{{1,1_{i} }} = \overline{B}_{{3,2_{i} }} = \overline{B}_{{7,4_{i} }} = \overline{B}_{{10,5_{i} }} = \overline{B}_{{12,3_{i} }} = \frac{{\partial N_{i} }}{\partial x}; \hfill \\ \overline{B}_{{2,2_{i} }} = \overline{B}_{{3,1_{i} }} = \overline{B} =_{{8,5_{i} }} = \overline{B}_{{9,4_{i} }} = \overline{B}_{{11,3_{i} }} = \frac{{\partial N_{i} }}{\partial y}; \hfill \\ \overline{B}_{{4,6_{i} }} = \overline{B}_{{6,7_{i} }} = - \frac{{\partial N_{i} }}{\partial x};\quad \overline{B}_{{5,7_{i} }} = \overline{B}_{{6,6_{i} }} = - \frac{{\partial N_{i} }}{\partial y}; \hfill \\ \overline{B}_{{4,4_{i} }} = {\Omega }_{x} \frac{{\partial N_{i} }}{\partial x};\quad \overline{B}_{{5,5_{i} }} = {\Omega }_{y} \frac{{\partial N_{i} }}{\partial y};\quad \overline{B}_{{6,4_{i} }} = {\Omega }_{y} \frac{{\partial N_{i} }}{\partial y}; \hfill \\ \overline{B}_{{6,5_{i} }} = {\Omega }_{y} \frac{{\partial N_{i} }}{\partial x};\quad \overline{B}_{{12,4_{i} }} = {\Omega }_{x} N_{i} ;\quad \overline{B}_{{11,5_{i} }} = {\Omega }_{y} N_{i} ; \hfill \\ \overline{B}_{{11,7_{i} }} = \overline{B}_{{12,6_{i} }} = - N_{i} ;\quad \overline{B}_{{13,5_{i} }} = \overline{B}_{{14,4_{i} }} = N_{i} \hfill \\ \end{gathered} $$

The elements of the vector ‘$\left[\overline{{\varvec{\varepsilon}} }\right]$’

$$ \begin{gathered} \overline{\overline{\varepsilon }}_{1} = \frac{{\partial u_{0} }}{\partial x},\quad \overline{\overline{\varepsilon }}_{2} = \frac{{\partial v_{0} }}{\partial y},\quad \overline{\overline{\varepsilon }}_{3} = \left( {\frac{{\partial u_{0} }}{\partial y} + \frac{{\partial v_{0} }}{\partial x}} \right),\quad \overline{\overline{\varepsilon }}_{4} = - \left( {\frac{{\partial \theta_{x} }}{\partial x} + \Omega_{x} \frac{{\partial \beta_{x} }}{\partial x}} \right), \hfill \\ \overline{\overline{\varepsilon }}_{5} = - \left( {\frac{{\partial \theta_{y} }}{\partial y} + \Omega_{y} \frac{{\partial \beta_{y} }}{\partial y}} \right),\quad \overline{\overline{\varepsilon }}_{6} = - \left( {\left( {\frac{{\partial \theta_{x} }}{\partial y} + \frac{{\partial \theta_{y} }}{\partial x}} \right) + \Omega_{x} \frac{{\partial \beta_{x} }}{\partial y} + \Omega_{y} \frac{{\partial \beta_{y} }}{\partial x}} \right), \hfill \\ \overline{\overline{\varepsilon }}_{7} = \frac{{\partial \beta_{x} }}{\partial x},\quad \overline{\overline{\varepsilon }}_{8} = \frac{{\partial \beta_{y} }}{\partial y},\quad \overline{\overline{\varepsilon }}_{9} = \frac{{\partial \beta_{x} }}{\partial y},\quad \overline{\overline{\varepsilon }}_{10} = \frac{{\partial \beta_{y} }}{\partial x},\overline{\overline{\varepsilon }}_{11} = \left( { - \theta_{y} + \frac{{\partial w_{0} }}{\partial y} + \Omega_{y} \beta_{y} } \right), \hfill \\ \overline{\overline{\varepsilon }}_{12} = \left( { - \theta_{x} + \frac{{\partial w_{0} }}{\partial x} + \Omega_{x} \beta_{x} } \right),\quad \overline{\overline{\varepsilon }}_{13} = \beta_{y} ,\quad \overline{\overline{\varepsilon }}_{14} = \beta_{x} \hfill \\ \end{gathered} $$