1 Introduction

Coating of surfaces is a very important activity with many industrial applications. The cooling of surfaces has also relevant applications in systems with heat generation. When the thin liquid films are falling down walls applications are found when coating or cooling surfaces where a temperature gradient exists across the film. The research on wall cooling has relevance in microchips located inside modern computers. Along with the advances of technology the microchips generate more and more heat that should be dissipated efficiently. Due to the usefulness of this subject extensive reviews were written some years ago by Oron et al. [1] and Dávalos-Orozco [2]. More recently, new advances in the problem of non-isothermal thin film flows were reviewed in Dávalos-Orozco [3].

Thin liquid films falling down walls have been investigated since many years ago under different boundary conditions. The stability of these flows is of interest because, when the film is not able to wet the wall, rivulets [4] may form and for some applications the film becomes useless. Usually it is difficult to control atmospheric temperature variations. Therefore, it is of interest to impose thermal boundary conditions to the wall-film system to solve the thermocapillary problem. The Marangoni instability has been investigated since many years ago. Pearson [5] studied the case of a flat free surface. Free surface deformation was first taken into account by Scriven and Sternling [6]. The effect of gravity was included by Takashima [7, 8]. This instability was considered by Dávalos-Orozco and You [9] and Moctezuma-Sánchez and Dávalos-Orozco [10] in a cylindrical wall. In [11] it is of interest to apply a horizontal temperature gradient. This is also relevant in annular pools [12,13,14].

The finite thickness and thermal conductivity of the wall were taken into account in thermocapillary phenomena by Takashima [15], Yang [16], Kabova et al. [17], Hernández-Hernández and Dávalos-Orozco [18] and Dávalos-Orozco [19]. The effect of a thick wall was also considered for liquid films falling down walls [20,21,22,23]. Also, in the case of cylinders, the sideband nonlinear instability was investigated in [24,25,26,27]. The influence of evaporation was taken into account in [28,29,30].

The no-slip condition at the wall surface is commonly used. However, it is possible to find surfaces where this condition is not satisfied [31, 32]. In some cases, the characteristics of the surface can be modified by changing its chemical composition [33]. When the wall has very small topography, the liquid trapped inside plays the role of lubricant when the liquid is in motion reducing the effective friction and presenting an apparent slip at the wall [34].

Thermocapillary effects were taken into account along with slip at the wall in Kowal et al. [35]. In the case of thin films falling down walls slip effect was considered in a number of works [36,37,38]. Slip was also contemplated in the presence of topography by Usha and Anjalaiah [39] and Zakaria and Selim [40]. The stability of a viscoelastic film was examined in Pal and Samanta [41] and Chattopadhyay et al. [42].

The finite thickness and thermal conductivity of the wall were not taken into account in the papers with slip and thermocapillary effects [35, 36, 38]. Therefore, in this paper the linear and nonlinear thermocapillary instability of a liquid layer falling down a thick wall with finite thermal conductivity is investigated. The liquid layer may be located above or below (Rayleigh-Taylor instability [43, 44]) the thick wall. It important to point out here that Karapetsas and Mitsoulis [45] have shown that the slip condition is necessary to have good agreement with experiments in newtonian and non-newtonian non-isothermal creeping flows.

In a previous paper [46], the Marangoni stability of a thin liquid layer coating a horizontal thick wall in the presence of gravity was investigated when slip is present at the interface between the wall and the liquid. There, it was found the possibility of a stabilizing effect of slip under different conditions. In some of the papers mentioned above stabilizing effects of slip have been mentioned. However, no definite analytical results have been given to determine the limits between stabilizing and destabilizing behavior of slip. Therefore, in this paper it is of interest to find out analytically and numerically the limits of the parameters in which slip may stabilize or destabilized when a main flow is present in a thin film flowing down above or below a hot or cold thick wall.

The structure of the paper is as follows. In the next section, the basic equations are presented along with the steps followed to obtain the nonlinear evolution equation of the free surface deformation under the lubrication approximation. Then, the linear results are presented in section three. The solutions of the nonlinear evolution equation are given in section four and section five are the conclusions.

Fig. 1
figure 1

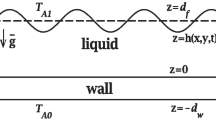
Sketch of the system. The liquid may slip on the wall falling down in the x-direction. The dashed line located at z \(= d_f\) shows the mean thickness of the liquid layer. The wall has thickness \(d_w\). In the sketch the wall is vertical and parallel to the gravity acceleration vector \(\overline{g}\). However, in the paper an inclination angle of \(45^{\circ }\) is also considered in two cases: \(\overline{g} > 0\) and \(\overline{g}< 0\) (Rayleigh-Taylor instability). The last condition corresponds to a thin film falling down below a thick wall. Two situations are considered with respect to the temperatures: \(T_{A0}>T_{A1}\) and \(T_{A0}<T_{A1}\)

Full size image

2 Equations of motion and evolution equation

The sketch of the system under investigation is shown in Fig. 1. Notice that gravity is in the x-direction and that the figure sketches the particular case of a vertical wall. However, in this paper also the case of a wall inclined at \(45^{\circ }\) degrees with respect to the horizontal is considered. Only when the wall is inclined \(45^{\circ }\) degrees gravity may have positive or negative (Rayleigh-Taylor) direction. The mean liquid layer thickness is \(d_f\) and the wall thickness is \(d_W\). The free surface height h(x, y, t), the unknown of the problem, is represented by a solid line. The origin is located at the interface between the liquid and the slippery thick wall. The atmospheres below the wall and above the free surface have different temperatures \(T_{A0}>T_{A1}\) or else \(T_{A0}<T_{A1}\).

The equations of motion, energy and continuity of the liquid, the energy equation of the wall and their corresponding boundary conditions are made non dimensional as follows. The distance in the z-direction is measured with d\(_f\) the thickness of the liquid layer. The distance in the x- and y-direction by \(\lambda /2\pi = d_f/\varepsilon \), where the wavelength \(\lambda \) is a representative longitude of the free surface deformation and the scaling parameter \(\varepsilon = 2\pi d_f/\lambda \), is assumed to be \(\varepsilon < 1\) in the small wavenumber (long wavelength) approximation. The time is scaled with \(d_f (\lambda /2\pi )/\nu = d_f^2/\varepsilon \nu \), velocity with \(\nu /\hbox {d}_f\) and pressure with \(\rho \nu ^2\)/ \(d_f^2\) where \(\rho \) and \(\nu \) are the density and the kinematic viscosity of the liquid, respectively. The temperature is scaled with \(\Delta T = T_{A0}\) - \(T_{A1}\), where \(T_{A0}\) is the temperature of the atmosphere close to the wall and \(T_{A1}\) is the temperature of the atmosphere close to the liquid free surface. These scalings mean that the variation in the x and y-directions is different from that in the z-direction. This will have consequences in the scaling of the equations of motion and boundary conditions.

The nonlinear evolution equation of the unknown h(x, y, t) is derived by means of an asymptotic method using the following expansions of the dependent variables in terms of \(\varepsilon \). They are

$$\begin{aligned}&u=u_0 + \varepsilon u_{1}+\varepsilon ^2 u_{2}+\cdots ,\text { } v=v_0 + \varepsilon v_{1}+\varepsilon ^2 v_{2}+\cdots ,\text { } w=\varepsilon (w_{1}+\varepsilon w_{2}+\cdots ),\nonumber \\&p=p_{0}+\varepsilon p_{1}+\cdots ,\text { } T=T_{0}+\varepsilon T_{1}+\cdots ,\text { } T_w=T_{w0}+\varepsilon T_{w1}+\cdots . \end{aligned}$$
(1)

The asymptotic method consists in substituting this expansions in the following equations and boundary conditions and solving recursively each resulting linearized set of equations. The scaled non dimensional equations of motion, continuity and energy of the liquid are:

$$\begin{aligned}{} & {} \varepsilon u_{t}+\varepsilon uu_{x}+\varepsilon vu_{y} +wu_{z} = -\varepsilon p_{x}+\varepsilon ^{2}u_{xx}+\varepsilon ^{2}u_{yy}+u_{zz} + G \sin (q). \end{aligned}$$
(2)
$$\begin{aligned}{} & {} \varepsilon v_{t}+\varepsilon uv_{x}+\varepsilon vv_{y} +wv_{z}= -\varepsilon p_{y}+\varepsilon ^{2}v_{xx}+\varepsilon ^{2}v_{yy}+v_{zz}. \end{aligned}$$
(3)
$$\begin{aligned}{} & {} \varepsilon w_{t}+\varepsilon uw_{x}+\varepsilon vw_{y} +ww_{z} = -p_{z} +\varepsilon ^{2}w_{xx}+\varepsilon ^{2}w_{yy}+w_{zz} - G \cos (q). \end{aligned}$$
(4)
$$\begin{aligned}{} & {} w_{z}=-\varepsilon u_{x}-\varepsilon v_{y}. \end{aligned}$$
(5)
$$\begin{aligned}{} & {} Pr\left( \varepsilon T_{t}+\varepsilon uT_{x}+\varepsilon vT_{y} +wT_{z} \right) = \varepsilon ^{2}T_{xx}+\varepsilon ^{2}T_{yy}+T_{zz}. \end{aligned}$$
(6)

The energy equation of the temperature \(T_w\) of the solid wall is:

$$\begin{aligned} Pr \varepsilon T_{wt} =\frac{\chi }{\frac{\rho _w}{\rho }\frac{c_{pw}}{c_{p}}} \left( \varepsilon ^{2}T_{wxx}+\varepsilon ^{2}T_{wyy}+T_{wzz} \right) . \end{aligned}$$
(7)

where \(G = g d_f^3/\nu ^2\) is the Galilei number, q is the angle of inclination of the thick wall and \(Pr = \nu /\alpha \) is the Prandtl number. Here, \(\alpha \) is the thermal diffusivity of the liquid, \(c_{p}\) is the heat capacity of the liquid and \(\rho _w\) and \(c_{pw}\) are the density and heat capacity of the wall, respectively. \(\chi \) is the ratio of the heat conductivity of the wall over that of the liquid. It is important to point out that the series expansion Eq. 1 is convergent in the present approximation when the Galilei number is order one or smaller.

The boundary conditions for the velocity and temperature of the liquid are the following. The slip boundary conditions (see [31]) and the condition of impenetrability at the wall are

$$\begin{aligned} u=\beta u_z, \qquad v=\beta v_z, \quad \qquad \text { and } \quad w=0.\qquad \text { at }z=0 \end{aligned}$$
(8)

where \(\beta = b/d_f\) is the non dimensional slip length of the wall and b is the longitudinal slip length. The no-slip boundary condition is attained setting \(\beta = 0\) at the wall. The ideal slip (friction free surface) limit is reached when \(\beta \) \(\rightarrow \infty \) and \(u_z = v_z = 0\) at the wall. Notice that the dimensional slip length b may have a range from \(10^{-9}\)m up to \(10^{-4}m\) for a superhydrophobic substrate [47]. However, there is also a variety of thin liquid film thicknesses from \(10^{-7}\hbox {m}\) (see [48]) up to \(10^{-4}\hbox {m}\) (see [49]) or more. Thus, the non dimensional parameter \(\beta \) also has a wide range of magnitudes. Here, the selection of the magnitude of \(\beta \) was made to show clearly the behavior of slip found in the analytical results.

The normal stress boundary condition at the free surface is

$$\begin{aligned}{} & {} -p + P_A +\frac{2}{N^{2}}[\varepsilon ^{3}(u_{x}h_{x}^{2}+v_{y}h_{y}^{2} )+\varepsilon ^{3}(u_{y}+v_{x})h_{x}h_{y}-\varepsilon (v_{z}+\varepsilon w_{y})h_{y}-\varepsilon (u_{z}+\varepsilon w_{x})h_{x}+w_{z}] \end{aligned}$$
(9)
$$\begin{aligned}{} & {} \quad =\frac{1}{N^{3}}S[(1+\varepsilon ^{2}h_{y}^{2} )h_{xx}+(1+\varepsilon ^{2}h_{x}^{2})h_{yy}-2\varepsilon ^{2}h_{x}h_{y} h_{xy}].\quad \text { at }z=h(x,y,t) \end{aligned}$$
(10)

where \(S = \gamma d_f \varepsilon ^2/3\rho \nu ^2\) is the surface tension number, \(\gamma \) is the surface tension and \(N=\sqrt{1+\varepsilon ^{2}h_{x}^{2}+\varepsilon ^{2}h_{y}^{2}}\). Note that the non dimensional \(h(x,y,t) = 1 + H(x,y,t)\) and that H(x, y, t) is the free surface deformation. Besides, \(\hbox {P}_A\) is the pressure of the atmosphere outside the liquid. The balance of shear stresses and surface tension temperature gradients on the free surface are the following. The first shear stress boundary condition is:

$$\begin{aligned}{} & {} \frac{2}{N}\left[ \varepsilon (w_{z}-\varepsilon u_{x})h_{x} -\frac{1}{2}\varepsilon ^{2} (u_{y}+v_{x})h_{y}+\frac{1}{2}(u_{z}+\varepsilon w_{x})(1-\varepsilon ^{2} h_{x}^{2}) \right. \nonumber \\{} & {} \left. -\frac{1}{2}\varepsilon ^{2}(\varepsilon w_{y}+v_{z})h_{x}h_{y} \right] = -Ma(\varepsilon T_{x}+\varepsilon h_{x}T_{z}).\qquad \text { at }z=h(x,y,t) \end{aligned}$$
(11)

and the second shear stress boundary condition is:

$$\begin{aligned}{} & {} \frac{2}{N}\left[ \varepsilon h_y \left( \varepsilon ^3 u_xh_x^2 - \varepsilon v_y \left( 1+\varepsilon ^2 h_x^2 \right) + w_z \right) + \frac{1}{2} \varepsilon ^2 \left( u_y+v_x\right) h_x \left( \varepsilon ^2 h_y^2-1 - \varepsilon ^2 h_x^2\right) \right. \nonumber \\{} & {} \left. -\varepsilon ^2 \left( \varepsilon w_x+u_z\right) h_x h_y + \frac{1}{2} \left( \varepsilon w_y+v_z\right) \left( 1+\varepsilon ^2 h_x^2 - \varepsilon ^2 h_y^2\right) \right] \nonumber \\{} & {} \quad =- Ma\left[ - \varepsilon ^3 T_xh_xh_y + \varepsilon T_y\left( 1 + \varepsilon ^2 h_x^2 \right) + \varepsilon T_z h_y \right] .\qquad \text { at }z=h(x,y,t) \end{aligned}$$
(12)

where \(Ma = Ma^*/Pr\) and \(Ma^* = -(d\gamma /dT)\Delta T d_f/\rho \nu \alpha \) is the usual Marangoni number and \(\gamma \) is the surface tension. The kinematic boundary condition at the free surface is

$$\begin{aligned} \varepsilon h_t + \varepsilon u h_x + \varepsilon v h_y - w = 0 . \qquad \text { at }z=h(x,y,t) \end{aligned}$$
(13)

The boundary conditions of the temperature in the liquid and the wall are as follows. At the free surface

$$\begin{aligned}{} & {} \frac{1}{N}\left( \varepsilon ^2 h_x T_x + \varepsilon ^2 h_y T_y - T_z \right) = Bi T. \qquad \text { at }z=h(x,y,t) \end{aligned}$$
(14)
$$\begin{aligned}{} & {} T = T_w \qquad \text { and }\qquad T_z = \chi T_{wz}. \qquad \text { at }z=0 \end{aligned}$$
(15)
$$\begin{aligned}{} & {} T_w = 1 \qquad \text { at }z=-d \end{aligned}$$
(16)

where \(d = d_W/d_f\), \(\hbox {Bi} = Q_{h} d_f / K\) is the Biot number and \(Q_{h}\) is the heat transfer coefficient at the free surface.

As explained above, the expansions Eq. 1 are substituted into the equations and corresponding boundary conditions and the solutions are calculated recursively at the different orders of \(\varepsilon \). Thus, from the equations of the temperatures, the basic temperature profiles which satisfy the boundary conditions are:

$$\begin{aligned} T_0= & {} \frac{1}{\delta }\left[ 1+Bi\left( h-z \right) \right] \end{aligned}$$
(17)
$$\begin{aligned} T_{W0}= & {} \frac{1}{\delta }\left[ 1+Bi\left( h-\frac{z}{\chi } \right) \right] \end{aligned}$$
(18)

The denominator is defined as

$$\begin{aligned} \delta (x,y,t) = 1+Bi\left( h(x,y,t)+\frac{d}{\chi } \right) \end{aligned}$$
(19)

which is in fact a function of x, y and t through the free surface deformation h(x, y, t). It is very important because it includes the ratio \(d/\chi \), which is able to control the stability of the flow, as will be shown presently. Notice that in the lubrication approximation, instead of evaluating the free surface at a specific magnitude of the z-coordinate, the evaluation is made at h(x, y, t), the unknown location of the free surface deformation. As will be demonstrated below, h(x, y, t) will satisfy an evolution equation derived using the kinematic boundary condition.

The solution of the pressure is

$$\begin{aligned} p_0 = P_A - G \cos (q)\left( z - h\right) - 3 S \nabla _\perp ^2 h \end{aligned}$$
(20)

where \(\nabla _\perp = (\partial /\partial x,\partial /\partial y)\) is the horizontal gradient. It is important to point out that under the present approximation, it is enough to have the main temperatures and pressure profiles given in Eqs. 18, 19 and 20.

The solution of the x and y-components of the velocity at the lowest order, that is, the main velocity profiles, are:

$$\begin{aligned} u_0= & {} -\frac{1}{2} G \sin (q)\left[ z^2 - 2 h \left( z+\beta \right) \right] \end{aligned}$$
(21)
$$\begin{aligned} v_0= & {} 0 \end{aligned}$$
(22)

The continuity equation is used to obtain the vertical component of velocity at the lowest order. That is:

$$\begin{aligned} w_1 = -\frac{1}{2} G \sin (q)\left[ z^2 + 2\beta z \right] h_x \end{aligned}$$
(23)

Substitution of these results of Eqs. 21, 22 and 23 into the kinematic boundary condition leads, at this order, to the equation:

$$\begin{aligned} h_t + G\sin (q) \left[ h^2 + 2 \beta h \right] h_x = 0 \end{aligned}$$
(24)

This approximation is used to substitute \(h_t\) in the places where it appears in the following steps of the asymptotic procedure. The expressions of the solutions of the velocity components in the next order are very large and will be presented in the Appendix. However, it is important to mention the form of the following factors which appear in the thermocapillary terms:

$$\begin{aligned}{} & {} T_{0x} + h_x T_{0z} = \frac{\partial }{\partial x} \left( \frac{1}{\delta } \right) \qquad at \qquad z=h\\{} & {} T_{0y} + h_y T_{0z} = \frac{\partial }{\partial y} \left( \frac{1}{\delta } \right) \qquad at \qquad z=h \end{aligned}$$

After substitution of these results into the kinematic boundary condition Eq. 13, it is possible to obtain the nonlinear evolution equation satisfied by the free surface perturbations in the presence of slip (\(\beta \)) at the wall. That is:

$$\begin{aligned}{} & {} h_t + G\sin (q) \left[ h^2 + 2 \beta h \right] h_x + \varepsilon \left\{ G^2\sin (q)^2 \frac{\partial }{\partial x}\left[ \frac{h^3}{15}\left( h+\beta \right) \left( 2 h^2+10h \beta +15\beta ^2 \right) h_x \right] \right. \nonumber \\{} & {} \quad - \nabla _\perp \cdot \left[ \left( \frac{1}{3}h^3 +\beta h^2 \right) \nabla _\perp \left( G \cos (q) h - 3 S \nabla _\perp ^2 h \right) \right] \nonumber \\{} & {} \quad \left. -Ma \nabla _\perp \cdot \left[ \left( \frac{1}{2}h^2 +\beta h \right) \nabla _\perp \left( \frac{1}{\delta } \right) \right] \right\} =0 \end{aligned}$$
(25)

Notice that when \(q = 0\), this evolution equation reduces to that of Dávalos-Orozco and Sánchez-Barrera [46]. In the same way, but with no-slip at the wall, this evolution equation reduces to that of Oron et al. [50] (in the absence of evaporation), to that of Oron [51] and to that of Podolny et al. [52] (when the liquid is not binary). When \(q > 0\) and \(Ma = 0\), Eq. 25 reduces to Eq. 3.7 of Samanta et al. [53].

In the next section, the linear stability is analyzed using this evolution equation. Then, in the following section, the nonlinear stability is investigated.

3 Linear stability

The linear instability is investigated linearizing the evolution Eq. 25 and assuming normal modes for the free surface deformation \(H(x,y,t)=A_h\,\exp (i k x+ \Omega t)\) found in \(h(x,y,t) = 1 + H(x,y,t)\). Here k is the x-component of the wavenumber vector. Besides, \(\Omega = \Gamma + i\omega \) where \(\Gamma \) is the growth rate and \(\omega \) is the frequency of oscillation. \(A_h\) is a constant amplitude of the free surface perturbation. Substitution leads to the dispersion relation for \(\Omega \). The result is separated into real and imaginary parts. The frequency of oscillation is: \(\omega = - G\sin (q)\left( 1+2 \beta \right) k\). Clearly, the frequency, and therefore the phase velocity, increases with \(\beta \).

The growth rate is obtained from the real part. That is:

$$\begin{aligned}{} & {} \Gamma =k^2 \left[ G^2\sin (q)^2 \frac{1}{15}\left( 1+\beta \right) \left( 2 +10 \beta + 15\beta ^2 \right) \right. \nonumber \\{} & {} \quad \left. - \left( \frac{1}{3}+\beta \right) \left( G \cos (q)+3 S k^2 \right) +\frac{Ma Bi}{\delta _L^2}\left( \frac{1}{2}+\beta \right) \right] \end{aligned}$$
(26)

where \(\delta _L = 1 + Bi(1 + d/\chi )\), is the linearized denominator \(\delta (x,y,t)\). As can be seen, \(\delta _L\) includes the ratio of thicknesses ratio d over the heat conductivities ratio \(\chi \) in one parameter \(d/\chi \), which will play an important role on the stability through thermocapillary effects. The critical wavenumber is obtained from the condition that the growth rate \(\Gamma \) = 0. Two solutions are found. One corresponds to \(k_c\) = 0 and the other one to

$$\begin{aligned} k_c = \frac{1}{\sqrt{3S}}\sqrt{ \frac{Ma Bi}{\delta _L^2} \left( \frac{\frac{1}{2}+\beta }{\frac{1}{3}+\beta } \right) +G^2\sin (q)^2 \left[ \frac{\frac{1}{15}\left( 1+\beta \right) \left( 2 +10 \beta + 15\beta ^2 \right) }{\frac{1}{3}+\beta } \right] - G \cos (q) } \end{aligned}$$
(27)

The wavenumber corresponding to the maximum growth rate is obtained making zero the k derivative of the growth rate.

$$\begin{aligned} k_{max}= & {} \frac{1}{\sqrt{2}} k_c \nonumber \\= & {} \frac{1}{\sqrt{6S}}\sqrt{ \frac{Ma Bi}{\delta _L^2} \left( \frac{\frac{1}{2}+\beta }{\frac{1}{3}+\beta } \right) +G^2\sin (q)^2 \left[ \frac{\frac{1}{15}\left( 1+\beta \right) \left( 2 +10 \beta + 15\beta ^2 \right) }{\frac{1}{3}+\beta } \right] - G \cos (q) } \end{aligned}$$
(28)

Notice the relation with respect to the critical wavenumber \(k_c\). The maximum growth rate is obtained after substitution of \(k_{max}\) into Eq. 26. That is

$$\begin{aligned}{} & {} \Gamma _{max} =\frac{1}{12 S \left( \frac{1}{3}+\beta \right) } \left[ G^2\sin (q)^2 \frac{1}{15}\left( 1+\beta \right) \left( 2 +10 \beta + 15\beta ^2 \right) \right. \nonumber \\{} & {} \quad \left. + \frac{Ma Bi}{\delta _L^2}\left( \frac{1}{2}+\beta \right) - G \cos (q)\left( \frac{1}{3}+\beta \right) \right] ^2 \end{aligned}$$
(29)

As can be seen, \(\Gamma _{max}\) in Eq. 29 represents a parabola in a plot \(\Gamma _{max}\) vs Ma. That is:

Fig. 2
figure 2

Growth rate \(\Gamma \) vs k. \(G = 0.1\): Fig. 2a, c and e. \(G = 0.3\): Fig. 2b, d and f (notice the different scales). \(d/\chi = 0.5\): Fig. 2a and b. \(d/\chi = 1.8\): Fig. 2c and d. From Fig. 2a–d: \(q = 90^{\circ }\) and \(Ma = 1.3\) (1), 1.5 (2), 1.7 (3). From Fig. 2e–f: \(q = 45^{\circ }\) and \(d/\chi = 0.5\). Figure 2e: \(Ma = 0.8\) (1), 1.2 (2), 1.6 (3). Figure 2f: \(Ma = 1.9\) (1), 2.2 (2), 2.5 (3). \(\beta = 0.0\) (solid line), 0.1 (dashed line), 0.3 (dotted line)

Full size image
$$\begin{aligned}{} & {} 4\left( \frac{3S \delta _L^4 \left( \frac{1}{3}+\beta \right) }{Bi^2 \left( \frac{1}{2}+\beta \right) ^2} \right) \Gamma _{max} \nonumber \\{} & {} \quad =\left( Ma +G^2\sin (q)^2 \frac{1}{15}\frac{\delta _L^2}{ Bi} \frac{\left( 1+\beta \right) \left( 2 +10 \beta + 15\beta ^2 \right) }{\frac{1}{2}+\beta } - G \cos (q) \frac{\delta _L^2}{ Bi} \left( \frac{\frac{1}{3}+\beta }{\frac{1}{2}+\beta } \right) \right) ^2 \end{aligned}$$
(30)

The focal distance \(p_f\) is

$$\begin{aligned} p_f = \left( \frac{3S \delta _L^4 \left( \frac{1}{3}+\beta \right) }{Bi^2 \left( \frac{1}{2}+\beta \right) ^2} \right) \end{aligned}$$
(31)

and the vertex is located at:

$$\begin{aligned}{} & {} \left( Ma_{\Gamma _{max}=0},\Gamma _{max}\right) \nonumber \\{} & {} \quad = \left( G \cos (q) \frac{\delta _L^2}{ Bi} \left( \frac{\frac{1}{3}+\beta }{\frac{1}{2}+\beta } \right) - G^2\sin (q)^2 \frac{1}{15}\frac{\delta _L^2}{ Bi} \frac{\left( 1+\beta \right) \left( 2 +10 \beta + 15\beta ^2 \right) }{\frac{1}{2}+\beta },0 \right) \end{aligned}$$
(32)

This means that at \(Ma_{\Gamma _{max}=0}\) the instability is neutral against any perturbations. Notice here that both the width of the parabola (see \(p_f\) in Eq. 31) and the location of the vertex through \(Ma_{\Gamma _{max}=0}\) are controlled by the ratio \(d/\chi \) and \(\beta \). This has important consequences on the results presented below. It is of interest to mention that when \(q = 0\), \(Ma_{\Gamma _{max}=0}\) reduces to that found in [46]. In that case \(Ma_{\Gamma _{max}=0}\) could be negative but here it could be positive. This may have major consequences, mainly in the behavior of the stability with respect to the slip factor \(\beta \) and the intersection of the curves of \(\Gamma _{max}\).

Next, the instability will be discussed based on the analytical results found above. First the case \(G > 0\) will be discussed for the two conditions \(q = 90^{\circ }\) and \(45^{\circ }\). Then, the case \(G < 0\) (Rayleigh-Taylor instability) will be discussed for the condition \(q = 45^{\circ }\). The flow will also be subjected to a destabilizing \(Ma > 0\) and a stabilizing \(Ma < 0\). Here it is assumed that the change in sign of Ma is due to a change in direction of the temperature gradient across the whole system. The number of parameters is large and therefore it is important to say that two parameters will be fixed through all the numerical calculations. They are \(Bi = 0.1\) and S = 1.

3.1 Flow down above a thick wall: \(G> 0\)

In Fig. 2 results of two magnitudes of G = 0.1 and 0.3, two magnitudes of \(d/\chi \), and two inclination angles \(q = 90^{\circ }\) and \(45^{\circ }\) are presented. The magnitude \(G = 0.1\) was selected with the goal to find intersections of the curves of \(\Gamma \) when \(\beta \) increases (see Fig. 2a and c). As can be seen, for \(q = 90^{\circ }\) and an increase to \(G = 0.3\) intersections are not possible (see Fig. 2b and d). The figure also shows the important role played by the ratio \(d/\chi \). Figure 2c and d demonstrate how this ratio decreases the instability when increasing from 0.5 to 1.8. In all cases, Ma destabilizes the flow increasing the magnitude of \(\Gamma \). Observe here that the solid curves correspond to the no-slip boundary condition and were plotted for the sake of comparison.

The intersections found in Fig. 2a and c are very important because they show that an increase of \(\beta \) stabilizes the flow after a particular wavenumber. As found for \(q = 45^{\circ }\), in Fig. 2e and f, it is still possible to find intersections even for \(G = 0.3\). The wavenumber for intersection between two curves with different \(\beta \), lets say \(\beta _1\) and \(\beta _2\), can be derived making equal the two corresponding expressions of \(\Gamma \). The result, for any angle of inclination, is:

Fig. 3
figure 3

First column: Critical wavenumber number \(k_c\) vs G for \(q = 90^{\circ }\) and \(45^{\circ }\) and \(Ma = 1.3\) (1), 1.5 (2), 1.7 (3). Second column: Maximum growth rate \(\Gamma _{max}\) vs Ma for \(d/\chi = 0.5\). Figure 3a: \(d/\chi = 0.5\). Figure 3b: \(G = 0.1\). Figure 3c: \(d/\chi = 1.8\). Figure 3d: \(G = 0.3\). \(\beta = 0.0\) (solid line), 0.1 (dashed line), 0.3 (dotted line)

Full size image
$$\begin{aligned} k_+ = \sqrt{\frac{G^2\sin (q)^2}{3S} \left[ \frac{4}{5} +\frac{5}{3}(\beta _1+\beta _2) + \beta _1^2+ \beta _1\beta _2 + \beta _2^2 \right] - \frac{G\cos (q)}{3S} + \frac{Ma Bi}{3S\delta _L^2}} \end{aligned}$$
(33)

This means that for a wavenumber \(k>k_+\), \(\beta \) has a stabilizing effect. Notice that \(k_+\) reduces to that found in [46] when q = 0 which is independent from \(\beta \). Furthermore, in order to have an intersection the radicand has to be positive. Beware that it is possible to have intersection for stable \(\Gamma < 0\). That is what is going on in Fig. 2b and d, as can be understood following the tendency and slope of the curves. Therefore, Eq. 33 should be used with care. This intersection was independent of \(\beta \) in the previous paper [46].

For example, the intersection of the curves \(\beta = 0\) and 0.1 in Fig. 2a for \(q = 90^{\circ }\), \(Ma = 1.3\) and \(d/\chi = 0.5\) occurs at \(k_+ = 0.1897\). That between the curves \(\beta = 0\) and 0.3 occurs at \(k_+ = 0.1933\) and that between the curves \(\beta = 0.1\) and 0.3 occurs at \(k_+ = 0.1951\). In the case of Fig. 2e for \(q = 45^{\circ }\) the intersections when \(Ma = 1.2\) and the other parameters are the same are as follows: the intersection of the curves \(\beta = 0\) and 0.1 occurs at \(k_+ = 0.0911\), that between the curves \(\beta = 0\) and 0.3 occurs at \(k_+ = 0.0948\) and that between the curves \(\beta = 0.1\) and 0.3 occurs at \(k_+ = 0.0966\). They are very close but different.

From Eq. 33 notice that \(\beta \) always stabilizes when

$$\begin{aligned} \frac{Ma Bi}{\delta _L^2}=G\cos (q) - G^2\sin (q)^2 \left[ \frac{4}{5} +\frac{5}{3}(\beta _1+\beta _2) + \beta _1^2+ \beta _1\beta _2 + \beta _2^2 \right] \end{aligned}$$
(34)

This may be verified in the left column of Fig. 2. This is more easy to verify in Fig. 2e and f for \(q = 45^{\circ }\), where clearly there is a tendency to move the \(k_+\) of intersection to the left, very close to the origin, by decreasing Ma. In contrast, \(\beta \) always destabilizes when \(k_+ = k_c\). In this case, \(k_c\) should be evaluated with either of the \(\beta \)’s, \(\beta _1\) or \(\beta _2\).

The critical wavenumber number is plotted against G in the left column of Fig. 3. The Maximum growth rate is plotted against Ma in the right column of Fig. 3. Two angles of inclination \(q = 90^{\circ }\) and \(45^{\circ }\) were used. Figure 3a corresponds to \(d/\chi = 0.5\) and Fig. 3b corresponds to \(d/\chi = 0.5\) and \(G = 0.1\). Figure 3c is for \(d/\chi = 1.8\) and Fig. 3d is for \(d/\chi = 0.5\) and \(G = 0.3\). Clearly, in the first column of Fig. 3, for \(q = 90^{\circ }\) intersections of the curves of \(k_c\) occur for certain G. However, this is not the case when \(q = 45^{\circ }\), where, in addition, \(k_c\) decreases with G, for both magnitudes of \(d/\chi \). The intersections between curves of \(k_c\) occur at the following G:

$$\begin{aligned} G_+=\pm \sqrt{ \frac{15Ma Bi/(2\delta _L^2 \sin ^2q)}{45(\beta _2\beta _1^2+\beta _1\beta _2^2)+15(\beta _1^2+\beta _2^2)+ 90\beta _1\beta _2 + 25(\beta _1+\beta _2)+6}} \end{aligned}$$
(35)

Notice that the intersections for \(q = 45^{\circ }\) occur for \(G_+ < 0\), using the minus sign in Eq. 35. This case of Rayleigh-Taylor instability is discussed below. It is important to point out that the role of the ratio \(d/\chi \) is to stabilize the flow when its magnitude increases. It also contributes to modify the point of intersection of the curves of \(k_c\) through \(\delta _L\) in \(G_+\). The angle of inclination q also has important influence on \(G_+\). However, the whole role of q on the stability is still more complex and it is discussed in different places below.

The Maximum growth rate in the right column of Fig. 3 shows that for \(q = 90^{\circ }\) the maximum growth rate \(\Gamma _{max}\) increases monotonically with an increase of \(\beta \) to the right of the vertex (\(Ma_{\Gamma _{max}=0}\)) of the parabola. However, the contrary occurs to the left of the vertex. It is of interest that this behavior is reversed with respect to the vertex for \(q = 45^{\circ }\). Therefore, from the point of view of the maximum growth rate \(\beta \) also has a stabilizing effect at \(q = 45^{\circ }\). This may be corroborated at the right column of Fig. 3 where the maximum growth rate is plotted against Ma for two angles of inclination \(q = 90^{\circ }\) and \(45^{\circ }\). Figure 3b corresponds to G = 0.1 and Fig. 3d to \(G = 0.3\). Notice how the vertex of the parabola Eq. 30 is displaced with the variation of the parameters (see Eq. 32). Moreover, the width of the parabola (latus rectum) also changes as four times Eq. 31. The curves are plotted, to the left and to the right of the figure, up to the place where intersections are found. For \(q = 90^{\circ }\), it is easy to observe two intersections. One is located just to the left of the vertex of the parabolas, for \(Ma< 0\). The second is located farther to the left. Apparently between these two intersections \(\beta \) stabilizes. On the contrary, the intersections when \(q = 45^{\circ }\) are located just to the right of the vertex and farther away. Between these two intersections \(\beta \) stabilizes.

It is important to be careful because the intersections of the parabolas made by \(\Gamma _{max}\) for \(q = 90^{\circ }\) are misleading. The reason is that the intersections occur for \(Ma<Ma_{\Gamma _{max}=0}\) where \(Ma< 0\) is stabilizing. Then, some of the curves are stable (\(\Gamma < 0\)) and therefore no intersections (that is \(\Gamma _{max}(\beta _1)\) = \(\Gamma _{max}(\beta _2)\)) are possible. This invalidates the meaning of the intersections found for \(q = 90^{\circ }\) to the left of the vertex due to the natural stabilizing (\(\Gamma < 0\)) effect of large enough \(Ma< 0\), not observed in Fig. 3b and d.

The case of \(q = 45^{\circ }\) is interesting because the stabilizing behavior of \(\beta \) in fact occurs between the two intersections. Again, to the left of the vertex it is found that the curves of \(\Gamma \) are stable, in the same way as for \(q = 90^{\circ }\), even in the region 0 \(<Ma<Ma_{\Gamma _{max}=0}\).

It is possible to show analytically that \(\Gamma < 0\) (stable) at \(Ma_{\Gamma _{max}=0}\) of the vertex. To this goal, it is enough to substitute \(Ma_{\Gamma _{max}=0}\) of Eq. 32 into \(\Gamma \) in Eq. 26. It is found that at \(Ma_{\Gamma _{max}=0}\) the growth rate \(\Gamma = - S k^4 (3 \beta + 1)\) is always negative for \(k>0\) and any \(\beta \), G and inclination angle q. As a consequence, \(\Gamma < 0\) for any magnitude of \(Ma\le Ma_{\Gamma _{max}=0}\). In particular, the result is valid for q = 0 [46].

The Ma for an intersection is found assuming that \(\Gamma _{max}\) and Ma are the same for two different \(\beta \), lets say \(\beta _1\) and \(\beta _2\). Two solutions are found and they are:

$$\begin{aligned} Ma_{++}= & {} -\frac{\delta _L^2}{Bi} \frac{Num_1-Num_2}{\left( \beta _1+\frac{1}{2} \right) \sqrt{\beta _2+\frac{1}{3}} - \left( \beta _2+\frac{1}{2} \right) \sqrt{\beta _1+\frac{1}{3}}} \end{aligned}$$
(36)
$$\begin{aligned} Ma_{--}= & {} -\frac{\delta _L^2}{Bi} \frac{Num_1+Num_2}{\left( \beta _1+\frac{1}{2} \right) \sqrt{\beta _2+\frac{1}{3}} + \left( \beta _2+\frac{1}{2} \right) \sqrt{\beta _1+\frac{1}{3}}} \end{aligned}$$
(37)

where

$$\begin{aligned}{} & {} Num_1= \left[ G^2\sin (q)^2 \frac{1}{15}\left( 1+\beta _1\right) \left( 2 +10 \beta _1 + 15\beta _1^2 \right) - G \cos (q)\left( \beta _1+\frac{1}{3}\right) \right] \sqrt{\beta _2+\frac{1}{3}}\\{} & {} Num_2= \left[ G^2\sin (q)^2 \frac{1}{15}\left( 1+\beta _2\right) \left( 2 +10 \beta _2 + 15\beta _2^2 \right) - G \cos (q)\left( \beta _2+\frac{1}{3}\right) \right] \sqrt{\beta _1+\frac{1}{3}} \end{aligned}$$

These two formulas Eqs. 36 and 37 reduce to those derived in [46] when \(q = 0^{\circ }\). They give the two limits of the regions of Ma where the behavior of \(\beta \) changes from destabilizing to stabilizing from the view point of the maximum growth rate. As mentioned above, this intersections are valid and have physical meaning only for \(Ma>Ma_{\Gamma _{max}=0}\).

Therefore, it is of interest to understand in a deeper way the behavior of the vertex of the parabola that is responsible of the intersections among the curves of different \(\beta \). To attain this goal first assume that \(Ma_{\Gamma _{max}=0}\) is a function of \(\beta \) and that it can be written as \(Ma_{\Gamma _{max}=0}(\beta )\). Then assume that \(\beta _2>\beta _1\). Subtract \(Ma_{\Gamma _{max}=0}(\beta _2)\) - \(Ma_{\Gamma _{max}=0}(\beta _1)\). The result has a number of positive factors, but the product of some other factors of the numerator determines if the difference is positive or negative. That part of the numerator is:

$$\begin{aligned} G \left( \beta _1 - \beta _2\right) \left[ G\sin (q)^2 f_{\beta _1\beta _2} - 5\cos (q) \right] \end{aligned}$$

where

$$\begin{aligned} f_{\beta _1\beta _2} = \left( 30\beta _1 \beta _2\left( \beta _1 + \beta _2\right) + 15\left( \beta _1^2+ \beta _2^2 \right) + 65\beta _1\beta _2 + 25\left( \beta _1 + \beta _2 \right) + 8\right) \end{aligned}$$

is always positive. Notice that by assumption \(\left( \beta _1 - \beta _2\right) < 0\) and therefore the term inside brackets determines the sign of the difference between the two Ma’s of the vertexes. To understand the behavior of the vertexes it is possible to calculate two critical values useful to determine the change of sign of \(Ma_{\Gamma _{max}=0}(\beta _2)\) - \(Ma_{\Gamma _{max}=0}(\beta _1)\). One critical value is:

$$\begin{aligned} G_*= \frac{5\cos (q)}{ \sin (q)^2 f_{\beta _1\beta _2} } \end{aligned}$$
(38)

which makes zero the numerator. It is also possible to derive a critical \(\cos (q)\) by substitution of \(\sin (q)^2 = 1 - \cos (q)^2\) and look at the change in sign from the point of view of the angle of inclination. The result is

$$\begin{aligned} \cos (q_*) = \frac{-5+\sqrt{4G^2f_{\beta _1\beta _2}^2+25}}{2Gf_{\beta _1\beta _2}} \end{aligned}$$
(39)

When \(G<G_*\), or else for q < \(q_*\), from the difference it is concluded that \(Ma_{\Gamma _{max}=0}(\beta _2)\) > \(Ma_{\Gamma _{max}=0}(\beta _1)\), that is, the vertex \(Ma_{\Gamma _{max}=0}(\beta _2)\) is located to the right of the vertex \(Ma_{\Gamma _{max}=0}(\beta _1)\). In case G > \(G_*\), or else, for q > \(q_*\) the contrary occurs and \(Ma_{\Gamma _{max}=0}(\beta _2)\) is located to the left of \(Ma_{\Gamma _{max}=0}(\beta _1)\). This is also the reason for the displacement of the intersections among the curves of different \(\beta \)’s. They change from left to right of the vertex depending on the magnitude of G (or q) with respect to the critical \(G_*\) (or \(q_*\)). In fact, the critical G (or q) of the subtraction of the Marangoni number of the intersections of the curves of maximum growth rate, that is \(Ma_{++}\) - \(Ma_{--}\), is exactly the same \(G_*\) Eq. 38 (or \(q_*\) Eq. 39). For G < \(G*\), it is found that \(Ma_{++}\) > \(Ma_{--}\), that is, \(Ma_{++}\) is located to the right of \(Ma_{--}\). The contrary is valid when G > \(G*\). Notice that in the following useful subtractions the critical is also \(G_*\). For the subtraction of \(Ma_{\Gamma _{max}=0}(\beta _2)\) - \(Ma_{++}\), when G < \(G_*\) it is found that \(Ma_{\Gamma _{max}=0}(\beta _2)\) < \(Ma_{++}\). For the subtraction of \(Ma_{\Gamma _{max}=0}(\beta _2)\) - \(Ma_{--}\), when G < \(G_*\) it is found that \(Ma_{\Gamma _{max}=0}(\beta _2)\) > \(Ma_{--}\). For the subtraction of \(Ma_{\Gamma _{max}=0}(\beta _1)\) - \(Ma_{++}\), when G < \(G_*\) it is found that \(Ma_{\Gamma _{max}=0}(\beta _1)\) < \(Ma_{++}\). For the subtraction of \(Ma_{\Gamma _{max}=0}(\beta _1)\) - \(Ma_{--}\), when G < \(G_*\) it is found that \(Ma_{\Gamma _{max}=0}(\beta _1)\) < \(Ma_{--}\). All these inequalities are reversed when G > \(G_*\). From all these inequalities, derived algebraically, it is concluded that:

$$\begin{aligned}{} & {} Ma_{\Gamma _{max}=0}(\beta _1)< Ma_{--}< Ma_{\Gamma _{max}=0}(\beta _2)< Ma_{++} \qquad {\textbf {if}} \qquad G < G_* \end{aligned}$$
(40)
$$\begin{aligned}{} & {} Ma_{++}< Ma_{\Gamma _{max}=0}(\beta _2)< Ma_{--} < Ma_{\Gamma _{max}=0}(\beta _1) \qquad {\textbf {if}} \qquad G > G_* \end{aligned}$$
(41)

These inequalities are very informative, but to give them a more precise meaning it will be helpful to employ the two extremal cases \(q = 0^{\circ }\) (which corresponds to Eq. 40) [46] and \(q = 90^{\circ }\) (which corresponds to Eq. 41). If \(\beta _2\) > \(\beta _1\), it can be shown analytically that for \(q = 0^{\circ }\) the vertex always has \(Ma_{\Gamma _{max}=0}> 0\), and the intersections of the maximum growth rate are located at \(Ma_{++}> 0\) and \(Ma_{--}> 0\). On the other extreme, for \(q = 90^{\circ }\) the vertex always has \(Ma_{\Gamma _{max}=0}\) < 0, \(Ma_{++}\) < 0 and \(Ma_{--}\) < 0. The change of these particular inequalities start to occur when G (or q) approaches and crosses the critical \(G_*\) Eq. 38 (or \(q_*\) Eq. 39). That is, in the process some of the terms of the inequalities in Eqs. 40 and 41, not all, might be negative.

Fig. 4
figure 4

Growth rate \(\Gamma \) vs k. Rayleigh-Taylor instability with \(q = 45^{\circ }\) and \(d/{\chi} = 0.5\) . G = 0.1: Fig. 4a, c. G = 0.3: Fig. 4b, d (notice the different scales). Figure 4a, b: destabilizing \(Ma= 1.3\) (1), 1.5 (2) and 1.7 (3). Figures 4c: stabilizing Ma = 0.1 (1), - 0.3 (2) and 0.5 (3). Figures 4d: stabilizing \(Ma = 0.1\) (1), 0.5 (2) and 0.9 (3). \(\beta = 0.0\) (solid line), 0.1 (dashed line), 0.3 (dotted line)

Full size image

Notice that in the case of G < 0 (Rayleigh-Taylor instability) the sign of the numerator is exclusively determined by \(\beta _1\) - \(\beta _2\) < 0. Thus the numerator is negative. Therefore, as will be shown presently, \(Ma_{\Gamma _{max}=0}(\beta _2)\) is located to the left of \(Ma_{\Gamma _{max}=0}(\beta _1)\). In this particular case, \(Ma_{++}\) < \(Ma_{--}\), that is, \(Ma_{--}\) is always located to the right of \(Ma_{++}\). Then, for \(q = 0^{\circ }\) the vertex always has \(Ma_{\Gamma _{max}=0}\) < 0, and the intersections \(Ma_{++}\) < 0 and \(Ma_{--}\) < 0 [46]. For \(q = 90^{\circ }\), that is, for a vertical wall, the results when G < 0 are of no interest because the phenomena are exactly the same as for \(G> 0\).

3.2 Flow down below a thick wall at \(q = 45^{\circ }\) (Rayleigh-Taylor instability) G < 0: destabilizing \(Ma>0\) and stabilizing \(Ma<0\)

From now on the angle of inclination is fixed at \(q = 45^{\circ }\) and the ratio is \(d/\chi = 0.5\). The numerical results for the destabilizing and stabilizing Ma are plotted in Fig. 4. The Fig. 4a and b correspond to a destabilizing \(Ma> 0\) and Fig. 4c and d to stabilizing Ma < 0. Besides, Fig. 4a and c correspond to \(G = -0.1\) and Fig. 4b and d correspond to \(G = -0.3\). It is important to note the different scales of the growth rate of each sub-figure. Observe that for the magnitudes of the parameters used, the intersections of the curves, where \(\beta \) changes its behavior from destabilizing to stabilizing, appear in Fig. 4a and b for \(\Gamma > 0\). The wavenumber \(k_+\) for these intersections is also predicted by the formula Eq. 33. No intersections were found for \(\Gamma > 0\) in Fig. 4c and d.

The critical wavenumber for the Rayleigh-Taylor instability is plotted against G in the first column of Fig. 5. Clearly, intersections of the curves are observed which are described by the formula in Eq. 35 of \(G_+\). In this case the minus sign in front of \(G_+\) should be used. It is found that the wavenumber increases with the magnitude of G but the growth is different for each \(\beta \).

As a consequence, only the right branches of the parabolas are physical and therefore \(\beta \) destabilizes from the point of view of the maximum growth rate. Notice that the curves are displaced to the left when \(d/\chi \) increases from 0.5 to 1.8.

The maximum growth rate against Ma is plotted in the right column of Fig. 5. For the sake of visibility of the separation of the curves, only \(G = - 0.1\) and - 0.2 were used in the figure. The ratio \(d/\chi = 0.5\) corresponds to Fig. 5b and \(d/\chi = 1.8\) corresponds to Fig. 5d. In each figure, the right hand intersection is found very close to the vertex of the parabolas. Therefore it is of interest to know if there is a possibility to have a real change of the stability behavior of \(\beta \) at those particular intersections. To this goal, again use is made of the result which says that at \(Ma_{\Gamma _{max}=0}\) the growth rate \(\Gamma \) = - \(S k^4 (3 \beta + 1)\) is always negative for any \(\beta \), G and inclination angle q. With this, it is possible to compare if any intersection occurs to the right of \(Ma_{\Gamma _{max}=0}\) to be of interest. It is found, using Eqs. 36 and 37, that the right hand intersection is always to the left of \(Ma_{\Gamma _{max}=0}\) and therefore the intersections between maxima of the growth rate are not real. In fact, the curves of the growth rate are stable.

Fig. 5
figure 5

Rayleigh-Taylor instability for G < 0 and \(q = 45^{\circ }\). Left column: Critical wavenumber number \(k_c\) vs G. Right column: Maximum growth rate \(\Gamma _{max}\) vs Ma for \(G = 0.1\) and 0.2. Figure 5a and b: \(d/\chi = 0.5\), Fig. 5c and d: \(d/\chi = 1.8\). \(\beta = 0.0\) (solid line), 0.1 (dashed line), 0.3 (dotted line)

Full size image

A discussion on the physical effects of slip is in order. As can be seen in Eqs. 25, 26 and 29 slip affects in a different way the Galilei number and the Marangoni number through their coefficients. Even more, the presence of gravity alone as a restoring force perpendicular to the wall and as promoting motion along the wall have different slip coefficients and therefore different slip effects which oppose each other from the stability point of view. Besides, when G and Ma oppose to each other a variation of \(\beta \) changes the relative magnitude between these two parameters. As a consequence this has the stabilizing effect found in the growth rate \(\Gamma \) after certain wavenumber \(k_+\) smaller than \(k_c\). In the case of the maximum growth rate \(\Gamma _{max}\) this effect occurs between a lower and an upper limit Marangoni numbers (which have to be positive to be valid intersections). Between these two limits the magnitude of \(\beta \) leads \(\Gamma _{max}\) to decrease when Ma increases. Therefore, the usual behavior of gravity and thermocapillary terms on stability is altered by slip through the modification of the coefficients of the different terms inside the equations. Notice that only the physical behavior of the phase velocity occurs as expected in the presence of slip. That is, the phase velocity just increases with \(\beta \).

4 Nonlinear free surface profiles

In this section the free surface profiles are analyzed using a normal mode expansion of the height h up to 5 modes. Seven modes were also investigated, but it was found that the free surface deformation profiles were almost the same.

The expansion is:

$$\begin{aligned}{} & {} h(x,t)=1 + A_1(t) \exp (i k x) + Ac_1(t) \exp (-i k x) +\nonumber \\{} & {} A_2(t) \exp (2 i k x) + Ac_2(t) \exp (-2 i k x) + A_3(t) \exp (3 i k x) + Ac_3(t)\exp (-3 i k x) +\nonumber \\{} & {} A_4(t) \exp (4 i k x) + Ac_4(t) \exp (-4 i k x) + A_5(t) \exp (5 i k x) + Ac_5(t) \exp (-5 i k x) \end{aligned}$$
(42)

However, a nine normal modes expansion was needed in the case where a relatively large Marangoni number was used. This h(x, t) is substituted into Eq. 25 to obtain a set of ten coupled nonlinear ordinary differential equations for \(A_i(t)\) and \(Ac_i(t)\), \(i = 1, \cdots \), 5. The initial value is assumed to be \(A_1(0) = Ac_1(0) = 0.01\), which corresponds to a cosine initial perturbation of the form 2cos(kx). Each solution of \(A_i(t)\) and \(Ac_i(t)\) is substituted back into Eq. 42 for h(x, t), which is plotted in the figures below. The goal is to have the free surface profile of the film flowing down a wall at a particular time. The dependance of the profiles on the parameter \(d/\chi \) is also investigated. In general, the sample data were selected from the linear problem. In particular, the wavenumber corresponding to the maximum growth rate was selected for each plotted curve in the numerical analysis. The free surface perturbations are initially unstable and then, after a large enough time, they reach nonlinear saturation.

4.1 Nonlinear films flowing down above a thick wall

The nonlinear results of the free surface profiles of a thin film flowing down above a thick wall are presented in Fig. 6. These results are based on those of Fig. 2 for linear instability. For each curve, the wavenumber corresponding to the maximum growth rate was selected. Notice that the wall is not drawn for the sake of presentation of the free surface profiles which have a small amplitude in comparison with the non dimensional thickness of the liquid layer. It is important to remember that the phase velocity of the perturbations differs for each given G and \(\beta \).

In Fig. 6 the first figures, from Fig. 6a to d, the angle of inclination is \(q = 90^{\circ }\) and for the last two figures, from Fig. 6e to f, \(q = 45^{\circ }\). In the first set of figures the Marangoni number is fixed to \(Ma = 1.3\). However, Fig. 6a: \(G = 0.1\) and \(d/\chi = 0.5\), Fig. 6b: \(G = 0.3\) and \(d/\chi = 0.5\), Fig. 6c: \(G = 0.1\) and \(d/\chi = 1.8\), Fig. 6d: \(G = 0.3\) and \(d/\chi = 1.8\). For the second set of figures different Marangoni numbers are used. For Fig. 6e \(Ma = 0.8\) with \(G = 0.1\) and for Fig. 6f \(Ma = 1.9\) with \(G = 0.3\). In general, the free surface profiles are plotted using the same lines of \(\beta \). That is, \(\beta = 0.0\) (solid line), 0.1 (dashed line), 0.3 (dotted line). The running time used for all the curves was 5000 units.

A comparison of Fig. 6a and c shows that and increase of \(d/\chi \) decreases the waves amplitudes. The same can be said about the curves in Fig. 6b and d. However, this increase stimulates the growth of the subharmonics (see Fig. 6c and d). On the contrary, it is observed that \(\beta \) works to decrease the amplitude of the subharmonics, as can be seen starting from the solid curve (no-slip) up to the dotted (\(\beta = 0.3\)) one. This may be considered a nonlinear stabilizing effect of \(\beta \) when the film flows down a vertical wall. However, in the Fig. 6a–d the amplitudes increase with \(\beta \), which is a destabilizing effect.

When the wall is inclined at \(q = 45^{\circ }\) and \(d/\chi = 0.5\), Fig. 6e shows no notable change when \(\beta \) increases. However, Fig. 6f presents an interesting picture. Here, 9 normal modes were used to describe the free surface profile. It is observed that an increase of \(\beta \) stimulates the increase of the amplitude of the subharmonics when going on from the solid curve (no-slip) up to the dotted (\(\beta = 0.3\)) one. This may be considered a nonlinear destabilizing effect of \(\beta \) when the film flows down above an inclined wall. Observe that in Fig. 6e \(\beta \) decreases the amplitude of the free surface perturbation but in Fig. 6d increases the amplitude of the surface deformation.

4.2 Nonlinear films flowing down below a thick wall: Rayleigh-Taylor instability

Here the curves are plotted below the x-axis of each sub figure of Fig. 7. That is because in the Rayleigh-Taylor instability \(h = 1 - H\) and the film is pulled in the direction parallel to gravity at the same time that it is flowing down and below the inclined thick wall. The angle of inclination is fixed to \(q = 45^{\circ }\) and \(d/\chi = 0.5\). The Galilei number of Fig. 7a is \(G = 0.1\) and that of Fig. 7b is \(G = 0.3\). However, both figures include a destabilizing effect of \(Ma = 1.3\). Besides, Fig. 7c is for \(G = 0.1\) and Fig. 7d is for \(G = 0.3\), but both include a stabilizing effect of \(Ma = 0.3\).

In Fig. 7a, for a destabilizing Ma, it is observed that the harmonics are suppressed by the increase of \(\beta \). However, the amplitude increases with \(\beta \). It is interesting that an increase of the magnitude of G in Fig. 7b changes the behavior of \(\beta \). As can be seen, \(\beta = 0.1\) first stabilizes and then destabilizes with a notably larger amplitude for \(\beta = 0.3\). Moreover, the appearence of sub harmonics is stimulated with \(\beta \).

Fig. 6
figure 6

Nonlinear free surface deformation. Figure 6a: \(G = 0.1\) and \(d/\chi = 0.5\), Fig. 6b: \(G = 0.3\) and \(d/\chi = 0.5\), Fig. 6c: \(G = 0.1\) and \(d/\chi = 1.8\), Fig. 6d: \(G = 0.3\) and \(d/\chi = 1.8\). From Fig. 6a–d: \(q = 90^{\circ }\) and \(Ma = 1.3\). From Fig. 6e–f: \(q = 45^{\circ }\) and \(d/\chi \) = 0.5. Figure 6e: \(Ma = 0.8\) with \(G = 0.1\). Figure 6f: \(Ma = 1.9\) with \(G = 0.3\). \(\beta = 0.0\) (solid line), 0.1 (dashed line), 0.3 (dotted line)

Full size image
Fig. 7
figure 7

Nonlinear free surface deformation: Rayleigh-Taylor instability. \(q = 45^{\circ }\) and \(d/\chi = 0.5\). Figure 7a: \(G = 0.1\) and destabilizing \(Ma = 1.3\), Fig. 7b: \(G = 0.3\) and destabilizing \(Ma = 1.3\), Fig. 7c: \(G = 0.1\) and stabilizing \(Ma = 0.3\), Fig. 7d: \(G = 0.3\) and stabilizing \(Ma = 0.3\). \(\beta = 0.0\) (solid line), 0.1 (dashed line), 0.3 (dotted line)

Full size image

In Fig. 7c, the Marangoni number Ma stabilizes and it is seen that \(\beta \) stimulates the presence of sub harmonics but works to decrease the amplitude of the free surface deformations. With the increase of the magnitude of G in Fig. 7d, \(\beta \) promotes the suppression of subharmonics but \(\beta \) increases the amplitude of the free surface perturbation. It is important to note the different amplitudes among the curves in Fig. 7a–d. For the sake of comparison the vertical axes present the same scale length in all the sub figures.

5 Conclusions

In this paper the linear and nonlinear thermocapillary instability of a thin film flowing down above or below on a thick wall with slip was investigated. It is important to point out that the results about the stabilizing and destabilizing effects of slip are new. The finite thickness and thermal conductivity of the wall showed to have a relevant role on the stability. Depending on the magnitude of the parameters, the growth rate is able to stabilize after a certain wavenumber \(k_+\) in the presence of slip. The curves of criticality may intersect among them at \(G_+\) when \(\beta \) increases. This intersections are a consequence of the stabilizing effect of slip on the growth rate. From the point of view of the maximum growth rate plotted against the Marangoni number, promising intersections among the curves brought about the possibility of a change in behavior of slip from destabilizing to stabilizing. A very detailed analysis was done from which it was concluded that a change of the stability behavior of slip is only possible to the right of the vertex of the parabola formed in a plot \(\Gamma _{max}\) vs Ma. The reason is that, starting from \(Ma_{\Gamma _{max}=0}\), the growth rate \(\Gamma \) is already negative. For Ma < \(Ma_{\Gamma _{max}=0}\) the growth rate is still more negative and there is no possibility of intersections of the maximum growth rate. The general result is that only intersections found to the right of the vertex are physically realizable. It was found that only when the film flows down above an inclined thick wall and for angles of inclination of the wall smaller than those of the vertical (q \(< 90^{\circ }\)), it is possible to find intersections of the curves of maximum growth rate to the right of the vertex. There were found intersections among the curves of maximum growth rate where the stability behavior of slip may change.

From the nonlinear point of view, for certain magnitudes of the parameters it was found that slip may suppress the appearance of sub harmonics and for other magnitudes slip stimulates their appearance. It was also observed that slip may increase or decrease the amplitude of the nonlinear free surface perturbations, depending of the magnitude of the parameters selected.