1 Introduction

In recent decades, many authors have paid a lot of attention to problems of falling liquid films, for example, but not limited, Chang [1], Oron et al. [2], Craster & Matar [3] and Ruyer-Quil et al. [4]. Surface coating processes are one of the applications of open flow in industry [5], chemical reactors [6], thermal protection design of combustion chambers in rocket engines [7], heat exchangers [8] and cooling microelectronic devices [9]. Many experiments have been carried out throughout the years to confirm and enhance theoretical studies on falling films ([10, 11, 12 and 13]).

The influence of electric field on the interfacial waves between immiscible fluids has been the subject of much research. The electrical stress existing within immiscible fluids due to different electrical properties is known as Maxwell stress. Immiscible two-fluids flows involving electric fields with Maxwell stresses lead to important electrohydrodynamic phenomena. Depending on their strength and orientation, electric fields can be either stabilizing or destabilizing.

The deformation of the flat interface is caused by the normal component of the Maxwell stress, which is caused by the action of the surface tension and normal viscous stress, and the tangential Maxwell stress is caused by the balance of the tangential viscous stresses. As a result, the electric field distribution is altered by the deforming contact [14, 15]. The electric fields can be used to control the dynamics of film flows by applying surface and volume pressures selectively. The electric field can be either stabilizing or destabilizing according to the fluid properties (perfect dielectric, leaky dielectric, or perfect conductive) and the electric field orientation. A variety of low-dimensional models for the study of electrified flows have been created in recent years. Kim & Bankoff [16] have presented a study on the interaction and instability of an electrostatic field with a thin liquid film flowing under gravity down an inclined plane. They have shown that the presence of the electric field can change the stability of the film, and that it can, for realistic values of the parameters, produce a negative pressure under the foil, which would stop a leak out of a puncture. Hammerton & Bassom.[17] have studied long-wavelength, small-amplitude disturbances on the surface of a fluid layer subject to a normal electric field. They have considered that the Reynolds number of the fluid flow is taken to be large, with viscous effects restricted to a thin boundary layer on the lower plate. The effects of surface tension and electric field enter the governing equation through an inverse Bond number and an electrical Weber number, respectively. The stability criteria were studied throughout different forms of modified Korteweg-de Vries equation. The rivulet creation in the transverse direction occurs in the three-dimensional situation, analogous to hanging liquid films by Scheid et al. [18] and Rietz et al. [19]. Wray, Matar & Papageorgiou [20] studied the leaky dielectric films under the influence of normal electric field using the two- and three-dimensional weighted residuals integral boundary-layer (WIBL) model. Their model is limited to include first-order electrostatic effects and ignore the interfacial charges. The long-wave dynamics of a gravity-driven conducting film subjected to a normal electric field were studied in three dimensions by Ref. [21]. Papageorgiou [22] introduced an overview of the various model techniques.

Tomlin et al.[21] studied the Benney equation and the Kuramoto–Sivashinsky equation to show that limited solutions exist for values of electric field are below a critical threshold, building on the work of Tseluiko & Papageorgiou [23]. Above the threshold, the Kuramoto–Sivashinsky equation predicts an unlimited exponential increase in transverse modes, comparable to the situation of hanging liquid film. Tomlin et al. [24] have investigated the two-dimensional development of a dielectric suspended film stabilized by the tangential electric field to the substrate. Using direct numerical techniques and the second-order approach WIBL, they proved that a sufficiently strong electric field may ensure linear and nonlinear stability of the film. They demonstrated that a sufficiently strong electric field may assure the film’s linear and nonlinear stability. They also demonstrated that the threshold of absolute instability may be used to approximate the limit for instantaneous dripping of the suspended film owing to the increase in primary instability. The absolute/convective transition is not a strong predictor of dripping after wave coalescence in the situation of dripping after wave coalescence [25]. The tangential electric field stabilizes the film and so the dripping is reduced. Dripping following coalescence becomes more evident in certain circumstances.

The shear-imposed falling film flows have studied by many authors. Smith & Davis [26] have investigated the effects of shear-imposed and the Reynolds number on the instability regime throughout Orr-Sommerfeld problem. Also, they have investigated the mechanism of the instability through an examination of the disturbance-energy equation. Smith [27] has presented two-groups of physical mechanism for the long-wave instability of thin liquid films in the presence of an imposed shear stress. The first group is related to the top surface with an imposed stress, while in the other, an imposed velocity is found. The study demonstrated how, in each of these scenarios, the specifics of the energy transfer from the basic state to the disturbance are handled differently and how a common growth mechanism results in the instability of the disturbance. Wei [28] has investigated the effect of an insoluble surfactant on the linear stability of a shear-imposed flow down an inclined plane in the long-wavelength limit. His results refereed to that a free falling film flow with surfactant is stable to long-wavelength disturbances at sufficiently small Reynolds numbers. The imposed additional interfacial shear causes instability due to the shear-induced Marangoni effect. Two modes of the stability are identified and the corresponding growth rates are derived. Samanta [29] have examined the film falling down an inclined plane in the presence of imposed shear stress. His simulations of the low-dimensional model have been performed in order to analyze the spatiotemporal behavior of nonlinear waves by applying a constant shear stress in the upstream and downstream directions. It is to be noticed that the presence of imposed shear stress in the upstream (downstream) direction makes the evolution of spatially growing waves weaker.

This study has two objectives. The first is dealing with investigating the linear motion of a falling layer of a perfect dielectric fluid in the presence external shear stress is predicted using a one-dimensional WIBL model. The second goal is to exploit the nonlinear dynamic model governing the problem to study the properties of solitary waves, while addressing the study of some limiting cases. This article is organized as follows. We have formulated the mathematical model of the problem, governing equations and the corresponding boundary conditions in sect. 2. In sect. 3, the simplified second-order weighted integral boundary layer model (WIBL) is introduced and then such model is normalized by Shkadov scaling. The primary instability of Whitham’s wave hierarchies is analyzed in sect. 4. Solitary-wave solutions are demonstrated in sect. 5. Section 6 investigates the evolution equation of extremely viscous liquid film with the linear instability discussion. Also, this section introduces the study of Kuramoto–Sivashinsky type equation for the solitary-wave as a limiting case. Finally, the concluding remarks are offered in sect. 7.

2 Statement of the problem

2.1 Model formulation

Fig. 1
figure 1

Skeleton of the considered problem

Full size image

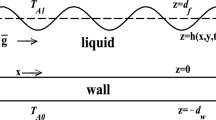
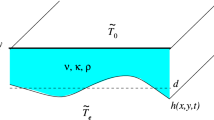
Assume a perfect dielectric viscous liquid film with constant density \(\rho\), dynamic viscosity \(\mu\) and kinematic viscosity \(\nu\), flowing under gravity on a substrate inclined at a nonzero angle \(\theta\) to the horizontal. Between two capacitor plates with a distance of \(\bar{H}\), the film and passive layer are placed as shown in Fig. 1. We have a uniform imposed shear stress \(\bar{\tau }\), acting parallel to the flat surface of the film. We have a uniform applied shear stress operating parallel to the unperturbed surface of the film. As shown in Fig. 1, we use coordinates \((\bar{x}, \bar{z})\) fixed in the plane with \(\bar{x}\) directed down the slope in the streamwise flow and \(\bar{z}\) perpendicular to the inclined substrate. Angle of inclination \(\theta\) increases, the plate and axes rotate; for \(\theta \in \left( 0, \pi /2\right)\) we have overlying liquid, vertical films for \(\theta = \pi /2\) and hanging films for \(\theta \in \left( \pi /2, \pi \right)\). The surface tension coefficient is denoted by \(\sigma\) (assumed constant), and the gravity is denoted by \({\textbf {g}} =\text {g} \{ \sin \theta , -\cos \theta \}\). The function \(\bar{h}(x, t)\) represents the local film thickness, with unperturbed thickness \(h_N\). Regions 1 and 2 indicate the liquid layer and ambient medium, respectively. The electric field is the gradient of electric potential \(\psi _i\) and \(\varepsilon _1 \varepsilon _0\) and \(\varepsilon _2\varepsilon _0\) denote the permittivity of the liquid and the passive layer, where \(\varepsilon _0=8.85 \times 10^{-12} \text {CVm}^{-1}\) the permittivity of vacuum. For the constant dielectric permittivity in each phase, the electric force will take values at the phase boundary only. It means that this force will be rewritten as a surface force (Zakaria & Sirwah[30] and Rohlfs et al. [31]). The electric field \({\bar{{\textbf {E}}}}_i={\bar{\nabla }} {\bar{\psi }}_i\) (\(i=1,2\)) can be analytically determined based on the Laplace equation

$$\begin{aligned} {\bar{\nabla }}^2 {\bar{\psi }}_i=0 \end{aligned}$$
(1)

subject to the conditions

$$\begin{aligned} {\bar{\psi }}_1=0 \text { at } \bar{z}=0, \text { and } {\bar{\psi }}_2=\Phi _0~\text { at }~\bar{z}=\bar{H} \end{aligned}$$

and

$$\begin{aligned} \varepsilon _1{\bar{\nabla }} {\bar{\psi }}_1\cdot {\textbf {n}}=\varepsilon _2{\bar{\nabla }} {\bar{\psi }}_2\cdot {\textbf {n}}, \text {and}\, {\bar{\psi }}_1= {\bar{\psi }}_2~\text {at}~\bar{z}=\bar{h} \end{aligned}$$
(2)

Up to a first-order approximation for boundary conditions of the normal electric field, the solutions of the Laplace equations are(Rohlfs et al.[31]):

$$\begin{aligned} {\bar{\psi }}_1=\frac{\varepsilon _2 \bar{z}}{\varepsilon _2 \bar{h}+\varepsilon _1 \left( \bar{H}-\bar{h}\right) }\,\text { and }\,{\bar{\psi }}_2=\frac{\varepsilon _1 \left( \bar{z}-\bar{H}\right) }{\varepsilon _2 \bar{h}+\varepsilon _1 \left( \bar{H}-\bar{h}\right) }+\Phi _0 \end{aligned}$$
(3)

The liquid film is governed by the continuity and momentum equations:

$$\begin{aligned}&{\bar{u}}_{\bar{x}}+{\bar{w}}_{\bar{z}}=0 \end{aligned}$$
(4)
$$\begin{aligned}&\rho \left( {\bar{u}}_{\bar{t}}+{\bar{u}}{\bar{u}}_{\bar{x}}+{\bar{w}} {\bar{u}}_{\bar{z}}\right) =-{\bar{p}}_{\bar{x}}+{\bar{u}}_{\bar{x}\bar{x}}+{\bar{u}}_{\bar{z}\bar{z}}+\rho \text {g} \sin \theta \end{aligned}$$
(5)
$$\begin{aligned}&\rho \left( {\bar{w}}_{\bar{t}}+{\bar{u}}{\bar{w}}_{\bar{x}}+{\bar{w}} {\bar{w}}_{\bar{z}}\right) =-{\bar{p}}_{\bar{z}}+{\bar{w}}_{\bar{x}\bar{x}}+{\bar{w}}_{\bar{z}\bar{z}}-\rho \text {g} \cos \theta \end{aligned}$$
(6)

subject to the conditions

$$\begin{aligned}&\mu ({\bar{u}}_{\bar{z}}+{\bar{w}}_{\bar{x}}-4 h_{\bar{x}} {\bar{u}}_{\bar{x}})|_{\bar{h}}-\bar{\tau }(1+\dfrac{3}{2}\bar{h}_{\bar{x}}^2)=0, \end{aligned}$$
(7)
$$\begin{aligned}&\left( {\bar{p}}_1-{\bar{p}}_2\right) |_{\bar{h}}+\frac{\varepsilon _0\Phi _0^2\varepsilon _1 \varepsilon _2 \left( \varepsilon _1-\varepsilon _2\right) }{2 \left( \varepsilon _1 \bar{H}-\left( \varepsilon _1-\varepsilon _2\right) \bar{h}\right) ^2}+\sigma \bar{h}_{\bar{x}\bar{x}}+2 \bar{\tau } \bar{h}_{\bar{x}}+2 \mu {\bar{u}}_{\bar{x}|_{\bar{h}}}=0, \end{aligned}$$
(8)

The kinematic condition, that the flow cannot travel across a free surface, assumes the following dimensional form

$$\begin{aligned} {\bar{w}}|_{\bar{h}}=\bar{h}_{\bar{t}}+ \bar{h}_{\bar{x}} {\bar{u}}|_{\bar{h}}, \end{aligned}$$
(9)

and for the liquid film, we have no-slip conditions at the solid substrate,

$$\begin{aligned} {\bar{{{\varvec{v}}}}}=0,~~at~~ {\bar{z}} =0, \end{aligned}$$
(10)

where \({\bar{{{\varvec{v}}}}}=({\bar{u}},{\bar{w}})\) is the velocity field, \({\bar{p}}_i\) are the pressures and the subscripts refer to the partial derivative with respect to \(\bar{t}\) or \(\bar{x}\) and \(\bar{z}\). The bar sign on physical quantities indicates that they are dimensional values.

2.2 Normalization of equations

The base states (Nusselt solution), in the dimensionless form, become( [21, 32]):

$$\begin{aligned} \bar{h}=h_N; {\bar{u}}=-\frac{\text {g} \rho \sin \theta }{2 \mu }\left( \bar{z}^2 -\bar{z} h_N\right) +\bar{\tau } \bar{z};~~{\bar{p}}_1={\bar{ p}}_2+\text {g} \rho \cos \theta \left( h_N-\bar{z}\right) +\frac{\varepsilon _0 \left( \varepsilon _1 \varepsilon _2^2-\varepsilon _1^2 \varepsilon _2\right) \Phi _0^2}{2 \left( \varepsilon _1 \bar{H}-\varepsilon _1 h_N+\varepsilon _2 h_N\right) ^2}, \end{aligned}$$
(11)

where \(h_N\) is the Nusselt thickness. We will non-dimensionalize \(\bar{x}\), \(\bar{h},\bar{z},\bar{H}\), velocity, \(\bar{t}\) and the pressure with \(\lambda\), \(h_N\), the characteristic velocity \(U=\frac{\rho \text {g} h_N^2\sin \theta }{\mu }\), \(\lambda /U\) and \(\dfrac{\mu U}{h_N}\), respectively, where \(\lambda\) is the wavelength of the generated waves and \(\bar{x}=\lambda x,\bar{h}=h_N h,\bar{z}=h_N z,\bar{H}=h_N H\). Making use of the normalization, we have the non-dimensional numbers

$$\begin{aligned} \text {Re}=\dfrac{\rho h_N U}{\mu };\text {We}=\dfrac{\sigma }{U \mu }=\dfrac{\sigma }{\rho \text {g} h_N^2 \sin \theta };B_{e}=\dfrac{\varepsilon _0\Phi _0^2 }{\rho \text {g} h_N^3 \sin \theta }, \end{aligned}$$

since Re is the Reynolds number, which measures the inertia to viscous force ratio, Weber number \(\text {We}\) measures the ratio of the capillary force to the viscous normal stress induced by gravity, and electric Bond number Be is used to calculate the ratio of crosswise electrostatic to streamwise gravitational forces. The aim is to construct equations of model that are consistent up to order \(\mathcal {O} (\epsilon )\) in terms of inertia and up to order \(\mathcal {O} (\epsilon ^2)\) in terms of viscous diffusion, where \(\epsilon \sim (h_N/\lambda ) \ll 1\). Consider a free surface evolves slowly downstream with respect to x coordinate and time, and so we have \(\partial _x = \mathcal {O} (\epsilon )\) and \(\partial _t = \mathcal {O}(\epsilon )\). According to this approximation, the normalized equations can be simplified and rewritten up to \(\mathcal {O} (\epsilon ^2)\) as follows:

$$\begin{aligned}&u_x+w_z=0 \end{aligned}$$
(12)
$$\begin{aligned}&\epsilon \text {Re} \left( u_t+u u_x+w u_z\right) =-\epsilon p_x+\epsilon ^2 u_{xx}+u_{\text {zz}}+1 \end{aligned}$$
(13)
$$\begin{aligned}&0=-p_z+\epsilon w_{zz}-\text {ct} \end{aligned}$$
(14)
$$\begin{aligned}&w|_{h}=h_t+ h_x u|_{h} \end{aligned}$$
(15)
$$\begin{aligned}&(u_z+\epsilon ^2 w_x-4 \epsilon ^2 h_x u_x)|_{h}=\tau (1+\dfrac{3\epsilon ^2 }{2}h_x^2) \end{aligned}$$
(16)
$$\begin{aligned}&\left( p_1-p_2\right) |_{h}+\frac{\text {B}_e\varepsilon _1 \varepsilon _2 \left( \varepsilon _1-\varepsilon _2\right) }{2 \left( \varepsilon _1 H-\left( \varepsilon _1-\varepsilon _2\right) h\right) ^2}+\epsilon ^2 \text {We} h_{xx}+2 \epsilon \tau h_x+2 \epsilon u_x|_{h}=0 \end{aligned}$$
(17)
$$\begin{aligned}&u=0,w=0,~\text{at}~ z =0, \end{aligned}$$
(18)

Taking advantage of the normal stress condition, the integration of the second component of Navier–Stokes equation yields

$$\begin{aligned} p=-\underbrace{\text {ct} (z-h)}_{p_g}-\underbrace{\frac{\varepsilon _1 \left( \varepsilon _1-\varepsilon _2\right) \varepsilon _2 \text {B}_e}{2 \left( \varepsilon _2 h+\varepsilon _1 (H-h)\right) {}^2}}_{p_{\text {el}}}-\underbrace{\epsilon \left( u_x-u_x|_{h}\right) }_{p_v}-\epsilon ^2 \underbrace{\text {We} h_{xx}}_{p_t}-\underbrace{2 \tau \epsilon h_x}_{p_{\text {sh}}} , \end{aligned}$$
(19)

where \(\text {ct}=\cot \theta\) and \(\tau =\dfrac{\bar{\tau } h_N}{\mu U}\) is the normalized imposed shear stress. Equation (19) shows the contributions to the pressure from gravitational ( \(p_g\)), capillary ( \(p_t\)), electrical ( \(p_{\text {el}}\)), viscous ( \(p_v\)) and external shear ( \(p_{\text {sh}}\)) origin . The term \(\text{ We } h_{xx}\) is found in the normal stress balance under consideration of the highest value to the magnitude of surface tension (\(\epsilon ^{2}\,\text{We} = \mathcal {O}(1)\)). This consideration is taken to show the stabilizing influence of which assists in preventing the breakup of nonlinear wave. According to the physical view, the increase in the strength of electric field leads to an increase in the interfacial pressure. This occurs as a result of the higher electrical permittivity of the liquid film, such that the total resistance decreases with increasing thickness of the liquid. Therefore, the increase in values of the electric field increases the amplitude of the interfacial waves, and this amplitude is directly proportional to the thickness of liquid film. This results in an agreement with the study of Di Marco & Grassi [33] and Rohlfs et al.[31] for a flat horizontal gas–liquid interfaces subjected to gravity and electric fields.

3 Weighted integral boundary layer model (WIBL)

The WIBL method by Ruyer-Quil & Manneville [35] for modeling falling liquid films reduces the two-dimensional conservation equations (for mass and momentum) and the boundary conditions into the model of one-dimensional evolution equations for the film thickness h and the streamwise flow rate q. WIBL models show good agreement with numerical simulations of the Navier–Stokes equations coupled to the appropriate electrical equations and experiment. The integration of the continuity equation (12) over the depth of the liquid film and use of the kinematic boundary condition (15) yield the averaged mass conservation equation

$$\begin{aligned} h_t+q_x=0, \end{aligned}$$
(20)

Using the continuity equation (12) together with the no-slip boundary condition on w, one can replace w everywhere by \(w=-\int _0^h\partial _x u dz\) and the streamwise velocity component u which, according to the concept of the WIBL method, is replaced by separation of variables as an expansion taken in the form

$$\begin{aligned} u=\sum _j a_j(x,t)f_j(z/h), \end{aligned}$$
(21)

where the expansion coefficients \(a_j(x,t)\) and test functions \(f_j(z/h)\) are assumed to be slowly varying functions of time t and the streamwise coordinate x. The simplified second-order model will be obtained by integrating the boundary layer equations according to the Galerkin method. The details of WIBL method are found in the work of Ruyer-Quil & Manneville [35]. The resulting conservation and momentum equations are

$$\begin{aligned} \epsilon \text {Re} \left( q_t+\frac{17 q q_x}{7 h}-\frac{9 q^2 h_x}{7 h^2}\right) &=\frac{5 h}{6}-\frac{5}{6} \epsilon~\text {ct}~ h h_x-\frac{5 q}{2 h^2}+\frac{5}{6} \epsilon \text {We}~ h h_{xxx}+\frac{5}{6}\epsilon \frac{\left( \varepsilon _1-\varepsilon _2\right) ^2 \varepsilon _2 B_e}{\varepsilon _1^2 H^3} \frac{h h_x}{(1-h \chi )^3}\\&\quad +\epsilon ^2\biggl [\frac{9q_{xx}}{2}-\frac{9 h_x q_x}{2 h}-\frac{6 q h_{xx}}{h}+\frac{4 q h_x^2}{h^2}\biggr ]\\&\quad +\tau \biggl [\frac{5}{4}-\epsilon ^2\frac{h_x^2}{8}+\epsilon ^2\frac{h h_{xx}}{6}-\epsilon \frac{5\text {Re}}{112} q h_x-\epsilon \frac{19\text {Re} }{336} h q_x-\epsilon \frac{19\text {Re}~ \tau }{672} h^2 h_x\biggr ], \end{aligned}$$
(22)

where \(\chi =\frac{\varepsilon _1-\varepsilon _2}{\varepsilon _1 H}\). The reduced-order model (22) can be normalized by setting \(\epsilon =1\) [36]. Model (22) includes the effects of second-order viscous dispersion as shown on the second line, which leads to the dependence of wave number on the wave speeds. This is especially essential for the prediction of capillary ripples, which is critical in pulse interaction theories. The electrostatic surface force is now accounted for in the conservation equations at the lowest order in which it exists, according to the least degeneracy principle. As a result, the electric fluxes in the streamwise direction are ignored when the film surface is considerably disturbed. In the case of minor changes in the flow field in the streamwise direction, the simplification accords with the general boundary-layer approximation.

3.1 Kapitza-Shkadov model

According to Shkadov scaling [37], namely

$$\begin{aligned} \left( x,t\right) \rightarrow \text {We}^{1/3} \left( x,t\right) ,\delta = \frac{\text {Re}}{\text {We}^{1/3}},\zeta = \frac{\text {ct}}{\text {We}^{1/3}},\eta = \frac{1}{\text {We}^{2/3}} \end{aligned}$$

the simplified WIBL model, the momentum equation, reads

$$\begin{aligned} \delta \left( q_t+\frac{17 q q_x}{7 h}-\frac{9 q^2 h_x}{7 h^2}\right) &=\frac{5 h}{6}-\frac{5 q}{2 h^2}-\frac{5}{6} \zeta h h_x+\frac{5 h h_{xxx}}{6}+\frac{5 \mathcal {E} h h_x}{6 (1-\chi h)^3}\\&\quad +\eta \left( \frac{4 q h_x^2}{h^2}-\frac{9 h_x q_x}{2 h}-\frac{6 q h_{xx}}{h}+\frac{9 q_{xx}}{2}\right) \\&\quad +\tau \left( \frac{5}{4}-\frac{5}{112} \delta q h_x-\frac{19}{336} \delta h q_x-\frac{1}{8} \eta h_x^2+\frac{1}{6} \eta h h_{xx}\right) -\frac{19}{672} \delta h^2 \tau ^2 h_x, \end{aligned}$$
(23)

where \(\delta\), \(\zeta\) and \(\eta\) denote the reduced Reynolds number, the reduced inclination number and the viscous dissipation, respectively, and

$$\begin{aligned} \mathcal {E}=\frac{\left( 1-\varepsilon _{21}\right) ^2 \text {Bo}_e}{H^3}, \end{aligned}$$

\(\text {Bo}_e=\frac{\varepsilon _2 B_e}{\root 3 \of {\text {We}}}\) is called the modified electric Bond number and \(\varepsilon _{21}=\dfrac{\varepsilon _2}{\varepsilon _1}\). Depending on whether the film is hanging, vertical, or overlaying, it is evident \(\zeta < 0\), \(\zeta =0\), or \(\zeta >0\). Because of the separation of scales in the streamwise and cross-stream directions in this region, which is due to the significant influence of surface tension, the Shkadov scaling is intrinsic to the falling film problem in the region of moderate Reynolds numbers.

It is necessary to maintain balance between all factors, such as inertia, gravity, viscosity, and surface tension, in order to sustain extremely nonlinear waves. The reduced Reynolds number \(\delta\) compares inertia force to surface tension and viscosity, capturing all three effects at the steep front of stationary elevations. The viscous dispersion parameter \(\eta\) appears along with streamwise dissipative terms and contributes in dispersion criteria of the waves. It means that the evolution equation (23) describes two distinct flow regimes: the drag-electrogravity regime, which occurs for \(\delta \ll 1\) and where the dynamics are controlled by a balance between the wall’s viscous force and gravity, electrostatic force and surface tension, with inertia playing the role of a perturbation, and the drag-electroinertia regime at \(\delta \gg 1\), at a dominated inertia effect. For \(\eta =0\), the model reduces to first order in the gradient expansion accounting for the boundary- layer theory. Model (23) recovers the same equation which is derived by Ruyer-Quil & Manneville [35] in the limit \(\mathcal {E} =0\) and \(\tau =0\) , i.e., when the electrostatic force and imposed shear stress are absent in the model. In the absence of electrostatic force, the evolution equation (23) is reduced to the model of Samanta [29] but with Shkadov scales. Also, the model of Rohlfs et al. [31] is obtained in the limit \(\tau =0\). The electrostatic force corresponding to a negative gravitational force at \(\zeta =-\mathcal {E}\) and \(\chi =0\). The type of flow with the negative gravity name associated with negative values of the inclination number \(\zeta\) . The film flow is destabilized in this situation because of the gravitational body force. The crosswise component of gravity is opposite the coordinate system in the case of positive gravity, and vice versa in the negative gravity case.

4 Primary instability by Whitham’s wave hierarchies

Fig. 2
figure 2

It is plotted to observe the stability of primary of creating linear waves on the surface of overlying falling film

Full size image
Fig. 3
figure 3

Displays the variations of the primary wave velocities as functions of the wave number corresponding to the case of a hanging falling film

Full size image
Fig. 4
figure 4

It is plotted to study the stability of primary waves in the case of vertical substrate

Full size image

The primary instability of linear dynamic of wavy film can be studied within the wave hierarchy framework according to Whitham [38]. The study of the Nusselt flow stability in terms of wave hierarchy has been offered by Alekseenko et al. [39], Ooshida [40], Samanta [41] and Kalliadasis et al. [37] extended the works of Alekseenko et al. and Ooshida to include viscous effects and connect with the shallow water theory. Noma et al. [42] studied experimentally the primary instability of a visco-plastic film flow down an inclined substrate, where downstream evolution is observed. They obtained the growth rates and cutoff frequencies for the generated surface waves. The experimental setup is a channel with a varying slope angle, in which a permanent flow of a Herschel–Bulkley fluid is established. In this work we extend the studies of Kalliadasis et al. [37] and Samanta [41] by the electrostatic force as a new parameter in the criteria of primary instability according to Whitham’s wave hierarchies. For various inclinations, Kalliadasis et al. [37] showed that the tail length behavior vs Reynolds number enables to discern the transition between the drag-gravity and drag-inertia regimes. Furthermore, the drag-gravity flow regime relates to flows with low Reynolds numbers, and the drag-inertia flow regime corresponds to flows with moderate Reynolds numbers. At a modified Reynolds number \(\delta\), the transition between the two regimes occurs. According to the normal mode decomposition, the infinitesimal perturbation is considered from a uniform parallel solution \(h=1, q=q_0\). So, we assume that

$$\begin{aligned} \left\{ \begin{array}{c} h\\ q \end{array}\right\} =\left\{ \begin{array}{c} 1\\ q_0 \end{array}\right\} +\left\{ \begin{array}{c} \tilde{h}\\ \tilde{q} \end{array}\right\} \text {exp}[ik(x-c t)],~k\in \mathbb {R}~~ \text {and}~~c\in \mathbb {C} \end{aligned}$$
(24)

where \((\tilde{h},\tilde{q})\ll 1\) and \(q_0=\dfrac{1}{3}+\dfrac{\tau }{2}\) is the flow rate of the base state. Substituting assumption (24) for h and q in the two equations model (20) and (23) and linearized with respect to the base solution, we obtain the dispersion relation which is a quadratic polynomial in c:

$$\begin{aligned} iR(k)(c-c_0(k))+k~ \delta (c-c_1(k))(c-c_2(k))=0, \end{aligned}$$
(25)

where

$$\begin{aligned}&c_0(k)=\frac{\eta k^2 (17 \tau +12)+15 (\tau +1)}{3 \left( 9 \eta k^2+5\right) }, \end{aligned}$$
(26)
$$\begin{aligned}&\quad c_{1,2}(k)=\left( \frac{61 \tau }{96}+\frac{17}{42}\pm \sqrt{\lambda }\right)~ \text {provided that}~ \lambda >0, \end{aligned}$$
(27)

with \(R(k)=\frac{5}{2}+\frac{9 \eta k^2}{2}\) and

$$\begin{aligned} \lambda =\tau _f+\dfrac{5}{6\delta }\zeta +\dfrac{5}{6\delta }k^2-\dfrac{5}{6}\frac{\text {Bo}_e\hat{\mathcal {E}}(1)}{\delta }, \end{aligned}$$

\(\hat{\mathcal {E}}(1)=\frac{\left( \varepsilon _{21}-1\right) ^2}{\left( \varepsilon _{21}+H-1\right) ^3}\) and \(\tau _f=\frac{1225 \tau ^2}{9216}+\frac{29 \tau }{288}+\frac{37}{1764}\). The positive sign of the discriminate \(\lambda\) depends on the comparison between the external shear stress \(\tau\), the modified inclination number \(\zeta\), and the electrostatic surface force. It can be seen from equation (25), the dispersion viscosity parameter, only, contributes in the velocity of the kinematic wave. The contribution of the electrostatic surface force in primary instability depends on the ratio \(\varepsilon _2/\varepsilon _1\), the distance between two capacitor plates H, and the modified electric Bond number \(\text {Bo}_e\).

According to Whitham [38], Alekseenko et al. [39], Ooshida [40], Ruyer-Quil et al. [44], Samanta [41] and Kalliadasis et al. [37], the dispersion relation (25) can also be written as a composition of two linear hyperbolic waves,

$$\begin{aligned} \underbrace{\left( \partial _t+c_0(k)\partial _x\right) h}_{\text {kinematic wave}}+\dfrac{\delta }{R(k)}\underbrace{\left( \partial _t+c_1(k)\partial _x\right) \left( \partial _t+c_2(k)\partial _x\right) h}_{\text {dynamic waves}}=0, \end{aligned}$$
(28)

The kinematic waves are generated from the equation of averaged mass conservation equation (20) which propagates with a speed \(c_0(k)\) and are dominant in the inertialess limit \((\delta /R(k))\rightarrow 0\). The wave fronts at the front and back of the dynamic wave packet travel at speeds \(c_1(k)\) and \(c_2(k)\), respectively. In other words, the fastest dynamic waves travel at the speed \(c_1(k),\) while the slowest ones travel at the speed \(c_2(k)\). The competition between lower-order waves (kinematic waves) and higher-order waves (dynamic waves), i.e., surface gravity waves advected by the flow, causes the instability. For positive \(\lambda\) values, the electrostatic forces are involved in the behavior of the dynamic waves. The dynamic waves influence on kinematic ones can be arisen via replacing \(\partial _t\) by \(-c_0(k)\partial _x\) in the dynamic wave section in hyperbolic waves equation (28), which leads to:

$$\begin{aligned} \underbrace{\left( \partial _t+c_0(k)\partial _x\right) h}_{\text {kinematic wave}}+\dfrac{\delta }{R(k)}\underbrace{\left( c_1(k)-c_0(k)\right) \left( c_2(k)-c_0(k)\right) \partial _{xx}h}_{\text {dynamic waves}}=0, \end{aligned}$$
(29)

Equation (29) shows that dynamic waves play a diffusive role for the kinematic waves. According to Whitham [38], the stability of the primary waves will be taken place in case of kinematic waves which travel at a speed that lies in an interval defined by the speed of dynamic waves, i.e.,

$$\begin{aligned} c_2(k)\leqq c_0(k)\leqq c_1(k), \end{aligned}$$
(30)

is satisfied. On the contrary, if the kinematic wave speed \(c_0(k)\) exceeds the speed of dynamic wave \(c_ 1(k)\), the infinitesimal disturbance will grow with time, and we obtain an unstable flow.

The plots of Fig. 2 aim to observe the movement of creating linear waves on the surface of overlying falling film. In the absence of the external shear stress and the electrostatic force, we note that the kinematic waves are not much affected by changes in viscosity, except for waves with a larger wavelength. Such observations can be extrapolated through numerical calculations of wave velocities displayed in Fig. 2(a,b). We note from the graphics of Fig. 2(b) that the dynamic waves are created accompanied by speeds that are confined between the speeds of the dynamic waves, especially at constant slow speeds. On the other hand, the speeds of kinematic waves will decline slowly with decreasing wavelength values. This indicates that in the absence of both the external influence of air and electricity the kinematic waves are not significantly affected by the drag-viscosity regime as shown in parts of Fig. 2. Fig. 3 displays the variations of the primary wave velocities as functions of the wave number corresponding to the case of a hanging falling film. It is noticed that there is a very slight change in \(c_0\) with the wave number in the absence of the effects of the electric forces and shear stress, as observed in the case of the overlying case. The long wave specified by \(k< 0.3\) is growing with time, while the else waves are stable. In part 3(b), there is a notable variation of \(c_0\) with k as well as an extension in the range of unstable waves due to increasing the values of \(\tau\), \(\delta\) and \(\eta\). In part 3(c), we examine the effect of electrostatic forces on the stability picture for the primary waves in the \(c-k\) plane as the effect of the imposed shear stress is switched off. By comparing the graphs of Fig. 3(a) and 3(c), we notice that there is a clear reduction in the values of all velocities as well as a contraction of the unstable wave region. A further increase in the values of the modified electric Bond number \(\text {Bo}_e\), as investigated in Fig. 3(d), leads to the demise of the growing waves. This confirms the stabilizing role of the electrostatic force. This is due to the role of the passive layer in controlling the effect of electrostatic force on reducing the energy of the kinematic waves and thus excludes the possibility of distillation of the liquid film for a longer time. The curves controlling the variation of wave velocities with the wave number, displayed in Fig. 3(e) and 3(f), clearly indicate a similarity in the behavior, except that there is an increase in the values of those waves, as well as an expansion in the wave number domain corresponding to rising waves with time on account of the shear stress and in the dielectric permittivity ratio. Throughout parts of Fig. 4, we study the stability of primary waves in the case of vertical substrate. Therefore, we re-investigate the behavior of the velocities of these waves with the wave number for the same system of selected parameters considered in parts of Fig. 3. When each part of Fig. 4 is compared to its counterpart in Fig. 3, we get the same qualitative results as reported for the case of hanging plate nevertheless the values of the wave velocities as well as the wave number range admitting disturbed waves increases strongly with increased the parameters \(\tau\), \(\delta\) and \(\eta\). Obviously, the electrostatic force comes into play a more effectively stabilizing role for the propagating waves in case of vertical plate rather than that remarked in hanging case. Moreover, the streamwise shear stress and the dielectric permittivity ratio have a stronger destabilizing influence for the waves propagating on the vertical plate. Hence, the liquid film is more susceptible to dripping regime. Conversely, the possibility of dripping is excluded when the shear stress is directed in the opposite direction to the flow.

5 Solitary waves

Fig. 5
figure 5

Represents the behavior of two fixed points in general case

Full size image

According to the experimental studies of Kliakhandler et al. [43]–[52], over long distances, the traveling waves (TWs) propagate with a stationary shape at constant speed. In downstream direction, the solitary waves are separated by fluid layers of constant thickness, or substrates, that are significantly longer than the waves characteristic length. The solitary waves can be seen as periodic TWs with the infinite long wavelength property. In this section, using the dynamical systems theory and elements from, we aim to study infinite-domain solitary waves. The flow is stationary in a frame of reference moving at the speed c of the waves with the dimension \(\xi = x - ct\), and thereby the set of partial differential equations (23) may be transformed to a set of ordinary differential equations.

The mass balance (20) can be integrated once,

$$\begin{aligned} q = c h +q_0 \end{aligned}$$
(31)

where \(q_0\) is the rate for Nusselt film flow. The averaged momentum balance (23) next reads

$$\begin{aligned} &\delta \left( c q'+\frac{9 q^2 h'}{7 h^2}-\frac{17 q q'}{7 h}\right) +\frac{5 h}{6}-\frac{5 q}{2 h^2}-\frac{5}{6} \zeta h h'+\frac{5 h'''}{6}+\frac{5 \text {Bo}_e\hat{\mathcal {E}}(h) h'}{6}-\frac{19}{672} \delta h^2 \tau ^2 h'\\&\quad +\eta \left( \frac{9 q''}{2}-\frac{6 q h''}{h}-\frac{9 h' q'}{2 h}+\frac{4 q h^{\prime 2}}{h^2}\right) +\tau \left( \frac{5}{4}+\frac{1}{6} h \eta h''-\frac{1}{8} \eta h^{\prime 2}-\frac{5}{112} \delta q h'-\frac{19}{336} \delta h q'\right) =0, \end{aligned}$$
(32)

where the primes refer to differentiation with respect to the moving coordinate \(\xi\). Using (31), (32) can be recast into \(h''' =f (h,h',h'')\), where f is a function of the thickness h, its first and second derivatives, and the parameters \(\delta , \eta , \tau , \mathcal {E},\chi\), and c. Then, ending up with a dynamical system of three dimensions,

$$\begin{aligned}&\begin{pmatrix} h_1' \\ h_2' \\ h_3' \end{pmatrix}=\begin{pmatrix} h_2 \\ h_3 \\ f\left( h_1, h_2, h_3\right) \end{pmatrix}, \end{aligned}$$
(33)
$$\begin{aligned}&\vec {\mathcal {H}}=\begin{pmatrix} h \\ h_{\xi } \\ h_{\xi \xi } \end{pmatrix}= \begin{pmatrix} h_1 \\ h_2 \\ h_3 \end{pmatrix} \end{aligned}$$
(34)

and

$$\begin{aligned} \begin{aligned} f=\zeta h_2-\frac{\text {Bo}_eh_2 h_1^2 \hat{\mathcal {E}}\left( h_1\right) +3 \mathcal {Q}_1\left( h_1\right) }{h_1^3}-\frac{3 \delta h_2 \mathcal {Q}_2\left( h_1\right) }{h_1^3} -\frac{\eta \left( 3 h_2^2 \mathcal {Q}_3\left( h_1\right) +3 h_3 \mathcal {Q}_4\left( h_1\right) \right) }{h_1^3}, \end{aligned} \end{aligned}$$
(35)

where

$$\begin{aligned}&\mathcal {Q}_1(h_1)=\frac{1}{6} \left( -6 c h_1+6 c+2 h_1^3+3 h_1^2 \tau -3 \tau -2\right) ,\\&\mathcal {Q}_2(h_1)=\frac{h_1 \left( 16 c (-6 c+3 \tau +2)-h_1 \left( 96 c^2+h_1 \tau (68 c+19 h_1 \tau )-30 c \tau +5 \tau (3 \tau +2)\right) \right) +24 (-6 c+3 \tau +2)^2}{1680},\\&\mathcal {Q}_3(h_1)=\frac{1}{60} (-3 h_1 (4 c+h_1 \tau )-96 c+48 \tau +32),\mathcal {Q}_4(h_1)=\frac{1}{15} h_1 \left( -9 c h_1+6 (6 c-3 \tau -2)+h_1^2 \tau \right) \end{aligned}$$

In phase space, solitary waves correspond to homoclinic orbits connecting a fixed point to itself. According to dynamical systems theory, the homoclinic orbits are structurally unstable, and their occurrence marks the beginning of chaotic dynamics. We will restrict the current study to single-loop homoclinic orbits corresponding to single-hump solitary waves. The fixed points of the equations of system (33) will be existed under consideration: \(h_1'= h_2'= h_3'=0\). The solution to (33) admits two fixed points:

$$\begin{aligned} \vec {\mathcal {H}}_1= \begin{pmatrix} h_I \\ 0 \\ 0 \end{pmatrix}= \begin{pmatrix} 1\\ 0 \\ 0 \end{pmatrix};\vec {\mathcal {H}}_2= \begin{pmatrix} h_{\text {II}} \\ 0 \\ 0 \end{pmatrix}= \begin{pmatrix} \frac{1}{4} \left( -3 \tau -2+\sqrt{3} \sqrt{16 c+(\tau -2) (3 \tau +2)}\right) \\ 0 \\ 0 \end{pmatrix} \end{aligned}$$
(36)

provided that

$$\begin{aligned} c>\text {Maximum}\left\{ \frac{1}{4}+4 \tau -\frac{3 \tau ^2}{16} ,\frac{17 \tau }{4}+\frac{1}{3}\right\} . \end{aligned}$$

In the limit \(\tau =0\), we recover the expression \(h_{\text {II}} =-\frac{1}{2}+\sqrt{3} \sqrt{c-\frac{1}{4}}\) corresponding to a film flowing down an inclined plane in the absence of impose shear stress ([49, 53, 54]).

It is noticeable that there is no viscous dispersion contribution, \(\eta\), and electrostatic force in formation of the two fixed points. Fig. 5 displays the variation of the fixed point with the wave speed \(\mathcal {C}\) corresponding to the down and up-stream shearing stress cases. The two fixed points coincide at \(c=1+\tau\) which is the speed of linear kinematic waves in the zero-wave-number limit, as observed in Eq. 26. We note that increasing the shear stress \(\tau\) values that take the same direction of flow will force the liquid film to flat state. On the other hand, it is clear that increasing the shear stress values that take the opposite direction of the flow tend to push the fluid away from the flat state. We can determine the shape of the tail and front of a solitary wave by considering how the corresponding homoclinic orbit in the phase space approaches and leaves the fixed point. So, let’s look at the linear instability of the fixed points.

The dispersion relation governing infinitesimal perturbations \(\sim \text {exp}(\varpi \xi )\) for the fixed points \(\vec {\mathcal {H}}_1\) and \(\vec {\mathcal {H}}_2\) is

$$\begin{aligned} \varpi ^3+\frac{3 \eta \mathcal {Q}_4\left( h_0\right) }{h_0^3} \varpi ^2+\varpi \left( \frac{\text {Bo}_e \hat{\mathcal {E}}\left( h_0\right) }{h_0}-\zeta +\frac{3 \delta \mathcal {Q}_2\left( h_0\right) }{h_0^3}\right) +\frac{3 \mathcal {Q}_1'\left( h_0\right) }{h_0^3}, \end{aligned}$$
(37)

where \(h_0\) represents the fixed point solution and the primes denote differentiation with respect to \(h_1\). Assuming that the contribution of viscous dispersion \(\eta\) is excluded and taking into account \(\mathcal {Q}_1'=0\), one of the eigenvalues \(\varpi\) vanishes which corresponding to an exchange of instabilities which leads to the velocity of solitary wave equals \(c=c_1=1+\tau\). In addition, we have an unstable manifold and another stable provided that the modified electric Bond number satisfies the condition

$$\begin{aligned} \text {Bo}_e<Bo_{e,c},Bo_{e,c}=\frac{4 \zeta h_0^6-12 \delta h_0^3 \mathcal {Q}_2\left( h_0\right) }{4 h_0^5 \hat{\mathcal {E}}\left( h_0\right) } \end{aligned}$$
(38)

If \(\text {Bo}_e=Bo_{e,c}\), the solitary waves will move through stationary stability regime. On the other hand, in case of \(\text {Bo}_e>Bo_{e,c}\), we obtain a complex conjugate pair solution for equation (37) as well as the neutral mode \(\varpi =0\). Accordingly, solitary waves under overstability mechanism regime are introduced on the surface of falling liquid film. Consider the case of contribution of viscosity dispersion parameter and \(\mathcal {Q}_1'=0\). We have an unstable manifold when \(\mathcal {Q}_4<0\) and another stable when \(\mathcal {Q}_4>0\) provided that the modified electric Bond number satisfies the condition

$$\begin{aligned} \text {Bo}_e>Bo_{e,c},Bo_{e,c}=\frac{4 \zeta h_0^6-12 \delta h_0^3 \mathcal {Q}_2\left( h_0\right) +9 \eta ^2 \mathcal {Q}_4\left( h_0\right) {}^2}{4 h_0^5 \hat{\mathcal {E}}\left( h_0\right) } \end{aligned}$$
(39)

Thus we can extract the Hopf bifurcation points from the consideration \(\mathcal {Q}_4=0\) for the two fixed point.

Returning to the general case, equation (37) can be reduced to the canonical form

$$\begin{aligned} \Omega ^3+\mathcal {P}_1\Omega +\mathcal {P}_0=0 \end{aligned}$$
(40)

by the changing:

$$\begin{aligned} \varpi =\Omega -\frac{\eta \mathcal {Q}_4\left( h_0\right) }{h_0^3}, \end{aligned}$$
(41)

where

$$\begin{aligned}\mathcal {P}_1&=\frac{\text {Bo}_e \hat{\mathcal {E}}\left( h_0\right) }{h_0}-\zeta +\frac{3 \delta \mathcal {Q}_2\left( h_0\right) }{h_0^3}-\frac{3 \eta ^2 \mathcal {Q}_4\left( h_0\right) {}^2}{h_0^6},\\&\quad \mathcal {P}_0=\eta \left( \frac{\zeta \mathcal {Q}_4\left( h_0\right) }{h_0^3}-\frac{\text {Bo}_e \mathcal {Q}_4\left( h_0\right) \hat{\mathcal {E}}\left( h_0\right) }{h_0^4}-\frac{3 \delta \mathcal {Q}_2\left( h_0\right) \mathcal {Q}_4\left( h_0\right) }{h_0^6}\right) +\frac{2 \eta ^3 \mathcal {Q}_4\left( h_0\right) {}^3}{h_0^9}+\frac{3 \mathcal {Q}_1'\left( h_0\right) }{h_0^3} \end{aligned}$$
(42)

Using the Cardano’s formulas, a real eigenvalue \(\Omega _{1,r}\) and a complex conjugate pair \(-\Omega _{2,r}\pm i \Omega _{2,i}\) can be obtained in the characteristic equation (40) when the discriminant \(\Delta =4\mathcal {P}_1^3 + 27\mathcal {P}_0^2> 0\). The related eigenvalue ratio is defined as \(\kappa =\Omega _{2,r}/\Omega _{1,r}\) which is the ratio of the saddle focus spiralling two-dimensional manifold rotation speed to its corresponding one-dimensional manifold ejection speed. In this case, the homoclinic orbit spirals back to the fixed point on the eigenspace covered by the complex pair’s eigenvectors. For the real eigenvalue it is a leaving monotonically case.

When \(\Delta < 0\), Eq. (40) admits three real eigenvalues. Thus, \(\vec {\mathcal {H}}_1\) changes from a saddle focus point to a saddle one at \(\Delta = 0\). In case of saddle fixed point, the homoclinic orbit moves out from and returns to the fixed point monotonically around the two eigenspaces corresponding to the smallest absolute value eigenvalues, and the corresponding tail and front are both monotonic.

6 Inertialess flow(extremely viscous film)

Fig. 6
figure 6

Illustrates the evolution of electrostatic force factor with the dielectric ratio

Full size image

In case of highly viscous liquid film, for example castor oil film, \(Re \rightarrow 0\) or equivalently \(\delta \rightarrow 0\), equation (23) enables us to have an expression for the flow rate q in terms of the elevation h :

$$\begin{aligned} q=-\frac{9 h^2\eta h_{x,t}}{2 \mathcal {L}(h)}+\frac{9 \eta h h_t h_x}{2 \mathcal {L}(h)}+\frac{\tau h^2 \left( \frac{5}{4}-\frac{1}{8} \eta h_x^2+\frac{1}{6} \eta h h_{xx}\right) }{\mathcal {L}(h)}+\frac{5 \mathcal {E} h^2h_x}{6 (1-h \chi )^3 \mathcal {L}(h)}-\frac{5 \zeta h^3 h_x}{6 \mathcal {L}(h)}+\dfrac{5h^3}{6}\frac{ h_{xxx}+1}{\mathcal {L}(h)}, \end{aligned}$$
(43)

where

$$\begin{aligned} \mathcal {L}(h)=\frac{5}{2}-4 \eta h_x^2+6 \eta h h_{xx}. \end{aligned}$$

In the absence of contribution of external shear stress and viscous dispersion \(\eta\), Dipin et al. [45] introduced the flow rate equation (43) in case of Rayleigh-Taylor instability, taking into account the difference in the choice of scalings. Substituting the flow rate equation (43) into the kinematic equation (20) leads to a single evolution equation:

$$\begin{aligned} \begin{aligned}&\left( 2 h^5 \mathcal {L}^2-9 \eta h^4 h_x \mathcal {L}_x+9 \eta h^4 \mathcal {L} h_{xx}-9 \eta h^3 \mathcal {L} h_x^2\right) h_t-\frac{5}{3} \zeta h^5 \left( \mathcal {L} \left( h_x^2+h h_{xx}\right) -h h_x \mathcal {L}_x\right) \\&\quad -\frac{1}{12} h^5 \tau \left( 2 \eta \mathcal {L} \left( h_x h_{xx}-2 h h_{xxx}\right) +\mathcal {L}_x \left( -3 \eta h_x^2+4 \eta h h_{xx}+30\right) \right) +h_{x,t} \left( 9 \eta h^5 \mathcal {L}_x+9 \eta h^4 \mathcal {L} h_x\right) -9 \eta h^5 \mathcal {L} h_{xx,t}\\&\quad +\frac{5 h^5 \mathcal {E} \left( \mathcal {L} \left( 3 \chi h_x^2+(1-h \chi ) h_{xx}\right) +(h \chi -1) h_x \mathcal {L}_x\right) }{3 (h \chi -1)^4}-\frac{5}{3} h^6 h_{xxx} \mathcal {L}_x-\frac{5 h^6 \mathcal {L}_x}{3}+\frac{5}{3} h^6 \mathcal {L} h_{xxxx}+\frac{5}{3} h^5 \mathcal {L} h_x h_{xxx} +\frac{5}{3} h^5 \mathcal {L} h_x=0 \end{aligned} \end{aligned}$$
(44)

In the case of excluding the contributions of both external shear stress and viscous dispersion, model (44) is transformed into the model of Ruyer-Quil et al. [44]. In the absence of viscous dispersion \(\eta\) contribution, we have a like Ruyer-Quil et al. model:

$$\begin{aligned} &h_t+h^2 h_x+\underbrace{ h^2 h_x h_{xxx}+\frac{h^3 h_{xxxx}}{3}}_{\text {Capillarity}}-\underbrace{\zeta h^2 \left( h_x^2+\frac{h h_{xx}}{3}\right) }_{\text {Gravity effect}}\\&\quad +\underbrace{\tau h h_x}_{\text {Shear force}}+\underbrace{\frac{\mathcal {E} h\left( (h \chi +2) h_x^2+h (1-h \chi ) h_{xx}\right) }{3 (h \chi -1)^4}}_{\text {Electric field contribution}}=0 \end{aligned}$$
(45)

The evolution equation (45) describes a flow with drag-electrogravity regime. Equation (45) is very similar to the evolution equation derived by Kliakhandler et al. [43] and Craster & Matar [3] without the effect of external shear stress \(\tau\) taking into account the difference in the choice of scalings. Tseluiko & Papageorgiou [23] derived a similar equation in the presence of normal electric field without the external shear. Tomlin et al. ([21, 24]) derived a long-wave Benney model similar to (45) in three-dimensional long wave dynamics of a gravity-driven thin film flow under the action of a normal electric field without an external shear stress. Benney type equation will be valid for Reynolds numbers near the critical value \((5/4)\cot \theta\) or we can say in inertialess flow regime. The dispersion relation for the Benney equation (44) will be obtained by using \(h = 1+\tilde{h}e^{i k x+\omega t}\left( \tilde{h}\ll 1\right)\), with k real and complex \(\omega =\omega _r+i \omega _i\). This gives

$$\begin{aligned} \omega _i=-\frac{k \left( \eta k^2 (17 \tau +12)+15 (\tau +1)\right) }{3 \left( 9 \eta k^2+5\right) };\omega _r=-\frac{5 \zeta k^2}{15+27 \eta k^2}-\frac{5 k^2 \mathcal {E}}{3 (\chi -1)^3 \left( 5+9 \eta k^2\right) }-\frac{5 k^4}{15+27 \eta k^2}. \end{aligned}$$
(46)

Gravitational force is stabilizing for overlying film \((\zeta < \pi /2)\), and destabilizing for hanging one \((\zeta > \pi /2)\). Fig. 6 illustrates the variation of the electrostatic force factor \(\mathcal {E}\) with the dielectric ratio \(\frac{\varepsilon _2}{\varepsilon _1}\) at the different values of modified electric Bond number \(Bo_e\). As we see in this figure, for all ratio values, the electrostatic values are always positive because \(H>1\). When the ratio is less than one and its value is heading towards zero, or when \(\varepsilon _1\) is much greater than \(\varepsilon _2\), we conclude that the absolute values of the electrostatic force increases. On the other hand, when the electrostatic ratio increases and moves away from one, we notice the growth in the absolute values, but not as much as the other side of the ratio increases. This behavior is due to the effect of the modified electric Bond number \(Bo_e\), which is evident when the dielectric ratio is less than one. According to what has been observed from the figure, it is clear that the effect of electrostatic force on the linear flow of waves in terms of stability or not depends on the value of parameter \(\chi\) whether it is less than one or not. This behavior of the force is illustrated by its contribution in the growth rate \(\omega _r\) in equation (46). According to the position of the viscous dispersion \(\eta\) in equation (46), it reduces the values of the maximum growth rate and thus it may be considered as a damping factor, or in other words a stabilizing factor in the waves dynamics. This indicates that it excludes the film dripping case. The phase velocity of the inertialess flow is \(\upsilon =-(\tau +1)+k^2 \left( \frac{2 \eta~ \tau }{3}+\eta \right) +\mathcal {O}(k^4)\). We note that the contribution of viscous dispersion \(\eta\) to the phase velocity of very long waves will disappear, and that the shear stress plays the most prominent role in changing the velocity.

6.1 Kuramoto–Sivashinsky type equation

Fig. 7
figure 7

Shows the possible two fixed points of weakly nonlinear model for Extremely viscous regime

Full size image

One of the most basic but widely applicable nonlinear equations in dissipative systems, such as hydrodynamics and moving interfaces, is the Kuramoto–Sivashinsky (KS) equation. Numerous circumstances involve the KS equation with a linear stabilizing term. These circumstances include terrace-edge evolution in step-How growth in the presence of step-step interaction and directed solidification where kinetics are critical. In recent years, a great deal of research has been done on the Kuramoto–Sivashinsky model equations and related ones, both in the setting of manifolds and finite-dimensional attractors and in numerical simulations of dynamical behavior. The Kuramoto–Sivashinsky type equation has been studied by many researchers, for examples, Tseluiko & Papageorgiou [23], Tsvelodub et al. [46], Tomlin et al. [21] and Mukhopadhyay & Mukhopadhyay [47]. Benney-type equation (45) forms a basis to extract the asymptotic corrected weakly nonlinear models that lead to the Kuramoto–Sivashinsky (KS) equation (see Tseluiko & Papageorgiou [23] and Tomlin et al. [21]), and references therein). The Kuramoto–Sivashinsky equation exhibits a wide range of dynamical behavior, including spatio-temporal instability. The asymptotic evolution of long-waves by assuming \(h=1+\epsilon \tilde{\mathcal {H}}(x,t)\) into equation (45) where \(\tilde{\mathcal {H}}=\mathcal {O}(1)\). Using a Galilean transformation and the slow time scale with the rescaling

$$\begin{aligned} \xi =x-(1+\tau )t,\mathcal {T}=\epsilon t \end{aligned}$$
(47)

gives the leading-order equation

$$\begin{aligned} \tilde{\mathcal {H}}_{\mathcal {T}}+\underbrace{(\tau +2) \tilde{\mathcal {H}} \tilde{\mathcal {H}}_{\xi }}_{\text {possible nonlinearity}}-\underbrace{\frac{1}{3}\left( \zeta -\text {Bo}_e~\hat{\mathcal {E}}(1)\right) \tilde{\mathcal {H}}_{\xi \xi }}_{\text {instability and energy production }} +\underbrace{\frac{1 }{3}\tilde{\mathcal {H}}_{\xi \xi \xi \xi }}_{\text {stability and energy dissipation}}=0 \end{aligned}$$
(48)

Notice that the nonlinearity in equation (48) arises from the nonlinear correction to the phase speed, larger waves move quicker than smaller waves due to a nonlinear kinematic effect. For thin film flows, the interfacial kinematics associated with mean flow cause the nonlinearity.

Now, to study the relationship between the gravity and electrostatic force and the extent of their influence on the traveling stationary wave with a constant velocity \(\mathcal {C}\), we consider the traveling wave solution \(\mathcal {H}(\xi -\mathcal {C} t)=\mathcal {H}(X)\) of (48). Then, equation (48) reduces to its stationary form:

$$\begin{aligned} -\mathcal {C}\mathcal {H}_X+(\tau +2)\mathcal {H} \mathcal {H}_X-\frac{1}{3}\mathcal {F} \mathcal {H}_{XX }+\frac{1 }{3}\mathcal {H}_{XXXX}=0, \end{aligned}$$
(49)

where \(\mathcal {F}=\left( \zeta -\text {Bo}_e\hat{\mathcal {E}}(1)\right)\) is the impact factor of drag-electrogravity regime.

Integrating equation (49) once and imposing the Nusselt condition \(\mathcal {H} = 0\) as a solution [48], we obtain

$$\begin{aligned} -\mathcal {C}\mathcal {H}+\dfrac{1}{2}(\tau +2)\mathcal {H}^2-\frac{1}{3}\mathcal {F} \mathcal {H}_{X}+\frac{1 }{3}\mathcal {H}_{XXX}=0. \end{aligned}$$
(50)

We observe the reversibility property of the Kuramoto–Sivashinsky equations (50) with respect to the transformation

$$\begin{aligned} X\rightarrow -X;\mathcal {C}\rightarrow -\mathcal {C};\mathcal {H}\rightarrow -\mathcal {H}, \end{aligned}$$
(51)

and this means that for every stationary wave(forward) traveling in the positive direction, there is a negative one(backward) traveling at the same speed but in opposite direction. So, we can merely consider \(\mathcal {C}>0\). Birkhoff’s normal form theory for Hamiltonian systems is nearly fully followed in the neighborhood of a fixed point or periodic solution of a reversible system. According to this theory on the periodic solution family of Kuramoto–Sivashinsky type equation (48) is used to show the effects of gravity and electrostatic forces on the different types of traveling waves. Periodic, doubly-periodic, solitary , kink, anti-kink and chaotic waves are examples for the types of these waves . Consider the vector \(\vec {\mathcal {H}}\), where

$$\begin{aligned} \vec {\mathcal {H}}= \begin{pmatrix} \mathcal {H} \\ \mathcal {H}_{X} \\ \mathcal {H}_{XX} \end{pmatrix}= \begin{pmatrix} \mathcal {H}_1 \\ \mathcal {H}_2 \\ \mathcal {H}_3 \end{pmatrix} \end{aligned}$$
(52)

and so equation (50) can be rewritten as a dynamical system

$$\begin{aligned} \begin{pmatrix} \mathcal {H}_1' \\ \mathcal {H}_2' \\ \mathcal {H}_3' \end{pmatrix}=\begin{pmatrix} \mathcal {H}_2 \\ \mathcal {H}_3 \\ 3\mathcal {C} \mathcal {H}_1 -3\left( \frac{\tau }{2}+1\right) \mathcal {H}_1^2+\mathcal {F} \mathcal {H}_2 \end{pmatrix}, \end{aligned}$$
(53)

where the prime denotes the derivative with respect to the coordinate \(X=\xi -\mathcal {C} t\). In phase space, solitary waves correspond to homoclinic orbits connecting a fixed point to itself. In this work, we focus on single-loop homoclinic orbits, which correspond to single-hump solitary waves in real space. The fixed points of the dynamical system (53) satisfy \(\mathcal {H}_1'=\mathcal {H}_2'=\mathcal {H}_3'= 0\) and

$$\begin{aligned} \vec {\mathcal {H}_0}= \begin{pmatrix} H_1 \\ 0 \\ 0 \end{pmatrix}= \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix};\vec {\mathcal {H}_1}= \begin{pmatrix} H_2 \\ 0 \\ 0 \end{pmatrix}= \begin{pmatrix} \frac{2 \mathcal {C}}{\tau +2} \\ 0 \\ 0 \end{pmatrix},~\text {provided that}~~\tau +2>0 \end{aligned}$$
(54)

whose positions are displayed in Fig. 7 as functions of the wave speed \(\mathcal {C}\) and the shear stress \(\tau\). This figure shows the behavior of the fixed point values with the changing of the wave speed \(\mathcal {C}\). We note that the increasing of the shear stress \(\tau\) values that take the same direction of flow transforms the liquid film to Nusselt case. On the contrary, it is clear that the increasing of the shear stress values that take the opposite direction of the flow takes the fluid away from the Nusselt state.

Considering the linear stability of the fixed points, the dispersion relations governing infinitesimal perturbations \(\sim \text {exp}(\Omega X)\) [34] for the fixed points \(H_1\) and \(H_2\) are

$$\begin{aligned} \Omega ^3-\left( \zeta -\text {Bo}_e\hat{\mathcal {E}}(1)\right) \Omega \mp 3\mathcal {C}=0, \end{aligned}$$
(55)

where the negative and positive signs refer to the fixed points \(H_1=0\) and \(H_2=\frac{2 \mathcal {C}}{\tau +2}\), respectively. Therefore, the points \(\vec {\mathcal {H}_{0,1}}\) change from a saddle focus to a saddle when the wave velocity \(\mathcal {C}\) takes the value

$$\begin{aligned} \mathcal {C}=\frac{2 \left( \zeta -\text {Bo}_e\hat{\mathcal {E}}(1) \right) ^{3/2}}{9 \sqrt{3}}, \end{aligned}$$
(56)

provided that \(\text {Bo}_e<\zeta /\hat{\mathcal {E}}(1)\). This condition can be satisfied for solitary waves on the surface of overlaying liquid film. In case of the saddle point, the homoclinic orbit travels over the two eigenspaces corresponding to the eigenvalues of least absolute value monotonically to and from the fixed point \(\mathcal {H}_1\), and the solitary wave’s tail and front are also monotonic. On the other hand , at the saddle focus point, the homoclinic orbit spirals on the eigenspace covered by the eigenvectors corresponding to the complex pair, leaving monotonically through the eigenspace spanned by the eigenvector corresponding to the real eigenvalue and returning to the fixed point \(\mathcal {H}_1\). The capillary ripples near the front of the solitary wave correspond to this spiral, while the tail stays monotonic. These behaviors depend the balance between the drag-gravity and drag-electrostatic regimes.

7 Conclusion

The second-order weighted integral boundary-layer model of Ruyer-Quil and Manneville [35] has been extended in this work to contain electrostatic surface forces for perfect dielectric liquids caused by an electric field normal to solid substrate in the presence of external shear stress. In the linear regime, the role of primary instability has been discussed within the Whitham wave hierarchy framework [38]. The contribution of the electrostatic surface force in primary instability depends on the ratio between the dielectric constants of liquid film and the ambient medium and the distance between two capacitor plates. The kinematic waves are not clearly affected by the drag-viscosity regime for overlying falling film in the absence of influence of external shear stress and electricity. In the absence of a contribution of the electrostatic force and external shear stress, theses result in agreement with studies of Ruyer-Quil et al. [44] and Samanta [29]. The electrostatic force comes into play a more effectively stabilizing role for the propagating waves in case of vertical plate rather than that remarked in hanging case. The external shear stress and the dielectric permittivity ratio have a stronger destabilizing influence for the waves propagating on the vertical plate. So, the liquid film is more susceptible to dripping regime. It is found that the possibility of dripping is excluded when the shear stress is directed in the opposite direction to the flow. Dripping process means that the liquid film transforms into droplet train phase. The gravitational dripping phenomena are associated with a pressure gradient that occurs crosswise. Based on a force balance between surface tension and the gravitational forces of the liquid film in the major wave hump, a criterion for the start of dripping is developed.

As for the nonlinear regime, the fixed points of solitary waves do not depend on the presence of viscous dispersion \(\eta\) in terms of its appearance or disappearance through a three-dimensional dynamical system. Only, the external shear stress has a significant role. When the viscous dispersion \(\eta\) is excluded, the fixed points of these solitary waves have an unstable manifold and another that is stable under specific electrostatic force and external shear stress conditions. In addition to other circumstances, we have observed that the solitary waves will be under overstability mechanism regime in agreement with remarks of Ruyer-Quil and Kalliadasis [55]. In other words, for overstability or oscillatory instability two opponent mechanisms, one stabilizing and the other destabilizing. It was also noted that when the contribution of viscosity parameter is taken into account and at certain value of the shear stress, Hopf bifurcation points are obtained. Hopf bifurcation point is considered as a new remark to the stationary waves due the effects of external forces regime on the wavy liquid film. Back to the general situation with Cardano’s formulas, the canonical dispersion relation is obtained. The saddle and saddle focus points are obtained. It has been shown that the locations of the two points are exchanged based on the fulfillment of certain conditions. This means that the saddle point bifurcation affects dramatically the interpretation of the convective instability. The saddle focus points mean that the system has an isolated equilibrium point.

A new complicated evolution equation (44) for the extremely viscous liquid film is obtained. The like-evolution equation of Ruyer-Quil et al. [44] is recovered by excluding contribution of external shear stress and viscous dispersion. The analogous evolution equation to the evolution equations derived by Kliakhandler et al. [43], Craster & Matar [3] and Tseluiko & Papageorgiou [23] is introduced to describe a flow with drag-electrogravity regime. In the presence of viscous dispersion parameter \(\eta\), the linear instability criteria of generated waves are studied. It is found that viscous dispersion parameter \(\eta\) play a damping factor. The viscous dispersion parameter \(\eta\) disappears its contribution to the phase velocity of very long waves, and that the shear stress is a major player in changing the velocity. The weakly nonlinear inertialess stationary traveling waves are analyzed through the Kuramoto–Sivashinsky type equation. A three-dimensional dynamical system is introduced from the Kuramoto–Sivashinsky type equation. For some value of wave velocity , the fixed points of the dynamical system change from a saddle focus to a saddle. It is found that the balance between the drag-gravity and drag-electrostatic regimes plays an effective role in the behaviors of the arisen solitary wave. It is found that, under some conditions, while the tail of the single wave remains monotonous, the capillary ripples near the wave’s front correspond to the spiral.