Analysis of the compressible, isotropic, neo-Hookean hyperelastic model

Abstract

The most widely-used representation of the compressible, isotropic, neo-Hookean hyperelastic model is considered in this paper. The version under investigation is that which is implemented in the commercial finite element software ABAQUS, ANSYS and COMSOL. Transverse stretch solutions are obtained for the following homogeneous deformations: uniaxial loading, equibiaxial loading in plane stress, and uniaxial loading in plane strain. The ground-state Poisson’s ratio is used to parameterize the constitutive model, and stress solutions are computed numerically for the physically permitted range of its values. Despite its broad application to a number of engineering problems, the physical limitations of the model, particularly in the small to moderate stretch regimes, are not explored. In this work, we describe and analyze results and make some critical observations, underlining the model’s advantages and limitations. For example, a snap-back feature of the transverse stretch is identified in uniaxial compression, a physically undesirable behavior unless validated by experimental data. The domain of this non-unique solution is determined in terms of the ground-state Poisson’s ratio and the state of stretch and stress. The analyses we perform are essential to enable the understanding of the characteristics of the standard, compressible, isotropic, neo-Hookean model used in ABAQUS, ANSYS and COMSOL. In addition, our results provide a framework for the parameter-fitting procedure needed to characterize this standard, compressible, isotropic neo-Hookean model in terms of experimental data.

1 Introduction

Hyperelasticity is used to characterize the finite-strain, nonlinear elastic behavior of rubber-like materials [1,2,3,4]. Since most rubber-like materials show nearly incompressible behavior, the fully incompressible approximation for those materials is often adopted for simplicity. We note that there exist numerous isotropic, incompressible, hyperelastic models, and researchers continue to propose new models to represent elastic deformations in the finite strain regime more accurately. Comparisons of existing models can be found in various papers [5,6,7,8]. It is difficult to choose a particular model as the best one to represent the nonlinear elastic behavior of different rubber-like materials. There are simpler models with fewer material parameters, but highly complex phenomenological versions also exist involving numerous material parameters. Some models are proposed for moderate but finite strain, whereas others can be used for very high strains at the cost of additional material parameters. The incompressible assumption can be used to obtain closed-form expressions of the transverse stretches for most models during standard homogeneous loadings (uniaxial loading, equibiaxial loading in plane stress, uniaxial loading in plane strain, pure shear loading, simple shear loading). Consequently, the stretch-stress relations for these incompressible, hyperelastic models can be expressed in closed-form analytical formulae, which can then be used in a parameter-fitting process to characterize a given rubber-like material in terms of experimental data.

The simplest isotropic, incompressible, hyperelastic model is undoubtedly the neo-Hookean formulation that was proposed by Rivlin [9]. It contains only one material parameter, and is utilized mainly in the moderate strain regime. It should be emphasized that it is widely used due to its simplicity. Although most researchers use Rivlin’s original representation, there exists a new, two-parameter generalized version [10, 11].

In cases where material compressibility cannot be neglected, the incompressible, isotropic, neo-Hookean hyperelastic model can be extended by addition of a term in the strain energy accounting for volumetric deformation. The compressible version of the resulting neo-Hookean model is not unique, and there exist several forms in the literature. The particular version implemented in the commercial finite element (FE) software ABAQUS [12], ANSYS [13], and COMSOL [14] is the most widely-used and widely-accepted. We reference this model in the following as the standard, compressible, isotropic, neo-Hookean model. However, it should be borne in mind that other models have been suggested [15,16,17,18,19].

Compressible, isotropic, neo-Hookean hyperelastic models (CNH) are used for various applications. Brock and Hanson [20] examine crack growth in a CNH material, deriving analytical formulae for wave speeds in the crack plane of their problem. It is important to emphasize that these authors use the CNH model for a highly compressible material having ground-state Poisson’s ratio of 0.25. Horgan and Saccomandi [16] investigate the variation of the apparent Poisson’s ratio, the Poisson function, in terms of the applied stretch for uniaxial tension in a nonlinear CNH model. They find that the Poisson function decreases with increasing stretch; the largest ground-state Poisson’s ratio they use is 0.45. The internal stability of a CNH model in homogeneous deformation is studied by Clayton and Bliss [17], using the formulation proposed by Simo and Pister [21]. This stability analysis is performed for both positive and negative ground-state Poisson’s ratios. Begley, Creton and McMeeking [22] obtain the displacement solution around a Mode I crack tip in plane strain for a CNH model, while Budday, Raybaud and Kuhl [23] model human brain tissue in the form of a stretch-driven growing inner core and a morphogenetically growing outer surface. The cortex of the brain is modeled using a CNH formulation with ground-state Poisson’s ratio of 0.458, and the authors infer that mechanical deformation plays a crucial role in brain development. Their material parameters are also used by Morin et al. [24]. Zhang [25] derives a lattice model to represent the mechanical behavior of a CNH material, demonstrating the lattice model’s performance and accuracy for ground-state Poisson’s ratios ranging from 0.417 to 0.495. Behera, Roy and Madenci [18] use a CNH model with a ground-state Poisson’s ration equal to 0.452 to study large deformation and rupture in rubber-like materials, employing the bond-associated weak form of peridynamics with non-uniform horizon in their analysis. We note that CNH models can be extended to characterize transversely isotropic porous solids. For example, Guo and Caner [26] use a novel anisotropic constitutive model developed for materials having aligned cylindrical pores, and Chen and Ravi-Chandar [27] develop an innovative CNH constitutive model to capture the nonlinear poroviscoelastic behavior of a gelatin-based hydrogel.

The complete understanding of the standard CNH model is essential not only for mechanical engineers but also for graphics and computer vison engineers working in computer graphics. In this application, a fundamental goal is to simulate natural phenomena realistically. This task includes the simulation of the movement and deformation of characters composed of soft solids (e.g., humans, animals, imaginary creatures). Bender et al. [28] utilize a CNH model to simulate the deformation of deformable solids and clothing, paying particular attention to the simulation of cloth, where achieving realistic wrinkling is crucial. The CNH model is used by these authors for a very low ground-state Poisson’s ratio, namely 0.1, demonstrating that CNH models are used for materials with significant compressibility. Smith, De Goes and Kim [19] conclude that to capture the fleshy appearance of virtual characters it is essential to use hyperelastic material models. These authors propose a new version of the compressible neo-Hookean model, and demonstrate that the new model behaves well for ground-state Poisson’s ratios in the range from 0 to 0.5. We note that Smith et al. [19] emphasize that biological tissues are nearly incompressible, but numerical simulations within this regime are extremely challenging. Sheen, Larionov and Pai [29] underline the popularity of the CNH model in computer graphics for enforcing incompressibility using a ground-state Poisson’s ratio close to 0.5. These authors comment that accurate simulation of the human body in contact with its environment is crucial in visual effects and apparel design. They propose a novel approach to alleviate numerical instabilities and locking in coarsely discretized bodies, and demonstrate the performance of their CNH material model in numerical examples. Macklin and Müller [30] emphasize that the neo-Hookean model has recently become popular in computer graphics, and employ the standard CNH formulation as implemented in ABAQUS, ANSYS and COMSOL. They present numerical examples with a range of ground-state Poisson’s ratios from 0.4 to 0.4995.

Although the expression for the strain energy associated with the standard, compressible, isotropic, neo-Hookean model is relatively simple, closed-form stress solutions cannot be obtained for homogeneous deformations, not even for simple uniaxial tension. Consequently, the determination of material parameters via a parameter-fitting procedure using experimental data is more complicated than for the incompressible models. One must use a numerical solution strategy to calculate the transverse stretch and the longitudinal stress in uniaxial loading. Furthermore, stress/stretch solutions for the standard CNH model in homogeneous loading, e.g., uniaxial loading, equibiaxial loading in plane stress, uniaxial loading in plane strain, are not yet reported in the literature. There is no paper presenting the effect of compressibility on stress/stretch solutions and on the uniqueness properties of the model. The theory guides and manuals for the commercial FE software ABAQUS, ANSYS, and COMSOL do not provide detailed information about the behavior of the compressible neo-Hookean model implemented in these codes. In particular, the effect of the value of the initial ground-state Poisson’s ratio on stress/stretch solutions is unclear, and the domains of uniqueness for stress and stretch are not identified. This is a serious challenge for the application of such models to understand experimental data obtained using compressible material systems, since, as will be demonstrated below, the standard CNH material model can yield multiple stress-stretch solutions in certain ranges of the applied stretch in uniaxial compression, and exhibits some other behavior that is unphysical unless validated by comparison with experimental data. In addition, the uniqueness, or its lack, and the stability of hyperelastic models are important, and must be understood completely in order to avoid physically unrealistic responses. Peng and Li [31] identified stable domains of volumetric deformation for a few compressible, hyperelastic material models, including an extended CNH model differing from the standard version. However, analysis of the standard CNH model for the standard loading cases is not included in their investigation. Pence and Gou [15], provide a detailed analysis of the behavior of three different CNH models, but exclude the standard CNH model. The authors also address the stability analysis of the non-standard CNH models only in uniaxial loading.

This paper provides a detailed analysis of the characteristics of the standard CNH model. Three commonly used, simple, homogeneous deformations (uniaxial loading, equibiaxial loading in plane stress, uniaxial loading in plane strain) are considered. It is shown that the transverse stretches parallel to zero stress directions cannot be expressed in closed-form, and are obtained using numerical calculations. The ground-state Poisson’s ratio, $\nu_{0}$, is used to quantify the ratio of the two material parameters involved in the constitutive model, and to parameterize the constitutive model and the results of the analysis. Computational results are presented for the entire permissible range, $- 1 < \nu_{0} < 0.5$. The variation of the transverse stretches in terms of the specified stretches is analyzed for each loading case. It is found that the model can yield multiple stress solutions for the same longitudinal stretch in uniaxial compression. The domain for unique solutions is determined, and stress solutions are calculated for the homogeneous deformations under investigation. These solutions are compared to those for the incompressible material to quantify numerically the differences resulting from the presence of compressibility. These new results give insight into the nature of the standard CNH model. Furthermore, these new solutions can be used in parameter-fitting procedures using experimental data, where compressibility of the material is not negligible.

2 Constitutive equations for the standard, compressible, isotropic, neo-Hookean model

The strain energy for isotropic, hyperelastic solids is expressed with use of the principal invariants $\left( {I_{1} , I_{2} , I_{3} } \right)$ of the left Cauchy-Green deformation tensor ${\varvec{b}} = {\varvec{FF}}^{T}$ [2]:

$$U = U\left( {I_{1} ,I_{2} ,I_{3} } \right),$$

(1)

$$I_{1} = {\text{tr}}\left( {\varvec{b}} \right) = \lambda_{1}^{2} + \lambda_{2}^{2} + \lambda_{3}^{2} ,$$

(2)

$$I_{2} = \frac{1}{2}\left( {I_{1}^{2} - {\text{tr}}\left( {{\varvec{b}}^{2} } \right)} \right) = \left( {\lambda_{1} \lambda_{2} } \right)^{2} + \left( {\lambda_{1} \lambda_{3} } \right)^{2} + \left( {\lambda_{2} \lambda_{3} } \right)^{2} ,$$

(3)

$$I_{3} = {\text{det}}\left( {\varvec{b}} \right) = \left( {\lambda_{1} \lambda_{2} \lambda_{3} } \right)^{2} = J^{2} ,$$

(4)

where ${\varvec{F}}$ is the deformation gradient, and $\lambda_{i}$ (with $i = 1,2,3)$ are the principal stretches, whereas the determinant of the deformation gradient defines the volume ratio as $J = {\text{det}}\left( {\varvec{F}} \right)$. The derivatives of the principal scalar invariants with respect to ${\varvec{b}}$ read

$$\frac{{\partial I_{1} }}{{\partial {\varvec{b}}}} = {\varvec{I}},\;\; \frac{{\partial I_{2} }}{{\partial {\varvec{b}}}} = I_{1} {\varvec{I}} - {\varvec{b}},\;\; \frac{{\partial I_{3} }}{{\partial {\varvec{b}}}} = I_{3} {\varvec{b}}^{ - 1} .$$

(5)

The Cauchy stress tensor is defined by the relation

$${\varvec{\sigma}} = 2J^{ - 1} \frac{\partial U}{{\partial {\varvec{b}}}}{\varvec{b}} = 2J^{ - 1} \left( {U_{,1} \frac{{\partial I_{1} }}{{\partial {\varvec{b}}}} + U_{,2} \frac{{\partial I_{2} }}{{\partial {\varvec{b}}}} + U_{,3} \frac{{\partial I_{3} }}{{\partial {\varvec{b}}}}} \right){\varvec{b}}.$$

(6)

$U_{,i}$ (with $i = 1,2,3)$ denote the partial derivative of $U$ with respect to the $i{\text{th}}$ principal scalar invariant. Using the relation $U_{,3} = U_{,J} /\left( {2J} \right)$ and Eq. (5), we find that the Cauchy stress tensor can be formulated as

$${\varvec{\sigma}} = 2J^{ - 1} \left( {\left( {U_{,1} + U_{,2} I_{1} } \right){\varvec{b}} - U_{,2} {\varvec{b}}^{2} } \right) + U_{,J} {\varvec{I}}.$$

(7)

The modified principal invariants are given by the relations

$$\overline{I}_{1} = J^{ - 2/3} I_{1},\;\; \overline{I}_{2} = J^{ - 4/3} I_{2} .$$

(8)

The decoupled representation of the strain energy function is assumed to be written as

$$U = U\left( {\overline{I}_{1} ,\overline{I}_{2} ,J} \right) = U_{{{\text{dev}}}} \left( {\overline{I}_{1} ,\overline{I}_{2} } \right) + U_{{{\text{vol}}}} \left( J \right),$$

(9)

where the term $U_{{{\text{dev}}}}$ represents the strain energy resulting from distortional (volume preserving) deformation and $U_{{{\text{vol}}}}$ denotes the energy associated with volumetric deformation. If the distortional part of $U$ is independent of $\overline{I}_{2}$ then the Cauchy stress solution reduces to

$${\varvec{\sigma}} = 2J^{ - 1} U_{,1} {\varvec{b}} + U_{,J} {\varvec{I}}.$$

(10)

The most common form of the strain energy for the compressible, isotropic, neo-Hookean (CNH) model (implemented in ABAQUS, ANSYS and COMSOL) is written as

$$U = \frac{G}{2}\left( {\overline{I}_{1} - 3} \right) + \frac{K}{2}\left( {J - 1} \right)^{2} ,$$

(11)

where $G$ and $K$ are two material parameters, equal to the ground-state shear and bulk moduli, respectively, as discussed in “Appendix 2”. The partial derivatives required for this model are

$$U_{,1} = \frac{G}{2}J^{ - 2/3} ,\;\; U_{,J} = K\left( {J - 1} \right) - \frac{1}{3}GI_{1} J^{ - 5/3} .$$

(12)

Consequently, the general form of the Cauchy stress tensor for the CNH model is given by

$${\varvec{\sigma}} = GJ^{ - 5/3} {\varvec{b}} + K\left( {J - 1} \right){\varvec{I}} - \frac{1}{3}GI_{1} J^{{ - \frac{5}{3}}} {\varvec{I}},$$

(13)

where as the first Piola–Kirchhoff stress tensor can be obtained from the Cauchy stress tensor as

$${\varvec{P}} = J\varvec{\sigma}\varvec{F}^{-T}.$$

(14)

If a deformation is imposed that is volume preserving,$\left( {J = 1} \right)$, the result in Eq. (13) reduces to ${\varvec{\sigma}} = G {\text{dev}}\left[ {\varvec{b}} \right].$ This is a valid prediction of the stress arising from volume preserving loading such as occurs in the idealized simple shear deformation of the double lap shear test. However, due to end effects, homogeneous deformation does not occur in practice in the double lap shear test. Furthermore, the single lap shear test is complicated by an applied moment as well as end effects, and thus this test lacks homogeneous deformation. Consequently, the analysis of the CNH model for lap shear tests is excluded from the paper, and we restrict our attention to tests that can have long gauge lengths or large gauge areas in which homogeneous deformations occur. These cases are uniaxial loading, equibiaxial loading in plane stress, and uniaxial loading in plane strain, where, in each case, volume change is involved during deformation. We note that the analysis of uniaxial loading in plane strain is a valid treatment of the deformation arising in the test of what is known as the pure shear specimen, as long as its height (i.e., in the direction subject to applied load) is large compared to its unconstrained thickness, and the length of the specimen is large compared to its height.

3 Homogeneous loading cases

3.1 Uniaxial loading

Uniaxial loading is depicted in Fig. 1a. The deformation gradient and the left Cauchy-Green deformation tensors are expressed with the help of the principal stretches as

$$\left[ {\varvec{F}} \right] = \left[ {\begin{array}{*{20}c} \lambda & 0 & 0 \\ 0 & {\lambda_{T} } & 0 \\ 0 & 0 & {\lambda_{T} } \\ \end{array} } \right], \;\; \left[ {\varvec{b}} \right] = \left[ {\begin{array}{*{20}c} {\lambda^{2} } & 0 & 0 \\ 0 & {\lambda_{T}^{2} } & 0 \\ 0 & 0 & {\lambda_{T}^{2} } \\ \end{array} } \right].$$

(15)

Fig. 1

Schematics of uniaxial loading (a), equibiaxial loading in plane stress (b) and uniaxial loading in plane strain (c). Note that in the undeformed state $\lambda = \lambda_{T} = 1.$ Values of $\lambda > 1$ represent tensile loading, while $\lambda < 1$ represent compression

The longitudinal stretch is $\lambda$ and the transverse stretch is denoted $\lambda_{T}$. The volume ratio and the first principal invariant are $J = \lambda \lambda_{T}^{2}$ and $I_{1} = \lambda^{2} + 2\lambda_{T}^{2}$.

Inserting these quantities into Eq. (13), (14) we can express the nominal stress components as:

$$P_{11} = \frac{2}{3}G\lambda_{T}^{2} \left( {\lambda \lambda_{T}^{2} } \right)^{ - 5/3} \left( {\lambda^{2} - \lambda_{T}^{2} } \right) + K\left( {\lambda \lambda_{T}^{4} - \lambda_{T}^{2} } \right),$$

(16)

$$P_{22} = P_{33} = \frac{1}{3}G\lambda \lambda_{T} \left( {\lambda \lambda_{T}^{2} } \right)^{ - 5/3} \left( {\lambda_{T}^{2} - \lambda^{2} } \right) + K\lambda \lambda_{T} \left( {\lambda \lambda_{T}^{2} - 1} \right).$$

(17)

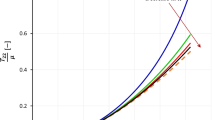
The zero transverse stress constraint, $P_{22} = P_{33} = 0$, cannot be solved analytically to obtain a closed-form expression for the stretch relation $\lambda_{T} = \lambda_{T} \left( \lambda \right)$. However, numerical schemes can be used to compute the transverse stretch. The solutions depend on the ratio $K/G$, i.e. on the ground-state Poisson’s ratio $\nu_{0}$. The definition of the ground-state Poisson’s ratio is explained in “Appendix 2”. Numerical solutions are obtained for various values of $\nu_{0}$ using Wolfram Mathematica [32]. The transverse stretch results are presented in Fig. 2b. The largest value for the ground-state Poisson’s ratio used in the plot is 0.4999 (red curve), whereas the smallest value is − 0.99 (purple curve). The color coding for the ground-state Poisson’s ratio, as shown in the bar in Fig. 2a, is used for all figures in this paper. Black curves indicate the solutions corresponding to a ground-state Poisson’s ratio equal to zero.

Fig. 2

a Color coding for the ground-state Poisson’s ratio. b Transverse stretch as a function of longitudinal stretch in uniaxial stress. Results are shown for various values of the ground-state Poisson ratio as indicated in the color coding. The black curve shows the result for $\nu_{0} = 0$. c Transverse stretch as a function of longitudinal stretch for uniaxial tension

One of the most critical observations in the results is the occurrence of “snap-back” of the transverse stretch in the compression regime for values of $\nu_{0} > 0.296$. It can be seen that in compression for $\lambda < 0.4$ there are multiple solutions for the transverse stretch for a given longitudinal stretch $\lambda$. This domain is therefore a regime of non-unique and possibly unstable behavior. The results show that if a material with such a non-unique characteristic is subjected to a uniaxial stress in compression with the longitudinal stretch being controlled monotonically, the component will at first thicken in the transverse direction. However, at a critical longitudinal stretch, the material will snap from being transversely thicker than its original width to being thinner than it. However, the exact behavior will depend on whether the longitudinal stretch or the axial load is being controlled, with different behavior occurring when the axial load is controlled monotonically, as will be described below. Note that for all values of ground-state Poisson’s ratio other than 0.5 the material eventually experiences transverse thinning for small longitudinal stretch ratios. Therefore, a positive value of ground-state Poisson ratio, other than 0.5, does not guarantee that transverse thickening will always occur in axial compression. However, for ground-state Poisson’s ratio values less than 0.296 the transition from transverse thickening to transverse thinning occurs smoothly and with continuity, and there is no snap-through. Note also that for longitudinal stretch approaching zero, the transverse stretch also approaches zero other than for $\nu_{0} = 0.5$. Therefore, the volume of the material approaches zero in this circumstance, in violation of quantum exclusion.

If $\nu_{0} < 0.296$ the phenomenon of multiple solutions is absent. The domain for multiple solutions is determined in the $\lambda - \nu_{0}$ plane and is shown in Fig. 3.

Fig. 3

Domain of multiple solutions in the $\lambda - \nu_{0}$ plane in uniaxial compression

The coordinates at the bottom-right corner of the domain in Fig. 3 are $\left( {0.3967, \;0.296} \right)$. Consequently, if the ground-state Poisson’s ratio is smaller than 0.296 ($K/G \approx 2.118$) then the model provides a unique solution in the entire regime of the possible stretches.

In uniaxial tension, the model for a material with a positive ground-state Poisson ratio behaves as expected in that the material thins transversely in a monotonic manner when the longitudinal stretch is increased. This can be seen in Fig. 2c where the transverse stretch is plotted versus the longitudinal stretch out to very large axial strains. The largest value for the ground-state Poisson’s ratio used in the plot is 0.4999 (red curve), whereas the smallest value is − 0.99 (purple curve). The black dashed line represents $\lambda_{T} = 1$. For negative ground-state Poisson’s ratios, Fig. 2c shows that the transverse stretch has a maximum when the longitudinal stretch is increased, and thereafter decreases monotonically. Eventually, the plots for negative ground-state Poisson’s ratios cross the axis for $\lambda_{T} = 1$ and the material begins to thin as the longitudinal stretch is increased. The longitudinal stretch values at which $\lambda_{T} = 1$ in uniaxial tension are shown in Fig. 4 for different values of $\nu_{0}$.

Fig. 4

Longitudinal stretch in uniaxial tension at which $\lambda_{T} = 1$. Results are shown as a function of ground-state Poisson’s ratio $\nu_{0} < 0$

Once the transverse stretch is determined, the nominal stress component $P_{11}$ can be obtained using Eq. (16). The result for $P_{11} /G$ is shown in Fig. 5a for different values of $\nu_{0}$. The largest value for the ground-state Poisson’s value used in the plot is 0.4999 (red curve), whereas the smallest value is − 0.99 (purple curve). It can be observed there are domains on the compression side of Fig. 5a where multiple stress solutions exist for the same longitudinal stretch value. This plot reveals that if the longitudinal stretch is controlled monotonically, there will be a “snap-back” feature in compression in some cases as $\lambda$ is reduced. It is also observed that the limit values for the nominal stress at $\lambda = 0$ is zero other than for the incompressible case, where infinite stress occurs. Due to quantum exclusion, a zero value for the nominal stress at $\lambda = 0$ is physically unrealistic as it would predict that zero force is needed to compress the material completely. Note that when the axial load is controlled monotonically during uniaxial stressing, other than for the incompressible material, the behavior is such that a limiting load is always reached where the nominal stress in Fig. 5a goes through a minimum. For magnitudes of the nominal stress in compression greater than the stress magnitude at the minima shown in Fig. 5a, the solution for stress ceases to exist. Such a behavior implies, though does not model, material failure.

Fig. 5

a Axial nominal stress $P_{11}$ as a function of longitudinal stretch in uniaxial loading. b Ratio, $\eta$, of the nominal stress for the compressible case to the nominal stress for the incompressible case shown as a function of the longitudinal stretch for uniaxial loading

We introduce the dimensionless parameter

$$\eta = \frac{{P_{11}^{{{\text{comp}}}} }}{{P_{11}^{{{\text{inc}}}} }}$$

(18)

measuring the ratio of the compressible $\left( {P_{11}^{{{\text{comp}}}} } \right)$ and incompressible $\left( {P_{11}^{{{\text{inc}}}} } \right)$ nominal stress results. The incompressible stress solutions are summarized in “Appendix 1”. With the help of this parameter, we can illustrate the effect of compressibility on the stress. The ratio $\eta$ is shown in Fig. 5b as a function of $\lambda$ for different values of $\nu_{0}$. The largest value for the ground-state Poisson’s ratio used in the plot is 0.4999 (red curve), whereas the smallest value is -0.99 (purple curve). It is noted that $\eta$ is undetermined at $\lambda = 1$, but its limit can be calculated. One can conclude that $\eta$ is always smaller than 1.

Results for the Cauchy stress are provided in “Appendix 3”.

3.2 Equibiaxial loading in plane stress

The schematic for equibiaxial loading in plane stress is shown in Fig. 1b. The deformation gradient and the left Cauchy-Green deformation tensors are expressed as

$$\left[ {\varvec{F}} \right] = \left[ {\begin{array}{*{20}c} \lambda & 0 & 0 \\ 0 & \lambda & 0 \\ 0 & 0 & {\lambda_{T} } \\ \end{array} } \right],\;\; \left[ {\varvec{b}} \right] = \left[ {\begin{array}{*{20}c} {\lambda^{2} } & 0 & 0 \\ 0 & {\lambda^{2} } & 0 \\ 0 & 0 & {\lambda_{T}^{2} } \\ \end{array} } \right].$$

(19)

The volume ratio and the first principal invariant are $J = \lambda^{2} \lambda_{T}$ and $I_{1} = 2\lambda^{2} + \lambda_{T}^{2}$.

Inserting the kinematic quantities in Eq. (13), (14) we can express the nominal stress components as:

$$P_{11} = P_{22} = \frac{1}{3}G\lambda \lambda_{T} \left( {\lambda^{2} \lambda_{T} } \right)^{ - 5/3} \left( {\lambda^{2} - \lambda_{T}^{2} } \right) + K\lambda \lambda_{T} \left( {\lambda^{2} \lambda_{T} - 1} \right),$$

(20)

$$P_{33} = \frac{2}{3}G\lambda^{2} \left( {\lambda^{2} \lambda_{T} } \right)^{ - 5/3} \left( {\lambda_{T}^{2} - \lambda^{2} } \right) + K\lambda^{2} \left( {\lambda^{2} \lambda_{T} - 1} \right).$$

(21)

The zero transverse stress constraint, $P_{33} = 0$, cannot be solved in closed-form for the transverse stretch, $\lambda_{T}$, as a function of the equibiaxial stretch, $\lambda$. Instead, the transverse stretch is obtained using a numerical method, and the results are presented in Fig. 6

Fig. 6

Transverse stretch as a function of equibiaxial stretch in plane stress. The black curve shows the result when $\nu_{0} = 0$. The largest value for the ground-state Poisson’s ratio used in the plot is 0.4999 (red curve), whereas the smallest value is − 0.99 (purple curve)

It is important to observe that the solution for transverse stretch is unique for each value of $\lambda$ in the entire domain of $\nu_{0}$, as shown in Fig. 6. However, there is a local maximum for the transverse stretch as $\lambda$ is reduced in the compression regime if $\nu_{0}$ is positive. As $\lambda$ is reduced in compression, the transverse stretch eventually transitions so that the transverse thickness of the material has reduced below $\lambda_{T} = 1$ instead of $\lambda_{T}$ being greater than unity, i.e., thinning instead of thickening. In addition, the transverse stretch tends to zero as $\lambda \to 0$. This is a physically unrealistic phenomenon unless validated by experiment, as in the uniaxial stress case. A local maximum in $\lambda_{T}$ also exists in tension in Fig. 6 for negative ground-state Poisson’s ratios.

The equibiaxial nominal stress is shown in Fig. 7a as a function of the equibiaxial stretch. The largest value for the ground-state Poisson’s ratio used in the plot is 0.49999 (red curve), whereas the smallest value is − 0.9999 (purple curve). In this case the equibiaxial nominal stress is unique for a given equibiaxial stretch. However, the equibiaxial stretch is not unique for a given equibiaxial nominal stress, i.e., the stress-stretch relationship is not monotonic. It can be seen that there is a minimum value for the equibiaxial nominal stress in compression, similar to the uniaxial loading case. Below this minimum value, the solution for equibiaxial nominal stress ceases to exist, with implications similar to those holding in the uniaxial loading case. It is notable that the limit equibiaxial nominal stress at $\lambda = 0$ is zero, as in the uniaxial stress case.

Fig. 7

a Equibiaxial nominal stress as a function of equibiaxial stretch in equibiaxial stretch in plane stress. b Stress ratio, $\eta$, in equibiaxial loading in plane stress

The ratio of the compressible stress solution and the incompressible stress solution for equibiaxial stretch in plane stress is denoted by the parameter $\eta$ as in the uniaxial stress case. The variation of $\eta$ as a function of biaxial stretch is shown in Fig. 7b. The largest value for the ground-state Poisson’s ratio used in the plot is 0.49999 (red curve), whereas the smallest value is − 0.9999 (purple curve). The results in Fig. 7b reveal that the stress solutions in the compressible case are always smaller in magnitude than the incompressible stress solutions.

Results for the Cauchy stress are provided in “Appendix 3”.

3.3 Uniaxial loading in plane strain

Uniaxial loading in plane strain is depicted in Fig. 1c It is axial stressing subject to plane strain constraint in direction 2. The deformation gradient and the left Cauchy-Green deformation tensors are expressed as

$$\left[ {\varvec{F}} \right] = \left[ {\begin{array}{*{20}c} \lambda & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & {\lambda_{T} } \\ \end{array} } \right], \;\; \left[ {\varvec{b}} \right] = \left[ {\begin{array}{*{20}c} {\lambda^{2} } & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & {\lambda_{T}^{2} } \\ \end{array} } \right].$$

(22)

The volume ratio and the first principal invariant are $J = \lambda \lambda_{T}$ and $I_{1} = 1 + \lambda^{2} + \lambda_{T}^{2}$. Substituting the kinematic variables into Eq. (13), (14), we can formulate the nominal stress components as:

$$P_{11} = G\lambda^{1/3} \lambda_{T}^{ - 2/3} - \frac{1}{3}G\lambda_{T} \left( {\lambda \lambda_{T} } \right)^{ - 5/3} \left( {\lambda^{2} + \lambda_{T}^{2} + 1} \right) + K\lambda_{T} \left( {\lambda \lambda_{T} - 1} \right),$$

(23)

$$P_{22} = - \frac{1}{3}G\left( {\lambda \lambda_{T} } \right)^{ - 2/3} \left( {\lambda^{2} + \lambda_{T}^{2} - 2} \right) + K\lambda \lambda_{T} \left( {\lambda \lambda_{T} - 1} \right),$$

(24)

$$P_{33} = G\lambda^{ - 2/3} \lambda_{T}^{1/3} - \frac{1}{3}G\lambda \left( {\lambda \lambda_{T} } \right)^{ - 5/3} \left( {\lambda^{2} + \lambda_{T}^{2} + 1} \right) + K\lambda \left( {\lambda \lambda_{T} - 1} \right).$$

(25)

The boundary conditions imply that $P_{33} = 0$. Due to its highly nonlinear nature, this equation cannot be solved in closed-form for the transverse stretch. We use a numerical scheme to determine $\lambda_{T}$ for a given $\lambda$ and the results are plotted in Fig. 8. For $\nu_{0} > 0$, we see the same phenomenon in compression as in the uniaxial and equibiaxial cases: the transverse stretch increases at first as $\lambda$ is reduced, goes through a maximum and then decreases. It is concluded that the transverse stretch tends to a finite value for $\lambda = 0$. This limiting value is $\lambda_{T} = 1/\sqrt 2$, in contrast to the zero limit observed in uniaxial loading and in equibiaxial loading in plane stress.

Fig. 8

Transverse stretch as a function of longitudinal stretch in uniaxial loading in plane strain. The black curve shows the result, when $\nu_{0} = 0$. The largest value for the ground-state Poisson’s ratio used in the plot is 0.4999 (red curve), whereas the smallest value is − 0.99 (purple curve)

The axial nominal stress, $P_{11}$, is shown in Fig. 9a as a function of the axial stretch. The largest value for the ground-state Poisson’s ratio used in the plot is 0.49999 (red curve), whereas the smallest value is – 0.9999 (purple curve). These stress versus stretch plots are monotonic and the stress tends toward $- \infty$ as $\lambda \to 0$. This limiting behavior is physically realistic, in contrast to the results for uniaxial loading and the case of equibiaxial loading in plane stress.

Fig. 9

a Axial nominal stress, $P_{11}$, as a function of axial stretch in uniaxial loading in plane strain. b Stress ratio, $\eta$, in uniaxial loading in plane strain

The stress ratio of Eq. (18) measures the ratio of the compressible and incompressible stress results. This ratio for uniaxial loading in plane strain is shown in Fig. 9b. The largest value for the ground-state Poisson’s ratio used in the plot is 0.49999 (red curve), whereas the smallest value is − 0.9999 (purple curve). The stresses in the compressible case are smaller in magnitude than in the incompressible case in the entire domain.

The numerical results for the transverse stress, $P_{22}$, are plotted in Fig. 10a. The largest value for the ground-state Poisson’s ratio used in the plot is 0.49999 (red curve), whereas the smallest value is – 0.9999 (purple curve). In axial compression for positive values of the ground-state Poisson’s ratios, $P_{22}$ at first decreases as $\lambda$ is reduced, goes through a minimum and then increases. For positive values of the ground-state Poisson ratio, the limit value for $P_{22}$ is $+ \infty$ at $\lambda = 0$. This result is physically unrealistic as a negative transverse stress is expected in axial compression when the ground-state Poisson’s ratio is positive.

Fig. 10

a Transverse stress, $P_{22}$, as a function of axial stretch in uniaxial loading in plane strain. b Transverse nominal stress, $P_{22}$, as a function of higher axial stretch in uniaxial loading in plane strain

The transverse nominal stress in axial tension in plane strain also exhibits unrealistic characteristics, but at relatively large axial stretch. Figure 10b presents the results for $P_{22}$ for higher axial stretches. The largest value for the ground-state Poisson’s ratio used in the plot is 0.499999 (red curve), whereas the smallest value is − 0.999999 (purple curve). In the incompressible case, $P_{22}$ approaches $G$ as $\lambda \to \infty$, consistent with the analytical solution in the limit of Eq. (30). If material compressibility is allowed, then the limiting value of $P_{22}$ is zero as $\lambda \to \infty$. As a result, as $\lambda$ is increased from unity, $P_{22}$ at first increases, goes through a maximum and then decreases to zero as $\lambda \to \infty$.

Results for the Cauchy stress are provided in “Appendix 3”.

4 Discussion

These results have important implications for the application of compressible, isotropic, neo-Hookean hyperelastic material models to the analysis of experimental data. The ability to robustly model the deformations of compressible materials in the moderate strain regime is required for broad classes of engineering materials, including most biological and biomimetic materials, which typically have a Poisson ratio in the range of 0.2–0.5 and exhibit nonlinear elastic responses [33,34,35,36,37,38]. The ability to accurately relate observed deformations to applied stress fields is particularly important for the development of traction force microscopy methods, which allow determination of cell-generated forces to understand the fundamental mechanobiology, as well as improved disease modeling and design of soft tissue replacements [39,40,41,42,43,44,45].

In this study, the behavior of the standard version of the compressible, isotropic, neo-Hookean hyperelastic material model for modeling such complex materials is analyzed. In uniaxial loading conditions, a stable regime producing unique solutions is found for $\nu_{0} < 0.296$. For larger values of $\nu_{0}$, multiple solutions are observed in a particular domain. This suggests the possibility of an unstable, but physically realizable, regime that may provide opportunities to leverage snap-through instabilities, which have been demonstrated to be useful in actuation with applications to soft robotics [46,47,48]. In the case of equibiaxial loading in plane stress, the nominal stress is unique for a given stretch; however, the stress-stretch relationship is not monotonic, just as it was not monotonic in the uniaxial loading case. In the case of uniaxial loading in plane strain the transverse stretch tends to a finite value $\lambda_{T} = 1/\sqrt 2$ and the axial nominal stress tends toward $- \infty$ as $\lambda$ approaches 0. This contrasts with the zero limit observed in uniaxial loading and in equibiaxial loading in plane stress. For uniaxial loading in plane strain, the numerical results for the transverse stress are not meaningful across all conditions, however. In particular, the limit value of the transverse stress at zero stretch is physically unrealistic for positive values of the ground-state Poisson’s ratio, and the transverse nominal stress in axial tension exhibits unrealistic characteristics at sufficiently large axial stretch values. Taken together, these observations place important bounds on the conditions under which such models produce physically meaningful results. The limit values of the transverse stretch, the nominal stress and the Cauchy stress are summarized in Fig. 11 for each loading case. The monotonicity of each result is also indicated in the table. Note that the Cauchy and nominal stress components, $\sigma_{22}$ and $P_{22}$, are equal in uniaxial loading with plane strain. This stress component tends to $+ \infty$ as $\lambda$ approaches 0, whereas the limit value is $0$ for $\lambda \to \infty$ as discussed in the previous section.

Fig. 11

Limit values and monotonicity of the solutions for each loading case. The following abbreviations are used: U (uniaxial loading), B (equibiaxial loading), UP (uniaxial loading in plane strain)

5 Conclusions

The standard version of the compressible, isotropic, neo-Hookean hyperelastic material model is considered in this paper. It is demonstrated that analytical, closed-form solutions for the model for transverse stretch and axial stress cannot be obtained for simple, homogenous deformation modes due to the highly nonlinear nature of the zero transverse stress constraints. The transverse stretch solutions are determined using numerical methods for the permitted values of material parameters. The results are presented with the help of the ground-state Poisson’s ratio, which has a practical and important physical meaning. The axial stress is calculated for the following homogeneous loading cases: uniaxial loading, equibiaxial loading (in plane stress) and uniaxial loading in plane strain. The characteristics of the model, including domains of non-unique behavior, are illustrated in a series of results and figure. Our results can be used in a parameter-fitting procedure to characterize the model in terms of experimental data. It is found that multiple solutions exist for the same applied longitudinal stretch in the uniaxial loading case in the compression regime for a specific range of the ground-state Poisson’s ratio and within a specific range of longitudinal stretch. The main results are summarized as follows: (a) Non-unique transverse stretch solutions are identified in uniaxial compression; (b) The domain for the unique solutions is identified; (c) Non-unique stress solutions are identified in uniaxial compression; (d) The particular values for the longitudinal stretch, where zero transverse strain is generated, are determined; (e) The numerical solutions for the nominal and Cauchy stresses are presented; (f) The ratio of the stresses in compressible and incompressible cases are obtained and presented; (g) The limit values for the stresses are determined in all loading modes; (h) A “snap-back” feature is identified in uniaxial compression.

Appendices

Appendices

1.1 Appendix 1: Results for the incompressible case

The strain energy in the incompressible case is defined as

$$U = \frac{G}{2}\left( {I_{1} - 3} \right).$$

(26)

The closed-form Cauchy stress solutions, including the added hydrostatic stress, are

$$\sigma_{U} = G\left( {\lambda^{2} - \lambda^{ - 1} } \right),\;\; \sigma_{B} = G\left( {\lambda^{2} - \lambda^{ - 4} } \right),$$

(27)

$$\sigma_{P} = G\left( {\lambda^{2} - \lambda^{ - 2} } \right),\;\; \sigma_{PC} = G\left( {1 - \lambda^{ - 2} } \right).$$

(28)

where $\sigma_{U}$, $\sigma_{B}$, $\sigma_{P}$ are the stresses in uniaxial loading, equibiaxial loading in plane stress and uniaxial loading in plane strain. The stress $\sigma_{P}$ is the axial stress while $\sigma_{PC}$ denotes the transverse stress in the direction of plane strain constraint. The limit value for $\sigma_{PC}$ is $G$ at $\lambda = \infty$.

The closed-form nominal stress solutions are given by formulae (29) and (30) and shown in Fig. 

Fig. 12

Nominal (a) and Cauchy (b) stresses for uniaxial loading, equibiaxial loading in plane stress and uniaxial loading in plane strain in the incompressible case

12

$$P_{U} = G\left( {\lambda - \lambda^{ - 2} } \right),\;\; P_{B} = G\left( {\lambda - \lambda^{ - 5} } \right),$$

(29)

$$P_{P} = G\left( {\lambda - \lambda^{ - 3} } \right),\;\; P_{PC} = G\left( {1 - \lambda^{ - 2} } \right).$$

(30)

1.2 Appendix 2: Linearized solutions in uniaxial loading

Inserting Eq. (15) in Eq. (13), we can express the Cauchy stress components as

$$\sigma_{11} = \frac{2}{3}G\left( {\lambda \lambda_{T}^{2} } \right)^{ - 5/3} \left( {\lambda^{2} - \lambda_{T}^{2} } \right) + K\left( {\lambda \lambda_{T}^{2} - 1} \right),$$

(31)

$$\sigma_{22} = \sigma_{33} = \frac{1}{3}G\left( {\lambda \lambda_{T}^{2} } \right)^{ - 5/3} \left( {\lambda_{T}^{2} - \lambda^{2} } \right) + K\left( {\lambda \lambda_{T}^{2} - 1} \right).$$

(32)

Linearization of these stress components are formulated as

$$\tilde{\sigma }_{11} = \frac{4}{3}G\left( {e - e_{T} } \right) + K\left( {e + 2e_{T} } \right),$$

(33)

$$\tilde{\sigma }_{22} = \frac{2}{3}G\left( {e_{T} - e} \right) + K\left( {e + 2e_{T} } \right),$$

(34)

where the engineering strains $e = \lambda - 1$ and $e_{T} = \lambda_{T} - 1$ are introduced for simplicity. The zero transverse stress constraint $\tilde{\sigma }_{22} = 0$ is solved for the transverse engineering strain, giving:

$$e_{T} = - \frac{3K - 2G}{{6K + 2G}}e = - \nu_{0} e.$$

(35)

The parameter $\nu_{0}$ denotes the ground-state Poisson’s ratio, which is related to the ratio of parameters $K$ and $G$ as

$$\frac{K}{G} = \frac{{2\left( {1 + \nu_{0} } \right)}}{{3\left( {1 - 2\nu_{0} } \right)}},\;\; \nu_{0} = \frac{3K/G - 2}{{6K/G + 2}}.$$

(36)

Insertion of the transverse strain Eq. (37) into Eq. (35) gives the stress along the loading direction:

$$\tilde{\sigma }_{11} = \frac{3KG}{{3K + G}}e = E_{0} e,$$

(37)

where $E_{0}$ represents the ground-state Young’s modulus. Combining Eq. (37) and Eq. (35), one finds that the material parameters in the CNH model are the ground-state shear and bulk moduli: $G = G_{0}$ and $K = K_{0}$. The dependence of the ratio $K/G$ on $\nu_{0}$ is visualized in Fig. 

Fig. 13

Ratio $K/G$ versus the ground-state Poisson’s ratio

13. The limit value for ratio $K/G$ is $0$ at $\nu_{0} = - 1$, whereas it is $\infty$ at $\nu_{0} = - 0.5$ (incompressible case).

Some numerical values are summarized in Table

Table 1 Some particular pairs for ratio $K/G$ and $\nu_{0}$

1. The value $\nu_{0} = 0.495$ (where $K/G$ is ~ 100) has a particular importance because ABAQUS/Standard recommends the use of solid continuum hybrid elements to avoid difficulties with convergence for materials with ground-state (or initial) Poisson’s ratio greater than this value. Furthermore, if the Poisson’s ratio is set to 0.5 (incompressible case) for an elastic material in ABAQUS/Standard, then the software changes it to $0.4999999$ (where $K/G$ is ~ $5 \times 10^{6}$).

1.3 Appendix 3: Cauchy stress solutions

Once the nominal stress components are obtained for the compressible cases, the Cauchy stress components are also calculated according to the formula in Eq. (14). The Cauchy stress $\sigma_{11}$ in uniaxial loading is shown in Fig. 

Fig. 14

a Cauchy stress $\sigma_{11}$ as a function of longitudinal stretch in uniaxial loading. b Biaxial Cauchy stress as a function of biaxial stretch in equibiaxial stretch in plane stress. c Axial Cauchy stress, $\sigma_{11}$, as a function of axial stretch in uniaxial loading in plane strain

14a for different values of $\nu_{0}$. The largest value for the ground-state Poisson’s ratio used in the plot is 0.4999 (red curve), whereas the smallest value is − 0.99 (purple curve). It can be observed there are domains on the compression side of Fig. 14a, where multiple Cauchy stress solutions exist for the same applied longitudinal stretch value. This plot reveals that if the longitudinal stretch is controlled monotonically, there will be a jump in Cauchy stress in compression in some cases as $\lambda$ is reduced. However, if the axial Cauchy stress is controlled, the behavior will be smooth and continuous in compression as far as $\lambda$ is concerned, although in some cases the material will go through a transient stage of incremental stretching even as the compressive stress magnitude is increased. It is also observed that the limit values for the Cauchy stress at $\lambda = 0$ is finite other than for the incompressible case. Due to quantum exclusion, a finite value for the Cauchy stress at $\lambda = 0$ is physically unrealistic. Numerical analysis reveals that the limiting value for $\sigma_{11}$ at $\lambda = 0$ in each case is exactly $- 3K$.

Cauchy stress results for equibiaxial loading in plane stress are plotted in Fig. 14b. The largest value for the ground-state Poisson’s ratio used in the plot is 0.49999 (red curve), whereas the smallest value is − 0.9999 (purple curve). It can be concluded that the equibiaxial Cauchy stress is unique for a given equibiaxial stretch. Similarly, the equibiaxial stretch is also unique for a given equibiaxial stress, i.e., the stress–stretch relationship is monotonic for the Cauchy stress. It is interesting to note that the limit Cauchy stress at $\lambda = 0$ is finite, as in the uniaxial loading case (see Fig. 14a). Numerical analysis reveals that the limiting value for $\sigma_{11} = \sigma_{22}$ at $\lambda = 0$ is exactly $- 3K/2$.

The axial Cauchy stress, $\sigma_{11}$, is shown in Fig. 13c as a function of the axial stretch in uniaxial loading in plane strain. The largest value for the ground-state Poisson’s ratio used in the plot is 0.49999 (red curve), whereas the smallest value is − 0.9999 (purple curve). These Cauchy stress versus stretch plots are monotonic and the stress tends toward $- \infty$ as $\lambda \to 0$. This limiting behavior is physically realistic.

The transverse Cauchy stress, $\sigma_{22}$, is identical to the transverse nominal stress, $P_{22}$, in uniaxial loading in plane strain. Therefore, the discussions and conclusions for the transverse nominal stress presented in Sect. 3.3 are also valid for the transverse Cauchy stress.