Fluid-filled toroidal membrane in contact with flat elastic substrate

Abstract

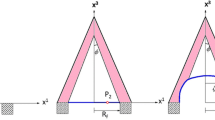
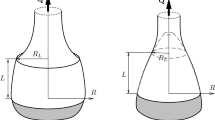
The present study aims to explore the contact mechanics of a fluid-filled toroidal hyperelastic membrane pressed against an elastic substrate. The deformable substrate is modeled as two flat elastic plates which are laterally pressed against the inflated torus. A stack of two bonded annular membranes is considered in the undeformed state, which results in toroidal topology upon internal pressurization. The air-inflated and liquid-filled membrane structure interaction with the elastic plate is studied under two different contact conditions: frictionless and no-slip contact. A variational formulation is adopted to obtain the equations of equilibrium of the membrane, and a numerical solution scheme coupled with an optimization technique is used with incremental step size. The pressing process is assumed to be quasi-static and axisymmetric. Frictionless contact allows the membrane material points to flow freely over the plate, thereby increasing the enclosed volume of the membrane during pressing. However, no-slip contact restricts the material point movement within the contact zone, and thus the volume of the membrane drops during contact. The contact stress generated in the elastic substrate and its indentation increase due to strain-hardening of the membrane. The plate indentation decreases due to increased stiffness, reducing the contact patch area. The force-displacement characteristics show a rapid increase in stiffness with increased plate displacement. Replacing the inflating air with liquid, the force required to maintain the contact is also found to increase for identical indentation levels.

A Appendix

The complete expressions for $F_1$ and $F_2$ of Eqs. (17) and (19) are given below.

$$\begin{aligned}&F_1(u_1,u_2,u_3,u_4,x,p)=A/B \\&F_2(u_1,u_2,u_3,u_4,x,p)=C/B \\&A=-u_{1}^3 x^2 \left( u_{2}^2+u_{4}^2\right) \left( \alpha u_{1}^2+x^2\right) \left( u_{1}^2 \left( u_{2}^2+u_{4}^2\right) ^3-x^2 \left( u_{2}^2-3 u_{4}^2\right) \right) A_1\\&\quad +4 u_{2} u_{4} \left( \alpha u_{1}^2 x^4+x^6\right) \left( u_{1} u_{2} (2 k (u_{3}-l) (H ({R_{0}} (u_{3}-l)))+p) + 4 u_{4} A_2 \right) \end{aligned}$$

Where,

$$\begin{aligned} A_1=&-\frac{u_{1} \left( u_{4} x (2 k (u_{3}-l) (H ({R_{0}} (u_{3}-l)))+p)+4 \alpha u_{2}^2-4 \alpha u_{4}^2-4\right) }{x}+\frac{4 \alpha u_{1}^2 u_{2}}{x^2}\\&+\frac{4 x^3 \left( -\alpha -\frac{1}{u_{2}^2+u_{4}^2}-\frac{2 u_{2}^2}{\left( u_{2}^2+u_{4}^2\right) ^2}\right) }{u_{1}^3}+\frac{12 u_{2} x^2}{u_{1}^2 \left( u_{2}^2+u_{4}^2\right) ^2}+4 u_{2} \left( \frac{\alpha }{\left( u_{2}^2+u_{4}^2\right) ^2}-1\right) , \end{aligned}$$

and

$$\begin{aligned} A_2\;\;\;=\;\;\;&\left( \frac{3 x^2}{u_{1}^2 \left( u_{2}^2+u_{4}^2\right) ^2}-\frac{2 u_{2} x^3}{u_{1}^3 \left( u_{2}^2+u_{4}^2\right) ^2}+\frac{\alpha u_{1}^2}{x^2}-\frac{2 \alpha u_{1} u_{2}}{x}+\frac{\alpha }{\left( u_{2}^2+u_{4}^2\right) ^2}-1\right) . \\ B\;\;\;=\;\;\;&4 u_{1} x \left( \alpha u_{1}^2+x^2\right) \left( -2 u_{1}^2 x^2 \left( u_{2}^2+u_{4}^2\right) ^2-u_{1}^4 \left( u_{2}^2+u_{4}^2\right) ^4+3 x^4\right) \\ C\;\;\;=\;\;\;&u_{1}^4 u_{2} x^3 \left( u_{2}^2+u_{4}^2\right) C_1-8 u_{2} u_{4} x^7 \left( 2 \alpha u_{2}^2+2 \alpha u_{4}^2+3\right) \\&-u_{1}^6 u_{2} x \left( u_{2}^2+u_{4}^2\right) ^4 (2 k x (u_{3}-l) (H (R_{0} (u_{3}-l)))+p x-8 \alpha u_{4})\\&-4 \alpha u_{1}^7 u_{4} \left( u_{2}^2+u_{4}^2\right) ^4+4 u_{1}^3 u_{4} x^4 \left( \alpha -8 u_{2}^2 u_{4}^2-4 u_{2}^4-4 u_{4}^4\right) \\&+4 u_{1}^5 u_{4} x^2 \left( u_{2}^2+u_{4}^2\right) ^4+8 u_{1}^2 u_{2} u_{4} x^5 \left( u_{2}^2+u_{4}^2\right) ^2+12 u_{1} u_{4} x^6, \end{aligned}$$

where

$$\begin{aligned} C_1=&-3 u_{2}^2 x (2 k (u_{3}-l) (H (R_{0} (u_{3}-l)))+p)+8 u_{4} \left( \alpha u_{2}^2+2\right) +8 \alpha u_{4}^3\\&-3 u_{4}^2 x (2 k (u_{3}-l) (H (R_{0} (u_{3}-l)))+p). \end{aligned}$$