An Anisotropic Hyperelastic Inflated Toroidal Membrane in Lateral Contact with Two Flat Rigid Plates

Abstract

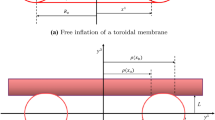
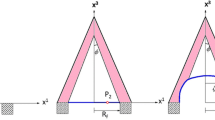
The present paper studies the contact problem of an inflated toroidal nonlinear anisotropic hyperelastic membrane laterally pressed between two flat rigid plates. The material is assumed to be homogeneous, and an anisotropic term is included in the incompressible Mooney–Rivlin hyperelastic model. Initially, two annular-shaped flat membranes, bonded at both equators, are considered in an undeformed state, which results in a toroidal geometry upon uniform internal pressurization. The contact problem of the inflated torus laterally pressed between two flat parallel plates is solved. Two different contact conditions, namely frictionless contact and no-slip contact, are considered within the contact region. The enclosed amount of gas within the inflated membrane is considered to be constant during the solution of the contact problem, which is solved in a quasi-static manner. In the case of no-slip contact, the stretch locking has been observed, and the frictionless contact causes the free flow of material points. The membrane’s stiffness increases with increasing anisotropic, material, and geometric parameters depicted in the force versus displacement curve under contact conditions.

Appendix A

The full expression of functions ${F}_{1}$ and ${F}_{2}$ applicable for free inflation and contact problem solution are given below

$$ F_{1} \left( {u_{1} ,u_{2} ,u_{4} ,x,p} \right) = A/B $$

(30)

$$ F_{2} \left( {u_{1} ,u_{2} ,u_{4} ,x,p} \right) = C/B $$

(31)

$$\begin{aligned} A & = - \left( {u_{1}^{6} x^{3} \left( {u_{2}^{2} + u_{4}^{2} } \right)\left( {2\zeta \left( {u_{2}^{2} + u_{4}^{2} } \right)^{3} \left( {u_{2}^{2} \left( {3pu_{4} x - 4\left( {\alpha + 2\alpha u_{4}^{2} + 1} \right)} \right) - \left( {3u_{4}^{2} - 1} \right)\left( { - pu_{4} x + 4\alpha u_{4}^{2} + 4} \right)\left. { + 4\alpha u_{2}^{4} } \right)} \right.} \right.} \right. \\ & \quad + 3pu_{2}^{4} u_{4}^{3} x + 3pu_{2}^{2} u_{4}^{5} x + 3\alpha pu_{2}^{2} u_{4} x + pu_{2}^{6} u_{4} x + 3\alpha pu_{4}^{3} x + pu_{4}^{7} x - 4\alpha ^{2} u_{2}^{4} + 4\alpha u_{2}^{8} + 4\alpha u_{2}^{2} - 16\alpha ^{2} u_{2}^{2} u_{4}^{2} + 8\alpha u_{2}^{6} u_{4}^{2} \\ & \quad \left. { - 8\alpha u_{2}^{2} u_{4}^{6} - 12u_{2}^{4} u_{4}^{2} - 12u_{2}^{2} u_{4}^{4} - 4u_{2}^{6} - 12\alpha ^{2} u_{4}^{4} - 4\alpha u_{4}^{8} - 12\alpha u_{4}^{2} - 4u_{4}^{6} } \right) + u_{1}^{4} x^{5} \left( {u_{2}^{2} + u_{4}^{2} } \right)\left( {3pu_{2}^{2} u_{4} x + 3pu_{4}^{3} x} \right. \\ & \quad \left. { + 4\alpha ^{2} \left( {u_{2}^{2} + u_{4}^{2} } \right)^{3} + 8\alpha \left( {u_{2}^{4} - u_{4}^{4} } \right) + 4u_{2}^{2} - 12u_{4}^{2} } \right) + \alpha u_{1}^{8} x\left( {u_{2}^{2} + u_{4}^{2} } \right)^{4} \left( {pu_{4} x + 4\alpha \left( {u_{2} - u_{4} } \right)\left( {u_{2} + u_{4} } \right) - 4} \right) \\ & \quad - 4\alpha ^{2} u_{1}^{9} u_{2} \left( {u_{2}^{2} + u_{4}^{2} } \right)^{4} + 4u_{1}^{5} u_{2} x^{4} \left( {\alpha ^{2} - 4\alpha u_{2}^{4} + 4\zeta \left( {u_{2}^{2} + u_{4}^{2} - 1} \right)\left( {u_{2}^{2} + u_{4}^{2} } \right)^{2} \left( {\left( {u_{2}^{2} + u_{4}^{2} } \right)^{2} - \alpha } \right)} \right. \\ & \quad \left. { - 8\alpha u_{2}^{2} u_{4}^{2} + 4\zeta ^{2} \left( {u_{2}^{2} + u_{4}^{2} - 1} \right)^{2} \left( {u_{2}^{2} + u_{4}^{2} } \right)^{4} + 4u_{2}^{6} u_{4}^{2} + 6u_{2}^{4} u_{4}^{4} + 4u_{2}^{2} u_{4}^{6} + u_{2}^{8} - 4\alpha u_{4}^{4} + u_{4}^{8} } \right) \\ & \quad + 4u_{1}^{2} x^{7} \left( { - \alpha ^{2} u_{2}^{4} + \alpha u_{2}^{8} - 3\alpha u_{2}^{2} } \right. + 2\alpha ^{2} u_{2}^{2} u_{4}^{2} + 2\zeta \left( {u_{2}^{2} + u_{4}^{2} } \right)^{2} \left( {\alpha \left( {u_{2}^{2} + 3u_{4}^{2} - 1} \right)\left( {u_{2}^{2} + u_{4}^{2} } \right)^{2} } \right. \\ & \quad \left. { + 3\left( {u_{2}^{2} + u_{2} + u_{4}^{2} } \right)\left( {\left( {u_{2} - 1} \right)u_{2} + u_{4}^{2} } \right) - u_{4}^{2} } \right) + 4\alpha u_{2}^{6} u_{4}^{2} + 6\alpha u_{2}^{4} u_{4}^{4} + 4\alpha u_{2}^{2} u_{4}^{6} + 7u_{2}^{4} u_{4}^{2} \\ & \quad \left. {\left. { + 5u_{2}^{2} u_{4}^{4} + 3u_{2}^{6} + 3\alpha ^{2} u_{4}^{4} + \alpha u_{4}^{8} + 3\alpha u_{4}^{2} + u_{4}^{6} } \right) + 16u_{1}^{3} u_{2} x^{6} \left( {\alpha - \left( {u_{2}^{2} + u_{4}^{2} } \right)^{2} \left( {2\zeta \left( {u_{2}^{2} + u_{4}^{2} - 1} \right) + 1} \right)} \right)} \right) \\ & \quad \left. { + 12u_{1} u_{2} x^{8} + 4x^{9} \left( { - \alpha u_{2}^{4} + u_{2}^{2} \left( {2\alpha u_{4}^{2} - 3} \right) + 3\left( {\alpha u_{4}^{4} + u_{4}^{2} } \right)} \right)} \right) \\ \end{aligned}$$

(32)

$$B=4{u}_{1}x\left(\alpha {u}_{1}^{4}{\left({u}_{2}^{2}+{u}_{4}^{2}\right)}^{2}+{u}_{1}^{2}{x}^{2}\left({\left({u}_{2}^{2}+{u}_{4}^{2}\right)}^{2}\left(2\zeta \left({u}_{2}^{2}+{u}_{4}^{2}-1\right)+1\right)-\alpha \right)-{x}^{4}\right)\left(\alpha {u}_{1}^{4}{\left({u}_{2}^{2}+{u}_{4}^{2}\right)}^{2}+{u}_{1}^{2}{x}^{2}\left(3\alpha +{\left({u}_{2}^{2}+{u}_{4}^{2}\right)}^{2}\left(\zeta \left(6{u}_{2}^{2}+6{u}_{4}^{2}-2\right)+1\right)\right)+3{x}^{4}\right)$$

(33)

$$ \begin{aligned} C & = - \left( {pu_{1}^{4} u_{2} x^{2} \left( {u_{2}^{2} + u_{4}^{2} } \right)^{2} \left( { - \left( {\alpha u_{1}^{2} + x^{2} } \right)\left( {u_{1}^{2} \left( {u_{2}^{2} + u_{4}^{2} } \right)^{2} + 3x^{2} } \right) - 2\zeta u_{1}^{2} x^{2} \left( {u_{2}^{2} + u_{4}^{2} } \right)^{2} \left( {3u_{2}^{2} + 3u_{4}^{2} - 1} \right)} \right)} \right. \\ & \quad + 4u_{4} \left( {\alpha ^{2} u_{1}^{9} \left( { - \left( {u_{2}^{2} + u_{4}^{2} } \right)^{4} } \right) + u_{1}^{5} x^{4} \left( {\alpha ^{2} - 4\alpha u_{2}^{4} + 4\zeta \left( {u_{2}^{2} + u_{4}^{2} - 1} \right)\left( {u_{2}^{2} + u_{4}^{2} } \right)^{2} \left( {\left( {u_{2}^{2} + u_{4}^{2} } \right)^{2} - \alpha } \right)} \right.} \right. \\ & \quad \left. { - 8\alpha u_{2}^{2} u_{4}^{2} + 4\zeta ^{2} \left( {u_{2}^{2} + u_{4}^{2} - 1} \right)^{2} \left( {u_{2}^{2} + u_{4}^{2} } \right)^{4} + 4u_{2}^{6} u_{4}^{2} + 6u_{2}^{4} u_{4}^{4} + 4u_{2}^{2} u_{4}^{6} + u_{2}^{8} - 4\alpha u_{4}^{4} + u_{4}^{8} } \right) + 2u_{1}^{2} u_{2} x^{7} \left( {\left( {u_{2}^{2} + u_{4}^{2} } \right)} \right. \\ & \quad \left. {\left( { - 2\alpha ^{2} - 2\zeta \left( {u_{2}^{2} + u_{4}^{2} } \right)\left( {\alpha \left( {u_{2}^{2} + u_{4}^{2} } \right)^{2} + 1} \right) + u_{2}^{2} + u_{4}^{2} } \right) - 3\alpha } \right) + 2u_{1}^{6} u_{2} x^{3} \left( {u_{2}^{2} + u_{4}^{2} } \right)\left( {2\zeta \left( {u_{2}^{2} + u_{4}^{2} } \right)^{3} \left( {\alpha \left( {2u_{2}^{2} + 2u_{4}^{2} - 1} \right) + 1} \right)} \right. \\ & \quad \left. { + \alpha \left( {\alpha \left( {u_{2}^{2} + u_{4}^{2} } \right) + \left( {u_{2}^{2} + u_{4}^{2} } \right)^{3} + 2} \right)} \right) + 4u_{1}^{3} x^{6} \left( {\alpha - \left( {u_{2}^{2} + u_{4}^{2} } \right)^{2} \left( {2\zeta \left( {u_{2}^{2} + u_{4}^{2} - 1} \right) + 1} \right)} \right) \\ & \quad \left. {\left. { + 4u_{1}^{4} u_{2} x^{5} \left( {u_{2}^{2} + u_{4}^{2} } \right)\left( {\alpha \left( {u_{2}^{2} + u_{4}^{2} } \right) + 1} \right) + 2\alpha ^{2} u_{1}^{8} u_{2} x\left( {u_{2}^{2} + u_{4}^{2} } \right)^{4} + 3u_{1} x^{8} - 2u_{2} x^{9} \left( {2\alpha \left( {u_{2}^{2} + u_{4}^{2} } \right) + 3} \right)} \right)} \right) \\ \end{aligned} $$

(34)