1 Introduction

In the last decades, fractional calculus has become a powerful mathematical tool to model a lot of physical processes. Because of the nature of fractional derivatives (nonlocal operators), they are especially used in describing nonlocal and multiscale phenomena. In this regard, we refer the reader works on the following topics: viscoelastic materials [6, 23, 28], heat conduction [24, 40, 54, 56], diffusion processes in complex systems [12, 30, 32], nonlocal constitutive laws [13, 19, 46], microscopic interaction forces [18, 25], nonlocal stress-strain constitutive relations [3], nonlocal beams [2, 8, 10, 41, 47]. A fairly broad overview of various aspects of fractional calculus applications can be found in the review paper by Failla and Zingales [20].

Notwithstanding this branch of mathematics is not new (the creation of fractional calculus dates back to the birth of the classical theory of differential calculus [27]) there are still remain a lot of problems that require attention. In particular, the branch of fractional calculus, that is devoted to differential equations containing simultaneously both the left and right fractional derivatives, is a research area where exists a large number of an unsolved/unexplored issues [15, 21, 29]. No exact solutions, for many of the aforementioned equations, have been found till now. For this reason, many researchers focus their attention on approximate solutions of equations containing various types of combinations of fractional derivatives. For this reason, many researchers focus their attention on approximate solutions of equations containing various types of combinations of fractional derivatives [1, 7, 11, 14, 22, 53].

On the other hand, certain types of phenomena in physics are better depicted when the order of the fractional operator is variable (it depends on the spatial or time variable) [26, 43]. Promising approaches have been presented in papers where authors studied: diffusion processes in an inhomogeneous and heterogeneous medium [16, 33, 44, 49,50,51, 55], control theory [17, 34, 35], mechanics [4, 31, 36, 38, 39, 42]. More details of the available applications of a variable order fractional calculus in the area of scientific and engineering modelling are presented in the following review papers: [37, 52].

In this paper we focus on the Riesz-Caputo fractional operator of variable order with fixed memory and its application in a strong form of the space-fractional continuum (1D case), which is just a straightforward extension of the results presented in [45]. Such approach allows, when adopted to the mechanical applications, for clear physical interpretation and moreover gives smooth passage to classical approach as a limit case [5, 48]. We propose three methods, based on polynomial interpolation, to approximation of the studied fractional operator. All presented numerical sachems were implemented in Python using library for real and complex floating-point arithmetic with arbitrary precision (http://mpmath.org/).

2 Approximation of the Riesz-Caputo fractional derivative with variable order

Let us consider the following Riesz-Caputo fractional derivative of variable order with \(\alpha\) depending on space variable

$$\begin{aligned}&^{RC}_{x-\ell }D^{\alpha (x)}_{x+\ell } f(x)=\frac{1}{2}(^C_{x-\ell }D^{\alpha (x)}_x f(x) +\nonumber \\&\quad (-1)^{n}{}^{C} _{x} D^{\alpha (x)}_{x+\ell } f(x)) \end{aligned}$$
(1)

Operators \(^C_{x-l}D^{\alpha (x)}_x\) and \(^C_{x}D^{\alpha (x)}_{x+\ell }\) are well known fractional Caputo derivatives, with fixed memory length \(\ell\) and variable order \(\alpha (x)>0\), defined as

$$\begin{aligned}&^C_{x-l}D^{\alpha (x)}_x f(x)\nonumber \\&\quad =\frac{1}{\varGamma (n-\alpha (x))}\int _{x-l}^x (x-\tau )^{n-\alpha (x)-1}f^{(n)}(\tau )d\tau \end{aligned}$$
(2)
$$\begin{aligned}&^C_{x}D^{\alpha (x)}_{x+\ell } f(x)\nonumber \\&\quad =\frac{(-1)^n}{\varGamma (n-\alpha (x))}\int _{x}^{x+\ell } (\tau -x)^{n-\alpha (x)-1}f^{(n)}(\tau )d\tau \end{aligned}$$
(3)

where \(n-1<\alpha (x)<n\).

In following, based on our previous work [9] where the numerical schemes for differential operators of constant order \(\alpha\) were developed, we elaborate the algorithms for the Riesz-Caputo derivative of variable order. For discretisation, we generate the grid of \((N+1)\) – equidistant nodes: \({x_{0}}< \ldots< {x_{i - m}}< {x_{i - m + 1}}< \ldots< {x_i}< \ldots< {x_{i + m - 1}}< {x_{i + m}}< \ldots < {x_{N}}\) where \({x_i} = {x_0} + i\varDelta x\), \(m = \ell /\varDelta x\) and \(\varDelta x = \left( {{x_N} - {x_0}} \right) /N\). Moreover, we introduce the following notation: \(f\left( {{x_i}} \right) = {f_i}\), \({f^{\left( n \right) }}\left( {{x_i}} \right) = f_i^{\left( n \right) }\), and \(\alpha \left( x_i\right) =\alpha _i\).

2.1 Method I: Approximation based on piecewise constant interpolation

$$\begin{aligned}&{\left. ^{RC}_{x-\ell }D^{\alpha (x)}_{x+\ell } f(x) \right| _{x = {x_i}}}\nonumber \\&\quad \approx ~\frac{1}{2}\left( \sum \limits _{k = i - m + 1}^i {f_k^{\left( n \right) }p_{i,k - 1}} + \sum \limits _{k = i}^{i + m - 1} {f_k^{\left( n \right) }q_{i,k}} \right) \end{aligned}$$
(4)

where

$$\begin{aligned} p_{i,k} = \frac{{{{\left( {\varDelta x} \right) }^{n - \alpha _i }}}}{{\varGamma \left( {n - \alpha _i + 1 } \right) }}\left[ {{{\left( {i - k} \right) }^{n - \alpha _i }} - {{\left( {i - k - 1} \right) }^{n - \alpha _i }}} \right] \end{aligned}$$
(5)

and

$$\begin{aligned} q_{i,k} = \frac{{{{\left( {\varDelta x} \right) }^{n - \alpha _i }}}}{{\varGamma \left( {n - \alpha _i + 1} \right) }}\left[ { {{\left( {k - i + 1} \right) }^{n - \alpha _i }} - {{\left( {k - i} \right) }^{n - \alpha _i }} } \right] \end{aligned}$$
(6)

2.2 Method II: Approximation based on piecewise linear interpolation

$$\begin{aligned}&{\left. ^{RC}_{x-\ell }D^{\alpha (x)}_{x+\ell } f(x) \right| _{x = {x_i}}}\nonumber \\&\quad \approx ~\frac{1}{2}\left( \sum \limits _{k = i - m}^i {f_k^{\left( n \right) }r_{i,k}} + \sum \limits _{k = i}^{i + m} {f_k^{\left( n \right) }s_{i,k}} \right) \end{aligned}$$
(7)

where

$$\begin{aligned}&r_{i,k} = \frac{{{{\left( {\varDelta x} \right) }^{n - \alpha _i }}}}{{\varGamma \left( {n - \alpha _i +2} \right) }} \nonumber \\&\times \left\{ {\begin{array}{*{20}{c}} {{{\left( {m - 1} \right) }^{n - \alpha _i +1}} + \left( {n - \alpha _i - m +1} \right) {m^{n - \alpha _i }}} &{} {\mathrm{{for}}\,k = i - m} \\ {{{\left( {i - k + 1} \right) }^{n - \alpha _i +1}} - 2{{\left( {i - k} \right) }^{n - \alpha _i +1}} + {{\left( {i - k - 1} \right) }^{n - \alpha _i + 1}}} &{} {\mathrm{{for}}\,k = i - m + 1 \ldots i - 1} \\ 1 &{} {\mathrm{{for}}\,k = i } \\ \end{array}} \right. \end{aligned}$$
(8)

and

$$\begin{aligned}&s_{i,k} = \frac{{ {{\left( {\varDelta x} \right) }^{n - \alpha _i }}}}{{\varGamma \left( {n - \alpha _i + 2} \right) }} \nonumber \\&\times \left\{ {\begin{array}{*{20}{c}} {{{\left( {m - 1} \right) }^{n - \alpha _i +1}} + \left( {n - \alpha _i - m + 1} \right) {m^{n - \alpha _i }}} &{} {\mathrm{{for}}\,k = i + m} \\ {{{\left( {k - i + 1} \right) }^{n - \alpha _i + 1}} - 2{{\left( {k - i} \right) }^{n - \alpha _i + 1}} + {{\left( {k - i - 1} \right) }^{n - \alpha _i +1}}} &{} {\mathrm{{for}}\,k = i + 1 \ldots i + m - 1} \\ 1 &{} {\mathrm{{for}}\,k = i } \\ \end{array}} \right. \end{aligned}$$
(9)

2.3 Method III: Approximation based on piecewise quadratic interpolation

$$\begin{aligned}&{\left. ^{RC}_{x-\ell }D^{\alpha (x)}_{x+\ell } f(x) \right| _{x = {x_i}}}\approx ~ \frac{1}{2}\left( \varDelta x\right) ^{n-\alpha _i} \nonumber \\&\times \left\{ \begin{array}{ll} \sum \limits _{k=-1}^{1} f_{i+k}^{\left( n \right) }u_k + \sum \limits _{k=i-m}^{i-1}f_k^{\left( n \right) }w_{i,k} + \sum \limits _{k=-1}^{1}f_{i-k}^{\left( n \right) }u_k + \sum \limits _{k=i+1}^{i+m}f_k^{\left( n \right) }v_{i,k} &{} \text {for odd } m\\ \sum \limits _{k=i-m}^{i} f_k^{\left( n \right) }w_{i,k} + \sum \limits _{k=i}^{i+m} f_k^{\left( n \right) }v_{i,k}&{} \text {for even } m \end{array} \right. \end{aligned}$$
(10)

where

$$\begin{aligned}&w_{i,k} = \nonumber \\&\left\{ {\begin{array}{*{20}{c}} \begin{array}{l} \frac{{{m^{n - \alpha _i + 2}} - {{(m - 2)}^{n - \alpha _i + 2}}}}{{\varGamma (n - \alpha _i + 3)}} - \frac{{3{m^{n - \alpha _i + 1}} + {{(m - 2)}^{n - \alpha _i + 1}}}}{{2\varGamma (n - \alpha _i + 2)}} \\ + \frac{{{m^{n - \alpha _i }}}}{{\varGamma (n - \alpha _i + 1)}} \\ \end{array} &{} \begin{array}{l} \\ {\hbox { for}\ k = i - m} \\ \end{array} \\ \begin{array}{l} - 2\frac{{{{(i - k + 1)}^{n - \alpha _i + 2}} - {{(i - k - 1)}^{n - \alpha _i + 2}}}}{{\varGamma (n - \alpha _i + 3)}} \\ + 2\frac{{{{(i - k + 1)}^{n - \alpha _i + 1}} + {{(i - k - 1)}^{n - \alpha _i + 1}}}}{{\varGamma (n - \alpha _i + 2)}} \\ \end{array} &{} \begin{array}{l} \\ {\hbox { for odd}\ k + i - m} \\ \end{array} \\ \begin{array}{l} \frac{{{{(i - k + 2)}^{n - \alpha _i + 2}} - {{(i - k - 2)}^{n - \alpha _i + 2}}}}{{\varGamma (n - \alpha _i + 3)}} \\ - \frac{{{{(i - k + 2)}^{n - \alpha _i + 1}} + 6{{(i - k)}^{n - \alpha _i + 1}} + {{(i - k - 2)}^{n - \alpha _i + 1}}}}{{2\varGamma (n - \alpha _i + 2)}} \\ \end{array} &{} \begin{array}{l} \\ {\hbox {for even}\ k + i - m\ \hbox {and}\ k < i - 1} \\ \end{array} \\ {\frac{{{2^{n - \alpha _i + 2}}}}{{\varGamma (n - \alpha _i + 3)}} - \frac{{{2^{n - \alpha _i + 1}}}}{{2\varGamma (n - \alpha _i + 2)}}} &{} {{\hbox {for even}\ m\ \hbox {and}\ k = i}} \\ {\frac{{{3^{n - \alpha _i + 2}} - 1}}{{\varGamma (n - \alpha _i + 3)}} - \frac{{{3^{n - \alpha _i + 1}} + 3}}{{2\varGamma (n - \alpha _i + 2)}} - \frac{1}{{\varGamma (n - \alpha _i + 1)}}} &{} {{\hbox {for odd}\ m\ \hbox {and}\ k = i - 1}} \\ \end{array}} \right. \end{aligned}$$
(11)

and

$$\begin{aligned}&v_{i,k} = \nonumber \\&\left\{ {\begin{array}{*{20}{c}} \begin{array}{l} \frac{{{m^{n - \alpha _i + 2}} - {{(m - 2)}^{n - \alpha _i + 2}}}}{{\varGamma (n - \alpha _i + 3)}} - \frac{{3{m^{n - \alpha _i + 1}} + {{(m - 2)}^{n - \alpha _i + 1}}}}{{2\varGamma (n - \alpha _i + 2)}} \\ + \frac{{{m^{n - \alpha _i }}}}{{\varGamma (n - \alpha _i + 1)}} \\ \end{array} &{} \begin{array}{l} \\ \hbox { for}\ k = i + m \\ \end{array} \\ \begin{array}{l} - 2\frac{{{{(k - i + 1)}^{n - \alpha _i + 2}} - {{(k - i - 1)}^{n - \alpha _i + 2}}}}{{\varGamma (n - \alpha _i + 3)}} \\ + 2\frac{{{{(k - i + 1)}^{n - \alpha _i + 1}} + {{(k - i - 1)}^{n - \alpha _i + 1}}}}{{\varGamma (n - \alpha _i + 2)}} \\ \end{array} &{} \begin{array}{l} \\ \hbox { for odd}\ k + i + m \\ \end{array} \\ \begin{array}{l} \frac{{{{(k - i + 2)}^{n - \alpha _i + 2}} - {{(k - i - 2)}^{n - \alpha _i + 2}}}}{{\varGamma (n - \alpha _i + 3)}} \\ - \frac{{{{(k - i + 2)}^{n - \alpha _i + 1}} + 6{{(k - i)}^{n - \alpha _i + 1}} + {{(k - i - 2)}^{n - \alpha _i + 1}}}}{{2\varGamma (n - \alpha _i + 2)}} \\ \end{array} &{} \begin{array}{l} \\ {\hbox {for even}\ k + i + m\ \hbox {and}\ k > i + 1} \\ \end{array} \\ {\frac{{{2^{n - \alpha _i + 2}}}}{{\varGamma (n - \alpha _i + 3)}} - \frac{{{2^{n - \alpha _i + 1}}}}{{2\varGamma (n - \alpha _i + 2)}}} &{} \hbox {for even}\ m\ \hbox {and}\ k = i \\ {\frac{{{3^{n - \alpha _i + 2}} - 1}}{{\varGamma (n - \alpha _i + 3)}} - \frac{{{3^{n - \alpha _i + 1}} + 3}}{{2\varGamma (n - \alpha _i + 2)}} - \frac{1}{{\varGamma (n - \alpha _i + 1)}}} &{} \hbox { for odd}\ m\ { and} \ k = i + 1 \\ \end{array}} \right. \end{aligned}$$
(12)

with

$$\begin{aligned} u_{-1}&=\frac{2(n-\alpha _i)^2+3(n-\alpha _i)}{2\varGamma (n-\alpha _i+3)} \\ u_{0}&=\frac{2+2(n-\alpha _i)}{\varGamma (n-\alpha _i+3)} \\ u_{1}&=\frac{-(n-\alpha _i)}{2\varGamma (n-\alpha _i+3)} \end{aligned}$$

3 Numerical analysis: errors and experimental rates of convergence

In this subsection, we report on a few numerical examples for checking the accuracy of the presented methods. Algebraic problems given by Eqs. (4), (7), and (10) were built using original procedures developed by the authors in Python.

Figure 1 shows graphs of approximations of the Riesz-Caputo derivative of functions \(x^2\), \(\exp x\), \(\sin x\), and \(\cos x\) for space-dependent orders \(\alpha \left( x\right) =\frac{1}{2}+\frac{x}{2}\) and \(\alpha \left( x\right) =1-\frac{x}{2}\). The calculations presented on the plots have been performed for \(N=2000\) and \(\ell = 0.2\).

Fig. 1
figure 1

Approximations of the Riesz-Caputo derivative of functions \(x^2\), \(\exp x\), \(\sin x\) and \(\cos x\) for space-dependent order \(\alpha \left( x\right) =\frac{1}{2}+\frac{x}{2}\) and \(\alpha \left( x\right) =1-\frac{x}{2}\)

Full size image

In Tables 1, 2, and 3 we present the absolute errors of numerical calculations carried out using the proposed methods (Method I, Method II, and Method III) for the following functions:

  • \(f\left( x\right) =\exp \left( x\right)\) and \(\alpha \left( x\right) =\exp \left( -x\right)\) (Table 1),

  • \(f\left( x\right) =\exp \left( x\right)\) and \(\alpha \left( x\right) =\frac{1+x^2}{2}\) (Table 2),

  • \(f\left( x\right) =\exp \left( x\right)\) and \(\alpha \left( x\right) =\sin \left( x\right) +1\) (Table 3).

The reported errors have been determined by comparing numerical results with exact values (using series representation of the Riesz-Caputo derivative [9]). We take a particular value of the Riesz-Caputo operator and compare it with a value received from the series at the same specific point. In this case, for each node \(x_i\) the order of derivative has the form \(\alpha \left( x_i\right)\) and is an established number (the order \(\alpha\) is constant for each node \(x_i\)). Moreover, all tables contain the experimental rates of convergence for each proposed method.

Table 1 Errors and experimental rates of convergence for the approximation of the Riesz-Caputo derivative of function \(f\left( x\right) =\exp \left( x\right)\) for variable order \(\alpha \left( x\right) =\exp \left( -x\right)\)
Full size table
Table 2 Errors and experimental rates of convergence for the approximation of the Riesz-Caputo derivative of function \(f\left( x\right) =\exp \left( x\right)\) for variable order \(\alpha \left( x\right) =\frac{1+x^2}{2}\)
Full size table
Table 3 Errors and experimental rates of convergence for the approximation of the Riesz-Caputo derivative of function \(f\left( x\right) =\exp \left( x\right)\) for variable order \(\alpha \left( x\right) =\sin \left( x\right) +1\)
Full size table

Analysing results presented in tables, one can observe that the convergence is the fastest for the piecewise quadratic interpolation (scheme 10), a little slower in case of the piecewise linear interpolation (scheme 7) and the slowest for the piecewise constant interpolation (scheme 4). Additionally, the errors generated by Method I are the biggest one, while for Method III are the smallest one.

4 Application of Riesz-Caputo derivative of variable order for the space-fractional continuum mechanics - numerical study

In this section we present the application of the Riesz-Caputo fractional derivative of variable order in continuum mechanics. We consider one-dimensional tension problem of the space-fractional continua in the following form [46]:

$$\begin{aligned} \frac{\partial }{\partial x}\left( \ell ^{\alpha (x)-1}\varGamma \left( 2-\alpha (x)\right) {}^{RC}_{x-\ell }D^{\alpha (x)}_{x+\ell } f(x) \right) +\frac{b}{E}=0 \end{aligned}$$
(13)

with Dirichlet’s boundary conditions

$$\begin{aligned} \left\{ \begin{array}{ll} f(0)=0 \\ f(l)=0.01l \end{array} \right. \end{aligned}$$
(14)

where \(\frac{b}{E}=0.1\) and \(l=1\). In Eq. (18), x denotes spatial variable, \(\ell\) is the length scale, f denotes the displacements, b is the body force, and E stands for the Young modulus.

We start from introducing the spatial discretization for the analysed one-dimensional continuum body that is presented in Fig. 2.

Fig. 2
figure 2

Spatial discretization for one-dimensional fractional continuum body

Full size image

Discrete form of the fractional operator \(\frac{\partial }{\partial x}\left( \ell ^{\alpha (x)-1}\varGamma \left( 2-\alpha (x)\right) {}^{RC}_{x-\ell }D^{\alpha (x)}_{x+\ell } f(x) \right)\) can be described by the trapezoidal formula (Method II) as:

$$\begin{aligned}&{\left. \dfrac{\partial }{\partial x}\left( \ell ^{\alpha (x)-1}\varGamma \left( 2-\alpha (x)\right) {}^{RC}_{x-\ell }D^{\alpha (x)}_{x+\ell } f(x) \right) \right| _{x = {x_i}}}\nonumber \\&\quad \approx \dfrac{\varGamma \left( 2-\alpha _i\right) \ell ^{\alpha _{i}-1}}{2\varDelta x} \nonumber \\&\times \left( \sum \limits _{k = i - m}^i {f'_k r_{i,k}} + \sum \limits _{k = i}^{i + m} {f'_k s_{i,k}} \right. \nonumber \\&\quad \left. -\sum \limits _{k = i - m-1}^{i-1} {f'_k r_{i-1,k}} - \sum \limits _{k = i-1}^{i + m-1} {f'_k s_{i-1,k}} \right) \end{aligned}$$
(15)

Next, after applying the backward difference formula, for the first order derivative, in Eq. (15) we obtain:

$$\begin{aligned}&{\left. \dfrac{\partial }{\partial x}\left( \ell ^{\alpha (x)-1}\varGamma \left( 2-\alpha (x)\right) {}^{RC}_{x-\ell }D^{\alpha (x)}_{x+\ell } f(x) \right) \right| _{x = {x_i}}} \nonumber \\&\quad \approx \dfrac{\varGamma \left( 2-\alpha _i\right) \ell ^{\alpha _{i}-1}}{2(\varDelta x)^2} \nonumber \\&\times \left( \sum \limits _{k = i - m}^i {((f_{k+1}-f_k ) r_{i,k})} + \sum \limits _{k = i}^{i + m} {((f_{k+1}-f_k) s_{i,k})} \right. \nonumber \\&\left. - \sum \limits _{k = i - m-1}^{i-1} {((f_{k+1}-f_k) r_{i-1,k})} - \sum \limits _{k = i-1}^{i + m-1} {((f_{k+1}-f_k) s_{i-1,k})} \right) \end{aligned}$$
(16)

Finally, the following system of linear equations equations can be formulated:

$$\begin{aligned}&\left\{ \begin{array}{ll} f_0=0 \\ \sum \limits _{k = i - m}^i {((f_{k+1}-f_k ) r_{i,k})} + \sum \limits _{k = i}^{i + m} {((f_{k+1}-f_k) s_{i,k})} \\ - \sum \limits _{k = i - m-1}^{i-1} {((f_{k+1}-f_k) r_{i-1,k})} - \sum \limits _{k = i-1}^{i + m-1} {((f_{k+1}-f_k) s_{i-1,k})}=\frac{-b}{F E} \\ f_n=0.01l \end{array} \right. \end{aligned}$$
(17)

where

$$\begin{aligned} F= \dfrac{\varGamma \left( 2-\alpha _i\right) \ell ^{\alpha _{i}-1}}{2(\varDelta x)^2} \end{aligned}$$

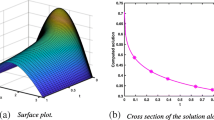
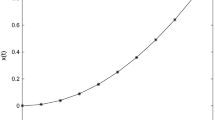
The system (17) (containing \(N+1\) equations) has been solved for two types of function \(\alpha\), namely \(\alpha \left( x\right) =\frac{1}{2}+\frac{x}{2}\) and \(\alpha \left( x\right) =1-\frac{x}{2}\) and the following parameters: \(N=200\) and \(\ell \in \{0.01;0.1;0.2;0.4\}\). The obtained results are presented in Fig. 3.

Fig. 3
figure 3

The comparison of displacements through the length of the body for variable order \(\alpha \left( x\right) =\frac{1}{2}+\frac{x}{2}\) (left side) and \(\alpha \left( x\right) =1-\frac{x}{2}\) (right side), and \(\ell \in \{0.01;0.1;0.2;0.4\}\)

Full size image

The analysis of Fig. 3 allows us to draw the conclusion that the deformation of the space-fractional continuum body solely depends on the length scale \(\ell\) and the order \(\alpha\). Moreover, the introduction of variable order of fractional continua makes the model more flexible, thus in perspective validation of this model with experimental data should be easier.

5 Conclusions

The approximation of the Riesz-Caputo fractional derivative of variable order and with fixed memory can be elaborated using different approaches. Herein, three original methods are considered based on the polynomial interpolation: piecewise constant (Method I), piecewise linear (Method II), and piecewise quadratic (Method III) interpolation. As presented, the convergence is the fastest for Method III, a little slower in case of Method II and the slowest for Method I. Moreover, the errors generated by Method I are the biggest one, while for Method III are the smallest one. Finally, the presented schemes can be directly applied for modelling of scale effect is terms of space-fractional continuum mechanics, making its ability to mimic experimental results higher.