1 Introduction

Although the origin of higher order continuum theories can be found in the second part of nineteenth century and in the beginning of twentieth century, the explosive growth of the application of nanostructures in several scientific and technological fields has renewed the interest on developing this kind of approaches. The reasons can be found in: (i) the impossibility to address with the classical approaches (scale-free) the size effect, which commonly appears in nanotechnology applications; (ii) the lower computational cost in comparison to molecular dynamic techniques.

In the last 15 years, the most widely used generalized continuum approaches to address mechanical problems at nanoscale are the modified strain gradient elasticity theory and the nonlocal elasticity frameworks. The modified strain gradient theory [1] is based in previous formulations by Mindlin [2] and Fleck and Hutchinson [3], and only three size-dependent constants are needed for the case of linear isotropic elastic materials. Thai et al. [4] recently published relevant examples of the application of this theory to the analysis of the mechanical behaviour of nanostructures. Moreover, it is worth to cite the works by Morassi and coworkers [5,6,7,8,9] to address problems related with nanosensors. Other widely used approaches to address the mechanical behaviour of nanomechanical systems fall into the nonlocal continuum mechanics framework. The bases of the theory were formulated by different authors in the 60s of the twentieth century [10,11,12]. Some time later, an integral constitutive model valid for linear isotropic elastic materials was proposed by Eringen et al. [13,14,15,16]. The main characteristics of the so called strain-driven nonlocal elasticity is that the stress at any point of the domain depends on the strain at each point in the solid through a convolution integral with a smoothing kernel. The nonlocal constitutive equation can be written in differential form, if a Helmholtz-type kernel is used in the integral formulation [16]. Based on this transformation, the differential approach has been widely used in a very large numbers of papers, starting with the work of Peddieson et al. [17]. The reader can found more details on the application of this differential model in the reviews recently published by Eltaher et al. [18], Rafii-Tabar et al. [19], and Thai et al. [4]. However, Romano et al. [20] recently pointed out that the pure nonlocal strain-driven elasticity theory leads to problems with no solution in general, due to the ill-posedness of the model. The reason is the requirement to accomplish additional boundary conditions related to the integral nature of the constitutive equations. To overcome these drawbacks, several alternatives have been developed inside the framework of nonlocal theories. Romano et al. [21] proposed the so-called stress-driven nonlocal model, in which the elastic strain at a certain point in the solid is related to the stress at all points of the domain by a convolution integral with a smoothing kernel of the Helmholtz-type. This approach allows to obtain consistent solutions corresponding to the mechanical behaviour of several kinds of nanostructures [22,23,24,25,26]. The mentioned ill-posedness affecting the pure strain-driven nonlocal approach can be also avoided using the two-phase local/nonlocal strain-driven constitutive approach, proposed by Eringen [13, 27] and recently applied by different authors to analyse both the static and dynamic behaviour of nanostructures [28,29,30,31,32]. Moreover, Barretta et al. [33, 34] have recently developed the two-phase local/nonlocal stress-driven formulation.

Lim et al. [35] combined both the fully nonlocal elasticity theory of Eringen and the strain gradient elasticity in a single framework called nonlocal strain gradient elasticity theory (NSGT). The new formulation allows to analyse stiffer (or more flexible) structures than those corresponding to the classical case, appropriately selecting the two scale-dependent material parameters included in the model. The theory has become very popular, and nowadays it is being currently used by a large number of authors, see [36,37,38,39,40,41,42,43,45] just to mention a few. When it is applied to bounded domains, the fulfilment of both standard and non-standard boundary conditions, together with the constitutive boundary conditions are required. In some of the quoted papers the solution only satisfies the standard and the non-standard boundary conditions, dismissing the constitutive ones [36, 37, 38, 39, 42, 45], meanwhile in other works only satisfies the standard and the constitutive boundary conditions, dismissing the non-standard ones [40, 41, 43, 44]. In this respect Zaera et al. [46] showed the inconsistency of the NSGT when applied to finite solids. The requirement to meet the three types of boundary conditions at once, standard, non-standard, and constitutive, makes the problem overconstrained, with no solution in general. Yet, given the large number of works using the NSGT being currently published in the field of generalized continuum mechanics, it is pertinent to evince the shortcomings of the application of this theory. Indeed, in a recent paper [44] it is claimed that, if the NSGT is properly formulated in variational terms, only the standard and the constitutive boundary conditions are required, thus amending the quoted inconsistency of the theory.

In order to stress the aforementioned inconsistency, in the present work we point out the consequences of dismissing certain mandatory boundary conditions, either non-standard or constitutive, to derive an apparently well-posed problem from a factually overconstrained problem. In particular, we analyse the bending behaviour of a simply supported Bernoulli–Euler beam subjected to an uniformly distributed static load, which was considered in different works [39, 44, 46]. Through this straightforward example we show that: (i) if constitutive boundary conditions are omitted, the equilibrium fields are incompatible with the constitutive equations of the material, as it was pointed out by Barretta and de Sciarra [40]; (ii) if non-standard boundary conditions are omitted, the energy conservation principle is infringed. Therefore the NSGT is inconsistent because, in general, there is no solution if it is applied to bounded solids. Consequently, its use must be definitely prevented to assess scale effects in mechanical nanosystems.

The paper is organised as follows. Section 2 presents the formulation of the studied problem. In Sect. 3, the consequences of dismissing the constitutive boundary conditions are highlighted, whereas Sect. 4 points out those of disregarding the non-standard ones. Finally, Sect. 5 stresses the main conclusion of this work.

2 Static bending of a NSGT Bernoulli–Euler beam

The essential hypothesis for the constitutive behaviour of the NSGT considers that the internal elastic energy is composed by two terms: one accounting for the nonlocal effects of the classical strain field and another one accounting for the nonlocality of the strain gradient field [35]. From this assumption and applying a classical variational principle it is possible to identify the total stress as the difference between the classical stress (work conjugate of classical strain) and the gradient of the higher order stress (work conjugate of strain gradient).

2.1 Governing equation, standard and non-standard boundary conditions

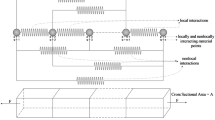
Let us consider a simply supported beam of length L and uniform section area A, inertia I, and Young modulus E, subject to a distributed transverse load \(q_z\). Axial, out-of-plane, and transverse coordinates are represented respectively as x, y, z, and the corresponding displacements as \(U_x\), \(U_y\), \(U_z\). According to the Bernoulli–Euler beam kinematics, we have

$$\begin{aligned} U_x = -z \,w^{\prime };\quad U_y=0; \quad U_z= w, \end{aligned}$$
(1)

where w represents the displacement of the section’s centroid in the transverse direction and, for simplicity, \(\left( \cdot \right) ^{\prime }\) denotes the derivative with respect to the spatial variable x. The axial strain, \(\varepsilon\), is given by

$$\begin{aligned} \varepsilon = U_x^{\prime } = - z\, w^{\prime \prime }. \end{aligned}$$
(2)

Specialising the general NSGT constitutive equation for the one dimensional problem, the normal axial stress is given by [35, 46]

$$\begin{aligned} \sigma = \sigma _0 - \sigma _1^{\prime } , \end{aligned}$$
(3)

where \(\sigma _0\) and \(\sigma _1\) represent nonlocal and higher order stresses, respectively defined as

$$\begin{aligned} \sigma _0 \left( x \right)&= E \int _a^b k\left( |x-{{\bar{x}}}|, \kappa \right) \, \varepsilon \left( {{\bar{x}}} \right) \, d {{\bar{x}}}, \end{aligned}$$
(4)
$$\begin{aligned} \sigma _1 \left( x \right)&= E l^2 \int _a^b k\left( |x-{{\bar{x}}}|, \kappa \right) \, \varepsilon ^{\prime } \left( {{\bar{x}}} \right) \, d {{\bar{x}}}, \end{aligned}$$
(5)

l and \(\kappa\) being parameters accounting for scale effects related to the strain gradient field \(\varepsilon ^{\prime }\) and to the nonlocal stress field respectively. The kernel appearing in above equations is given by

$$\begin{aligned} k \left( | x - {{\bar{x}}} |,\kappa \right) = \frac{1}{2 \kappa } e^{-\frac{| x - {{\bar{x}}} |}{\kappa }}. \end{aligned}$$
(6)

Assuming the previous hypotheses, the bending moment is given by

$$\begin{aligned} M = \int _A \sigma z \,dA = M_0 - M_1^{\prime } , \end{aligned}$$
(7)

with

$$\begin{aligned} M_0 =-EI \int _0^L k\left( |x-{{\bar{x}}}|, \kappa \right) w^{\prime \prime } \left( {{\bar{x}}} \right) \,d {{\bar{x}}} \end{aligned}$$
(8)

and

$$\begin{aligned} M_1 =-l^2 EI \int _0^L k\left( |x-{{\bar{x}}}|, \kappa \right) w^{\prime \prime \prime } \left( {{\bar{x}}} \right) \,d {{\bar{x}}} \end{aligned}$$
(9)

being respectively nonlocal and higher order moments.

According to Lim et al. [35], and particularizing the general 3D formulation to the 1D case, the internal energy density potential (per unit volume) U is given by the product of work conjugate pairs \(\sigma _0\) and \(\varepsilon\), on one side, and \(\sigma _1\) and \(\varepsilon ^{\prime }\), on the other

$$\begin{aligned} U&= \frac{1}{2} \sigma _0 \varepsilon + \frac{l^2}{2} \sigma _1 \varepsilon ^{\prime } \nonumber \\&= \frac{1}{2} \varepsilon E \int _0^L k\left( |x-{{\bar{x}}}|, \kappa \right) \varepsilon \left( {{\bar{x}}} \right) d {{\bar{x}}} + \frac{l^2}{2} \varepsilon ^{\prime } E \int _0^L k\left( |x-{{\bar{x}}}|, \kappa \right) \varepsilon ^{\prime } \left( {{\bar{x}}} \right) d {{\bar{x}}} . \end{aligned}$$
(10)

From the kinematics of the Bernoulli–Euler beam model, the internal energy of the whole beam is derived as

$$\begin{aligned} {\mathcal {U}} = {\mathcal {U}}_{M_0} +{\mathcal {U}}_{M_1} \end{aligned}$$
(11)

with

$$\begin{aligned} {\mathcal {U}}_{M_0}&= \frac{1}{2} EI \int _0^L \left[ \int _0^L k\left( |x-{{\bar{x}}}|, \kappa \right) w^{\prime \prime } \left( {{\bar{x}}} \right) \, d \bar{x} \right] w^{\prime \prime } \left( x \right) \, dx , \end{aligned}$$
(12)
$$\begin{aligned} {\mathcal {U}}_{M_1}&= \frac{l^2}{2} EI \int _0^L \left[ \int _0^L k\left( |x-{{\bar{x}}}|, \kappa \right) w^{\prime \prime \prime } \left( {{\bar{x}}} \right) \, d {{\bar{x}}} \right] w^{\prime \prime \prime } \left( x \right) \, dx . \end{aligned}$$
(13)

Due to the conservative character of the system, governing equation and boundary conditions are derived from the principle of minimum total potential energy \(\delta \varPi = \delta {\mathcal {U}} - \delta {\mathcal {V}} = 0\), where \(\varPi\) and \({\mathcal {V}}\) are the total potential energy and the potential of applied forces, respectively. This principle implicitly imposes the equivalence between the work of external forces and the internal energy of the solid, implying conservation of energy.

Now, integrating by parts and considering the symmetry of the 1D kernel [Eq. (6)] with respect to axial coordinates x and \({{\bar{x}}}\), we get the first variation \(\delta {\mathcal {U}} = \delta {\mathcal {U}}_{M_0} + \delta {\mathcal {U}}_{M_1}\), with

$$\begin{aligned} \delta {\mathcal {U}}_{M_0}& = \left. \left[ EI \int _0^L k\left( |x-{{\bar{x}}}|, \kappa \right) w^{\prime \prime } \left( {{\bar{x}}} \right) \, d {{\bar{x}}} \right] \delta w^{\prime } \left( x \right) \right| _0^L \nonumber \\&\quad -\left. \left[ EI \int _0^L k\left( |x-{{\bar{x}}}|, \kappa \right) w^{\prime \prime } \left( {{\bar{x}}} \right) \, d {{\bar{x}}} \right] ^{\prime } \delta w \right| _0^L \nonumber \\&\quad+ \int _0^L \left[EI \int _0^L k\left( |x-{{\bar{x}}}|, \kappa \right) w^{\prime \prime } \left( {{\bar{x}}} \right) \, d {{\bar{x}}} \right] ^{\prime \prime } \delta w \, dx , \end{aligned}$$
(14)
$$\begin{aligned} \delta {\mathcal {U}}_{M_1}&= \left. \left[ l^2 EI \int _0^L k\left( |x-{{\bar{x}}}|, \kappa \right) w^{\prime \prime \prime } \left( {{\bar{x}}} \right) \, d {{\bar{x}}} \right] \delta w^{\prime \prime } \left( x \right) \right| _0^L \nonumber \\&\quad -\left. \left[l^2 EI \int _0^L k\left( |x-{{\bar{x}}}|, \kappa \right) w^{\prime \prime \prime } \left( {{\bar{x}}} \right) \, d {{\bar{x}}} \right] ^{\prime } \delta w^{\prime } \left( x \right) \right| _0^L \nonumber \\&\quad + \left. \left[l^2 EI \int _0^L k\left( |x-{{\bar{x}}}|, \kappa \right) w^{\prime \prime \prime } \left( {{\bar{x}}} \right) \, d {{\bar{x}}} \right] ^{\prime \prime } \delta w \right| _0^L \nonumber \\&\quad -l^2 EI \int _0^L \left[ \int _0^L k\left( |x-{{\bar{x}}}|, \kappa \right) w^{\prime \prime \prime } \left( {{\bar{x}}} \right) \, d {{\bar{x}}} \right] ^{\prime \prime \prime } \delta w \, dx . \end{aligned}$$
(15)

The first variation of \(\delta {\mathcal {V}}\) is given by

$$\begin{aligned} \delta {\mathcal {V}} = \int _0^L q_z \, \delta w \, dx. \end{aligned}$$
(16)

By virtue of the principle of minimum total potential energy [47], we get the equilibrium equation

$$\begin{aligned} M^{\prime \prime } + q_z =0, \end{aligned}$$
(17)

as well as the standard essential and natural boundary conditions to be imposed at \(x=0\) and \(x=L\)

$$\begin{aligned} w&= 0;\quad {\text {or}}\,\, M^{\prime } =0, \end{aligned}$$
(18)
$$\begin{aligned} w^{\prime }&= 0;\quad {\text {or}}\,\,M =0, \end{aligned}$$
(19)

as well as non-standard ones

$$\begin{aligned} w^{\prime \prime } =0;\quad {\text {or}}\,\,M_1 =0. \end{aligned}$$
(20)

It should be noted that non-standard boundary conditions (20)—whether essential or natural—have to be fulfilled, together with the standard boundary conditions (18) and (19), to achieve equilibrium (\(\delta \varPi =0\)).

Now introducing the following nondimensional variables and parameters

$$\begin{aligned} {{\bar{w}}}&= \frac{w}{L};\quad \xi =\frac{x}{L};\quad s=\frac{{{\bar{x}}}}{L};\nonumber \\ {{\bar{M}}}&= \frac{L}{EI} M;\quad {{\bar{M}}}_0 = \frac{L}{EI} M_0;\quad {{\bar{M}}}_1 = \frac{1}{EI} M_1;\nonumber \\ {{\bar{q}}}_z&= {{\bar{q}}} =\frac{q L^3}{EI};\quad h=\frac{\kappa }{L};\quad g=\frac{l}{L}; \end{aligned}$$
(21)

the dimensionless governing equation is given by

$$\begin{aligned} {{\bar{M}}}^{\prime \prime } + {{\bar{q}}}_z =0. \end{aligned}$$
(22)

Standard and non-standard boundary conditions to be imposed at \(\xi =0\) and \(\xi = 1\) are written as

$$\begin{aligned} {{\bar{w}}}&= 0;\quad {\text {or}}\,\,{{\bar{M}}}^{\prime } = 0, \end{aligned}$$
(23)
$$\begin{aligned} {{\bar{w}}}^{\prime }&= 0;\quad {\text {or}}\,\,{{\bar{M}}} =0, \end{aligned}$$
(24)
$$\begin{aligned} {{\bar{w}}}^{\prime \prime }&= 0;\quad {\text {or}}\,\,{{\bar{M}}}_1 =0, \end{aligned}$$
(25)

where now \(\left( \cdot \right) ^{\prime }\) represents derivative with respect to the nondimensional spatial variable \(\xi\). For the study case (simply supported beam), the standard boundary conditions read \(\bar{w}\left( 0 \right) = {{\bar{w}}}\left( 1 \right) =0\), \({{\bar{M}}}\left( 0 \right) = {{\bar{M}}}\left( 1 \right) =0\). Non-standard essential boundary conditions, i.e. \({{\bar{w}}}^{\prime \prime }\left( 0 \right) = {{\bar{w}}}^{\prime \prime }\left( 1 \right) =0\), have been selected as in [39].

The integral constitutive equations read

$$\begin{aligned} {{\bar{M}}} = {{\bar{M}}}_0 - {{\bar{M}}}_1^{\prime }, \end{aligned}$$
(26)

where nonlocal moment is given by

$$\begin{aligned} {{\bar{M}}}_0 = - \int _0^1 \frac{1}{2h} e^{-\frac{|\xi - s|}{h}} {{\bar{w}}}^{\prime \prime } \left( s \right) \,d s, \end{aligned}$$
(27)

and higher order moment by

$$\begin{aligned} {{\bar{M}}}_1 =-g^2 \int _0^1 \frac{1}{2h} e^{-\frac{|\xi - s|}{h}} \bar{w}^{\prime \prime \prime } \left( s \right) \,d s. \end{aligned}$$
(28)

2.2 Constitutive boundary conditions

The equivalence between the integral and differential constitutive equations, the last one equipped with constitutive boundary conditions, can be set as follows [48].

The linear Fredholm integral equation of first kind with exponential kernel

$$\begin{aligned} \int _a^b e^{\mu |\xi - s|} \, \varphi \,d s = f,\quad -\infty<a<b<\infty \end{aligned}$$
(29)

is equivalent to a boundary value problem consisting on the ordinary differential equation

$$\begin{aligned} \varphi = \frac{1}{2 \mu } \left( f^{\prime \prime } - \mu ^2 f \right) . \end{aligned}$$
(30)

As stated by Romano et al. [20], the quoted integral equation implicitly contains the boundary conditions

$$\begin{aligned} f^{\prime }\left( a\right) + \mu f(a) =0,\quad f^{\prime }(b) - \mu f\left( b\right) =0. \end{aligned}$$
(31)

which are necessary and sufficient for the existence and uniqueness of its solution.

The constitutive equation (27) relates the nonlocal moment with the curvature through the integral equation (29), with \(a=0\), \(b=1\), \(\mu =-1/h\), \(\varphi = \bar{w}^{\prime \prime } \left( s \right)\), and \(f=-2h {{\bar{M}}}_0\), thus being equivalent to the differential constitutive equation

$$\begin{aligned} {{\bar{w}}}^{\prime \prime } = h^2 {{\bar{M}}}_0^{\prime \prime } - {{\bar{M}}}_0 \end{aligned}$$
(32)

subject to the constitutive boundary conditions

$$\begin{aligned} {{\bar{M}}}_0\left( 0\right) - h {{\bar{M}}}_0^{\prime }\left( 0\right) =0;\quad \bar{M}_0\left( 1\right) + h {{\bar{M}}}_0^{\prime }\left( 1\right) =0. \end{aligned}$$
(33)

Likewise, the integral constitutive equation (28) relates the higher order moment with the derivative of the curvature through the integral equation (29), with \(a=0\), \(b=1\), \(\mu =-1/h\), \(\varphi = {{\bar{w}}}^{\prime \prime \prime } \left( s \right)\), and \(f=-2h/g^2 {{\bar{M}}}_1\), thus being equivalent to the differential constitutive equation

$$\begin{aligned} {{\bar{w}}}^{\prime \prime \prime } = \frac{h^2}{g^2} {{\bar{M}}}_1^{\prime \prime } - \frac{1}{g^2} {{\bar{M}}}_1 \end{aligned}$$
(34)

subject to the constitutive boundary conditions

$$\begin{aligned} {{\bar{M}}}_1\left( 0\right) - h {{\bar{M}}}_1^{\prime }\left( 0\right) =0;\quad \bar{M}_1\left( 1\right) + h {{\bar{M}}}_1^{\prime }\left( 1\right) =0. \end{aligned}$$
(35)

The differential equation relating the total moment and the curvature is derived from the two previous BVPs. From Eqs. (26), (32), and (34) we get the constitutive equation

$$\begin{aligned} -{{\bar{w}}}^{\prime \prime } +g^2 {{\bar{w}}}^{IV} = {{\bar{M}}} - h^2 {{\bar{M}}}^{\prime \prime }, \end{aligned}$$
(36)

Differentiating Eq. (26) and considering Eq. (34)

$$\begin{aligned} {{\bar{M}}}^{\prime } = {{\bar{M}}}_0^{\prime } - \frac{1}{h^2} \left( {{\bar{M}}}_1 + g^2 {{\bar{w}}}^{\prime \prime \prime } \right) . \end{aligned}$$
(37)

Particularizing Eq. (37) for \(\xi =0\) and using BCs (33) and (35), we get

$$\begin{aligned} {{\bar{M}}}^{\prime } \left( 0\right) - \frac{1}{h} {{\bar{M}}}\left( 0 \right) = -\frac{g^2}{h^2} {{\bar{w}}}^{\prime \prime \prime }\left( 0\right) . \end{aligned}$$
(38)

Similarly for \(\xi =1\), we get

$$\begin{aligned} {{\bar{M}}}^{\prime } \left( 1\right) + \frac{1}{h} {{\bar{M}}}\left( 1 \right) = -\frac{g^2}{h^2} {{\bar{w}}}^{\prime \prime \prime } \left( 1\right) . \end{aligned}$$
(39)

The constitutive boundary conditions (38) and (39) are necessary and sufficient for the existence and uniqueness of the solution of the integral constitutive relation (26) [40]. Similarly, the integral constitutive equation (26) is equivalent to the differential constitutive equation (36) equipped with constitutive boundary conditions (38) and (39).

2.3 Formulation in the displacement variable

Now the problem will be formulated in terms of the displacement \({{\bar{w}}}\). From Eqs. (36) and (22), the total bending moment follows the expression

$$\begin{aligned} {{\bar{M}}} = - h^2 {{\bar{q}}}_z -{{\bar{w}}}^{\prime \prime } +g^2 {{\bar{w}}}^{IV}. \end{aligned}$$
(40)

Taking now \({{\bar{M}}}^{\prime \prime }\) from Eq. (40), the governing Eq. (22) can be written as

$$\begin{aligned} g^2 {{\bar{w}}}^{VI} - {{\bar{w}}}^{IV} - h^2 {{\bar{q}}}_z^{\prime \prime } + {{\bar{q}}}_z =0, \end{aligned}$$
(41)

The previous equation is subject to the following boundary conditions:

  • Four standard boundary conditions: \({{\bar{w}}}\left( 0 \right) = {{\bar{w}}}\left( 1 \right) =0\), \({{\bar{M}}}\left( 0 \right) = {{\bar{M}}}\left( 1 \right) =0\).

  • Two non-standard boundary conditions: \({{\bar{w}}}^{\prime \prime }\left( 0 \right) = {{\bar{w}}}^{\prime \prime }\left( 1 \right) =0\).

  • Two constitutive boundary conditions for the total moment \({{\bar{M}}}\): expressed, using Eqs. (40), (38) and (39), as

    $$\begin{aligned}&h \left( {{\bar{q}}}_z \left( 0 \right) -h \,{{\bar{q}}}_z\! ^{\prime } \left( 0 \right) \right) + \frac{1}{h} {{\bar{w}}}^{\prime \prime }\left( 0 \right) - \left( 1 - \frac{g^2}{h^2} \right) {\bar{w}}^{\prime \prime \prime }\left( 0 \right) \nonumber \\&\quad -\frac{g^2}{h} {{\bar{w}}}^{IV} \left( 0 \right) + g^2 {{\bar{w}}}^V\left( 0 \right) = 0, \end{aligned}$$
    (42)
    $$\begin{aligned}&h \left( {{\bar{q}}}_z \left( 1 \right) + h \,{{\bar{q}}}_z\! ^{\prime } \left( 1 \right) \right) + \frac{1}{h} {{\bar{w}}}^{\prime \prime }\left( 1 \right) + \left( 1 - \frac{g^2}{h^2} \right) {{\bar{w}}}^{\prime \prime \prime }\left( 1 \right) \nonumber \\&\quad -\frac{g^2}{h} {{\bar{w}}}^{IV} \left( 1 \right) - g^2 {{\bar{w}}}^V\left( 1 \right) = 0. \end{aligned}$$
    (43)

For the reasons stated above, the previous eight boundary conditions are all of them mandatory, and the sixth-order governing Eq. (41) has more boundary conditions than those required. In the following sections, we outline the serious implications of dismissing the constitutive boundary conditions, as well as those of not using the non-standard ones. To that aim, we consider the bending behaviour of a simply supported Bernoulli–Euler beam subjected to an uniformly distributed static load \({{\bar{q}}}_z = {{\bar{q}}}\), which was considered in different works [39, 44, 46] as pointed out in the introduction section. After that, the inconsistence of the NSGT clearly emerges.

3 Consequences of dismissing the constitutive boundary conditions

The general solution of Eq. (41) for uniformly distributed load (\({{\bar{q}}}_z = {{\bar{q}}}\)) is given by

$$\begin{aligned} {{\bar{w}}} = {{\bar{q}}} \frac{\xi ^4}{24} + A_0 + A_1 \xi + A_2 \xi ^2 + A_3 \xi ^3 + A_4 \sinh \frac{\xi }{g} + A_5 \cosh \frac{\xi }{g} \end{aligned}$$
(44)

\(A_0\) to \(A_5\) being six arbitrary constants that have to be determined imposing six boundary conditions.

First, the problem is solved with the four classical boundary conditions (\({{\bar{w}}}\left( 0\right) = {{\bar{w}}}\left( 1\right) = 0\), \(\bar{M} \left( 0\right) = - h^2 {{\bar{q}}} -{{\bar{w}}}^{\prime \prime }\left( 0\right) +g^2 \bar{w}^{IV}\left( 0\right) =0\), \({{\bar{M}}} \left( 1\right) = - h^2 {{\bar{q}}} -\bar{w}^{\prime \prime }\left( 1\right) +g^2 {{\bar{w}}}^{IV}\left( 1\right) =0\)), and two non-standard boundary conditions (\({{\bar{w}}}^{\prime \prime }\left( 0\right) = \bar{w}^{\prime \prime }\left( 1\right) = 0\)), thus disregarding the two constitutive boundary conditions (42) and (43). In this case, and after some algebra, the displacement field is given by

$$\begin{aligned} {{\bar{w}}}&= {{\bar{q}}} \left[ \frac{\xi ^4}{24} - \frac{ \xi ^3}{12} + \frac{1}{2} (g-h) (g+h) \xi ^2 + \frac{1}{24} \left( -12 g^2+12 h^2+1\right) \xi \right. \nonumber \\& \left.\quad -g^2 (g-h) (g+h) \left( {\text {sech}}\left( \frac{1}{2 g}\right) \cosh \left( \frac{1-2 \xi }{2 g}\right) -1\right) \right] , \end{aligned}$$
(45)

which provides the same results presented in Table 2 of [39] for the parameters considered in that work. The displacement field does not fulfil the constitutive boundary conditions since both left terms of expressions (42) and (43) are non-nil in general

$$\begin{aligned} \frac{{{\bar{q}}} (g-h) (g+h) \left( 2 g \tanh \left( \frac{1}{2 g}\right) -1\right) }{2 h^2} \ne 0 . \end{aligned}$$
(46)

Thus the bending moment field derived from the constitutive equation is different to that derived from the internal equilibrium equation, as it will be shown next.

Using expressions (27) and (28), the nonlocal and higher order bending moments read, respectively

$$\begin{aligned} {{\bar{M}}}_0&= \frac{1}{4} {{\bar{q}}} \Bigg[ 4 g^2 \cosh \left( \frac{\xi }{g}\right) + \left( h-2 g h \tanh \left( \frac{1}{2 g}\right) \right) \left( e^{\frac{\xi -1}{h}}+e^{-\frac{\xi }{h}} \right) \nonumber \\&\quad -2 \left( 2 g^2 \tanh \left( \frac{1}{2 g}\right) \sinh \left( \frac{\xi }{g}\right) +2 g^2+(\xi -1) \xi \right) \Bigg] , \end{aligned}$$
(47)
$$\begin{aligned} {{\bar{M}}}_1&= \frac{1}{4} g^2 {{\bar{q}}} e^{-\frac{\xi +1}{h}} \left[ -2 e^{\frac{\xi +1}{h}} \Biggl( 2 g \, {\text {sech}}\left( \frac{1}{2 g}\right) \sinh \left( \frac{1-2 \xi }{2 g}\right) +2 \xi -1\Biggr) \right. \nonumber \\ & \left. \quad +\left( 1-2 g \tanh \left( \frac{1}{2 g}\right) \right) \left( e^{\frac{2 \xi }{h}} - e^{\frac{1}{h}} \right) \right] . \end{aligned}$$
(48)

Finally, the bending moment field derived from the nonlocal strain gradient constitutive equation is given by

$$\begin{aligned} {{\bar{M}}}&= {{\bar{M}}}_0 - {{\bar{M}}}_1^{\prime } =\frac{{{\bar{q}}}}{4h} \Bigg[ -2 h (\xi -1) \xi \nonumber \\&\quad +\left( 2 g \tanh \left( \frac{1}{2 g}\right) -1 \right) \left( g - h \right) \left( g + h \right) \left( e^{\frac{\xi -1}{h}} + e^{-\frac{\xi }{h}} \right) \Bigg] , \end{aligned}$$
(49)

On the other side, due to the isostatic character of the considered beam, the distribution of bending moments can be also determined by integration of the internal equilibrium Eq. (22) subject to the standard boundary conditions \({{\bar{M}}}\left( 0 \right) =0\) and \({{\bar{M}}}\left( 1 \right) =0\), leading to

$$\begin{aligned} {{\bar{M}}} = \frac{1}{2} {{\bar{q}}} \xi \left( 1 - \xi \right) . \end{aligned}$$
(50)

Therefore, the bending moment field derived from the constitutive equation, given by expression (49), is incompatible with that derived from the equilibrium equation. The mismatch is also evident in Fig. 1, and is the consequence of dismissing the constitutive boundary conditions in the integration of the governing equation.

Fig. 1
figure 1

Fields of bending moments \({{\bar{M}}}\) obtained with the internal equilibrium equation and with the constitutive equation. Solution derived dismissing constitutive boundary conditions

Full size image

4 Consequences of dismissing the non-standard boundary conditions

Now, the sixth-order governing Eq. (41) is solved with the four classical boundary conditions (\(\bar{w}\left( 0\right) = 0\), \({{\bar{M}}} \left( 0\right) = - h^2 {{\bar{q}}} -\bar{w}^{\prime \prime }\left( 0\right) +g^2 {{\bar{w}}}^{IV}\left( 0\right) =0\), \(\bar{w}\left( 1\right) = 0\), \({{\bar{M}}} \left( 1\right) = - h^2 {{\bar{q}}} -\bar{w}^{\prime \prime }\left( 1\right) +g^2 {{\bar{w}}}^{IV}\left( 1\right) =0\)), and the two constitutive boundary conditions (42) and (43) as presented in both [46] and [44], thus disregarding the two non-standard boundary conditions. It has to be noted that the solutions derived herein are fully equivalent to that considered in [44] when the mixture parameter \(\alpha\) used in the quoted work is set to zero to recover the pure NSGT theory. Nevertheless, the inconsistency that will apear for \(\alpha =0\) still holds for a mixed nonlocal strain gradient formulation with \(\alpha \ne 0\).

In the present case (\(\alpha =0\)), the displacement field is given by

$$\begin{aligned} {{\bar{w}}}&= {{\bar{q}}} \left[ \frac{\xi ^4}{24}- \frac{\xi ^3}{12} + \frac{1}{2}(g-h) (g+h) \xi ^2 + \frac{1}{24} \left( -12 g^2+12 h^2+1\right) \xi \right. \nonumber \\&\quad \left. +\frac{1}{2} g (g-h) (g+h) \left( \sinh \left( \frac{\xi }{g}\right) -\coth \left( \frac{1}{2 g}\right) \left( \cosh \left( \frac{\xi }{g}\right) -1\right) \right) \right] , \end{aligned}$$
(51)

which does not satisfy the non-standard boundary conditions, neither essential nor natural, as shown in [46]. Equation  (51) provides results coincident to those presented in Tables 3 and 4 of [44] for the parameters considered in that work.

Using expressions (27) and (28), the nonlocal and higher order bending moments read, respectively

$$\begin{aligned} {{\bar{M}}}_0&= \frac{{{\bar{q}}}}{4 \left( e^{\frac{1}{g}}-1\right) } \left[ g \left( -2 g+e^{\frac{1}{g}} (2 g-1)-1\right) \left( e^{\frac{\xi -1}{h}}+e^{-\frac{\xi }{h}} \right) - 2 \xi \right. \nonumber \\&\quad \left. +\,2 \left( e^{\frac{1}{g}} \left( -2 g^2-\xi ^2+\xi \right) +2 g^2+g e^{\frac{1-\xi }{g}}+g e^{\frac{\xi }{g}}+\xi ^2\right) \right] , \end{aligned}$$
(52)
$$\begin{aligned} {{\bar{M}}}_1&= \frac{g \, {{\bar{q}}}}{4 \left( 1 - e^{\frac{1}{g}} \right) } \left[ \left( e^{\frac{1}{g}} (1-2 g)+2 g+1\right) h \left( e^{\frac{\xi -1}{h}}-e^{-\frac{\xi }{h}} \right) \right. \nonumber \\&\quad \left. +\,2 g \left( \left( e^{\frac{1}{g}}-1\right) (2 \xi -1)+e^{\frac{1- \xi }{g}}-e^{\frac{\xi }{g}}\right) \right] . \end{aligned}$$
(53)

It can be shown that now the bending moment field \({{\bar{M}}} = {{\bar{M}}}_0 - {{\bar{M}}}_1^{\prime }\) is consistent with that derived from the internal equilibrium equations, given by Eq. (50). However, a deep inconsistency still arises when non-standard boundary conditions are dismissed, as it will be discussed next.

External work in the beam is given by

$$\begin{aligned} {{\bar{W}}}_{ext}&= \frac{1}{2} \int _{0}^{1} {{\bar{q}}} \, {{\bar{w}}} \, d\xi \nonumber \\&= \frac{1}{48} {{\bar{q}}}^2 \left( -2 g^2+12 g (g^2-h^2) \left( \coth \left( \frac{1}{2 g}\right) -2 g\right) +2 h^2+\frac{1}{5}\right) . \end{aligned}$$
(54)

On the other side, the internal energy is calculated as (see Eqs. (11)–(13) in this paper, or Eq. (10) in [44])

$$\begin{aligned} \bar{{\mathcal {U}}}&= \frac{1}{2} \int _{0}^{1} - {{\bar{M}}}_0 {{\bar{w}}}^{\prime \prime } \, d \xi + \frac{1}{2} \int _{0}^{1} - {{\bar{M}}}_1 {{\bar{w}}}^{\prime \prime \prime } \, d \xi \nonumber \\&= \frac{e^{-1/h} {{\bar{q}}}^2}{240 \left( e^{\frac{1}{g}}-1\right) ^2} \Bigg[ 30 \left( e^{\frac{1}{g}} (1-2 g)+2 g+1\right) ^2 h (g-h) (g+h) \nonumber \\&\quad \left. +\left( e^{2/g}+1\right) e^{\frac{1}{h}} \left( -120 g^4 (h+3)+10 g^2 (3 h (8 h-1)-2)+10 h^2+1\right) \right. \nonumber \\&\quad \left. +2 e^{\frac{1}{g}+\frac{1}{h}} \Biggl ( -1 + 10 (g - h) (g + h) (1 - 3 h + 12 g^2 (1 + h)) \right. \nonumber \\&\quad \left. +10 \left( 24 g^4+g^2 \left( 12 (h-1) h^2+1\right) +3 h^3\right) \cosh \left( \frac{1}{g}\right) \right. \nonumber \\&\quad +\,60 g (2 h+1) (g-h) (g+h) \sinh \left( \frac{1}{g}\right) \Biggr ) \Bigg] , \end{aligned}$$
(55)

where the minus sign in the integrands of Eq. (55) appears due to the specific sign criterion considered here. The previous expressions (54) and (55) show that, in general, \(\bar{W}_{ext}\) and \(\bar{{\mathcal {U}}}\) are not equal (see Fig. 2 for a comparison of both expressions for a particular case with \({{\bar{q}}}=1\)). The implications of the mismatch between external work and internal energy are profound, since the conservation of energy is infringed by a solution that only fulfils the standard and constitutive boundary conditions, dismissing non-standard ones.

Recently, in the paper by Barretta and Marotti de Sciarra [44] it is claimed that no ill-posedness holds when dismissing non-standard boundary conditions if the NSGT is established by an adequate variational formulation with appropriate test fields. This approach is posed through the application of the principle of virtual work (Eq. (1) in [44]), being fully equivalent to the principle of minimum total potential energy for elastic solids. This principle is stated through the definition of the internal work as

$$\begin{aligned} {{\bar{W}}}_{int} = \frac{1}{2} \int _{0}^{1} - {{\bar{M}}} \, {{\bar{w}}}^{\prime \prime } \, d\xi , \end{aligned}$$
(56)

where here we are considering the work variables integrated along the loading process. This definition of the internal work, valid for the classical bending problem, is not applicable to NSGT beams. The correct one has to be derived as the product of conjugate pairs as in Eq. (11) [or Eq. (55)]. Therefore, in order to sort out this shortcoming, these authors impose a second variational condition (Eq. (11) in [44]) stating the equivalence between internal work, defined as in (56), and internal energy, defined as in Eq. (55) [or in Eq. (10) of [44], taking the mixture parameter \(\alpha =0\)]. When the first variation of the internal energy is further developed, a boundary term appears [see Eq. (12) of that paper]. This term is then dismissed by choosing a virtual field of curvatures taking null value at the boundaries, \(\delta {{\bar{w}}}^{\prime \prime }\left( 0\right) =0\) and \(\delta {{\bar{w}}}^{\prime \prime }\left( 1\right) =0\). However, it has to be pointed out that selecting a virtual field with null values at \(\xi =0\) and \(\xi =1\) implies that the primary variable \({{\bar{w}}}^{\prime \prime }\) has to be specified at these points, i.e. essential boundary conditions are imposed [49]. Alternatively, the boundary term could be cancelled by imposing the natural boundary conditions \(\bar{M}_1\left( 0\right) =0\) and \({{\bar{M}}}_1\left( 1\right) =0\), or any other suitable choice of essential and natural boundary conditions. All in all, from the nature of the variational problem, the fulfillment of the surplus non-standard boundary conditions, not considered in the quoted paper, are required. The verification of this statement comes from the integration along the loading process of the boundary term

$$\begin{aligned} {{\bar{W}}}_{B}&= \int _{0}^{{{\bar{q}}}} - \left( {{\bar{M}}}_1\left( 1 \right) \, \frac{d {{\bar{w}}}^{\prime \prime }\left( 1 \right) }{d {{\bar{q}}}} - {{\bar{M}}}_1\left( 0 \right) \, \frac{d {{\bar{w}}}^{\prime \prime }\left( 0 \right) }{d {{\bar{q}}}} \right) d {{\bar{q}}} \nonumber \\&= -\frac{1}{2} \left( {{\bar{M}}}_1\left( 1 \right) \, {{\bar{w}}}^{\prime \prime }\left( 1 \right) - {{\bar{M}}}_1\left( 0 \right) \, {{\bar{w}}}^{\prime \prime }\left( 0 \right) \right) \nonumber \\&= \frac{1}{4} e^{-\frac{1}{2h}} {{\bar{q}}}^2 h (h^2 - g^2) \left( \coth \left( \frac{1}{2 g}\right) -2 g\right) ^2 \sinh \left( \frac{1}{2 h}\right) . \end{aligned}$$
(57)

The addition of this term to the external work now equals the strain potential, i.e., \({{\bar{W}}}_{ext} + {{\bar{W}}}_B = \bar{{\mathcal {U}}}\), as it can be deduced from Eqs. (54), (55) and (57) (see Fig. 2).

There are specific cases where the equivalence \({{\bar{W}}}_{ext} \equiv \bar{{\mathcal {U}}}\) holds. The first one, of limited conceptual interest for the current discussion, is that corresponding to \(h=g\), for which both energies are coincident with those derived for the classical (local) beam \({{\bar{W}}}_{local}=\bar{{\mathcal {U}}}_{local } = {{\bar{q}}}^2/240\) (Fig. 2). In this case, the stiffening effect of the gradient part appears to offset the softening effect of the nonlocal part, and the displacement field equals that of a classical supported beam. The second case is of much greater interest and deserves to be commented. If the nonlocal parameter h tends to zero, the energy balance is also achieved for any value of the gradient parameter g. Here the nonlocal kernel becomes the Dirac delta and both the constitutive and the governing equations drop to the strain gradient ones, for which non-standard boundary conditions are also required [50]. It may appear contradictory that now a solution obtained without imposing mandatory non-standard boundary conditions does satisfy the energy balance. The rationale is found in the imposed constitutive boundary conditions  (42) and (43) leading to \({{\bar{w}}}^{\prime \prime \prime }\left( 0 \right) = 0\) and \({{\bar{w}}}^{\prime \prime \prime }\left( 1 \right) = 0\) when \(h \rightarrow 0\), which are coincident with the non-standard natural boundary contitions \({{\bar{M}}}_1(0)=0\) and \({{\bar{M}}}_1(1)=0\) (notice that, if the nonlocal parameter tends to zero, \({{\bar{M}}}_1=-g^2 {{\bar{w}}}^{\prime \prime \prime }\), see Eq. (82) in [46]). As a particular case, the classical (local) formulation recovered for \(h \rightarrow 0\) and \(g \rightarrow 0\) also satisfies the energy balance between external work and internal energy.

Fig. 2
figure 2

Variation of the external work \({{\bar{W}}}_{ext}\), of the strain energy \(\bar{{\mathcal {U}}}\), and of the work due to the boundary term \(\bar{W}_B\) with the nonlocal parameter h, for a simply supported beam with uniformly distributed load \({{\bar{q}}}=1\). a\(g\rightarrow 0\); b\(g=0.1\); c\(g=0.2\). Solution derived dismissing non-standard boundary conditions. All energies have been nondimensionalized with the external work corresponding to the classical (local) case, \(\bar{W}_{local} = {{\bar{q}}}^2/240\)

Full size image

5 Conclusion

The mandatory character of the standard boundary conditions, as well as of the non-standard and constitutive ones, leads to an overconstained problem with no solution in general, as stated in [46]. In this work it is showed that, if constitutive boundary conditions are dismissed, the equilibrium fields are not compatible with the constitutive equations of the material. Moreover, we pointed out that if non-standard boundary conditions are omitted, the energy conservation principle is infringed. Therefore, the inconsistency of the NSGT when applied to finite structures is corroborated, and its use to assess scale effects in nanostructures must be definitely prevented.

However, there are other fully consistent nonlocal models: the two-phase local/nonlocal strain driven elasticity [13, 29, 32], the nonlocal stress-driven elasticity [21], or the two-phase local/nonlocal stress-driven elasticity [33]. All of them emerge as alternatives to the NSGT.

6 Remarks

A typo detected in the expression of the displacement field \({{\bar{w}}}\) in Section 6.3 of [46] has been corrected in Eq. (51) of the current manuscript. However, the expression of the curvature and the values presented in Fig. 3a of the quoted work are correct.

All the closed-form expression in the present communication have been obtained with the Mathematica programming environment [51].