1 Introduction

Layered composites with a periodic structure can be found in nature as sedimentary rocks and modern engineering constructions. Their role in geophysics and engineering is significant and leads to necessity of forecasting, among others, stress distributions in these types of materials. The level of complexity of problems for such materials leads, for practical reasons, to the use of approximate models in which the approximation error is small compared to the ease of obtaining a solution. The approximate models used in problems related to layered materials are most often based on the averaging of certain material parameters. In this way, a continuum theory for laminate mediums [4] was used to analyze dynamic problems; the asymptotic homogenization approach [5] applied to mixtures for the wave propagation; an approach using thick plate theory [6], used for problems related to vibrations; matrix methods [7], theory of tolerance [2], applied to composites with parallel layer boundary. One of the approaches to dealing with this type of problems may be the model of a transversely isotropic medium. A lot of information on the analysis of models of this type can be found, among others in the works [8,9,10]. For such models, the constituents of the stress vector in the direction of layering are continuous, which in the case of multi-component materials does not occur.

A different approach to the problem is presented by the theory of non-asymptotic homogenization derived by Woźniak [1] and applied to the multi-layered micropertiodic composites by Matysiak [11], which allows prediction of local stresses and heat fluxes in microperiodic composites. The valuable of this approach is that it permits to calculate local values of displacement and stress tensor components in every component of the laminated body, as well as the mechanical continuity conditions on interfaces are satisfied. The homogenized model with microlocal parameters is widely developed in the analysis of such problems as contact mechanics [3], fracture problems [12], heat conduction [13], wave propagation [14] etc. Comparisons of the results obtained within the classical theory of elasticity with the solutions based on the homogenized model with microlocal parameters were presented in [15,16,17]. Results obtained in this work shows good consistencies of results for both approaches in considered cases.

Pressure load problems at the boundary surface of materials are frequently encountered mechanics problems that can often be extended to other types of problems. However, the cases usually considered layering parallel and perpendicular to the edge. Problems of this type were considered, among others, in works [3, 18, 19] and [20]. To a lesser extent, the problems discussed concern materials with a boundary normal to the layering. Known solved problems focuses mainly on problems for layered composites with perpendicular or parallel boundary surface to stratification.

This work is an attempt to fill the gap in the problems under consideration for microperiodic elastic composites and will describe problems for a composite medium loaded locally with normal and tangential loads on the boundary surface of the medium for any form load functions. In considered problems displacement vector and stress tensor components will be designated for materials with an inclined stratification at any considered angle of layering. Comparison with existing solutions has been made on the basis of comparison with existing results for layering perpendicular to the edge, see [16, 21].

2 Formulation of the problem

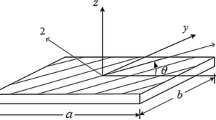
Considered material consists of thin layers of thickness l (periodic cells), which are made of two isotropic components (Fig. 1). Thickness of each alternating layer is respectively l1 and l2. Periodic cell saturation with material 1 could be written as:

Fig. 1
figure 1

Scheme of considered problem of boundary load

Full size image
$$\chi = \frac{{l_{1} }}{{l_{1} + l_{2} }} = \frac{{l_{1} }}{l}.$$
(2.1)

Let \(\lambda_{1} ,\,\,\lambda_{2} ,\,\,\mu_{1} ,\,\,\mu_{2}\) be Lame constants and \(\nu_{1} ,\,\,\nu_{2}\) be Poisson ratios of layers 1 and 2, respectively. Let  \(\vec{u}\left( {x, y} \right) = \left[ {u_{x} \left( {x,y} \right),\,\,u_{y} \left( {x,y} \right),\,\,0} \right]\) denote the displacement vector and  \(\sigma_{xx} ,\,\,\sigma_{xy} ,\,\,\sigma_{yy}\) be the non–zero components of stress tensor in coordinate system related to the layering orientation \(\left( {x,\,\,y,\,\,z} \right).\) Let \(\left( {\xi ,\,\,\eta ,\,\,z} \right)\) be the coordinate system rotated relative to the  \(\left( {x,\,\,y,\,\,z} \right)\) system around the z axis by the angle ϕ. Vector \(\vec{n}\) is a normal vector of the boundary plane. Boundary conditions for the considered problem could be expressed as:

$$\begin{aligned} \sigma_{{^{\eta \eta } }}^{(m)} \left( {\xi ,0} \right) & = -\, p\left( \xi \right){\text{H}}\left( {a - \left| \xi \right|} \right),\,\,\,\,\xi \in {\text{R}}, \\ \sigma_{\xi \eta }^{(m)} \left( {\xi ,0} \right) & = -\, \tau \left( \xi \right){\text{H}}\left( {a - \left| \xi \right|} \right),\,\,\,\,\xi \in {\text{R}}, \\ \end{aligned}$$
(2.2)

It is assumed that stress tensor components tend to zero at infinity:

$$\sigma_{\xi \xi }^{(m)} ,\,\,\sigma_{\xi \eta }^{(m)} ,\,\,\sigma_{\eta \eta }^{(m)} \to 0,\,\,\,\xi^{2} + \eta^{2} \to \infty ,\,\,\,m = 1,2,$$
(2.3)

where \(p\left( \xi \right)\) normal load function, \(\tau \left( \xi \right)\) tangential load function, \({\text{H}}\left( \cdot \right)\) Heaviside’s step function, \(a\) given constant of half-width of the pressure area, \(a > 0\), \(m\) number of composite’s component material, m = 1, 2.

The homogenized model with microlocal parameters in the plane state of strains is described by the following equations [12]:

$$\begin{aligned} & A_{1} \frac{{\partial^{2} U}}{{\partial x^{2} }} + \left( {B + C} \right)\frac{{\partial^{2} V}}{\partial x\partial y} + C\frac{{\partial^{2} U}}{{\partial y^{2} }} = 0, \\ & A_{2} \frac{{\partial^{2} V}}{{\partial y^{2} }} + \left( {B + C} \right)\frac{{\partial^{2} U}}{\partial x\partial y} + C\frac{{\partial^{2} V}}{{\partial x^{2} }} = 0, \\ \end{aligned}$$
(2.4)

and the stresses in the m-th kind of composite component [16]:

$$\begin{aligned} \sigma_{xx}^{(m)} & = A_{1} \frac{\partial U}{\partial x} + B\frac{\partial V}{\partial y},\,\,\sigma_{xy}^{(m)} = C\left( {\frac{\partial U}{\partial y} + \frac{\partial V}{\partial x}} \right), \\ \sigma_{yy}^{(m)} & = D_{m} \frac{\partial U}{\partial x} + E_{m} \frac{\partial V}{\partial y},\,\,\sigma_{zz}^{(m)} = \frac{{\lambda_{m} }}{{\lambda_{m} + 2\mu_{m} }}\left( {\sigma_{xx}^{\left( m \right)} + \sigma_{yy}^{\left( m \right)} } \right), \\ \end{aligned}$$
(2.5)

where \(U = U\left( {x,y} \right)\) and \(V = V\left( {x,y} \right)\) are unknown functions interpreted as a components of macro-displacement vector in the direction of the x and y axes respectively and \(A_{1} ,\,\,A_{2} ,\,\,B\) and C are constants from homogenized model in the form:

$$\begin{aligned} A_{1} & = \frac{{\left( {\lambda_{1} + 2\mu_{1} } \right)\left( {\lambda_{2} + 2\mu_{2} } \right)}}{{\left( {1 - \chi } \right)\left( {\lambda_{1} + 2\mu_{1} } \right) + \chi \left( {\lambda_{2} + 2\mu_{2} } \right)}} > 0, \\ A_{2} & = A_{1} + \frac{{4\chi \left( {1 - \chi } \right)\left( {\mu_{1} - \mu_{2} } \right)\left( {\lambda_{1} - \lambda_{2} + \mu_{1} - \mu_{2} } \right)}}{{\left( {1 - \chi } \right)\left( {\lambda_{1} + 2\mu_{1} } \right) + \chi \left( {\lambda_{2} + 2\mu_{2} } \right)}} > 0, \\ B & = \frac{{\left( {1 - \chi } \right)\lambda_{2} \left( {\lambda_{1} + 2\mu_{1} } \right) + \chi \lambda_{1} \left( {\lambda_{2} + 2\mu_{2} } \right)}}{{\left( {1 - \chi } \right)\left( {\lambda_{1} + 2\mu_{1} } \right) + \chi \left( {\lambda_{2} + 2\mu_{2} } \right)}} > 0, \\ C & = \frac{{\mu_{1} \mu_{2} }}{{\left( {1 - \chi } \right)\mu_{1} + \chi \mu_{2} }} > 0,\,\,D_{m} = \frac{{\lambda_{m} }}{{\lambda_{m} + 2\mu_{m} }}A_{1} > 0, \\ E_{m} & = \frac{{4\mu_{m} \left( {\lambda_{m} + \mu_{m} } \right)}}{{\lambda_{m} + 2\mu_{m} }} + \frac{{\lambda_{m} }}{{\lambda_{m} + 2\mu_{m} }}B > 0,\,\,\,m = 1,\,2. \\ \end{aligned}$$
(2.6)

It should be mentioned here that the approach, which is the homogenized model with microlocal parameters, successfully allows to use well known methods of solving boundary problems for classical theory of elasticity- e.g. Fourier, Hankel’s, etc., and potential methods [22].

3 Solution method

The solution of the system of Eq. (2.4) was sought using the elastic potentials method, where macro-displacement components could be represented in the form [16]:

$$U\left( {x,y} \right) = \kappa_{1} \frac{{\partial \varPsi_{1} }}{\partial x} + \kappa_{2} \frac{{\partial \varPsi_{2} }}{\partial x},\,\,\,\,V\left( {x,y} \right) = \frac{{\partial \varPsi_{1} }}{\partial y} + \frac{{\partial \varPsi_{2} }}{\partial y},\,\,\,\,\kappa_{k} = \frac{{A_{2} \gamma_{k}^{2} - C}}{B + C},\,\,\,\,k = 1,\,2,$$
(3.1)

where \(\Psi _{i} { = }\Psi _{i} \left( {x,y} \right),\,\,\,i = 1,2\) and are sought functions of elastic potentials. The values of the \(\gamma_{k} ,\,\,k = 1,\,2\) constants are determined from characteristic equation, given as [16]:

$$A_{2} C\gamma_{k}^{4} + \left( {B^{2} + 2BC - A_{1} A_{2} } \right)\gamma_{k}^{2} + A_{1} C = 0.$$
(3.2)
$$\gamma_{k}^{2} \frac{{\partial^{2} \varPsi_{k} }}{{\partial x^{2} }} + \frac{{\partial^{2} \varPsi_{k} }}{{\partial y^{2} }} = 0,\,\,\,\,\gamma_{k} = \left( {\frac{{A_{1} A_{2} - 2BC - B^{2} + \left( { - 1} \right)^{k} \sqrt \Delta }}{{2A_{2} C}}} \right)^{{\frac{1}{2}}} ,\,\,\,k = 1,\,2,$$
(3.3)
$$\Delta = \left( {B^{2} + 2BC - A_{1} A_{2} } \right)^{2} - 4A_{1} A_{2} C^{2} > 0,$$
(3.4)

where \(\Delta > 0\) for general case of \(\mu_{1} \ne \mu_{2}\). Other case of \(\mu_{1} = \mu_{2}\) and full analysis of solution method could be found in [23, 24]. Stress tensor components in m-th material, \(m = 1,\,2,\) in the coordinate system associated with the lamina orientation \(\left( {x,\,\,y,\,\,z} \right)\) could be expressed by elastic potentials as [16]:

$$\begin{aligned} \sigma_{xx}^{\left( m \right)} & = \mathop \sum \limits_{k = 1}^{2} \left( {A_{1} \kappa_{k} \frac{{\partial^{2} \varPsi_{k} }}{{\partial x^{2} }} + B\frac{{\partial^{2} \varPsi_{k} }}{{\partial y^{2} }}} \right),\,\,\,\,\,\sigma_{xy}^{\left( m \right)} = C\mathop \sum \limits_{k = 1}^{2} \left( {1 + \kappa_{k} } \right)\frac{{\partial^{2} \varPsi_{k} }}{\partial x\partial y}, \\ \sigma_{yy}^{\left( m \right)} & = \mathop \sum \limits_{k = 1}^{2} \left( {D_{m} \kappa_{k} \frac{{\partial^{2} \varPsi_{k} }}{{\partial x^{2} }} + E_{m} \frac{{\partial^{2} \varPsi_{k} }}{{\partial y^{2} }}} \right),\,\,\,\,\,\sigma_{zz}^{\left( m \right)} = \frac{{\lambda_{m} }}{{2\left( {\lambda_{m} + \mu_{m} } \right)}}\left( {\sigma_{xx}^{\left( m \right)} + \sigma_{yy}^{\left( m \right)} } \right),\,\,\,\,m = 1,2. \\ \end{aligned}$$
(3.5)

Layering inclined at an angle relative to the edge of the half-plane makes it necessary to move from the coordinate system associated with the boundary surface \(\left( {\xi ,\,\eta } \right)\) to the coordinate system associated with direction of layering \(\left( {x,\,y} \right)\). Dependencies between the coordinates can be written in the form:

$$\left\{ {\begin{array}{*{20}c} {\xi = x\,{ \cos }\left( \phi \right) - y\,{ \sin }\left( \phi \right)} \\ {\eta = x\,{ \sin }\left( \phi \right) + y\,{ \cos }\left( \phi \right).} \\ \end{array} } \right.$$
(3.6)

Taking into account dependencies (3.1) in Eq. (2.4), we can write Eq. (3.1) in the following form:

$$\begin{aligned} \frac{{\partial^{2} \varPsi }}{{\partial \xi^{2} }}\left( {\gamma_{k}^{2} { \cos }^{2} \left( \phi \right) + { \sin }^{2} \left( \phi \right)} \right) + 2\frac{{\partial^{2} \varPsi }}{\partial \xi \partial \eta }\sin \left( \phi \right)\cos \left( \phi \right)\left( {\gamma_{k}^{2} - 1} \right) \hfill \\ \quad + \,\frac{{\partial^{2} \varPsi }}{{\partial \eta^{2} }}\left( {\gamma_{k}^{2} { \sin }^{2} \left( \phi \right) + { \cos }^{2} \left( \phi \right)} \right) = 0,\,\,\,\,k = 1,\,2. \hfill \\ \end{aligned}$$
(3.7)

To solve partial differential Eq. (3.7), the integral Fourier transform method was used, where Fourier transforms of elastic potentials are given by [11]:

$$\tilde{\varPsi }_{k} \left( {s,\eta } \right) = \frac{1}{{\sqrt {2\uppi} }}\mathop \smallint \limits_{ - \infty }^{\infty } \varPsi_{k} \left( {\xi ,\eta } \right)\exp \left( { - {\text{i}}\xi s} \right){\text{d}}\xi ,\,\,\,k = 1,\,2.$$
(3.8)

Functions being the solution to Eqs. (3.7) which satisfies (2.3) are sought in the form:

$$\tilde{\varPsi }_{k} \left( {s,\eta } \right) = A_{k} \left( s \right){ \exp }\left( { - \left( {a_{1}^{k} \left| s \right| + {\text{i}}a_{2}^{k} s} \right)\eta } \right),\,\,\,\,k = 1,2,$$
(3.9)

where

$$a_{1}^{k} = \frac{{\gamma_{k} }}{{\gamma_{k}^{2} { \sin }^{2} \left( \phi \right) + { \cos }^{2} \left( \phi \right)}},\,\,\,\,\,a_{2}^{k} = \frac{{\left( {\gamma_{k}^{2} - 1} \right){ \sin }\left( \phi \right){ \cos }\left( \phi \right)}}{{\gamma_{k}^{2} { \sin }^{2} \left( \phi \right) + { \cos }^{2} \left( \phi \right)}},\,\,\,k = 1,\,2.$$
(3.10)

Functions \(A_{k} \left( s \right)\) will be determined in the way of solving the adequate boundary problem. In this paper for considered problem boundary conditions on the surface of the half-plane could be written as follows:

$$\left[ {\begin{array}{*{20}l} {\sigma_{\xi \eta }^{\left( m \right)} } \hfill \\ {\sigma_{\eta \eta }^{\left( m \right)} } \hfill \\ {\sigma_{\eta z}^{\left( m \right)} } \hfill \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {\sigma_{xx}^{\left( m \right)} } \hfill & {\sigma_{xy}^{\left( m \right)} } \hfill & 0 \hfill \\ {\sigma_{xy}^{\left( m \right)} } \hfill & {\sigma_{yy}^{\left( * \right)} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {\sigma_{zz}^{\left( m \right)} } \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} { - { \sin }\left( \phi \right)} \hfill \\ { - { \cos }\left( \phi \right)} \hfill \\ 0 \hfill \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} { - \sigma_{xx}^{\left( m \right)} \sin \left( \phi \right) - \sigma_{xy}^{\left( m \right)} \cos \left( \phi \right)} \hfill \\ { - \sigma_{xy}^{\left( m \right)} \sin \left( \phi \right) - \sigma_{yy}^{\left( * \right)} \cos \left( \phi \right)} \hfill \\ 0 \hfill \\ \end{array} } \right],\quad m = 1,2,$$
(3.11)

where \(\sigma_{yy}^{(*)}\) is the averaged stress tensor component in the direction of layering [3]:

$$\sigma_{yy}^{\left( * \right)} \left( {\xi ,\eta } \right) = \chi \sigma_{yy}^{\left( 1 \right)} \left( {\xi ,\eta } \right) + \left( {1 - \chi } \right)\sigma_{yy}^{\left( 2 \right)} \left( {\xi ,\eta } \right) = B\frac{{\partial U\left( {\xi ,\eta } \right)}}{\partial x} + A_{2} \frac{{\partial V\left( {\xi ,\eta } \right)}}{\partial y}.$$
(3.12)

Equation (3.11) describes boundary condition with respect to the averaged part. The averaged boundary condition proposed by Perkowski [3] has been verified in the context of solutions from the classical approach for both the theory of elasticity and heat conduction [10].

Using Fourier transform (3.8) to equations describing the boundary condition (3.11) and taking into account the form of constitutive Eq. (3.5), the matrix equation can be written as a system of equations:

$$\left\{ {\begin{array}{*{20}l} {\mathop \sum \limits_{k = 1}^{2} \left( {D_{11}^{\left( k \right)} \frac{{\partial^{2} \tilde{\varPsi }_{k} \left( {s,\eta } \right)}}{{\partial \eta^{2} }} + {\text{i}}sD_{12}^{\left( k \right)} \frac{{\partial \tilde{\varPsi }_{k} \left( {s,\eta } \right)}}{\partial \eta } - s^{2} D_{13}^{\left( k \right)} \tilde{\varPsi }_{k} \left( {s,\eta } \right)} \right)} \hfill \\ {\quad = - \tilde{p}\left( s \right)\sin \left( \phi \right) - \tilde{\tau }\left( s \right)\cos \left( \phi \right)} \hfill \\ {\mathop \sum \limits_{k = 1}^{2} \left( {D_{21}^{\left( k \right)} \frac{{\partial^{2} \tilde{\varPsi }_{k} \left( {s,\eta } \right)}}{{\partial \eta^{2} }} + {\text{i}}sD_{22}^{\left( k \right)} \frac{{\partial \tilde{\varPsi }_{k} \left( {s,\eta } \right)}}{\partial \eta } - s^{2} D_{23}^{\left( k \right)} \tilde{\varPsi }_{k} \left( {s,\eta } \right)} \right)} \hfill \\ {\quad = - \tilde{p}\left( s \right)\cos \left( \phi \right) + \tilde{\tau }\left( s \right)\sin \left( \phi \right),\quad k = 1,2,} \hfill \\ \end{array} } \right.$$
(3.13)

where

$$\begin{aligned} D_{11}^{\left( k \right)} & = \left( {A_{1} \kappa_{k} \sin^{2} \left( \phi \right) + B{ \cos }^{2} \left( \phi \right) + C\left( {1 + \kappa_{k} } \right){ \cos }^{2} \left( \phi \right)} \right)\sin \left( \phi \right), \\ D_{12}^{\left( k \right)} & = \left( {2\left( {A_{1} \kappa_{k} - B} \right)\sin^{2} \left( \phi \right) + C\left( {1 + \kappa_{k} } \right)\left( {\cos^{2} \left( \phi \right) - { \sin }^{2} \left( \phi \right)} \right)} \right)\cos \left( \phi \right), \\ D_{13}^{\left( k \right)} & = \left( {A_{1} \kappa_{k} \cos^{2} \left( \phi \right) + B{ \sin }^{2} \left( \phi \right) - C\left( {1 + \kappa_{k} } \right){ \cos }^{2} \left( \phi \right)} \right)\sin \left( \phi \right), \\ D_{21}^{\left( k \right)} & = \left( {B\kappa_{k} \sin^{2} \left( \phi \right) + A_{2} { \cos }^{2} \left( \phi \right) + C\left( {1 + \kappa_{k} } \right){ \sin }^{2} \left( \phi \right)} \right)\cos \left( \phi \right), \\ D_{22}^{\left( k \right)} & = \left( {2\left( {B\kappa_{k} - A_{2} } \right)\cos^{2} \left( \phi \right) + C\left( {1 + \kappa_{k} } \right)\left( {\cos^{2} \left( \phi \right) - { \sin }^{2} \left( \phi \right)} \right)} \right)\sin \left( \phi \right), \\ D_{23}^{\left( k \right)} & = \left( {B\kappa_{k} \cos^{2} \left( \phi \right) + A_{2} { \sin }^{2} \left( \phi \right) - C\left( {1 + \kappa_{k} } \right){ \sin }^{2} \left( \phi \right)} \right)\cos \left( \phi \right),\quad k = 1,2. \\ \end{aligned}$$
(3.14)

Considering (3.9) in (3.13) the system of equations, in which functions \(A_{k} \left( s \right)\) are searched for, can be written as follows:

$$\left\{ {\begin{array}{*{20}l} {\left( {A_{11}^{\left( 1 \right)} + {\text{isgn}}\left( s \right)A_{11}^{\left( 2 \right)} } \right)A_{1} \left( s \right) + \left( {A_{12}^{\left( 1 \right)} + {\text{isgn}}\left( s \right)A_{12}^{\left( 2 \right)} } \right)A_{2} \left( s \right) = \left( { - \tilde{p}\sin \left( \phi \right) - \tilde{\tau }{ \cos }\left( \phi \right)} \right) s^{ - 2} ,} \hfill \\ {\left( {A_{21}^{\left( 1 \right)} + {\text{isgn}}\left( s \right)A_{21}^{\left( 2 \right)} } \right)A_{1} \left( s \right) + \left( {A_{22}^{\left( 1 \right)} + {\text{isgn}}\left( s \right)A_{22}^{\left( 2 \right)} } \right)A_{2} \left( s \right) = \left( { - \tilde{p}\cos \left( \phi \right) + \tilde{\tau }{ \sin }\left( \phi \right)} \right) s^{ - 2} ,} \hfill \\ \end{array} } \right.$$
(3.15)

where

$$\begin{aligned} A_{1k}^{\left( 1 \right)} & = \left( {\left( {a_{1}^{k} } \right)^{2} - \left( {a_{2}^{k} } \right)^{2} } \right)D_{11}^{\left( k \right)} + a_{2}^{k} D_{12}^{\left( k \right)} - D_{13}^{\left( k \right)} ,\quad A_{1k}^{\left( 2 \right)} = 2a_{1}^{k} a_{2}^{k} D_{11}^{\left( k \right)} - a_{1}^{k} D_{12}^{\left( k \right)} , \\ A_{2k}^{\left( 1 \right)} & = \left( {\left( {a_{1}^{k} } \right)^{2} - \left( {a_{2}^{k} } \right)^{2} } \right)D_{21}^{\left( k \right)} + a_{2}^{k} D_{22}^{\left( k \right)} - D_{23}^{\left( k \right)} ,\quad A_{2k}^{\left( 2 \right)} = 2a_{1}^{k} a_{2}^{k} D_{21}^{\left( k \right)} - a_{1}^{k} D_{22}^{\left( k \right)} ,\quad k = 1,2. \\ \end{aligned}$$
(3.16)

The \(A_{k} \left( s \right),\quad k = 1,2\) functions describing elastic potentials in the form of a general dependence on the function of normal pressure \(\tilde{p}\left( s \right)\) and tangential load \(\tilde{\tau }\left( s \right)\) could be written in the following form:

$$A_{1} \left( s \right) = \frac{{\left( {\tilde{p}\left( s \right)\Delta_{1}^{\left( 1 \right)} - \tilde{\tau }\,\left( s \right)\Delta_{2}^{\left( 1 \right)} } \right)s^{ - 2} }}{{\Delta_{1} + {\text{isgn}}\left( s \right)\Delta_{2} }},\quad A_{2} \left( s \right) = \frac{{\left( {\tilde{p}\left( s \right)\Delta_{1}^{\left( 2 \right)} + \tilde{\tau }\left( s \right)\,\Delta_{2}^{\left( 2 \right)} } \right)s^{ - 2} }}{{\Delta_{1} + {\text{isgn}}\left( s \right)\Delta_{2} }},$$
(3.17)

where

$$\begin{aligned} \Delta_{1}^{\left( 1 \right)} & = A_{12}^{\left( 1 \right)} \cos \left( \phi \right) - A_{22}^{\left( 1 \right)} \sin \left( \phi \right) + {\text{isgn}}\left( s \right)\left( {A_{12}^{\left( 2 \right)} \cos \left( \phi \right) - A_{22}^{\left( 2 \right)} \sin \left( \phi \right)} \right), \\ \Delta_{1}^{\left( 2 \right)} & = A_{21}^{\left( 1 \right)} \sin \left( \phi \right) - A_{11}^{\left( 1 \right)} \cos \left( \phi \right) + {\text{isgn}}\left( s \right)\left( {A_{21}^{\left( 2 \right)} \sin \left( \phi \right) - A_{11}^{\left( 2 \right)} \cos \left( \phi \right)} \right), \\ \Delta_{2}^{\left( 1 \right)} & = A_{22}^{\left( 1 \right)} \cos \left( \phi \right) + A_{12}^{\left( 1 \right)} \sin \left( \phi \right) + {\text{isgn}}\left( s \right)\left( {A_{22}^{\left( 2 \right)} \cos \left( \phi \right) + A_{12}^{\left( 2 \right)} \sin \left( \phi \right)} \right), \\ \Delta_{2}^{\left( 2 \right)} & = A_{11}^{\left( 1 \right)} \sin \left( \phi \right) + A_{21}^{\left( 1 \right)} \cos \left( \phi \right) + {\text{isgn}}\left( s \right)\left( {A_{11}^{\left( 2 \right)} \sin \left( \phi \right) + A_{21}^{\left( 2 \right)} \cos \left( \phi \right)} \right). \\ \end{aligned}$$
(3.18)

Received dependencies describing functions \(A_{k} \left( s \right)\) can be used to describe both the friction and frictionless problems. General form of elastic potential could be written as:

$$\begin{aligned} \varPsi_{k} \left( {\xi ,\eta } \right) & = \frac{1}{{\sqrt {2\uppi} }}\mathop \smallint \limits_{ - \infty }^{\infty } \left( {\left( {A_{k}^{\left( 1 \right)p} + {\text{isgn}}\left( s \right)A_{k}^{\left( 2 \right)p} } \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{p} \left( s \right){ + }\left( { - 1} \right)^{k} \left( {A_{k}^{\left( 1 \right)\tau } + {\text{isgn}}\left( s \right)A_{k}^{\left( 2 \right)\tau } } \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\tau } \left( s \right)} \right) \\ & \quad \cdot { \exp }\left( { - a_{1}^{k} \left| s \right|\eta + {\text{i}}s\left( {\xi - a_{2}^{k} \eta } \right)} \right)s^{ - 2} {\text{d}}s,\quad k = 1,2, \\ \end{aligned}$$
(3.19)

where

$$\begin{aligned} & A_{k}^{\left( 1 \right)p} = \frac{{\Delta_{1} \Delta_{11}^{\left( k \right)} + \Delta_{2} \Delta_{12}^{\left( k \right)} }}{{\Delta_{1}^{2} + \Delta_{2}^{2} }},\quad A_{k}^{\left( 2 \right)p} = \frac{{\Delta_{1} \Delta_{12}^{\left( k \right)} - \Delta_{2} \Delta_{11}^{\left( k \right)} }}{{\Delta_{1}^{2} + \Delta_{2}^{2} }},\, \\ & A_{k}^{\left( 1 \right)\tau } = \frac{{\Delta_{1} \Delta_{21}^{\left( k \right)} + \Delta_{2} \Delta_{22}^{\left( k \right)} }}{{\Delta_{1}^{2} + \Delta_{2}^{2} }},\quad A_{k}^{\left( 2 \right)\tau } = \frac{{\Delta_{1} \Delta_{22}^{\left( k \right)} - \Delta_{2} \Delta_{21}^{\left( k \right)} }}{{\Delta_{1}^{2} + \Delta_{2}^{2} }},\quad k = 1,2. \\ \end{aligned}$$
(3.20)

Having the form of an elastic potential function \(\Psi _{i} { = }\Psi _{i} \left( {x,y} \right),\quad i = 1,2\), (3.19) components of the displacement vector could be written as following:

$$\begin{aligned} U\left( {\xi ,\eta } \right) & = \mathop \sum \limits_{k = 1}^{2} \frac{{\kappa_{k} }}{{\sqrt {2\uppi} }}\mathop \smallint \limits_{ - \infty }^{\infty } \left( {\left( {A_{k}^{\left( 1 \right)p} + {\text{isgn}}\left( s \right)A_{k}^{\left( 2 \right)p} } \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{p} \left( s \right){ + }\left( { - 1} \right)^{k} \left( {A_{k}^{\left( 1 \right)\tau } + {\text{isgn}}\left( s \right)A_{k}^{\left( 2 \right)\tau } } \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\tau } \left( s \right)} \right) \\ & \quad \left( { - \left( {a_{1}^{k} \left| s \right| + {\text{i}}a_{2}^{k} s} \right)\sin \left( \phi \right) + {\text{i}}s\cos \left( \phi \right)} \right){ \exp }\left( { - a_{1}^{k} \left| s \right|\eta + {\text{i}}s\left( {\xi - a_{2}^{k} \eta } \right)} \right)s^{ - 2} {\text{d}}s, \\ \end{aligned}$$
(3.21)
$$\begin{aligned} V\left( {\xi ,\eta } \right) & = \mathop \sum \limits_{k = 1}^{2} \frac{1}{{\sqrt {2\uppi} }}\mathop \smallint \limits_{ - \infty }^{\infty } \left( {\left( {A_{k}^{\left( 1 \right)p} + {\text{isgn}}\left( s \right)A_{k}^{\left( 2 \right)p} } \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{p} \left( s \right){ + }\left( { - 1} \right)^{k} \left( {A_{k}^{\left( 1 \right)\tau } + {\text{isgn}}\left( s \right)A_{k}^{\left( 2 \right)\tau } } \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\tau } \left( s \right)} \right) \\ & \quad \left( { - \left( {a_{1}^{k} \left| s \right| + {\text{i}}a_{2}^{k} s} \right)\cos \left( \phi \right) - {\text{i}}s\sin \left( \phi \right)} \right){ \exp }\left( { - a_{1}^{k} \left| s \right|\eta + {\text{i}}s\left( {\xi - a_{2}^{k} \eta } \right)} \right)s^{ - 2} {\text{d}}s. \\ \end{aligned}$$
(3.22)

For any form of the function describing load at the boundary (both normal and tangential load), components of the stress tensor for m-th kind of material in the coordinate system related to the layering direction \(\left( {x,y,z} \right)\) take the form:

$$\begin{aligned} \sigma_{ij}^{\left( m \right)} \left( {\xi ,\eta } \right) & = \frac{1}{{\sqrt {2\pi } }}\mathop \smallint \limits_{ - \infty }^{\infty } \mathop \sum \limits_{k = 1}^{2} \left\{ {\left( {P_{ijm}^{\left( 1 \right)k} + {\text{isgn}}\left( s \right)P_{ijm}^{\left( 2 \right)k} } \right)\tilde{p}\left( s \right) + \left( { - 1} \right)^{k} \left( {Q_{ijm}^{\left( 1 \right)k} + {\text{isgn}}\left( s \right)Q_{ijm}^{\left( 2 \right)k} } \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\tau } \left( s \right)} \right\} \\ & \quad \cdot \exp \left( { - a_{1}^{k} \left| s \right|\eta + {\text{is}}\left( {\xi - a_{2}^{k} \eta } \right)} \right){\text{d}}s,\quad i,j = x,y;\quad m = 1,2, \\ \end{aligned}$$
(3.23)

where

$$\begin{aligned} & P_{xxm}^{\left( l \right)k} = A_{1} \kappa_{k} C_{1k}^{\left( l \right)p} + BC_{3k}^{\left( l \right)p} ,\quad Q_{xxm}^{\left( l \right)k} = A_{1} \kappa_{k} C_{1k}^{\left( l \right)\tau } + BC_{3k}^{\left( l \right)\tau } , \\ & P_{xym}^{\left( l \right)k} = C\left( {1 + \kappa_{k} } \right)C_{2k}^{\left( l \right)p} ,\quad Q_{xym}^{\left( l \right)k} = C\left( {1 + \kappa_{k} } \right)C_{2k}^{\left( l \right)\tau } , \\ & P_{yym}^{\left( l \right)k} = D_{m} \kappa_{k} C_{1k}^{\left( l \right)p} + E_{m} C_{3k}^{\left( l \right)p} ,\quad Q_{yym}^{\left( l \right)k} = D_{m} \kappa_{k} C_{1k}^{\left( l \right)\tau } + E_{m} C_{3k}^{\left( l \right)\tau } ,\quad m,l,k = 1,2. \\ \end{aligned}$$
(3.24)

and:

$$\begin{aligned} & C_{1k}^{\left( 1 \right)X} = A_{k}^{\left( 1 \right)X} b_{1}^{k} - A_{k}^{\left( 2 \right)X} b_{2}^{k} ,\quad C_{1k}^{\left( 2 \right)X} = A_{k}^{\left( 2 \right)X} b_{1}^{k} + A_{k}^{\left( 1 \right)X} b_{2}^{k} , \\ & C_{2k}^{\left( 1 \right)X} = A_{k}^{\left( 1 \right)X} b_{3}^{k} - A_{k}^{\left( 2 \right)X} b_{4}^{k} ,\quad C_{2k}^{\left( 2 \right)X} = A_{k}^{\left( 2 \right)X} b_{3}^{k} + A_{k}^{\left( 1 \right)X} b_{4}^{k} , \\ & C_{3k}^{\left( 1 \right)X} = A_{k}^{\left( 1 \right)X} b_{5}^{k} - A_{k}^{\left( 2 \right)X} b_{6}^{k} ,\quad C_{3k}^{\left( 2 \right)X} = A_{k}^{\left( 2 \right)X} b_{5}^{k} + A_{k}^{\left( 1 \right)X} b_{6}^{k} ,\quad X = p,\tau ;\quad k = 1,2, \\ \end{aligned}$$
(3.25)
$$\begin{aligned} & b_{1}^{k} = \left( {a_{1}^{k} } \right)^{2} { \sin }^{2} \left( \phi \right) - \left( {{ \cos }\left( \phi \right) - a_{2}^{k} { \sin }\left( \phi \right)} \right)^{2} ,\quad b_{2}^{k} = - 2a_{1}^{k} { \sin }\left( \phi \right)\left( {\cos \left( \phi \right) - a_{2}^{k} { \sin }\left( \phi \right)} \right), \\ & b_{3}^{k} = \left( {a_{1}^{k} } \right)^{2} \sin \left( \phi \right)\cos \left( \phi \right) + \left( {\cos \left( \phi \right) - a_{2}^{k} { \sin }\left( \phi \right)} \right)\left( {\sin \left( \phi \right) + a_{2}^{k} { \cos }\left( \phi \right)} \right), \\ & b_{4}^{k} = a_{1}^{k} \sin \left( \phi \right)\left( {\sin \left( \phi \right) + a_{2}^{k} { \cos }\left( \phi \right)} \right) - a_{1}^{k} \cos \left( \phi \right)\left( {\cos \left( \phi \right) + a_{2}^{k} { \sin }\left( \phi \right)} \right), \\ & b_{5}^{k} = \left( {a_{1}^{k} } \right)^{2} { \cos }^{2} \left( \phi \right) - \left( {{ \sin }\left( \phi \right) + a_{2}^{k} { \cos }\left( \phi \right)} \right)^{2} ,\quad b_{6}^{k} = 2a_{1}^{k} { \cos }\left( \phi \right)\left( {\sin \left( \phi \right) + a_{2}^{k} { \cos }\left( \phi \right)} \right),\quad k = 1,2. \\ \end{aligned}$$
(3.26)

In the next step three special cases of distributed load at the boundary will be investigated:

Special case 1 normal load (Fig. 2a).

Fig. 2
figure 2

Schemes of considered special cases of distributed load: a normal load, b tangential load

Full size image

Special case 2 tangential load (Fig. 2b).

Special case 3 combination of normal and tangential load (Fig. 1).

4 Special case 1 of normal pressure load

For the purpose of analysis only normal pressure will be considered, hence \(\tau \left( \xi \right) = 0\). For any form of the function describing the normal load, components of the stress tensor in the coordinate system related to the layering direction \(\left( {x,y,z} \right)\) take the form:

$$\begin{aligned} \sigma_{ij}^{\left( m \right)} \left( {\xi ,\eta } \right) & = \frac{1}{{\sqrt {2\uppi} }}\mathop \smallint \limits_{ - \infty }^{\infty } \mathop \sum \limits_{k = 1}^{2} \left( {P_{ijm}^{\left( 1 \right)k} + {\text{isgn}}\left( s \right)P_{ijm}^{\left( 2 \right)k} } \right) \\ & \quad \cdot \exp \left( { - a_{1}^{k} \left| s \right|\eta + {\text{i}}s\left( {\xi - a_{2}^{k} \eta } \right)} \right)\tilde{p}\left( s \right){\text{d}}s,\quad i,j = x,y;\quad m = 1,2. \\ \end{aligned}$$
(4.1)

In the further part of this paper a special case of an elliptical pressure will be presented, where the pressure function is in the form:

$$p\left( \xi \right) = p_{\hbox{max} } \sqrt {\left( {1 - \left( {\frac{\xi }{a}} \right)^{2} } \right)} \,{\text{H}}\left( {1 - \left| {\frac{\xi }{a}} \right|} \right), \quad \xi \in {\text{R}},\quad p_{\hbox{max} } = {\text{const}}.$$
(4.2)

Determination of stress distributions for this form of load function plays a significant role in contact mechanics (Hertz’s problem).

Fourier transform of expression (4.2) is equal [25]:

$$\tilde{p}\left( s \right) = \sqrt {\frac{\uppi}{2}} \frac{{p_{\hbox{max} } {\text{J}}_{1} \left( {a\left| s \right|} \right)}}{\left| s \right|},$$
(4.3)

where \({\text{J}}_{1} \left( s \right)\) is the Bessel function of the first kind.

We could determine expressions for components of stress tensor in the form:

$$\begin{aligned} \sigma_{ij}^{\left( m \right)} \left( {\xi ,\eta } \right) & = \mathop \smallint \limits_{0}^{\infty } \mathop \sum \limits_{k = 1}^{2} \frac{{p_{\hbox{max} } {\text{J}}_{1} \left( {as} \right)}}{s}\exp \left( { - a_{1}^{k} s\eta } \right) \\ & \quad \cdot \left( {P_{ijm}^{\left( 1 \right)k} \cos \left( {\left( {\xi - a_{2}^{k} \eta } \right)s} \right) - P_{ijm}^{\left( 2 \right)k} \sin \left( {\left( {\xi - a_{2}^{k} \eta } \right)s} \right)} \right){\text{d}}s,\quad i,j = x,y;\quad m = 1,2, \\ \end{aligned}$$
(4.4)

Considering dimensionless coordinates \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\xi } = \frac{\xi }{a},\,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } = \frac{\eta }{a},\,\,s = \frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{s} }}{a}\) and stress tensor components in m-th kind of material related to the average pressure \(p_{0}\) at the load area:

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma }_{yy}^{\left( m \right)} = \frac{{\sigma_{yy}^{\left( m \right)} }}{{p_{0} }},\quad \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma }_{xx}^{\left( m \right)} = \frac{{\sigma_{xx}^{\left( m \right)} }}{{p_{0} }},\quad \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma }_{xy}^{\left( m \right)} = \frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma }_{xy}^{\left( m \right)} }}{{p_{0} }},\quad m = 1,2,$$
(4.5)

where average pressure is related to the maximum pressure in the form \(p_{0} = \frac{\uppi}{4}p_{\hbox{max} }\), expression (4.4) could be rewritten in the form:

$$\begin{aligned} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma }_{ij}^{\left( m \right)} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\xi } ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } } \right) & = \frac{4}{\uppi}\mathop \sum \limits_{k = 1}^{2} \int\limits_{0}^{\infty } {\frac{{{\text{J}}_{1} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{s} } \right)}}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{s} }}\exp \left( { - a_{1}^{k} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{s} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } } \right)} \\ & \quad \cdot \left( {P_{ijm}^{\left( 1 \right)k} \cos \left( {\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\xi } - a_{2}^{k} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } } \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{s} } \right) - P_{ijm}^{\left( 2 \right)k} \sin \left( {\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\xi } - a_{2}^{k} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } } \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{s} } \right)} \right){\text{d}}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{s} ,\quad i,j = x,y;\quad m = 1,2. \\ \end{aligned}$$
(4.6)

On the basis of obtained analytical dependences, distributions of stress tensor components in coordinate system related to the layering orientation \(\left( {x,y,z} \right)\) were made to show smooth transitions between layering perpendicular and parallel to the boundary (Figs. 3, 4, 5). This approach will show stresses in directions perpendicular and parallel to the layering \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma }_{xx}^{(m)} ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma }_{yy}^{(m)}\) and will also determine shear stresses between alternate layers \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma }_{xy}^{(m)}\).

Fig. 3
figure 3

Isolines of dimensionless stress tensor component \({{\sigma_{yy}^{(m)} } \mathord{\left/ {\vphantom {{\sigma_{yy}^{(m)} } {p_{0} }}} \right. \kern-0pt} {p_{0} }},m = 1,2\) for \({{E_{1} } \mathord{\left/ {\vphantom {{E_{1} } {E_{2} }}} \right. \kern-0pt} {E_{2} }} = 4\,\); \(\nu_{1} = \nu_{2} = 0.3\); \(\chi = 0.5\) for layering angles: a\(\phi = 0^{ \circ }\), b\(\phi = 30^{ \circ }\), c\(\phi = 45^{ \circ }\), d\(\phi = 60^{ \circ }\), e\(\phi = 90^{ \circ }\)

Full size image
Fig. 4
figure 4

Isolines of dimensionless stress tensor component \({{\sigma_{xy}^{(m)} } \mathord{\left/ {\vphantom {{\sigma_{xy}^{(m)} } {p_{0} }}} \right. \kern-0pt} {p_{0} }}\) for \({{E_{1} } \mathord{\left/ {\vphantom {{E_{1} } {E_{2} }}} \right. \kern-0pt} {E_{2} }} = 4\,\); \(\nu_{1} = \nu_{2} = 0.3\,\); χ = 0.5 for layering angles: aϕ = 0°, bϕ = 30°, cϕ = 45°, dϕ = 60° eϕ = 90°, m = 1,2

Full size image
Fig. 5
figure 5

Isolines of dimensionless stress tensor component \({{\sigma_{xx}^{(m)} } \mathord{\left/ {\vphantom {{\sigma_{xx}^{(m)} } {p_{0} }}} \right. \kern-0pt} {p_{0} }}\) for E1/E2 = 4; \(\nu_{1} = \nu_{2} = 0.3\); \(\chi = 0.5\) for layering angles: aϕ = 0°, bϕ = 30°, cϕ = 45°, dϕ = 60°, eϕ = 90°, m = 1,2

Full size image

As can be seen in formula (4.6), stress distributions depend on the periodic cell component. In the presented examples, in the case of normal stresses \(\sigma_{yy}^{(m)}\) acting along the laminas for better illustration, they were drawn separately for cells of the first and second kind as continuous lines.

Figure 3 presents isolines of dimensionless stress tensor component \({{\sigma_{yy}^{(1)} } \mathord{\left/ {\vphantom {{\sigma_{yy}^{(1)} } {p_{0} }}} \right. \kern-0pt} {p_{0} }}\) and \({{\sigma_{yy}^{\left( 2 \right)} } \mathord{\left/ {\vphantom {{\sigma_{yy}^{\left( 2 \right)} } {p_{0} }}} \right. \kern-0pt} {p_{0} }}\) at different angles of lamina orientation. It is possible to observe smooth transitions of stress zones in the direction consistent with the rotation of the layering system. In addition, the distributions also show that isolines of highest values “approach” the pressure zone along with the rotation of the material system. This is related to taking over loads at higher extent by a component with higher Young’s module. Stress distributions \(\sigma_{yy}^{\left( 2 \right)}\) for the second cell periodicity component have a similar character to stress distributions \(\sigma_{yy}^{\left( 1 \right)}\), but due to the lower value of Young’s modulus, stress values are correspondingly lower.

Analyzing distributions of dimensionless shear stresses \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma }_{xy}^{(m)} ,\quad m = 1,2\) in the plane of stratification from Fig. 4 it can be noticed that for angles \(\phi = 0^{ \circ }\) and \(\phi = 90^{ \circ }\) there are two zones of local maximum stress (Fig. 4a, e). When changing the angle \(\phi\) there are three local zones of maximum shear stresses, with the stress value being the largest of those considered for the angle approximately \(45^{ \circ }\) at depth \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } \approx 0.7\).

It should be noticed that location and values of local maximum shear stresses \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma }_{xy}^{\left( m \right)}\) could provide information about potential delamination effects.

In Fig. 5 it can be seen that for cases where \(\phi = 0^{ \circ }\) and \(\phi = 90^{ \circ }\) the distributions of normal stresses \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma }_{xx}^{\left( m \right)}\) correspond to the shape of appropriate distributions of stresses \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma }_{yy}^{\left( m \right)}\) for perpendicular and longitudinal lamination (Fig. 3a, e) in the proportion related to the stiffness ratio of both materials of the periodic cell.

In the next step, the distributions of stress tensor components will be presented in relation to the coordinate system associated with the edge of material \(\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma }_{\xi \xi }^{\left( m \right)} ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma }_{\xi \eta }^{\left( m \right)} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma }_{\eta \eta }^{\left( m \right)} } \right)\) at two different depths \(\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } = 0.5,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } = 1} \right)\) and for two different Young’s modulus ratios \(\left( {{{E_{1} } \mathord{\left/ {\vphantom {{E_{1} } {E_{2} }}} \right. \kern-0pt} {E_{2} }} = 4,\,\,{{E_{1} } \mathord{\left/ {\vphantom {{E_{1} } {E_{2} }}} \right. \kern-0pt} {E_{2} }} = 8} \right)\).

In Fig. 6 we can see that for the angles \(0^{ \circ }\) and \(90^{ \circ }\), the tensor components \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma }_{\xi \xi }^{\left( m \right)}\) and \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma }_{\xi \xi }^{\left( m \right)}\) for m-th kind of material are equal for both components as well as the average stresses. Graphs of changes in stress values for different angles \(\phi\) are presented for two different depths \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } = 0.5\), \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } = 1\) and for two different Young’s modules ratios: \({{E_{1} } \mathord{\left/ {\vphantom {{E_{1} } {E_{2} }}} \right. \kern-0pt} {E_{2} }} = 4\) and \({{E_{1} } \mathord{\left/ {\vphantom {{E_{1} } {E_{2} }}} \right. \kern-0pt} {E_{2} }} = 8\).

Fig. 6
figure 6

Dimensionless stress tensor components \(\sigma_{\eta \eta }^{\left( m \right)}\) and \(\sigma_{\xi \xi }^{\left( m \right)}\) for \(\nu_{1} = \nu_{2} = 0.3\); \(\chi = 0.5\) for: a\({{E_{1} } \mathord{\left/ {\vphantom {{E_{1} } {E_{2} }}} \right. \kern-0pt} {E_{2} }} = 4,\,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } = 0.5\); b\({{E_{1} } \mathord{\left/ {\vphantom {{E_{1} } {E_{2} }}} \right. \kern-0pt} {E_{2} }} = 4,\,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } = 1\); c\({{E_{1} } \mathord{\left/ {\vphantom {{E_{1} } {E_{2} }}} \right. \kern-0pt} {E_{2} }} = 8,\,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } = 0.5\); d\({{E_{1} } \mathord{\left/ {\vphantom {{E_{1} } {E_{2} }}} \right. \kern-0pt} {E_{2} }} = 8,\,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } = 1\)

Full size image

From Fig. 6 it can be read that for the angle \(\phi = 0^{ \circ }\) (layering perpendicular to the edge), the components \(\sigma_{\xi \xi }^{\left( 1 \right)}\) and \(\sigma_{\xi \xi }^{\left( 2 \right)}\) are equal, while the stresses \(\sigma_{\eta \eta }^{\left( m \right)}\) coincide with the assumptions with the average boundary condition [3]. A similar situation takes place for layering parallel to the edge \((\phi = 90^{ \circ } )\), where the components \(\sigma_{\eta \eta }^{\left( 1 \right)}\) and \(\sigma_{\eta \eta }^{\left( 2 \right)}\) are equal. It can be seen that regardless of the angle of the lamination with respect to the edge the maximum stress values in the component with a higher stiffness increase with increasing the stiffness ratio of the components (Fig. 6).

5 Special case 2 of tangential load

For the purpose of this case only tangential load will be considered, hence \(p\left( \xi \right) = 0.\) For any form of the function describing tangential load, components of the stress tensor in the coordinate system related to the layering direction \(\left( {x,y,z} \right)\) take the form:

$$\begin{aligned} & \sigma_{ij}^{\left( m \right)} \left( {\xi ,\eta } \right) = \frac{1}{{\sqrt {2\uppi} }}\mathop \smallint \limits_{ - \infty }^{\infty } \mathop \sum \limits_{k = 1}^{2} \left( {Q_{ijm}^{\left( 1 \right)k} + {\text{isgn}}\left( s \right)Q_{ijm}^{\left( 2 \right)k} } \right) \\ & \quad \cdot \exp \left( { - a_{1}^{k} \left| s \right|\eta + {\text{i}}s\left( {\xi - a_{2}^{k} \eta } \right)} \right)\tilde{\tau }\left( s \right){\text{d}}s,\quad i,j = x,y;\;\;m = 1,2. \\ \end{aligned}$$
(5.1)

By analogy to the case of normal pressure a special case of an elliptical tangential load will be presented, where the tangential load function is in the form:

$$\tau \left( \xi \right) = \tau_{\hbox{max} } \sqrt {\left( {1 - \left( {\frac{\xi }{a}} \right)^{2} } \right)} \,{\text{H}}\left( {1 - \left| {\frac{\xi }{a}} \right|} \right), \quad \xi \in {\text{R}},\;\;\tau_{\hbox{max} } = {\text{const,}}$$
(5.2)

so expressions for stress tensor components could be easily written as:

$$\begin{aligned} & \sigma_{ij}^{\left( m \right)} \left( {\xi ,\eta } \right) = \mathop \smallint \limits_{0}^{\infty } \mathop \sum \limits_{k = 1}^{2} \left( { - 1} \right)^{k} \frac{{\tau_{\hbox{max} } {\text{J}}_{1} \left( {as} \right)}}{s}\exp \left( { - a_{1}^{k} s\eta } \right) \\ & \quad \cdot \left( {Q_{ijm}^{\left( 1 \right)k} \cos \left( {\left( {\xi - a_{2}^{k} \eta } \right)s} \right) - Q_{ijm}^{\left( 2 \right)k} \sin \left( {\left( {\xi - a_{2}^{k} \eta } \right)s} \right)} \right){\text{d}}s,\quad i,j = x,y;\;\;m = 1,2. \\ \end{aligned}$$
(5.3)

Considering dimensionless coordinates \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\xi } = \frac{\xi }{a},\,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } = \frac{\eta }{a},\,\,s = \frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{s} }}{a}\) and stress tensor components in m-th kind of material related to the average tangential load \(\tau_{0} = \frac{\uppi}{4}\tau_{\hbox{max} }\) at the load area:

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma }_{yy}^{\left( m \right)} = \frac{{\sigma_{yy}^{\left( m \right)} }}{{\tau_{0} }},\quad \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma }_{xx}^{\left( m \right)} = \frac{{\sigma_{xx}^{\left( m \right)} }}{{\tau_{0} }},\quad \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma }_{xy}^{\left( m \right)} = \frac{{\sigma_{xy}^{\left( m \right)} }}{{\tau_{0} }},\quad m = 1,2.$$
(5.4)

Expression (5.3) could be rewritten in the form:

$$\begin{aligned} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma }_{ij}^{\left( m \right)} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\xi } ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } } \right) & = \frac{4}{\uppi}\mathop \sum \limits_{k = 1}^{2} \int\limits_{0}^{\infty } {\left( { - 1} \right)^{k} \frac{{{\text{J}}_{1} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{s} } \right)}}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{s} }}\exp \left( { - a_{1}^{k} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{s} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } } \right)} \\ & \quad \cdot \left( {Q_{ijm}^{\left( 1 \right)k} \cos \left( {\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\xi } - a_{2}^{k} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } } \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{s} } \right) - Q_{ijm}^{\left( 2 \right)k} \sin \left( {\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\xi } - a_{2}^{k} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } } \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{s} } \right)} \right){\text{d}}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{s} ,\quad i,j = x,y;\;\;m = 1,2. \\ \end{aligned}$$
(5.5)

On the basis of obtained analytical dependences, distributions of stress tensor components were made to show smooth transitions between layering perpendicular and parallel to the boundary (Figs. 7, 8, 9).

Fig. 7
figure 7

Isolines of dimensionless stress tensor component \({{\sigma_{yy}^{(1)} } \mathord{\left/ {\vphantom {{\sigma_{yy}^{(1)} } {\tau_{0} }}} \right. \kern-0pt} {\tau_{0} }}\) and \({{\sigma_{yy}^{\left( 2 \right)} } \mathord{\left/ {\vphantom {{\sigma_{yy}^{\left( 2 \right)} } {\tau_{0} }}} \right. \kern-0pt} {\tau_{0} }}\) for \({{E_{1} } \mathord{\left/ {\vphantom {{E_{1} } {E_{2} }}} \right. \kern-0pt} {E_{2} }} = 4\,\)\(\nu_{1} = \nu_{2} = 0.3\); \(\chi = 0.5\) for layering angles: a\(\phi = 0^{ \circ }\), b\(\phi = 30^{ \circ }\), c\(\phi = 45^{ \circ }\), d\(\phi = 60^{ \circ }\), e\(\phi = 90^{ \circ }\)

Full size image
Fig. 8
figure 8

Isolines of dimensionless stress tensor component \({{\sigma_{xy}^{(m)} } \mathord{\left/ {\vphantom {{\sigma_{xy}^{(m)} } {\tau_{0} }}} \right. \kern-0pt} {\tau_{0} }}\) for E1/E2 = 4; \(\nu_{1} = \nu_{2} = 0.3\,\); χ = 0.5 for layering angles: aϕ = 0°, bϕ = 30°, cϕ = 45°, dϕ = 60° eϕ = 90°, m = 1,2

Full size image
Fig. 9
figure 9

Isolines of dimensionless stress tensor component \({{\sigma_{xx}^{(m)} } \mathord{\left/ {\vphantom {{\sigma_{xx}^{(m)} } {\tau_{0} }}} \right. \kern-0pt} {\tau_{0} }}\) for E1/E2 = 4; \(\nu_{1} = \nu_{2} = 0.3\,\); \(\chi = 0.5\) for layering angles: aϕ = 0°, bϕ = 30°, cϕ = 45°, dϕ = 60°, eϕ = 90°

Full size image

In Fig. 8 it can be seen that for angles \(\phi = 0^{ \circ }\) and \(\phi = 90^{ \circ }\) stress distributions \(\sigma_{xy}^{\left( m \right)}\) are similar to each other, and for other angles \(\phi\) there are stress accumulation near the ends of the load zone.

6 Special case 3 of combined normal and tangential load

Considering that values of maximal normal and tangential loads are equal \(\left( {p_{\hbox{max} } = \tau_{\hbox{max} } = \bar{p}} \right)\) and they are applied in the same area and described by elliptical functions, as in points 4 and 5, we have:

$$\tilde{p}\left( s \right) = \sqrt {\frac{\uppi}{2}} \frac{{\bar{p}\,{\text{J}}_{1} \left( {a\left| s \right|} \right)}}{\left| s \right|}\cos \left( \beta \right),\quad \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\tau } \left( s \right) = \sqrt {\frac{\uppi}{2}} \frac{{\bar{p}\,{\text{J}}_{1} \left( {a\left| s \right|} \right)}}{\left| s \right|}\sin \left( \beta \right).$$
(6.1)

Considering stress tensor components in m-th kind of material related to the average load \(\bar{p}_{0} = \frac{\uppi}{4}\bar{p}\) at the load area dimensionless stress tensor components \({{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma }_{ij}^{\left( m \right)} = \sigma_{ij}^{\left( m \right)} } \mathord{\left/ {\vphantom {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma }_{ij}^{\left( m \right)} = \sigma_{ij}^{\left( m \right)} } {\bar{p}_{0} }}} \right. \kern-0pt} {\bar{p}_{0} }}\) could be written as the following:

$$\begin{aligned} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma }_{ij}^{\left( m \right)} \left( {\xi ,\eta } \right) & = \mathop \smallint \limits_{0}^{\infty } \mathop \sum \limits_{k = 1}^{2} \frac{{{\text{J}}_{1} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{s} } \right)}}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{s} }}\exp \left( { - a_{1}^{k} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{s} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } } \right) \cdot \left( {\left( {P_{ijm}^{\left( 1 \right)k} \cos \left( \beta \right) + \left( { - 1} \right)^{k} Q_{ijm}^{\left( 1 \right)k} \sin \left( \beta \right)} \right)\cos \left( {\left( {\xi - a_{2}^{k} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } } \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{s} } \right)} \right. \\ & \quad \left. { - \left( {P_{ijm}^{\left( 2 \right)k} \cos \left( \beta \right) + \left( { - 1} \right)^{k} Q_{ijm}^{\left( 2 \right)k} \sin \left( \beta \right)} \right)\sin \left( {\left( {\xi - a_{2}^{k} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } } \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{s} } \right)} \right){\text{d}}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{s} ,\quad i,j = x,y;\;\;m = 1,2. \\ \end{aligned}$$
(6.2)

For the case of loading the half-plane with normal and tangential loads, stress distributions were made at depth \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } = 0.1\), assuming that the surface load vector \({\varvec{\upsigma}}\) would take the form:

$${\varvec{\upsigma}} = \tau \left( \xi \right)\vec{i} + p\left( \xi \right)\vec{j} = \sigma \left( \xi \right)\sin \left( \beta \right)\vec{i} + \sigma \left( \xi \right)\cos \left( \beta \right)\vec{j}.$$
(6.3)

In the shear stress \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma }_{xy}^{(m)}\) and normal stress \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma }_{xx}^{(m)}\) graphs (Figs. 10,  11), the parity of stress distribution \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma }_{xx}^{(m)}\) for parallel and perpendicular layers to the edge can be observed (Fig. 10a, c), and the oddity of \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma }_{xy}^{(m)}\) stresses (Fig. 11a, c).

Fig. 10
figure 10

Dimensionless stress tensor component \({{\sigma_{xx}^{(m)} } \mathord{\left/ {\vphantom {{\sigma_{xx}^{(m)} } {\bar{p}}}} \right. \kern-0pt} {\bar{p}}}\) for E1/E2 = 4; \(\nu_{1} = \nu_{2} = 0.3\,\); \(\chi = 0.5\); at \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } = 0.1\) for different layering angles ϕ: aϕ = 0°, bϕ = 45°, cϕ = 90° and loads: \(1 - \beta = 0^{ \circ }\); \(2 - \beta = - 45^{ \circ }\); \(3 - \beta = 45^{ \circ }\); \(4 - \beta = - 90^{ \circ }\); \(5 - \beta = 90^{ \circ }\)

Full size image
Fig. 11
figure 11

Dimensionless stress tensor component \({{\sigma_{xy}^{(m)} } \mathord{\left/ {\vphantom {{\sigma_{xy}^{(m)} } {\bar{p}}}} \right. \kern-0pt} {\bar{p}}}\) for E1/E2 = 4; \(\nu_{1} = \nu_{2} = 0.3\,\); \(\chi = 0.5\); at \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } = 0.1\) for different layering angles ϕ: aϕ = 0°, bϕ = 45°, cϕ = 90° and loads: \(1 - \beta = 0^{ \circ }\); \(2 - \beta = - 45^{ \circ }\); \(3 - \beta = 45^{ \circ }\); \(4 - \beta = - 90^{ \circ }\); \(5 - \beta = 90^{ \circ }\)

Full size image

From the stress distribution \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma }_{yy}^{(m)}\) it can be seen that the stress values \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma }_{yy}^{(1)}\) for the first component are much higher than for the second component \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma }_{yy}^{(2)}\), regardless of the angle of layering \(\phi\) (Fig. 12).

In the next step, based on the received dependencies, the basic problem will be solved when the half-plane is loaded with concentrated force (Fig. 13).

Fig. 12
figure 12

Dimensionless stress tensor components \({{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma }_{yy}^{(m)} } \mathord{\left/ {\vphantom {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma }_{yy}^{(m)} } {\bar{p}}}} \right. \kern-0pt} {\bar{p}}}\) for E1/E2 = 4; \(\nu_{1} = \nu_{2} = 0.3\,\); \(\chi = 0.5\); at \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } = 0.1\) for different layering angles ϕ: a, bϕ = 0°, c, dϕ = 45°, e, fϕ = 90° and loads: \(1 - \beta = 0^{ \circ }\); \(2 - \beta = - 45^{ \circ }\); \(3 - \beta = 45^{ \circ }\); \(4 - \beta = - 90^{ \circ }\); \(5 - \beta = 90^{ \circ }\)

Full size image

7 Special case of concentrated load

We will now consider the case of boundary load with concentrated force \(\sigma_{0}\) applied at an angle \(\theta\) to the surface of the material with a certain shift relative to the origin of the coordinate system given by the constant \(a\) (Fig. 13).

Fig. 13
figure 13

Scheme of considered concentrated load problem

Full size image

Forces at the surface could be written in the forms:

$$P = \sigma_{0} \sin \left( \theta \right),\quad Q = \sigma_{0} \cos \left( \theta \right),\quad \sigma_{0} = {\text{const,}}$$
(7.1)

hence functions describing load distribution are formulated as follows:

$$p\left( \xi \right) = P\updelta\left( {a - \xi } \right),\quad \tau \left( \xi \right) = Q\updelta\left( {a - \xi } \right),\quad P,Q = {\text{const}},$$
(7.2)

where \(\updelta\left( \cdot \right)\) is Dirac delta function.

Fourier transforms of functions (7.2) could be written as:

$$\tilde{p}\left( s \right) = \frac{P}{{\sqrt {2\uppi} }}\exp \left( { - {\text{i}}as} \right),\quad \tilde{\tau }\left( s \right) = \frac{Q}{{\sqrt {2\uppi} }}\exp \left( { - {\text{i}}as} \right).$$
(7.3)

In the next step Fourier transforms of boundary loads were applied in expressions describing elastic potentials - expression (1.23), hence for the case of concentrated load elastic potentials are expressed as:

$$\begin{aligned} \varPsi_{k} \left( {\xi ,\eta } \right) & = \frac{1}{{2\uppi}}\mathop \smallint \limits_{ - \infty }^{\infty } \left( {A_{k}^{\left( 1 \right)p} P + \left( { - 1} \right)^{k} A_{k}^{\left( 1 \right)\tau } Q + {\text{isgn}}\left( s \right)\left( {A_{k}^{\left( 2 \right)p} P + \left( { - 1} \right)^{k} A_{k}^{\left( 2 \right)\tau } Q} \right)} \right) \\ & \quad \cdot { \exp }\left( { - a_{1}^{k} \left| s \right|\eta + {\text{i}}s\left( {\xi - a - a_{2}^{k} \eta } \right)} \right)\frac{{{\text{d}}s}}{{s^{2} }},\quad k = 1,2. \\ \end{aligned}$$
(7.4)

Stress tensor components for the problem of concentrated load for composite with slant lamination could be written in the form of closed solutions:

$$\begin{aligned} \sigma_{xx}^{(m)} \left( {\xi ,\eta } \right) & = \sqrt {\frac{2}{\uppi}} \sum\limits_{k = 1}^{2} {\frac{{A_{1} \kappa_{k} \left( {a_{1}^{k} \eta C_{1k}^{\left( 1 \right)p} + \left( {a_{2}^{k} \eta + a - \xi } \right)C_{1k}^{\left( 2 \right)p} } \right) + B\left( {a_{1}^{k} \eta C_{3k}^{\left( 1 \right)p} + \left( {a_{2}^{k} \eta + a - \xi } \right)C_{3k}^{\left( 2 \right)p} } \right)}}{{\left( {a_{1}^{k} \eta } \right)^{2} + \left( {\xi - a - a_{2}^{k} \eta } \right)^{2} }}} P \\ & \quad + \left( { - 1} \right)^{k} \frac{{A_{1} \kappa_{k} \left( {a_{1}^{k} \eta C_{1k}^{\left( 1 \right)\tau } + \left( {a_{2}^{k} \eta + a - \xi } \right)C_{1k}^{\left( 2 \right)\tau } } \right) + B\left( {a_{1}^{k} \eta C_{3k}^{\left( 1 \right)\tau } + \left( {a_{2}^{k} \eta + a - \xi } \right)C_{3k}^{\left( 2 \right)\tau } } \right)}}{{\left( {a_{1}^{k} \eta } \right)^{2} + \left( {\xi - a - a_{2}^{k} \eta } \right)^{2} }}Q, \\ \end{aligned}$$
(7.5)
$$\begin{aligned} \sigma_{xy}^{(m)} \left( {\xi ,\eta } \right) & = \sqrt {\frac{2}{\uppi}} \sum\limits_{k = 1}^{2} {\frac{{\left( {1 + \kappa_{k} } \right)\left( {a_{1}^{k} \eta C_{2k}^{\left( 1 \right)p} + \left( {a_{2}^{k} \eta + a - \xi } \right)C_{2k}^{\left( 2 \right)p} } \right)}}{{\left( {a_{1}^{k} \eta } \right)^{2} + \left( {\xi - a - a_{2}^{k} \eta } \right)^{2} }}P} \\ & \quad + \left( { - 1} \right)^{k} \frac{{\left( {1 + \kappa_{k} } \right)\left( {a_{1}^{k} \eta C_{2k}^{\left( 1 \right)\tau } + \left( {a_{2}^{k} \eta + a - \xi } \right)C_{2k}^{\left( 1 \right)\tau } } \right)}}{{\left( {a_{1}^{k} \eta } \right)^{2} + \left( {\xi - a - a_{2}^{k} \eta } \right)^{2} }}Q, \\ \end{aligned}$$
(7.6)
$$\begin{aligned} \sigma_{yy}^{(m)} \left( {\xi ,\eta } \right) & = \sqrt {\frac{2}{\uppi}} \sum\limits_{k = 1}^{2} {\frac{{D_{m} \kappa_{k} \left( {a_{1}^{k} \eta C_{1k}^{\left( 1 \right)p} + \left( {a_{2}^{k} \eta + a - \xi } \right)C_{1k}^{\left( 2 \right)p} } \right) + E_{m} \left( {a_{1}^{k} \eta C_{3k}^{\left( 1 \right)p} + \left( {a_{2}^{k} \eta + a - \xi } \right)C_{3k}^{\left( 2 \right)p} } \right)}}{{\left( {a_{1}^{k} \eta } \right)^{2} + \left( {\xi - a - a_{2}^{k} \eta } \right)^{2} }}} P \\ & \quad + \,\left( { - 1} \right)^{k} \frac{{D_{m} \kappa_{k} \left( {a_{1}^{k} \eta C_{1k}^{\left( 1 \right)\tau } + \left( {a_{2}^{k} \eta + a - \xi } \right)C_{1k}^{\left( 2 \right)\tau } } \right) + E_{m} \left( {a_{1}^{k} \eta C_{3k}^{\left( 1 \right)\tau } + \left( {a_{2}^{k} \eta + a - \xi } \right)C_{3k}^{\left( 2 \right)\tau } } \right)}}{{\left( {a_{1}^{k} \eta } \right)^{2} + \left( {\xi - a - a_{2}^{k} \eta } \right)^{2} }}Q. \\ \end{aligned}$$
(7.7)

Stress tensor components (7.5)–(7.7) in dimensionless coordinates \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\xi } ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta }\) take forms:

$$\begin{aligned} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma }_{xx}^{(m)} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\xi } ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } } \right) & = \sqrt {\frac{2}{\uppi}} \sum\limits_{k = 1}^{2} {\frac{{A_{1} \kappa_{k} \left( {a_{1}^{k} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } C_{1k}^{\left( 1 \right)p} + \left( {a_{2}^{k} \eta + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\xi } } \right)C_{1k}^{\left( 2 \right)p} } \right) + B\left( {a_{1}^{k} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } C_{3k}^{\left( 1 \right)p} + \left( {a_{2}^{k} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\xi } } \right)C_{3k}^{\left( 2 \right)p} } \right)}}{{\left( {a_{1}^{k} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } } \right)^{2} + \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\xi } - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a} - a_{2}^{k} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } } \right)^{2} }}} \sin \left( \theta \right) \\ & \quad + \,\left( { - 1} \right)^{k} \frac{{A_{1} \kappa_{k} \left( {a_{1}^{k} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } C_{1k}^{\left( 1 \right)\tau } + \left( {a_{2}^{k} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\xi } } \right)C_{1k}^{\left( 2 \right)\tau } } \right) + B\left( {a_{1}^{k} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } C_{3k}^{\left( 1 \right)\tau } + \left( {a_{2}^{k} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\xi } } \right)C_{3k}^{\left( 2 \right)\tau } } \right)}}{{\left( {a_{1}^{k} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } } \right)^{2} + \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\xi } - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a} - a_{2}^{k} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } } \right)^{2} }}\cos \left( \theta \right), \\ \end{aligned}$$
(7.8)
$$\begin{aligned} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma }_{xy}^{(m)} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\xi } ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } } \right) & = \sqrt {\frac{2}{\uppi}} \sum\limits_{k = 1}^{2} {\frac{{\left( {1 + \kappa_{k} } \right)\left( {a_{1}^{k} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } C_{2k}^{\left( 1 \right)p} + \left( {a_{2}^{k} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\xi } } \right)C_{2k}^{\left( 2 \right)p} } \right)}}{{\left( {a_{1}^{k} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } } \right)^{2} + \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\xi } - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a} - a_{2}^{k} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } } \right)^{2} }}\sin \left( \theta \right)} \\ & \quad + \,\left( { - 1} \right)^{k} \frac{{\left( {1 + \kappa_{k} } \right)\left( {a_{1}^{k} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } C_{2k}^{\left( 1 \right)\tau } + \left( {a_{2}^{k} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\xi } } \right)C_{2k}^{\left( 1 \right)\tau } } \right)}}{{\left( {a_{1}^{k} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } } \right)^{2} + \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\xi } - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a} - a_{2}^{k} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } } \right)^{2} }}\cos \left( \theta \right), \\ \end{aligned}$$
(7.9)
$$\begin{aligned} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma }_{yy}^{(m)} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\xi } ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } } \right) & = \sqrt {\frac{2}{\uppi}} \sum\limits_{k = 1}^{2} {\frac{{D_{m} \kappa_{k} \left( {a_{1}^{k} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } C_{1k}^{\left( 1 \right)p} + \left( {a_{2}^{k} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\xi } } \right)C_{1k}^{\left( 2 \right)p} } \right) + E_{m} \left( {a_{1}^{k} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } C_{3k}^{\left( 1 \right)p} + \left( {a_{2}^{k} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\xi } } \right)C_{3k}^{\left( 2 \right)p} } \right)}}{{\left( {a_{1}^{k} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } } \right)^{2} + \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\xi } - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a} - a_{2}^{k} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } } \right)^{2} }}} \sin \left( \theta \right) \\ & \quad + \,\left( { - 1} \right)^{k} \frac{{D_{m} \kappa_{k} \left( {a_{1}^{k} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } C_{1k}^{\left( 1 \right)\tau } + \left( {a_{2}^{k} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\xi } } \right)C_{1k}^{\left( 2 \right)\tau } } \right) + E_{m} \left( {a_{1}^{k} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } C_{3k}^{\left( 1 \right)\tau } + \left( {a_{2}^{k} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\xi } } \right)C_{3k}^{\left( 2 \right)\tau } } \right)}}{{\left( {a_{1}^{k} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } } \right)^{2} + \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\xi } - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a} - a_{2}^{k} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } } \right)^{2} }}\cos \left( \theta \right). \\ \end{aligned}$$
(7.10)

where dimensionless stresses are related to the value of force \(\sigma_{0}\) in considered boundary condition:

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma }_{xx}^{(m)} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma }_{xy}^{(m)} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma }_{yy}^{(m)} = \,\frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma }_{xx}^{(m)} }}{{\sigma_{0} }},\frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma }_{xy}^{(m)} }}{{\sigma_{0} }},\frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\sigma }_{yy}^{(m)} }}{{\sigma_{0} }},\quad \sigma_{0} = const$$
(7.11)

and dimensionless coordinates are related to the thickness of periodic cell as:

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\xi } = \frac{\xi }{l},\,\,\,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\eta } = \frac{\eta }{l},\,\,\,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a} = \frac{a}{l}.$$
(7.12)

The solutions obtained in the general form for concentrated forces could allow solving boundary problems described by other pressure distributions, using appropriate functions describing load distribution. The stress distribution given by Eqs. (7.5)–(7.7) stands for the fundamental solution for a periodically laminated half-plane with the slant lamination to the boundary, and can be used to solve some boundary value problems of a heterogeneous body (for example: a crack or inclusion angled to the layering in the composite space, contact problems).

8 Conclusions

The normal pressure problem for the elastic microperiodic composite half-plane with slant layering was solved in the general form and for the special case of an elliptic normal pressure. Stress tensor components were determined and their distributions were made numerically. Also the basic problem was solved involving the loading of half-plane with focused force and an analytical form of solutions for this problem was obtained. Presented analytical solutions are the generalization of problems of pressure load on microperiodic half-plane with layers perpendicular parallel to the edge given in [3] and [5], respectively and their extension to materials with an angular arrangement of layers relative to the boundary surface with stratification angle.

Obtained solutions allow to draw following conclusions:

  1. 1.

    The averaged boundary condition can be successfully used in solving plane problems elasticity for microperiodic composite materials with layering inclined at an angle to the boundary.

  2. 2.

    Obtained solutions regarding stress tensor components under the surface of the material can provide basic information during the design process of connections exposed to damage in the pressure zone of bodies made of layered materials and their possible optimization in terms of the layering angle.

  3. 3.

    Dependencies obtained in this paper can be used to solve problems such as: fracture problems, contact problems (with and without frictional forces), inclusions passing at an angle to stratification etc.