Sommerfeld effect in a two-disk rotor dynamic system at various unbalance conditions

Abstract

Near resonance behavior of a shaft-rotor system driven by a motor with limited power gives rise to the Sommerfeld effect wherein the rotor speed gets stuck till a specific level of excitation power is reached. In this paper, a semi-analytical method is used to observe the Sommerfeld effect of a two-disk rotor system driven through a direct current motor. The effect of relative unbalance position on vibration amplitude of a two disk rotor-shaft system is studied in detail. We observe the change in critical power input for passage through resonance by changing the unbalance positions on the disks. We also investigate the case where two close resonance frequencies interfere with the jump phenomenon associated with the Sommerfeld effect. Prediction of critical power input in complex rotor system is highly essential. Else the system may be destroyed due to large vibration amplitudes generated during operations. In this article, drive and rotor dynamics are modeled together by using multi-energy domain bond graph approach and theoretically obtained steady-state characteristics are validated through transient simulations.

Appendices

Appendix 1

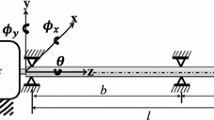
The disc locations are specified as $a_{1} = 0.3{\text{ m}}$, $b_{1} = 0.6{\text{ m}}$, $a_{2} = 0.7{\text{ m}}$, $b_{2} = 0.2{\text{ m}}$, with $a_{1} + b_{1} = a_{2} + b_{2} = L$ (Fig. 20). The expressions for influence coefficients in Eqs. (1, 2) are given as follows:

$$\begin{aligned} u_{l11} = & \frac{{a_{1} b_{1} }}{6EIL}\left( {L^{2} - b_{1}^{2} - a_{1}^{2} } \right),\quad u_{l\phi 11} = \frac{{a_{1} }}{6EIL}\left( {6a_{1} L - 3a_{1}^{2} - 2L^{2} - a_{1}^{2} } \right),\quad u_{\phi l11} = \frac{{b_{1} }}{6EIL}\left( {L^{2} - b_{1}^{2} - 3a_{1}^{2} } \right), \\ u_{\phi 11} = & \frac{{ - \left( {6a_{1} L - 3a_{1}^{2} - 2L^{2} - 3a_{1}^{2} } \right)}}{6EIL},\quad u_{l22} = \frac{{a_{2} b_{2} }}{6EIL}\left( {L^{2} - b_{2}^{2} - a_{2}^{2} } \right),\quad u_{l\phi 22} = \frac{{a_{2} }}{6EIL}\left( {6a_{2} L - 3a_{2}^{2} - 2L^{2} - a_{2}^{2} } \right) \\ u_{\phi l22} = & \frac{{b_{2} }}{6EIL}\left( {L^{2} - b_{2}^{2} - 3a_{2}^{2} } \right),\quad u_{\phi 22} = \frac{{ - \left( {6a_{2} L - 3a_{2}^{2} - 2L^{2} - 3a_{2}^{2} } \right)}}{6EIL},\quad u_{l12} = \frac{{b_{1} }}{6EIL}\left( {\frac{L}{{b_{1} }}\left( {a_{2} - a_{1} } \right)^{3} + a_{2} \left( {L^{2} - b_{1}^{2} } \right) - a_{2}^{3} } \right) \\ u_{l\phi 12} = & \frac{{\left( {a_{2}^{3} - 3a_{2}^{2} L + 3a_{2} a_{1}^{2} - 3a_{1}^{2} L + 2a_{2} L^{2} } \right)}}{6EIL},\quad u_{\phi l12} = \frac{{\left( {3L(a_{2} - a_{1} )^{2} + b_{1} \left( {L^{2} - b_{1}^{2} } \right) - 3b_{1} a_{2}^{2} } \right)}}{6EIL}, \\ u_{\phi 12} = & \frac{{ - \left( {6a_{2} L - 3a_{1}^{2} - 2L^{2} - 3a_{2}^{2} } \right)}}{6EIL},\quad u_{l21} = \frac{{b_{2} a_{1} }}{6EIL}\left( {L^{2} - b_{2}^{2} - a_{1}^{2} } \right),\quad u_{l\phi 21} = \frac{{ - a_{1} }}{6EIL}\left( {6a_{2} L - 3a_{2}^{2} - 2L^{2} - a_{1}^{2} } \right) \\ u_{\phi l21} = & \frac{{b_{2} }}{6EIL}\left( {L^{2} - b_{2}^{2} - 3a_{1}^{2} } \right),\quad u_{\phi 21} = \frac{{ - \left( {6a_{2} L - 3a_{2}^{2} - 2L^{2} - 3a_{1}^{2} } \right)}}{6EIL}. \\ \end{aligned}$$

Fig. 20

Load and deflection location definitions for computation of influence coefficients

Appendix 2

The sub-matrices of $\left[ {\mathbf{A}} \right]_{16 \times 16}$ in Eq. (22) are detailed as follows:

$$\left[ {{\mathbf{A}}_{{\mathbf{1}}} } \right] = \left[ {\begin{array}{*{20}l} {\frac{{ - (R_{e} + \lambda_{i} K_{l1} )}}{{m_{1} }}} \hfill & {\frac{{ - (R_{l\phi } + \lambda_{i} K_{l\phi 1} )}}{{m_{1} }}} \hfill & 0 \hfill & 0 \hfill & {\frac{{ - K_{l1} }}{{m_{1} }}} \hfill & {\frac{{ - K_{l\phi 1} }}{{m_{1} }}} \hfill & {\frac{{ - \dot{\theta }\lambda_{i} K_{l1} }}{{m_{1} }}} \hfill & {\frac{{ - \dot{\theta }\lambda_{i} K_{l\phi 1} }}{{m_{1} }}} \hfill \\ {\frac{{ - (R_{l\phi } + \lambda_{i} K_{\phi l1} )}}{{I_{d1} }}} \hfill & {\frac{{ - (R_{e\phi } + \lambda_{i} K_{\phi 1} )}}{{I_{d1} }}} \hfill & 0 \hfill & {\frac{{ - \dot{\theta }I_{p1} }}{{I_{d1} }}} \hfill & {\frac{{ - K_{\phi l1} }}{{I_{d1} }}} \hfill & {\frac{{ - K_{\phi 1} }}{{I_{d1} }}} \hfill & {\frac{{ - \dot{\theta }\lambda_{i} K_{\phi l1} }}{{I_{d1} }}} \hfill & {\frac{{ - \dot{\theta }\lambda_{i} K_{\phi 1} }}{{I_{d1} }}} \hfill \\ 0 \hfill & 0 \hfill & {\frac{{ - (R_{e} + \lambda_{i} K_{l1} )}}{{m_{1} }}} \hfill & {\frac{{ - (R_{l\phi } + \lambda_{i} K_{l\phi 1} )}}{{m_{1} }}} \hfill & {\frac{{\dot{\theta }\lambda_{i} K_{l1} }}{{m_{1} }}} \hfill & {\frac{{\dot{\theta }\lambda_{i} K_{l\phi 1} }}{{m_{1} }}} \hfill & {\frac{{ - K_{l1} }}{{m_{1} }}} \hfill & {\frac{{ - K_{l\phi 1} }}{{m_{1} }}} \hfill \\ 0 \hfill & {\frac{{\dot{\theta }I_{p1} }}{{I_{d1} }}} \hfill & {\frac{{ - (R_{l\phi } + \lambda_{i} K_{\phi l1} )}}{{I_{d1} }}} \hfill & {\frac{{ - (R_{e\phi } + \lambda_{i} K_{\phi 1} )}}{{I_{d1} }}} \hfill & {\frac{{\dot{\theta }\lambda_{i} K_{\phi l1} }}{{I_{d1} }}} \hfill & {\frac{{\dot{\theta }\lambda_{i} K_{\phi 1} }}{{I_{d1} }}} \hfill & {\frac{{ - K_{\phi l1} }}{{I_{d1} }}} \hfill & {\frac{{ - K_{\phi 1} }}{{I_{d1} }}} \hfill \\ {\frac{{ - \lambda_{i} K_{l12} }}{{m_{2} }}} \hfill & {\frac{{ - \lambda_{i} K_{l\phi 12} }}{{m_{2} }}} \hfill & 0 \hfill & 0 \hfill & {\frac{{ - K_{l12} }}{{m_{2} }}} \hfill & {\frac{{ - K_{l\phi 12} }}{{m_{2} }}} \hfill & {\frac{{ - \dot{\theta }\lambda_{i} K_{l12} }}{{m_{2} }}} \hfill & {\frac{{ - \dot{\theta }\lambda_{i} K_{l\phi 12} }}{{m_{2} }}} \hfill \\ {\frac{{ - \lambda_{i} K_{\phi l12} }}{{I_{d2} }}} \hfill & {\frac{{ - \lambda_{i} K_{\phi 12} }}{{I_{d2} }}} \hfill & 0 \hfill & 0 \hfill & {\frac{{ - K_{\phi l12} }}{{I_{d2} }}} \hfill & {\frac{{ - K_{\phi 12} }}{{I_{d2} }}} \hfill & {\frac{{ - \dot{\theta }\lambda_{i} K_{\phi l12} }}{{I_{d2} }}} \hfill & {\frac{{ - \dot{\theta }\lambda_{i} K_{\phi 12} }}{{I_{d2} }}} \hfill \\ 0 \hfill & 0 \hfill & {\frac{{ - \lambda_{i} K_{l12} }}{{m_{2} }}} \hfill & {\frac{{ - \lambda_{i} K_{l\phi 12} }}{{m_{2} }}} \hfill & {\frac{{\dot{\theta }\lambda_{i} K_{l12} }}{{m_{2} }}} \hfill & {\frac{{\dot{\theta }\lambda_{i} K_{l\phi 12} }}{{m_{2} }}} \hfill & {\frac{{ - K_{l12} }}{{m_{2} }}} \hfill & {\frac{{ - K_{l\phi 12} }}{{m_{2} }}} \hfill \\ 0 \hfill & 0 \hfill & {\frac{{ - \lambda_{i} K_{\phi l12} }}{{I_{d2} }}} \hfill & {\frac{{ - \lambda_{i} K_{\phi 12} }}{{I_{d2} }}} \hfill & {\frac{{\dot{\theta }\lambda_{i} K_{\phi l12} }}{{I_{d2} }}} \hfill & {\frac{{\dot{\theta }\lambda_{i} K_{\phi 12} }}{{I_{d2} }}} \hfill & {\frac{{ - K_{\phi l12} }}{{I_{d2} }}} \hfill & {\frac{{ - K_{\phi 12} }}{{I_{d2} }}} \hfill \\ \end{array} } \right]$$

$$\left[ {{\mathbf{A}}_{{\mathbf{2}}} } \right] = \left[ {\begin{array}{*{20}l} {\frac{{ - \lambda_{i} K_{l21} }}{{m_{1} }}} \hfill & {\frac{{ - \lambda_{i} K_{l\phi 21} }}{{m_{1} }}} \hfill & 0 \hfill & 0 \hfill & {\frac{{ - K_{l21} }}{{m_{1} }}} \hfill & {\frac{{ - K_{l\phi 21} }}{{m_{1} }}} \hfill & {\frac{{ - \dot{\theta }\lambda_{i} K_{l21} }}{{m_{1} }}} \hfill & {\frac{{ - \dot{\theta }\lambda_{i} K_{l\phi 21} }}{{m_{1} }}} \hfill \\ {\frac{{ - \lambda_{i} K_{\phi l21} }}{{I_{d1} }}} \hfill & {\frac{{ - \lambda_{i} K_{\phi 21} }}{{I_{d1} }}} \hfill & 0 \hfill & 0 \hfill & {\frac{{ - K_{\phi l21} }}{{I_{d1} }}} \hfill & {\frac{{ - K_{\phi 21} }}{{I_{d1} }}} \hfill & {\frac{{ - \dot{\theta }\lambda_{i} K_{\phi l21} }}{{I_{d1} }}} \hfill & {\frac{{ - \dot{\theta }\lambda_{i} K_{\phi 21} }}{{I_{d1} }}} \hfill \\ 0 \hfill & 0 \hfill & {\frac{{ - \lambda_{i} K_{l21} }}{{m_{1} }}} \hfill & {\frac{{ - \lambda_{i} K_{l\phi 21} }}{{m_{1} }}} \hfill & {\frac{{\dot{\theta }\lambda_{i} K_{l21} }}{{m_{1} }}} \hfill & {\frac{{\dot{\theta }\lambda_{i} K_{l\phi 21} }}{{m_{1} }}} \hfill & {\frac{{ - K_{l21} }}{{m_{1} }}} \hfill & {\frac{{ - K_{l\phi 21} }}{{m_{1} }}} \hfill \\ 0 \hfill & 0 \hfill & {\frac{{ - \lambda_{i} K_{\phi l21} }}{{I_{d1} }}} \hfill & {\frac{{\lambda_{i} K_{\phi 21} }}{{I_{d1} }}} \hfill & {\frac{{\dot{\theta }\lambda_{i} K_{\phi l21} }}{{I_{d1} }}} \hfill & {\frac{{\dot{\theta }\lambda_{i} K_{\phi 21} }}{{I_{d1} }}} \hfill & {\frac{{ - K_{\phi l21} }}{{I_{d1} }}} \hfill & {\frac{{ - K_{\phi 21} }}{{I_{d1} }}} \hfill \\ {\frac{{ - (R_{e} + \lambda_{i} K_{l2} )}}{{m_{2} }}} \hfill & {\frac{{ - (R_{e\phi } + \lambda_{i} K_{l\phi 2} )}}{{m_{2} }}} \hfill & 0 \hfill & 0 \hfill & {\frac{{ - K_{l2} }}{{m_{2} }}} \hfill & {\frac{{ - K_{l\phi 2} }}{{m_{2} }}} \hfill & {\frac{{ - \dot{\theta }\lambda_{i} K_{l2} }}{{m_{2} }}} \hfill & {\frac{{ - \dot{\theta }\lambda_{i} K_{l\phi 2} }}{{m_{2} }}} \hfill \\ {\frac{{ - (R_{l\phi } + \lambda_{i} K_{\phi l2} )}}{{I_{d2} }}} \hfill & {\frac{{ - (R_{e\phi } + \lambda_{i} K_{\phi 2} )}}{{I_{d2} }}} \hfill & 0 \hfill & {\frac{{\dot{\theta }I_{p2} }}{{I_{d2} }}} \hfill & {\frac{{ - K_{\phi l2} }}{{I_{d2} }}} \hfill & {\frac{{ - K_{\phi 2} }}{{I_{d2} }}} \hfill & {\frac{{ - \dot{\theta }\lambda_{i} K_{\phi l2} }}{{I_{d2} }}} \hfill & {\frac{{ - \dot{\theta }\lambda_{i} K_{\phi 2} }}{{I_{d2} }}} \hfill \\ 0 \hfill & 0 \hfill & {\frac{{ - (R_{e} + \lambda_{i} K_{l2} )}}{{m_{2} }}} \hfill & {\frac{{ - (R_{l\phi } + \lambda_{i} K_{l\phi 2} )}}{{m_{2} }}} \hfill & {\frac{{\dot{\theta }\lambda_{i} K_{l2} }}{{m_{2} }}} \hfill & {\frac{{\dot{\theta }\lambda_{i} K_{l\phi 2} }}{{m_{2} }}} \hfill & {\frac{{ - K_{l2} }}{{m_{2} }}} \hfill & {\frac{{ - K_{l\phi 2} }}{{m_{2} }}} \hfill \\ 0 \hfill & {\frac{{\dot{\theta }I_{p2} }}{{I_{d2} }}} \hfill & {\frac{{ - (R_{l\phi } + \lambda_{i} K_{\phi l2} )}}{{I_{d2} }}} \hfill & {\frac{{ - (R_{e\phi } + \lambda_{i} K_{\phi 2} )}}{{I_{d2} }}} \hfill & {\frac{{\dot{\theta }\lambda_{i} K_{\phi l2} }}{{I_{d2} }}} \hfill & {\frac{{\dot{\theta }\lambda_{i} K_{\phi 2} }}{{I_{d2} }}} \hfill & {\frac{{ - K_{\phi l2} }}{{I_{d2} }}} \hfill & {\frac{{ - K_{\phi 2} }}{{I_{d2} }}} \hfill \\ \end{array} } \right]$$

$\left[ {{\mathbf{A}}_{{\mathbf{3}}} } \right] = \left[ I \right]_{8 \times 8}$ and $\left[ {{\mathbf{A}}_{{\mathbf{4}}} } \right] = \left[ 0 \right]_{8 \times 8}$.

Appendix 3

The 16 numbers of equations after separating the $\cos \left( {\omega t} \right)$ and $\sin \left( {\omega t} \right)$ parts as detailed in Sect. 2.3 are

$$\begin{aligned} & - m_{1} A_{1} \omega^{2} \cos \zeta_{1} - R_{e} A_{1} \omega \sin \zeta_{1} - R_{l\phi } B_{1} \omega \sin \xi_{1} + K_{l1} A_{1} \cos \zeta_{1} + K_{l\phi 1} B_{1} \cos \xi_{1} + K_{l21} A_{2} \cos \zeta_{2} \\ & \quad + K_{l\phi 21} B_{2} \cos \xi_{2} = me_{1} \omega^{2} \cos \left( {\delta_{1} } \right) \\ & m_{1} A_{1} \omega^{2} \sin \zeta_{1} - R_{e} A_{1} \omega \cos \zeta_{1} - R_{l\phi } B_{1} \omega \cos \xi_{1} - K_{l1} A_{1} \sin \zeta_{1} - K_{l\phi 1} B_{1} \sin \xi_{1} - K_{l21} A_{2} \sin \zeta_{2} \\ & \quad - K_{l\phi 21} B_{2} \sin \xi_{2} = - me_{1} \omega^{2} \sin \left( {\delta_{1} } \right) \\ & - I_{d1} B_{1} \omega^{2} \cos \xi_{1} - B_{1} R_{e\phi } \omega \sin \xi_{1} + \omega^{2} I_{p} B_{1} \cos \xi_{1} - R_{l\phi } A_{1} \omega \sin \zeta_{1} + K_{\phi l1} A_{1} \cos \zeta_{1} + K_{\phi 1} B_{1} \cos \xi_{1} \\ & \quad + K_{\phi l21} A_{2} \cos \zeta_{2} + K_{\phi 21} B_{2} \cos \xi_{2} = 0 \\ & I_{d1} B_{1} \omega^{2} \sin \xi_{1} - B_{1} R_{e\phi } \omega \cos \xi_{1} - \omega^{2} I_{p} B_{1} \sin \xi_{1} - R_{l\phi } A_{1} \omega \cos \zeta_{1} - K_{\phi l1} A_{1} \sin \zeta_{1} - K_{\phi 1} B_{1} \sin \xi_{1} \\ & \quad - K_{\phi l21} A_{2} \sin \zeta_{2} - K_{\phi 21} B_{2} \sin \xi_{2} = 0 \\ & - m_{1} A_{1} \omega^{2} \sin \zeta_{1} + R_{e} A_{1} \omega \cos \zeta_{1} + R_{l\phi } B_{1} \omega \cos \xi_{1} + K_{l1} A_{1} \sin \zeta_{1} + K_{l\phi 1} B_{1} \sin \xi_{1} + K_{l21} A_{2} \sin \zeta_{2} \\ & \quad + K_{l\phi 21} B_{2} \sin \xi_{2} = me_{1} \omega^{2} \sin \left( {\delta_{1} } \right) \\ & - m_{1} A_{1} \omega^{2} \cos \zeta_{1} - R_{e} A_{1} \omega \sin \zeta_{1} - R_{l\phi } B_{1} \omega \sin \xi_{1} + K_{l1} A_{1} \cos \zeta_{1} + K_{l\phi 1} B_{1} \cos \xi_{1} + K_{l21} A_{2} \cos \zeta_{2} \\ & \quad + K_{l\phi 21} B_{2} \cos \xi_{2} = me_{1} \omega^{2} \cos \left( {\delta_{1} } \right) \\ & - I_{d1} B_{1} \omega^{2} \sin \xi_{1} + B_{1} R_{e\phi } \omega \cos \xi_{1} + \omega^{2} I_{p} B_{1} \sin \xi_{1} + R_{l\phi } A_{1} \omega \cos \zeta_{1} + K_{\phi l1} A_{1} \sin \zeta_{1} + K_{\phi 1} B_{1} \sin \xi_{1} \\ & \quad + K_{\phi l21} A_{2} \sin \zeta_{2} + K_{\phi 21} B_{2} \sin \xi_{2} = 0 \\ & - I_{d1} B_{1} \omega^{2} \cos \xi_{1} - B_{1} R_{e\phi } \omega \sin \xi_{1} + \omega^{2} I_{p} B_{1} \cos \xi_{1} - R_{l\phi } A_{1} \omega \sin \zeta_{1} + K_{\phi l1} A_{1} \cos \zeta_{1} + K_{\phi 1} B_{1} \cos \xi_{1} \\ & \quad + K_{\phi l21} A_{2} \cos \zeta_{2} + K_{\phi 21} B_{2} \cos \xi_{2} = 0 \\ & - m_{2} A_{2} \omega^{2} \cos \zeta_{2} - R_{e} A_{2} \omega \sin \zeta_{2} - R_{l\phi } B_{2} \omega \sin \xi_{2} + K_{l12} A_{1} \cos \zeta_{1} + K_{l\phi 12} B_{1} \cos \xi_{1} + K_{l2} A_{2} \cos \zeta_{2} \\ & \quad + K_{l\phi 2} B_{2} \cos \xi_{2} = me_{2} \omega^{2} \sin \left( {\delta_{2} } \right) \\ & m_{2} A_{2} \omega^{2} \sin \zeta_{2} - R_{e} A_{2} \omega \cos \zeta_{2} - R_{l\phi } B_{2} \omega \cos \xi_{2} - K_{l12} A_{1} \sin \zeta_{1} - K_{l\phi 12} B_{1} \sin \xi_{1} - K_{l2} A_{2} \sin \zeta_{2} \\ & \quad - K_{l\phi 2} B_{2} \sin \xi_{2} = me_{2} \omega^{2} \cos \left( {\delta_{2} } \right) \\ & - I_{d2} B_{2} \omega^{2} \cos \xi_{2} - B_{2} R_{e\phi } \omega \sin \xi_{1} + \omega^{2} I_{p} B_{2} \cos \xi_{2} - R_{l\phi } A_{2} \omega \sin \zeta_{2} + K_{\phi l12} A_{1} \cos \zeta_{1} + K_{\phi 12} B_{1} \cos \xi_{1} \\ & \quad + K_{\phi l2} A_{2} \cos \zeta_{2} + K_{\phi 2} B_{2} \cos \xi_{2} = 0 \\ & I_{d2} B_{2} \omega^{2} \sin \xi_{2} - B_{2} R_{e\phi } \omega \cos \xi_{2} - \omega^{2} I_{p} B_{2} \sin \xi_{2} - R_{l\phi } A_{2} \omega \cos \zeta_{2} - K_{\phi l12} A_{1} \sin \zeta_{1} - K_{\phi 12} B_{1} \sin \xi_{1} \\ & \quad - K_{\phi l2} A_{2} \sin \zeta_{2} - K_{\phi 2} B_{2} \sin \xi_{2} = 0 \\ & - m_{2} A_{2} \omega^{2} \sin \zeta_{2} + R_{e} A_{2} \omega \cos \zeta_{2} + R_{l\phi } B_{2} \omega \cos \xi_{2} + K_{l12} A_{1} \sin \zeta_{1} + K_{l\phi 12} B_{1} \sin \xi_{1} + K_{l2} A_{2} \sin \zeta_{2} \\ & \quad + K_{l\phi 2} B_{2} \sin \xi_{2} = me_{2} \omega^{2} \sin \left( {\delta_{2} } \right) \\ & - m_{2} A_{2} \omega^{2} \cos \zeta_{2} - R_{e} A_{2} \omega \sin \zeta_{2} - R_{l\phi } B_{2} \omega \sin \xi_{2} + K_{l12} A_{1} \cos \zeta_{1} + K_{l\phi 12} B_{1} \cos \xi_{1} + K_{l2} A_{2} \cos \zeta_{2} \\ & \quad + K_{l\phi 2} B_{2} \cos \xi_{2} = me_{2} \omega^{2} \cos \left( {\delta_{2} } \right) \\ & - I_{d2} B_{2} \omega^{2} \sin \xi_{2} + B_{2} R_{e\phi } \omega \cos \xi_{2} + \omega^{2} I_{p} B_{2} \sin \xi_{2} + R_{l\phi } A_{2} \omega \cos \zeta_{2} + K_{\phi l12} A_{1} \sin \zeta_{1} + K_{\phi 12} B_{1} \sin \xi_{1} \\ & \quad + K_{\phi l2} A_{2} \sin \zeta_{2} + K_{\phi 2} B_{2} \sin \xi_{2} = 0 \\ & - I_{d2} B_{2} \omega^{2} \cos \xi_{2} - B_{2} R_{e\phi } \omega \sin \xi_{1} + \omega^{2} I_{p} B_{2} \cos \xi_{2} - R_{l\phi } A_{2} \omega \sin \zeta_{2} + K_{\phi l12} A_{1} \cos \zeta_{1} + K_{\phi 12} B_{1} \cos \xi_{1} \\ & \quad + K_{\phi l2} A_{2} \cos \zeta_{2} + K_{\phi 2} B_{2} \cos \xi_{2} = 0 \\ \end{aligned}$$