Double resonance capture of a two-degree-of-freedom oscillator coupled to a non-ideal motor

Abstract

This work presents the development of a discrete parameter model consisting of a concentrated mass which is supported by a set of springs and dampers positioned in two orthogonal directions, such that the mass can move horizontally and vertically in a plane. A non-ideal motor is attached to the mass such that the phenomenon of resonance capture can occur. Resonance capture occurs in structures with low damping which are attached to rotating machines with limited power supply. When resonance capture occurs, the mean angular velocity of the motor remains constant and the displacement of the structure increases. An investigation on the influence of the two orthogonal resonance frequencies is presented. It was found that this model can illustrate the dynamics of a more complex structure consisting of a portal frame coupled to a non-ideal unbalanced motor. Experimental tests are used to support numerical simulations and the analytical model.

Appendix

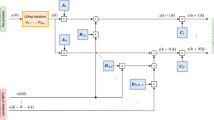
The equations of motion in terms of the uncoupled accelerations are given in Eqs. 17, 18 and 19.

$$\begin{aligned} \ddot{x}= & {} -\frac{\mu _1\mathrm {sin}\left( \phi \right) {\mathfrak{M}}({\dot{\phi}})}{J_1\left( \mu _1\mu _2-1\right) } +\frac{\mu _1\mu _2\mathrm {cos}\left( \phi \right) \mathrm {sin}\left( \phi \right) \left( \mu _1\mathrm {sin}\left( \phi \right) \dot{\phi }^2-F_y\right) }{\mu _1\mu _2-1}+\frac{\left( \mu _1\mu _2{\mathrm {cos}\left( \phi \right) }^{2}-1\right) \left( \mu _1\mathrm {cos}\left( \phi \right) \dot{\phi }^2-F_x\right) }{\mu _1\mu _2-1} \end{aligned}$$

(17)

$$\begin{aligned} \ddot{y}= & {} \frac{\mu _1\mathrm {cos}\left( \phi \right) {\mathfrak{M}}({\dot{\phi}})}{J_1\left( \mu _1\mu _2-1\right) } +\frac{\left( \mu _1\mu _2{\mathrm {sin}\left( \phi \right) }^{2}-1\right) \left( \mu _1\mathrm {sin}\left( \phi \right) \dot{\phi }^2-F_y\right) }{\mu _1\mu _2-1}+\frac{\mu _1\mu _2\mathrm {cos}\left( \phi \right) \mathrm {sin}\left( \phi \right) \left( \mu _1\mathrm {cos}\left( \phi \right) \dot{\phi }^2-F_x\right) }{\mu _1\mu _2-1} \end{aligned}$$

(18)

$$\begin{aligned} \ddot{\phi }= & {} -\frac{{\mathfrak{M}}(\dot{\phi })}{J_1\left( \mu _1\mu _2-1\right) } +\frac{\mu _2\mathrm {cos}\left( \phi \right) \left( \mu _1\mathrm {sin}\left( \phi \right) \dot{\phi }^2-F_y\right) }{\mu _1\mu _2-1}-\frac{\mu _2\mathrm {sin}\left( \phi \right) \left( \mu _1\mathrm {cos}\left( \phi \right) \dot{\phi }^2-F_x\right) }{\mu _1\mu _2-1} \end{aligned}$$

(19)

in which,

$$\begin{aligned} F_x\,= & \omega _x^2 x +2\xi _x\omega _x \dot{x} \end{aligned}$$

(20)

$$\begin{aligned} F_y\,= & \omega _y^2 x +2\xi _y\omega _y \dot{y} \end{aligned}$$

(21)

$$\begin{aligned} J_1\,= & J_0 + mr^2 \end{aligned}$$

(22)

$$\begin{aligned} \mu _1= & \frac{mr}{M+m} \end{aligned}$$

(23)

$$\begin{aligned} \mu _2= & \frac{mr}{J_1} \end{aligned}$$

(24)

1.1 Encoder

Figure 22 shows the optical sensor used to measure the angular velocity of the motor during the experimental tests.

Fig. 22

Optical sensor used to measure the angular velocity in the motor