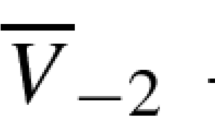Abstract
We investigate a relation between the super topological recursion and Gaiotto vectors for \({\mathcal {N}}=1\) superconformal blocks. Concretely, we introduce the notion of the untwisted and \(\mu \)-twisted super topological recursion and construct a dual algebraic description in terms of super Airy structures. We then show that the partition function of an appropriate super Airy structure coincides with the Gaiotto vector for \({\mathcal {N}}=1\) superconformal blocks in the Neveu–Schwarz or Ramond sector. Equivalently, the Gaiotto vector can be computed by the untwisted or \(\mu \)-twisted super topological recursion. This implies that the framework of the super topological recursion—equivalently super Airy structures—can be applied to compute the Nekrasov partition function of \({\mathcal {N}}=2\) pure U(2) supersymmetric gauge theory on \({\mathbb {C}}^2/{\mathbb {Z}}_2\) via a conjectural extension of the Alday–Gaiotto–Tachikawa correspondence.




Similar content being viewed by others
Notes
The AGT correspondence can be, in fact, thought of a particular example of a wider class of duality, the so-called BPS/CFT correspondence reviewed in [27,28,29,30] which describes a relation between supersymmetric gauge theory, integrable systems, and 2d conformal field theory. Another descendant of the BPS/CFT correspondence is the so-called Bethe/Gauge correspondence [32,33,34] which indeed predates the AGT correspondence.
They found Airy structures for \({\mathcal {W}}({\mathfrak {g}})\)-algebras of type D or E as well.
In the context of superconformal structures of super Riemann surfaces, a completely nonintegrable subbundle \({\mathcal {D}}\) of rank 0|1 normally refers to \({\mathcal {D}}\subset T{\mathbb {C}}_z\) (e.g. [38, Sect. 2.2]) instead of \(T^*{\mathbb {C}}_z\). Thus, one might find \(\tilde{{\mathcal {D}}}\) a dual description of \({\mathcal {D}}\).
The original definition in [9] considers only power series of \(\hbar \) rather than \(\hbar ^{\frac{1}{2}}\). However, there is no issue with extending the algebra with \(\hbar ^{\frac{1}{2}}\) because \(\deg \hbar ^{\frac{1}{2}}=1\). In particular, Theorem 3.2 stands because their proof considers induction with respect to \(\chi =2g+n\), and \(\chi \) remains integers even with \(\hbar ^{\frac{1}{2}}\).
This point is already addressed in [9, Sect. 5.1] when \(\tau _l=\delta _{l,-N+1}\) and \(Q_l=\phi _{kl}=\psi _{kl}=0\).
Since \(\{{{\bar{H}}}_i,{{\bar{F}}}_i\}\) and \(\{ H_i,F_i\}\) are linearly related by some upper triangular matrix, the resulting differential constraints \(H_ie^{{\mathcal {F}}}= F_ie^{{\mathcal {F}}}=0\) are equivalent to \(\bar{H}_ie^{{\mathcal {F}}_F}=\bar{F}_ie^{{\mathcal {F}}_F}=0\).
Without supersymmetry, a vector \(\vert w\rangle \) in the Verma module satisfying \(L_1 \vert w\rangle =\Lambda \vert w\rangle \) and \(L_{n\ge 2}\vert w\rangle =0\) is called the “Whittaker vector”, whereas the corresponding Gaiotto vector is rather defined as a formal sum of some cohomology classes of an appropriate instanton moduli space [7, Sect. 2.1]. Thus, strictly speaking, one may call \(\vert G\rangle \) in Definition 4.3 the Whittaker vector instead of the Gaiotto vector, though the AGT correspondence states that these two vectors are equivalent to each other. In the present paper, however, we call it the Gaiotto vector in order to emphasise a relation to four-dimensional supersymmetric gauge theory.
We abuse the notation and \(\vert M\rangle \) without any subscript refers to the Gaiotto vector of level M in the Neveu–Schwarz sector while \(\vert M\rangle _{\pm }\) with subscript are in the Ramond sector.
This is analogous to [7, Lemma 4.5].
[19] computed up to level 2.
This is because graphs in \(\hat{{\mathbb {G}}}\) are defined up to permutations.
See [7, Sect. 4.4] for the graphical interpretation without fermions where the symmetry factor is explicitly written. We omit an explicit formula for the symmetry factor for brevity of notation
To the authors’ best knowledge, an analogous vector in the Neveu–Schwarz sector is not discussed in the literature.
In the previous section, we denoted by I, J a collection of bosonic and fermionic variables. We abuse the notation here, but one should be able to decode whether they are collections of indices or variables from the context.
References
Alday, L.F., Gaiotto, D., Tachikawa, Y.: Liouville correlation functions from four-dimensional gauge theories. Lett. Math. Phys. 91, 167–197 (2010). arXiv:0906.3219
Andersen, J.E., Borot, G., Chekhov, L.O., Orantin, N.: The ABCD of topological recursion. arXiv:1703.03307
Braverman, A., Finkelberg, M., Nakajima, H.: Instanton moduli spaces and \({\cal{W}}\)-algebras. arXiv:1406.2381
Belavin, V., Feigin, B.: Super Liouville conformal blocks from N=2 SU(2) quiver gauge theories. JHEP 07, 079 (2011). arXiv:1105.5800
Belavin, A., Belavin, V., Bershtein, M.: Instantons and 2d Superconformal field theory. JHEP 09, 117 (2011). arXiv:1106.4001
Bonelli, G., Maruyoshi, K., Tanzini, A.: Gauge theories on ALE space and super Liouville correlation functions. Lett. Math. Phys. 101, 103–124 (2012). arXiv:1107.4609
Borot, G., Bouchard, V., Chidambaram, N.K., Creutzig, T.: Whittaker vectors for \({\cal{W}}\)-algebras from topological recursion. arXiv:2104.04516
Borot, G., Bouchard, V., Chidambaram, N.K., Creutzig, T., Noshchenko, D.: Higher airy structures, W algebras and topological recursion. arXiv:1812.08738
Bouchard, V., Ciosmak, P., Hadasz, L., Osuga, K., Ruba, B., Sułkowski, P.: Super quantum airy structures. arXiv:1907.08913
Bouchard, V., Eynard, B.: Think globally, compute locally. JHEP 02, 143 (2013). arXiv:1211.2302
Bouchard, V., Osuga, K.: Supereigenvalue models and topological recursion. JHEP 1804, 138 (2018)
Bouchard, V., Osuga, K.: “\({\cal{N}}=1\) Super Topological Recursion,” arXiv:2007.13186
Chekhov, L., Eynard, B., Orantin, N.: Free energy topological expansion for the 2-matrix model. JHEP 0612, 053 (2006). arXiv:math-ph/0603003
Ciosmak, P., Hadasz, L., Jaskólski, Z., Manabe, M., Sułkowski, P.: From CFT to Ramond super-quantum curves. JHEP 05, 133 (2018)
Eynard, B., Orantin, N.: Invariants of algebraic curves and topological expansion. Commun. Number Theory Phys. 1(2), 347–452 (2007)
Eynard, B., Orantin, N.: Topological recursion in random matrices and enumerative geometry. J. Phys. A Math. Theor. 42(29) (2009) arXiv:0811.3531
Gaiotto, D.: Asymptotically free \({\cal{N}} = 2\) theories and irregular conformal blocks. J. Phys. Conf. Ser. 462(1), 012014 (2013) arXiv:0908.0307
Gottsche, L., Nakajima, H., Yoshioka, K.: Instanton counting and Donaldson invariants. J. Differ. Geom. 80(3), 343–390 (2008)
Ito, Y.: Ramond sector of super Liouville theory from instantons on an ALE space. Nucl. Phys. B 861, 387–402 (2012). arXiv:1110.2176
Ito, Y.: Supersymmetric gauge theories on various four-dimensional spaces and two-dimensional conformal field theories. Ph.D Thesis
Kontsevich, M., Soibelman, Y.: Airy structures and symplectic geometry of topological recursion. arXiv:1701.09137
Le Floch, B.: A slow review of the AGT correspondence. arXiv:2006.14025
Manabe, M.: \(n\)-th parafermion \({\cal{W}_{N}}\) characters from \(U(N)\) instanton counting on \({\mathbb{C}^{2}}/{\mathbb{Z}_{n}}\). JHEP 06, 112 (2020) arXiv:2004.13960
Nakajima, H., Yoshioka, K.: Instanton counting on blowup. 1. Invent. Math. 162, 313–355 (2005). arXiv:math/0306198
Nakajima, H., Yoshioka, K.: Lectures on instanton counting. arXiv:math/0311058
Nekrasov, N.A.: Seiberg-Witten prepotential from instanton counting. Adv. Theor. Math. Phys. 7(5), 831–864 (2003) arXiv:hep-th/0206161
Nekrasov, N.: BPS/CFT correspondence: non-perturbative Dyson–Schwinger equations and qq-characters. JHEP 03, 181 (2016) arXiv:1512.05388
Nekrasov, N.: BPS/CFT correspondence III: Gauge Origami partition function and qq-characters. Commun. Math. Phys. 358(3), 863–894 (2018) arXiv:1701.00189
Nekrasov, N.: BPS/CFT correspondence IV: sigma models and defects in gauge theory. Lett. Math. Phys. 109(3), 579–622 (2019) arXiv:1711.11011
Nekrasov, N.: BPS/CFT correspondence V: BPZ and KZ equations from qq-characters. arXiv:1711.11582
Nekrasov, N., Okounkov, A.: Seiberg-Witten theory and random partitions. Prog. Math. 244, 525–596 (2006). arXiv:hep-th/0306238
Nekrasov, N.A., Shatashvili, S.L.: Supersymmetric vacua and Bethe ansatz. Nucl. Phys. B Proc. Suppl. 192–193, 91–112 (2009). arXiv:0901.4744
Nekrasov, N.A., Shatashvili, S.L.: Quantum integrability and supersymmetric vacua. Prog. Theor. Phys. Suppl. 177, 105–119 (2009). arXiv:0901.4748
Nekrasov, N.A., Shatashvili, S.L.: Quantization of integrable systems and four dimensional gauge theories. arXiv:0908.4052
Osuga, K.: Topological recursion in the Ramond sector. JHEP 1910, 286 (2019) https://doi.org/10.1007/JHEP10(2019)286arXiv:1909.08551
Tachikawa, Y.: A review on instanton counting and W-algebras. arXiv:1412.7121
Tachikawa, Y.: A brief review of the 2d/4d correspondences. J. Phys. A 50(44), 443012 (2017) arXiv:1608.02964
Witten, E.: Notes on super Riemann surfaces and their moduli. Pure Appl. Math. Quart. 15(1), 57–211 (2019) arXiv:1209.2459
Acknowledgements
The author owes many thanks to Nitin Chidambaram for inspirational discussions and for helpful explanations of the recent results of BBCC [7]. The author thanks Andrea Brini, Omar Kidwai, and Piotr Sułkowski for various comments. The author also acknowledges the Young Researchers Integrability School and Workshop 2020 (YRISW) for a series of introductory lectures at which the author learnt about some topics discussed in the present paper. This work is supported by the Engineering and Physical Sciences Research Council under grant agreement ref. EP/S003657/2, by the TEAM programme of the Foundation for Polish Science co-financed by the European Union under the European Regional Development Fund (POIR.04.04.00-00-5C55/17- 00), and also during the revision by Grant-in-Aid for JSPS Fellows (KAKENHI Grant Number: 22J00102). Finally, the author appreciates various helpful comments by the editors and referees for the improvements of the presentation.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A. Computational details
Appendix A. Computational details
1.1 A.1 Computations for the proof of Proposition 3.3
We show that there exists a linear transformation that brings \(H_{i} ,F_{i}\) to the form of (3.3). Note that \(\Phi _N\) acts on Heisenberg modes \((J_a)_{a\in {\mathbb {Z}}}\) and \((\Gamma _r)_{r\in {\mathbb {Z}}+f}\) as:
where we conventionally defined \(\phi _{0,k}=0\), and \(\tau _{l-N+1}=Q_{l-N+1}=\phi _{l,k}=\psi _{l,k}=0\) for \(l\in {\mathbb {Z}}_{<0}\). Using (A.2) and (A.3), one can explicitly write \(H_{i} ,F_{i}\) as
where
Recall that \(\tau _{-(N-1)}\ne 0\), which implies \(C_0\ne 0\). Then, from the degree 1 terms in \(H_i\) and \(F_i\), one notices that there exists an (infinite dimensional) upper triangular matrix that takes \(H_i,F_i\) to \({{\bar{H}}}_i, {{\bar{F}}}_i\) of the form of (3.3), that is,
It is important that there is only one \(D_i\) for each i in \(\bar{H}_i\). This is exactly why we define \({{\tilde{D}}}_i\) by (3.18). Therefore, \(\{H_{i} ,F_{i}\}_{ i\in {\mathbb {Z}}_{\ge 1}}\) and \(\{\bar{H}_{i} ,{{\bar{F}}}_{i}\}_{ i\in {\mathbb {Z}}_{\ge 1}}\) are related by a linear transformation, and this proves that \(\tilde{{\mathcal {S}}}_F\) forms a super Airy structure.
1.2 A.2. Computations for the proof of Theorem 3.4
We first consider the differential constraints given by the operators \({{\bar{H}}}_i,{{\bar{F}}}_i\) defined in (A.11). Then, for \((g,n,m)=(1,1,0)\), it is easy to see that \(\bar{H}_ie^{{\mathcal {F}}}={{\bar{F}}}_ie^{{\mathcal {F}}}=0\) gives
See, for example, [9, Theorem 2.20] for justifying this consequence. On the other hand, \(\omega _{1,1|0}\) is a part of the defining data of the super spectral curve. Thus, (3.23) holds for \((g,n,m)=(1,1,0)\). Note that for \((g,n,m)=(0,3,0)\) and \((g,n,m)=(0,1,2)\), one can also show that \(F_{0,3|0}=F_{0,1|2}=0\).
For any other (g, n, m) with \(2g+n+2m-2>0\), the strategy is the same as the proof given in [12, Appendix A.3]. It turns out that it is more convenient to consider the constraints coming from \(H_ie^{{\mathcal {F}}}= F_ie^{{\mathcal {F}}}=0\) in order to match with the super topological recursion (see Footnote 7). Let us denote by \(I=\{i_1,i_2,\ldots \}\) a collections of positive integers and by \(J=\{j_1,j_2,\ldots \}\) by a collection of nonnegative integersFootnote 16. Then, we introduce the following quantities:
Then, order by order in \(\hbar \) as well as in variables \(x^j,\theta ^j\), we find from \(H_i^2Z=0\) a sequence of constraints on the free energy \(F_{g,n+1|2m}\) for \(2g+n+2m-2>0\) with \((g,n,m)\ne (1,0,0)\) as follows:
where the \(\delta _{f,0}\delta _{j_l,0}\) in the last term is a consequence of the fermionic zero mode \(\Gamma _0\). Similarly, \(F_i^2Z=0\) gives a sequence of constraints for \(F_{g,n|2m}\) for \(2g+n+2m-2>1\) with \(m\ge 1\)
We now will show that exactly the same equations can be derived for \({{\hat{F}}}_{g,n|2m}\) for \(2g+n+2m-2>0\) with \((g,n,m)\ne (1,1,0)\) from the abstract super loop equations. The abstract loop equations imply that
where the extra power of \(z^{2f-1}\) is inserted because \((\Theta _z^R)^2=zdz\) whereas \((\Theta _z^{NS})^2=\mathrm{d}z\).
Let us compute terms that involve \(\omega _{0,1|0}\) in (A.20). Since \(\omega _{g,n|2m}\) respects polarization by definition, we find that
where we used that \(\phi _{kl}=0\) for any \(l\le 0\) and \(C_k\) agrees with (A.6). Note that \(C_k\) depends on \(\phi _{kl}\) due to nonzero \(\tau _{l<1}\) unlike (A.37) in [12, Appendix A.2]. Next, terms with \(\omega _{\frac{1}{2},1|0}\) in (A.20) are
Also, the \(Q_0\)-dependent terms in (A.20) give
The sum of (A.22), (A.23), and (A.24) precisely agrees with the first term in (A.18), i.e. \(\Xi _{g,n+1|2m}[i,I|J]\) when we drop the \(\bigotimes d\xi _I\otimes \bigotimes \eta _J\) factor.
Similarly, terms involving \(\omega _{0,1|0}\) \(\omega _{\frac{1}{2},1|0}\), and the \(Q_0\)-dependent terms in (A.21) are, respectively, computed as
The sum of (A.25), (A.26), and (A.27) precisely agrees with the first term in (A.19), i.e. \(\Xi _{g,n|2m}[I|i,J]\) when we drop the \(\bigotimes d\xi _I\otimes \bigotimes \eta _J\) factor.
Computations for the rest of the terms are completely parallel to those in [12, Appendix A.2], but here are even simpler thanks to the absence of the involution operator \(\sigma \). Thus, we omit tedious yet trivial computations and refer to the reader [12]. As a computational note, the difference between \((\Theta _z^R)^2=zdz\) and \((\Theta _z^{NS})^2=dz\) should be taken carefully. After all, one finds that \({\hat{F}}_{g,n|2m}\) satisfy precisely the same set of equations as the one that \(F_{g,n|2m}\) do, i.e. (A.18) and (A.19). Since uniqueness of solution is clear, \({\hat{F}}_{g,n|2m}=F_{g,n|2m}\). This proves Theorem 3.4.
Rights and permissions
About this article
Cite this article
Osuga, K. Super topological recursion and Gaiotto vectors for superconformal blocks. Lett Math Phys 112, 48 (2022). https://doi.org/10.1007/s11005-022-01541-2
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11005-022-01541-2