Topological twists of massive SQCD, Part I

Abstract

We consider topological twists of four-dimensional $\mathcal {N}=2$ supersymmetric QCD with gauge group SU(2) and $N_f\le 3$ fundamental hypermultiplets. The twists are labelled by a choice of background fluxes for the flavour group, which provides an infinite family of topological partition functions. In this Part I, we demonstrate that in the presence of such fluxes the theories can be formulated for arbitrary gauge bundles on a compact four-manifold. Moreover, we consider arbitrary masses for the hypermultiplets, which introduce new intricacies for the evaluation of the low-energy path integral on the Coulomb branch. We develop techniques for the evaluation of these path integrals. In the forthcoming Part II, we will deal with the explicit evaluation.

1 Introduction

Correlations functions of topologically twisted quantum field theories provide many insights into non-perturbative aspects of quantum field theory as well as the geometry of four-manifolds [1,2,3]. We consider topologically twisted $\mathcal {N}=2$ supersymmetric Yang–Mills theories with additional matter multiplets on a compact four-manifold, which were introduced in [4,5,6,7,8,9]. After the work by Seiberg and Witten on the full non-perturbative solution [3, 10, 11], these theories have received much attention in physics [12,13,14,15,16,17,18,19,20,21,22,23,24,25,26] and mathematics [27,28,29,30,31,32,33,34,35,36,37,38].¹ Their path integrals can in many cases be explicitly evaluated after topologically twisting. The study of the analytical structure of partition functions as function of the parameters such as the masses and UV couplings allows to study the limits in parameters space, as well as relations between different field theories. Moreover, the Q-fixed equations give rise to topological invariants of the underlying space-time geometry. The path integral derivation relates distinct notions of invariants for the same space-time geometry and improves the understanding of such invariants [21, 24, 25, 33, 43,44,45,46,47,48,49].

We consider in this article topological twists of $\mathcal {N}=2$ QCD with gauge group SU(2) and matter multiplets in the fundamental representation of the gauge group. By including background fluxes for the flavour group, we obtain an infinite family of topological theories [16]. The choice of a background flux makes it possible to formulate topologically twists for $\mathcal {N}=2$ SQCD for arbitrary ’t Hooft fluxes, or first Chern classes of the gauge bundle. This is similar to the topological twist of $\mathcal {N}=2^*$ SU(2) gauge theory, which requires a non-vanishing background flux on a non-spin four-manifold [25]. We moreover develop techniques to determine correlation functions for arbitrary values of the masses of the hypermultiplets.

The starting point of our approach is the low-energy effective field theory on the Coulomb branch. This phase of the theory contributes for a compact four-manifold X with the topological condition that $b_2^+(X)=1$ [12]. In this way, the classical Donaldson invariants can be derived starting from the Seiberg–Witten (SW) solution to $\mathcal {N}=2$ supersymmetric Yang–Mills theory with gauge group SU(2). The Coulomb branch integral (or u-plane integral) reduces to an integral over zero modes [12] and reads schematically

$$\begin{aligned} \Phi =\int _{\mathcal {B}} \hbox {d}a\wedge \hbox {d}{\bar{a}}\,\rho (a) \, \Psi (a,{\bar{a}}), \end{aligned}$$

(1.1)

where $\mathcal {B}$ is the Coulomb branch with local coordinates a and ${\bar{a}}$, $\rho (a)$ contains the couplings to the background and $\Psi (a,{\bar{a}})$ is a sum over fluxes of the unbroken U(1) gauge group. For simplicity, we have suppressed the dependence on the metric and not included observables here. For the pure SU(2) theory, the Coulomb branch integral can be formulated and evaluated for arbitrary four-manifolds, without a requirement for Kähler or toric properties.

Recently, progress has been made on evaluating these u-plane integrals using a change of variables from a to the running coupling $\tau$. As a result, the integration domain becomes a fundamental domain $\mathcal {F}\subseteq \mathbb H$ in the upper half-plane $\mathbb H$ for the running coupling [23, 25, 50,51,52,53,54,55,56,57,58]. The integral then takes the form

$$\begin{aligned} \Phi =\int _{\mathcal {F}} \hbox {d}\tau \wedge \hbox {d}{\bar{\tau }}\,\nu (\tau )\,\Psi (\tau ,{\bar{\tau }}), \end{aligned}$$

(1.2)

where the measure factor $\nu (\tau )$ further contains the Jacobian for the change of variables from a to $\tau$. The domain $\mathcal {F}$ is a modular fundamental domain in previous analyses, corresponding to the duality group $\Gamma ^0(4)$ for the pure SU(2) theory [12, 54, 56], $\Gamma (2)$ for the $\mathcal {N}=2^*$ theory [25] and similarly $\Gamma (2)$ and $\Gamma _0(4)$ for the theories with two and three massless flavours [50].

As mentioned above, we aim to apply this approach to $\mathcal {N}=2$ supersymmetric SU(2) theories with $N_f\le 3$ hypermultiplets in the fundamental representation. Topological correlators of these asymptotically free theories have been considered in various papers before, in particular the formulation of the low-energy path integral in [12, 13], SW contributions for four-manifolds with $b_2^+>1$ [12, 20, 21, 24], the u-plane integral for $\mathbb {P}^2$ [50], and the calculation of the partition function of the AD theory within the $N_f=1$ theory [23]. Since no background fluxes are included in these works, the ’t Hooft flux necessarily matches the second Stiefel-Whitney class of the four-manifold, $w_2(E)=w_2(X)$, since the twisted hypermultiplets are not well-defined otherwise.

Extending to generic ’t Hooft fluxes, and application of the above approach (1.2) to fundamental hypermultiplets with generic masses, gives rise to several new aspects. In particular:

• 1. The fundamental domain of the effective coupling constant becomes more intricate for massive theories and does for generic masses not correspond to a modular fundamental domain for a subgroup of $\text {PSL}(2,\mathbb Z)$. The domain contains generically a set of branch points, and branch cuts starting from these points [59,60,61]. These aspects have to be dealt with appropriately.

• 2. We couple the hypermultiplets to background fluxes ${\varvec{k}}_j$ for the flavour group to formulate the theories for arbitrary ’t Hooft fluxes. This gives rise to additional couplings in (1.1) and (1.2),

  $$\begin{aligned} \prod _{j,k=1}^{N_f} \exp \!\left( -2\pi i \frac{\partial ^2 F}{\partial m_j\partial m_k}B({\varvec{k}}_j,{\varvec{k}}_k)\right) , \end{aligned}$$

  (1.3)

  where F is the prepotential of the massive theory, and $B(\cdot ,\cdot )$ is the quadratic form associated to the intersection form on the middle homology $H_2(X,\mathbb {Z})$ of X. Such couplings were suggested by Shapere and Tachikawa [62] and are also essential for the formulation of the $\mathcal {N}=2^*$ Yang–Mills theory on a non-spin four-manifold [25]. Similarly to [25], we also deduce a non-holomorphic coupling to ${\varvec{k}}_j$. Moreover, for arriving at a single-valued integrand, we fix an ambiguity in the quadratic terms of the prepotential. These terms have appeared earlier in the literature in the context of singularities of the SW differential and winding numbers [11, 63].

• 3. Special points on the Coulomb branch give rise to superconformal theories, such as the Argyres–Douglas (AD) theories [64, 65] and the massless $N_f=4$ theory [11]. Their topological partition functions and correlators can be found by considering them in certain mass deformations. The case of $N_f=1$ is analysed in [42].

The paper is organised as follows. In Sect. 2, we present the Seiberg–Witten solution of SU(2) $\mathcal {N}=2$ SQCD in flat space, focusing on the fundamental domains for the effective coupling, which we illustrate in several interesting examples. In Sect. 3, we formulate the topological twist by coupling the hypermultiplets to external fluxes, such that the topological field theory is well-defined for arbitrary ’t Hooft flux and non-spin manifolds. The topological low-energy effective theory coupled to $N_f$ background fluxes is then modelled in Sect. 4 as a $\textrm{SU}(2)\times \textrm{U}(1)^{N_f}$ theory, with the matter fields corresponding to frozen U(1) factors. This allows to compute the path integral explicitly as an integral over the u-plane. In Sect. 5, we formulate the u-plane integral as an integral over the fundamental domains. We prove that the single-valuedness under monodromies holds for a specific choice of magnetic winding numbers. Finally, in Sect. 6 we demonstrate that such integrals may be evaluated using mock modular forms, and we show that they localise at the cusps, elliptic points and interior singularities of the fundamental domains.

A following paper, Part II, will be dedicated to explicit analyses and computations for specific examples. There, we will give a detailed discussion on the contribution from the AD points for each type, as briefly mentioned in point 3 above, as well as calculating the u-plane integrals for a number of examples.

2 Special geometry and SW theories

In this section, we review aspects of the non-perturbative solution for the low-energy effective theory of $\mathcal {N}=2$ SQCD with gauge group SU(2) and $0\le N_f\le 3$ fundamental hypermultiplets [10, 11]. See [66] for a review. Throughout, we let $\Lambda _{N_f}$ denote the scale of the theory with $N_f$ hypermultiplets having masses $m_j$, $j=1,\dots ,N_f$, and a the mass of the W-boson on the Coulomb branch.

2.1 Field content

The $\mathcal {N}=2$ theories we consider contain a vector multiplet and $N_f\le 3$ hypermultiplets. The fields in these multiplets form representations of $\textrm{Spin}(4)=\text {SU}(2)_+\times \text {SU}(2)_-$ and $\text {SU}(2)_R$, which we denote by $({\varvec{k}},{\varvec{l}}, {\varvec{m}})$, with ${\varvec{k}},{\varvec{l}}$ and ${\varvec{m}}$ dimensions of the representations.

The vector multiplet consists of a gauge field $A_\mu$, complex scalar field $\phi$ and a pair of Weyl fermions $\Psi ^I_\alpha$, ${\bar{\Psi }}^I_{\dot{\alpha }}$. This multiplet transforms under the adjoint representation of the gauge group G. The representation of $\text {SU}(2)_+\times \text {SU}(2)_- \times \text {SU}(2)_R$ formed by the bosonic fields is,

$$\begin{aligned} ({\textbf {2}}, {\textbf {2}},{\textbf {1}})\oplus ({\textbf {1}}, {\textbf {1}},{\textbf {1}}) \oplus ({\textbf {1}}, {\textbf {1}},{\textbf {1}}), \end{aligned}$$

(2.1)

while the representation for the fermions is

$$\begin{aligned} ({\textbf {1}}, {\textbf {2}},{\textbf {2}})\oplus ({\textbf {2}}, {\textbf {1}},{\textbf {2}}). \end{aligned}$$

(2.2)

The hypermultiplet consists of a pair of complex scalar fields, q and ${\tilde{q}}$, and Weyl fermions, $\lambda _\alpha$, $\bar{\lambda }_{\dot{\alpha }}$, $\chi _\alpha$ and ${\bar{\chi }}_{\dot{\alpha }}$. We fix the gauge group $G=\text {SU}(2)$, and let the hypermultiplets transform under the fundamental representation of this group. With the same notation as above, the bosonic fields of this multiplet form the representation,

$$\begin{aligned} ({\textbf {1}}, {\textbf {1}},{\textbf {2}})\oplus ({\textbf {1}}, {\textbf {1}},{\textbf {2}}), \end{aligned}$$

(2.3)

while the fermions form the representation

$$\begin{aligned} ({\textbf {2}}, {\textbf {1}},{\textbf {1}})\oplus ({\textbf {1}}, {\textbf {2}},{\textbf {1}})\oplus ({\textbf {2}}, {\textbf {1}},{\textbf {1}})\oplus ({\textbf {1}}, {\textbf {2}},{\textbf {1}}). \end{aligned}$$

(2.4)

2.2 Seiberg–Witten geometry

The Seiberg–Witten geometry underlies the Coulomb branch of $\mathcal {N}=2$ gauge theory. The Coulomb branch is the phase of the theory where $\text {SU}(2)$ is broken to $\text {U}(1)$ by a vacuum expectation value (vev) of the vector multiplet scalar $\phi$. The vev is semi-classically parametrised by a complex parameter a,

$$\begin{aligned} \phi =\left( \begin{array}{cc} a &{} \quad 0 \\ 0 &{} \quad -a \end{array}\right) , \end{aligned}$$

(2.5)

up to gauge transformations. In particular, $a\rightarrow -a$ is a gauge transformation. The gauge invariant order parameter is the Coulomb branch expectation value of the theory in $\mathbb {R}^4$,

$$\begin{aligned} u=\frac{1}{16\pi }\left<\textrm{Tr}(\phi ^2)\right>_{\mathbb {R}^4}. \end{aligned}$$

(2.6)

The non-perturbative effective action of $\mathcal {N}=2$ SQCD is characterised by the prepotential $F(a,{\varvec{m}})$, with ${\varvec{m}}$ the mass vector ${\varvec{m}}=(m_1,\dots ,m_{N_f})$. The semi-classical part of F reads [63, 67,68,69]

$$\begin{aligned}&F(a,{\varvec{m}})=\frac{2i}{\pi } a^2 \left( \log (4a/\Lambda _{N_f})-\frac{3}{2}\right) -\frac{1}{2}\sum _{j=1}^{N_f}\left( n_j\frac{m_j}{\sqrt{2}}\,a+\, C\, (a^2+m_j^2/2)\right) \nonumber \\&\quad -\frac{i}{4\pi } \sum _{j=1}^{N_f} \left( a+\tfrac{m_j}{\sqrt{2}}\right) ^2\log ((a+\tfrac{m_j}{\sqrt{2}})/\Lambda _{N_f})+\left( a-\tfrac{m_j}{\sqrt{2}}\right) ^2\log ((a-\tfrac{m_j}{\sqrt{2}})/\Lambda _{N_f})\nonumber \\&\quad +\dots , \end{aligned}$$

(2.7)

where the $\dots$ indicates further non-perturbative corrections. Here $C=\frac{1}{2}+\frac{i}{2\pi }\log (2)-\frac{3i}{2\pi }$. The classical terms proportional to $a^2$ and $m^2$ on the first line are chosen to facilitate the decoupling of hypermultiplets, which will be discussed later in more detail.

The $n_j\in \mathbb {Z}$ in (2.7) are the magnetic winding numbers of the periods $a_D{:}{=}\frac{\partial F}{\partial a}$ dual to a [63, 67, 70]. These numbers seem to be only rarely discussed in the literature beyond these references.² Generally, the theory allows for $N_f$ electric winding numbers for a and $N_f$ magnetic winding numbers for $a_D$. These appear in the massive $N_f>0$ theories since the Seiberg–Witten differentials now have poles with nonzero residues [67]. See also Appendix C. The choice (2.7) of the prepotential corresponds to fixing the electric winding numbers to be zero, or equivalently fixing the monodromy at infinity to map $a\rightarrow e^{\pi i}a$. Compare for example with [67, Eq. (2.17)]. In Sect. 5, we will discuss that the single-valuedness of the u-plane integral requires $n_j\equiv -1 \mod 4$.

We introduce the period $a_D$ dual to a, and the parameters $m_{D,j}$ dual to $m_j$ by

$$\begin{aligned} a_D=\frac{\partial F}{\partial a},\qquad m_{D,j}=\sqrt{2}\frac{\partial F}{\partial m_j}. \end{aligned}$$

(2.8)

These parameters are further combined into the $(2+2N_f)-$dimensional vector $\Pi$,

$$\begin{aligned} \Pi =\left( \begin{array}{c} a_D \\ a \\ m_{D,1} \\ \tfrac{m_{1}}{\sqrt{2}} \\ \vdots \\ m_{D,N_f} \\ \tfrac{m_{N_f}}{\sqrt{2}} \end{array}\right) . \end{aligned}$$

(2.9)

This vector forms a local system over the u-plane. The elements of the vector form the symplectic form,

$$\begin{aligned} \omega _{N_f}=\hbox {d}a_D\wedge \hbox {d}a+ \frac{1}{\sqrt{2}}\sum _{j=1}^{N_f}\hbox {d}m_{D,j}\wedge \hbox {d} m_j. \end{aligned}$$

(2.10)

The effective gauge coupling is related to the prepotential through

$$\begin{aligned} \tau =\frac{\partial ^2 F}{\partial a^2}. \end{aligned}$$

(2.11)

We also introduce the couplings $v_j$ and $w_{jk}$ with $j,k\in 1,\dots , N_f$ [72,73,74],³

$$\begin{aligned} v_j=\sqrt{2}\frac{\partial ^2 F}{\partial a \partial m_j}, \qquad w_{jk}=2\frac{\partial ^2 F}{\partial m_j\partial m_k}. \end{aligned}$$

(2.12)

The derivative of the prepotential with respect to the scale $\Lambda _{N_f}$ provides the order parameter u (2.6) on the Coulomb branch,

$$\begin{aligned} u=\frac{4\pi i}{4-N_f} \Lambda _{N_f} \frac{\partial F(a,{\varvec{m}})}{\partial \Lambda _{N_f}}+\frac{1}{4-N_f}\sum _j m_j^2. \end{aligned}$$

(2.13)

Using the different relations introduced above together with the fact that the prepotential satisfies the homogeneity equation [75,76,77]

$$\begin{aligned} 2 F=\Lambda _{N_f} \frac{\partial F}{\partial \Lambda _{N_f}} +\sum _{j=1}^{N_f}m_j\frac{\partial F}{\partial m_j}+a \frac{\partial F}{\partial a}, \end{aligned}$$

(2.14)

we can find some non-trivial relations between the respective quantities. For instance, from the perturbative prepotential (2.7), we deduce that the leading terms of u are

$$\begin{aligned} u=2\,a^2+\mathcal {O}(a^{-2}) \end{aligned}$$

(2.15)

The weak-coupling limit then becomes in our conventions⁴

$$\begin{aligned} \left\{ \begin{array}{l} \tau \rightarrow +i\infty , \\ a\rightarrow -i\infty , \\ u\rightarrow -\infty . \end{array} \right. \end{aligned}$$

(2.16)

The Seiberg–Witten (SW) solution provides a family of elliptic curves parametrised by the order parameter u and the masses $m_i$, whose complex structure corresponds to the running coupling $\tau =\frac{\theta }{\pi }+\frac{8\pi i}{g^2}$. For the theories of interest in this paper, the curves $\mathcal {S}_{N_f}$ are given by [11]

$$\begin{aligned} \begin{aligned} N_f=0:\quad y^2&=x^3-ux^2+\frac{1}{4}\Lambda _0^4x, \\ N_f=1:\quad y^2&=x^2(x-u)+\frac{1}{4}m\Lambda _1^3x-\frac{1}{64}\Lambda _1^6, \\ N_f=2:\quad y^2&=(x^2-\frac{1}{64}\Lambda _2^4)(x-u)+\frac{1}{4}m_1m_2\Lambda _2^2x-\frac{1}{64}(m_1^2+m_2^2)\Lambda _2^4, \\ N_f=3:\quad y^2&= x^2(x-u)-\frac{1}{64}\Lambda _3^2(x-u)^2-\frac{1}{64}(m_1^2+m_2^2+m_3^2)\Lambda _3^2(x-u)\\ {}&\quad +\frac{1}{4}m_1m_2m_3\Lambda _3x-\frac{1}{64}(m_1^2m_2^2+m_2^2m_3^2+m_1^2m_3^2)\Lambda _3^2. \end{aligned} \end{aligned}$$

(2.17)

The family of SW curves (2.17) are Jacobian rational elliptic surfaces with singular fibres [78,79,80]. These surfaces are well studied in the mathematical literature [81,82,83]. Rational in this context means that $g_2$ and $g_3$ are polynomials in u of degree at most 4 and 6, respectively [84]. In Appendix B, we summarise the class $\mathcal {S}$ representation of the SW curves [85].

The curve for $N_f$ hypermultiplets reduces to the curve for $N_f-1$ hypermultiplets upon decoupling a hypermultiplet in the double scaling limit [86]

$$\begin{aligned} m_{N_f}\rightarrow \infty , \quad \Lambda _{N_f}\rightarrow 0, \quad m_{N_f}\Lambda _{N_f}^{4-N_f}=\Lambda _{N_f-1}^{4-(N_f-1)}. \end{aligned}$$

(2.18)

The curves (2.17) provide the exact results for the vevs of the scalar a and its dual $a_D$ as period integrals. We have explicitly,

$$\begin{aligned} a=\int _A \lambda ,\qquad a_D=\int _B \lambda , \end{aligned}$$

(2.19)

with $\lambda$ the SW differential, for which we refer to [11, 63, 67].

2.3 Characteristic functions on the Coulomb branch

In this subsection, we discuss various characteristic functions on the Coulomb branch, which are instrumental for determining the u-plane integral. They are:

• the physical discriminant $\Delta _{N_f}$,

• the order parameter u,

• the period da/du, and

• the derivatives $\hbox {d}u/\hbox {d}\tau$ and $\hbox {d}a/\hbox {d}\tau$.

The physical discriminant $\Delta _{N_f}$

We define the physical discriminant $\Delta _{N_f}$ as the monic polynomial

$$\begin{aligned} \Delta _{N_f}=\prod _{j=1}^{N_f+2}(u-u_j), \end{aligned}$$

(2.20)

where $u_j$ for $j=1,\dots , N_f+2$ are the singular points of the effective theory. We let $j=1,\dots , N_f$ label the singular points where one of the matter hypermultiplets becomes massless, and $j=N_f+1, N_f+2$ denote the strong coupling singularities where a monopole and a dyon, respectively, become massless.

The discriminant is a polynomial of degree $2+N_f$ in u. It can also be determined directly from the SW curve [59],

$$\begin{aligned} \Delta _{N_f}=(-1)^{N_f}\Lambda _{N_f}^{2N_f-8}(g_2^3-27g_3^2), \end{aligned}$$

(2.21)

where $g_2$ and $g_3$ are the Weierstraß invariants of the SW curve. Up to the sign and scale, the physical discriminant $\Delta _{N_f}$ equals the mathematical discriminant $g_2^3-27g_3^2$ for these theories.

As the masses are tuned, some of the singularities on the Coulomb branch can collide. If we consider $\Delta _{N_f}$ as a polynomial in u, its discriminant $D(\Delta _{N_f})$ vanishes if and only if two roots coincide. It is straightforward to show that for $N_f\le 3$,

$$\begin{aligned} D(\Delta _{N_f})=\left( D^{\text {AD}}_{N_f}\right) ^3\prod _{i<j}(m_i-m_j)^2(m_i+m_j)^2. \end{aligned}$$

(2.22)

This factorises the locus in mass space where singularities collide into two orthogonal components: The first component is the Argyres–Douglas (AD) locus given by the polynomial equation $D^{\text {AD}}_{N_f}=0$, where mutually non-local singularities collide [59, 65, 87]. The other component is characterised by the equations $m_i=\pm m_j$, and one can check that this gives rise to mutually local singularities colliding. Here, the flavour symmetry gets enhanced and a Higgs branch opens up [11]. This extends the analysis of [59].

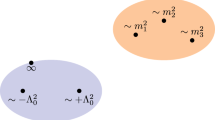
Given a mass configuration ${\varvec{m}}=(m_1,\dots , m_{N_f})$, we can denote by $k_l$ the weight (or multiplicity) of the l-th singularity, and by ${\varvec{k}}({\varvec{m}})=(k_1,k_2,\dots )$ the vector of those weights. Since the Coulomb branch $\mathcal {B}_{N_f}({\varvec{m}})$ contains $2+N_f$ singularities aside from weak coupling $u=\infty$, it is clear that ${\varvec{k}}({\varvec{m}})$ provides a partition of $2+N_f$. This in turn partitions the mass space $\mathbb C^{N_f}\ni {\varvec{m}}$ into finitely many regions where ${\varvec{k}}({\varvec{m}})$ is locally constant. As an example, in Fig. 1 we plot the contours of (2.22) for $N_f=2$ in the real ${\varvec{m}}=(m_1,m_2)$ plane.

Fig. 1

Partitioning of the real $\varvec{m}=(m_1,m_2)$ plane in $N_f=2$, in units of $\Lambda _2=1$. On the AD component the Coulomb branch $\mathcal B_{2}(\varvec{m})$ contains an AD point of Kodaira type II (blue) or III (green). On the other component (orange), mutually local singularities collide. If $\varvec{m}$ is varied along a continuous path that does not cross the partitioning $0=D(\Delta _{N_f})$, the weight vector ${\varvec{k}} ({\varvec{m}})$ is constant (colour figure online)

The possible singularity structures of the rational elliptic curves (2.17) are classified in Persson’s list of allowed configurations of singular fibres [88, 89]. From Kodaira’s classification, it follows that any solution to (2.22) gives rise to a singularity on the Coulomb branch of Kodaira type $I_k$, II, III or IV. As described in [59, 80], the solutions to $0=D^{\text {AD}}_{N_f}$ give rise to AD points of Kodaira type II, III and IV. The second component $0=\prod _{i<j}(m_i-m_j)(m_i+m_j)$ can be studied in more detail. These are $2(N_f-1)$ independent equations. Whenever one of the factors vanishes, the SW surface contains an $I_k$ singularity with $k\ge 2$. For $N_f=2$, the only possibility is $I_2$, while for $N_f=3$ singularities of type $I_2$, $I_3$ and $I_4$ are possible. The point in the Coulomb branch $\mathcal {B}_{N_f}$ corresponding to an $I_k$ singularity with $k\ge 2$ intersects with a Higgs branch of quaternionic dimension $k-1\ge 1$ [11]. Further merging these $I_k$ singularities with a mutually non-local singularity does not affect the Higgs branch, such that the points with a III or IV singularity also intersect with a Higgs branch of quaternionic dimension one or two, respectively, while the points with AD theories of type II do not intersect with any Higgs branch.

Order parameter u

The order parameter u, introduced in (2.6), is invariant under monodromies on the Coulomb branch. By bringing the SW curve to Weierstraß form, u can be expressed in terms of the running coupling $\tau \in \mathbb {H}$ (2.11) [59, 61, 90,91,92]. As in [59], we restrict the domain for $\tau \in \mathbb {H}$ to $\mathcal {F}({\varvec{m}})\subseteq \mathbb {H}$, such that u is 1-to-1. In specific cases, u can be expressed in terms of modular forms. We follow the conventions of [59, Sect. 2.2] in picking the solutions. We discuss the order parameters in more detail in the following Sect. 2.4.

The period $\hbox {d}a/\hbox {d}u$

The period $\frac{\text {d}a}{\text {d}u}$ can be related to the complex structure $\tau$ of the curve through [91]

$$\begin{aligned} \frac{\text{ d }a}{\text {d}u}=\frac{1}{6}\sqrt{\frac{g_2}{g_3}\frac{E_6}{E_4}}, \end{aligned}$$

(2.23)

where the Weierstraß invariants $g_2$, $g_3$ are polynomials in u, and $E_4=E_4(\tau )$, $E_6=E_6(\tau )$ are the Eisenstein series of modular weights four and six, respectively, defined in Eq. (A.7). The square root in (2.23) leads to an ambiguity in the sign of da/du. This can be resolved by taking a branch of the square root, for example at weak coupling. On the other hand, da/du is not a single-valued function on the u-plane. It changes by a sign under monodromies at weak coupling and transforms with a modular weight under monodromies around strong coupling singularities.

The derivatives $\hbox {d}u/\hbox {d}\tau$ and $\hbox {d}a/\hbox {d}\tau$

The derivative $\hbox {d}u/\hbox {d}\tau$ is related to the period $\frac{\text{ d }a}{\text {d}u}$ through [59, 93]

$$\begin{aligned} \frac{\text{ d }u}{\text {d}\tau }=-\frac{16\pi i}{4-N_f}\frac{\Delta _{N_f}}{P^{\text {M}}_{N_f}}\left( \frac{\text{ d }a}{\text {d}u}\right) ^2, \end{aligned}$$

(2.24)

where $P^{\text {M}}_{N_f}$ is a polynomial in u. For $N_f\le 3$, it reads

$$\begin{aligned} P^{\text {M}}_{N_f}=\frac{6}{4-N_f}(-1)^{N_f}\Lambda _{N_f}^{2N_f-8}(2g_2g_3'-3g_2'g_3), \end{aligned}$$

(2.25)

where the prime denotes differentiation with respect to u. It appears naturally in differential equations associated with elliptic surfaces (see e.g. [94]).

When u is known in terms of modular forms, it is also straightforward to determine $\frac{\text{ d }u}{\text {d}\tau }$ by differentiating modular forms [59]. For generic masses ${\varvec{m}}$, we can compute the q-series of u and thus $\frac{\text{ d }u}{\text {d}\tau }$ to any order. We will not explicitly need $\hbox {d}u/\hbox {d}\tau$ for evaluating the u-plane integral, but through

$$\begin{aligned} \frac{\text{ d }a}{\text {d}\tau }=\frac{\text{ d }a}{\text {d}u}\frac{\text{ d }u}{\text {d}\tau } \end{aligned}$$

(2.26)

we can use it to evaluate $\hbox {d}a/\hbox {d}\tau$. This derivative appears as the Jacobian for the change of integration variables from the periods a to the couplings $\tau$.

2.4 Fundamental domains

The recent progress in computing u-plane integrals has been enabled by mapping the u-plane to a modular fundamental domain, on which the u-plane integrand can be related to mock modular forms and thus be efficiently evaluated [23, 25, 50,51,52,53,54,55,56,57,58]. It has been known since the 1990 s that the u-planes for $\mathcal {N}=2$ SQCD with $N_f=0,2,3$ massless hypermultiplets are modular and correspond to fundamental domains for congruence subgroups of $\text {PSL}(2,\mathbb Z)$ [90]. On the other hand, the generic mass case including the peculiar role of massless $N_f=1$ has remained elusive.

The order parameter u for a given mass ${\varvec{m}}=(m_1,\dots , m_{N_f})$ can be considered as a function

$$\begin{aligned} u: \mathbb H\rightarrow \mathcal {B}_{N_f}({\varvec{m}}), \end{aligned}$$

(2.27)

where $\mathcal {B}_{N_f}({\varvec{m}})$ is the Coulomb branch of the theory with $N_f$ hypermultiplets of mass ${\varvec{m}}$. In [59], it was found that for $N_f\ge 1$ and generic masses the duality group does not act on $\tau$ by fractional linear transformations. This prevents the preimage $u^{-1}(\mathcal {B}_{N_f}({\varvec{m}}))$ from being a modular fundamental domain for a subgroup of $\text {PSL}(2,\mathbb Z)$. Instead, we can define a fundamental domain $\mathcal {F}_{N_f}({\varvec{m}})$ through the equivalence relation $\tau \sim \tau ' \Leftrightarrow u(\tau )=u(\tau ')$, such that $u: \mathcal {F}_{N_f}({\varvec{m}})\rightarrow \mathcal {B}_{N_f}({\varvec{m}})$ is bijective. In [59, 61], such fundamental domains for the effective gauge coupling have been found explicitly for $\mathcal {N}=2$ SQCD with $N_f\le 4$ generic masses. They decompose as

$$\begin{aligned} \mathcal {F}_{N_f}({\varvec{m}})=\bigcup _{j=1}^{n}\alpha _j\mathcal {F}, \end{aligned}$$

(2.28)

where $\mathcal {F}=\text {PSL}(2,\mathbb Z)\backslash \mathbb H$ is the key-hole fundamental domain of $\text {PSL}(2,\mathbb Z)$, and $\alpha _j\in \text {PSL}(2,\mathbb Z)$ are $n\le 6$ maps that are locally constant as functions of the masses ${\varvec{m}}$. More precisely, $\mathcal {F}_{N_f}({\varvec{m}})$ is constant on any of the finitely many connected components of $\{{\varvec{m}}\in \mathbb C^{N_f}\, | \, D(\Delta _{N_f})=0\}$, where $D(\Delta _{N_f})$ is given in (2.22). We also call n the index of the domain $\mathcal {F}_{N_f}({\varvec{m}})$.

The geometry of $\mathcal {F}_{N_f}({\varvec{m}})$ agrees with that of the Coulomb branch $\mathcal {B}_{N_f}({\varvec{m}})$. Namely, $\mathcal {B}_{N_f}({\varvec{m}})$ is the complex plane with $2+N_f$ singular points removed. In (2.28), those singularities are reflected in the cusps $\alpha _j(\infty )$, where the number of $\alpha _j$ with the same $\alpha _j(\infty )$ (giving the width of the cusp) agrees with the multiplicity of the singularity $u(\alpha _j(\infty ))$.

The domains $\mathcal {F}({\varvec{m}}){:}{=}\mathcal {F}_{N_f}({\varvec{m}})$ are endowed with further data. For generic masses ${\varvec{m}}$, there are $N_f$ pairs of branch points on $\mathcal {F}({\varvec{m}})$ that are connected by branch cuts. The branch points are determined by the non-removable singularities of the rational function $\Delta _{N_f}(u)/P^{\text {M}}_{N_f}(u)$, as it appears in Matone’s relation (2.24). They correspond to the non-trivial zeros of the discriminant of the sextic equation associated with the SW curve [59]. As the masses are varied, the branch points move on continuous paths in the fundamental domain.

When two branch points collide, there appears an elliptic point, which is a further dedicated point on the domain $\mathcal {F}({\varvec{m}})$. These elliptic points correspond to the superconformal Argyres–Douglas (AD) points [64, 65]. By Kodaira’s classification of singular fibres, they are always in the $\text {PSL}(2,\mathbb Z)$ orbit of i or $e^{\pi i/3}$. Their presence is also responsible for the index n of the domain to be reduced. The possible values are $n=2,3,4$ if $\mathcal {F}({\varvec{m}})$ contains such an elliptic point, and $n=6$ otherwise.

The $N_f=4$ theory furthermore contains a UV coupling $\tau _{\text {{UV}}}$. Since $u(\tau )\rightarrow \infty$ for $\tau \rightarrow \tau _{\text {{UV}}}$, it can be viewed as a puncture of the fundamental domain, and has to be excluded from the integration domain.

Let us review the explicit construction of $\mathcal {F}({\varvec{m}})$ in a few important examples. Many more examples can be found in [59, 61]. Here, we are mainly considering the masses to be small compared to the period a, such that the mass singularities discussed in previous sections can be considered as strong coupling singularities, or in other words as cusps on the real line of the fundamental domains. When the masses are increased it is more natural to think of the mass singularities as weakly coupled.

The pure SU(2) $N_f=0$ theory

It is well-known that the pure SU(2) Coulomb branch corresponds to the fundamental domain for the congruence subgroup $\Gamma ^0(4)$ of $\text {PSL}(2,\mathbb Z)$. The order parameter can be explicitly determined in terms of a modular function for the duality group [95],

$$\begin{aligned} \begin{aligned} \frac{u}{\Lambda _0^2}=&-\frac{1}{2}\frac{\vartheta _2^4+\vartheta _3^4}{\vartheta _2^2\vartheta _3^2}, \end{aligned} \end{aligned}$$

(2.29)

where the Jacobi theta functions $\vartheta _i$ are defined in Appendix A.1. A fundamental domain for the pure SU(2) theory is given in Fig. 2. Since the domain is modular, the branch points are absent.

Fig. 2

Fundamental domain of $\Gamma ^0(4)$. This is the duality group of the pure SU(2) theory. The two cusps on the real line correspond to the strong coupling singularities of the gauge theory, while the cusp at $\tau =i\infty$ corresponds to weak coupling. Boundaries of the same colour are identified (colour figure online)

The massless $N_f=1$ theory

From the massless $N_f=1$ SW curve, one directly finds [90]

$$\begin{aligned} \begin{aligned} \frac{u}{\Lambda _1^2}=&-\frac{3}{2^{\frac{7}{3}}}\frac{E_4^{\frac{1}{2}}}{(E_4^{\frac{3}{2}}-E_6)^{\frac{1}{3}}}, \end{aligned} \end{aligned}$$

(2.30)

where $E_4$ and $E_6$ are the Eisenstein series defined in (A.7). This function also appears as an order parameter in pure SU(3) SW theory [60] as well as in the description of certain elliptically fibred Calabi–Yau spaces [96]. Due to the presence of the square root, this function is not modular. The massless $N_f=1$ curve has three distinct strongly coupled singularities, which become the three cusps of the fundamental domain aside from the weakly coupled region $u\rightarrow \infty$. The fundamental domain is plotted in Fig. 3. Note that, this is not the fundamental domain of any subgroup of $\text {PSL}(2,\mathbb Z)$.

Fig. 3

Fundamental domain for massless $N_f=1$

When a positive mass m is turned on, the branch points move in the fundamental domain emerging from those of the massless case. They move as a function of the mass as shown in [59] and depicted in Fig. 4. This further incorporates the hypermultiplet decoupling on the level of the fundamental domain.

Fig. 4

Choice of branch cuts (zigzag lines) for varying (real) mass in $N_f=1$. Lines with the same colour are identified. Starting with a small mass in (a), we cut along the arcs of radius 1 around $\tau =1$ and $\tau =2$. At the AD mass we can use the identifications of the different boundaries to reorganise the domain in (b) to the one of (c). When we increase the mass further the cuts of (c) move upwards as in (d) eventually reaching infinity and disappearing, leaving us with the domain in Fig. 2 of the pure theory (colour figure online)

The equal mass $N_f=2$ theory

For $N_f=2$ with $m_1=m_2=m$, the order parameter can be determined explicitly [59],

$$\begin{aligned} \frac{u}{\Lambda _2^2}=-\frac{\vartheta _4^8+\vartheta _2^4\vartheta _3^4+(\vartheta _2^4+\vartheta _3^4)\sqrt{16\frac{m^2}{\Lambda _2^2}\vartheta _2^4\vartheta _3^4+\vartheta _4^8}}{8\vartheta _2^4\vartheta _3^4}. \end{aligned}$$

(2.31)

The curve has a double singularity at $u_*=m^2+\frac{\Lambda _2^2}{8}$ and two simple singularities at $u_\pm =-\frac{\Lambda _2^2}{8}\pm m\Lambda _2$. When m is varied, it can be determined how the branch point $\tau _{\text {bp}}$ moves in the fundamental domain. When m is not zero and not equal to $m_{\text {AD}}=\tfrac{\Lambda _2}{2}$, the singularities $u_*$, $u_+$ and $u_-$ are distinct and the fundamental domain $\mathcal {F}(m,m)$ is given in Fig. 5. For any such mass, there is a pair of branch points in $\mathcal {F}(m,m)$, which are connected by a branch cut. Near a branch point $\tau _\textrm{bp}$, u reads

$$\begin{aligned} u(\tau )=u_\textrm{bp}+c(\tau _\textrm{bp})\,(\tau -\tau _{\textrm{bp}})^{1/2}, \end{aligned}$$

(2.32)

for some constant $c(\tau _\textrm{bp})$.

Fig. 5

Fundamental domain $\mathcal F_2(m,m)$ of the massive $\varvec{m}=(m,m)$ $N_f=2$ theory. The dashed lines correspond to the paths of the branch points from zero to infinite mass. For given positive mass m, the two branch points are identified under $TST^{-1}$, such that there is only one branch point $u_{\text {bp}}=2m^2-\tfrac{\Lambda _2^2}{8}$ on the u-plane

The massless limit in $N_f=2$

In the limit where $m_1=m_2=m\rightarrow 0$, one finds from (2.31) that

$$\begin{aligned} \frac{u}{\Lambda _2^2}=-\frac{1}{8}\frac{\vartheta _3^4+\vartheta _4^4}{\vartheta _2^4} \end{aligned}$$

(2.33)

This expression is a modular function for the principal congruence subgroup $\Gamma (2)$ of $\text {PSL}(2,\mathbb Z)$. The holomorphy of (2.33) is explained by the fact that the pair of branch points for $m\ne 0$ collides in the limit $m\rightarrow 0$, which annihilates the branch cut. This is because the mutually local singularities $u_\pm \rightarrow -\frac{\Lambda _2^2}{8}$ collide, and thus the singularities corresponding to $\tau \rightarrow 0$ and $\tau \rightarrow 2$ in Fig. 5 are identified. The fundamental domain of the massless theory is thus the modular fundamental domain for the duality group $\Gamma (2)$, as depicted in Fig. 6.

Fig. 6

Fundamental domain for $\Gamma (2)$, the duality group of the massless $N_f=2$ theory

The AD limit in $N_f=2$

When $m\rightarrow m_{\text {AD}}=\tfrac{\Lambda _2}{2}$, the singularities $u_*$ and $u_+$ collide and form the superconformal AD point $(A_1,A_3)$ of Kodaira type III. As studied in detail in [59, 80, 97], this AD point forms an elliptic point of the fundamental domain. Since three mutually non-local singularities collide for this mass, the index of the domain $\mathcal {F}(m_{\text {AD}},m_{\text {AD}})$ is reduced by 3, giving a domain of index $6-3=3$. By taking the limit from (2.31), one finds that the square root resolves by virtue of the Jacobi identity (A.4). This restores holomorphy and even modularity. One finds that the order parameter

$$\begin{aligned} \frac{u}{\Lambda _2^2}=-\frac{1}{64}\left( \frac{16\vartheta _4^8}{\vartheta _2^4\vartheta _3^4}+40\right) \end{aligned}$$

(2.34)

is a modular function for the congruence subgroup $\Gamma _0(2)$ of $\text {PSL}(2,\mathbb Z)$ [59]. Its elliptic fixed point $\tau _{\text {AD}}=1+i$ is precisely the AD point. We depict the corresponding fundamental domain in Fig. 7.

Fig. 7

Fundamental domain of the $N_f=2$ theory with equal AD mass $m_1=m_2=m_{\text {AD}}=\frac{\Lambda _2}{2}$. It is the modular fundamental domain for the congruence subgroup $\Gamma _0(2)$ of $\text {PSL}(2,\mathbb Z)$. The AD point $\tau _{\text {AD}}=1+i$ is the elliptic fixed point of $\Gamma _0(2)$. The three singularities collided in $u_{\text {AD}}$ result in a reduction of the index from 6 to 3

The $N_f=4$ theory

In $N_f=4$, the fundamental domain for the effective coupling $\tau$ can be found analogously to the asymptotically free cases. One notable new feature is the additional singularity of the theory when $\tau$ approaches the UV coupling $\tau _{\text {{UV}}}$. For example, with the mass configuration ${\varvec{m}}=(m,m,0,0)$ one finds [61]

$$\begin{aligned} u(\tau ,\tau _{\text {{UV}}})=-\frac{m^2}{3}\vartheta _3(\tau _{\text {{UV}}})^4\frac{\lambda (\tau _{\text {{UV}}})^2+2\left( \lambda (\tau )-1\right) \lambda (\tau _{\text {{UV}}})-\lambda (\tau )}{\lambda (\tau _{\text {{UV}}})-\lambda (\tau )}, \end{aligned}$$

(2.35)

where $\lambda = \frac{\vartheta _2^4}{\vartheta _3^4}$. This function is a meromorphic $\Gamma (2)$ modular form of weight 2 in $\tau _{\text {{UV}}}$ for fixed $\tau$ and of weight 0 in $\tau$ for fixed $\tau _{\text {{UV}}}$. Furthermore, it has mixed weight (0, 2) under $\text {PSL}(2,\mathbb Z)$ acting on $\tau$ and $\tau _{\text {{UV}}}$ simultaneously. As such, it is an example of a bimodular form for the triple $(\Gamma (2),\Gamma (2);\text {PSL}(2,\mathbb Z))$ [25, 61]. Since $u(\tau ,\tau _{\text {{UV}}})$ has a pole as $\tau \rightarrow \tau _{\text {{UV}}}$, the fundamental domain $\mathcal {F}_4({\varvec{m}})$ has a puncture at $\tau _{\text {{UV}}}$. This is depicted in Fig. 8.

Fig. 8

Fundamental domain of the $N_f=4$ theory with mass $\varvec{m}=(m,m,0,0)$. The six singularities on the Coulomb branch $\mathcal B_4$ are described by the three cusps, each of width 2. The $I_0^*$ singularity corresponding to $u=\infty$ sits at $\tau =\tau _{\text {{UV}}}$

2.5 Monodromies

This section determines the monodromies around the $N_f+2$ monodromies. Duality transformations of such couplings in $\mathcal {N}=2$ supersymmetric theories have also been studied in [72,73,74]. We leave the winding numbers $n_j$, $j=1,\dots , N_f$, for $a_D$ generic. Starting with the monodromy around infinity, $a\rightarrow e^{\pi i}a$, we deduce from the (2.7) that the vector $\Pi$ transforms as $\Pi \rightarrow {\textbf {M}}_\infty \,\Pi$, with ${\textbf {M}}_\infty$ given by

$$\begin{aligned} {\textbf {M}}_\infty =\begin{pmatrix} -1&{} 4-N_f&{} 0&{}-n_1&{}\cdots &{}0&{}-n_{N_f}\\ 0&{}-1&{}0&{}0&{}\cdots &{}0&{}0\\ 0&{}n_1&{}1&{}1&{}\cdots &{}0&{}0\\ 0&{}0&{}0&{}1&{}\cdots &{}0&{}0\\ \vdots &{}\vdots &{}&{}&{}\ddots &{}&{}\\ 0&{}n_{N_f}&{}0&{}0&{}\cdots &{}1&{}1\\ 0&{}0&{}0&{}0&{}\cdots &{}0&{}1 \end{pmatrix}. \end{aligned}$$

(2.36)

The monodromy matrix ${\textbf {M}}_\infty$ is in $\text {SL}(2+2N_f,\mathbb {Z})$, while it acts on the couplings by a symplectic transformation, i.e. it preserves the symplectic form (2.10). This can be checked by requiring that any monodromy ${\textbf {M}}_\infty$ satisfies ${\textbf {M}}^T {\textbf {J}} {\textbf {M}}={\textbf {J}}$, with

$$\begin{aligned} {\textbf {J}}=\begin{pmatrix}0&{} \quad 1\\ -1&{}\quad 0\end{pmatrix}^{\oplus N_f+1}. \end{aligned}$$

(2.37)

The action on the couplings $\tau$ (2.11), $v_j$ and $w_{jk}$ (2.12) is thus

$$\begin{aligned} {\textbf {M}}_\infty : {\left\{ \begin{array}{ll} \tau \rightarrow \tau +N_f-4,\\ v_j\rightarrow -v_j-n_j,\\ w_{jk}\rightarrow w_{jk}+\delta _{jk}, \end{array}\right. } \end{aligned}$$

(2.38)

with $\delta _{jk}$ the Kronecker delta.

If we assume that the mass $m_j$ is large, we can also deduce the monodromies around $a=\tfrac{m_j}{\sqrt{2}}$, $j=1,\dots , N_f$ from the perturbative prepotential (2.7). For a encircling $\tfrac{m_1}{\sqrt{2}}$ counterclockwise, $\Pi \rightarrow {\textbf {M}}_1 \Pi$, we find for the monodromy matrix ${\textbf {M}}_1$,

$$\begin{aligned} {\textbf {M}}_1=\begin{pmatrix} 1&{} 1 &{} 0&{}-1&{}\cdots &{}0&{} 0\\ 0&{}1&{}0&{}0&{}\cdots &{}0&{}0\\ 0&{}-1&{}1&{} 1&{}\cdots &{}0&{}0\\ 0&{}0&{}0&{}1&{}\cdots &{}0&{}0\\ \vdots &{}\vdots &{}&{}&{}\ddots &{}&{}\\ 0&{}0&{}0&{}0&{}\cdots &{}1&{}0\\ 0&{}0&{}0&{}0&{}\cdots &{}0&{}1 \end{pmatrix}, \end{aligned}$$

(2.39)

while the ${\textbf {M}}_j$ for other values of j are given by permutations. Its action on the couplings is

$$\begin{aligned} {\textbf {M}}_j: {\left\{ \begin{array}{ll} \tau \rightarrow \tau +1,\\ v_k\rightarrow v_k-\delta _{jk},\\ w_{kl}\rightarrow w_{kl}+\delta _{kl}\delta _{jl}. \end{array}\right. } \end{aligned}$$

(2.40)

To visualise the monodromies with large $\textrm{Im}(\tau )$ for $N_f=1$, we refer to Fig. 4(d). In this regime of the masses, there is one monodromy with periodicity 3 and one with periodicity 1.

Besides the monodromies ${\textbf {M}}_\infty$ and ${\textbf {M}}_j$, there are monodromies ${\textbf {M}}_m$ and ${\textbf {M}}_d$ around the points where a monopole and a dyon become massless, respectively. By requiring that the electro-magnetic charges of the massless particles are $(n_m,n_e)=(1,0)$ and $(1,-2)$, respectively, we can fix the upper left blocks of the monodromies. We fix the remaining entries by assuming that the masses remains invariant, $m_j\rightarrow m_j$, and that the other periods only change by a multiple of the vanishing cycle at the corresponding cusp, together with the requirement that

$$\begin{aligned} {\textbf {M}}_\infty ={\textbf {M}}_m {\textbf {M}}_d \prod _{j=1}^{N_f}{} {\textbf {M}}_j. \end{aligned}$$

(2.41)

For $N_f=1$ and $n_1=n$, this gives for ${\textbf {M}}_{m}$,

$$\begin{aligned} {\textbf {M}}_m=\begin{pmatrix} 1&{}\quad 0 &{}\quad 0&{} \quad 0 \\ -1 &{}\quad 1&{}\quad 0&{}\quad -(n+1)/2 \\ (n+1)/2 &{}\quad 0&{}\quad 1&{}\quad (n+1)^2/4\\ 0&{}\quad 0&{}\quad 0&{}\quad 1 \end{pmatrix}. \end{aligned}$$

(2.42)

This acts on the couplings as

$$\begin{aligned} {\textbf {M}}_m: {\left\{ \begin{array}{ll} \tau \rightarrow \frac{\tau }{-\tau +1},\\ v\rightarrow \frac{v+(n+1)\tau /2}{-\tau +1},\\ w\rightarrow w+\frac{(v+(n+1)/2)^2}{-\tau +1}. \end{array}\right. } \end{aligned}$$

(2.43)

The monodromy ${\textbf {M}}_{d}$ around the dyon singularity for $N_f=1$ is

$$\begin{aligned} {\textbf {M}}_d=\begin{pmatrix} -1&{} \quad 4 &{} \quad 0&{}\quad -n-1 \\ -1 &{}\quad 3&{}\quad 0&{}\quad -(n+1)/2 \\ (n+1)/2&{}\quad -n-1&{}\quad 1&{}\quad (n+1)^2/4\\ 0&{}\quad 0&{}\quad 0&{}\quad 1 \end{pmatrix}, \end{aligned}$$

(2.44)

This acts on the couplings as

$$\begin{aligned} {\textbf {M}}_d: {\left\{ \begin{array}{ll} \tau \rightarrow \frac{-\tau +4}{-\tau +3},\\ v\rightarrow \frac{v+(n+1)\tau -n-1}{-\tau +3},\\ w\rightarrow w+\frac{(v+(n+1)/2)^2}{-\tau +3}. \end{array}\right. } \end{aligned}$$

(2.45)

We can note that all the above monodromy matrices leave the symplectic form (2.10) invariant and are independent of the masses.

For a small mass m, the fourth “hypermultiplet” cusp of the fundamental domain for $N_f=1$ lies naturally near the real axis, $\tau \rightarrow 1$. See for example Fig. 4a. Having determined ${\textbf {M}}_\infty$, ${\textbf {M}}_m$ and ${\textbf {M}}_d$, we can easily determine the monodromy ${\tilde{{\textbf {M}}}_1}$ in this regime as

$$\begin{aligned} {\tilde{{\textbf {M}}}_1}={\textbf { M}}_m^{-1} {\textbf {M}}_\infty {\textbf {M}}_d^{-1}=\begin{pmatrix} 0 &{}\quad 1 &{}\quad 0 &{}\quad (1-n)/2 \\ -1 &{}\quad 2 &{}\quad 0&{}\quad (1-n)/2 \\ (n-1)/2&{} \quad (1-n)/2 &{}\quad 1&{}\quad (n-1)^2/4\\ 0&{}\quad 0&{}\quad 0&{}\quad 1 \end{pmatrix} \end{aligned}$$

(2.46)

Thus for $n=-1$, the massless particle has charge $\pm (-1,1,0,1)$.

We get similar monodromies for $N_f=2,3$. The action on the running couplings $\tau$ is the same for all $N_f$, by construction. The transformations of $v_j$ and $w_{jk}$ also take the same form for all $N_f$ and can be summarised as

$$\begin{aligned} \begin{aligned}&{\textbf {M}}_m: {\left\{ \begin{array}{ll}v_j&{}\rightarrow \frac{v_j+(n_j+1)\tau /2}{-\tau +1},\\ w_{jk}&{} \rightarrow w_{jk}+\frac{(v_j+(n_j+1)/2)(v_k+(n_k+1)/2)}{-\tau +1},\end{array}\right. }\\&{\textbf {M}}_d: {\left\{ \begin{array}{ll} v_j&{}\rightarrow \frac{v_j+(n_j+1)\tau -n_j-1}{-\tau +3},\\ w_{jk}&{} \rightarrow w_{jk}+\frac{(v_j+(n_j+1)/2)(v_k+(n_k+1)/2)}{-\tau +3}.\end{array}\right. } \end{aligned} \end{aligned}$$

(2.47)

3 The UV theory on a four-manifold

We review various aspects of the formulation of the UV theory on a compact smooth four-manifold.

3.1 Aspects of four-manifolds

We let X be a smooth, compact, oriented Riemannian four-manifold, with Euler number $\chi =\chi (X)$ and signature $\sigma =\sigma (X)=b_2^+-b_2^{-}$. The u-plane integral is non-vanishing only for four-manifolds X with $b_2^+\le 1$. In this article, we consider manifolds with $b_2^+=1$. Such four-manifolds admit a linear complex structure $\mathcal {J}$ on the tangent space $TX_p$ at each point p of X. The complex structure varies smoothly on X, such that TX is a complex bundle. We introduce furthermore the canonical class $K_X=-c_1(TX)$ of X, with $c_1(TX)$ the first Chern class of TX. For a manifold X with $(b_1,b_2^+)=(0,1)$, we have that

$$\begin{aligned} K_X^2=8+\sigma (X). \end{aligned}$$

(3.1)

The middle cohomology $H^2(X,\mathbb {Z})$ of X gives rise to the uni-modular lattice L. More precisely, we identify L with the natural embedding of $H^2(X,\mathbb {Z})$ in $H^2(X,\mathbb {Z})\otimes \mathbb {R}$, which mods out the torsion of $H^2(X,\mathbb {Z})$. A characteristic element $K\in L$ is an element which satisfies ${\varvec{l}}^2+ B(K,{\varvec{l}})\in 2\mathbb Z$ for all ${\varvec{l}}\in L$. The Riemann–Roch theorem demonstrates that the canonical class $K_X$ of X is a characteristic element of L. The Wu formula furthermore shows that any characteristic vector K of L is a lift of $w_2(X)$.

The quadratic form Q of the lattice L for a 4-manifold with $(b_1,b_2^+)=(0,1)$ can be brought to a simple standard form depending on whether Q is even or odd [98]. This divides such manifolds into two classes, for which the evaluation of their u-plane integrals needs to be done separately [56, 99]. The period point $J\in H^2(X,\mathbb R)$ is defined as the unique class in the forward light cone of $H^2(X,\mathbb R)$ that satisfies $J=*J$ and $J^2=1$.

All four-manifolds without torsion and even intersection form admit a Spin structure. More generally, for any oriented four-manifold one can define a $\text {Spin}^c$-structure. The group $\text {Spin}^c(4)$ can be defined as pairs of unitary $2\times 2$ matrices with coinciding determinant,

$$\begin{aligned} \text {Spin}^c(4)= \{ (u_1,u_2)\in \textrm{U}(2)\times \textrm{U}(2)|\det {u_1}=\det u_2\}. \end{aligned}$$

(3.2)

There exists a short exact sequence

$$\begin{aligned} 1 \longrightarrow U(1)\longrightarrow \text {Spin}^c(4)\longrightarrow SO(4) \longrightarrow 1. \end{aligned}$$

(3.3)

A $\text {Spin}^c$-structure $\mathfrak {s}$ on a four-manifold X is then a reduction of the structure group of the tangent bundle on X, i.e. SO(4), to the group $\text {Spin}^c(4)$. The different $\text {Spin}^c$-structures correspond to the inequivalent ways of choosing transition functions of the tangent bundle such that the cocycle condition is satisfied. The $\text {Spin}^c$-structure defines two rank two hermitian vector bundles $W^\pm$. We let $c(\mathfrak {s})$ be the first Chern class of the determinant bundles, $c(\mathfrak {s}){:}{=}c_1(\det W^\pm )\in H^2(X,\mathbb {Z})$.

If $\mathfrak {s}$ is the canonical $\text {Spin}^c$ structure associated to an almost complex structure on X, then $c(\mathfrak s)^2=2\chi +3\sigma$. More generally,

$$\begin{aligned} c_1(\mathfrak {s})^2\equiv \sigma \mod 8. \end{aligned}$$

(3.4)

3.2 Topological twisting with background fluxes

We discuss in this section topological twisting of theories with fundamental hypermultiplets including background fluxes. The discussion is parallel to the case of $\mathcal {N}=2^*$ [25], where the hypermultiplet is in the adjoint representation of the gauge group.

We let $(E\rightarrow X,\nabla )$ be a principal $\text {SU}(2)/\mathbb {Z}_2\cong \text {SO}(3)$-bundle with connection $\nabla$. The second Stiefel-Whitney class $w_2(E)\in H^2(X,\mathbb {Z}_2)$ measures the obstruction to lift E to an SU(2) bundle, which will exist locally but not globally if $w_2(E)\ne 0$. We denote a lift of $w_2(E)$ to the middle cohomology lattice L by ${\bar{w}}_2(E)\in L$ and define the ’t Hooft flux ${\varvec{\mu }}={\bar{w}}_2(E)/2\in L/2$. The instanton number of the principal bundle is defined as $k=-\frac{1}{4}\int _X p_1(E)$ and satisfies $k\in -{\varvec{\mu }}^2 + \mathbb {Z}$, where $p_1$ is the first Pontryagin class.

To formulate the theories with $N_f$ fundamental hypermultiplets on a compact four-manifold, we perform a topological twist. Coupling the four-dimensional $\mathcal {N}=2$ $\text {SU}(2)$ theory to background fields means choosing two sets of data:

• A principal $\text {SU}(2)_R$ R-symmetry bundle, with connection $\nabla _R$,

• and a principal bundle $\mathcal {L}$ with connection for global symmetries (the flavour symmetries) [25].

The relevant twist for the $\mathcal {N}=2$ supersymmetry algebra in four dimensions is the Donaldson-Witten twist. This twist is the local identification of the SU(2)${}_+$ with the diagonal subgroup of the SU(2)${}_+\times$SU(2)${}_R$ factor of the spin lift of the local spin group $\text {Spin}(4)\cong \text {SU}(2)_+\times \text {SU}(2)_-$ [1]. Alternatively, one can view the fields as sections of a non-trivial R-symmetry bundle, isomorphic to the spin bundle $S^+$. Application of this to the representations of the vector multiplet (2.1) and (2.4) gives:

$$\begin{aligned} \begin{aligned}&\text {bosons:}\quad{} & {} ({\textbf {2}}, {\textbf {2}})\oplus ({\textbf {1}}, {\textbf {1}}) \oplus ({\textbf {1}}, {\textbf {1}}), \\&\text {fermions:}\quad{} & {} ({\textbf {2}},{\textbf {2}})\oplus ({\textbf {3}}, {\textbf {1}})\oplus ({\textbf {1}},{\textbf {1}}). \end{aligned} \end{aligned}$$

(3.5)

Thus the bosons remain unchanged, a vector and a complex scalar, while the fermions reorganise to a vector, self-dual two-form and real scalar, which we denote as $\psi$, $\chi$ and $\eta$, respectively. We note that none of these fields are spinors and can thus be considered on a non-spin four-manifold. The original supersymmetry generators also transform in the representations for the fermions above. Thus the theory contains a scalar fermionic supercharge $\mathcal {Q}=\epsilon ^{\dot{A} \dot{B}}\overline{\mathcal {Q}}_{\dot{A}\dot{B}}$, whose cohomology provides the operators in the topological theory [1].

For the fields of a hypermultiplet, (2.3) and (2.4), one finds

$$\begin{aligned} \begin{aligned}&\text {bosons:}\quad{} & {} ({\textbf {1}}, {\textbf {2}})\oplus ({\textbf {1}}, {\textbf {2}}), \\&\text {fermions:}\quad{} & {} ({\textbf {2}}, {\textbf {1}})\oplus ({\textbf {1}},{\textbf {2}})\oplus ({\textbf {2}}, {\textbf {1}})\oplus ({\textbf {1}}, {\textbf {2}}). \end{aligned} \end{aligned}$$

(3.6)

Thus hypermultiplet bosons become spinors, i.e. sections of the spin bundle $S^+$, while the fermions are sections of $S^+$ and $S^-$. Thus the twisted hypermultiplets can in this case only be formulated on four-manifolds which are spin, i.e. $w_2(X)=0$ [12, 16].

However, if the hypermultiplets are charged under a gauge field or flux, the product of these bundles with $S^\pm$ may be a Spin$^c$ bundle, $W^+$ or $W^-$ [16, 25, 39]. The latter are defined for arbitrary four-manifolds. For example, an almost complex structure on X determines two canonical Spin$^c$ bundles $W^\pm \simeq S^\pm \otimes K^{-1/2}_X$ with $K_X$ the canonical class determined by the almost complex structure. Since the hypermultiplets are in the fundamental, two-dimensional representation of SU(2), the topologically twisted hypermultiplets are well-defined on a non-spin four-manifold if ${\varvec{\mu }}=-K_X/2$ [12].

Let us state this also in terms of the gauge bundle E. To this end, we label the two components of the fundamental, two-dimensional representation of SU(2) by ±. The two components are sections of a line bundle $\mathcal {L}_E^{\pm 1/2}$ with $c_1(\mathcal {L}_E)={\bar{w}}_2(E)$. Of course, the square root $\mathcal {L}_E^{1/2}$ only exists if $w_2(E)\in 2L$. On the other hand, the physical requirement is that $S^+\otimes \mathcal {L}_E^{1/2}$ is well defined, or ${\bar{w}}_2(X)+{\bar{w}}_2(E)\in 2\,L$. Therefore, the obstructions can cancel each other for a suitable choice of $w_2(E)$. Thus the topological twisted theory is not well-defined for an arbitrary choice of ’t Hooft flux ${\varvec{\mu }}{:}{=}\frac{1}{2} {\bar{w}}_2(E)$, but rather ${\varvec{\mu }}$ has to satisfy ${\varvec{\mu }}=\frac{1}{2} {\bar{w}}_2(X) \mod L$ [12], or

$$\begin{aligned} {\bar{w}}_2(X)={\bar{w}}_2(E) \mod 2\,L. \end{aligned}$$

(3.7)

To consider more general ’t Hooft fluxes ${\varvec{\mu }}$ or equivalently $w_2(E)$, we can couple the j’th hypermultiplet to a background flux or line bundle $\mathcal {L}_j$, with $\mathcal {L}_j$ possibly different for each j. We let $\mathcal {E}_j=\mathcal {L}_E\otimes \mathcal {L}_j$. Then the requirement that $S^\pm \otimes \mathcal {E}_j^{\pm 1/2}$ is globally well-defined is that

$$\begin{aligned} c_1(\mathcal {E}_j)\in {\bar{w}}_2(X) +2\,L, \end{aligned}$$

(3.8)

which can be satisfied for any ${\bar{w}}_2(E)$ for a suitable choice of $\mathcal {L}_j$. Thus we can formulate the u-plane integral for arbitrary ${\bar{w}}_2(E)$, if we require that the background fluxes satisfy

$$\begin{aligned} c_1(\mathcal {L}_j)\in {\bar{w}}_2(X)+{\bar{w}}_2(E) +2\,L, \end{aligned}$$

(3.9)

for each j. This is consistent with (3.7) for $c_1(\mathcal {L}_j)=0$.

The Chern classes $c_1(\mathcal {L}_j)$ can also be seen as the splitting classes of the $\text {Spin}(2N_f)$ principal bundle $\mathcal {L}$. The Chern class of $\mathcal {L}$ reads

$$\begin{aligned} c(\mathcal {L})=\sum _{l=0}^2 c_l(\mathcal {L})=\prod _{j=1}^{N_f} (1+c_1(\mathcal {L}_j)). \end{aligned}$$

(3.10)

The scalar generators of the equivariant cohomology of $\text {Spin}(2N_f)$ are the masses $m_j$, which generate the $N_f$-dimensional Cartan subalgebra of $\text {Spin}(2N_f)$. The gauge bundle $E_k$ is also $\text {Spin}(2N_f)$ equivariant. For generic masses, the flavour group is U(1)$^{N_f}$ and is enhanced for special loci of the masses, for example to $\text {U}(N_f)$ for equal masses [11].

The $\mathcal {Q}$-fixed equations are the non-Abelian monopole equations with $N_f$ matter fields in the fundamental representation. For generic gauge group G and with representation R, these equations read [15]

(3.11)

where $T^a$ is a generator of the Lie algebra in the representation R. Including the sum over matrix elements, we have

$$\begin{aligned} M^j_{(\alpha } T^a M^j_{\beta )}=\sum _{k,l}(M^j)^k_{(\alpha } (T^a)^{kl} (M^j)^l_{\beta )}. \end{aligned}$$

(3.12)

We denote the moduli space of solutions to (3.11) by $\mathcal {M}^{Q,N_f}_{k,\mathcal {L}_j}$, and leave the dependence on the ’t Hooft flux ${\varvec{\mu }}$ and the metric J implicit. For $N_f=4$ on $X=\mathbb{C}\mathbb{P}^2$, such moduli spaces are studied in [32].

The moduli spaces $\mathcal {M}^{Q,N_f}_{k,\mathcal {L}_j}$ are non-compact for vanishing masses [24, 36, 100]. This is improved upon turning on masses and localizing with respect to the $\text {U}(1)^{N_f}$ flavour symmetry, $M^j_\alpha \rightarrow e^{i\,\varphi _j} M^j_{\alpha }$, which leave the invariant $\mathcal {Q}$-fixed equations (3.11). There are two components:

• the instanton component, with $F^+=0$ and $M^j=0$, $j=1,\dots ,N_f$. The moduli space for this component is denoted $\mathcal {M}^\textrm{i}_k$. Since the hypermultiplet fields vanish, this component is associated to the Coulomb branch.

• the abelian or monopole component, for which a U(1) subgroup of the flavour group acts as pure gauge. Here the connection is reducible, and a U(1) subgroup of the SU(2) gauge group is preserved. For generic masses, there are $N_f$ such components, where $M^\ell$ is upper or lower triangular for some $\ell$, and $M^j=0$ for all $j\ne \ell$. The moduli space of this component is denoted $\mathcal {M}^{\textrm{a},j}_k$, $j=1,\dots , N_f$. Since some of the hypermultiplet fields are non-vanishing, this component is associated to the Higgs branch [21, 100].

The instanton component $\mathcal {M}^\textrm{i}_k$ is non-compact due to point-like instantons. This can be cured using the Uhlenbeck compactification or algebraic-geometric compactifications. We assume that the physical path integral chooses a specific compactification, whose details are however not manifest at the level of the low-energy effective field theory other than that the compactification must be in agreement with the correlation functions.

The topological twist for $\mathcal {N}=2$ supersymmetric QCD can be further made dependent on a cocycle $\zeta _{\alpha \beta \gamma }^{\text {gauge}}$ representing the ’t Hooft flux, and $\zeta _{\alpha \beta \gamma }^s$ a cocycle representing $w_2(X)$ (the cocycles are the U(1)-valued functions measuring the obstruction of the cocycle condition for transition functions) [25]. Without additional line bundles, $\bar{w}_2(X)={\bar{w}}_2(E)$ is equivalent to the cocycle $\zeta _{\alpha \beta \gamma }^{\text {gauge}}\zeta _{\alpha \beta \gamma }^s$ being trivialisable. We leave it for future work to explore whether the invariants depend on the choice of trivialisation.

3.3 Correlation functions and moduli spaces

The $\mathcal {Q}$-fixed equations (3.11) include a Dirac equation for each hypermultiplet $j=1,\dots ,N_f$ in the fundamental representation. The corresponding index bundle $W_k^j$ defines an element of the K-group of $\mathcal {M}^\textrm{i}_k$. Its virtual rank $\text {rk}(W^j_k)$ is the formal difference of two infinite dimensions. It is given by an index theorem and reads

$$\begin{aligned} \text {rk}(W^j_k)=-k+\frac{1}{4}(c_1(\mathcal {L}_j)^2-\sigma )\in \mathbb {Z}, \end{aligned}$$

(3.13)

where $c_1(\mathcal {L}_j)$ is the first Chern class of the bundle $\mathcal {L}_j$. Note that the rhs is not an integer for an arbitrary $c_1(\mathcal {L}_j)\in H^2(X,\mathbb {Z})$. To verify that the rhs is integral for the $c_1(\mathcal {L}_j)$’s satisfying (3.9), we rewrite $\text {rk}(W^j_k)$ as

$$\begin{aligned} \text {rk}(W^j_k)=-(k+{\varvec{\mu }}^2)-c_1(\mathcal {L}_j)\cdot {\varvec{\mu }}+\frac{1}{4}\left( (c_1(\mathcal {L}_j)+2{\varvec{\mu }})^2-\sigma \right) . \end{aligned}$$

(3.14)

Then the first term on the rhs is an integer since $k\in -\frac{1}{4}w_2(E)^2+\mathbb {Z}$ for an $\text {SO}(3)$ bundle. The second term is an integer because $c_1(\mathcal {L}_j)\cdot {\varvec{\mu }}=(\bar{w}_2(X)-2{\varvec{\mu }})\cdot {\varvec{\mu }}\mod \mathbb {Z} \in \mathbb {Z}$, and the third term is an integer using (3.4) and the fact that $c_1(\mathcal {L}_j)+2{\varvec{\mu }}$ equals the characteristic class of a $\text {Spin}^c$-structure $\mathfrak {s}_j$ by (3.9),

$$\begin{aligned} c_1(\mathcal {L}_j)+2{\varvec{\mu }}=c(\mathfrak {s}_j), \end{aligned}$$

(3.15)

for each j.

The mass $m_j$ is the equivariant parameter of the U(1) flavour symmetry associated to the j’th hypermultiplet. The equivariant Chern class of $W^j_k$ reads in terms of the splitting class $x_l$,

$$\begin{aligned} c(W_k^j)=\prod _{l=0}^{-\text {rk}(W^j_k)} (x_l+m_j)=m_j^{-\text {rk}(W^j_k)} \sum _l \frac{c_l(W_k^j)}{m_j^l}. \end{aligned}$$

(3.16)

We abbreviate $c_l(W_k^j)$ to $c_{l,j}$, and let $c(W_k)=\prod _{j=1}^{N_f} c(W_k^j)$.

The moduli space $\mathcal {M}_{k,{\varvec{\mu }},\mathcal {L}_j}^{Q}$ for $N_f$ hypermultiplets corresponds to the vanishing locus of the obstructions for the existence of $N_f$ zero modes of the Dirac operator. As a result, the virtual complex dimension of the moduli space $\mathcal {M}_{k,{\varvec{\mu }},\mathcal {L}_j}^{Q}$ is that of the instanton moduli space plus the sum of (typically negative) ranks of the index bundles $W_k^j$, $\text {vdim}(\mathcal {M}^{Q,N_f}_{k,\mathcal {L}_j})=\text {vdim}(\mathcal {M}^{Q}_k)_{N_f=0}+\sum _{j=1}^{N_f}\text {rk}(W_k^j)$ [17, 25, 31, 36]. This gives

$$\begin{aligned} \text {vdim}(\mathcal {M}_{k,\mathcal {L}_j}^{Q,N_f})=(4-N_f)k+\frac{1}{4}\left( -3\chi -(3+N_f)\sigma +\sum _{j=1}^{N_f} c_1(\mathcal {L}_j)^2\right) . \end{aligned}$$

(3.17)

It is argued in [13] that the inclusion of massive matter amounts to inserting an integral of the equivariant Euler class of the Dirac index bundle over the moduli space. Therefore, the correlation functions are the generating functions for the intersection numbers of the standard Donaldson observables and the Poincaré duals to the Chern classes of the various vector bundles.

The correlation functions on X in the theory with $N_f$ massive fundamental hypermultiplets are conjectured to be

$$\begin{aligned} \langle \mathcal {O}_1\dots \mathcal {O}_p\rangle =\sum _k \Lambda _{N_f}^{\textrm{vdim}(\mathcal {M}^{Q,N_f}_{k,\mathcal {L}_j})} \, \int _{\mathcal {M}_{k,\mathcal {L}_j}^{Q,N_f}} c(W_k)\, \omega _1\wedge \dots \wedge \omega _p, \end{aligned}$$

(3.18)

where $\omega _i=\mu (\mathcal {O}_i)$ are the Donaldson classes associated to the physical observable $\mathcal {O}_i$, and c(M) is the Euler class of the matter bundle [101,102,103,104]. Localising to the fixed point locus in $\mathcal {M}^{Q,N_f}_{k,\mathcal {L}_j}$ with respect to $U(1)^{N_f}$ gives

$$\begin{aligned} \begin{aligned} \langle \mathcal {O}_1\dots \mathcal {O}_p\rangle&=\sum _k \Lambda _{N_f}^{\textrm{vdim}(\mathcal {M}^{Q,N_f}_{k,\mathcal {L}_j})}\\&\quad \times \int _{\mathcal {M}^\textrm{i}_k \cup \mathcal {M}^\textrm{a}_k} \left( \prod _{j=1}^{N_f} m_j^{-\text {rk}( W^j_k)}\sum _l \frac{c_{l,j}}{m_j^l}\right) \, \omega _1\wedge \dots \wedge \omega _p. \end{aligned} \end{aligned}$$

(3.19)

where the integral is over the union $\mathcal {M}^\textrm{i}_k \cup \mathcal {M}^\textrm{a}_k$ of the instanton component $\mathcal {M}^\textrm{i}_k$ [13, Eq. (5.13)] and the monopole component $\mathcal {M}^\textrm{a}_k$ [25, 105]. The equation together with the dimension of the moduli spaces (3.17) demonstrates a selection rule for observables together with powers of $\Lambda _{N_f}$ and $m_j$.

In the decoupling limit $m_{N_f}\rightarrow \infty$, $\Lambda _{N_f}\rightarrow 0$ (2.18), the only contribution for $j=N_f$ is from $l=0$, $c_{0,N_f}=1$. The powers of $m_j$ and $\Lambda _{N_f}$ work out such that the correlation functions reduce to those of the theory with $N_f-1$ hypermultiplets [21]

$$\begin{aligned} \left( \frac{\Lambda _{N_f}}{\Lambda _{N_f-1}}\right) ^{-\alpha } \langle \mathcal {O}_1\dots \mathcal {O}_p\rangle _{N_f} \rightarrow \langle \mathcal {O}_1\dots \mathcal {O}_p\rangle _{N_f-1}, \end{aligned}$$

(3.20)

We deduce from (3.19) that

$$\begin{aligned} \begin{aligned} \alpha&=\textrm{vdim}(\mathcal {M}^{Q,N_f}_k)+(4-N_f)\, \text {rk}(W_k^{N_f})\\&=\frac{1}{4}\Big (-3\chi -7\sigma +(5-N_f)\,c_1(\mathcal {L}_{N_f})^2+\sum _{j=1}^{N_f-1}c_1(\mathcal {L}_j)^2 \Big ). \end{aligned} \end{aligned}$$

(3.21)

The overall factor can be accounted for by an overall renormalization in the decoupling limit.

The correlation function has a smooth massless limit $m_j\rightarrow 0$, for which only terms with the top Chern classes contribute. These are given by

$$\begin{aligned} \langle \mathcal {O}_1\dots \mathcal {O}_p\rangle =\sum _k \prod _{j=1}^{N_f} \Lambda _{N_f}^{\textrm{vdim}(\mathcal {M}^{Q,N_f}_{k,\mathcal {L}_j})} \int _{\mathcal {M}^\textrm{i}_k \cup \mathcal {M}^\textrm{a}_k} c_{l_j,j}\, \omega _1\wedge \dots \wedge \omega _p \end{aligned}$$

(3.22)

with $l_j=-\textrm{rk}(W^j_k)$ for each $c_{l,j}$. For a non-vanishing result, the degree of $\omega _1\dots \omega _p$ must equal $\textrm{vdim}(\mathcal {M}^{Q,N_f}_{k,\mathcal {L}_j})$.

By comparing the form degrees (or ghost numbers) of operators with the virtual dimension of the moduli space, one derives selection rules for correlation functions of point and surface operators. Since u has ghost number 4, the fugacity p naturally has ghost number $-4$. Similarly, we associate ghost number $-2$ to the surface ${\varvec{x}}$. The mass $m_j$ finally has ghost number 2. Thus correlation functions will evaluate to sums of monomials of the form $p^s{\varvec{x}}^t\prod _{j=1}^{N_f}m_j^{r_j}$, with the selection rule

$$\begin{aligned} -4s-2t+2\sum _{j=1}^{N_f}r_j=-\text {vdim}_{\mathbb R}(\mathcal {M}_{k,\mathcal {L}_j}^{Q,N_f}). \end{aligned}$$

(3.23)

4 The effective theory on a four-manifold

We consider in this section the low-energy effective field theory on a four-manifold. We derive the semi-classical action of the theory coupled to background $\text {U}(1)$ fields. As in previous cases [12, 25, 62, 106], the final expression takes the form of a Siegel–Narain theta series multiplied by a measure factor.

4.1 Hypermultiplets and background fields

The effective theory coupled to $N_f$ background fluxes can be modelled as that of a theory with gauge group $\text {SU}(2)\times \text {U}(1)^{N_f}$, where the fields of the U(1) factors have been frozen in a special way [25, 107]. To derive the precise form, we recall the low-energy effective Lagrangian for the r multiplets $(\phi ^J,\eta ^J,\chi ^J,\psi ^J,F^J)$ of the topologically twisted $\text {U}(1)^r$ SYM theory [108]. Since the u-plane integral reduces to an integral over zero-modes [12], it suffices to only include the zero-modes in the Lagrangian. For simply connected four-manifolds, there is no contribution from the one-form fields $\psi ^J$. The Lagrangian is then given in terms of the prepotential $F(\{a^J\})$ and its derivatives to the vevs $\langle \phi ^J \rangle =a^J$, as

$$\begin{aligned} \begin{aligned} \mathcal {L}&= \frac{i}{16\pi }({\bar{\tau }}_{JK}F^J_+\wedge F_+^K+\tau _{JK}F^J_-\wedge F^K_-)-\frac{1}{8\pi }y_{JK}D^J\wedge D^K\\&\quad \qquad +\frac{i\sqrt{2}}{16\pi }{\bar{\mathcal {F}}}_{JKL}\eta ^J\chi ^K\wedge (D+F_+)^L, \end{aligned} \end{aligned}$$

(4.1)

with $y_{JK}=\text {Im}(\tau _{JK})$, $\tau _{JK}=\partial _J\partial _K F(\{a^J\})$ and $\mathcal {F}_{JKL}=\partial _J\partial _K\partial _L F(\{a^J\})$. It is left invariant by the BRST operator Q, which acts on the zero modes as

$$\begin{aligned} \begin{alignedat}{2} [Q,A^J]&=\psi ^J=0,\qquad{} & {} [Q,\psi ^J]=4\sqrt{2}da^J,\\ [Q,a^J]&=0,\qquad{} & {} [Q,{\bar{a}}^J]=\sqrt{2}i\eta ^J,\\ [Q,\eta ^J]&=0,\qquad{} & {} [Q,\chi ^J]=i(F_+-D_+)^J,\\ [Q,D^J]&=(\hbox {d}\psi ^J)_+=0. \end{alignedat} \end{aligned}$$

(4.2)

Using this operator, we can write $\mathcal {L}$ as the sum of a topological, holomorphic term and a Q-exact term,

$$\begin{aligned} \mathcal {L}=\frac{i}{16\pi }\tau _{JK}F^J\wedge F^K+\{Q,W\}, \end{aligned}$$

(4.3)

with

$$\begin{aligned} W=-\frac{i}{8\pi }y_{JK}\chi ^J(F_++D)^K. \end{aligned}$$

(4.4)

The low-energy theory of $\text {SU}(2)$ gauge theory with $N_f$ hypermultiplets coupled to $N_f$ background fluxes can then be modelled by the above rank r description with $r=N_f+1$. We identify $F(\{a^J\})$ with $F(a,{\varvec{m}})$. We let the indices J, K run from 0 to $N_f$ and identify the index 0 with the unbroken U(1) of the SU(2) gauge group and the indices $j,k,l=1,\dots , N_f$ with that of the frozen $\text {U}(1)^{N_f}$ factors. We further set $\phi ^0{:}{=}\phi$ for any field $\phi$. We will proceed by using lower indices for j, k, l, except where the summation convention is explicitly used, to avoid confusion with powers of the fields.

The masses of the hypermultiplets are the vevs of the frozen scalar fields of the corresponding vector multiplets, $\tfrac{m_{j}}{\sqrt{2}}=\langle \phi _{j}\rangle =a_{j}$ [107]. We set $[F_{j}]=4\pi {\varvec{k}}_{j}$ with

$$\begin{aligned} {\varvec{k}}_{j}=c_1(\mathcal {L}_j)/2\in L/2. \end{aligned}$$

(4.5)

To make the BRST variations of the fields from the frozen U(1) factors vanish, we set $\eta _j=\chi _j=0$, as well as $D^j=F_+^j$. With these identifications, the Lagrangian becomes

$$\begin{aligned} \begin{aligned} \mathcal {L}=\,&\frac{i}{16\pi }\tau _{JK}F^J\wedge F^K+\frac{1}{8\pi }y_{00}F_+\wedge F_+-\frac{1}{8\pi }y_{00}D\wedge D\\&+\frac{i\sqrt{2}}{16\pi }{\bar{\mathcal {F}}}_{000}\eta \chi \wedge (D+F_+)+\frac{i\sqrt{2}}{8\pi }{\bar{\mathcal {F}}}_{00j}\eta \chi \wedge F_+^j\\&+\frac{1}{4\pi }y_{0j}(F_+-D)\wedge F_+^j. \end{aligned} \end{aligned}$$

(4.6)

Integrating over D, $\eta$ and $\chi$ in the standard way [12, 25, 108], we end up with

$$\begin{aligned} \begin{aligned}&\int \hbox {d}D \hbox {d}\eta \hbox {d}\chi \, e^{-\int _X \mathcal {L}} \\&=\frac{\partial }{\partial {\bar{a}}}\left( i\sqrt{y_{00}}\,B\left( F+\frac{y_{0j}}{y_{00}}F^j,J\right) \right) e^{-\int _X\mathcal {L}_0}, \end{aligned} \end{aligned}$$

(4.7)

where

$$\begin{aligned} \mathcal {L}_0&=\frac{i}{16\pi }\tau _{JK}F^J\wedge F^K+\frac{1}{8\pi }y_{00}F_+\wedge F_++\frac{y_{0j}}{4\pi }F_+\wedge F_+^j+\frac{1}{8\pi }\frac{y_{0j}y_{0k}}{y_{00}}F^j_+\wedge F^k_+\nonumber \\&= \frac{i}{16\pi } ({\bar{\tau }} F_+\wedge F_++\tau F_-\wedge F_-)+\frac{i}{8\pi }(v_j F_-\wedge F_-^j+{\bar{v}}_jF_+\wedge F^j_+)\nonumber \\&\quad +\frac{i}{16\pi } w_{jk}F^j\wedge F^k+\frac{ y}{8\pi }\text {Im}(v_j)\text {Im}(v_k)F_+^j\wedge F_+^k, \end{aligned}$$

(4.8)

and we identified $\tau {:}{=}\tau _{00}$, $y=\textrm{Im}(\tau )=y_{00}$, $v_j{:}{=}\tau _{0j}$ and $w_{jk}{:}{=}\tau _{jk}$. Thus the coupling $w_{jk}$ is holomorphic, but the coupling $v_j$ is non-holomorphic. This is similar to the couplings for $\mathcal {N}=2^*$ [25].

4.2 Sum over fluxes

The path integral includes a sum over fluxes ${\varvec{k}}=[F]/4\pi \in L/2$. After summing the exponentiated action (4.7) over the fluxes ${\varvec{k}}$ and multiplying by $\frac{\text{ d }{\bar{a}} }{\text {d}{\bar{\tau }}}$, we find that this takes the form

$$\begin{aligned} \sum _{{\varvec{k}}\in L+{\varvec{\mu }}}\int \hbox {d}D \hbox {d}\eta \hbox {d}\chi \, e^{-\int _X \mathcal {L}}=\left( \prod _{j,k=1}^{N_f} C_{jk}^{B({\varvec{k}}_j,{\varvec{k}}_k)}\right) \,\Psi _{{\varvec{\mu }}}^J(\tau ,{\bar{\tau }},{\varvec{z}},{\bar{{\varvec{z}}}}). \end{aligned}$$

(4.9)

The couplings $C_{jk}$ are given in terms of $w_{jk}$ (2.12) by

$$\begin{aligned} C_{jk}=e^{-\pi iw_{jk}}, \end{aligned}$$

(4.10)

for $j,k=1,\dots , N_f$. Such couplings were first put forward in [62] and were also crucial in [25].

The term $\Psi _{{\varvec{\mu }}}^J$ is an example of a Siegel–Narain theta function. It reads explicitly

$$\begin{aligned} \begin{aligned} \Psi _{{\varvec{\mu }}}^J(\tau ,{\bar{\tau }},{\varvec{z}},{\bar{{\varvec{z}}}})&=e^{-2\pi y{\varvec{b}}^2_+} \sum _{{\varvec{k}}\in L+{\varvec{\mu }}}\partial _{\bar{\tau }}\left( 4\pi i\sqrt{y}B( {\varvec{k}}+{\varvec{b}}, J)\right) \\&\times (-1)^{B({\varvec{k}},K)} q^{-{\varvec{k}}_-^2/2}{\bar{q}}^{{\varvec{k}}_+^2/2} e^{-2\pi iB({\varvec{z}},{\varvec{k}}_-)-2\pi iB({\bar{{\varvec{z}}}}, {\varvec{k}}_+)},\end{aligned} \end{aligned}$$

(4.11)

and discussed in more detail in Appendix A.2. The elliptic variable reads in terms of $v_j$ and ${\varvec{k}}_j$,

$$\begin{aligned} {\varvec{z}}=\sum _{j=1}^{N_f}v_j{\varvec{k}}_j,\quad \text {and} \quad {\varvec{b}}=\frac{\text {Im}({\varvec{z}})}{y}, \end{aligned}$$

(4.12)

thus inducing a non-holomorphic dependence on $v_j$. Furthermore, K appearing in the fourth root of unity $(-1)^{B({\varvec{k}},K)}$ is a characteristic vector of L. Note that $\Psi _{\varvec{\mu }}^J$ changes by the sign $(-1)^{B({\varvec{\mu }},K-K')}$ upon replacing K by a different characteristic vector $K'$ [12, 25, 109].

For $N_f=0$, this phase can be understood as arising from integrating out massive fermionic modes [106]. It also appears naturally in decoupling the adjoint hypermultiplet in the analogous function for $\mathcal {N}=2^*$ [25]. For $N_f>0$, the constant part of the couplings $v_j$ (2.12) effectively contributes to the phase, such that the total phase reads

$$\begin{aligned} e^{\pi i B({\varvec{k}},K)} \prod _{j=1}^{N_f} e^{\pi i\, n_j\,B({\varvec{k}}_j,{\varvec{k}})}, \end{aligned}$$

(4.13)

with $n_j$ the magnetic winding numbers. For arbitrary $n_j\in \mathbb {Z}$, the phase is an eighth root of unity. It would be interesting to understand this phase from integrating out massive modes.

We deduce from (4.13) that the summand of $\Psi ^J_{\varvec{\mu }}$ changes by a phase

$$\begin{aligned} e^{\pi i (n_j'-n_j) B({\varvec{k}}_j,{\varvec{k}})} \end{aligned}$$

(4.14)

if the winding numbers $n_j$ are replaced by $n'_j$. Since ${\varvec{k}}_j\in K/2-{\varvec{\mu }}\mod L$ (see (3.9)) and ${\varvec{k}}\in L+{\varvec{\mu }}$, this phase is 1 if $n_j'-n_j=0\mod 4$. We can therefore restrict to $n_j\in \mathbb {Z}_4$. For specific choices of ${\varvec{\mu }}$ and ${\varvec{k}}_j$, the $n_j$ can lie in a subgroup of $\mathbb {Z}_4$.

The modular transformations of $\Psi ^J_{\varvec{\mu }}$ are discussed in Appendix A.2, which are crucial input for single-valuedness of the u-plane integrand. We will demonstrate in Sect. 5.2 that the u-plane integrand is single-valued if we impose further constraints on the winding numbers $n_j$.

Finally, if the theory is considered on a curved background, topological couplings arise in the effective field theory [106]. These terms couple to the Euler characteristic and the signature of the four-manifold X, respectively, denoted A and B. These take the form [12, 106],

$$\begin{aligned} A=\alpha \left( \frac{\text{ d }u}{\text {d}a}\right) ^{1/2},\qquad B=\beta \Delta _{N_f}^{1/8}. \end{aligned}$$

(4.15)

Here, $\Delta _{N_f}$ is the physical discriminant incorporating the singularities of the effective theory, while $\frac{\text{ d }u}{\text {d}a}$ is the (reciprocal of) the periods of the SW curves as introduced in Sect. 2. Both can be determined directly from the SW curve, as described in Sect. 2.3. The prefactors $\alpha$ and $\beta$ are independent of u, but can be functions of other moduli such as the masses ${\varvec{m}}$, the dynamical scale $\Lambda _{N_f}$ or the UV coupling $\tau _{\text {{UV}}}$. However, it turns out that for the theories with fundamental matter they are independent of the masses and only depend on the scale [21, 110]. They satisfy several constraints from holomorphy, RG flow, homogeneity and dimensional analysis and can in principle be fixed for any Lagrangian theory from a computation in the $\Omega$-background [21, 23, 80, 110].

4.3 Observables and contact terms

The observables in the topologically twisted theories are the point observable or 0-observable u, as well as d-observables supported on a d-dimensional submanifold of X. The d-observables are only non-vanishing if the submanifold corresponds to a non-trivial homology class. For $b_1=0$, the d-observables with d odd therefore do not contribute.

To introduce the surface observable, let ${\varvec{x}}\in H_2(X,\mathbb {Q})$. Then the surface observable reads in terms of the UV fields,

$$\begin{aligned} I({\varvec{x}})=\frac{1}{4\pi ^2}\int _{{\varvec{x}}} \textrm{Tr}\left[ \psi \wedge \psi -\frac{1}{\sqrt{2}}\phi \,F \right] . \end{aligned}$$

(4.16)

In the effective infrared theory, this operator becomes,

$$\begin{aligned} {\tilde{I}}({\varvec{x}})=\frac{i}{\sqrt{2}\pi } \int _{\varvec{x}}\frac{1}{32} \frac{\text{ d}^2u}{\text {d}a^2}\,\psi \wedge \psi -\frac{\sqrt{2}}{4}\frac{\text{ d }u}{\text {d}a}(F_-+D). \end{aligned}$$

(4.17)

Generating functions of correlation functions are obtained by inserting

$$\begin{aligned} e^{p\,u/\Lambda _{N_f}^2+{\tilde{I}}({\varvec{x}})/\Lambda _{N_f}} \end{aligned}$$

(4.18)

in the path integral. The surface observable leads to a change in the argument of the sum over fluxes (4.11),

$$\begin{aligned} {\varvec{z}}\rightarrow {\varvec{z}}+ \frac{{\varvec{x}}}{2\pi \,\Lambda _{N_f}}\,\frac{\text{ d }u}{\text {d}a},\qquad {\bar{{\varvec{z}}}} \rightarrow {\bar{{\varvec{z}}}}. \end{aligned}$$

(4.19)

and to analytically continue ${\varvec{b}}$ (4.12) to the complex number by setting ${\varvec{b}}=({\varvec{z}}-{\bar{{\varvec{z}}}})/(2iy)$.

The inclusion of the surface observable also gives rise to a contact term [2, 12, 103], which in particular ensures that the u-plane integrand is single-valued. For $0\le N_f\le 3$, the contact term is $\exp ({\varvec{x}}^2\,G_{N_f})$ with [13, 22, 111]

$$\begin{aligned} G_{N_f}=-\frac{1}{24\,\Lambda _{N_f}^2}E_2\left( \frac{\text{ d }u}{\text {d}a}\right) ^{2}+\frac{1}{3\,\Lambda _{N_f}^2}\left( u+\frac{\Lambda _3^2}{64}\delta _{N_f,3}\right) , \end{aligned}$$

(4.20)

while for $N_f=4$ it is given by [22, 112]

(4.21)

This expression (4.20) is valid for the theories with $N_f$ arbitrary hypermultiplet masses. The reason for it is the following [22, 74, 108]: G is guaranteed to be ${\bar{\mathcal {Q}}}$-closed and hence locally holomorphic. First, notice that $\frac{\partial F}{\partial \tau _0}=\frac{u}{4}$, where $\Lambda _{N_f}^{4-N_f}{=}{:} e^{\pi i\tau _0}$ for the asymptotically free theories ($N_f\le 3$) and $\tau _0=\tau _{\text {{UV}}}$ for $N_f=4$. The real part of the exponential prefactor of $\Psi _{\varvec{\mu }}^J$ can be added to G to give a monodromy-invariant contribution ${\hat{G}}$ which multiplies the intersection ${\varvec{x}}^2$. From the action of a duality transformation on ${\hat{G}}$ it can be inferred that

$$\begin{aligned} G_{N_f}=-\frac{4i}{\pi \Lambda _{N_f}^2}\frac{\partial ^2 F}{\partial \tau _0^2}. \end{aligned}$$

(4.22)

The expression (4.20) follows by direct computation. A more general scheme to fix the contact terms is proposed in [13]. Contact terms can also be derived from the corresponding Whitham hierarchies [111, 113]. In the presence of surface observables, there are additional mixed contact terms $\frac{\partial ^2\mathcal {F}}{\partial \tau _0\partial m}$ for the external fluxes $\{{\varvec{k}}_j\}$ as encountered in [25] for the $\mathcal {N}=2^*$ theory.

5 The u-plane integral

In this section, we set up the u-plane integral schematically given in (1.2), and demonstrate that it is well-defined on the integration domain for any ${\varvec{\mu }}$ with appropriate background fluxes. The case ${\varvec{\mu }}={\bar{w}}_2(X)/2$ and ${\varvec{k}}_j=0$ was analysed in [12].

5.1 Definition of the integrand

As discussed in the previous sections, the u-plane integral on a closed four-manifold X with $(b_1, b_2^+)=(0,1)$ depends on many parameters. We summarise:

• The scale $\Lambda _{N_f}$ and masses ${\varvec{m}}=(m_1,\dots ,m_{N_f})$ of the theory. See Sect. 2.

• The magnetic winding numbers $n_j$, $j=1,\dots , N_f$. See Sect. 2.2.

• The four-manifold X, in particular its signature $\sigma =\sigma (X)$, Euler characteristic $\chi =\chi (X)$, period point J and intersection form Q. See Sect. 3.1.

• The ’t Hooft flux ${\varvec{\mu }}$, and the external fluxes $\{{\varvec{k}}_j\}=({\varvec{k}}_1,\dots ,{\varvec{k}}_{N_f})$. See Sect. 3.3.

• The fugacities for the point and surface observables p and ${\varvec{x}}$. See Sect. 4.3.

In terms of these parameters, the u-plane path integral reduces to the following finite-dimensional integral over $\mathcal {F}_{N_f}({\varvec{m}})$,

$$\begin{aligned} \boxed {\begin{aligned}&\Phi _{{\varvec{\mu }}, \{{\varvec{k}}_j\}}^{J}(p,{\varvec{x}}, {\varvec{m}}, \Lambda _{N_f})\\&\quad =\int _{\mathcal {F}_{N_f}({\varvec{m}})}\hbox {d}\tau \wedge \hbox {d}{\bar{\tau }} \, \nu (\tau ;\{{\varvec{k}}_j\})\,\Psi _{\varvec{\mu }}^J(\tau ,{\bar{\tau }},{\varvec{z}},{\bar{{\varvec{z}}}})\,e^{2pu/\Lambda _{N_f}^2+{\varvec{x}}^2 G_{N_f}}. \end{aligned}} \end{aligned}$$

(5.1)

We summarise the different elements on the rhs:

• The integration domain $\mathcal {F}_{N_f}({\varvec{m}})$ in (5.1) is crucially the fundamental domain of the effective gauge coupling. As discussed in Sect. 2.4, this domain requires new aspects compared to integration domains for earlier discussions of u-plane integrals. The evaluation of integrals over $\mathcal {F}_{N_f}({\varvec{m}})$ will be discussed in more detail in Sect. 6.

• $\nu$ is the “measure factor" [12, 13, 21, 25, 106]

  $$\begin{aligned} \nu (\tau ;\{{\varvec{k}}_j\})= \mathcal {K}_{N_f}\,\frac{\text{ d }a}{\text {d}\tau } \,A^\chi B^\sigma \prod _{i,j=1}^{N_f}C_{ij}^{B({\varvec{k}}_i,{\varvec{k}}_j)}. \end{aligned}$$

  (5.2)

  It combines the topological couplings (4.15) and the couplings to the background fluxes (4.10) with the Jacobian $\frac{\text{ d }a}{\text {d}\tau }$ of the change of variables from a to $\tau$. $\mathcal {K}_{N_f}$ is an overall normalisation factor. For $N_f=0$, it is fixed by matching to known Donaldson invariants. Since $\chi +\sigma =4$, there is an ambiguity [23]

  $$\begin{aligned} (\mathcal {K}_{N_f},\alpha ,\beta )\sim (\zeta ^{-4}\mathcal {K}_{N_f},\zeta \alpha ,\zeta \beta ), \end{aligned}$$

  (5.3)

  with $\alpha$ and $\beta$ the u-independent prefactors in (4.15).

• The function $\Psi ^J_{\varvec{\mu }}$ arises from the sum over U(1) fluxes. It is a Siegel–Narain theta function (4.11) and discussed in detail in Sect. 4.2. The elliptic parameter ${\varvec{z}}$ of the Siegel–Narain theta function reads

  $$\begin{aligned} \begin{aligned} {\varvec{z}}&= \frac{{\varvec{x}}}{2\pi \,\Lambda _{N_f}}\frac{\text{ d }u}{\text {d}a}+\sum _{j=1}^{N_f} v_j{\varvec{k}}_j,\\ {\bar{{\varvec{z}}}}&= \sum _{j=1}^{N_f} {\bar{v}}_j{\varvec{k}}_j. \end{aligned} \end{aligned}$$

  (5.4)

• Finally, $G_{N_f}$ is the contact term, discussed in more detail in Sect. 4.3.

While the path integral set up in Sect. 4 integrates the exponentiated action over the local coordinates a and ${\bar{a}}$, in (5.1) we have changed variables to $\tau$ and ${\bar{\tau }}$. This change of variables $(a,{\bar{a}})\rightarrow (\tau ,{\bar{\tau }})$ is valid as long as the Jacobian is non-singular in the integration region. Since the coordinates a and ${\bar{a}}$ are holomorphic and anti-holomorphic, respectively, the Jacobian is diagonal and the functional determinant accordingly reads $\frac{{\text{ d }}a}{\text {d}\tau }\frac{\text{ d }{\bar{a}}}{\text {d}{\bar{\tau }}}$. We thus need to show that $\frac{\text{ d }a}{\text {d}\tau }$ is not singular away from isolated points in $\mathcal {F}_{N_f}({\varvec{m}})$, which in (5.1) we remove implicitly from the integration domain.

Using $\frac{\text{ d }a}{\text {d}u}=\frac{\text{ d }a}{\text {d}u}\frac{du}{\text {d}\tau }$, we can study the singular points in detail. First, it is shown in [59] that the singularities of $\frac{\text{ d }u}{\text {d}\tau }$ are in one-to-one correspondence with the branch points. In fact, both $\frac{\text{ d }u}{\text {d}\tau }=0$ and $\frac{\text{ d }u}{\text {d}\tau }=\infty$ are realised as branch points in $\mathcal {N}=2$ SQCD. In the following Sect. 6, we remove a small circle in $\mathcal {F}_{N_f}({\varvec{m}})$ around the branch points and show that they do not give an extra contribution. Furthermore, the solutions to $\frac{\text{ d }u}{\text {d}a}=0$ are shown to be the Argyres–Douglas (AD) points. We exclude them from the integration region and study their contribution also in Sect. 6. Finally, we know that $\eta ^{24}\propto \left( \frac{\text{ d }a}{\text {d}u}\right) ^{12}\Delta _{N_f}$ [59], with $\eta$ the Dedekind eta-function as defined in (A.5). Since $\eta \ne 0$ and $\Delta _{N_f}$ does not have poles, we find that $\frac{\text{ d }a}{\text {d}u}$ never vanishes. This agrees with the fact that $\frac{\text{ d }a}{\text {d}u}$ is the period of a holomorphic differential and therefore is never zero.

We conclude that the functional determinant is singular in $\mathbb H$ precisely at the branch points and AD points; however, with the proper exclusion of those as done in the following section, it is non-singular and the change of variables is well-defined. This furthermore conveniently solves the problem that there is no natural integration region in $(a, {\bar{a}})$ space [12].

5.2 Monodromy transformations of the integrand

We continue by explicitly verifying that the u-plane integral is single-valued around the singular points of the moduli space. We find that this puts a constraint on the magnetic winding numbers $n_j$, in addition to the constraints on the background fluxes ${\varvec{k}}_j$ discussed in Sect. 3.3.

5.2.1 Monodromy around infinity

Let us determine how the u-plane integrand transforms under the monodromy around infinity. As a function of the effective coupling $\tau$, the measure factor (5.2) is proportional to $\frac{\text{ d }a}{\text {d}\tau }\left( \frac{\text{ d }u}{\text {d}a}\right) ^{\frac{\chi }{2}}\Delta ^{\frac{\sigma }{8}}$ times the product over the couplings $C_{ij}$. We take the monodromy at infinity to be oriented as $u\rightarrow e^{2\pi i}u$ and $a\rightarrow e^{\pi i}a$, as in Sect. 2.5. Then this path also encircles all singularities $u_j$, which are the roots of the physical discriminant, $\Delta =\prod _{j=1}^{N_f+2}(u-u_j)$. We thus have that $\Delta \rightarrow e^{2\pi i(N_f+2)}\Delta$, and hence

$$\begin{aligned} \Delta ^{\frac{\sigma }{8}}\rightarrow e^{\pi i (N_f+2)\sigma /4}\Delta ^{\frac{\sigma }{8}} \end{aligned}$$

(5.5)

Next, since $u\rightarrow e^{2\pi i}u$ and $a\rightarrow e^{\pi i}a$ we find $\frac{\text{ d }u}{\text {d}a}\rightarrow e^{\pi i}\frac{\text{ d }u}{\text {d}a}$, and therefore

$$\begin{aligned} \left( \frac{\text{ d }u}{\text {d}a}\right) ^{\frac{\chi }{2}}\rightarrow e^{\pi i \chi /2}\left( \frac{\text{ d }u}{\text {d}a}\right) ^{\frac{\chi }{2}}. \end{aligned}$$

(5.6)

For $\frac{\text{ d }a}{\text {d}\tau }$ we have that $a\rightarrow e^{\pi i}a$, while $\hbox {d}\tau \rightarrow \hbox {d}\tau$, and thus

$$\begin{aligned} \frac{\text{ d }a}{\text {d}\tau }\rightarrow -\frac{\text{ d }a}{\text {d}\tau }. \end{aligned}$$

(5.7)

From (2.38) we recall that $w_{ij}\rightarrow w_{ij}+\delta _{ij}$, such that with the definition (4.10) we find $C_{ij}\rightarrow e^{-\pi i \delta _{ij}}C_{ij}$. The couplings $C_{ij}$ transform in the measure factor as

$$\begin{aligned} \prod _{i,j=1}^{N_f}C_{ij}^{B({\varvec{k}}_i,{\varvec{k}}_j)}\rightarrow e^{-\pi i\sum _{j}{\varvec{k}}_j^2}\prod _{i,j=1}^{N_f}C_{ij}^{B({\varvec{k}}_i,{\varvec{k}}_j)}. \end{aligned}$$

(5.8)

Combining (5.5), (5.6), (5.7), (5.8), and using $\chi =4-\sigma$, we obtain

$$\begin{aligned} \nu \rightarrow -e^{\pi iN_f\sigma /4}e^{-\pi i\sum _{j}{\varvec{k}}_j^2}\, \nu . \end{aligned}$$

(5.9)

This phase for ${\varvec{k}}_j=0$ can be checked directly by taking q-expansions from the SW curves, for generic masses.

From (2.38) we recall that under the monodromy around infinity $v_j \rightarrow -v_j-n_j$, and thus

$$\begin{aligned} {\varvec{z}}\rightarrow -{\varvec{z}}-\sum _{j=1}^{N_f}n_j{\varvec{k}}_j. \end{aligned}$$

(5.10)

For the sum over fluxes we can now deduce using (A.12) that

$$\begin{aligned} \begin{aligned}&\Psi _{\varvec{\mu }}^J\Big (\tau +N_f-4,-{\varvec{z}}-\sum _{j=1}^{N_f}n_j{\varvec{k}}_j\Big )\\&\quad =e^{\pi i(N_f-4)({\varvec{\mu }}^2-{\varvec{\mu }}\cdot K)}\,\Psi ^J_{\varvec{\mu }}\Big (\tau ,-{\varvec{z}}-\sum _{j=1}^{N_f}n_j{\varvec{k}}_j+(N_f-4)({\varvec{\mu }}-\tfrac{K}{2})\Big ), \end{aligned} \end{aligned}$$

(5.11)

where we suppressed the dependence on the anti-holomorphic parts. Recall from (3.9) that

$$\begin{aligned} c_1(\mathcal {L}_j)\equiv K-2{\varvec{\mu }}\mod 2L. \end{aligned}$$

(5.12)

and as such we can express ${\varvec{k}}_j=c_1(\mathcal {L}_j)/2$ as

$$\begin{aligned} {\varvec{k}}_j=\frac{K}{2}-{\varvec{\mu }}+{\varvec{\ell }}_j,\qquad {\varvec{\ell }}_j\in L. \end{aligned}$$

(5.13)

We have then

$$\begin{aligned} {\varvec{k}}^2_j=\frac{\sigma }{4}-K\cdot {\varvec{\mu }}+{\varvec{\mu }}^2-2{\varvec{\mu }}\cdot {\varvec{\ell }}_j \mod 2\mathbb {Z}, \end{aligned}$$

(5.14)

where we used that K is a characteristic vector of L, and $K^2=\sigma \mod 8$. Using (A.12) and substitution of (5.13) in this expression, (5.11) equals

$$\begin{aligned} e^{\pi i(N_f-4)({\varvec{\mu }}^2-{\varvec{\mu }}\cdot K)}\,\Psi ^J_{\varvec{\mu }}\left( \tau ,-{\varvec{z}}-\sum _{j=1}^{N_f}n_j{\varvec{\ell }}_j+(N_f-4+\sum _j n_j)({\varvec{\mu }}-\tfrac{K}{2})\right) . \end{aligned}$$

(5.15)

Our aim is to write this as a phase times $\Psi ^J_{\varvec{\mu }}(\tau ,{\varvec{z}})$. The constraints on the winding numbers should be independent of ${\varvec{\mu }}$ and ${\varvec{k}}_j$, since the prepotential is. From (A.15), we therefore get the first constraint

$$\begin{aligned} \sum _j n_j=N_f\mod 2. \end{aligned}$$

(5.16)

Using identity (A.15), $2{\varvec{\mu }}^2-K\cdot {\varvec{\mu }}\in \mathbb {Z}$ and $4({\varvec{\mu }}-\tfrac{K}{2})\in 2L$, this simplifies to

$$\begin{aligned} \begin{aligned}&e^{\pi i(N_f-4)({\varvec{\mu }}^2-{\varvec{\mu }}\cdot K)+2\pi i {\varvec{\mu }}\cdot \sum _j n_j{\varvec{\ell }}_j-2\pi i (N_f+\sum _j n_j)({\varvec{\mu }}^2-{\varvec{\mu }}\cdot K/2)}\Psi ^J_{\varvec{\mu }}(\tau ,-{\varvec{z}})\\&\quad =-e^{\pi iN_f({\varvec{\mu }}^2-{\varvec{\mu }}\cdot K)+2\pi i {\varvec{\mu }}\cdot \sum _j n_j {\varvec{\ell }}_j-2\pi i (N_f+\sum _j n_j)({\varvec{\mu }}^2-{\varvec{\mu }}\cdot K/2)}\,\Psi ^J_{\varvec{\mu }}(\tau ,{\varvec{z}})\\&\quad =-e^{-\pi iN_f{\varvec{\mu }}^2+2\pi i {\varvec{\mu }}\cdot \sum _j n_j {\varvec{\ell }}_j-2\pi i \sum _j n_j({\varvec{\mu }}^2-{\varvec{\mu }}\cdot K/2)}\,\Psi ^J_{\varvec{\mu }}(\tau ,{\varvec{z}}). \end{aligned} \end{aligned}$$

(5.17)

Finally using (5.14), we can express the phase in terms of ${\varvec{k}}_j$,

$$\begin{aligned} {\textbf {M}}_\infty :\qquad \Psi ^J_{\varvec{\mu }}(\tau ,{\varvec{z}})\rightarrow -e^{-\pi i N_f {\varvec{\mu }}^2 - \pi i \sum _j n_j ({\varvec{k}}_j^2+{\varvec{\mu }}^2-\sigma /4) }\,\Psi _{\varvec{\mu }}^J(\tau ,{\varvec{z}}). \end{aligned}$$

(5.18)

By multiplying (5.9) with (5.18), we find

$$\begin{aligned} \nu (\tau ;\{{\varvec{k}}_j\})\, \Psi _{{\varvec{\mu }}}^J(\tau ,{\varvec{z}}) \rightarrow e^{-\pi i \sum _j(n_j+1){\varvec{k}}_j^2+\frac{\pi i}{4}\sum _j (\sigma -4{\varvec{\mu }}^2)(n_j+1)}\, \nu (\tau ;\{{\varvec{k}}_j\})\, \Psi _{{\varvec{\mu }}}^J(\tau ,{\varvec{z}}). \end{aligned}$$

(5.19)

Combining (3.15) with (3.4), we have that $4({\varvec{k}}_j+{\varvec{\mu }})^2 \equiv \sigma \mod 8$ for every $j=1,\dots , N_f$. We insert this into the second exponential of (5.19), such that

$$\begin{aligned} {\textbf {M}}_\infty :\qquad \nu (\tau ;\{{\varvec{k}}_j\})\, \Psi _{{\varvec{\mu }}}^J(\tau ,{\varvec{z}}) \rightarrow e^{2\pi i {\varvec{\mu }}\sum _j(n_j+1){\varvec{k}}_j} \,\nu (\tau ;\{{\varvec{k}}_j\}) \,\Psi _{{\varvec{\mu }}}^J(\tau ,{\varvec{z}}), \end{aligned}$$

(5.20)

and the u-plane integrand is invariant under $T^{N_f-4}$ if and only if ${\varvec{\mu }}\sum _j(n_j+1){\varvec{k}}_j\in \mathbb Z$. Using (5.13) and the fact that K is a characteristic vector of L, we find

$$\begin{aligned} n_j=1 \mod 2 \end{aligned}$$

(5.21)

for all $j=1, \dots , N_f$, which implies the above constraint (5.16).

5.2.2 Monodromy ${\textbf {M}}_j$

Let us determine how the integrand transforms under the monodromy $M_j$ around the mass singularity $m_j/\sqrt{2}$. Since the mass singularity corresponds to a singularity $u_j$ on the u-plane, we have that $(u-u_j)\rightarrow e^{2\pi i}(u-u_j)$. This implies that $\Delta =(u-u_j)\prod _{i\ne j}^{2+N_f}(u-u_i)\rightarrow e^{2\pi i}\Delta$, such that $\Delta ^{\frac{\sigma }{8}}\rightarrow e^{\pi i \sigma /4}\Delta ^{\frac{\sigma }{8}}$. The transformation of $\frac{\text{ d }a}{\text {d}u}$ can be determined from (2.23): While $u\rightarrow u_j$, both $g_2$ and $g_3$ remain finite and nonzero (otherwise $u_j$ would be an AD point). This implies that $\frac{g_3}{g_2}$ contains no factors of $(u-u_j)$, and thus $\frac{\text{ d }u}{\text {d}a}\rightarrow \frac{\text{ d }u}{\text {d}a}$. Similarly, we have that $\frac{\text{ d }a}{\text {d}\tau }\rightarrow \frac{\text{ d }a}{\text {d}\tau }$. From (2.40) we finally have that $w_{ik}\rightarrow w_{ik}+\delta _{ij}\delta _{ik}$. We combine

$$\begin{aligned} {\textbf {M}}_j: \quad \nu \rightarrow e^{\pi i\sigma /4}e^{-\pi i{\varvec{k}}_j^2}\nu . \end{aligned}$$

(5.22)

For the monodromy around the mass singularity $m_j/\sqrt{2}$, we find for $\Psi _{\varvec{\mu }}^J$ with (A.12)

$$\begin{aligned} \begin{aligned}&\Psi _{{\varvec{\mu }}}^{J}(\tau +1,{\varvec{z}}-{\varvec{k}}_j)=e^{\pi i ({\varvec{\mu }}^2-{\varvec{\mu }}\cdot K)}\Psi _{{\varvec{\mu }}}^{J}(\tau ,{\varvec{z}}-{\varvec{\ell }}_j)\\&=e^{\pi i ({\varvec{\mu }}^2-{\varvec{\mu }}\cdot K)+2\pi i B({\varvec{\mu }},{\varvec{\ell }}_j)}\,\Psi _{{\varvec{\mu }}}^{J}(\tau ,{\varvec{z}})\\&=e^{-\pi i \sigma /4+\pi i {\varvec{k}}_j^2}\,\Psi _{{\varvec{\mu }}}^{J}(\tau ,{\varvec{z}}). \end{aligned} \end{aligned}$$

(5.23)

The phases thus cancel precisely,

$$\begin{aligned} {\textbf {M}}_j: \quad \nu (\tau +1)\,\Psi _{{\varvec{\mu }}}^{J}(\tau +1,{\varvec{z}}-{\varvec{k}}_j)=\nu (\tau )\,\Psi _{{\varvec{\mu }}}^{J}(\tau ,{\varvec{z}}), \end{aligned}$$

(5.24)

without any constraints.

5.2.3 Monodromy ${\textbf {M}}_m$

For the monopole singularity in $N_f=1$ we find that

$$\begin{aligned} \begin{aligned}&\Psi _{{\varvec{\mu }}}^J(\tfrac{\tau }{-\tau +1},\tfrac{v{\varvec{k}}_1+(n+1)/2\,\tau {\varvec{k}}_1}{-\tau +1})=e^{\pi i (n+1)\frac{v}{-\tau +1}{\varvec{k}}_1^2+\pi i \frac{(n+1)^2}{4}\frac{\tau }{-\tau +1}{\varvec{k}}_1^2}\,(-1)^{(n+1){\varvec{k}}_1\cdot K/2}\\&\qquad \qquad \times \Psi _{{\varvec{\mu }}+(n+1){\varvec{k}}_1/2}^J(\tfrac{\tau }{-\tau +1},\tfrac{v{\varvec{k}}_1}{-\tau +1}), \end{aligned} \end{aligned}$$

(5.25)

where we have used (A.16). Then using (A.13), we arrive at

$$\begin{aligned} \begin{aligned}&\Psi _{{\varvec{\mu }}}^J(\tfrac{\tau }{-\tau +1},\tfrac{v{\varvec{k}}_1+(n+1)/2\,\tau {\varvec{k}}_1}{-\tau +1})\\&\quad =(-\tau +1)^{b_2/2}(-{\bar{\tau }}+1)^2\,e^{\pi i (n+1){\varvec{k}}_1\cdot K/2-(n+1)^2{\varvec{k}}_1^2/4}\,e^{-\pi i \sigma /4}\\&\qquad \times \exp \!\left[ \pi i \frac{(v+(n+1)/2)^2}{-\tau +1}{\varvec{k}}_1^2 \right] \Psi _{{\varvec{\mu }}+(n+1){\varvec{k}}_1/2}^J(\tau ,{\varvec{z}}). \end{aligned} \end{aligned}$$

(5.26)

Since $\Psi _{\varvec{\mu }}^J$ is required to transform to itself up to an overall factor, we must demand that $(n+1){\varvec{k}}_1/2 \in L$. Therefore for ${\varvec{k}}_1\in L/2$, we find the requirement that $n=-1 \in \mathbb {Z}_4$. This simplifies the transformations considerably, and we find

$$\begin{aligned} \Psi _{{\varvec{\mu }}}^J(\tau ,{\varvec{z}})\rightarrow (-\tau +1)^{b_2/2}(-{\bar{\tau }}+1)^2e^{-\pi i \sigma /4} e^{\pi i{\varvec{k}}_1^2\frac{v^2}{-\tau +1}} \Psi _{{\varvec{\mu }}}^J(\tau ,{\varvec{z}}). \end{aligned}$$

(5.27)

The ${\varvec{k}}_j$-independent part of the measure factor transforms precisely as under ${\textbf {M}}_j$ (see (5.22)), as the same argument holds. However, due to the transformation $\tau \rightarrow \frac{\tau }{-\tau +1}$, the measure also picks up its modular weight $\frac{\sigma }{2}+1$. From (2.43) we furthermore find the transformation of $C_{11}$, such that

$$\begin{aligned} \nu (\tau ,{\varvec{k}}_1)\rightarrow e^{\pi i \sigma /4}e^{-\pi i{\varvec{k}}_1^2\frac{v^2}{-\tau +1}}(-\tau +1)^{\frac{\sigma }{2}+1}\nu (\tau ,{\varvec{k}}_1), \end{aligned}$$

(5.28)

where we have already used $n=-1 \in \mathbb {Z}_4$. If we multiply (5.27) and (5.28) with $\hbox {d}\tau \wedge \hbox {d}{\bar{\tau }}$ (which has modular weight $(-2,-2)$), then

$$\begin{aligned} {\textbf {M}}_m:\quad \hbox {d}\tau \wedge \hbox {d}{\bar{\tau }} \nu (\tau ,{\varvec{k}}_1)\,\Psi _{{\varvec{\mu }}}^J(\tau ,{\varvec{z}})\rightarrow \hbox {d}\tau \wedge \hbox {d}{\bar{\tau }} \nu (\tau ,{\varvec{k}}_1)\,\Psi _{{\varvec{\mu }}}^J(\tau ,{\varvec{z}}), \end{aligned}$$

(5.29)

where we have used $\sigma +b_2=2$. Thus, the u-plane integrand is also invariant under ${\textbf {M}}_m$.

For $N_f>1$ we find the same condition, namely that $n_j=-1 \mod 4$ for all j.

5.2.4 Monodromy ${\textbf {M}}_d$

Given the relation (2.41), it is not necessary to explicitly check single-valuedness of the integrand under this monodromy, as it is a product of the above monodromies.

To conclude this section, let us stress the constraints for the winding number $n_j$, such that the u-plane integral is invariant under all monodromies in $N_f\le 3$. To this end, we need to satisfy the constraints $n_j=1\mod 2$ (5.21) from ${\textbf {M}}_\infty$, and $n_j=-1\mod 4$ for ${\textbf {M}}_m$. Since the latter is the stronger constraint, we require

$$\begin{aligned} n_j=-1\mod 4, \end{aligned}$$

(5.30)

for all $j=1,\dots ,N_f$.

6 Integration over fundamental domains

As discussed in Sects. 2 and 5, u-plane integrals for massive $\mathcal {N}=2$ theories with fundamental hypermultiplets include new aspects. This section discusses how to evaluate such integrals (5.1). More concretely, we aim to define and evaluate integrals of the form

$$\begin{aligned} \mathcal {I}_f=\int _{\mathcal {F}({\varvec{m}})} \hbox {d}\tau \wedge \hbox {d}{\bar{\tau }}\,y^{-s}\,f(\tau ,{\bar{\tau }}), \end{aligned}$$

(6.1)

with $s\le 1$. The domain $\mathcal {F}({\varvec{m}})$ is the fundamental domain for the effective coupling constant as discussed in Sect. 2.4, and f a non-holomorphic function of weight $(2-s,2-s)$ arising from the topologically twisted Yang–Mills theory. For $\mathcal {F}({\varvec{m}})$ a fundamental domain of a congruence subgroup, such integrals (6.1) have been studied in the context of theta lifts of weakly holomorphic modular forms and harmonic Maass forms [114,115,116] as well as one-loop amplitudes in string theory [117,118,119].

We assume that the integrand $y^{-s}\,f(\tau ,{\bar{\tau }})$ can be expressed as

$$\begin{aligned} \partial _{{\bar{\tau }}} {\widehat{h}}(\tau ,{\bar{\tau }})=y^{-s}\,f(\tau ,{\bar{\tau }}), \end{aligned}$$

(6.2)

for a suitable function ${\widehat{h}}(\tau ,{\bar{\tau }})$ using mock modular forms. This was indeed the case in [25, 54, 55] and will be demonstrated for massive $\mathcal {N}=2$ theories with fundamental hypermultiplets. The integral $\mathcal {I}_f$ then reads

$$\begin{aligned} \mathcal {I}_f=-\int _{\partial \mathcal {F}({\varvec{m}})} \hbox {d}\tau \,{\widehat{h}}(\tau ,{\bar{\tau }}), \end{aligned}$$

(6.3)

with $\partial \mathcal {F}({\varvec{m}})$ the boundary of $\mathcal {F}({\varvec{m}})$. We will carry this out evaluation in Part II [99].

There are a number of aspects to be addressed in order to evaluate integrals over $\mathcal {F}({\varvec{m}})$:

• 1. Identifications of boundary components of $\mathcal {F}({\varvec{m}})$ due to monodromies on the u-plane.

• 2. Contributions from the cusps, that is $\tau \rightarrow i\infty$ or $\tau \rightarrow \gamma (i\infty )\in \mathbb {Q}$ for an element $\gamma \in \text {PSL}(2,\mathbb Z)$.

• 3. Contributions from a singular point in the interior of $\mathcal {F}({\varvec{m}})$.

• 4. Contributions from an elliptic point $p\in \mathbb {H}$ of $\text {PSL}(2,\mathbb Z)$.

• 5. Branch points and branch cuts.

We will discuss these aspects 1.–5. in the following.

1. Identifications

The modular transformation induced by monodromies identifies components of the boundary of the fundamental domain $\partial \mathcal {F}({\varvec{m}})$ pairwise. Their contributions to the integral (6.3) vanish, which is, for example, familiar from deriving valence formulas for modular forms [120, Fig. 2]. See Fig. 4 for an example.

2. Cusps

Contributions near the cusps require a regularisation [12, 55]. Such regularisations have been developed in the context of string amplitudes [117,118,119] and analytic number theory [120,121,122].

Let us first consider the cusp $\tau \rightarrow i\infty$. To regularise the divergence, one introduces a cut-off $\text {Im}\, \tau = Y\gg 1$, and takes the limit $Y \rightarrow \infty$ after evaluation. We require that f near $i\infty$ has a Fourier expansion of the form⁵

$$\begin{aligned} f(\tau ,{\bar{\tau }})=\sum _{m\gg -\infty ,n\ge 0} c(m,n)\,q^m\,{\bar{q}}^n. \end{aligned}$$

(6.4)

Then the function ${\widehat{h}}$ has the form,

$$\begin{aligned} {\widehat{h}}(\tau ,{\bar{\tau }})=h(\tau )+2^s\int ^{i\infty }_{-{\bar{\tau }}} \frac{f(\tau ,-v)}{(-i(v+\tau ))^s}\hbox {d}v, \end{aligned}$$

(6.5)

where $h(\tau )$ is a weakly holomorphic q-series, with expansion

$$\begin{aligned} h(\tau )=\sum _{m\gg -\infty } d(m)\,q^m. \end{aligned}$$

(6.6)

The cusp $\tau \rightarrow i\infty$ then contributes

$$\begin{aligned} \left[ \mathcal {I}_f \right] _\infty = w_\infty \,d(0), \end{aligned}$$

(6.7)

with d(0) the constant term of $h(\tau )$ (6.6), and $w_\infty$ the width of the cusp $\mathcal {F}({\varvec{m}})$ at $i\infty$. For $N_f\le 3$, $w_\infty$ is $4-N_f$ [59].

The other cusps can be treated in a similar fashion using modular transformations. We label the $n_c$ cusps in $\mathcal {F}({\varvec{m}})$ by $j=1,\dots ,n_c$. If the cusp is on the horizontal axis at $-\frac{d_j}{c_j}\in \mathbb {Q}$ with relative prime $(c_j,d_j)\in \mathbb {Z}^2$, we can map the cusp to $i\infty$ by a modular transformation

$$\begin{aligned} \gamma _j=\begin{pmatrix} a_j &{} \quad b_j \\ c_j &{}\quad d_j \end{pmatrix}. \end{aligned}$$

(6.8)

We let $\tau _j=\gamma _j \tau$. Then the holomorphic part $h_j(\tau _j)$ of $(c_j\tau +d_j)^{-2}\,\widehat{h}(\gamma \tau _j,\gamma {\bar{\tau }}_j)$ can be expanded for $\tau$ near $-\frac{d_j}{c_j}$ as

$$\begin{aligned} h_j(\tau _j)=\sum d_j(n)\,q_j^n,\qquad q_j=e^{2\pi i \tau _j}. \end{aligned}$$

(6.9)

As a result, the cusp j contributes

$$\begin{aligned} \left[ \mathcal {I}_f \right] _j= w_j\,d_j(0). \end{aligned}$$

(6.10)

3. Singular points in the interior of $\mathcal {F}({\varvec{m}})$

The integrand can be singular at a point $\tau _\textrm{s}$ in the interior of $\mathcal {F}({\varvec{m}})$. Such singularities appear typically for deformations of superconformal theories, such as the $\mathcal {N}=2^*$ theory and the $N_f=4$ theory, where the UV coupling $\tau _{\text {{UV}}}$ gives rise to such a singularity [25, 61]. See Fig. 8 for an example. We require that the expansion of f near such a singularity reads,

$$\begin{aligned} f(\tau ,{\bar{\tau }})=\sum _{m\gg -\infty ,n\ge 0} c_s(m,n)\,(\tau -\tau _\textrm{s})^m\,({\bar{\tau }}-{\bar{\tau }}_\textrm{s})^n. \end{aligned}$$

(6.11)

Then, the anti-derivative ${\widehat{h}}(\tau ,{\bar{\tau }})$ has similar expansion,

$$\begin{aligned} {\widehat{h}}(\tau ,{\bar{\tau }})=\sum _{m\gg -\infty ,n\ge 0} d_s(m,n)\,(\tau -\tau _\textrm{s})^m\,({\bar{\tau }}-{\bar{\tau }}_\textrm{s})^n. \end{aligned}$$

(6.12)

The contour integral for a small contour around $\tau _\textrm{s}$,

$$\begin{aligned} C_\varepsilon (\tau _\textrm{s})= \left\{ \tau =\tau _\textrm{s}+\varepsilon \, e^{i\varphi }, \varphi \in [0,2\pi )\right\} , \end{aligned}$$

(6.13)

is bounded for such a function. Moreover, in the limit $\varepsilon \rightarrow 0$, the contour integral is finite. We define the “residue” of a non-holomorphic function $g(\tau ,{\bar{\tau }})$

$$\begin{aligned} \begin{aligned} \underset{\tau =\tau _\textrm{s}}{\text {nRes}}\left[ g(\tau ,{\bar{\tau }})\right]&=\frac{1}{2\pi i}\lim _{\varepsilon \rightarrow 0}\oint _{C_\varepsilon (\tau _\textrm{s})}g(\tau ,{\bar{\tau }})\,\hbox {d}\tau . \end{aligned} \end{aligned}$$

(6.14)

For the expansion (6.11) this evaluates to

$$\begin{aligned} \left[ \mathcal {I}_f\right] _s=2\pi i\, \underset{\tau =\tau _\textrm{s}}{\text {nRes}}\left[ {\widehat{h}}(\tau ,{\bar{\tau }})\right] =d_s(-1,0), \end{aligned}$$

(6.15)

with $d_s(-1,0)$ the coefficient in the expansion (6.12).

4. Elliptic points

For $\mathcal {N}=2$ QCD, AD points are the elliptic points of the duality group, and lie on the boundary of $\mathcal {F}({\varvec{m}})$. See Fig. 7 for an example. The elliptic points are $\alpha =e^{\pi i/3}$ and i, and their images under $\text {PSL}(2,\mathbb Z)$. Contour integrals around such points can be regularised using a cut-off $\varepsilon$. We assume that the anti-derivative ${\widehat{h}}$ has the following expansion near an elliptic point $\tau _e$,

$$\begin{aligned} {\widehat{h}}(\tau ,{\bar{\tau }})=\sum _{m\gg -\infty ,n\ge 0} d_\textrm{e}(m,n)\,(\tau -\tau _\textrm{e})^m\,({\bar{\tau }}-{\bar{\tau }}_\textrm{e})^n. \end{aligned}$$

(6.16)

As a result, the boundary arc around $\tau _\textrm{AD}$ in $\mathbb {H}$ is a fraction of $2\pi$, which needs to be properly accounted for. These neighbourhoods have an angle $\frac{2\pi }{k_e}$, with $k_e=2$ for $\tau _e=i$, and $k_e=6$ for $\tau _e=\alpha$ [123]. Furthermore, it is important how many images of $\mathcal {F}$ in $\mathcal {F}({\varvec{m}})$ coincide at the elliptic point. We denote this number by $n_e$. For $\mathcal {N}=2$ SQCD, we found examples with $n_e=2$ and 4 for $\tau _e\sim \alpha$, while for $\tau _e\sim i$, $n_e=1$ [59]. The contribution from an elliptic point is then,

$$\begin{aligned} \left[ \mathcal {I}_f\right] _e=2\pi i \frac{n_{\text {e}}}{k_\textrm{e}}\, \underset{\tau =\tau _\textrm{e}}{\text {nRes}}\left[ {\widehat{h}}(\tau ,{\bar{\tau }})\right] =\frac{n_{\text {e}}}{k_\textrm{e}}\,d_e(-1,0), \end{aligned}$$

(6.17)

5. Branch points and cuts

Branch points and cuts are a new aspect compared to previous analyses (see for instance Figs. 4, 5). We will demonstrate that their contribution vanishes for the integrands of interest.

We assume that the integrand f satisfies

$$\begin{aligned} {\widehat{h}}(\tau ,{\bar{\tau }})= (\tau -\tau _{\textrm{bp}})^{n}\,g(\tau ,{\bar{\tau }}), \end{aligned}$$

(6.18)

with $n\in \mathbb {Z}/2$ and $n\ge -1/2$, $g(\tau ,{\bar{\tau }})$ being a real analytic function near $\tau _\textrm{bp}$. This assumption is satisfied for the twisted Yang–Mills theories [99]. To treat this type of singularity, we remove a $\delta$ neighbourhood and analyse the $\delta \rightarrow 0$ limit. Let $C_\delta$ be the contour

$$\begin{aligned} C_\delta =\{ \tau _\textrm{bp}+\delta \, e^{i\theta }\,\vert \, \theta \in (0,2\pi )\} \end{aligned}$$

(6.19)

around $\tau _\textrm{bp}$ with radius $\delta >0$. Therefore, on the contour $|y^{-s} f|$ is bounded by

$$\begin{aligned} |{\widehat{h}}|\le \delta ^n\,K \end{aligned}$$

(6.20)

for some $K>0$. The integral around the branch point therefore vanishes in the limit,

$$\begin{aligned} \begin{aligned} \mathcal {I}^\textrm{bp}_f&=\lim _{\delta \rightarrow 0}\,\int _{C_\delta } {\widehat{h}}\,|\hbox {d}\tau |\le \lim _{\delta \rightarrow 0}\,\int _0^{2\pi } \delta ^n\,K\,\delta \,\hbox {d}\theta \\&=\lim _{\delta \rightarrow 0}\,2\pi K \delta ^{n+1}=0. \end{aligned} \end{aligned}$$

(6.21)

The branch points necessarily give rise to branch cuts. For the purpose of integration, we remove a neighbourhood with distance r from the cut and take the limit $r\rightarrow 0$ after determining the integral. Since the value of the integrand is finite near the branch cut, the contribution to the integral vanishes.

Summary

Combining all the contributions discussed above, we find

$$\begin{aligned} \mathcal {I}_f=\sum _{j=1}^n w_j\,d_j(0)+\sum _{s} d_{s}(-1,0)+\sum _e\, \frac{n_{\text {e}}}{k_\textrm{e}}\,d_e(-1,0). \end{aligned}$$

(6.22)

This formula generalises [12] for the pure $N_f=0$ theory on a smooth four-manifold X that admits a metric of positive scalar curvature, [56, Equation (5.10)] for the pure theory on generic X, [25, Equation (4.88)] for the $\mathcal {N}=2^*$ theory on X, and [50] for the massless $N_f=2$ and $N_f=3$ theories on $X=\mathbb{C}\mathbb{P}^2$.

Appendices

A Modular forms

In this Appendix, we collect some properties of modular forms for subgroups of $\text {PSL}(2,\mathbb Z)$. For further reading, see [120, 123,124,125,126,127].

1.1 A.1 Theta functions and Eisenstein series

We make use of modular forms for the congruence subgroups $\Gamma _0(n)$ and $\Gamma ^0(n)$ of $\text {PSL}(2,\mathbb Z)$. These subgroups are defined as

$$\begin{aligned} \begin{aligned} \Gamma _0(n) = \left\{ \begin{pmatrix}a&{}b\\ c&{}d\end{pmatrix}\in \text {SL}(2,\mathbb Z)\big | \, c\equiv 0 \; \mod n\right\} ,\\ \Gamma ^0(n) = \left\{ \begin{pmatrix}a&{}b\\ c&{}d\end{pmatrix}\in \text {SL}(2,\mathbb Z)\big | \, b\equiv 0 \; \mod n\right\} , \end{aligned} \end{aligned}$$

(A.1)

and are related by conjugation with the matrix $\text {diag}(n,1)$. We furthermore define the principal congruence subgroup $\Gamma (n)$ as the subgroup of $\text {SL}(2,\mathbb Z)\ni A$ with $A\equiv \mathbbm {1}\mod n$. A subgroup $\Gamma$ of $\text {SL}(2,\mathbb Z)$ is called a congruence subgroup if it contains $\Gamma (n)$ for some $n\in \mathbb N$.

The above-introduced congruence subgroups host a number of interesting modular forms. The Jacobi theta functions $\vartheta _j:\mathbb {H}\rightarrow \mathbb {C}$, $j=2,3,4$, are defined as

$$\begin{aligned} \begin{aligned} \vartheta _2(\tau )= \sum _{r\in \mathbb {Z}+\frac{1}{2}}q^{r^2/2},\quad \vartheta _3(\tau )= \sum _{n\in \mathbb {Z}}q^{n^2/2},\quad \vartheta _4(\tau )= \sum _{n\in \mathbb {Z}} (-1)^nq^{n^2/2}, \end{aligned} \end{aligned}$$

(A.2)

with $q=e^{2\pi i\tau }$. These functions transform under $T,S\in \text {SL}(2,\mathbb Z)$ as

$$\begin{aligned} \begin{aligned} S:\quad&\begin{array}{l} \vartheta _2(-1/\tau )=\sqrt{-i\tau }\vartheta _4(\tau ), \\ \vartheta _3(-1/\tau )=\sqrt{-i\tau }\vartheta _3(\tau ), \\ \vartheta _4(-1/\tau )=\sqrt{-i\tau }\vartheta _2(\tau ),\end{array}\\ T:\quad&\begin{array}{l}\vartheta _2(\tau +1)=e^{\frac{\pi i}{4}}\vartheta _2(\tau ), \\ \vartheta _3(\tau +1)=\vartheta _4(\tau ), \\ \vartheta _4(\tau +1)=\vartheta _3(\tau ). \end{array} \end{aligned} \end{aligned}$$

(A.3)

They furthermore satisfy the Jacobi abstruse identity

$$\begin{aligned} \vartheta _2^4+ \vartheta _4^4= \vartheta _3^4. \end{aligned}$$

(A.4)

The Dedekind eta function $\eta : \mathbb H\rightarrow \mathbb C$ is defined as the infinite product

$$\begin{aligned} \eta (\tau )=q^{\frac{1}{24}}\prod _{n=1}^{\infty }(1-q^n), \quad q=e^{2\pi i\tau }. \end{aligned}$$

(A.5)

It transforms under the generators of $\text {SL}(2,\mathbb Z)$ as

$$\begin{aligned} \begin{aligned} S: \quad&\eta (-1/\tau )=\sqrt{-i\tau }\, \eta (\tau ),\\ T: \quad&\eta (\tau +1)=e^{\frac{\pi i}{12}}\, \eta (\tau ), \end{aligned}\end{aligned}$$

(A.6)

and relates to the Jacobi theta series as $\eta ^{3}=\frac{1}{2}\vartheta _2\vartheta _3\vartheta _4$.

1.1.1 Eisenstein series

We let $\tau \in \mathbb {H}$ and define $q=e^{2\pi i \tau }$. Then the Eisenstein series $E_k:\mathbb {H}\rightarrow \mathbb {C}$ for even $k\ge 2$ are defined as the q-series

$$\begin{aligned} E_{k}(\tau )=1-\frac{2k}{B_k}\sum _{n=1}^\infty \sigma _{k-1}(n)\,q^n, \end{aligned}$$

(A.7)

where $B_k$ are the Bernoulli numbers and $\sigma _k(n)=\sum _{d|n} d^k$ is the divisor sum. For $k\ge 4$ even, $E_{k}$ is a modular form of weight k for ${\text {SL}}(2,\mathbb {Z})$. Any modular form for $\text {SL}(2,\mathbb Z)$ can be related to the Jacobi theta functions (A.2) by

$$\begin{aligned} E_4=\frac{1}{2}(\vartheta _2^8+\vartheta _3^8+\vartheta _4^8),\qquad E_6=\frac{1}{2}(\vartheta _2^4+\vartheta _3^4)(\vartheta _3^4+\vartheta _4^4)(\vartheta _4^4-\vartheta _2^4). \end{aligned}$$

(A.8)

With our normalisation (A.7), the j-invariant can be written as

$$\begin{aligned} j=1728\frac{E_4^3}{E_4^3-E_6^2}=256\frac{(\vartheta _3^8-\vartheta _3^4\vartheta _4^4+\vartheta _4^8)^3}{\vartheta _2^8\vartheta _3^8\vartheta _4^8}. \end{aligned}$$

(A.9)

1.2 A.2 Siegel–Narain theta function

Let L be an n-dimensional uni-modular lattice with signature $(1,n-1)$. For the application to the u-plane integral, $n=b_2(X)$. Let K be a characteristic vector of L. Its defining property is ${\varvec{l}}^2={\varvec{l}}\cdot K\mod 2$ for every ${\varvec{l}}\in L$. Furthermore, we have that ${\varvec{\mu }}\in L/2$.

We consider the Siegel–Narain theta function $\Psi _{{\varvec{\mu }}}^J:\mathbb H\times \mathbb C\rightarrow \mathbb C$ defined in the main text in (4.11). We repeat it here for convenience,

$$\begin{aligned} \begin{aligned} \Psi _{{\varvec{\mu }}}^J(\tau ,{\bar{\tau }},{\varvec{z}},{\bar{{\varvec{z}}}})&=e^{-2\pi y{\varvec{b}}^2_+} \sum _{{\varvec{k}}\in L+{\varvec{\mu }}}\partial _{\bar{\tau }}\left( 4\pi i\sqrt{y}B( {\varvec{k}}+{\varvec{b}},J)\right) \\&\quad \times (-1)^{B({\varvec{k}},K)} q^{-{\varvec{k}}_-^2/2}{\bar{q}}^{{\varvec{k}}_+^2/2} e^{-2\pi iB({\varvec{z}},{\varvec{k}}_-)-2\pi iB({\bar{{\varvec{z}}}}, {\varvec{k}}_+)}, \end{aligned} \end{aligned}$$

(A.10)

where J is a normalized positive vector in $L\otimes \mathbb {R}$, ${\varvec{k}}_+=B({\varvec{k}},J)\,J$, ${\varvec{k}}_-={\varvec{k}}-{\varvec{k}}_+$ and ${\varvec{b}}=\text {Im}({\varvec{z}})/y$. The transformations under the generators S and T of $\text {PSL}(2,\mathbb Z)$ are most easily determined if we shift ${\varvec{\mu }}\rightarrow {\varvec{\mu }}+K/2$. One finds [54, 56]

$$\begin{aligned} \begin{aligned}&S:\qquad \Psi ^J_{{\varvec{\mu }}+K/2}(-1/\tau ,-1/{\bar{\tau }},{\varvec{z}}/\tau ,{\bar{{\varvec{z}}}}/{\bar{\tau }})= -i(-i\tau )^{n/2}(i{\bar{\tau }})^2\\&\hspace{3cm}\times \,e^{-\pi i{\varvec{z}}^2/\tau +\pi iK^2/2}\,(-1)^{B({\varvec{\mu }},K)} \,\Psi _{K/2}^J(\tau ,{\bar{\tau }},{\varvec{z}}-{\varvec{\mu }},{\bar{{\varvec{z}}}}-{\varvec{\mu }}), \\&T:\qquad \Psi ^J_{{\varvec{\mu }}+K/2}(\tau +1,{\bar{\tau }}+1,{\varvec{z}},{\bar{{\varvec{z}}}})=\\&\hspace{3cm} e^{\pi i({\varvec{\mu }}^2-K^2/4)}\,\Psi ^J_{{\varvec{\mu }}+K/2}(\tau ,{\bar{\tau }},{\varvec{z}}+{\varvec{\mu }},{\bar{{\varvec{z}}}}+{\varvec{\mu }}). \end{aligned} \end{aligned}$$

(A.11)

Using these transformations, one finds for the periodicity in $\tau$,

$$\begin{aligned} \begin{aligned} \Psi _{{\varvec{\mu }}}^J(\tau +1,{\bar{\tau }}+1,{\varvec{z}},{\bar{{\varvec{z}}}})&=e^{\pi i({\varvec{\mu }}^2-B({\varvec{\mu }},K))}\Psi _{{\varvec{\mu }}}^J(\tau ,{\bar{\tau }},{\varvec{z}}+{\varvec{\mu }}-K/2,{\bar{{\varvec{z}}}}+{\varvec{\mu }}-K/2) \\ \end{aligned} \end{aligned}$$

(A.12)

and for $S^{-1}T^{-k}S=\left( {\begin{matrix}1&{}0\\ k&{}1\end{matrix}}\right)$,

$$\begin{aligned} \Psi ^J_{\varvec{\mu }}\!\left( \tfrac{\tau }{k\tau +1},\tfrac{{\bar{\tau }}}{k\bar{\tau }+1}, \tfrac{{\varvec{z}}}{k\tau +1},\tfrac{{\bar{{\varvec{z}}}}}{k{\bar{\tau }}+1} \right) =(k\tau +1)^{\frac{n}{2}}(k{\bar{\tau }}+1)^2e^{-\frac{\pi ik{\varvec{z}}^2}{k\tau +1}}e^{\frac{\pi i}{4}kK^2}\Psi ^J_{{\varvec{\mu }}}(\tau ,\bar{\tau },{\varvec{z}},{\bar{{\varvec{z}}}}). \end{aligned}$$

(A.13)

We furthermore list the following transformations for ${\varvec{z}}$:

• For the reflection ${\varvec{z}}\rightarrow -{\varvec{z}}$,

  $$\begin{aligned} \Psi ^J_{\varvec{\mu }}(\tau ,{\bar{\tau }},-{\varvec{z}},-{\bar{{\varvec{z}}}})=-e^{2\pi iB({\varvec{\mu }},K)}\,\Psi ^J_{\varvec{\mu }}(\tau ,{\bar{\tau }},{\varvec{z}},{\bar{{\varvec{z}}}}). \end{aligned}$$

  (A.14)

• For shifting ${\varvec{z}}\rightarrow {\varvec{z}}+{\varvec{\nu }}$ with ${\varvec{\nu }}\in L$,

  $$\begin{aligned} \Psi ^J_{\varvec{\mu }}(\tau ,{\bar{\tau }},{\varvec{z}}+{\varvec{\nu }},{\bar{{\varvec{z}}}}+{\varvec{\nu }})=e^{-2\pi iB({\varvec{\nu }},{\varvec{\mu }})}\, \Psi ^J_{{\varvec{\mu }}}(\tau ,{\bar{\tau }},{\varvec{z}},{\bar{{\varvec{z}}}}). \end{aligned}$$

  (A.15)

• For shifting ${\varvec{z}}\rightarrow {\varvec{z}}+{\varvec{\nu }}\tau$ with ${\varvec{\nu }}\in L \otimes \mathbb {R}$,

  $$\begin{aligned} \Psi ^J_{\varvec{\mu }}(\tau ,{\varvec{z}}+{\varvec{\nu }}\tau )=e^{2\pi iB({\varvec{z}},{\varvec{\nu }})} q^{{\varvec{\nu }}^2/2} (-1)^{-B({\varvec{\nu }},K)}\, \Psi ^J_{{\varvec{\mu }}+{\varvec{\nu }}}(\tau ,{\bar{\tau }},{\varvec{z}},{\bar{{\varvec{z}}}}). \end{aligned}$$

  (A.16)

  We can restrict to ${\varvec{\nu }}\in L/2$, if the characteristic ${{\varvec{\mu }}+{\varvec{\nu }}}$ is required to be in L/2.

B Class $\mathcal {S}$ representation

A different parametrisation of the SW curves (2.17) is the class $\mathcal {S}$ representation. This representation gives the SW differential in a canonical form

$$\begin{aligned} \lambda ^2=p_{N_f}(z,u,\Lambda _{N_f},{\varvec{m}})\hbox {d}z^2, \end{aligned}$$

(B.1)

where the Laurent polynomials $p_{N_f}$ read [85, Sect. 10]

$$\begin{aligned} \begin{aligned} p_0&=\frac{\Lambda _0^2}{z^3}+\frac{2u}{z^2}+\frac{\Lambda _0^2}{z},\\ p_1&=\frac{\Lambda _1^2}{z^3}+\frac{3u}{z^2}+\frac{2\Lambda _1m}{z}+\Lambda _1^2,\\ p_2&=\frac{\Lambda _2^2}{z^4}+\frac{2\Lambda _2 m_1}{z^3}+\frac{4u}{z^2}+\frac{2\Lambda _2m_2}{z}+\Lambda _2^2. \end{aligned}\end{aligned}$$

(B.2)

The corresponding elliptic curves can be found as $x^2=z^4\,p_{N_f}$, which is quartic for $N_f=0,1$ and cubic for $N_f=2$. By comparing invariants of the SW curves (2.17) with those of the class $\mathcal {S}$ curve (B.1), one finds the dictionary

$$\begin{aligned} \begin{aligned} N_f=0: \quad&u_{\mathcal {S}}=u_{\text {SW}}, \\ N_f=1: \quad&u_{\mathcal {S}}=\frac{4}{3} u_{\text {SW}}, \quad m_{\mathcal {S}}=2m_{\text {SW}}, \\ N_f=2: \quad&u_{\mathcal {S}}=4 u_{\text {SW}}, \quad m_{\mathcal {S},i}=4m_{\text {SW},i}. \end{aligned}\end{aligned}$$

(B.3)

These relations merely amount to a rescaling of the parametrisation of the Coulomb branch and in particular leave its geometry invariant. For this reason, we proceed above with using the SW curves (2.17).

C Winding numbers

In this Appendix, we discuss the winding numbers appearing in (2.7) in some more detail. As mentioned in Sect. 2.2, generally the theory admits $N_f$ electric winding numbers and $N_f$ magnetic winding numbers. While in the main text we set the electric winding numbers to zero, in this Appendix we keep the possibility open for them to be nonzero.

The $\mathcal {N}=2$ supersymmetry algebra requires that the central charge Z is a linear combination of conserved charges. The U(1) conserved charges $S_i$ of the hypermultiplets must appear in Z as follows [11],

$$\begin{aligned} Z= n_m a_D+n_e a +\sum _{j=1}^{N_f} S_j \frac{m_j}{\sqrt{2}}. \end{aligned}$$

(C.1)

We note that Z is an inner product of periods $(a_D,a, \frac{1}{\sqrt{2}}{\varvec{m}})$ and conserved charges $(n_m, n_e,\varvec{S})$. The periods are given by contour integrals

$$\begin{aligned} a=\int _{\gamma _1}\lambda , \qquad a_D=\int _{\gamma _2}\lambda , \end{aligned}$$

(C.2)

where $\gamma _1,\gamma _2$ generate $H_1(E,\mathbb Z)$, and $\lambda$ is a meromorphic 1-form, the SW differential. In massive SQCD, $\lambda$ has poles with nonzero residues. If the contours $\gamma _i$ are deformed across poles of $\lambda$, then a and $a_D$ pick up contributions from the residues. By invariance of (C.1), these jumps are linear combinations of the masses,

$$\begin{aligned} \sum _{j=1}^{N_f} \Delta S_j \frac{m_j}{\sqrt{2}}, \end{aligned}$$

(C.3)

i.e. the global charges of the hypermultiplets are shifted as $S_j\rightarrow S_j+\Delta S_j$. From the residue theorem, the shift in the periods gives

$$\begin{aligned} 2\pi i \sum _{i=1}^{N_f}n_i\text {Res}(\lambda ,x_i), \end{aligned}$$

(C.4)

where $x_i$ are the $N_f$ poles of $\lambda$, and $n_i\in \mathbb Z$ are the winding numbers of the contour deformation. Since both $a_D$ and a are given by contour integrals of the same differential, a deformation of either $\gamma _1$ or $\gamma _2$ or both results in such a shift.

Example. In order to see how $n_i$ and $\Delta S_j$ are related, let us study $N_f=2$ as an example. In $N_f=2$, the $S_j$ are integers for fundamental particles and half-integers for monopoles [11]. The two poles of $\lambda$ are $x^\pm =\pm \frac{1}{8}\Lambda _2^2$, with residue [11, (15.4)]

$$\begin{aligned} 2\pi i\text {Res}(\lambda ,x^\pm )=\pm \frac{m_1+m_2}{2\sqrt{2}}. \end{aligned}$$

(C.5)

Then,

$$\begin{aligned} \sum _{j=1}^{2} \Delta S_j \frac{m_j}{\sqrt{2}}=2\pi i \sum _{i=1}^{2}n_i\text {Res}(\lambda ,x_i)=\sum _{j=1}^2\frac{n_1-n_2}{2}\frac{m_j}{\sqrt{2}}, \end{aligned}$$

(C.6)

such that $\Delta S_j=\frac{n_1-n_2}{2}\in \mathbb Z/2$ for both $j=1,2$. Constraints on the $n_i$ entail constraints on the change $\Delta S_j$. For instance, if both $n_1$ and $n_2$ are odd, or if both are even, then $\Delta S_1$ and $\Delta S_2$ are integers. In the main text of this paper, we find such a constraint.

For generic $N_f\le 3$, by construction of the SW curves the residues of $\lambda$ are linear combinations of the masses

$$\begin{aligned} 2\pi i\text {Res}(\lambda , x_i)=\sum _{j=1}^{N_f}l_{i j} \frac{m_j}{\sqrt{2}}, \end{aligned}$$

(C.7)

with $i=1,\dots , N_f$, and $l_{ij}\in \mathbb Z/2$ [11, (17.1)]. Then we can compute

$$\begin{aligned} \sum _{j=1}^{N_f} \Delta S_j \frac{m_j}{\sqrt{2}}=2\pi i \sum _{i=1}^{N_f}n_i\text {Res}(\lambda ,x_i)=\sum _{i=1}^{N_f}\sum _{j=1}^{N_f} n_i l_{i j} \frac{m_j}{\sqrt{2}}=\sum _{j=1}^{N_f} \frac{m_j}{\sqrt{2}} \sum _{i=1}^{N_f}l_{i j}n_i. \end{aligned}$$

(C.8)

We find that the change in the abelian global charges $\Delta S_j$ is given by a half-integral linear combination of winding numbers,

$$\begin{aligned} \Delta S_j=\sum _{i=1}^{N_f} l_{i j}n_i. \end{aligned}$$

(C.9)

In order to relate the winding numbers $n_i$ to those for the periods $a_i$ and $a_{D,i}$ as found in [63], we can expand

$$\begin{aligned} {\textbf {M}}_\infty ^{\text {Ohta}}: \quad a_D\rightarrow -a_D+ (4-N_f)a-\frac{1}{\sqrt{2}}\left( \frac{n^{a_D}_{N_f}}{n^a_{N_f}}-\frac{4-N_f}{2}\right) \sum _{j=1}^{N_f}n_j^am_j, \end{aligned}$$

(C.10)

with $n_j^a$ being the coefficients of $-\frac{1}{2\sqrt{2}}m_j$ in the constant term of a, and similarly $n_j^{a_D}$ those for $a_D$ [63, (5.2)]⁶. We are aiming to compare this to (2.36),

$$\begin{aligned} {\textbf {M}}_\infty : \quad a_D\rightarrow -a_D+ (4-N_f)a-\frac{1}{\sqrt{2}}\sum _{j=1}^{N_f}n_jm_j. \end{aligned}$$

(C.11)

Since in (C.10) we divide and multiply by $n_j^a$, we cannot directly relate the two expressions by setting $n_j^a=0$. However, if we relate first

$$\begin{aligned} n_j^a = \frac{n^a_{N_f}}{n^{a_D}_{N_f}} n_j^{a_D}, \qquad j=1,\dots N_f-1, \end{aligned}$$

(C.12)

then we find

$$\begin{aligned} \begin{aligned} {\textbf {M}}_\infty ^{\text {Ohta}}: \quad a_D\rightarrow&-a_D+ (4-N_f)a-\frac{1}{\sqrt{2}}\sum _{j=1}^{N_f}\left( n_j^{a_D}-\frac{4-N_f}{2}n_j^a\right) m_j. \end{aligned} \end{aligned}$$

(C.13)

In this case, it is well-defined to set $n_j^a=0$, such that the action of ${\textbf {M}}_\infty ^{\text {Ohta}}$ and ${\textbf {M}}_\infty$ coincide for $n_j=n_j^{a_D}$, as anticipated.

The $N_f-1$ condition (C.12) reproduces the constraints on the winding numbers in [63, (5.3)]: For $N_f=1$, the condition is empty. For $N_f=2$, it agrees precisely with Ohta. For $N_f=3$ finally, the $N_f-1=2$ equations (C.12) are equivalent to those found in [63]. It seems however that our result $n_j^a =0, n_j^{a_D}=-1$ (5.30) is merely one particular of the infinitely many solutions to the geometric constraint (C.12).⁷ Thus it appears that the formulation of the theory on a compact four-manifold introduces further constraints. It would be interesting to understand whether it is possible to introduce non-vanishing electric winding numbers in the u-plane integral, and whether this leads to different correlation functions.