1 Introduction

The global positioning system (GPS) position time series features seasonal signals that are routinely modeled as sinusoids with a constant amplitude over time (Blewitt and Lavallée 2002; Ding et al. 2005; Santamaría-Gómez et al. 2011; Bogusz and Figurski 2014). The environmental loading effects contribute largely to the annual and semi-annual amplitude variations (van Dam and Wahr 1987; van Dam et al. 2001, 2012); however, they are not the only causes of seasonal changes recorded by the GPS receivers. Other contributors are systematic errors, either due to variations in satellite orbits (Ray et al. 2008) or of a numeric origin (Penna and Stewart 2003), which may sometimes be as large as the loading effects. Klos et al. (2018c) demonstrated that the seasonal signals in loading models do not remain constant over time. This means that the seasonal changes in the GPS position time series may be also time-variable (Freymueller 2009; Chen et al. 2013; Bogusz et al. 2015a; Gruszczynska et al. 2016). Therefore, amplitudes given as constants over time, typically derived with the weighted least-squares method, do not provide the most accurate description of them.

Beyond the time variability of seasonal changes, the noise present in the GPS position time series is another issue that needs inclusion in order to achieve reliable modeling of the observations. This has already been widely described in numerous studies by Zhang et al. (1997), Mao et al. (1999), Williams et al. (2004), Bos et al. (2010) and Klos et al. (2016), that a power-law process being close to flicker noise with a spectral index of −1 is the optimum noise model to describe the stochastic part of the GPS data. The impact of this phenomena on the velocity uncertainties may be reduced by spatial filtering using different methods, such as stacking or principal component analysis (PCA), which help to estimate a common mode error (CME; Dong et al. 2006; Bogusz et al. 2015b; Gruszczynski et al. 2018). Some authors observed that the instability of monuments may be another contributor to site-specific noise. If significant enough, it will change the character from flicker to random-walk noise, with a spectral index of −2 (Beavan 2005).

The power-law character of the GPS position time series may be incorrectly interpreted if some of the processes are mismodeled or incorrectly modeled during the time series analysis. As an example, the character of flicker noise may be under- or over-estimated if too many or too few frequencies are modeled and removed. Removing the autocorrelation from the stochastic part of the time series results in an artificial improvement in a velocity uncertainty of up to 56% (Bogusz and Klos 2016; Klos et al. 2018e). Besides this, the undetected offsets in the time series can lead to an artificial shift in the character of the stochastic part from flicker to random-walk noise (Williams 2003a), which leads to unrealistic overestimates of velocity uncertainty (Williams 2003b).

All of the above indicate that the time-varying curves need to be properly modeled during the GPS time series analysis, including the site-specific noise level, in order to produce reliable velocity estimates. Different methods have been employed to estimate the time-varying curves. Santamaría-Gómez et al. (2011) used a non-linear iterative least squares method to remove all significant peaks from the GPS position time series. They noted that the effect of the remaining peaks was insignificant to the noise analysis. Xu and Yeu (2015) and Gruszczynska et al. (2016) proposed using the singular spectrum analysis (SSA) approach to model the time-varying curves. Chen et al. (2013) compared the estimates obtained with the SSA and Kalman filter (KF) techniques, and emphasized that the SSA is much faster than the KF and features a lower computational cost. They also found that both methods gave a similar response. Klos et al. (2018b) emphasized that the reliability of seasonal signals estimated with the SSA, KF, wavelet decomposition (WD) and Chebyshev polynomials (CP) depends on the level of the noise present in the data. The SSA is based on selecting the frequencies of interest from the power spectrum of the data, with no separation between signal and noise. The KF, when not properly tuned, begins to model the seasonals together with the noise; the WD removes most of the power from the frequency band of interest; while the CP absorbs noise when the order of the polynomial is incorrectly chosen. Thus, the time-varying curves estimated with any of these methods change, depending on the noise level, as these methods absorb some part of the power of noise into the seasonal estimates.

In this study, the merits of the Wiener filter (WF) (Wiener 1930) to model the varying part of the seasonal signal are investigated. The WF is used to analyze the geodetic time series, but is only applied to gravity records, with Li and Sideris (1994) applying the WF to filter the noise out from the gravity series. Kotsakis and Sideris (2001) emphasized that the WF was an efficient tool for denoising the gravity data in the frequency domain. Migliaccio et al. (2004) used a time-wise WF to estimate the gravity potential, taking the colored noise into consideration. Reguzzoni and Tselfes (2009) applied an iterative procedure based on the WF to remove the colored noise from the gravity field and steady-state ocean circulation explorer (GOCE) data. Liu et al. (2010) performed Wiener-based filtering for unconstrained solutions of the gravity recovery and climate experiment (GRACE) satellite mission. Sampietro (2015) employed the WF to determine the depth of the Moho from the GOCE gravity field model. Kleinherenbrink et al. (2016) applied the WF to analyze the gravity field from the GRACE. However, no attempts were made to employ the WF to filter the noise or seasonal signals from the GPS position time series.

The work by Klos et al. (2018b) is continued in this study, and the problem of reliable modeling of time-varying seasonal curves with the noise level present in the data being taken into consideration is addressed. The time-variable curves are provided by a first-order autoregressive process which, when properly tuned, enables modeling the seasonal amplitudes varying over time. This process is employed for residuals with time-constant curves already removed, ensuring a better expression of time variability. Then, the WF is adapted to the level of noise that characterized the data, assuming the proper power spectral density function of the noise, and applied to the original time series. By using an inverse fast Fourier transform (IFFT) and the level of noise present in the observations, the seasonal signal provided by the autoregressive process refined by the level of noise is estimated. The entire methodology is named the adaptive WF (AWF), as the filtering of seasonalities is adapted to the level of noise. Within this study, annual and semi-annual variations are analyzed, although this method could be successfully employed for any other type of oscillations or higher harmonics in the annual changes, which must also introduce additional correlations if not removed (Bogusz and Klos 2016).

The analyses start with a synthetic dataset, proving the effectiveness of the AWF in modeling the time-varying curves. The maximum likelihood estimation (MLE) is then used to characterize the noise content of a set of 385 international GPS service (IGS) permanent stations, which is applied to construct the AWF for real data. The next step is to estimate the time-varying seasonal curves for a real dataset. The final step is to cross-compare the estimates provided by the AWF with those obtained by the KF or SSA, and, in this way, proving that the AWF was able to separate the signal from the noise effectively. Only the GPS position time series are focused on, although there was no apparent reason why this methodology could not be successfully applied to any other type of geodetic data, such as Zenith total delay or integrated water vapor series, as well as tide gauges or gravity records.

2 Data

This section provides a description of all the real and synthetic datasets. For the synthetic series, two different datasets are considered. Synthetic series 1 has a constant noise character, where different time-varying amplitudes of the seasonal signals are added. Synthetic series 2 is based on different noise characters: different amplitudes and spectral indices of noise, with the same time-varying seasonal signal.

2.1 Synthetic Series 1

The GPS position time series are best characterized by a power-law noise close to the flicker noise (Williams et al. 2004; Bos et al. 2010; Klos and Bogusz 2017). Several studies have been carried out that prove that an incorrect assumption in the noise type may cause over- or under-estimation of the uncertainty of velocity, leading to incorrect interpretations (Bos et al. 2010; Langbein 2012; Klos et al. 2016). Therefore, to test the impact of the noise character and its level on the estimates of seasonal signals, a series of 100 synthetic 22-year sets, equivalent to the longest time series available from the IGS, are produced. A pure flicker noise with a spectral index of −1 and an amplitude of 8 mm/year0.25 is assumed, which agrees with the average amplitude of the power-law noise found in the vertical changes in the GPS position time series (Santamaría-Gómez et al. 2011). The amplitudes of the seasonal signals are set to vary over 3.0–10.0 mm for the annual signal and over 1.5–4.0 mm for the semi-annual signal. Their variation over time is expressed by standard deviations of 1.0 and 0.5 mm for the annual and semi-annual periods, respectively. The standard deviation of the seasonal signals indicates the value of which the amplitude of the seasonal signal may differ from year to year. Phase lags vary between 1 and 6 months within the synthetic dataset.

2.2 Synthetic Series 2

Five hundred synthetic time series for a 22-year period are generated, in which a pure flicker noise, spectral index of −1, and various noise amplitudes from 1 to 25 mm/year0.25 are assumed, covering the low and high noise levels present in the GPS position time series. The annual and semi-annual signals of the amplitudes, 3.0 and 1.0 mm, respectively, and the standard deviations of 1.0 and 0.5 mm are added, which were also used by Klos et al. (2018b).

2.3 Real GPS Position Time Series

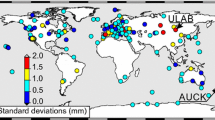
The IGS GPS position time series from 385 permanently working stations (Rebischung et al. 2016) are employed, with 8 years being the minimum time span of observations. The series appear in the latest release of the International Terrestrial Reference System (ITRF2014; Altamimi et al. 2016) (Fig. 1). The offsets are removed using the epochs defined by the IGS and supported by additional epochs detected with the sequential T test analysis of regime shifts (STARS; Rodionov and Overland 2005). To remove the outliers, the interquartile range (IQR) approach (Langbein and Bock 2004) is used. The time series are characterized by a small percentage of gaps, at 3.5% for the entire data. Since the modified MLE for time series with missing data (Bos et al. 2013) is used, no interpolation is performed, excluding small gaps lasting a few days. The north and east components are omitted and only on the vertical changes are analyzed, as the time variability of the seasonal signals is the greatest for the "Up" component (Klos et al. 2018b).

Fig. 1
figure 1

Geographical distribution of the 385 ITRF2014 IGS GPS stations employed in the analysis. The length of each series is marked in a specific color

Full size image

3 Methodology

To estimate the time-varying seasonal signals, the AWF is employed. It is adapted to the noise level of the observations, in this way ensuring the best separation between noise and signal. In this section, a detailed description of the AWF algorithm is provided, as well as the MLE algorithm and the methods used to compare the seasonal signals estimated with the AWF.

3.1 Adaptive Wiener Filter

Following Davis et al. (2012), the seasonal signal si can be modeled as a periodic time-constant signal s c i and a random process s r i

$$ \begin{aligned} s_{i} & = \left( {a + \delta a_{i} } \right)\cos \left( {\omega_{0} t_{i} } \right) + \left( {b + \delta b_{i} } \right)\sin \left( {\omega_{0} t_{i} } \right) \\ & = \left[ {a\cos \left( {\omega_{0} t_{i} } \right) + b\sin \left( {\omega_{0} t_{i} } \right)} \right] + \left[ {\delta a_{i} \cos \left( {\omega_{0} t_{i} } \right) + \delta b_{i} \sin \left( {\omega_{0} t_{i} } \right)} \right] \\ & = s_{i}^{c} + s_{i}^{r} , \\ \end{aligned} , $$
(1)

where a and b are constants. The variable ω0 is the normalized angular frequency of the annual signal (\( \omega_{0} = \frac{{\pi f_{0} }}{{2f_{s} }} \) where fs is the sampling frequency, equal to 1 day in this study). The random variables δai and δbi are the first-order autoregressive, AR(1), processes

$$ \begin{aligned} \delta a_{i} & = \phi \delta a_{i - 1} + v_{i} \\ \delta b_{i} & = \phi \delta b_{i - 1} + w_{i} . \\ \end{aligned} $$
(2)

Here, vi and wi are the two Gaussian variables with standard deviations σv and σw (mm), respectively. If ϕ = 1, then δai and δbi become the random-walk variables (Davis et al. 2012). However, this implies that the amplitude of the varying seasonal signal is increasing over time, which is not supported by observations. Therefore, in the presented case, the ϕ defined for the AR(1) process is slightly smaller than 1, that is 0.9999.

The least-squares method is an estimator used for s c i . However, since s r i is a random process, the least-squares method cannot provide estimates for it. Therefore, the problem of time-varying seasonal curves is reduced to estimating s r i from the noisy observations from which s c i has been removed with the least-squares. Note that during the least-squares estimation it is possible to include offsets and other deterministic signals in order that the residuals only contain noise and the seasonal signal. Next, assume that δbi = 0, so that the autocovariance γ for s r i is

$$ \begin{aligned} \gamma \left( {s_{i}^{r} ,s_{i + k}^{r} } \right) & = \text{cov} \left( {\delta a_{i} \delta a_{i + k} \cos \left( {\omega_{0} t_{i} } \right)\cos \left( {\omega_{0} t_{i + k} } \right)} \right) \\ & = \text{cov} \left( {\delta a_{i} \delta a_{i + k} \frac{1}{2}\left[ {\cos \left( {\omega_{0} \left( {t_{i} + t_{i + k} } \right)} \right) + \cos \left( {\omega_{0} k} \right)} \right]} \right). \\ \end{aligned} $$
(3)

While the AR(1) process is time-invariant, sr is not due to the modulation with the cosine. Therefore, by introducing the average autocovariance function \( \overline{\gamma } \)

$$ \overline{\gamma } \left( k \right) = \mathop {\lim }\limits_{T \to \infty } \frac{1}{T}\int\limits_{0}^{T} {\gamma {\text{d}}t} = \frac{1}{2}\frac{{\sigma_{v}^{2} }}{{\left( {1 - \phi^{2} } \right)}}\phi^{k} \cos \left( {\omega_{0} k} \right), $$
(4)

where \( \sigma_{v}^{2} /\left( {1 - \phi^{2} } \right)\phi^{k} \) is the autocovariance of the AR(1) process, dependent on lag k. An example of the autocovariance function is given in Fig. 2.

Fig. 2
figure 2

An example of the average autocovariance function \( \overline{\gamma } \left( k \right) \)

Full size image

Using the Wiener–Khinchin theorem, the average autocovariance function [Eq. (4)] can be employed to compute the one-sided spectral density function S(ω) with the unit mm2/rad

$$ S\left( \omega \right) = \frac{{2\sigma_{v}^{2} }}{\pi }\left[ {\frac{1}{{\left( {1 - 2\phi \cos \left( {\omega + \omega_{0} } \right) + \phi^{2} } \right)}} + \frac{1}{{\left( {1 - 2\phi \cos \left( {\omega - \omega_{0} } \right) + \phi^{2} } \right)}}} \right]. $$
(5)

An example of S(ω) for the annual signal, with a period of 365.25 days, is shown in Fig. 3. In addition to S(ω), also provided is the power spectral density of the power-law noise process, W(f), plotted in grey, to compare the behavior of the variations in both. The closer the value of ϕ is to 1, the sharper the peak of the annual signal. The assumption so far is σw = 0. Now, σ 2 v can be replaced by (σ 2 v  + σ 2 w ) to also include σw.

Fig. 3
figure 3

An example of power spectral density function S(f) of the time-varying annual signal. The power-law noise is plotted in grey

Full size image

By employing all the information provided above, the WF can be constructed. Assuming the time series xi with its Fourier transform X(ωj)

$$ X\left( {\omega_{j} } \right) = F\left( {x_{i} } \right). $$
(6)

Next the optimal filter \( \Phi \left( {\omega_{j} } \right) \) is defined in the frequency domain as

$$ \Phi \left( {\omega_{j} } \right) = \frac{{S\left( {\omega_{j} } \right)}}{{S\left( {\omega_{j} } \right) + W\left( {\omega_{j} } \right)}}. $$
(7)

The power spectral density of noise W(ωj) is employed to adapt the WF for the noise present in the time series being considered. For the GPS observations, for which the power-law noise model is preferred, the one-sided power spectral density is estimated with (Agnew 1992)

$$ W\left( {\omega_{j} } \right) = \frac{{\sigma_{pl}^{2} }}{\pi }\left( {2\sin \frac{{\omega_{j} }}{2}} \right)^{\kappa } \approx \frac{{\sigma_{pl}^{2} }}{\pi }\omega^{\kappa } , $$
(8)

where κ is the spectral index of power-law noise and ωj is the normalized angular frequency. The spectral index of 0 means pure white noise, while values of −1 and −2 mean pure flicker noise and random-walk noise, respectively. σpl, the standard deviation of the power-law noise, with units of mm, is the constant estimated with the MLE. For example, assuming flicker and white noise generates the following one-sided power spectral density

$$ W\left( {\omega_{j} } \right) = 2\sigma_{pl}^{2} \left( {2\sin \frac{{\omega_{j} }}{2}} \right)^{ - 1} + 2\sigma_{w}^{2} , $$
(9)

with σw being the standard deviation of the white noise component estimated with the MLE. The noise model employed to create the WF is estimated from the real observations to provide the best separation between signal and noise.

The estimated varying seasonal signal \( \widehat{{s_{i} }} \) is computed with the inverse Fourier transform

$$ \widehat{s}_{i} = F^{ - 1} \left( {\Phi \left( {\omega_{j} } \right)X\left( {\omega_{j} } \right)} \right). $$
(10)

Both the forward and backward Fourier transforms have been implemented using the FFT. So far, it is assumed that the annual signal only varies over time. To derive the time-varying semi-annual signal, a period of 182.63 days, the two spectra are added to obtain the total power spectral density function, as given in Fig. 4.

Fig. 4
figure 4

An example of the power spectral density function S(f) of the time-varying annual and semi-annual signals. Power-law noise is plotted in grey

Full size image

To obtain the total time-varying seasonal signal estimates with the AWF, the constant seasonal signal derived with the weighted least-squares is added to the variations estimated with Eq. (10), derived with the proper noise model assumed.

3.2 Maximum Likelihood Estimation

The MLE has been already widely used to estimate the time-constant seasonal oscillations and trends simultaneously with the character of the noise (Williams et al. 2004; Bos et al. 2008; Langbein 2012). In this analysis, the GPS vertical position time series are described as a sum of the initial value, trend and seasonal components of the frequencies of interest, as in Bogusz and Klos (2016). The stochastic part that remains after the deterministic model has been removed, named residuals, is characterized by the white plus power-law noise model with spectral index κ and the standard deviation of noise, which can then be re-estimated to the amplitudes of the individual contributors. Such a model is assumed in the MLE analysis for the real GPS data in order to estimate the parameters of noise to construct the AWF.

The MLE is also applied in this study to assess the character of the residuals: to estimate the parameters of power-law noise, when the AWF-derived seasonal curves are removed from the synthetic and real series. On this basis, the parameters of noise are compared between original series, using both synthetic and real data, and their residuals to define the effectiveness of the AWF.

3.3 Comparison to Other Algorithms

To compare the time-varying seasonal signal obtained using the AWF, two other methods, namely the KF and SSA are employed. These approaches were used by Klos et al. (2018b) to evaluate the reliability of the seasonal curve estimates. It was emphasized that both the KF and SSA were able to provide reliable seasonal signals under different noise levels.

In this study, the parameters of the KF and SSA estimated for both approaches by Klos et al. (2018b) are applied. For the KF, the traditional KF is tuned to include the third-order autoregressive process, which mimics the power-law noise present in the residuals. For the SSA, the 3-year windows are employed. See Klos et al. (2018b) for more details.

4 Results

The methodology described above is applied to analyze the synthetic and real datasets, and to estimate the time-varying curves that are optimally separated from the noise affecting the observations. The comparison between the AWF estimates of the seasonal signals and those derived with the KF and SSA algorithms is presented.

4.1 Synthetic Series 1

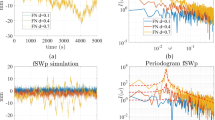
The series of 100 synthetic data sets with pure flicker noise, spectral index of −1 and amplitude of 8 mm/year0.25, is subjected to estimates of seasonal oscillations using the AWF. The different cases are summarized in Table 1 and shown in Fig. 5. For all cases, synthetic series 1 is used with spectral index κ = −1 and a 2.0-mm standard deviation of noise, to which different seasonal time-varying amplitudes are added. The AWF is created in five different versions, assuming different noise levels. The too-low noise levels are described by cases 1 and 2, the ideal case, which agrees with the simulated parameters, by case 3, and too-high noise levels by cases 4 and 5.

Table 1 A set of parameters assumed to assess the performance of Wiener-based filtering to estimate the time-varying seasonal signals
Full size table
Fig. 5
figure 5

Left panel: Synthetic series 1 and synthetic seasonal signal plotted in, respectively, grey and yellow. Right panel: Power spectral density generated for synthetic series 1 and the residuals after AWF curves are removed

Full size image

Different levels of noise are assumed when the AWF is created, in order to intentionally impose improper noise levels while estimating the seasonal oscillations. The too-low noise levels (cases 1 and 2), with a too-low spectral index or too-low amplitude of noise, result in the mean variance of differences between the synthetic and estimated curves of 0.97 and 0.78 mm2, respectively. The too-high noise levels (cases 4 and 5), with too-high amplitude of noise or too-high spectral index, result in the mean variances of 0.67 and 0.69 mm2, respectively. When the proper noise level is assumed during the creation of the AWF (case 3), the mean variance is 0.70 mm2.

The differences between individual variances in each case, from 1 to 5, depend on the amplitude of the seasonal signal being synthesized. If it is assumed that the time series being analyzed has a large amplitude of the annual signal and a small amplitude of the semi-annual signal, then estimating the seasonal signal with cases 4 and 5 allows for a minor time variability in the annual signal, which is only higher than the assumed noise level. In these cases, the semi-annual signal will probably not be detected due to its too-small amplitude. In this way, the resulting seasonal signal will have a small time variability in the annual signal, which will not be fully modeled and include no semi-annual curve. Setting too-low noise levels (cases 1 and 2) results in the artificial estimation of the time variability, which does not necessarily arise from the seasonal signals, but can stem from the noise character of the analyzed time series. In this case, both the annual and semi-annual signals are detected, as they are larger than the assumed noise level, but are in fact modeled with a too large time variability. As a consequence, a part of the autocorrelation originally included in the noise is transferred to the estimates of the seasonal signals, resulting in biased estimates of the noise type. This can be also easily noticed in Fig. 5, where different assumptions of the AWF result in dissimilar estimates of the residuals: the time series for which the seasonal model is removed.

To summarize Table 1, the large mean variances in cases 1 and 2 arise from the fact that part of the time variability which characterizes the noise is modeled and included in the seasonal signals due to the too-low noise levels employed during the creation of the AWF. On the other hand, the underestimated mean variances from cases 4 and 5 prove that too-high noise levels, set incorrectly during the AWF creation, do not permit the modeling of the full-time variability of the seasonal signal being simulated.

4.2 Synthetic Series 2

This synthetic series is compared with the KF and SSA approaches, both applied with the parameters described in the previous section and by Klos et al. (2018b). In this case, seasonal signals with an equal time variability are assumed, but with different underlying noise levels added. This provides an insight into the effectiveness of the AWF for various noise conditions. The results of this analysis are presented in Table 2 and compared with the KF- and SSA-derived estimates. Two characteristic noise levels are listed: a low noise level, meaning a noise amplitude of 1 mm/year0.25, which is very rarely met in the GPS position time series, and a high noise level, with a noise amplitude of 10 mm/year0.25, a level of noise usually found in the vertical changes of GPS stations.

Table 2 The results of the noise analysis, trend uncertainties and misfits between the synthesized and estimated seasonal curves for the different approaches: KF, SSA and AWF, from 500 simulations of synthetic series 2
Full size table

For the low noise level, the misfits between the synthesized and estimated seasonal curves are the greatest when no seasonal signal is assumed in the estimates. All three methods tested give similar misfit results, of 0.17 or 0.16 mm. The misfit created when the seasonal signals are derived is then transferred to the residuals. For these, a noise analysis with the MLE is performed and the spectral indices and the amplitudes of power-law noise are provided in Table 2. The estimates of trend uncertainty (mm/year), spectral index κ and the amplitude of the power-law noise (mm/year−κ/4) are delivered. Two different noise levels are presented: (1) the low noise level of spectral index −1 and noise amplitude 1 mm/year0.25 and (2) the high noise level of spectral index −1 and noise amplitude 10 mm/year0.25. The actual parameters that should be obtained from each method are presented in the ‘Actual’ row. From Table 2, it is clear that the largest amplitude and spectral index of noise are found for the case when no seasonal is assumed, as the seasonal signals which are not modeled would be transferred to the residuals as the long-term correlation. The KF, SSA and AWF all resulted in similar spectral indices and amplitudes of power-law noise, being close to the actual synthesized value. Using Eq. (29) of Bos et al. (2008), the trend uncertainty is estimated for noise parameters present in the residuals. Due to the fact that the KF-, SSA- and AWF-delivered curves provide similar misfits and parameters of noise, the trend uncertainties estimated here are almost equal to the actual value.

For the high noise level, the estimates of the seasonal curves provided by the different methods produce a larger misfit than the one observed for the low noise level. Here, when no seasonal was assumed, a misfit of 2.44 mm is obtained. The seasonal curves estimated with the SSA give a mean misfit of 1.08 mm, while the KF and AWF, respectively, allow computing a seasonal curve which differs by only 0.73 and 0.67 mm from the synthesized one. Although the misfits are similar, the real impact of the different methods may be observed for the noise parameters delivered for the residuals. The lowest amplitude of the power-law noise is found for the residuals when the SSA-delivered curve is removed. The AWF gives the amplitude closest to the actual synthesized one. Similar results are observed for spectral indices, for which both the SSA and KF model a part of the noise along with seasonal oscillations. For the AWF, the estimated spectral index is equal to that synthesized, due to the optimal separation between seasonal signal and noise.

The above analyses performed for the synthetic datasets demonstrate that the AWF can distinguish the seasonal signal from noise, and, in this way, prevent the noise power being transferred to the seasonal estimates.

4.3 Noise Analysis of Real Data

The values of the trends and amplitudes of annual and semi-annual seasonal signals and noise parameters are also estimated simultaneously for a set of 385 IGS stations using the MLE approach. Only the vertical time series are chosen for analysis, as they feature the greatest variability in seasonal oscillations over time. The seasonal amplitudes range between 0 and 11 mm for the annual signal, and between 0 and 3 mm for the semi-annual curve (Fig. 6). The greatest amplitude in the annual signal occurs in the data for the IMPZ (Imperatriz, Brazil) station. The amplitude of the annual curve is much greater for Asian stations than for any other region. However, the amplitudes are very consistent regionally. For Europe, the smallest amplitudes are found for the coastal stations, while the inland ones are characterized by amplitudes of between 3 and 6 mm. The amplitudes of the semi-annual signal are the smallest for Europe, Australia, Oceania and Southern parts of both North and South America. The greatest amplitudes of the semi-annual signal occur for central Asia, the northern part of North America and a few stations situated in Antarctica.

Fig. 6
figure 6

The estimates of the amplitudes of the annual and semi-annual seasonal oscillations in the vertical direction with the MLE method for the 385 IGS stations used in this study

Full size image

The draconitic signal for the 351.60-day period, which has been already found to be present in the GPS position time series (Amiri-Simkooei 2013), is estimated in this study to vary between 0.2 and 1.7 mm for the set of stations examined. This is a clear improvement over the previous estimates delivered from earlier reprocessing of the GPS observations, and which has also been stated by Amiri-Simkooei et al. (2017).

The parameters of the stochastic part, or so-called noise, are examined, assuming the combination of the power-law and white noises during the MLE analysis. These parameters include the fraction of the power-law noise, meaning a percentage of the power-law noise contribution in the considered combination, the spectral index and the amplitude of power-law noise. These parameters are then used a priori in the creation of the AWF to filter the seasonal curves from the real GPS observations.

The fraction of the power-law noise is large and equal to almost 1 (or 100%) for the majority of stations with latitudes higher than 40° (Figs. 7 and 8). For the remaining stations, the percentage of the contribution of the power-law noise is much smaller. It drops dramatically for latitudes lower than 10°. These results are consistent with those published in Williams et al. (2004), who analyzed the latitude dependencies of white and flicker noises. They showed that white noise is much greater for lower than for higher latitudes.

Fig. 7
figure 7

The estimates of noise parameters delivered with the MLE for the GPS height residuals. These noise parameters are used further to create and run the Adaptive Wiener Filter

Full size image
Fig. 8
figure 8

Parameters of the stochastic part plotted with respect to the latitude of the station. The amplitudes of white (left) and power-law noise (middle) are given, along with a fraction of the power-law noise estimated for the combination of the white plus power-law noises (right)

Full size image

4.4 The AWF-Based Estimates of Seasonals from the Real Dataset

As demonstrated for the synthetic datasets, assuming incorrect parameters of noise may lead to incorrect estimates of the seasonal signals. Therefore, to create the AWF filter for the real dataset, noise parameters estimated individually for each IGS GPS station are employed, as presented in the previous section. To provide the time-changeability of the seasonal curves, the AWF is run with the AR(1) process, as described in the Methodology section. The residuals are analyzed after the AWF seasonal curve is removed, using the MLE algorithm to compare the noise parameters of the original and filtered residuals.

Figure 9 presents the detrended time series in the vertical direction for six GPS stations for the original GPS time series and the seasonal curves estimated with the AWF. These stations are characterized by large seasonal variations, of up to several millimeters when different time spans are compared.

Fig. 9
figure 9

Detrended "Up" component for six permanent stations, i.e. RAMO (Mitzpe Ramon, Israel), NICO (Nicosia, Cyprus), NEAH (Neah Bay, USA), MAS1 (Maspalomas, Spain), LPAL (La Palma, Canary Islands) and YAR2 (Yaragadee, Australia)

Full size image

After the time-varying curves are removed from the IGS dataset, the parameters of the noise created for the original residuals are compared with those for which the AWF seasonal signals are removed. The differences between the fraction of power-law noise, spectral indices and the standard deviations of noise (Fig. 10) are cross-compared. The differences in the fraction of power-law noise are in the range −0.3 to 0.1, meaning the maximum change in the fraction of the power-law noise is 30%, towards flicker noise. This is only observed for the ZHN1 station (Honolulu, Hawaiian Islands). For the majority of stations, the differences in the fraction of the PL noise lay in the range −0.1 to 0.1.

Fig. 10
figure 10

The differences in the fraction of power-law noise, spectral index of power-law noise and standard deviation of noise (mm) when the AWF seasonal curve is removed from the GPS data. The differences are estimated between the original (see Fig. 7) and the filtered residuals (parameters for the original minus parameters for the filtered residuals)

Full size image

The differences in the spectral index of the power-law noise lay in the range −0.3 to 0.1. The maximum difference is found for the NAUR (Nauru, Australia), MCIL (Marcus Island, Japan) and MERI (Merida, Mexico) stations, which are characterized by an abnormally low fraction of power-law noise of less than 20% for the original residuals. The spectral indices of the power-law noise lay in the range −0.1 to 0.1 for the majority of stations, meaning no significant change in the character of the noise when the two types of residuals are compared.

The differences in the standard deviations of noise when the AWF curves are removed vary between −0.25 and 0.25 mm for the majority of stations, which are relatively low values, meaning no change in the power of the stochastic part when the seasonal signals are estimated and removed. This also means that the AWF method provides the optimal separation between signal and noise, with no absorption of noise into the seasonal estimates.

5 Conclusions

The GPS position time series are affected by the time-varying seasonal curves arising from the environmental loadings, systematic errors or numerical artifacts. Whether they are affected more by the former or the latter, these seasonal changes have to be modeled on a station-by-station basis using site-specific information on the noise level, as undetected correlations present in the series will affect the noise parameters estimated from the data and, therefore, also the uncertainties of the estimated velocities (Klos et al. 2018b).

Various methods have been used to model the time-varying curves, such as the SSA, KF or WD. In addition to these methods, the AWF method is introduced in this study, which has been used in geodesy only to denoise gravity records.

Klos et al. (2018c) showed how the power spectral densities change when the environmental loading models are removed directly from the GPS position time series. The CANT (Santander, Spain), IRKT (Irkutsk, Russia), VARS (Vardo, Norway) and GUAT (Guatemala City, Guatemala) stations were indicated. In this study, the differences between the noise parameters delivered for the residuals determined upon the constant amplitude assumption and the AWF-derived curves being removed are estimated. These differences in the spectral index vary from −0.06 for CANT, −0.02 for IRKT to −0.03 for GUAT, meaning a change towards white noise. Almost all of the 385 series analyzed show no evident change between the spectral index estimated for the AWF-based residuals and the original residuals. This means that the AWF approach maintains the noise properties of the signals and removes only the time-varying curves which are greater than the noise level.

Among others, Gu et al. (2016) presented the power spectra for the GPS position time series and noticed the 4th and 5th harmonics for a tropical year of stacked PSDs, while Bogusz and Klos (2016) showed the significance of even the 9th overtone. Khelifa (2016) presented the seasonal curves of 118 and 59 days estimated for the Doppler orbitography and radiopositioning integrated by satellite (DORIS) time series. The presented method can be extended to model these higher frequencies.

The proposed AWF is easy to implement and is a computationally low method that allows us to determine the seasonal oscillations, including information on the level of noise. If assumed properly during the creation of the AWF, the noise present in the data will remain intact. Not only the level of noise but also its type has to be included. Different geodetic observations are characterized by different kinds of noise. As an example, zenith total delays are well-approximated by the autoregressive process (Klos et al. 2018d), while DORIS observations are represented by pure power-law noise (Klos et al. 2018a). For all these cases, the AWF constitutes an alternative approach to how to split the original geodetic signal into seasonal signals and noise. Also, the AWF provides a good separation between both, which means no influence is observed by the noise on the seasonal estimates.