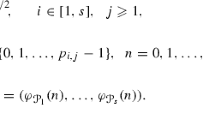The Halton sequence and its discrepancy in the Cantor expansion

Abstract

We consider variants of the Halton sequence in a generalized numeration system, called the Cantor expansion. We show that it provides a wealth of low-discrepancy sequences by giving an estimate of the (star) discrepancy of the Halton sequence in each bounded Cantor base. The techniques used in our estimation of the discrepancy are adapted from those developed by E.I. Atanassov.

1 Introduction

Let $\omega = (x_n)_{n=1}^\infty$ be a sequence in $[0,1)^s$. A standard problem in numerical analysis is estimating the integral of a function, through a knowledge of its value at a finite number of points of the sequence. This is known as the Monte Carlo method in the case of stochastic sequences $(x_n)_{n=1}^N$ or the quasi-Monte Carlo method in the case of deterministic $(x_n)_{n=1}^N.$ This is encapsulated in the famous Koksma–Hlawka inequality

$$\begin{aligned} \bigg | \int _{[0,1]^s} f(x)\, dx - \frac{1}{N}\sum _{n=1}^N f(x_n)\bigg | \le V(f) D^*_N(\omega ) \end{aligned}$$

for an arbitrary function f on $[0,1]^s$ with bounded variation V(f) in the sense of Hardy and Krause and any finite set of points $(x_n)_{n=1}^N$ with discrepancy

$$\begin{aligned} D^*_N(\omega ) = \sup _{J = \prod _{i=1}^s [0,z_i) \subseteq [0,1)^s}\bigg | \frac{A(J;N;\omega )}{N}- \lambda _s(J)\bigg |. \end{aligned}$$

Here $A(J;N;\omega ) = \#\{ 1\le n\le N:x_n\in J\}$ is the counting function, where $\lambda _s(J)$ denotes the s-dimensional Lebesgue measure of J and the above supremum is taken over all rectangular solids $J=\prod _{i=1}^s [0,z_i)$ with $0< z_i \le 1$ $(1\le i\le s)$. Note that $\lambda _s(J) = \prod _{i=1}^s z_i.$ For more details on numerical integration, the reader can consult [3, 11] or [14]. Evidently, to estimate $\int _{[0,1]^s} f(x)\,dx$ sufficiently precisely, what is needed is a good bound for $D^*_N(\omega ).$ The discrepancy is nothing other than a quantitative measure of uniformity of distribution. In particular, the sequence $\omega$ is uniformly distributed on $[0,1)^s$, if and only if $D^*_N(\omega )\rightarrow 0$ as $N\rightarrow \infty .$ In a sense, the faster $D^*_N(\omega )$ decays as a function of N,  the better uniformly distributed the sequence $\omega$ is. One of the fundamental obstructions in this subject is that there is a limit to how well distributed any sequence can be. This is encapsulated in the elementary inequality $D^*_N(\omega ) \ge 1/2^sN$ $(N\in {\mathbb {N}})$ whose proof makes an entertaining exercise. This opens the door to the deep subject of irregularities of distribution which addresses just what limitations there are to the uniformity of distribution of an arbitrary sequence, and the complementary problem of constructing sequences with discrepancy as small as possible. This latter issue is clearly central to the initial issue mentioned in this paper.

Perhaps the most famous example of a low-discrepancy sequence is the van der Corput sequence. In 1935, van der Corput [21] introduced a procedure to generate low-discrepancy sequences on [0, 1). These sequences are considered to be among the best distributed over [0, 1),  and no other infinitely generated sequences can have discrepancy of smaller order of magnitude than van der Corput sequences. The technique of van der Corput is based on a very simple idea. Let $b>1$ be a natural number. Then every nonnegative integer n has a b-adic representation of the form

$$\begin{aligned} n = \sum _{j=1}^\infty n_jb^{j-1} = n_1+n_2b+n_3b^2+n_4b^3+\cdots , \end{aligned}$$

where $n_j\in \{0,1,\ldots , b-1\}$ $(j\in {\mathbb {N}}).$ The van der Corput sequence $(\phi _b(n))_{n=0}^\infty$ in base b is constructed by reversing the base b representation of the sequence of nonnegative integers, where the radical-inverse function $\phi _b:{\mathbb {N}}_0\rightarrow [0,1)$ is defined by

$$\begin{aligned} \phi _b\bigg (\sum _{j=1}^\infty n_jb^{j-1}\bigg ) = \sum _{j=1}^\infty \frac{n_j}{b^j} = \frac{n_1}{b}+\frac{n_2}{b^2} +\frac{n_3}{b^3}+\cdots . \end{aligned}$$

In practical applications, a generalization of the van der Corput sequence to higher dimensions is more likely to be of practical use. In 1960, this was proposed by Halton [7]. Given coprime integers $b_1,\ldots , b_s$ all greater than 1,  the sequence $(\phi _{b_1}(n),\ldots ,\phi _{b_s}(n))_{n=0}^\infty$ is called the Halton sequence in bases $b_1,\ldots , b_s.$

It was known for a long time that the discrepancy of the first N elements of the Halton sequence in bases $b_1,\ldots , b_s$ can be bounded by

$$\begin{aligned} c(b_1,\ldots , b_s)\frac{(\log N)^s}{N} + O\bigg (\frac{(\log N)^{s-1}}{N}\bigg ), \end{aligned}$$

(1.1)

for some constant $c(b_1,\ldots , b_s)>0$. For example, this was shown in [4, 6, 7, 15] and [18]. It is believed that the order $(\log N)^s/N$ is the best possible for an arbitrary infinite sequence. That this is the case when $s=1$ was proved by Schmidt [20]. For $s>1,$ the question remains open. We shall call an infinite sequence $\omega$ in $[0,1)^s$ a low-discrepancy sequence if $D^*_N(\omega ) = O((\log N)^s/N).$

The question of how small the constant $c(b_1,\ldots , b_s)$ in (1.1) can be interesting from both a theoretical and a practical viewpoint. The articles referred to above show that this constant depends very strongly on the dimension s. The minimal value for this quantity can be obtained if we choose $b_1,\ldots , b_s$ to be the first s prime numbers. But even in this case $c(b_1,\ldots ,b_s)$ grows very fast to infinity if s increases. This deficiency was overcome by Atanassov [1] who proved that

$$\begin{aligned} c(b_1,\ldots , b_s) = \frac{1}{s!} \prod _{i=1}^s \frac{b_i -1}{\log b_i}. \end{aligned}$$

This estimate is so impressive that, when $b_1,\ldots , b_s$ are the first s prime numbers, $c(b_1,\ldots , b_s)\rightarrow 0$ as $s\rightarrow \infty .$

In this paper, we introduce the Halton sequence in a generalized numeration system, which is induced by the a-adic integers and which is called the Cantor expansion, and give an estimate of its discrepancy by adapting the techniques developed by Atanassov. It is worth noting here that the van der Corput sequence and some one-dimensional low-discrepancy sequences with respect to the Cantor expansion were studied in [2] and [5]. Note also that it was mentioned in [8] about the Halton sequence in a more generalized numeration system than the Cantor expansion, called the G-expansion; however, the paper aimed to study the Halton sequence in some fixed non-integer bases and did not touch on the Halton sequence with respect to dynamical bases.

We now summarize the contents of this paper. In Sect. 2, we introduce the concept of a generalized numeral system. Then we define the Halton sequence induced by this generalized system and state our main result on the estimate of discrepancy of the Halton sequence. In Sects. 3 and 4, we collect all preliminary lemmas and prove our main result, respectively. In Sect. 5, we prove an estimate of discrepancy of the van der Corput sequence in a generalized numeration system without the restriction on boundedness of inducing sequences. Then we pose an open problem regarding an extension of our results. Finally, we introduce in Sect. 6 the Hammersley point set induced by the generalized numeration system and show that it provides a wealth of low-discrepancy point sets by giving an estimate of its discrepancy.

2 A generalized Halton sequence

Let $\underline{b}=(b_j)_{j=1}^\infty$ be a sequence of natural numbers greater than 1. Then it is clear that every nonnegative integer n has a unique $\underline{b}$-adic representation of the form

$$\begin{aligned} n = \sum _{j=1}^\infty n_jb_1\cdots b_{j-1} = n_1 + n_2b_1 + n_3b_1b_2+n_4b_1b_2b_3+\cdots , \end{aligned}$$

where $n_j\in \{0,1,\ldots , b_j-1\}$ $(j\in {\mathbb {N}}).$ This $\underline{b}$-adic representation is also called the Cantor expansion of n with respect to the Cantor base $\underline{b}$. Moreover, every real number $x\in [0,1)$ has a $\underline{b}$-adic expansion of the form

$$\begin{aligned} x = \sum _{j=1}^\infty \frac{x_j}{b_1\cdots b_j} = \frac{x_1}{b_1} + \frac{x_2}{b_1b_2} + \frac{x_3}{b_1b_2b_3} + \cdots , \end{aligned}$$

where $x_j\in \{0,1,\ldots , b_j-1\}$ $(j\in {\mathbb {N}})$. The $x_j$ can be calculated by the greedy algorithm

$$\begin{aligned} x_1 = [xb_1]\qquad \text{ and }\qquad x_j = [\{xb_1\cdots b_{j-1}\}b_j], \end{aligned}$$

where $[\alpha ]$ and $\{\alpha \}$ denote the integer part and the fractional part of $\alpha ,$ respectively. The idea of this generalized numeration system stems from the a-adic integers, which is a class of locally compact topological groups and possesses a symbolic dynamical structure. For more details on the a-adic integers, see [9, pp. 106–117].

Define the radical-inverse function $\phi _{\underline{b}}:{\mathbb {N}}_0\rightarrow [0,1)$ by

$$\begin{aligned} \phi _{\underline{b}}\bigg (\sum _{j=1}^\infty n_jb_1\cdots b_{j-1}\bigg ) = \sum _{j=1}^\infty \frac{n_j}{b_1\cdots b_j} = \frac{n_1}{b_1}+\frac{n_2}{b_1b_2} +\frac{n_3}{b_1b_2b_3}+ \cdots . \end{aligned}$$

The van der Corput sequence in base $\underline{b}$ is defined as $(\phi _{\underline{b}}(n))_{n=0}^\infty .$ This sequence was studied in [2] and [5], where it was proved to be a low-discrepancy sequence with some restriction on the Cantor base $\underline{b}.$ Furthermore, the sequence was shown, without any restriction on the Cantor base, to be uniformly distributed mod 1 in [13] and to be a low-discrepancy sequence in [12].

Let $\underline{b}_1=(b_{1,j})_{j=1}^\infty ,\ldots , \underline{b}_s=(b_{s,j})_{j=1}^\infty$ be s sequences of natural numbers greater than 1 such that, for all $j_1,j_2\in {\mathbb {N}}$ and all $1\le i_1<i_2\le s,$ we have $b_{i_1,j_1}$ and $b_{i_2,j_2}$ coprime. The Halton sequence in bases $\underline{b}_1,\ldots , \underline{b}_s$ is defined to be $\omega = (\phi _{\underline{b}_1}(n),\ldots , \phi _{\underline{b}_s}(n))_{n=0}^\infty$.

The following is our main result and gives an estimate of the discrepancy of the Halton sequence in bases of bounded sequences.

Main Theorem 2.1

Let $\underline{b}_1=(b_{1,j})_{j=1}^\infty ,\ldots , \underline{b}_s=(b_{s,j})_{j=1}^\infty$ be s bounded sequences of natural numbers greater than 1 such that, for all $j_1,j_2\in {\mathbb {N}}$ and all $1\le i_1<i_2\le s,$ we have $b_{i_1,j_1}$ and $b_{i_2,j_2}$ coprime. Suppose that $\omega$ is the Halton sequence in bases $\underline{b}_1,\ldots , \underline{b}_s.$ Then, for any $N\ge 1,$ we have

$$\begin{aligned} N D_N^*(\omega ) \le \frac{1}{s!}\prod _{i=1}^s\bigg (\frac{\lfloor M_i/2\rfloor \log N}{\log m_i} + s\bigg ) + \sum _{l=0}^{s-1}\frac{M_{l+1}}{l!}\prod _{i=1}^l\bigg ( \frac{\lfloor M_i/2\rfloor \log N}{\log m_i} +l \bigg ), \end{aligned}$$

where $M_i=\max (b_{i,j})_{j=1}^\infty$ and $m_i=\min (b_{i,j})_{j=1}^\infty$ $(1\le i\le s).$

Corollary 2.2

Let $\underline{b}_1=(b_{1,j})_{j=1}^\infty ,\ldots , \underline{b}_s=(b_{s,j})_{j=1}^\infty$ be s bounded sequences of natural numbers greater than 1 such that, for all $j_1,j_2\in {\mathbb {N}}$ and all $1\le i_1<i_2\le s,$ we have $b_{i_1,j_1}$ and $b_{i_2,j_2}$ coprime. Suppose that $\omega$ is the Halton sequence in bases $\underline{b}_1,\ldots , \underline{b}_s.$ Then, for any $N\ge 1,$ we have

$$\begin{aligned} D_N^*(\omega ) \le c(\underline{b}_1,\ldots ,\underline{b}_s) \frac{(\log N)^s}{N} + O\bigg (\frac{(\log N)^{s-1}}{N}\bigg ) \end{aligned}$$

with

$$\begin{aligned} c(\underline{b}_1,\ldots ,\underline{b}_s) = \frac{1}{s!}\prod _{i=1}^s\frac{\lfloor M_i/2\rfloor }{\log m_i}, \end{aligned}$$

where $M_i=\max (b_{i,j})_{j=1}^\infty$ and $m_i=\min (b_{i,j})_{j=1}^\infty$ $(1\le i\le s).$

This shows that the Halton sequence is a low-discrepancy sequence.

3 Preliminary lemmas

In order to prove Theorem 2.1, we need the following five lemmas. These preliminary results are adapted from [3] whose ideas go back to Atanassov [1].

Lemma 3.1

Let $\underline{b}_1=(b_{1,j})_{j=1}^\infty ,\ldots , \underline{b}_s=(b_{s,j})_{j=1}^\infty$ be s arbitrary sequences of natural numbers greater than 1 such that, for all $j_1,j_2\in {\mathbb {N}}$ and all $1\le i_1<i_2\le s,$ we have $b_{i_1,j_1}$ and $b_{i_2,j_2}$ coprime. Suppose that $\omega$ is the Halton sequence in bases $\underline{b}_1,\ldots , \underline{b}_s.$ Let J be an interval of the form

$$\begin{aligned} J=\prod _{i=1}^s \bigg [\frac{u_i}{b_{i,1}\cdots b_{i,k_i}}, \frac{v_i}{b_{i,1}\cdots b_{i,k_i}}\bigg ) \end{aligned}$$

with integers $0\le u_i<v_i \le b_{i,1}\cdots b_{i,k_i}$ and $k_i\ge 1$ for all $1\le i\le s.$ Then the inequality

$$\begin{aligned} | A(J;N;\omega ) - N\lambda _s(J) | \le \prod _{i=1}^s (v_i-u_i) \end{aligned}$$

holds for every $N\in {\mathbb {N}}.$ Moreover, for every $N\le \prod _{i=1}^s b_{i,1}\cdots b_{i,k_i},$ we have $A(J;N;\omega ) \le \prod _{i=1}^s (v_i-u_i).$

Proof

For each $n\in {\mathbb {N}}_0,$ we denote the $\underline{b}_i$-adic expansion of n by

$$\begin{aligned} n = n_1^{(i)} + n_2^{(i)}b_{i,1} + n_3^{(i)}b_{i,1}b_{i,2} + n_4^{(i)}b_{i,1}b_{i,2}b_{i,3} +\cdots , \end{aligned}$$

where $n_j^{(i)}\in \{0,1,\ldots , b_{i,j}-1\}$ $(j\in {\mathbb {N}}).$ Choose $\ell = (l_1,\ldots , l_s)\in {\mathbb {N}}_0^s$ such that, for all $1\le i\le s,$ we have $0\le l_i <b_{i,1}\cdots b_{i,k_i}$ with the expansion

$$\begin{aligned} l_i = l_{i,k_i} + l_{i,k_i-1}b_{i,k_i} +l_{i,k_i-2}b_{i,k_i}b_{i,k_i-1} +\cdots + l_{i,1}b_{i,k_i}\cdots b_{i,2}, \end{aligned}$$

where $l_{i,k_i-j}\in \{0,1,\ldots , b_{i,k_i-j}-1\}$ $(0\le j\le k_i-1).$ We consider the interval

$$\begin{aligned} J_\ell = \prod _{i=1}^s\bigg [\frac{l_i}{b_{i,1}\cdots b_{i,k_i}}, \frac{l_i +1}{b_{i,1}\cdots b_{i,k_i}}\bigg ). \end{aligned}$$

Then the nth element $\omega _n$ of the Halton sequence is contained in $J_\ell ,$ if and only if, for all $1\le i\le s,$

$$\begin{aligned} \frac{l_{i,1}}{b_{i,1}} +\cdots + \frac{l_{i,k_i}}{b_{i,1}\cdots b_{i,k_i}} \le \frac{n_1^{(i)}}{b_{i,1}} + \frac{n_2^{(i)}}{b_{i,1}b_{i,2}} +\cdots < \frac{l_{i,1}}{b_{i,1}} +\cdots + \frac{l_{i,k_i}}{b_{i,1}\cdots b_{i,k_i}} + \frac{1}{b_{i,1}\cdots b_{i,k_i}}. \end{aligned}$$

This is however equivalent to $n_1^{(i)} = l_{i,1},\ldots , n_{k_i}^{(i)} = l_{i,k_i}$ which in turn is equivalent to $n\equiv l_{i,1}+ l_{i,2}b_{i,1}+\cdots + l_{i,k_i}b_{i,1}\cdots b_{i,k_i-1}\pmod { b_{i,1}\cdots b_{i,k_i}}$ for all $1\le i\le s.$

As $b_{1,j_1},\dots , b_{s,j_s}$ are pairwise coprime for all $(j_1,\ldots , j_s)\in {\mathbb {N}}^s,$ we obtain from the Chinese Remainder Theorem that every $\prod _{i=1}^s b_{i,1}\cdots b_{i,k_i}$ consecutive elements of the Halton sequence, contain exactly one element in $J_\ell$ or, in other words, $A(J_\ell ; t\prod _{i=1}^s b_{i,1}\cdots b_{i,k_i};\omega ) = t$ for all $t\in {\mathbb {N}},$ and hence

$$\begin{aligned} A\bigg (J_\ell ;t\prod _{i=1}^s b_{i,1}\cdots b_{i,k_i};\omega \bigg ) - \bigg (t\prod _{i=1}^s b_{i,1}\cdots b_{i,k_i}\bigg )\lambda _s(J_\ell ) = 0. \end{aligned}$$

Therefore, for every $N\in {\mathbb {N}},$ we obtain

$$\begin{aligned} |A(J_\ell ; N;\omega ) - N\lambda _s(J_\ell )| \le 1. \end{aligned}$$

Now we write the interval J as a disjoint union of intervals of the form $J_\ell ,$

$$\begin{aligned} J = \bigcup _{l_1=u_1}^{v_1-1}\cdots \bigcup _{l_s=u_s}^{v_s-1} J_\ell , \end{aligned}$$

where $\ell = (l_1,\ldots , l_s).$ We then have

$$\begin{aligned} | A(J;N;\omega )-N\lambda _s(J)| \le \sum _{l_1=u_1}^{v_1-1}\cdots \sum _{l_s=u_s}^{v_s-1} |A(J_\ell ;N;\omega )- N\lambda _s(J_\ell )| \le \prod _{i=1}^s (v_i-u_i), \end{aligned}$$

which proves the first assertion.

For every $N\le \prod _{i=1}^s b_{i,1}\cdots b_{i,k_i},$ we always have $A(J_\ell ; N;\omega )\le 1$ for each $\ell = (l_1,\ldots , l_s)\in {\mathbb {N}}_0^s$ with $0\le l_i< b_{i,1}\cdots b_{i,k_i}$ for all $1\le i\le s,$ and hence

$$\begin{aligned} A(J;N;\omega ) = \sum _{l_1=u_1}^{v_1-1}\cdots \sum _{l_s=u_s}^{v_s-1} A(J_\ell ; N;\omega ) \le \prod _{i=1}^s (v_i-u_i). \end{aligned}$$

This was the second assertion of the lemma. $\square$

Lemma 3.2

Let $\underline{b}_1=(b_{1,j})_{j=1}^\infty ,\ldots , \underline{b}_s=(b_{s,j})_{j=1}^\infty$ be s arbitrary sequences of natural numbers greater than 1. For each $N\in {\mathbb {N}},$ let $d(\underline{b}_1,\ldots , \underline{b}_s;N)$ be the number of tuples $(k_1,\ldots , k_s)\in {\mathbb {N}}^s$ such that $\prod _{i=1}^s b_{i,1}\cdots b_{i,k_i} \le N.$ Then we have

$$\begin{aligned} d(\underline{b}_1,\ldots , \underline{b}_s;N) \le \frac{1}{s!}\prod _{i=1}^s\frac{\log N}{\log m_i}, \end{aligned}$$

where $m_i=\min (b_{i,j})_{j=1}^\infty$ $(1\le i\le s).$

Proof

Let $N\in {\mathbb {N}}.$ Assume that $k=(k_1,\ldots , k_s)\in {\mathbb {N}}^s$ satisfies $\prod _{i=1}^s b_{i,1}\cdots b_{i,k_i} \le N.$ Notice that we immediately have $m_1^{k_1}\cdots m_s^{k_s} \le N.$ Then the interval $E_k = \prod _{i=1}^s [k_i-1,k_i)$ of volume 1 is entirely contained in the simplex

$$\begin{aligned} S = \big \{ (x_1,\ldots , x_s)\in [0,\infty )^s:x_1\log m_1+\cdots +x_s\log m_s \le \log N \big \} \end{aligned}$$

of volume $\frac{1}{s!}\prod _{i=1}^s\frac{\log N}{\log m_i}.$ Hence, we obtain

$$\begin{aligned} d(\underline{b}_1,\ldots , \underline{b}_s; N) = \lambda _s\bigg ( \bigcup _{E_k\subseteq S} E_k\bigg )\le \lambda _s(S) = \frac{1}{s!}\prod _{i=1}^s\frac{\log N}{\log m_i}, \end{aligned}$$

as required. $\square$

Lemma 3.3

Let $\underline{b}_1=(b_{1,j})_{j=1}^\infty ,\ldots , \underline{b}_s=(b_{s,j})_{j=1}^\infty$ be s arbitrary sequences of natural numbers greater than 1. Suppose that $(z_k^{(1)})_{k=0}^\infty ,\ldots , (z_k^{(s)})_{k=0}^\infty$ are s bounded sequences of nonnegative real numbers such that $z_0^{(i)}\le 1$ and $z_k^{(i)}\le f_i$ for all $k\in {\mathbb {N}}$ and all $1\le i\le s.$ Then, for any $N\ge 1,$ we have

$$\begin{aligned} \sum _{\begin{array}{c} (k_1,\ldots , k_s)\in {\mathbb {N}}_0^s \\ \prod _{i=1}^s b_{i,1}\cdots b_{i,k_i} \le N \end{array}} \prod _{i=1}^s z_{k_i}^{(i)} \le \frac{1}{s!}\prod _{i=1}^s \bigg (f_i\frac{\log N}{\log m_i} +s\bigg ), \end{aligned}$$

where $m_i=\min (b_{i,j})_{j=1}^\infty$ $(1\le i\le s).$

Proof

Let $\mathfrak {u}\subseteq \{1,\ldots , s\}.$ By Lemma 3.2, the number of s-tuples $(k_1,\ldots , k_s)$ such that $k_i>0$ if $i\in \mathfrak {u},$ $k_i=0$ if $i\notin \mathfrak {u},$ and $\prod _{i\in \mathfrak {u}}b_{i,1}\cdots b_{i,k_i}\le N$ is bounded above by $\frac{1}{|\mathfrak {u}|!}\prod _{i\in \mathfrak {u}}\frac{\log N}{\log m_i}.$ Moreover, each of these s-tuples contributes at most $\prod _{i\in \mathfrak {u}} f_i$ to the sum on the left hand side in the statement of the lemma. From this, invoking the inequality $\frac{1}{|\mathfrak {u}|!} \le \frac{s^{s-|\mathfrak {u}|}}{s!},$ we obtain

$$\begin{aligned} {\begin{matrix} \sum _{\begin{array}{c} (k_1,\ldots , k_s)\in {\mathbb {N}}_0^s \\ \prod _{i=1}^s b_{i,1}\cdots b_{i,k_i} \le N \end{array}} \prod _{i=1}^s z_{k_i}^{(i)} &{}\le \sum _{\mathfrak {u}\subseteq \{1,\ldots , s\}} \frac{1}{|\mathfrak {u}|!} \prod _{i\in \mathfrak {u}} f_i\frac{\log N}{\log m_i} \\ &{} \le \frac{1}{s!}\sum _{\mathfrak {u}\subseteq \{1,\ldots , s\}} s^{s-|\mathfrak {u}|}\prod _{i\in \mathfrak {u}} f_i\frac{\log N}{\log m_i} \\ &{} = \frac{1}{s!}\prod _{i=1}^s \bigg (f_i\frac{\log N}{\log m_i} +s\bigg ), \end{matrix}} \end{aligned}$$

and this is the desired result. $\square$

Now we need to introduce some notation. Let $J\subseteq {\mathbb {R}}^s$ be an interval. Then a signed splitting of J is a collection of not necessarily disjoint intervals $J_1,\ldots , J_r$ together with signs $\varepsilon _1,\ldots ,\varepsilon _r\in \{-1,1\}$ such that, for all $x\in J,$ we have

$$\begin{aligned} \sum _{\begin{array}{c} i=1 \\ x\in J_i \end{array}}^r \varepsilon _i = 1. \end{aligned}$$

A function $\nu$ on the class of intervals in ${\mathbb {R}}^s$ is said to be additive if, for each pair of disjoint intervals A, B in ${\mathbb {R}}^s,$ we have $\nu (A\cup B)=\nu (A)+\nu (B).$ It is not hard to see that the s-dimensional Lebesgue measure $\lambda _s$ and the counting function $A(\cdot ;N;\omega )$ are the examples we are particularly interested in. It is not hard to check that, for any additive function $\nu$ on the class of intervals in ${\mathbb {R}}^s,$ we have

$$\begin{aligned} \nu (J) = \sum _{i=1}^r\varepsilon _i\nu (J_i), \end{aligned}$$

where $(J_1,\ldots ,J_r;\varepsilon _1,\ldots ,\varepsilon _r)$ is a signed splitting of J,  and here we use $\nu (J_i)=\nu (J_i\cap J)$ $(1\le i\le r).$ The following result is taken directly from [1] (see also [3] for a detailed proof).

Lemma 3.4

([1, Lemma 3.5]) Let $J=\prod _{i=1}^s [0,z_i)$ be an s-dimensional box. For each $1\le i\le s,$ let $(z_{k,i})_{k=1,\ldots , n_i}$ be an arbitrary finite sequence of numbers in [0, 1]. Define further $z_{0,i}=0$ and $z_{n_i+1,i}= z_i$ for all $1\le i\le s.$ Then the collection of intervals

$$\begin{aligned} \prod _{i=1}^s [\min (z_{k_i,i},z_{k_i+1,i}),\,\max (z_{k_i,i},z_{k_i+1,i})) \end{aligned}$$

together with the signs $\varepsilon _{k_1,\ldots , k_s} = \prod _{i=1}^s \mathrm {sgn}(z_{k_i+1,i}-z_{k_i,i})$ for $0\le k_i\le n_i$ and $1\le i\le s$ define a signed splitting of the interval J.

For the proof of Theorem 2.1, we need a digit expansion of reals $z\in [0,1)$ in $(b_j)_{j=1}^\infty$-adic base which uses signed digits. The next lemma shows that such an expansion exists.

Lemma 3.5

Let $\underline{b}=(b_j)_{j=1}^\infty$ be an arbitrary sequence of natural numbers greater than 1. Then every $z\in [0,1)$ can be written in the form

$$\begin{aligned} z= a_0 + \frac{a_1}{b_1}+\frac{a_2}{b_1b_2}+\frac{a_3}{b_1b_2b_3}+\cdots \end{aligned}$$

with integer digits $a_0,a_1,a_2,\ldots$ such that $a_0\in \{0,1\}$ and $-\lfloor \frac{b_j-1}{2}\rfloor \le a_j\le \lfloor \frac{b_j}{2}\rfloor$ for all $j\in {\mathbb {N}}.$ This expansion is called a signed $\underline{b}$-adic expansion of z.

Proof

For each $j\in {\mathbb {N}},$ let $c_j=\lfloor \frac{b_j-1}{2}\rfloor .$ Define

$$\begin{aligned} x= \frac{c_1}{b_1} +\frac{c_2}{b_1b_2}+\frac{c_3}{b_1b_2b_3}+\cdots \in [0,1). \end{aligned}$$

For $z\in [0,1),$ we have $z+x\in [0,2)$ with $\underline{b}$-adic expansion

$$\begin{aligned} z+x = u_0+\frac{u_1}{b_1}+\frac{u_2}{b_1b_2}+\frac{u_3}{b_1b_2b_3} +\cdots , \end{aligned}$$

where $u_0\in \{0,1\},$ and where $u_j\in \{0,1,\ldots , b_j-1\}$ $(j\in {\mathbb {N}}).$ Therefore,

$$\begin{aligned} z = u_0 +\frac{u_1-c_1}{b_1}+\frac{u_2-c_2}{b_1b_2} +\frac{u_3-c_3}{b_1b_2b_3}+\cdots \end{aligned}$$

with $-\lfloor \frac{b_j-1}{2}\rfloor \le u_j-c_j\le b_j-1-\lfloor \frac{b_j-1}{2}\rfloor = \lfloor \frac{b_j}{2}\rfloor$ for all $j\in {\mathbb {N}},$ as required. $\square$

4 Proof of the main theorem

Proof of Theorem 2.1

Let $J= \prod _{i=1}^s [0,z_i)\subseteq [0,1)^s.$ According to Lemma 3.5, for all $1\le i\le s,$ we consider the signed $\underline{b}_i$-adic expansion of $z_i$ of the form

$$\begin{aligned} z_i= a_{i,0}+\frac{a_{i,1}}{b_{i,1}}+\frac{a_{i,2}}{b_{i,1}b_{i,2}} +\frac{a_{i,3}}{b_{i,1}b_{i,2}b_{i,3}}+\cdots \end{aligned}$$

with $a_{i,0}\in \{0,1\}$ and $-\lfloor \frac{b_{i,j}-1}{2}\rfloor \le a_{i,j} \le \lfloor \frac{b_{i,j}}{2}\rfloor$ $(j\in {\mathbb {N}}).$

For all $1\le i\le s,$ let $n_i = \lfloor \frac{\log N}{\log m_i}\rfloor + 1,$ and for $1\le k\le n_i,$ define the truncations of the expansions

$$\begin{aligned} z_{k,i} = a_{i,0}+\frac{a_{i,1}}{b_{i,1}}+ \frac{a_{i,2}}{b_{i,1}b_{i,2}} +\cdots + \frac{a_{i,k-1}}{b_{i,1}\cdots b_{i,k-1}}, \end{aligned}$$

and let $z_{0,i}=0$ and $z_{n_i+1,i}=z_i.$

According to Lemma 3.4, the collection of intervals

$$\begin{aligned} J_{k_1,\ldots , k_s} = \prod _{i=1}^s [\min (z_{k_i,i},z_{k_i+1,i}), \max (z_{k_i,i},z_{k_i+1,i})) \end{aligned}$$

together with the signs $\varepsilon _{k_1,\ldots , k_s} = \prod _{i=1}^s \mathrm {sgn}(z_{k_i+1,i}-z_{k_i,i})$ for $0\le k_i\le n_i$ and $1\le i\le s$ defines a signed splitting of the interval J.

Since both $\lambda _s$ and $A(\cdot ;N;\omega )$ are additive functions on the set of intervals, we obtain that

$$\begin{aligned} A(J;N;\omega )-N\lambda _s(J)&= \sum _{k_1=0}^{n_1}\cdots \sum _{k_s=0}^{n_s} \varepsilon _{k_1,\ldots , k_s}( A(J_{k_1,\ldots , k_s};N;\omega ) - N\lambda _s(J_{k_1,\ldots , k_s}) ) \\&= \Sigma _1 + \Sigma _2, \end{aligned}$$

where $\Sigma _1$ denotes the sum over all $(k_1,\ldots ,k_s)$ such that $\prod _{i=1}^s b_{i,1}\cdots b_{i,k_i}\le N$ and $\Sigma _2$ denotes the remaining part of the above sum.

First we deal with the sum $\Sigma _1.$ For any $1\le i\le s,$ the length of the interval $[\min (z_{k_i,i},z_{k_i+1,i}), \max (z_{k_i,i},z_{k_i+1,i}))$ is $|a_{i,k_i}/b_{i,1}\cdots b_{i,k_i}|,$ and also the limit points of this interval are rationals with denominator $b_{i,1}\cdots b_{i,k_i}.$ It is worth keeping in mind that, due to the choice of $n_i,$ we must have $k_i<n_i$ when $\prod _{i=1}^s b_{i,1}\cdots b_{i,k_i}\le N$. Accordingly, the intervals $J_{k_1,\ldots , k_s}$ are of the form as considered in Lemma 3.1 from which we obtain

$$\begin{aligned} |A(J_{k_1,\ldots , k_s};N;\omega )-N\lambda _s(J_{k_1,\ldots , k_s})| \le \prod _{i=1}^s |a_{i,k_i}|. \end{aligned}$$

We have $|a_{i,k_i}|\le \lfloor \frac{b_{i,k_i}}{2}\rfloor \le \lfloor \frac{M_i}{2}\rfloor =: f_i.$ An application of Lemma 3.3 yields that

$$\begin{aligned} \Sigma _1 \le \frac{1}{s!}\prod _{i=1}^s\bigg ( \frac{\lfloor M_i/2\rfloor \log N}{\log m_i} + s \bigg ). \end{aligned}$$

It remains to estimate $\Sigma _2.$ To this end, we split the set of s-tuples $(k_1,\ldots , k_s)$ for which $\prod _{i=1}^s b_{i,1}\cdots b_{i,k_i} >N$ into disjoint sets $B_0,B_1,\ldots , B_{s-1}$ where we set $B_0 = \{(k_1,\ldots ,k_s)\in {\mathbb {N}}_0^s:b_{1,1}\cdots b_{1,k_1} >N\}$ and, for $1\le l\le s-1,$

$$\begin{aligned} B_l = \bigg \{(k_1,\ldots ,k_s)\in {\mathbb {N}}_0^s:\prod _{i=1}^l b_{i,1}\cdots b_{i,k_i}\le N\>\text{ and }\> \prod _{i=1}^{l+1}b_{i,1}\cdots b_{i,k_i}>N\bigg \}. \end{aligned}$$

For a fixed $1\le l\le s-1$ and a fixed l-tuple $(k_1,\ldots , k_l)$ with $\prod _{i=1}^l b_{i,1}\cdots b_{i,k_i}\le N,$ define r to be the largest integer such that

$$\begin{aligned} \bigg (\prod _{i=1}^l b_{i,1}\cdots b_{i,k_i}\bigg )(b_{l+1,1}\cdots b_{l+1,r-1})\le N. \end{aligned}$$

It follows that the tuple $(k_1,\ldots , k_l,k_{l+1},\ldots , k_s)$ is contained in $B_l,$ if and only if $k_{l+1}\ge r.$

Therefore, for any $0\le l\le s-1$ and fixed $k_1,\ldots , k_l\in {\mathbb {N}}_0$ such that $\prod _{i=1}^l b_{i,1}\cdots b_{i,k_i}\le N,$ we have that

$$\begin{aligned} \sum _{\begin{array}{c} k_{l+1},\ldots , k_s\in {\mathbb {N}} \\ (k_1,\ldots ,k_s)\in B_l \end{array}} \varepsilon _{k_1,\ldots , k_s}( A(J_{k_1,\ldots , k_s};N;\omega ) - N\lambda _s(J_{k_1,\ldots , k_s})) = \pm (A(L;N;\omega )-N\lambda _s(L)), \end{aligned}$$

where

$$\begin{aligned} L&= \prod _{i=1}^l [\min (z_{k_i,i},z_{k_i+1,i}),\max (z_{k_i,i},z_{k_i+1,i})) \\&\quad \times [\min (z_{r,l+1},z_{l+1}),\max (z_{r,l+1},z_{l+1})) \times \prod _{i=l+2}^s [0,z_i). \end{aligned}$$

Let $(k_1,\ldots ,k_s)\in B_l.$ As

$$\begin{aligned} |z_{l+1}-z_{r,l+1}|&= \bigg | \frac{a_{l+1,r}}{b_{l+1,1}\cdots b_{l+1,r}} +\frac{a_{l+1,r+1}}{b_{l+1,1}\cdots b_{l+1,r+1}} + \frac{a_{l+1,r+2}}{b_{l+1,1}\cdots b_{l+1,r+2}} +\cdots \bigg | \\&= \frac{1}{b_{l+1,1}\cdots b_{l+1,r-1}}\bigg | \frac{a_{l+1,r}}{b_{l+1,r}} +\frac{a_{l+1,r+1}}{b_{l+1,r} b_{l+1,r+1}} + \frac{a_{l+1,r+2}}{b_{l+1,r}b_{l+1,r+1}b_{l+1,r+2}} +\cdots \bigg | \\&\le \frac{1}{b_{l+1,1}\cdots b_{l+1,r-1}}\bigg ( \frac{\lfloor b_{l+1,r}/2\rfloor }{b_{l+1,r}}+\frac{\lfloor b_{l+1,r+1}/2\rfloor }{b_{l+1,r} b_{l+1,r+1}} + \frac{\lfloor b_{l+1,r+2}/2 \rfloor }{b_{l+1,r}b_{l+1,r+1}b_{l+1,r+2}} +\cdots \bigg ) \\&\le \frac{1}{b_{l+1,1}\cdots b_{l+1,r-1}}\bigg ( \frac{1}{2}+\frac{1}{2 b_{l+1,r}} + \frac{1}{2b_{l+1,r}b_{l+1,r+1}}+\cdots \bigg ) \\&\le \frac{1}{b_{l+1,1}\cdots b_{l+1,r-1}}\bigg ( \frac{1}{2} + \frac{1}{2^2} + \frac{1}{2^3}+\cdots \bigg ) \\&= \frac{1}{b_{l+1,1}\cdots b_{l+1,r-1}}, \end{aligned}$$

it follows that the interval $[\min (z_{r,l+1},z_{l+1}), \max (z_{r,l+1},z_{l+1}) )$ is contained in some interval

$$\begin{aligned} \bigg [\frac{u}{b_{l+1,1}\cdots b_{l+1,r}}, \frac{v}{b_{l+1,1}\cdots b_{l+1,r}}\bigg ) \end{aligned}$$

for $u,v\in {\mathbb {N}}_0$ with $v-u\le b_{l+1,r}.$ Hence, L is contained in the interval

$$\begin{aligned} L'= & {} \prod _{i=1}^l [\min (z_{k_i,i},z_{k_i+1,i}),\max (z_{k_i,i},z_{k_i+1,i}))\\&\times \bigg [\frac{u}{b_{l+1,1}\cdots b_{l+1,r}}, \frac{v}{b_{l+1,1}\cdots b_{l+1,r}}\bigg ) \times [0,1)^{s-l-1}. \end{aligned}$$

Since $(k_1,\ldots , k_s)\in B_l$, we have $N<(\prod _{i=1}^l b_{i,1}\cdots b_{i,k_i})(b_{l+1,1}\cdots b_{l+1,r})$ and $N\ge \prod _{i=1}^l b_{i,1}\cdots b_{i,k_i}.$ The latter fact implies that $k_i<n_i$ for all $1\le i\le s.$ Thus, an application of Lemma 3.1 yields that

$$\begin{aligned} A(L;N;\omega ) \le A(L';N;\omega ) \le b_{l+1,r}\prod _{i=1}^l |a_{i,k_i}|. \end{aligned}$$

But on the other hand, we also have that $N\lambda _s(L)\le b_{l+1,r}\prod _{i=1}^l |a_{i,k_i}|.$ Hence,

$$\begin{aligned} |A(L;N;\omega ) - N\lambda _s(L)| \le b_{l+1,r}\prod _{i=1}^l |a_{i,k_i}| \le M_{l+1}\prod _{i=1}^l c_{i,k_i}, \end{aligned}$$

where $c_{i,k_i} = 1$ if $k_i=0$ and $c_{i,k_i}=\lfloor \frac{M_i}{2}\rfloor$ otherwise.

Summing up, we obtain

$$\begin{aligned} |\Sigma _2|&\le \sum _{l=0}^{s-1} \sum _{\begin{array}{c} k_1,\ldots , k_l\in {\mathbb {N}}_0 \\ \prod _{i=1}^l b_{i,1}\cdots b_{i,k_i} \le N \end{array}} \bigg | \sum _{(k_1,\ldots , k_s)\in B_l} \epsilon _{k_1,\ldots , k_s}(A(J_{k_1,\ldots , k_s};N;\omega ) - N\lambda _s(J_{k_1,\ldots , k_s}) ) \bigg | \\&\le \sum _{l=0}^{s-1} \sum _{\begin{array}{c} k_1,\ldots , k_l\in {\mathbb {N}}_0 \\ \prod _{i=1}^l b_{i,1}\cdots b_{i,k_i} \le N \end{array}} M_{l+1} \prod _{i=1}^l c_{i,k_i} \le \sum _{l=0}^{s-1}\frac{M_{l+1}}{l!}\prod _{i=1}^l\bigg ( \frac{\lfloor M_i/2\rfloor \log N}{\log m_i} +l \bigg ), \end{aligned}$$

where we have used Lemma 3.3 again. Hence, the result follows. $\square$

5 An open problem

We have seen that the Halton sequence in bases of bounded sequences $\underline{b}_1,\ldots ,\underline{b}_s$ is a low-discrepancy sequence. It is of theoretical interest to ask whether the assumption of boundedness of the base sequences $\underline{b}_1,\ldots ,\underline{b}_s$ can be removed or not.

The following statement shows that we can remove the restriction on the boundedness when $s=1.$ That is, the van der Corput sequence in base $\underline{b}=(b_j)_{j=1}^\infty$ of an arbitrary sequence of natural numbers greater than 1 is a low-discrepancy sequence. Note that the proof is developed from the classical dyadic case in [10, pp. 127–128].

Proposition 5.1

Let $\underline{b}=(b_j)_{j=1}^\infty$ be an arbitrary sequence of natural numbers greater than 1. Suppose that $\omega$ is the van der Corput sequence in base $\underline{b}.$ Then, for any $N\in {\mathbb {N}},$ we have

$$\begin{aligned} N D_N^*(\omega ) \le \frac{\log N}{\log m} +1, \end{aligned}$$

where $m = \min (b_j)_{j=1}^\infty .$

Note that Proposition 5.1 gives a better estimation of discrepancy than the case $s=1$ of Theorem 2.1 and also that of [2, Théorème 4.5]. To prove this result, we need to introduce a notation and two preliminary lemmas.

A finite sequence $0\le c_1< c_2<\cdots < c_L$ of points from the interval [0, 1) is called an arithmetic progression with difference $\eta$ if $c_{i+1}-c_i = \eta$ for all $1\le i\le L-1.$

The first lemma gives an estimation of discrepancy of an arithmetic progressions.

Lemma 5.2

([16, Theorem 2.1]) Let $c_1<c_2<\cdots < c_L$ be an arithmetic progression with difference $\eta$. Then we have

$$\begin{aligned} D_L^*(c_1,\ldots , c_L) \le \min (\eta ,1/L) \end{aligned}$$

The next simple lemma is useful for estimating the discrepancy of a sequence which can be decomposed into a number of subsequences with small discrepancy.

Lemma 5.3

([18, Theorem 2.6, Ch. 2]) For $1\le k\le K,$ let $\omega _k$ be a sequence of $N_k$ elements in [0, 1) with discrepancy $D^*_{N_k}(\omega _k).$ Let $\omega$ be a superposition of $\omega _1,\ldots , \omega _K,$ that is, a sequence obtained by listing in some order the terms of $\omega _k.$ We set $N= N_1+\cdots + N_K,$ which will be the number of elements of $\omega .$ Then we have

$$\begin{aligned} ND^*_N(\omega ) \le \sum _{k=1}^K N_k D^*_{N_k}(\omega _k). \end{aligned}$$

Proof of Proposition 5.1

We can always represent a given $N\in {\mathbb {N}}$ by its $\underline{b}$-adic expansion

$$\begin{aligned} N = N_1 + N_2b_1 + N_3b_1b_2 +\cdots + N_k b_1\cdots b_{k-1}, \end{aligned}$$

(5.1)

where $k\in {\mathbb {N}}$ and $N_j\in \{0,1,\ldots , b_j-1\}$ $(1\le j\le k).$ Partition the interval [0, N] of integers into k subintervals $I_1,\ldots , I_k$ as follows. First, put $I_1 = [0,N_kb_1\cdots b_{k-1}].$ Then, for each $1<j\le k,$ we define $I_j$ as the interval

$$\begin{aligned}{}[N_kb_1\cdots b_{k-1} +\cdots + N_{k-j+2}b_1\cdots b_{k-j+1} + 1, N_kb_1\cdots b_{k-1} + \cdots + N_{k-j+1}b_1\cdots b_{k-j}]. \end{aligned}$$

Note that the proof idea of splitting up the range of $0,1,\ldots , N$ in this way is due to Niederreiter [17].

An integer $n\in I_j$ $(1\le j\le k)$ can be written in the form

$$\begin{aligned} n = N_kb_1\cdots b_{k-1} + \cdots + N_{k-j+2}b_1\cdots b_{k-j+1} + 1 + \sum _{i=1}^{k-j+1} n_i b_0\cdots b_{i-1}, \end{aligned}$$

(5.2)

where $b_0 = 1$ and $n_i\in \{0,1,\ldots , b_i-1\}$ $(1\le i\le k-j+1)$ such that $n_{k-j+1} < N_{k-j+1}.$ In fact, we get all $N_{k-j+1}b_1\cdots b_{k-j}$ integers in $I_j$ if we let $n_i$ run through all possible combinations. It now follows that

$$\begin{aligned} \phi _{\underline{b}}(n)&= \frac{N_k}{b_1\cdots b_k} +\cdots + \frac{N_{k-j+2}}{b_1\cdots b_{k-j+2}} + \frac{1}{b_1\cdots b_{k-j+1}} +\sum _{i=1}^{k-j+1} \frac{n_i}{b_1\cdots b_i} \\&= x_j + \sum _{i=1}^{k-j+1} \frac{n_i}{b_1\cdots b_i}, \end{aligned}$$

where $x_j$ only depends on j,  and not on n. If n runs through $I_j,$ then $\sum _{i=1}^{k-j+1}\frac{n_i}{b_1\cdots b_i}$ runs through all fractions $0,\frac{1}{b_1},\ldots , \frac{b_1-1}{b_1},\frac{1}{b_1b_2},\ldots , \sum _{i=1}^{k-j} \frac{b_i-1}{b_1\cdots b_i} + \frac{N_{k-j+1}}{b_1\cdots b_{k-j+1}}$ in some order. Moreover, we note that

$$\begin{aligned} 0\le x_j = \frac{N_k}{b_1\cdots b_k} + \cdots + \frac{N_{k-j+2}}{b_1\cdots b_{k-j+2}} \le \frac{b_k\cdots b_{k-j+2}-1}{b_1\cdots b_k} \le \frac{1}{b_1\cdots b_{k-j+1}}. \end{aligned}$$

We deduce that if the $\phi _{\underline{b}}(n)$ $(n\in I_j)$ are ordered according to their magnitude, then we obtain a sequence $\omega _j$ of $N_{k-j+1}b_1\cdots b_{k-j}$ elements that is a true arithmetic progression with parameters $\eta _j = \frac{1}{b_1\cdots b_{k-j+1}}.$ It now follows immediately from Lemma 5.2 that the discrepancy of each $\omega _j,$ multiplied by the number of elements in $\omega _j,$ is at most 1. Combining this with Lemma 5.3 and the fact that $\phi _{\underline{b}}(0),\phi _{\underline{b}}(1),\ldots , \phi _{\underline{b}}(N)$ is decomposed into k sequences $\omega _j,$ we obtain $N D^*_N(\omega ) \le k.$

It remains to estimate k in terms of N. By (5.1), we have $N\ge b_1\cdots b_{k-1} \ge m^{k-1},$ and so we obtain $k\le (\log N/\log m) + 1.$ This completes the proof of Proposition 5.1. $\square$

In general, it is likely to be true that the Halton sequence in arbitrary bases of sequences is a low-discrepancy sequence.

Problem 5.4

Let $s>1,$ and let $\underline{b}_1 = (b_{1,j})_{j=1}^\infty ,\ldots , \underline{b}_s = (b_{s,j})_{j=1}^\infty$ be s arbitrary sequences of natural numbers greater than 1 such that, for all $j_1,j_2\in {\mathbb {N}}$ and all $1\le i_1<i_2 \le s,$ we have $b_{i_1,j_1}$ and $b_{i_2,j_2}$ coprime. Suppose that $\omega$ is the Halton sequence in bases $\underline{b}_1,\ldots , \underline{b}_s.$ Then we have

$$\begin{aligned} D_N^*(\omega ) \le c(\underline{b}_1,\ldots ,\underline{b}_s)\frac{(\log N)^s}{N} + O\bigg ( \frac{(\log N)^{s-1}}{N}\bigg ), \end{aligned}$$

where $c(\underline{b}_1,\ldots ,\underline{b}_s)>0$ is a constant.

If the conjecture is true, then it is natural to ask further whether the constant $c(\underline{b}_1,\ldots ,\underline{b}_s)$ can be reduced to a similar form to that in Corollary 2.2.

6 A generalized Hammersley point set

Based on the $(s-1)$-dimensional Halton sequence, we can introduce a finite s-dimensional point set which is known as the Hammersley point set.

Let $\underline{b}_1=(b_{1,j})_{j=1}^\infty ,\ldots , \underline{b}_{s-1}=(b_{s-1,j})_{j=1}^\infty$ be $s-1$ sequences of natural numbers greater than 1 such that, for all $j_1,j_2\in {\mathbb {N}}$ and all $1\le i_1<i_2\le s-1,$ we have $b_{i_1,j_1}$ and $b_{i_2,j_2}$ coprime. The Hammersley point set in bases $\underline{b}_1,\ldots , \underline{b}_{s-1}$ consisting of N points in $[0,1)^s$ is defined to be the point set

$$\begin{aligned} \mathcal {P} = \bigg \{\bigg (\frac{n}{N} , \phi _{\underline{b}_1}(n),\ldots , \phi _{\underline{b}_{s-1}}(n)\bigg ):0\le n\le N-1\bigg \}. \end{aligned}$$

We deduce a discrepancy bound for the Hammersley point set with the help of Theorem 2.1 in combination with the following general result from [18] that goes back to Roth [19].

Lemma 6.1

([18, Lemma 3.7]) Let $\omega =(x_n)_{n=0}^\infty$ be an arbitrary sequence in $[0,1)^{s-1}$ with discrepancy $D^*_N(\omega ).$ For $N\in {\mathbb {N}},$ let $\mathcal {P}$ be the point set consisting of $(n/N, x_n)$ in $[0,1)^s$ for $n=0,1,\ldots , N-1.$ Then we have

$$\begin{aligned} N D^*_N(\mathcal {P}) \le \max _{1\le N'\le N} N' D^*_{N'}(\omega ) +1. \end{aligned}$$

Theorem 6.2

Let $\underline{b}_1=(b_{1,j})_{j=1}^\infty ,\ldots , \underline{b}_{s-1}=(b_{s-1,j})_{j=1}^\infty$ be $s-1$ arbitrary sequences of natural numbers greater than 1 such that, for all $j_1,j_2\in {\mathbb {N}}$ and all $1\le i_1<i_2\le s-1,$ we have $b_{i_1,j_1}$ and $b_{i_2,j_2}$ are coprime. For $N\in {\mathbb {N}},$ let $\mathcal {P}$ be the Hammersley point set in bases $\underline{b}_1,\ldots , \underline{b}_{s-1}$ consisting of N points. Then, for any $N\ge 2,$ we have

$$\begin{aligned} N D^*_N(\mathcal {P}) \le \frac{1}{(s-1)!}\prod _{i=1}^{s-1}\bigg (\frac{\lfloor M_i/2\rfloor \log N}{\log m_i} + s-1\bigg ) + \sum _{l=0}^{s-2}\frac{M_{l+1}}{l!}\prod _{i=1}^l\bigg ( \frac{\lfloor M_i/2\rfloor \log N}{\log m_i} +l \bigg ) +1, \end{aligned}$$

where $M_i=\max \{b_{i,j}\in \underline{b}_i:b_{i,1}\cdots b_{i,j}\le N\}$ and $m_i=\min \{b_{i,j}\in \underline{b}_i:b_{i,1}\cdots b_{i,j}\le N\}$ $(1\le i\le s-1).$

Corollary 6.3

Let $\underline{b}_1=(b_{1,j})_{j=1}^\infty ,\ldots , \underline{b}_{s-1}=(b_{s-1,j})_{j=1}^\infty$ be $s-1$ bounded sequences of natural numbers greater than 1 such that, for all $j_1,j_2\in {\mathbb {N}}$ and all $1\le i_1<i_2\le s-1,$ we have $b_{i_1,j_1}$ and $b_{i_2,j_2}$ coprime. For $N\in {\mathbb {N}},$ let $\mathcal {P}$ be the Hammersley point set in bases $\underline{b}_1,\ldots , \underline{b}_{s-1}$ consisting of N points. Then, for any $N\ge 2,$ we have

$$\begin{aligned} D^*_N(\mathcal {P}) \le c(\underline{b}_1,\ldots , \underline{b}_{s-1}) \frac{(\log N)^{s-1}}{N} + O\bigg (\frac{(\log N)^{s-2}}{N}\bigg ) \end{aligned}$$

with

$$\begin{aligned} c(\underline{b}_1,\ldots , \underline{b}_{s-1}) = \frac{1}{(s-1)!}\prod _{i=1}^{s-1} \frac{\lfloor M_i/2\rfloor }{\log m_i}, \end{aligned}$$

where $M_i=\max (b_{i,j})_{j=1}^\infty$ and $m_i=\min (b_{i,j})_{j=1}^\infty$ $(1\le i\le s).$

A point set $\mathcal {P}$ consisting of N points in $[0,1)^s$ is called a low-discrepancy point set if $D_N^*(\mathcal {P}) = O((\log N)^{s-1}/N).$ In this sense, the generalized Hammersley point set is a low-discrepancy point set.