Abstract
Let \( (H_s(n))_{n \geqslant 1} \) be an s-dimensional generalized Halton’s sequence. Let \(D^{*}_N\) be the discrepancy of the sequence \( (H_s(n) )_{n = 1}^{N} \). It is known that  as \(N \rightarrow \infty \). In this paper, we prove that this estimate is exact. Namely, there exists a constant \(C(H_s)>0\) such thats
as \(N \rightarrow \infty \). In this paper, we prove that this estimate is exact. Namely, there exists a constant \(C(H_s)>0\) such thats

Similar content being viewed by others
1 Introduction
Let \((\beta _{n})_{n \geqslant 1}\) be a sequence in the unit cube  ,
,  ,
,

where \(\mathbf{1}_{B_{\mathbf{y}}}(\mathbf{x}) =1\) if \(\mathbf{x}\in B_{\mathbf{y}}\), and \( \mathbf{1}_{B_{\mathbf{y}}}(\mathbf{x}) =0\) if \( \mathbf{x}\notin B_{\mathbf{y}}\).
We define the star discrepancy of an N-point set \((\beta _{n})_{n=1}^{N}\) as

In 1954, K. Roth proved that
According to the well-known conjecture (see, e.g., [1, p. 283]), this estimate can be improved to
In 1972, W. Schmidt proved this conjecture for \(s=1\). For \(s=2\), Faure and Chaix [4] proved (3) for a class of (t, s)-sequences. See [2] for the most important results on this conjecture.
There exists another conjecture on the lower bound for the discrepancy function: there exists a constant \(\dot{c}_3>0 \) such that

for all N-point sets \((\beta _{k,N})_{k=0}^{N-1}\) (see [2, p. 147]).
Definition
An s-dimensional sequence \(((\beta _{n})_{n \geqslant 1})\) is of low discrepancy (abbreviated l.d.s.) if  for
for  .
.
Let \( p\geqslant 2 \) be an integer,

van der Corput proved that \( (\phi _p(n))_{n\geqslant 0}\) is a 1-dimensional l.d.s. (see [12]). Let
where \(\widehat{p}_1,\ldots ,\widehat{p}_s\geqslant 2\) are pairwise coprime integers. Halton proved that \( ( \widehat{H}_{s}(n))_{n\geqslant 0}\) is an s-dimensional l.d.s. (see [6]). For other examples of l.d.s. see, e.g., [1, 5, 11]. In [9], we proved that Halton’s sequence satisfies (3). In this paper we generalize this result.
Let \(Q=(q_1,q_2,\dots )\) and \(Q_j=q_1q_2\cdots q_j\), where \(q_j\geqslant 2\), \(j=1,2,\dots \), is a sequence of integers. Consider Cantor’s expansion of  :
:

The Q-adic representation of x is then unique. We define the odometer transform as

\(n=2,3,\dots \), \(T_Q^0(x)=x\), where  .
.
For \(Q=(q,q,\dots )\), we obtain von Neumann–Kakutani’s q-adic adding machine (see, e.g., [5]). As is known, the sequence \((T_{Q}^n(x))_{n\ge 1}\) coincides for \(x=0\) with the van der Corput sequence (see, e.g., [5, Section 2.5]).
Let \(q_0 \geqslant 4\), \(p_{i,j} \geqslant 2\), \(s\geqslant i\geqslant 1\), \(j\geqslant 1\), be integers, \(\mathrm{g.c.d.}(p_{i,k},p_{j,l})=1\) for \(i\ne j\), \(\mathscr {P}_i = (p_{i,1},p_{i,2},\dots )\), \(\varvec{\mathscr {P}}=(\mathscr {P}_1,\dots ,\mathscr {P}_s)\), \(T_{\varvec{\mathscr {P}}}(\mathbf{x}) = (T_{\mathscr {P}_1}(x_1),\dots ,T_{\mathscr {P}_s}(x_s))\),

We note that \(H_{\varvec{\mathscr {P}}}(n) =T^n_{\varvec{\mathscr {P}}}(\mathbf{0})\) for \(n=0,1,\dots \)
Let  be a sequence of corresponding permutations \(\sigma _{i,j}\) of
be a sequence of corresponding permutations \(\sigma _{i,j}\) of  for \(j \geqslant 1\), \(\varvec{\mathrm{\Sigma }}=(\mathrm{\Sigma }_1,\dots ,\mathrm{\Sigma }_s)\), \(\mathbf{x}=(x_1,\dots ,x_s)\),
for \(j \geqslant 1\), \(\varvec{\mathrm{\Sigma }}=(\mathrm{\Sigma }_1,\dots ,\mathrm{\Sigma }_s)\), \(\mathbf{x}=(x_1,\dots ,x_s)\),

We consider the following generalization of Halton’s sequence (see [3, 5, 7]):
We note that \((H_{\varvec{\mathscr {P}}}^{\varvec{\mathrm{\Sigma }}}(n,\mathbf{x}))_{n \geqslant 0} \) coincides for \(\mathbf{x}=\mathbf{0}\) and \(s=1\) with the Faure sequence \(S_Q^{\mathrm{\Sigma }}\) [3]. Similarly to [11, pp. 29–31], we get that \( (H_{\varvec{\mathscr {P}}}^{\varvec{\mathrm{\Sigma }}}(n,\mathbf{x}))_{n \geqslant 0}\) is of low discrepancy.
2 Theorem and its proof
In this section we will prove
Theorem
Let \(s \geqslant 2\), \(C_1=s q_0^{s+1} \log _2 q_0\),  and
and  . Then
. Then

This result supports conjecture (3) (see also [8, 10]).
The proof of Theorem is similar to the proof of [9, Theorem]. The main part of the proof in [9] and in this paper is the construction of the bounded vector \((y_1,\dots ,y_s)\) and the application of the Chinese Remainder Theorem. In the paper [9], we take \(y_i = \sum _{j=1}^m p_i^{-\tau _{i,j}}\), \( i=1,\dots ,s\), where

In this paper we take  , with some special sequences \((\tau _{i,j})_{1 \leqslant i \leqslant s, j \geqslant 1}\). In order to obtain the ‘periodic’ properties similar to (8), we need a more complicated construction of \((\tau _{i,j})_{s \geqslant i \geqslant 1, j \geqslant 1}\):
, with some special sequences \((\tau _{i,j})_{1 \leqslant i \leqslant s, j \geqslant 1}\). In order to obtain the ‘periodic’ properties similar to (8), we need a more complicated construction of \((\tau _{i,j})_{s \geqslant i \geqslant 1, j \geqslant 1}\):
-
\( p_{i,\tau _{i,j}}=p_{i,\tau _{i,1}}\), \(j=1,2,\dots \),
-
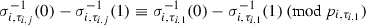 , \(j=1,2,\dots \),
, \(j=1,2,\dots \), -
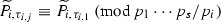 , \(j=1,2,\dots \),
, \(j=1,2,\dots \),
in such a way that the sets  would receive the greatest length, where
would receive the greatest length, where  , \(s \geqslant i \geqslant 1\). We need all these conditions to prove statement (26).
, \(s \geqslant i \geqslant 1\). We need all these conditions to prove statement (26).
In order to construct \((\tau _{i,j})_{1 \leqslant i \leqslant s, j \geqslant 1}\), we define auxiliary sequences \(\mathscr {L}_{i,j}^{(\mathfrak m)}\!, L^{(\mathfrak m)}_i \!\), \(l_{i,j}, \mathscr {F}_{i,b}^{(\mathfrak m)}\!,\dots \)
2.1 Construction of the sequence \((\tau _{i,j})\)
Let  ,
,  . By (5), we get
. By (5), we get

Hence

Let \(a_{i,j} \equiv \sigma ^{-1}_{i,j}(0) - \sigma ^{-1}_{i,j}(1) \, (\mathrm{mod}\, p_{i,j})\),  ,
,  ,
,

It is easy to see that there exist  and
and  such that
such that

We enumerate the set \(\mathscr {L}_{i,g_{i,\mathfrak m}, \mathfrak a_{i}}^{(\mathfrak m)}\):

For  we have
we have

Let  ,
,  , \(\dot{p}_i =p_0/p_i \leqslant q_0^{s-1}\) and
, \(\dot{p}_i =p_0/p_i \leqslant q_0^{s-1}\) and

We define \( F_i, m\) and \(b_i=b_i^{(\mathfrak m)}\) as follows:

We enumerate the set \(F_{i,b_i}^{(\mathfrak m)}\):

Bearing in mind that  and \(C_1=s q_0^{s+1} \log _2 q_0\), we have
and \(C_1=s q_0^{s+1} \log _2 q_0\), we have

Let \(\mathbf{k}=(k_1,\dots ,k_s)\), \(\tau _{i, j} =l_{i,f_{i,j}}\), \(\varvec{\tau }_{\mathbf{k}} =(\tau _{1, k_1},\dots , \tau _{s, k_s})\), \(P_{i,k} = \widetilde{P}_{i,\tau _{i,k}}\),

Applying (10), we get \(\tau _{i,m} = l_{i,f_{i,m}} \leqslant l_{i,F^{(\mathfrak m)}_i} \leqslant l_{i,L^{(\mathfrak m)}_i} \leqslant \mathfrak m\). Let \(\mathbf{m}=(m,\dots ,m)\). From (5) and (14), we derive

We will need the following properties of integers \(\mathfrak a_{i}\), \(1 \leqslant i \leqslant s\), (see (16), (17)): By (11), we have that \((b_i,\dot{p}_i) =1\) and \((b_j,p_i) =1\) for \(i\ne j \), \(i,j=1,\dots ,s\). Let \( c_i \equiv \prod _{1 \leqslant j \leqslant s,j \ne i} b_j \, (\mathrm{mod} \, p_i)\). According to (10), (11) and (14), we obtain

Let

 . Hence
. Hence
2.2 Using the Chinese Remainder Theorem
Let  , with
, with  , \(i=1,\dots ,s\). We define the truncation
, \(i=1,\dots ,s\). We define the truncation

If  , then the truncation
, then the truncation  is defined coordinatewise, that is,
is defined coordinatewise, that is,  , where \(\mathbf{r}=(r_1,\dots ,r_s)\).
, where \(\mathbf{r}=(r_1,\dots ,r_s)\).
By (6), we have

Applying (14) and the Chinese Remainder Theorem, we get

Now we will find the relation between \(T_{\varvec{\mathscr {P}}}^n(\mathbf{x})\) and \(H_{\varvec{\mathscr {P}}}(n)\) (see (20). It is easy to verify that if \(r_i' \geqslant r_i\), \(i=1,\dots ,s\), then  . According to (4), we get
. According to (4), we get

From (4), (6) and (18), we obtain

Hence

Let  . Therefore
. Therefore

2.3 Construction of boundary points \(y_1,\dots ,y_s\) and \(u_1,\dots ,u_s\)
Let \(\mathbf{y}=(y_1,\dots ,y_s)\) with  , and let
, and let  , \(k_i \geqslant 1\), \(i=1,\dots ,s\), \(\mathbf{k}=(k_1,\dots ,k_s)\),
, \(k_i \geqslant 1\), \(i=1,\dots ,s\), \(\mathbf{k}=(k_1,\dots ,k_s)\),

We deduce

Consider the following condition:
In order to express this condition in terms of the sequence \((H_{\varvec{\mathscr {P}}}(n))_{n \geqslant 1}\), we will construct boundary points \(u_1,\dots ,u_s\). Next we will construct auxiliary sequences \(\mathbf{u}^{(\mathbf{k})}\!,\check{u}^{(\mathbf{k})}\!,A_{\mathbf{k}},\dots \) Applying (18), we will get in (26) the solution of (23).
Let \(\mathbf{u}=(u_1,\dots ,u_s)\), \(u_i =\sum _{j \geqslant 1}^{\tau _{i,m}} u_{i,j}\widetilde{P}_{i,j}^{-1}\) with \(u_{i,j} =\sigma _{i,j}^{-1}(y_{i,j}) \), \(u_{i,j}^{*} =\sigma _{i,j}^{-1}(0)\),

According to (9)–(14), we have \( p_{i, \tau _{i,k_i}}= p_i\), \(k_i=1,\dots ,m\), \(i=1,\dots ,s\). By (9), we get  .
.
From (16), we obtain  , \(k_i=1,\dots ,m\), \(i=1,\dots ,s\). Hence
, \(k_i=1,\dots ,m\), \(i=1,\dots ,s\). Hence

with  .
.
Let \(\mathbf{w}=(w_1,\dots ,w_s)= H_{\varvec{\mathscr {P}}}^{\varvec{\mathrm{\Sigma }}}(n,\mathbf{x})=\widetilde{\varvec{\mathrm{\Sigma }}}(T_{\varvec{\mathscr {P}}}^n(\mathbf{x}))\). We see from (21) and (24) that

Applying (18), (19), (20), (24) and (25), we have

where \(v_m \equiv -W_{\mathbf{m}}(\mathbf{x}) + \check{\mathbf{u}}_{\mathbf{m}} \equiv -W_{\mathbf{m}}(\mathbf{x}) + \check{\mathbf{u}}_{\mathbf{k}} \, (\mathrm{mod} \, P_{\mathbf{k}})\) and  .
.
Hence

2.4 Completion of the proof of Theorem
Bearing in mind that

we get that it is sufficient to find the lower bound of the main value of discrepancy function to prove Theorem.
Lemma 1
Let

Then

Proof
Let \(\mathscr {H}_n =H_{\varvec{\mathscr {P}}}^{\varvec{\mathrm{\Sigma }}}(n,\mathbf{x})\). Using (26), we have

and

with \(M_1 \geqslant 0\) and  , \(M_1,M_2 \in \mathbb Z\). From (1) and (22), we get
, \(M_1,M_2 \in \mathbb Z\). From (1) and (22), we get

By (27), we obtain

Bearing in mind (29)–(30), we derive

Using (31), we have

\(\square \)
Lemma 2
With notations as above,
Proof

Applying (17) and (28), we derive

\(( d_i, \widehat{p}_i)=1\), \(\widehat{p}_i >1\), \(i=1,\dots ,s\), and  is the fractional part of x. We have that if \(\widehat{p}_0 =\widehat{p}_1\widehat{p}_2\cdots \widehat{p}_s \not \equiv 0 \, (\mathrm{mod} \, 2)\) then \( \alpha \not \equiv 1/2 \, (\mathrm{mod} \, 1)\). Let \(\widehat{p}_{\nu } \equiv 0 \, (\mathrm{mod} \, 2)\) for some
is the fractional part of x. We have that if \(\widehat{p}_0 =\widehat{p}_1\widehat{p}_2\cdots \widehat{p}_s \not \equiv 0 \, (\mathrm{mod} \, 2)\) then \( \alpha \not \equiv 1/2 \, (\mathrm{mod} \, 1)\). Let \(\widehat{p}_{\nu } \equiv 0 \, (\mathrm{mod} \, 2)\) for some  , and let \( \alpha \equiv 1/2 \, (\mathrm{mod} \, 1)\). Then
, and let \( \alpha \equiv 1/2 \, (\mathrm{mod} \, 1)\). Then

with \( a_1 = \widehat{p}_0(\widehat{p}_{\nu }/2-d_{\nu })/\widehat{p}_{\nu } \) and \(a_2 = \sum _{i \ne \nu }\widehat{p}_0d_i/\widehat{p}_i \). Let  and \(j \ne \nu \). We see that \(a_1 \equiv 0 \, (\mathrm{mod} \,\widehat{p}_j)\) and \(a_2 \not \equiv 0 \, (\mathrm{mod} \, \widehat{p}_j)\). We get a contradiction. Hence \( \alpha \not \equiv 1/2 \, (\mathrm{mod} \, 1)\). We have
and \(j \ne \nu \). We see that \(a_1 \equiv 0 \, (\mathrm{mod} \,\widehat{p}_j)\) and \(a_2 \not \equiv 0 \, (\mathrm{mod} \, \widehat{p}_j)\). We get a contradiction. Hence \( \alpha \not \equiv 1/2 \, (\mathrm{mod} \, 1)\). We have

Thus  with \(p_0=p_1\cdots p_s\), \((p_0,\widehat{p}_0)=\widehat{p}_0\).
with \(p_0=p_1\cdots p_s\), \((p_0,\widehat{p}_0)=\widehat{p}_0\).
Bearing in mind that \(P_{ \mathbf{k}} \geqslant 2^{k_1+k_2 + \cdots +k_s}\), we obtain from (32) that

This completes the proof. \(\square \)
Going back to the proof of Theorem, by (7) and (13), we get

where \(C_1=s q_0^{s+1} \log _2 q_0\),  and \(q_0^s \geqslant p_0\).
and \(q_0^s \geqslant p_0\).
Using (15) and (26), we have that \(v_m + P_{\varvec{\tau }m} \leqslant 2P_{\mathbf{m}} \leqslant N\). According to (33), (27) and (2), we obtain

Hence Theorem is proved.
References
Beck, J., Chen, W.W.L.: Irregularities of Distribution. Cambridge Tracts in Mathematics, vol. 89. Cambridge University Press, Cambridge (1987)
Bilyk, D.: On Roth’s orthogonal function method in discrepancy theory. Unif. Distrib. Theory 6(1), 143–184 (2011)
Faure, H.: Discrépances de suites associées à un système de numération (en dimension un). Bull. Soc. Math. France 109(2), 143–182 (1981)
Faure, H., Chaix, H.: Minoration de discrépance en dimension deux. Acta Arith. 76(2), 149–164 (1996)
Faure, H., Kritzer, P., Pillichshammer, F.: From van der Corput to modern constructions of sequences for quasi-Monte Carlo rules. Indag. Math. (N.S.) 26(5), 760–822 (2015)
Halton, J.H.: On the efficiency of certain quasi-random sequences of points in evaluating multi-dimensional integrals. Numer. Math. 2, 84–90 (1960)
Hellekalek, P.: Regularities in the distribution of special sequences. J. Number Theory 18(1), 41–55 (1984)
Levin, M.B.: On the lower bound in the lattice point remainder problem for a parallelepiped. Discrete Comput. Geom. 54(4), 826–870 (2015)
Levin, M.B.: On the lower bound of the discrepancy of Halton’s sequences: I. C. R. Math. Acad. Sci. Paris Sér. I Math. (to appear)
Levin, M.B.: On the lower bound of the discrepancy of \((t,s)\) sequences: II (2015). arXiv:1505.04975v2
Niederreiter, H.: Random Number Generation and Quasi-Monte Carlo Methods. CBMS-NSF Regional Conference Series in Applied Mathematics, vol. 63. Society for Industrial and Applied Mathematics (SIAM), Philadelphia (1992)
van der Corput, J.G.: Verteilungsfunktionen I-II. Proceedings. Akadamie van Wetenschappen Amsterdam 38, 813–821, 1058–1066 (1935)
Acknowledgments
The author is very grateful to the referee for corrections and suggestions which improved this paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Levin, M.B. On the lower bound of the discrepancy of Halton’s sequence II. European Journal of Mathematics 2, 874–885 (2016). https://doi.org/10.1007/s40879-016-0103-7
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-016-0103-7



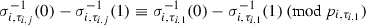 ,
, 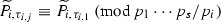 ,
,