Speeding-up one-versus-all training for extreme classification via mean-separating initialization

Abstract

In this paper, we show that a simple, data dependent way of setting the initial vector can be used to substantially speed up the training of linear one-versus-all classifiers in extreme multi-label classification (XMC). We discuss the problem of choosing the initial weights from the perspective of three goals. We want to start in a region of weight space (a) with low loss value, (b) that is favourable for second-order optimization, and (c) where the conjugate-gradient (CG) calculations can be performed quickly. For margin losses, such an initialization is achieved by selecting the initial vector such that it separates the mean of all positive (relevant for a label) instances from the mean of all negatives – two quantities that can be calculated quickly for the highly imbalanced binary problems occurring in XMC. We demonstrate a training speedup of up to $5\times$ on Amazon-670K dataset with 670,000 labels. This comes in part from the reduced number of iterations that need to be performed due to starting closer to the solution, and in part from an implicit negative-mining effect that allows to ignore easy negatives in the CG step. Because of the convex nature of the optimization problem, the speedup is achieved without any degradation in classification accuracy. The implementation can be found at https://github.com/xmc-aalto/dismecpp.

1 Introduction

Extreme classification: In this work we consider extreme multi-label classification (XMC) problems, where the number of labels $l$ is very large, possibly in the millions. Such problems arise in various domains, such as annotating large encyclopedia (Partalas et al., 2015), image-classification (Deng et al., 2010), next word prediction (Mikolov et al., 2013; Mnih et al., 2009), as well as recommendation systems, web-advertising and prediction of related searches (Agrawal et al., 2013; Prabhu & Manik, 2014; Jain et al., 2019).

We assume that the fraction of positive training instances for most labels is very low – the label frequency has a long-tailed distribution (Dekel et al., 2010). This is a good approximation for the large dataset from the extreme classification repository (Bhatia et al., 2016) (cf. Fig. 1 in Qaraei et al. (2021), Babbar & Schölkopf (2017), and Partalas et al. (2015) for some examples), and for many types of data that are gathered at internet-scale (Adamic et al., 2002).

One-versus-all classifiers: Many XMC methods employ some form of a One-versus-all (OvA) classifier as the last stage of the classification procedure: For each label $j \in [l]$, a score is calculated as ${{\textbf {w}}}_j^\mathsf {T}f({{\textbf {x}}})$, and the k highest-scoring labels are selected as the prediction of the classifier,

$$\begin{aligned} \hat{y} = \text {top}_k \{ {{\textbf {w}}}_j^\mathsf {T}f({{\textbf {x}}}) : j \in [l] \}, \end{aligned}$$

(1)

where ${{\textbf {w}}}_j$ is the weight vector for label j and f is a fixed function of the instance. The training objective is to minimize, with some additional regularization terms, a binary margin loss $\phi$ for each label j,

$$\begin{aligned} \phi ( y_j {{\textbf {w}}}_j^\mathsf {T}f({{\textbf {x}}})), \end{aligned}$$

(2)

where $y_j \in \{-1, 1\}$ indicates whether the label is relevant to the instance.

Algorithms that follow this general structure are DiSMEC (Babbar & Schölkopf, 2017) and ProXML (Babbar & Schölkopf, 2019) for sparse representations f, and Slice (Jain et al., 2019) where f is some pre-trained mapping of instances to dense vectors. Other examples are Parabel (Prabhu et al., 2018), Bonsai (Khandagale et al., 2020) and PPDSparse (Yen et al., 2017). Embedding-based approaches where the mapping f itself is learnt, such as XML-CNN (Liu et al., 2017) and AttentionXML (You et al., 2019) are incompatible with the method presented in this paper. In some cases the training is organized in two phases, first the deep network f is trained and then frozen, after which the OVA classifier can be trained. This approach is taken e.g. by X-Transformer (Chang et al., 2020) and its successor XR-Transformer (Zhang et al., 2021).

Despite the substantial contemporary research effort on designing deep classifiers in the XMC setting, efficient learning of sparse One-versus-rest linear classifiers remains useful. This is attributed to their: (i) easier interpretability for explaining the model outputs in terms of input features, (ii) comparable, and at times better performance, compared to deeper methods in short-text XMC problems (DiSMEC vs AttentionXML in Table 1 of Dahiya et al. (2021)), and (iii) complementary learning capabilities using sparse features vis-à-vis dense representation using deep transformer models, as shown in the recent work XR-Transformer (Zhang et al., 2021).

Fast training: Minimizing the objective in eq. (2) using a gradient-based iterative algorithm is very computation-intensive. To reduce compute requirements – and thus energy consumption – we can make use of three generic principles:

• 1. Try to achieve more progress per step, e.g. by using a second-order method (Babbar & Schölkopf, 2017; Keerthi et al., 2005; Galli et al., 2021) or an adaptive step size. (Duchi et al., 2011; Ruder, 2017)

• 2. Make the computations of each step faster, e.g. by approximating the true loss with negative mining. (Jain et al., 2019; Dahiya et al., 2021; Prabhu et al., 2018; Yen et al., 2017; Reddi et al., 2019).

• 3. Reducing the number of necessary steps by taking a good guess for the initial weight vector in the iterative optimization process. (Fang et al., 2019; Keerthi et al., 2005).

In this work, we focus on the second-order optimization approach using a truncated conjugate-gradient (CG) Newton optimization, as it is used in recent versions of Liblinear (Galli et al., 2021).¹

Implicit negative-mining with hinge-like losses: To a degree, faster per-step calculations are achieved implicitly when using a loss function that is zero for points classified correctly with sufficient margin. Such a training point makes no contribution to the gradient or Hessian, and thus can be skipped in the computations. This can be seen as a form of implicit negative-mining, where the list of negatives is updated each iteration (similar to Yen et al. (2017)) based on the values of $y_i {{\textbf {w}}}^\mathsf {T}f({{\textbf {x}}}_i)$. Unlike explicit negative-mining, this process is not an approximation. However, it does not enforce sparsity, but only exploits its existence. Fortunately, close to convergence, when most instances are correctly classified, this leads to very sparse computations for the CG procedure. Thus, one aim in choosing the initial weights is to get into this fast regime as quickly as possible.

Choice of initial vector: The third idea, choosing a suitable starting weight, is used in Liblinear to speed up hyperparameter sweeps. It is assumed that the solutions for two similar hyperparameter values are closely related, and as such the final weight vector of one training run can be used to warm-start the next. The feasibility of this approach in cold-start XMC has been shown in Fang et al. (2019), which presented OvA-Primal (OvAP) and OvA-Primal++ (OvAP++) as two strategies for finding initial vectors that result in low initial loss. We provide a short summary of these methods at the end of Sect. 2.

Shortcomings of the existing work: OvAP, though simple and easy to implement, completely ignores the positive instances for each label. We will show that there is a computationally cheap method that allows taking them into account.

In contrast, OvAP++ makes use of the positives, but requires much more care to implement, as it breaks the embarrassingly parallel nature of the original OvA approach. Hence, the individual binary problems need to be solved in a certain (partial) order. This also precludes the application of this strategy to situations where all labels have to be trained simultaneously, e.g. when fine-tuning the feature representations f.

The existing analysis in Fang et al. (2019) focuses only on finding an initial weight vector that has loss as low as possible. Important properties of the loss function (such as local smoothness / Lipschitz constant) sometimes are more favourable after some training epochs than right at initialization time, as evidenced e.g. by the success of cyclical learning rates (Smith & Leslie, 2017) and warmup phases (Goyal et al., 2018). However, the impact of these properties is not considered in Fang et al. (2019).

Contributions: Our contributions in this work are:

• 1. We explicate via extensive empirical evaluation that, when employed in conjunction with the squared-hinge loss, the benefit of initialization methods is not limited to just starting closer to the final weight vector. Good initialization also leads to much faster computations in each training step, because of an implicit negative-mining effect.

• 2. We present a novel initialization strategy that is computationally efficient, keeps the simplicity of OvAP, but incorporates information about the positive instances for each label to find even better initial weights. This is achieved by selecting the initial vector such that it separates the mean of all positive instances from the mean of all negatives.

• 3. We show experimentally that this leads to a speedup of up to $5\times$ relative to Zero-initialization for our code-base on the Amazon-670K dataset, and demonstrate that this enables training of DiSMEC-style models with up to 3 million labels on a single 128-core node in a reasonable amount of time.

• 4. We provide a new implementation of DiSMEC that can adapt to the NUMA characteristics of modern many-core processors. Combined with the new choice of the initial vector, this can lead to a speedup of up to 14$\times$ in wallclock time.

Outline: In Sect. 2, we formally introduce our learning setting and recap the key concept of optimization using conjugate-gradients. This is followed by a presentation of the key results from Fang et al. (2019), the OvAP and OvAP++ initialization methods. In Sect. 3, we investigate which properties an initial weight vector needs to have to be beneficial for optimization. In particular, we show that low loss alone is not a sufficient criterion by providing a counter-example. We investigate why it fails, and thus highlight the importance of the local loss landscape and the implicit negative-mining effect. The description of our proposed method is given in Sect. 4, together with an evaluation of its effect on the local loss landscape and implicit negative-mining. In Sect. 5, an extensive empirical evaluation of the new initialization method with a variety of datasets and settings is presented. Finally, Sect. 6 discusses the limitations of our approach and given an outlook on how it could be applied more broadly in XMC.

2 Background

Setup: We are given a dataset $\mathcal {D} = \{({{\textbf {x}}}_i,{{\textbf {y}}}_i): i \in [n]\}$ with $n$ training instances ${{\textbf {x}}}_i \in \mathcal {X}= \mathbb {R}^d$ and their corresponding labels ${{\textbf {y}}}_i \in \mathcal {Y}= \{-1, 1\}^l$. For a label $j \in [l]$ we denote with $\mathsf {P}(j) {:}{=}\{{{\textbf {x}}}_i:y_{i}^{(j)} = 1\}$ the set of instances for which the label is relevant, and analogously $\mathsf {N}(j) {:}{=}\mathsf {X}\setminus \mathsf {P}(j)$, where $\mathsf {X}{:}{=}\{{{\textbf {x}}}_i: i \in [n]\}$ is the set of all training instances. This corresponds to a label vector ${{\textbf {y}}}^{(j)}$ which has entries 1 for each positive instance, $y^{(j)}_i = 1 \Leftrightarrow i \in \mathsf {P}(j)$, and $-1$ otherwise.

In the linear OVA setting, we have to solve $l$ independent problems of size $O(n)$. We assume that the number of labels $l$ is large enough so that an additional $O(n)$ computation does not significantly influence the overall training time. In particular, the initialization method that will be presented in Sect. 4 requires calculating the mean of all instances, $\bar{{{\textbf {x}}}}= \sum _{i=1}^{n} {{\textbf {x}}}_i$, which is a cheap operation compared to solving the $l$ subproblems. In addition, we assume that the labels are sparse, in the sense that for most $j \in [l]$ we have $|\mathsf {P}(j)| \ll |\mathsf {N}(j)|$. These two assumptions are part of the characterization of an XMC problem.

The goal in linear XMC is to find a weight vector ${{\textbf {w}}}_j^*$ for each label $j \in [l]$ that minimizes the risk of the corresponding binary problem with some convex margin loss $\phi$, combined with a regularizer $\mathcal {R}$:

$$\begin{aligned} \mathcal {L} \left[ {{\textbf {w}}}, {{\textbf {y}}}^{(j)} \right]&{:}{=}\sum _{i=1}^{n} \phi \left( y^{(j)}_{i}{{\textbf {w}}}^\mathsf {T}{{\textbf {x}}}_i \right) + \mathcal {R}[{{\textbf {w}}}] \end{aligned}$$

(3)

$$\begin{aligned} {{\textbf {w}}}^*_j {:}{=}{{\textbf {w}}}^* \left( \mathsf {X}, {{\textbf {y}}}^{(j)}\right)&{:}{=}\mathop {{\mathrm {argmin}}}\limits _{{{\textbf {w}}}} \mathcal {L}\left[ {{\textbf {w}}}, {{\textbf {y}}}^{(j)}\right] . \end{aligned}$$

(4)

Throughout this paper, we use the $L_2$-norm $\mathcal {R}[{{\textbf {w}}}] = 0.5\Vert {{\textbf {w}}}\Vert _2^2$ as the regularizer. From hereon, we will focus on the independent binary sub-problems, and consequently drop the superscript ${{\textbf {y}}}^{(j)}$ and write ${{\textbf {y}}}\in \{-1, 1\}^{n}$ for the vector indicating the relevance of instances for a given label. Following Jain et al. (2019), Babbar & Schölkopf (2017, 2019), as the margin loss $\phi$ we use the squared hinge-loss

$$\begin{aligned} \phi (m) = \max (0, 1 - m)^2. \end{aligned}$$

(5)

Even though this function’s second derivative does not exist at $m=1$, it can be used for second-order optimization (Galli et al., 2021).

Conjugate-gradient Newton optimization: The minimization of eq. (3) is carried out using a CG Newton procedure inspired by Liblinear (Fan et al., 2008; Galli et al., 2021). The algorithm works as follows: First, a descent direction ${{\textbf {p}}}$ is determined by minimizing a local quadratic approximation $\hat{\mathcal {L}}$ to the loss function

$$\begin{aligned} \hat{\mathcal {L}}({{\textbf {w}}}+ \varvec{\delta }) = \mathcal {L}({{\textbf {w}}}) + \nabla \mathcal {L} \cdot \varvec{\delta } + \frac{1}{2} \varvec{\delta }^\mathsf {T}\mathsf {H}_{\mathcal {L}} \varvec{\delta }, \end{aligned}$$

(6)

where $\mathsf {H}$ denotes the Hessian of $\mathcal {L}$. The stationarity condition for a local minimum,

$$\begin{aligned} 0 = \nabla \mathcal {L} + \mathsf {H}_{\mathcal {L}} \varvec{\delta }^*, \end{aligned}$$

(7)

shows that the optimal change $\varvec{\delta }^*$ of weights – in quadratic approximation – can be found by solving a system of linear equations. The conjugate-gradient algorithm provides a way of solving the equations without ever requiring an explicit representation of the matrix $\mathsf {H}_{\mathcal {L}}$. Instead, only Hessian-vector products are needed, which can be calculated for a pointwise regularization $\mathcal {R}[{{\textbf {w}}}] = \sum _{j=1}^m \rho (w_j)$ as (Keerthi et al., 2005)

$$\begin{aligned} \mathsf {H} {{\textbf {d}}}&= \left( \sum _{i=1}^{n} \nabla ^2_{{{\textbf {w}}}} \phi (y_{i}{{\textbf {w}}}^\mathsf {T}{{\textbf {x}}}_i) + \sum _{j=1}^m \nabla ^2_{{{\textbf {w}}}} \rho (w_j) \right) {{\textbf {d}}} \end{aligned}$$

(8)

$$\begin{aligned}&= \left( \sum _{i=1}^{n} y_i {{\textbf {x}}}_i \nabla _{\!{{\textbf {w}}}} \phi ^{\prime }(y_{i}{{\textbf {w}}}^\mathsf {T}{{\textbf {x}}}_i) \right) {{\textbf {d}}} + \mathrm {diag}(\rho ^{\prime \prime }({{\textbf {w}}})) {{\textbf {d}}} \end{aligned}$$

(9)

$$\begin{aligned}&= \left( \sum _{i=1}^{n} y_i^2 {{\textbf {x}}}_i {{\textbf {x}}}_i^\mathsf {T}\phi ^{\prime \prime }(y_{i}{{\textbf {w}}}^\mathsf {T}{{\textbf {x}}}_i) \right) {{\textbf {d}}} + \mathrm {diag}(\rho ^{\prime \prime }({{\textbf {w}}})) {{\textbf {d}}} \end{aligned}$$

(10)

$$\begin{aligned}&= \sum _{i=1}^{n} {{\textbf {x}}}_i \phi ^{\prime \prime }(y_{i}{{\textbf {w}}}^\mathsf {T}{{\textbf {x}}}_i) \langle {{\textbf {x}}}_i {{\textbf {d}}} \rangle + \mathrm {diag}(\rho ^{\prime \prime }({{\textbf {w}}})) {{\textbf {d}}} \end{aligned}$$

(11)

For the case of $L_2$ regularization, the second term simplifies to $\mathrm {diag}(\rho ^{\prime \prime }({{\textbf {w}}})) = \mathbbm {1}$. In practice, (7) need not be solved exactly, and the conjugate-gradient procedure can be terminated after a few iterations.

Once the quadratically optimal step ${{\textbf {p}}}$ has been found, a line-search using a backtracking approach is carried out over ${{\textbf {w}}}+ \lambda {{\textbf {p}}}$, $\lambda \in (0, 1]$. This ensures that the loss at the new weight vector is actually an improvement, $\mathcal {L}[{{\textbf {w}}}+ \lambda ^* {{\textbf {p}}}] < \mathcal {L}[{{\textbf {w}}}]$, even if the quadratic approximation deviates from the true loss. If the new point fulfills the stopping criterion as discussed below, the optimization terminates. Otherwise a new quadratic approximation around ${{\textbf {w}}}+ \lambda ^*{{\textbf {p}}}$ is formed and the next update step is calculated.

Stopping criterion: Whether or not the optimization is stopped depends on the magnitude of the gradient. We use the criterion given by Liblinear:

$$\begin{aligned} \Vert \nabla \mathcal {L}[{{\textbf {w}}}^*]\Vert \le \epsilon \Vert \nabla \mathcal {L}[{{\textbf {0}}}]\Vert . \end{aligned}$$

(12)

The scaling factor $\epsilon$ depends on the imbalance in the data and is calculated through

$$\begin{aligned} \epsilon = \epsilon _0 \cdot \frac{\mathrm {max}(1, \mathrm {min}(|\mathsf {P}|, |\mathsf {N}|))}{n}. \end{aligned}$$

(13)

This means that the convergence criterion gets stricter the more imbalanced the training data, which ensures that simply predicting the majority class for all instances is not accepted as a solution. Unless otherwise noted, we use $\epsilon _0=0.01$, the default value of Liblinear.

OvA-primal and OvA-primal++: In order to reduce the number of iterations needed to achieve the stopping criterion, Fang et al. (2019) propose two schemes for selecting the initial weights ${{\textbf {w}}}_0$, based on the following observation: For $\alpha$-Lipschitz loss functions and bounded weights $\Vert {{\textbf {w}}}\Vert _2 < B$, the optimal weight vector ${{\textbf {w}}}^*({{\textbf {y}}})$ for one label vector ${{\textbf {y}}}$ results in good performance also for a different label vector ${{\textbf {y}}}^\prime$ if the two label vectors are close in Hamming distance $\ell _{\text {H}}$:

$$\begin{aligned} \mathcal {L}[{{\textbf {w}}}^*({{\textbf {y}}}), {{\textbf {y}}}^\prime ] - \mathcal {L}[{{\textbf {w}}}^*({{\textbf {y}}}^\prime ), {{\textbf {y}}}^\prime ] \le \text {const} \cdot \ell _{\text {H}}({{\textbf {y}}}, {{\textbf {y}}}^\prime ). \end{aligned}$$

(14)

Given that for tail labels it holds that $\ell _{\text {H}}({{\textbf {y}}}, {\textbf {-1}}_n) \ll n$, they conclude that using ${{\textbf {w}}}^*(-{{\textbf {1}}}_n)$ makes the initial vector result in much lower loss than using Zero-initialized weights. Formally, the goal is to find the optimal weight for all-negative labels by solving

$$\begin{aligned} {{\textbf {w}}}^*(-{{\textbf {1}}}_n) = \mathop {{\mathrm {argmin}}}\limits _{{{\textbf {w}}}} \sum _{i=1}^{n} \phi \left( -{{\textbf {w}}}^\mathsf {T}{{\textbf {x}}}_i \right) + \mathcal {R}[{{\textbf {w}}}]. \end{aligned}$$

(15)

This strategy is called OvA-Primal (OvAP). As discussed above, the number of labels $l$ is assumed to be large enough that this one additional training run will not take a significant portion of the overall training time.

Then, based on convergence rates of iterative minimizers, they estimate the speedup that OvA-Primal, given by ${{\textbf {w}}}_0={{\textbf {w}}}^*(-{{\textbf {1}}}_n)$, provides over ${{\textbf {w}}}_0={{\textbf {0}}}_d$. For an optimization algorithm that has linear convergence, i.e. that needs

$$\begin{aligned} O\left( \log \frac{\mathcal {L}[{{\textbf {w}}}_0, {{\textbf {y}}}] - \mathcal {L}[{{\textbf {w}}}^*({{\textbf {y}}}), {{\textbf {y}}}]}{\epsilon } \right) \end{aligned}$$

(16)

steps for training to precision $\epsilon$, the speedup in the asymptotic bound is $\log n$ (Fang et al., 2019,Thm.3.2) if the average number of samples per label does not scale with $n$ or $l$.

OvA-Primal++ (OvAP++) extends the idea of OvAP by additionally re-using the final weight vectors ${{\textbf {w}}}_j^*$ of one label j as the initial weights for similar labels $j^\prime$. To achieve this, they first build a minimum spanning tree over the labels, including the virtual all-negative label as the root, where the cost of an edge is given by the Hamming distance between the label vectors. Starting from the root, one can initialize the descendants of a label by the final weights of that label. Due to the low Hamming-distance, this should provide a good starting point. This process is implemented as a blocked depth-first search over the tree as a compromise between parallelism and memory requirements. OvAP++ provides further speedups over OvAP, but at the cost of significantly increased implementation complexity. In particular, the sub-problems can no longer be solved independently from each other.

3 Analysis of criteria for initial weights

In this section, we investigate which properties an initial weight vector needs to fulfill in order to improve the training speed. The first criterion – to start with a low loss value, and correspondingly closer to the optimal weight vector – has been used to motivate the OvA-Primal method described above. Here, we show that low initial loss alone is not a sufficient criterion for successful initial weights. In particular, we present a counterexample, in which the weight vector leads to very low initial loss, orders of magnitude smaller than initializing by zero, yet does not provide any significant speed-up. We identify two reasons for this: First, the loss landscape around the initial vector needs to be favourable for second-order optimization. Second, a significant part of the speed-up is in fact not due to the reduced distance to the optimal vector and correspondingly smaller number of iterations, but is instead caused by faster computations in each iteration, owing to an implicit negative-mining effect.

To illustrate these phenomena, we take the AmazonCat-13K dataset (details in the appendix) from the extreme classification repository (Bhatia et al., 2016; McAuley & Jure, 2013) as a running example in this section and the next.

Fig. 1

Objective value at different iterations for starting with Zero vector, OvAP and with Bias-initialization ${{\textbf {w}}}_{b}$. The right side shows the progress for different values of the bias weight. The shaded area spans the 5–95% quantiles. Note that the slight increase in objective for the later iterations is just an artifact due to the fact that we plot the loss values averaged for the binary sub-problems that have not yet terminated at the given iteration. The sub-problems with low loss value terminate earlier, causing an increase in average of the remaining trajectories. Figure 12 shows the number of iterations until convergence for the different bias values

Insufficiency of low loss: A simple way to calculate an approximation to ${{\textbf {w}}}^*(-{{\textbf {1}}}_{n})$, the optimal weight-vector that predicts the absence of the label for every instance, is to use a weight vector ${{\textbf {w}}}_{\mathrm {b}} = (-1, 0,\ldots )^\mathsf {T}$, where we assume that the bias feature $x_0 = 1$ is at index 0.²

Then, the score for any instance ${{\textbf {x}}}$ will be $m = {{\textbf {w}}}_{\mathrm {b}}^\mathsf {T}{{\textbf {x}}}= -1$, which means that it is classified as negative with margin one. Therefore, this weight vector is a minimizer of the squared hinge-loss without regularization. As can be seen in Fig. 1 (left), the initial value of the loss is decreased by three orders of magnitude, to a lower value than with the OvAP initializer. Yet, after some iterations, the OvAP based optimization overtakes Bias. In particular, the Bias-initialized optimization does not make any substantial progress during the first iteration.

This does not contradict the previous result, because the asymptotic convergence rate based on the number of iterations does not need to agree with actual computation time, for example if each iteration provides more progress towards the minimum due to a benign loss landscape as described in the next paragraph, or if the computations for a single iteration become faster due to implicit negative-mining.

Importance of loss landscape: Certain regions in the weight space may be more benign towards the chosen minimization procedure than others. For example, in deep networks one often chooses an initialization procedure that preserves variance and mean over layers, to prevent vanishing or exploding gradients (Glorot et al., 2010). Such a technique does not provide any reduced loss for the starting point, but can be very effective in speeding up the training.

Fig. 2

Approximation errors $e(\delta ; m_0)$ for $m_0 = 0$ (solid blue) and $m_0=1$ (dashed red) over $\delta$, as described by eq. (17) (Color figure online)

For the concrete case of Newton optimization, this means that we require the local quadratic approximation to fit the true loss well. As $\phi$ is piecewise-quadratic, this is fulfilled only when m is far from the discontinuity at $m=1$. Let ${\hat{\phi }}_{m_0}$ be the quadratic approximation, then we can calculate the approximation error based on the step size as

$$\begin{aligned}&e(\delta ; m_0) {:}{=}{\hat{\phi }}_{m_0}(\delta ) - \phi (m_0 + \delta ), \end{aligned}$$

(17)

$$\begin{aligned} \text {where}&{\hat{\phi }}_{m_0}(\delta ) = \phi (m_0) + \delta \left. \phi ^{\prime } \right| _{m_0} + 0.5 \delta ^2 \left. \phi ^{\prime \prime } \right| _{m_0}. \end{aligned}$$

(18)

Two examples are shown in Fig. 2. For an instance right at the discontinuity, improving the classification margin to exceed one causes the quadratic approximation to over-estimate the true loss value, leading to smaller proposed update vectors ${{\textbf {p}}}$. On the other hand, for any instance classified with at least margin 1, the quadratic approximation cannot “see" the increased error as the margin shrinks, and may propose overly large steps ${{\textbf {p}}}$ that have to be shrunk using line search.

Fig. 3

Multiplier found by backtracking line search, i.e. the fraction of the descent direction as found by the CG solver that can be applied to the real objective function and still lead to sufficient reduction in loss. The shaded area indicates ± one standard deviation. Having a value smaller than one indicates that the quadratic approximation to the loss is overly optimistic in the given direction, and the real step has to be scaled down. As discussed in the main text (Fig. 2), this happens when the direction in question is such that it reduces the margin of an instance that is classified correctly with margin more than one. This effect can be seen here: For $\text {bias} = -0.9$, all the negative instances still have non-zero error, so the update will choose a direction that makes them more negative, which is a direction in which the quadratic approximation is overestimating the loss. On the other hand, with $\text {bias} = -1$, the only nonzero signal is coming from the positive instances, which will cause the bias to be reduced. Thus, most of the negative instances will get nonzero error, and the quadratic approximation severely underestimates the true loss. Consequently, the line search shows that only a minute step towards the desired direction is allowed. For $\text {bias} = -2$, the situation is similar, but this time the distance for each negative instance until it gets nonzero error is much larger, and as such the underestimation effect is reduced and larger step size multipliers are possible

By choosing $-1$ for the bias weight, the initial weights are exactly at the discontinuity of the Hessian. This suggests that it might be beneficial to use a different value for the bias, e.g. ${{\textbf {w}}}_0= 0.9{{\textbf {w}}}_{\mathrm {b}}$ or ${{\textbf {w}}}_0= 2 {{\textbf {w}}}_{\mathrm {b}}$. This intuition is confirmed by Fig. 1 (right), where we can see that both variations make significant progress in the first iteration, with $2{{\textbf {w}}}_{\mathrm {b}}$ clearly outperforming ${{\textbf {w}}}_{\mathrm {b}}$. A more detailed look at this phenomenon is provided by Fig. 3, which shows that the acceptable step size along the chosen descent direction is very small if ${{\textbf {w}}}_0$ is close to ${{\textbf {w}}}_{\mathrm {b}}$. This indicates that the quadratic approximation is overly optimistic, and proposes much larger steps than optimal. This happens very strongly in the first epoch of $\text {bias=-1}$, and to some degree during the first few epochs of $\text {bias}=-2$.

For the squared hinge-loss, a vector that minimizes eq. (15) perfectly will have similar characteristics to the Bias initialization ${{\textbf {w}}}_{b}$, in that for many instances the prediction will be close to the hinge location. Thus the starting point will be in a location unfavourable to the Newton optimizer. A remedy is to stop training of ${{\textbf {w}}}^*(-{{\textbf {1}}}_{n})$ early. This results in larger initial loss, but makes the training progresses more smoothly. More details on this phenomenon are presented in appendix 7.2.

Even though the local loss landscape can explain why the first Newton-optimization step makes so little progress, this alone is not sufficient to explain the vastly different training durations: For $2{{\textbf {w}}}_{\mathrm {b}}$, training takes only 558 seconds, much faster than ${{\textbf {w}}}_{\mathrm {b}}$ and $0.9{{\textbf {w}}}_{\mathrm {b}}$ at 1161 and 995 seconds. In addition to fewer iterations, the initialization method can also influence the amount of computation necessary during each iteration, through an implicit negative-mining step as discussed below.

Implicit negative-mining: As the weight vector ${{\textbf {w}}}$ approaches its optimum ${{\textbf {w}}}^*$, the calculations of Hessian-vector products become sparse, because only instances with non-zero loss need to be taken into account: For $m > 1$ we have $\phi (m) = \phi ^\prime (m) = \phi ^{\prime \prime }(m) = 0$, which implies that the sum over all data points in eq. (11) can be replaced with a sum over implicitly-mined hard instances

$$\begin{aligned} \mathcal {A} = \{i: \phi ^{\prime \prime } ({{\textbf {x}}}_i^\mathsf {T} {{\textbf {w}}} \cdot y_i) \ne 0\} = \{i: {{\textbf {x}}}_i^\mathsf {T} {{\textbf {w}}} \cdot y_i < 1\}. \end{aligned}$$

(19)

Therefore, the computations in eq. (11) can be written as

$$\begin{aligned} \mathsf {H} {{\textbf {d}}} = \sum _{i=1}^{n} {{\textbf {x}}}_i \phi ^{\prime \prime }(y_{i}{{\textbf {w}}}^\mathsf {T}{{\textbf {x}}}_i) \langle {{\textbf {x}}}_i {{\textbf {d}}} \rangle + {{\textbf {d}}} = \sum _{i \in \mathcal {A}} \phi ^{\prime \prime } ({{\textbf {x}}}_i^\mathsf {T} {{\textbf {w}}} \cdot y_i) y_i \langle {{\textbf {x}}}_i, {{\textbf {d}}} \rangle \cdot {{\textbf {x}}}_i + {{\textbf {d}}} , \end{aligned}$$

(20)

which can be computationally much more efficient than the full sum (Keerthi et al., 2005). The active set $\mathcal {A}$ has to be re-calculated after each weight update. Because each weight update requires multiple $\mathsf {H} {{\textbf {d}}}$ calculations for the conjugate-gradient procedure, this still results in a net speed-up.

Fig. 4

The average sparsity of Hessian-vector product computations, and corresponding duration of one iteration of the Newton optimization. The averages are taken over the individual binary problems, and the shaded area shows the $2\sigma$ error of the mean. The total computation time includes a (sparse) matrix multiplication and a varying number of CG steps. As this data shows, even though $\text {bias}=-1$ and $\text {bias}=-2$ start very sparse, much of the sparsity is lost during the first training steps. For the later iterations, $-2$ results in slightly less sparsity and slower iterations, however the effect on total running time is far overshadowed by the much faster earlier iterations (note the logarithmic axes). Furthermore, as indicated by Fig. 12, for $\text {bias}=-2$ fewer iterations are needed, so the timings of iterations after the tenth are less important

For different Bias-initializations $\lambda {{\textbf {w}}}_{\mathrm {b}}$, $\lambda \ge 1$, the active set at the first iteration is given by are all the negatives, $\mathcal {A} = \mathsf {N}$. However, for $\lambda =1$ the very first optimization step undoes the sparsity, so even though the first iteration is fast, it does not make progress towards the objective and makes the following iterations slow again, see Fig. 4. To a much lesser degree, this also happens for $\lambda =2$. For $\lambda < 1$, the initial weights are not at the discontinuity of the Hessian, but the quadratic approximation now overestimates the actual loss function. Further, there is no sparsity in the first iteration, causing it to be very slow.

The implicit negative-mining effect, even though not explicitly considered by Fang et al. (2019), still contributes to the speed-up of OvAP and OvAP++. The OvAP leads to significant sparsity in the first iteration, as Fig. 6 below will indicate.

Thus, our goal is to find a new initialization method that starts with a high sparsity, in such a way that the first optimization steps do not turn the Hessian computations dense again as is the case with Bias. Such an initialization procedure is presented in the next section.

4 Mean-separating initialization

Motivation: In this section, we derive a simple way to generate an initial vector, motivated by the following observation: If the data is linearly separable with margin, then the final weight vector will separate the convex hull of the negatives $\mathsf {N}$ from that of the positives $\mathsf {P}$, which in particular implies that it separates the centres of mass $\bar{{{\textbf {p}}}}$ of the positives and $\bar{{{\textbf {n}}}}$ of the negatives. This means that we can restrict the search space of weight vectors to those that separate $\bar{{{\textbf {p}}}}$ and $\bar{{{\textbf {n}}}}$. A sketch of this situation is given in Fig. 5.

Even though perfect separability might not be achieved on real data, it needs to hold at least approximately. Fortunately, the high-dimensional tf-idf³ text data that is commonly used in XMC fulfills this property, as evidenced by the high performance achievable with linear classifiers.

Derivation: Without making use of any additional information about the training data (as we want a computationally cheap procedure), there are only very general conditions we can impose to choose among these hyperplanes. As a first step, we can parameterize the search space based on the margins of $\bar{{{\textbf {p}}}}$ and $\bar{{{\textbf {n}}}}$, setting

$$\begin{aligned} \langle {{\textbf {w}}}_0, \bar{{{\textbf {p}}}}\rangle = s, \quad \langle {{\textbf {w}}}_0, \bar{{{\textbf {n}}}}\rangle = t, \end{aligned}$$

(21)

for two hyperparameters s and t.

These are only two linear constraints in the high dimensional weight space. However, for good generalization, we prefer weight vectors with minimal norm. If we want a minimum $L_2$-norm solution, then the search space becomes restricted to $\mathrm {span}(\bar{{{\textbf {p}}}}, \bar{{{\textbf {n}}}})$, and we can parameterize ${{\textbf {w}}}_0= u \bar{{{\textbf {p}}}}+ {\tilde{v}} \bar{{{\textbf {n}}}}$. This leads to a system of two linear equations in the two unknowns u and ${\tilde{v}}$, with a unique solution except in the unlikely event that $\bar{{{\textbf {p}}}}$ and $\bar{{{\textbf {n}}}}$ are linearly dependent.

Fig. 5

Motivation for the Average-of-Positives initialization. If the data is linearly separable, then the feature-means of the positives (blue) and the negatives (red) will lie on the correct side of the optimal separating hyperplane (black line). Thus we may restrict our search for the initial vector to the set of the separating planes of $\bar{{{\textbf {p}}}}$ and $\bar{{{\textbf {n}}}}$ (orange). In order to achieve strong implicit negative mining in the first epoch, we choose a solution where the center of mass of the negatives is classified correctly with a large margin (dashed orange lines), so that most of the negatives (light red) will be classified correctly with a margin over 1 and thus not enter the Hessian computation (Color figure online)

Reparameterization for efficiency: Since most labels have only few positive instances, their mean $\bar{{{\textbf {p}}}}$ can be calculated quickly, but calculating $\bar{{{\textbf {n}}}}$ directly would be an $O(n)$ operation for each label. However, we can precompute the mean of all instances $\bar{{{\textbf {x}}}}$, and use the property

$$\begin{aligned} |\mathsf {N}| \bar{{{\textbf {n}}}}+ |\mathsf {P}| \bar{{{\textbf {p}}}}= |\mathsf {X}| \bar{{{\textbf {x}}}}. \end{aligned}$$

(22)

Because $\mathrm {span}(\bar{{{\textbf {p}}}}, \bar{{{\textbf {n}}}}) = \mathrm {span}(\bar{{{\textbf {p}}}}, \bar{{{\textbf {x}}}})$, we can make the equivalent parameterization ${{\textbf {w}}}_0= u \bar{{{\textbf {p}}}}+ v \bar{{{\textbf {n}}}}$, leading to the equations

$$\begin{aligned} s = \langle {{\textbf {w}}}_0, \bar{{{\textbf {p}}}}\rangle&= \langle u \bar{{{\textbf {p}}}}+ v \bar{{{\textbf {x}}}}, \bar{{{\textbf {p}}}}\rangle = v \langle \bar{{{\textbf {x}}}}, \bar{{{\textbf {p}}}}\rangle + u \langle \bar{{{\textbf {p}}}}, \bar{{{\textbf {p}}}}\rangle \\ |\mathsf {N}| t = |\mathsf {N}| \langle {{\textbf {w}}}_0, \bar{{{\textbf {n}}}}\rangle&= \langle u \bar{{{\textbf {p}}}}+ v \bar{{{\textbf {x}}}}, |\mathsf {X}| \bar{{{\textbf {x}}}}- |\mathsf {P}| \bar{{{\textbf {p}}}}\rangle . \end{aligned}$$

This is solved by

$$\begin{aligned} u&= \frac{\langle \bar{{{\textbf {x}}}}, \bar{{{\textbf {p}}}}\rangle (t + (s - t) |\mathsf {P}| / |\mathsf {X}| ) - s \langle \bar{{{\textbf {x}}}}, \bar{{{\textbf {x}}}}\rangle }{\langle \bar{{{\textbf {p}}}}, \bar{{{\textbf {x}}}}\rangle ^2 - \langle \bar{{{\textbf {p}}}}, \bar{{{\textbf {p}}}}\rangle \langle \bar{{{\textbf {x}}}}, \bar{{{\textbf {x}}}}\rangle } \end{aligned}$$

(23)

$$\begin{aligned} v&= (s - u \langle \bar{{{\textbf {p}}}}, \bar{{{\textbf {p}}}}\rangle ) / \langle \bar{{{\textbf {x}}}}, \bar{{{\textbf {p}}}}\rangle . \end{aligned}$$

(24)

A short discussion on the situations if the denominators become zero is given in appendix 7.3.

As we want the loss vector corresponding to the initial weights to be sparse, we want the distance of $\bar{{{\textbf {n}}}}$ to the decision boundary to be larger than that of $\bar{{{\textbf {p}}}}$. On the other hand, it needs to be small enough that the resulting weight vector is not too far from the optimal weights. Empirically, we found $s=1$, $t=-2$ (cf. appendix 7.3) to work well.

Fig. 6

Sparsity of the Hessian calculation over different training epochs. Even though Bias-initialization starts out very sparse, this property is lost after the first update step. In contrast, MSI maintains sparsity over the entire range of training iterations

Evaluation: Does this initialization method work as we expect? As shown in Fig. 6, the method induces loss vectors that are more sparse than the ones for OvAP, and keeps this property over the course of training, resulting in faster update times for each iteration. As expected, tail labels benefit most, because the situation depicted in Fig. 5 is better approximated in the tail than for head labels. Because most labels in XMC are tail labels, training time improvements for them are most important for overall speed-up. Still, our method is faster or at least as fast as any of the other methods across the entire range of number of positives.

Fig. 7

Number of Newton optimization steps required for convergence (left) and training time for a single label (right). The average and the 95% quantiles are plotted as a function of the number of positive instances

Figure 7 shows that using the MSI initialization drastically reduces the number of iterations needed for convergence for tail labels. Whereas for Zero and OvAP initialization the number of iterations increases as the number of positive instances decreases, for Bias and MSI initialization it remains almost constant. This cannot be explained by looking only at the distance the optimization algorithm has to travel, neither in terms of the initial loss value, nor in terms of the distance between initial and final weight vector. The corresponding graphs are presented in appendix 7.3.

Fig. 8

Duration per iteration (left), and line search step multiplier (right). The MSI initialization manages to have the early iterations as fast as the later ones, while still working much better in terms of the quadratic approximation than the Bias initialization. The decrease of the step multiplier, and the slight increase in duration, for late iterations is not relevant, because as Fig. 7 shows most of the binary problems will have finished by iteration 10

Until about iteration 8, the duration per iteration with MSI is faster than the other initialization methods, as depicted in Fig. 8. Because MSI very rarely needs more than 10 iterations of training, and on average if finished before 8 iterations (Fig. 7), the slight speed advantage of the other methods for later iterations only applies to very few binary sub-problems, and such has little effect on the overall training time.

5 Benchmarks

In this section, we demonstrate the effectiveness of MSI initialization on a wide range of datasets and settings. We first provide timings for training with sparse tf-idf data on a singe, large compute node, the setting in which we expect linear OVA models to be run typically. We then show how changes in the training data affect the speed-up of our method: In particular, we present timing for the case of training with a dense input representation, and timings for training with the logistic loss, which does not admit the implicit negative-mining effect. Finally, to allow for a meaningful comparison with the method by Fang et al. (2019), we also run training on smaller hardware.

Infrastructure and training configuration: Our code is a re-implementation of the conjugate-gradient Newton procedure of recent versions of Liblinear (Galli et al., 2021). The hyperparameters related to stopping condition for conjugate-gradient iterations ($\epsilon = 0.5$), preconditioner ($\alpha =0.01$), back-tracking line search ($\alpha =0.5$, $\eta =0.01$, $\text {max\_steps}=20$), and stopping condition for the optimization ($\epsilon _0=0.01$) have been taken from their code. To reduce model size, all weights below a threshold of 0.01 have been clipped to zero.

Our main experiments were run on a single compute node equipped with two AMD Rome 7H12 CPUs. The code is NUMA-aware and produces a copy of the training data for each NUMA-node, but memory bandwidth still is the limiting factor in scalability. We observed very good scaling for 64 cores, but sublinear improvements for more cores.

All nodes in the compute cluster have identical hardware and jobs were run with exclusive access to the node. In the absence of any other user-jobs running on the same node, and hence no significant randomness⁴ in the run times, we have not systematically collected data from multiple runs of the same setting.

Sparse data: We tested the initialization methods on Eurlex-3k (Mencia & Loza, 2008), AmazonCat-13k (McAuley & Jure, 2013), WikiSeeAlsoTitles-350K, WikiTitles-500k, Amazon-670k (McAuley & Jure, 2013), WikiLSHTC-325k (Partalas et al., 2015), Amazon-3M (McAuley et al., 2015, 2015), and Delicious-200k (Wetzker et al., 2008) in their train/test splits as available from Bhatia et al. (2016). The run-time results are shown in the Tabel 1 under the columns Zero, Bias, OvAP, and MSI.

Table 1 Training time (in minutes) for different datasets and initialization methods

As shown in the Ratio column, the proposed method (MSI) is 3–4 times faster than Zero initialization, and also significantly faster than Bias and OvAP initialization. For Amazon-3M it is only possible to run the proposed MSI initializer due to the large computational cost involved for the Zero initialization baseline. Therefore, the relative speed-up cannot be reported. However, our training of 1360 minutes ($< 1$ day), using MSI as a starting point of the optimization process, shows that learning a DiSMEC-style (Babbar & Schölkopf, 2017) model is feasible even for datasets with millions of labels, on a single node.

The Zero setting corresponds to the vanilla DiSMEC algorithm, under our new and faster implementation. Due to improvements in implementation quality, in particular the NUMA-awareness of our code, our timings with this initialization are already much faster than running original DiSMEC on the same node.

Because the optimization problem is convex, the minimum is not affected by the choice of initial parameter. However, because in practice only an approximate minimum is found, there are slight variations (around 0.1%) in precision@k metrics for the different methods. The exact numbers can be found in Table 4.

Dense data: We also ran the tests on the same dataset of dense features as used for slice⁵. The default setting for the stopping condition as specified by Liblinear, $\epsilon _0=0.01$, is far too strict in this setting. Therefore, we increased this parameter to $\epsilon _0=1$ here. For these settings, we observed larger variability in the classification accuracy, and a slightly reduced, but still significant speed-up.

Logistic loss: We also ran a test where we replaced the squared hinge-loss with the logistic loss. As the logistic loss only vanishes asymptotically, this is a setting that does not benefit from implicit negative-mining. This means that later iterations will take approximately as long as earlier ones, and there is less benefit from being able to skip the first iterations. The result is a much reduced benefit from our proposed initialization, as can be seen in Table 2.

Due to the vast number of negatives (for a tail label), the loss function’s minimum will not be achieved when the negatives are classified correctly with margin one as is the case with squared-hinge, but will in fact train a larger margin for the negatives. This suggests that by decreasing the t parameter further, our initial guess for the separating hyperplane will be closer to the final weight vector. Thus we have used $t = -3$.

Table 2 Training time (in minutes) for different datasets and initialization methods when minimizing the logistic loss

Table 3 Training time (in minutes) and speed-up on smaller hardware comparing OvAP++ and MSI

Comparison with OvAP++: Finally, in order to allow for a meaningful comparison with the code by Fang et al. (2019), we also ran trainings with the smaller datasets on a Xeon Gold 6148 processor, with both our own implementation and with their code. For these experiments, instead of taking the dataset directly from the XMC repository (Bhatia et al., 2016), we applied their preprocessing script. Because the two methods still use slightly different optimization procedures (theirs uses a trust-region instead of a line search, as in older Liblinear versions) and implementations, we still need compare the relative speed-ups between the different initialization methods. The results can be seen in Table 3. MSI initialization consistently leads to more speed-up than OvAP++ initialization.

6 Discussion

We have provided a way to initialize the weights of a linear OvA extreme classifier in such a way as to reduce training times. Our experiments show that aside from the initial loss value investigated in Fang et al. (2019), the implicit sparsity and local smoothness properties of the loss landscape also play an important role in the success of the method.

Limitations: The initialization method discussed in this work is mainly applicable to linear One-versus-rest XMC algorithms. This rules out label-embedding schemes (Guo et al., 2019; Bhatia et al., 2015), decision-tree based classifiers (Prabhu & Manik, 2014; Majzoubi & Anna, 2020) and deep-learning methods in which the classifier is jointly learnt with the intermediate representations (You et al., 2019).

Outlook: The choice of initial vector is an underexplored design tool in XMC that is orthogonal to many other design choices such as explicit negative-mining (Reddi et al., 2019; Jain et al., 2019), training meta classifiers over buckets of labels (Medini et al., 2019; Dahiya et al., 2021), or the choice of regularizer. Future work should thus look into combining these, for example integrating our initialization into the OvA parts of Slice (Jain et al., 2019), Parabel (Prabhu et al., 2018) XR-Transformer (Zhang et al., 2021), Probabilistic Label Trees (Wydmuch et al., 2018), or Astec (Dahiya et al., 2021).

Appendix

1.1 Information on AmazonCat data

To evaluate the initialization methods and investigate their properties, we took the AmazonCat-13K dataset from the extreme classification repository Bhatia et al. (2016); McAuley and Jure (2013) as a running example during sects. 3 and 4. In this dataset the input features are sparse tf-idf values of a bag-of-words representation augmented by an additional bias feature that is set to 1. The train/test split is taken from the repository. The dataset consists of 1 186 239 training instances and 306 782 test instances in a 203 882 dimensional feature space. These instances are mapped to 13 330 labels, with an average of 5 labels per instance.

1.2 Early stopping for OVA-primal

For the squared-hinge loss, a vector that minimizes (15) perfectly will have similar characteristics to the Bias initialization ${{\textbf {w}}}_{b}$, in that for many instances the prediction will be close to the hinge location. Thus the starting point will be in a location unfavourable to the Newton optimizer. A remedy is to stop training of ${{\textbf {w}}}^*(-{\textbf {1}})$ early. This results in larger initial loss, but makes the training progresses more smoothly.

Since the label vector $-{\textbf {1}}$ is maximally imbalanced, according to equation (13) the weight should be trained to high precision $\epsilon = \epsilon _0 / n$. If instead we use the much less strict $\epsilon = \epsilon _0$, the initial loss is much larger, but at the same time the training progresses more smoothly.

The resulting training durations are shown in Fig. 9. Overall, the loose stopping criterion performs much better, except for labels with less than three positives. This is because for these labels, the initial vector is very close to the final vector, and thus the number of iterations that are required for training decreases, cf. Fig. 10. This is in contrast to the $\text {bias}=-1$ setting, which has similar characteristics in the second-order optimization, but does not benefit from fewer iterations and consequently does not show a decrease of overall training time for the extreme tail.

In Fig. 11 (left), the training progress over the iterations is shown. Here we can see that, similar to Bias initialization, the strict setting results in very little progress in the first iteration, and overall much slower progress also for the other iterations, such that loose turns out to be the faster setting, even though its initial loss is an order of magnitude larger. The right side of this figure shows the step multiplier during the line-search phase, which shows that during the first iteration, for strict the second-order approximation is overly optimistic and the real step size has to be much smaller than the CG procedure suggests.

Fig. 9

Histogram (left) and average with 95% confidence interval in dependence of the number of positive instance (right) of the training time, measured in milliseconds. Overall, the loose training configuration is much faster, though for extreme tail labels with less than 3 positive instances, strict actually performs slightly better

Fig. 10

Histogram (left) and average with 95% confidence interval in dependence of the number of positive instance (right) of the number of weight updates until convergence

Fig. 11

Letting the OvA-Primal initial vector be the result of training the all-zero-label problem until convergence (strict) results in much worse performance than doing early stopping (loose). We suspect that this is because strict training brings the weight vectors into a regime that is qualitatively similar to the $\text {bias}=-1$ setting: All training instances will predict a negative label with a margin very close to 1. Even though this results in much lower initial loss (left), it also leads to a useless first iteration in which little progress is made (right)

Fig. 12

Total duration of the individual binary problems when trained with different Bias-init variations. The histogram on the left has bins corresponding to the number of binary problems taking a certain amount of time, on the right the average time and 95% quantiles are shown in dependence of the number of positive instances. Duration is measured in milliseconds. The graphs show that $\text {bias} = -1$ is a local maximum in terms of computation time

Fig. 13

Number of Newton optimization steps required for convergence. On the left, the data is shown as a histogram, with the bins corresponding to the number of binary problems that required the corresponding number of steps. On the right, the average number of steps, and the 95% quantiles, are plotted as a function of the number of positive instances. The data shows that the benefit of the $\text {bias}=-2$ initialization is not limited purely to faster iterations because of increased sparsity, but it also needs fewer steps, despite having slightly larger initial loss than $\text {bias}=-1$. This indicates that each step has to make more progress, i.e. the loss landscape is more benign to the Newton optimization around the $\text {bias}=-2$ trajectory. The right-hand graph also shows that most of the benefit comes from the tail labels

1.3 Additional Results for Bias Initialization

Some additional graphs showing details about the training process with Bias initialization. In Fig. 12 the training duration of different Bias variations is shown in terms of training time for each individual binary problem. For $\text {bias}=-1$, the binary problems take roughly the same amount of time independent of the number of positives, but for $\text {bias}=-2$ the tail labels can be trained much faster.

The training duration as measured in number of iterations is presented in Fig. 13.

1.4 Additional results for mean-separating initialization

In Fig. 14 (left) we show how the initial loss depends on the number of positive instances. For Bias and MSI, we can see that tail labels result in very low initial loss, whereas for head labels MSI gives slightly larger loss than Bias and OvAP. On the other hand, OvAP ’s loss remains significantly larger for tail labels. The right side of Fig. 14 shows how that initial loss translates to initial distance in weight space. Here, we can see that for tail labels, OvAP ’s initial weight vector is an order of magnitude further from the optimum than for the other methods.

Fig. 14

Loss of the initial weight vector (left) and distance between initial and final vector (right). The shaded area shows 95% quantiles. For all except Zero initialization, loss and distance are much lower for tail labels than for head labels

What happens if the denominator of MSI is zero The expression in equation (23) diverges if $\bar{{{\textbf {p}}}}$ and $\bar{{{\textbf {x}}}}$ are linearly dependent, which implies that the means of features for negatives and positives only differs by a factor. In that case, we cannot (except in unlikely special cases) find an initial vector that fulfills our condition, so we return the zero vector.

A second numerical instability occurs if $\left| {\langle \bar{{{\textbf {x}}}}, \bar{{{\textbf {p}}}}\rangle }\right| \ll 1$, during the calculation of v. To investigate this setting, we substitute $\langle \bar{{{\textbf {x}}}}, \bar{{{\textbf {p}}}}\rangle$ with 0 in (23) and (24).

$$\begin{aligned} s&= u \langle \bar{{{\textbf {p}}}}, \bar{{{\textbf {p}}}}\rangle \end{aligned}$$

(25)

$$\begin{aligned} |\mathsf {N}| t&= v |\mathsf {X}| \langle \bar{{{\textbf {x}}}}, \bar{{{\textbf {x}}}}\rangle - u |\mathsf {P}| \langle \bar{{{\textbf {p}}}}, \bar{{{\textbf {p}}}}\rangle \end{aligned}$$

(26)

This leads to

$$\begin{aligned} u = \frac{s}{\langle \bar{{{\textbf {p}}}}, \bar{{{\textbf {p}}}}\rangle }, \qquad v = \frac{|\mathsf {N}| t + |\mathsf {P}| s}{|\mathsf {X}| \langle \bar{{{\textbf {x}}}}, \bar{{{\textbf {x}}}}\rangle }. \end{aligned}$$

(27)

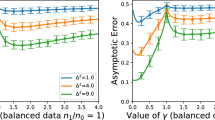
Choice of hyperparameters for MSI As argued in the main text, in order to achieve sparsity in the Hessian calculations, having the average of the negative instances be classified very strongly as a negative would be beneficial. Interestingly, Fig. 15 shows not only the expected speedup in per-iteration time, but also that $t=-1$ requires significantly more iterations than the other two settings.

Fig. 15

Average duration of the iterations (top left, in $\mu$ s), and number of iterations for different numbers of positive instances (top right). The bottom left graph shows the development of the objective function. At first glance, this seems paradoxical, as the algorithm is designed so that for each binary problem, the loss strictly decreases over the iterations. The apparent increase is caused by the fact that the sample of binary problems shrinks for later iterations, as the labels for which the loss is already low before will terminate the optimization. Finally, the bottom right graph shows the Euclidian distance between the initial weight vector and the approximately optimal weight vector for which the minimization is terminated. The shaded area marks the 95% quantile

This is not too surprising, given that we expect that the large number of negative instances fill a larger proportion of the space than the few positives, so the separating hyperplane should be closer to the mean of the positives. One reason for this could be that $t=-1$ induces a higher initial loss than the other two settings, as shown in the bottom left graph. However, if we measure the distance that the optimization procedure covers, i.e. the distance between the initial and final weight vector, it turns out that $t=-1$ actually starts closest.

1.5 Full result table

Since the actual loss function is based on binary classification, we have also calculated the precision and recall as averaged over the individal binary problems. The metrics remain mostly unchanged for tf-idf data, but there is significant fluctuation when slice features are used (Table 4).

Table 4 Durations (as given in main paper) and precision@{1,3,5} for training different datasets with the given initialization methods

0