Optimal policy trees

Abstract

We propose an approach for learning optimal tree-based prescription policies directly from data, combining methods for counterfactual estimation from the causal inference literature with recent advances in training globally-optimal decision trees. The resulting method, Optimal Policy Trees, yields interpretable prescription policies, is highly scalable, and handles both discrete and continuous treatments. We conduct extensive experiments on both synthetic and real-world datasets and demonstrate that these trees offer best-in-class performance across a wide variety of problems.

1 Introduction

The ever-increasing availability of high-quality and granular data is driving a shift away from one-size-fits-all policies towards personalized and data-driven decision making. In medicine, different treatment courses can be recommended based on individual patient characteristics rather than following general rules of thumb. In insurance, underwriting decisions could be made at the individual level, rather than relying on aggregate populations and actuarial tables. In e-commerce, consumers may experience a personalized version of a website, tailored to their shopping tastes. In all domains, the ability to understand the underlying phenomena in the data to aid decision making is critical.

In this paper, we consider the problem of determining the best prescription policy for assigning treatments to a given observation (e.g. a customer or a patient) as a function of the observation’s features. A common context is that we have observational data of the form $\left\{ (\varvec{\mathbf {x}}_i, y_i, z_i) \right\} _{i = 1}^n$ consisting of n observations. Each observation i consists of features $\varvec{\mathbf {x}}_i \in {\mathbb {R}}^p$, an applied prescription $z_i$, and an observed outcome $y_i \in {\mathbb {R}}$. Depending on the scenario, the prescription may be one choice from a set of m available treatments ($z_i \in \{1, \ldots , m\}$, noting that discrete treatments in higher dimensions can be flattened and numbered 1 to m without loss of generality), or could be the dosage of one or more continuous treatments ($z_i \in {\mathbb {R}}^m$). Our prescriptive task is to develop a policy that, given $\varvec{\mathbf {x}}$, prescribes the treatment z that results in the best outcome y.

Decision trees are an appealing class of model to apply to this problem, as their interpretability and transparency allows humans to inspect and understand the decision-making process, to both develop their understanding of the underlying phenomenon and to identify and correct flaws in the model. The interpretability is arguably more important in prescriptive problems than in predictive problems, as a prescriptive model recommends actions with direct and often significant consequences, requiring more transparency and justification than models that simply make predictions.

One of the key difficulties in learning from observational data is the lack of complete information. In the data, we only observe the outcome corresponding to the treatment that was applied. Crucially, we do not observe what would have happened if we had applied other treatments to each observation, the so-called counterfactual outcomes.

Previous approaches (Bertsimas et al. 2019; Kallus 2017) for decision tree-based prescriptions from observational data dealt with the lack of information by embedding a counterfactual estimation model inside the prescriptive decision tree, combining the tasks of estimating the counterfactuals and learning the optimal prescription policy. While this approach has the attractive property of learning from the data in a single step, it also makes the learning problem more complicated and thus limits the complexity of counterfactual estimation to approaches than can be practically embedded in a tree-training process.

Some recent works (Biggs et al. 2020; Zhou et al. 2018) have proposed decision tree approaches to this problem that separate the counterfactual estimation and policy learning steps. Instead of a single learning step, the counterfactuals are first estimated using a method that models the data well, and than a decision tree is trained against these estimates to learn an optimal prescription policy (see Table 1 for an example of the counterfactual estimation process). These approaches use greedy heuristics to train the decision trees, rather than aiming for global optimality (Zhou et al. 2018 also include an exhaustive tree search, which does not scale beyond shallow trees and small datasets).

Table 1 Example reward estimation problem

The limitations of such a greedy search are well-known in the literature, evidenced by the extensive research into approaches for training decision trees that are globally-optimal, particularly in recent years (see Carrizosa et al. 2021 for a survey covering many such methods). Experiments on both synthetic datasets and real-world applications have shown that modern optimization techniques can be applied to such problems and achieve solutions that achieve performance comparable to black-box methods while maintaining the interpretability of a single decision tree.

In this paper, we propose an approach that extends our earlier work on training globally-optimal trees to construct policy trees that are interpretable, highly scalable, handle both discrete and continuous treatments, and have best-in-class performance on both synthetic and real-world datasets. Specifically, we summarize our contributions in this paper:

• We extend the Optimal Trees framework of Bertsimas and Dunn (2017, 2019); Bertsimas et al. (2019) to the problem of learning prescription policies based on complete counterfactual information estimated using state-of-the-art approaches from the causal inference literature. The resulting Optimal Policy Trees are interpretable and highly scalable, and can handle problems where we must choose one treatment from a set of possible options, as well as problems where we need to prescribe continuous-valued doses for one or more treatments.

• We demonstrate through comprehensive synthetic experiments and number of real-world applications that Optimal Policy Trees have best-in-class performance, outperforming prescriptive tree approaches by a significant margin, and also offering significant performance gains over the existing greedy policy tree approaches.

The structure of the paper is as follows. In Sect. 2, we review related literature in decision tree induction and general policy learning from observational data. In Sect. 3, we present Optimal Policy Trees and algorithm we propose for training these trees in greater detail, including a summary of the methods used for counterfactual estimation. In Sect. 4, we conduct comprehensive experiments with synthetic data to compare the performance of Optimal Policy Trees to other methods across a variety of problem classes. In Sect. 5, we present a number of applications of Optimal Policy Trees to real-world problems. Finally, in Sect. 6 we summarize our conclusions.

2 Related literature

Decision tree methods like CART (Breiman et al. 1984) are one of the most popular methods for machine learning, primarily due to their interpretability. Because they split on a single feature at a time, it is simple for a human to follow the decision logic of the tree. However, the performance of these trees is often much weaker than approaches that sacrifice interpretability by aggregating multiple trees, such as random forests (Breiman 2001) or gradient boosting (Friedman 2001), forcing practitioners to choose between interpretability or performance.

Recent advances in modern optimization have led to approaches that eschew the traditional greedy heuristics used to train decision trees in favor of approaches rooted in global optimization. A variety of methodologies have been proposed to solve this problem, including linear programming (Bennett 1992), integer programming (Verwer and Zhang 2017), constraint programming (Nijssen and Fromont 2010; Verhaeghe et al. 2020), and branch-and-bound search (Aglin et al. 2020), among many others (see Carrizosa et al. (2021) for a survey covering many such works in great detail). Many works have promising performance gains compared to their greedy counterpart, but are often limited in the scalability where the trees are limited to depth 4 or 5 and the datasets are limited to 1000 observations (Verwer and Zhang 2017). One such approach is Optimal Classification Trees (Bertsimas and Dunn 2017), later extended to a general-purpose framework in Bertsimas and Dunn (2019). The Optimal Trees framework solves a mixed-integer optimization formulation of the decision tree problem using coordinate descent, permitting optimization of decision trees according to an arbitrary loss function, and has tailored algorithms for tuning its hyperparameters to avoid overfitting. Moreover, this approach also scales well to datasets with millions of observations and thousands of features, making it one of the more practical options for learning optimal decision trees. Comprehensive experiments on synthetic and real-world datasets have shown that these Optimal Trees achieve performance levels comparable to black-box methods without sacrificing interpretability.

There have been a number of tree-based approaches to prescriptive decision making. Personalization trees (Kallus 2017) use a greedy approach to simultaneously estimate counterfactuals and learn the optimal prescription policy directly from the data. These personalization trees can also be aggregated into personalization forests that improve performance at the cost of interpretability. Optimal Prescriptive Trees (Bertsimas et al. 2019) are similar to personalization trees, and apply the Optimal Trees framework to a similar problem modified to incorporate the accuracy of the counterfactual estimation in the objective function. Both personalization trees and Optimal Prescriptive Trees offer the ability to estimate the counterfactuals and learn the optimal prescription policy from data in a single step, but this has the limitation that the class of model used for counterfactual estimation is limited to what can be embedded in a tree-learning procedure without sacrificing tractability. In particular, Optimal Prescriptive Trees can estimate the counterfactuals as piecewise-constant or piecewise-linear function s, but the structure of the outcomes is often more complicated in practice. Another drawback is that embedding the counterfactual estimation inside the tree can detract from the interpretability of the prescription policy, as the splits of the tree are used not just to develop the prescription policy, but also to refine and improve the counterfactual estimates. As such, it can be difficult to understand which parts of the tree relate directly to the prescription policy alone. Finally, the trees rely on having enough data in each leaf to estimate the outcome for each treatment, which can mean that a lot of data is required if the number of possible treatments is high.

Recent works have proposed separating the counterfactual estimation and policy learning tasks, using a decision tree for the latter to construct an interpretable prescription policy. In contrast to prescriptive trees, which simultaneously predict counterfactual outcomes and prescribe the corresponding optimal treatment assignments, these policy trees only learn to prescribe the best treatment assignment. Zhou et al. (2018) use doubly-robust estimators from the causal inference literature (Dudík et al. 2011) to estimate the counterfactual outcomes from observational data with discrete treatments. Their use of this doubly-robust estimator is important, as it is able to account for treatment assignment bias in the observed data, whereas a naive approach that predicts the outcomes directly may lead to biased estimates that can mislead any subsequent prescription policy. Using these estimates, they proceed to learn a tree-based prescription policy, considering both a greedy approach and an exhaustive optimal approach to training trees, with the latter unsurprisingly exhibiting poor scalability (results from this exhaustive method are only shown for trees with three splits). Another approach for greedy policy trees is proposed by Biggs et al. (2020), where a black-box model is trained to predict the outcomes from observational data with continuous treatments. This model is used to estimate the counterfactual outcomes under possible candidate treatment options, and used to feed a greedy tree-learning process. Both of these approaches share the common approach of using the best model available for counterfactual estimation, and then using a decision tree to learn an interpretable prescription policy based on these estimates. They also share the common limitation that using a greedy heuristic for training trees is likely to result in sub-optimal policies that do not attain maximum performance and also likely results in larger trees that are harder to interpret.

In addition to interpretable decision trees, there are a number of black-box methods that can be used for prescription in this setting, including the aforementioned personalization forests as well as causal forests (Wager and Athey 2018), causal boosting (Powers et al. 2018), and causal MARS (Powers et al. 2018), although these causal approaches only deal with the case where the treatment is a binary decision. These methods give high-quality estimates of the treatment effect, which can be used for prescription based on whether the predicted effect is positive or negative, but offer no further insight into the reasons behind prescriptions.

Another class of black-box methods is the so-called regress-and-compare approach, which involves training models for each treatment option to predict the outcome function under that treatment. To make a prescription for a new observation, these models are used to predict the outcome under each candidate treatment option, and the treatment with the best predicted outcome is prescribed. A recent example of this method is Bertsimas et al. (2017), where in the context of diabetes management a k-nearest-neighbors approach is used to estimate the counterfactual outcomes under a range of different treatment options, and the combination of drugs with the best outcome is prescribed. Unlike the doubly-robust estimator used by Zhou et al. (2018), the regress-and-compare method is susceptible to treatment assignment bias in the observed data, and as a result may not be able to correctly identify causal relationships in the data. Unfortunately, it is not possible to use the doubly-robust estimates in a regress-and-compare setting, as they are only meaningful when used in aggregate to compare alternative policies, and should not be interpreted on a per-observation basis (Dudík et al. 2011). It is also difficult to interpret the results of a regress-and-compare approach, because we have to investigate the details of each of the treatment models in order to understand why a given treatment has the best prediction. Another limitation is that this approach spreads the data across separate learning tasks for each treatment option, which can limit the amount of data available for learning and prohibits joint learning across all treatments together, which may affect the accuracy of the outcome estimates and in turn impact the quality of the resulting prescriptions. In particular, because the determination of the optimal prescription is made separately for each observation, the policy is very sensitive to overfitting, as even a single low-quality outcome estimate can lead to suboptimal prescription for the corresponding observation. In contrast, encoding the prescription policy as a decision tree may help to regularize the prescriptions and reduce their sensitivity to the input data and training process. Finally, it can be a problem that the outcome estimation models are trained separately from the policy evaluation task, as they may focus on predicting the outcomes in areas that are not as relevant for deciding which treatment is best. This can lead to less efficient use of data compared to other methods that focus directly on learning the decision boundary.

3 Optimal policy trees

In this section, we introduce Optimal Policy Trees and detail the algorithm that we propose for training these trees.

Suppose we have n observations in the training data, {$\varvec{\mathbf {x}}_i\}_{i=1}^n$, and there are m possible treatment options (in the case of continuous treatments, this can be achieved by discretizing, as discussed in Sect. 3.2). Further, assume we are given the reward that is attained for every observation i under every prescription option t, denoted $\Gamma _{it}$. Without loss of generality, assuming lower reward is better, the problem we seek to solve is

$$\begin{aligned} \min _{\tau (.)} \sum _{i = 1}^n \sum _{t = 1}^m \mathbbm {1}\{ \tau (\varvec{\mathbf {x}}_i) = t \} \cdot \Gamma _{it}, \end{aligned}$$

(1)

where $\tau (\varvec{\mathbf {x}})$ is a policy that assigns prescriptions to observations based solely on their features $\varvec{\mathbf {x}}$, and $\mathbbm {1}\{.\}$ is the indicator function that takes value 1 if its argument is true, and 0 otherwise.

If we knew the outcome for every observation under each prescription option, we could simply use these outcomes as the rewards $\Gamma _{it}$. Of course, in reality we often do not know the outcomes for every observation under each prescription. In particular, for observational data, we only have the outcome corresponding to the treatment that was applied in the historical data. Nevertheless, we will proceed with solving Problem (1) assuming that these rewards are known. In Sect. 3.2 we will discuss strategies for estimating these rewards when they are not known.

3.1 Learning optimal policy trees

We will now solve Problem (1) using a decision tree-based model. Specifically, our prescription policy function $\tau (\varvec{\mathbf {x}})$ will make prescriptions following a decision tree that seeks to optimize the total overall cost of the policy according to the rewards.

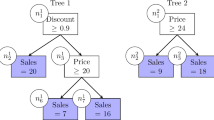
The splits of this tree will use the feature values to direct observations to one of the leaves of the tree, and each leaf will assign the same prescription to all observations that fall into the leaf. An example of such a tree, which we call policy trees, is shown in Fig. 1.

Fig. 1

Example of a policy tree that prescribes one of two treatment options based on feature values

While the tree looks similar to a classification tree, there is an important difference in how they are trained. A classification tree focuses only on whether the predicted label is correct, whereas the policy tree uses the rewards to take into account the relative cost of each treatment option. For instance, consider a setting with three treatment options and an observation with rewards under these treatments of [1, 2, 10]. Assuming that we seek to minimize the rewards, a classification view of this problem would deem that the first treatment (with the lowest reward) is the “correct” label, and we would get equal penalty for prescribing the second or third treatments. In contrast, the policy view of the problem would incur a relative penalty of 1 and 9 for prescribing the second and third treatments, respectively. In this way, the policy tree makes use of the relative values of the rewards rather than simply focusing on which treatment gives the best reward for each observation.

We denote the leaf of the tree into which an observation $\varvec{\mathbf {x}}$ falls as $v(\varvec{\mathbf {x}})$, and the prescription made in each leaf $\ell$ as $z_\ell$. Without loss of generality, we can assume the treatments are enumerated as $1, 2, \ldots , m$ so that $z_\ell \in \{1, 2, \ldots , m\}$. We can then express the prescription policy in terms of the leaf assignment function $v(\varvec{\mathbf {x}})$ as

$$\begin{aligned} \tau (\varvec{\mathbf {x}}) = \sum _{\ell } \mathbbm {1}\{ v(\varvec{\mathbf {x}}) = \ell \} \cdot z_\ell . \end{aligned}$$

(2)

Combining (1) and (2) yields the following optimization problem:

$$\begin{aligned} \min _{v(.), \varvec{\mathbf {z}}} \sum _{i = 1}^n \sum _{\ell } \mathbbm {1}\{ v(\varvec{\mathbf {x}}_i) = \ell \} \cdot \Gamma _{iz_\ell } \end{aligned}$$

(3)

Specifically, for each observation i, we identify the leaf $\ell = v(\varvec{\mathbf {x}}_i)$ containing this observation, and use the reward $\Gamma _{iz_\ell }$ corresponding to the prescription in this leaf.

To solve Problem (3), we note that it is separable in the leaves of the problem:

$$\begin{aligned} \min _{v(.), \varvec{\mathbf {z}}} \sum _{\ell } \sum _{i : v(\varvec{\mathbf {x}}_i) = \ell } \Gamma _{iz_\ell } \end{aligned}$$

(4)

This means that given a tree structure $v(\varvec{\mathbf {x}})$, we can find the optimal prescription in each leaf $\ell$ by solving the following problem:

$$\begin{aligned} z_\ell = \arg \min _{t} \sum _{i : v(\varvec{\mathbf {x}}_i) = \ell } \Gamma _{it}, \end{aligned}$$

(5)

which can be solved simply by enumerating the possible prescription options.

Note that this problem formulation is equivalent to the classification tree problem under misclassification loss, with the addition of per-observation, per-class losses $\Gamma _{iz_\ell }$. We can thus use any approach for training classification trees to solve this problem, provided that they support the specification of such custom loss weights.

In this case, we will utilize the Optimal Trees framework (Bertsimas and Dunn 2019) to optimize the tree structure and determine $v(\varvec{\mathbf {x}})$. Our particular choice of optimal decision tree learning algorithm is based both on the scalability and performance of the Optimal Trees approach, as well as our existing familiarity with this particular method. This approach uses a coordinate descent algorithm to optimize an arbitrary objective function that depends only on the tree assignment function $v(\varvec{\mathbf {x}})$. Concretely, the objective we optimize is Problem (3), and at each step of the coordinate descent process, we use the current tree structure to evaluate the currently-optimal values of $z_\ell$ according to Eq. (5). Plugging these values of $z_\ell$ back into (3) yields the current objective value, guiding the coordinate descent procedure. The full details of the general-purpose tree optimization algorithm used by Optimal Trees are presented in Section 8.3 of Bertsimas and Dunn (2019), but for clarity, the exact problem being solved is

$$\begin{aligned} \min _{v(.), \varvec{\mathbf {z}}} ~&~ \biggl ( \sum _{\ell } \sum _{i : v(\varvec{\mathbf {x}}_i) = \ell } \Gamma _{iz_\ell } \biggr )+ \alpha \cdot \text {numsplits}(v) \\ \text {s.t.} ~&~ \text {depth}(v) \le D_{\max } \nonumber \\&~ |\{i : v(\varvec{\mathbf {x}}_i) = \ell \}| \ge n_{\min } ~~~ \forall l \nonumber \end{aligned}$$

(6)

where $\text {numsplits}(v)$ is the number of splits in the tree v, and $\text {depth}(v)$ is the depth of the tree. There are three hyperparameters that control the size of the resulting trees to prevent overfitting, and must be specified by the user:

• $D_{\max }$: the maximum depth of the tree;

• $\alpha$: the complexity parameter that controls the tradeoff between training accuracy and tree complexity;

• $n_{\min }$: the minimum number of samples required in each leaf.

The first two of these are the most critical parameters to tune, and the Optimal Trees framework details a tailored tuning algorithm for determining these parameters in Section 8.4 of (Bertsimas and Dunn 2019). For example, $D_{\max }$ is tuned using a normal grid search over discrete values, whereas $\alpha$ is tuned using a pruning procedure based on generating a sequence of related trees and finding the value of $\alpha$ that would minimize the validation error.

As noted earlier, Problem (3) is also solved in the same fashion with a tree-based model by Biggs et al. (2020) and Zhou et al. (2018), but in both cases a greedy heuristic is used to train the tree. For other problem classes like classification and regression, there are significant performance and interpretability advantages to training trees with globally optimal methods rather than greedily (Bertsimas and Dunn 2017, 2019; Bertsimas et al. 2019). Our experiments in Sects. 4 and 5.1 demonstrate that this is also the case for the optimal policy problem.

3.2 Estimating rewards

In Sect. 3.1, we assumed that we had access to reward information $\Gamma _{it}$ for every observation i and every treatment option t. In some cases, we have access to this full information about the problem (see Sect. 5.3 for an example), but often we have observational data and thus only observe the outcome for the treatment that was applied in the data. In these cases, we will need to estimate the missing counterfactual outcomes. The method we use to estimate depends on the type of prescription decision being made.

3.2.1 Estimating rewards for discrete treatments

When the prescription is a choice of one treatment from a set of possible options, we draw on the causal inference literature and use doubly-robust estimates (Dudík et al. 2011) for the outcomes, as outlined by Zhou et al. (2018) and Athey and Wager (2017).

For clarity, we present the estimation process here. There are three steps:

• 1. Propensity score estimation We train a model to estimate the probability ${\hat{p}}_{it}$ that a given observation i is assigned a given treatment t. We use the features $\varvec{\mathbf {x}}_i$ and the assigned treatments $z_i$ observed in the data to train a multi-class classification model (such as random forests or boosting), and use this model to estimate treatment assignment probabilities. To avoid overfitting to the data, a k-fold cross-validation process is used for estimation, where the probabilities for the data in each fold are estimated using a model trained on the remaining data not in the fold.

• 2. Outcome estimation We train a model to estimate the outcome ${\hat{r}}_{it}$ for each observation i under each treatment option t. For each treatment t, we train a regression model on the subset of training data that received this treatment, and predict the observed outcomes $y_i$ as a function of the features $\varvec{\mathbf {x}}_i$. We then use these models to estimate the outcomes ${\hat{r}}_{it}$ for all observations under all treatments. As for propensity score estimation, random forests and boosting models can be used for this prediction. A variant approach combining random forests with multiple causal forests is also presented in Zhou et al. (2018).

• 3. Doubly-robust estimation Finally, the estimated propensity scores ${\hat{p}}_{it}$ and outcomes ${\hat{r}}_{it}$ are combined to give the final doubly-robust estimates:

  $$\begin{aligned} \Gamma _{it} = \frac{y_i - {\hat{r}}_{it}}{{\hat{p}}_{it}} \cdot \mathbbm {1}\left\{ z_i = t \right\} + {\hat{r}}_{it} \end{aligned}$$

Using these estimated values $\Gamma _{it}$ in Eq. (1) results in a so-called doubly-robust estimate of the policy quality. This means that the estimated total reward under the policy has low bias if at least one of the propensity score or outcome sub-estimators has low bias, thus the name doubly-robust  (Dudík et al. 2011).

Compared to using the outcome estimates directly as the rewards, an important advantage of the doubly-robust estimator is the ability to correct for treatment assignment bias in the observed data. Treatments in observational data are often not assigned at random, and this bias can influence the outcome estimation process, leading to poor estimates if not accounted for. For instance, consider a medical example where a specific treatment is typically given to sicker patients. This means that the group receiving this treatment is composed of sicker patients to begin with, and thus despite receiving the treatment, we might see that the outcomes in the treated group are lower than in the untreated group. This could cause the outcome estimator to predict lower outcomes when the treatment is applied, whereas in reality the treatment might still be helpful, as the outcomes in the treated group would be even worse without the treatment application. Combining the propensity scores with the outcome estimates helps to correct for any such treatment assignment bias in the data, to ensure that the estimated rewards are fair.

3.2.2 Estimating rewards for continuous treatments

When the prescription is choosing the dosing level for one or more treatments, we estimate the counterfactual outcomes with a regression model.

We denote by $z_{it}$ the dose of each treatment t for each observation i, and treat the dose for each treatment as a separate continuous feature in the dataset. We then train a regression model (such as random forests or boosting) to predict the outcome $y_i$ based on the features $\varvec{\mathbf {x}}_i$ and the treatment doses $z_{it}$. Given this trained model, we can estimate rewards by predicting the outcome under any combination of treatment doses for a given observation i with features $\varvec{\mathbf {x}}_i$. In practice, we discretize the range of possible treatment doses to create a set of candidate doses, and estimate the outcome under each such set. The policy tree will then learn to prescribe one of the candidate doses works best in any given situation.

Note that if the outcomes $y_i$ are binary (e.g. denoting a success or failure), then a classification model can be used for estimation in place of regression. In this case, the estimated probabilities from the classification model can be used as the estimated outcomes.

3.3 Estimation and evaluation procedure in practice

To train and evaluate Optimal Policy Trees from observational data, we combine the approaches in Sects. 3.1 and 3.2. The exact workflow is:

• 1. Given observational data ($\mathbf {x_i}, y_i, z_i$), split into training and testing sets

• 2. On the training set, conduct reward estimation following Sect. 3.2 to estimate the reward $\Gamma _{it}$ for every observation i under each treatment option t

• 3. Train Optimal Policy Tree using the training set features $\mathbf {x_i}$ and the estimated rewards $\Gamma _{it}$ from the previous step (further splitting the data into training/validation sets to validate hyperparameters as necessary)

• 4. Evaluate the trained policy tree on the training set by summing the reward corresponding to the prescribed treatment for each observation.

• 5. On the testing set, conduct reward estimation following Sect. 3.2 to estimate the reward $\Gamma _{it}$ for every observation i under each treatment option t. It is necessary that this estimation step is separate to the reward estimation on the training set, to avoid information leaking between the training and testing sets.

• 6. Evaluate the trained policy tree on the testing set by summing the reward corresponding to the prescribed treatment for each observation. This constitutes a fair out-of-sample evaluation of the quality of the prescription policy.

To select the class of model and their associated hyperparameters for the reward estimation procedures in Steps 2 and 5, we recommend considering a range of model classes (e.g. boosted decision trees, random forests, linear regression) and using cross-validation to tune hyperparameters for each such model, before selecting the model class with the best estimated out-of-sample performance, so as to lead to high-quality reward estimates. Empirically, we have found that the highest estimated out-of-sample performance generally comes from boosted decision trees or random forests.

Note that in Step 5, training a separate estimation model in the test data purely serves the purpose of obtaining an unbiased evaluation of the policies, which is not necessary if the purpose is only for inference. In online settings where new observations arrive one-by-one, the Optimal Policy Tree model can still make prescriptions for these new observations, but we may not be able to provide a fair estimate of the policy performance for this new data.

3.4 Weighted-loss classification

Throughout this section, we have assumed that the reward $\Gamma _{it}$ for a given observation can depend on the features $\varvec{\mathbf {x}}_i$ as well as the observed outcome $y_i$ and observed treatment $z_i$. We note that a special case of this problem is when $\Gamma _{it}$ depends only on the observed treatment $z_i$. This gives rise to a weighted-loss classification problem, where there is a penalty matrix $\varvec{\mathbf {L}}$, where $L_{jk}$ specifies the penalty when an observation of class j is assigned to class k by the model. If $\varvec{\mathbf {L}}$ has zeros on the diagonal and ones everywhere else, the problem is equivalent to standard multi-class misclassification.

4 Performance on synthetic data

In this section, we conduct a number of experiments on synthetically-generated data in order to evaluate the relative performance of optimal policy trees against other methods for prescriptive decision making.

Our experimental setup follows that used in Powers et al. (2018) and Bertsimas et al. (2019). We generate n data points $\varvec{\mathbf {x}}_i, i = 1, \ldots , n$ where each $\varvec{\mathbf {x}}_i \in {\mathbb {R}}^d$, with $d = 10$. Each $\varvec{\mathbf {x}}_i$ is generated i.i.d. with the odd-numbered coordinates j sampled $x_{ij} \sim \text {Normal}(0, 1)$ and the even-numbered coordinates j sampled $x_{ij} \sim \text {Bernoulli}(0.5)$.

4.1 Binary treatment

First, we consider scenarios with a single binary treatment. We define a baseline function that generates the baseline outcome for each observation, and an effect function that models the effect of the treatment being applied. The different functional forms we consider are presented in Table 2. Each function is further centered and scaled so that the generated values have zero mean and unit variance. In each experiment, we model the outcomes under “no treatment” and “treatment” ($Y_0$ and $Y_1$, respectively) as

$$\begin{aligned} Y_0(\varvec{\mathbf {x}}) = \text {baseline}(\varvec{\mathbf {x}}) - \frac{1}{2}\text {effect}(\varvec{\mathbf {x}}), \qquad Y_1(\varvec{\mathbf {x}}) = \text {baseline}(\varvec{\mathbf {x}}) + \frac{1}{2}\text {effect}(\varvec{\mathbf {x}}). \end{aligned}$$

We will adopt the convention that lower outcomes are desirable for all experiments. We assign treatments in a biased way to simulate an observational study where observations are more likely to receive the treatment option with the better outcome. Concretely, we assign the treatment with probability

$$\begin{aligned} {\mathbb {P}}(Z = 1 | \varvec{\mathbf {X}} = \varvec{\mathbf {x}}) = \frac{e^{Y_0(\varvec{\mathbf {x}})}}{1 + e^{Y_0(\varvec{\mathbf {x}})}} \end{aligned}$$

The outcomes in the training set have additional i.i.d. noise added in the form $\epsilon _i \sim \text {Normal}(0, 0.1)$.

Table 2 Functions used for discrete-treatment synthetic experiments

In summary, for each $\varvec{\mathbf {x}}_i$, we calculate the outcome under each treatment as $Y_0(\varvec{\mathbf {x}}_i)$ and $Y_1(\varvec{\mathbf {x}}_i)$. For the training set, we assign a treatment $z_i$ to 0 or 1 at random following the distribution above, and then finally assign the observed outcome as $(1 - z_i)Y_0(\varvec{\mathbf {x}}_i) + z_i Y_1(\varvec{\mathbf {x}}_i) + \epsilon _i$. These triplets $(\varvec{\mathbf {x}}_i, y_i, z_i)$ constitute the training data for each experiment.

To explore performance of the methods in a variety of scenarios, we consider seven different experiments, with different configurations of the baseline and effect functions as shown in Table 3.

Table 3 Experiment design for synthetic experiments with binary treatments

For each experiment, we generate training data with n from 100 to 5,000 to observe the effect of the increasing amount of training data on the model performance. We train models on the training set and evaluate on a testing set with $n=60,000$ where we know the true outcomes for each prescription. We evaluate the mean regret of the model’s prescriptions on the testing set, defined as the difference between the outcome under the prescribed treatment and the outcome under the optimal treatment, averaged across all points in the testing set. Each experiment was repeated 100 times and the results averaged.

We compare the following methods:

• Prescriptive Trees We include both greedy and optimal prescriptive trees as presented in Bertsimas et al. (2019). We set $\mu =0.5$ and consider trees up to depth 5, using validation to select the best depth and complexity parameter $\alpha$.

• Policy Trees We include both greedy and optimal policy trees as presented in Sect. 3. We consider trees up to depth 5, using validation to select the best depth and complexity parameter $\alpha$. We estimate rewards on the training set using the doubly-robust estimator with random forests for propensity estimation and causal forests for outcome estimation (following the process described in Zhou et al. (2018)). All forests used 100 trees.

• Regress & Compare We include a regress-and-compare approach using random forests. We train a random forest with 100 trees to predict the outcome under each prescription, and then for each point in the test set we prescribe the option that has the lowest predicted outcome.

• Causal Forests Because there is just a single treatment, we can include causal forests (Wager and Athey 2018) to predict the treatment effect. If this predicted treatment effect is negative, we prescribe the treatment, otherwise we prescribe no treatment. To match the other methods, we use 100 trees in the forest, with all other parameters taking their default values.

When validation is used, the original training data is further split 70%/30% into training and validation sets to determine the optimal hyperparameter values. These tuned values are then used to train the final model on the combined training and validation sets.

Fig. 2

Results for synthetic experiments with binary treatments

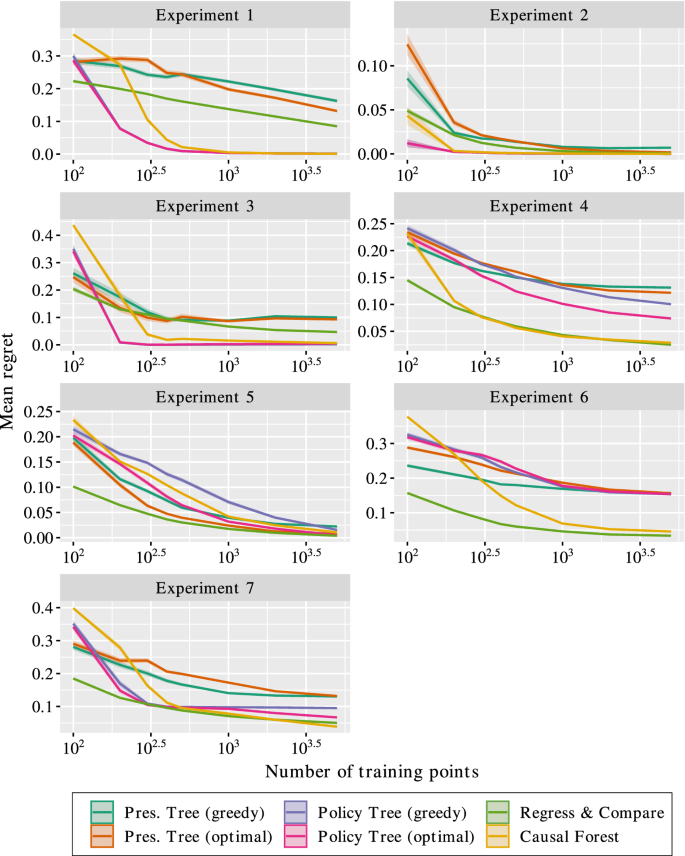
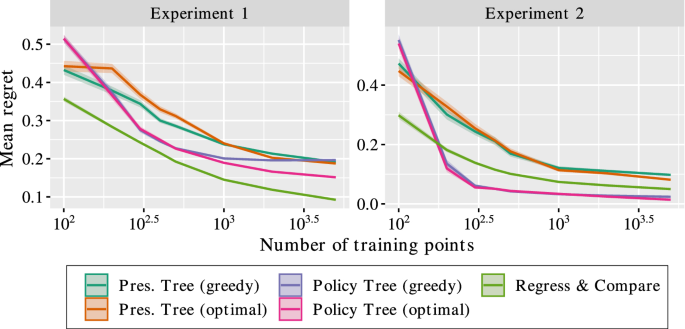
Figure 2 presents the results of the experiments. We make the following observations:

• Experiment 1 Here the baseline function is linear, while the effect is piecewise-constant with two pieces. We see that the policy tree approaches perform strongest and quickly reach zero regret, as they simply have to learn the structure of the effect function, which is a tree with a single split. Causal forests also achieve zero regret but require more training data. R&C and prescriptive tree approaches exhibit much slower improvement in regret, due to having to also learn and model the linear baseline function.

• Experiment 2 The baseline function is piecewise-constant and the effect function is linear in a single feature. Policy trees again exhibit fast convergence to zero regret, as the optimal policy is simply to prescribe based on the sign of $x_1$ which is achieved by a tree with a single split. Causal forests also converge to zero regret quickly, as do the other methods with much more training data. In particular, since both baseline and effect functions can be modeled using a tree structure, the prescriptive trees can approach zero regret.

• Experiment 3 The baseline function is quadratic and the effect function is piecewise-constant. Since the effect function can be modeled by a tree structure, the policy trees converge quickly to zero regret, followed closely by causal forests. The other methods struggle due to the complexity of modeling the non-linearity of the baseline function.

• Experiment 4 Both baseline and effect functions are linear. In this case, policy trees do not converge as quickly as before since the effect function is not modeled exactly through a tree structure. In fact, both flavors of trees have to learn linear functions in this case, but we can see that the policy approaches make better use of the data, and the optimal policy tree performs significantly stronger than the greedy approach. Both R&C and causal forests can more quickly learn the linear structure in the data, and exhibit similar performance.

• Experiment 5 The baseline function is constant and the effect function is piecewise linear. Here, prescriptive and policy trees face exactly the same problem structure due to the absence of a baseline function. We can see that both optimal tree methods converge towards zero regret, with the prescriptive approach converging slightly faster. Causal forests also exhibit slow convergence to zero, while R&C performs the strongest.

• Experiment 6 The baseline function is piecewise-constant with two pieces and the effect function is quadratic. Again, prescriptive and policy trees face very similar problems as the non-linearity of the effect function dominates the complexity of the problem compared to the simple baseline. All tree methods converge to the same non-zero regret, whereas R&C and causal forests converge to much lower values due to being able to better model the non-linearity.

• Experiment 7 Both baseline and effect functions are piecewise-linear. While the nature of the function is the same for prescriptive and policy trees, the policy approach performs much stronger due to only having to learn the effect part of this piecewise-linear function. The policy, R&C and causal forests exhibit roughly similar convergence, with optimal policy trees outpe rforming the greedy alternative.

To summarize the results, the performance of policy trees depends on the nature of the effect function, but is largely independent of the baseline function. This is because the policy tree only considers the relative effects of each treatment and does not need to estimate the raw outcome under each treatment, and therefore does not depend on the complexity of the underlying baseline function. When the effect function can be modeled well by a tree structure, the policy trees pe rform among the best methods, with the optimal approach outperforming the greedy method when the solution is non-trivial. On the other hand, the performance of prescriptive trees depends heavily on the complexity of both baseline and effect functions, and perform worse than policy trees when the baseline is non-trivial. R&C and causal forests perform well in most cases, but suffer from a lack of interpretability and in some cases exhibit slower convergence than policy trees.

4.2 Multiple treatments

In this section, we extend the previous experiment setup to consider problems with more than two treatment options. We again borrow the setup from Bertsimas et al. (2019) and add an additional experiment. In this case, the outcomes are generated as

$$\begin{aligned} Y_0(\varvec{\mathbf {x}})&= \text {baseline}(\varvec{\mathbf {x}}), \\ Y_1(\varvec{\mathbf {x}})&= \text {baseline}(\varvec{\mathbf {x}}) + \text {effect}_1(\varvec{\mathbf {x}}),\\ Y_2(\varvec{\mathbf {x}})&= \text {baseline}(\varvec{\mathbf {x}}) + \text {effect}_2(\varvec{\mathbf {x}}). \end{aligned}$$

The treatments are assigned so that the “no treatment” option is more likely to be assigned when the baseline is small, and treatments 1 and 2 are equally likely to be assigned:

$$\begin{aligned} {\mathbb {P}}(Z = 0 | \varvec{\mathbf {X}} = \varvec{\mathbf {x}})&= \frac{1}{1 + e^{Y_0(\varvec{\mathbf {x}})}} \\ {\mathbb {P}}(Z = 1 | \varvec{\mathbf {X}} = \varvec{\mathbf {x}})&= {\mathbb {P}}(Z = 2 | \varvec{\mathbf {X}} = \varvec{\mathbf {x}}) = \frac{1}{2} \left( 1 - {\mathbb {P}}(Z = 0 | \varvec{\mathbf {X}} = \varvec{\mathbf {x}}) \right) \end{aligned}$$

The experiments we consider as shown in Table 4. As before, the outcomes in the training set have additional i.i.d. noise added in the form $\epsilon _i \sim \text {Normal}(0, 0.1)$. We again report the mean regret for each method on the testing set. Because there are multiple treatments, we do not include causal forests.

Table 4 Experiment design for synthetic experiments with multiple discrete treatments

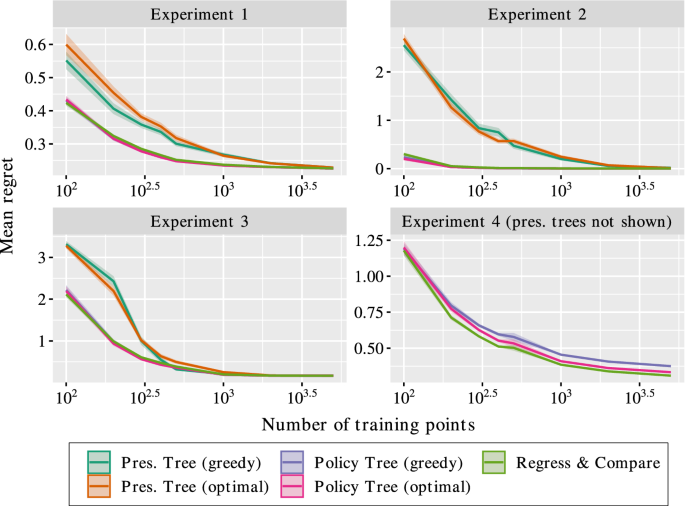
Figure 3 presents the results of the experiments. We make the following observations:

• Experiment 1 The baseline function is piecewise-linear and the effect functions are piecewise-constant and quadratic. R&C performs the strongest as it is best able to model the complicated non-linear effect function of the second treatment. Policy trees are capable of easily learning the first effect function, and do not have to worry about the baseline, so the optimal policy trees outperform the prescriptive methods. Due to the complexity of the second effect function, the optimal policy tree approach significantly outpe rforms the greedy approach.

• Experiment 2 The baseline function is quadratic and the effect functions are both piecewise-constant. The policy tree approaches converge towards zero regret as they are capable of learning both effect functions exactly. The optimal approach performs slightly better than the greedy method. The prescriptive approaches and R&C exhibit slower convergence as they additionally have to deal with the complexity of learning the quadratic baseline.

To summarize, these results mirror those of the binary treatment case. The policy trees approach depends solely on the complexity of the effect functions, and the baseline function is not important. In the case where the effect functions are non-trivial, the optimal policy trees outpe rform the greedy method as they are better at learning these difficult functions.

Fig. 3

Results for synthetic experiments with multiple discrete treatments

4.3 Continuous treatment

Now, we consider experiments where the outcomes are a continuous function of the treatment. In this case, our prescription is the dose level of the treatment to apply, rather than choosing one treatment option from the available set.

For these experiments, we define an outcome function $y(\varvec{\mathbf {x}}, z)$ that depends on both the features $\varvec{\mathbf {x}}$ of the datapoint and the treatment dose z that is applied. Table 5 shows the functional forms that we consider. We consider treatment doses between $-4$ and 4, and again treat lower outcomes as more desirable.

Table 5 Functions used for continuous-treatment synthetic experiments

We generate the training and testing data as before. We assign treatment doses to the training data in a biased fashion similar to before so that better treatment assignments are more likely. Concretely, for each point we sample five candidate doses $t_k \sim \text {Uniform}(-4, 4)$ and calculate the outcome under each such dose, $y(\varvec{\mathbf {x}}, t_k)$. We then assign the treatments according to a softmax probability:

$$\begin{aligned} {\mathbb {P}}(Z = t_k | \varvec{\mathbf {X}} = \varvec{\mathbf {x}}) = \frac{e^{-y(\varvec{\mathbf {x}}, t_k)}}{\sum _j e^{-y(\varvec{\mathbf {x}}, t_j)}} \end{aligned}$$

As before, the outcomes in the training set have additional i.i.d. noise added in the form $\epsilon _i \sim \text {Normal}(0, 0.1)$. For the test set, we assign the dose that minimizes the outcome function for the given $\varvec{\mathbf {x}}$.

We consider four experiments as detailed in Table 6.

Table 6 Experiment design for synthetic experiments with a single continuous treatments

For consistency, we provide the same dosing options to all methods. We discretize the $(-4,4)$ interval into 10 evenly spaced values and use these as the candidate doses for methods to prescribe. We consider the following methods:

• Prescriptive Trees We include both greedy and optimal prescriptive trees. We round all observed doses in the training data to the nearest candidate dose before training, and use the candidate doses as the prescription options. We set $\mu =0.5$ and consider trees up to depth 5, using validation to select the best depth and complexity parameter $\alpha$.

• Policy Trees We include both greedy and optimal policy trees as presented in Sect. 3. We consider trees up to depth 5, using validation to select the best depth and complexity parameter $\alpha$. We estimate rewards on the training set by first training an XGBoost (Chen and Guestrin 2016) model to predict the outcome as a function of the features x and the treatment z, and then using this model to predict the outcome under each candidate dose for each observation to use as the rewards matrix. We ran XGBoost for 100 rounds with default parameters.

• Regress & Compare We include a regress-and-compare approach using XGBoost. We use the training data to train an XGBoost model with default parameters for 100 rounds to predict the outcome as a function of the features x and the treatment z. For each point in the test set we prescribe the candidate dose that has the lowest predicted outcome.

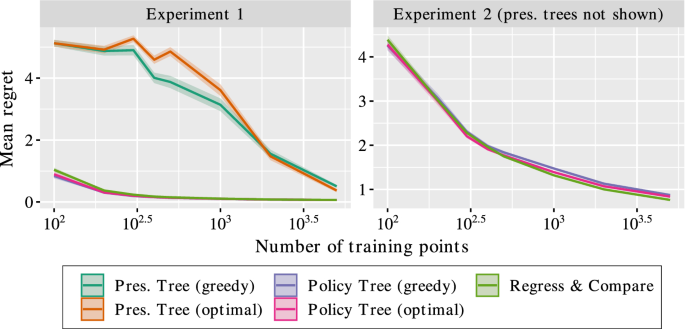
The results are shown in Fig. 4. We make the following observations:

• Experiment 1 The optimal dose is to prescribe $z = x_1$, so the learned dosing function should be linear. The policy tree approaches learn this linear function increasingly well as the size of the training data increases, matching R&C. The prescriptive trees learn much more slowly.

• Experiment 2 Here the optimal dose is either $-4$ or 4 based on the sign of $x_1$, so the optimal prescription policy should be a tree with a single split. Indeed, the policy tree and R&C approaches quickly reach zero regret, but prescriptive trees require much more data to discover this optimal policy.

• Experiment 3 The optimal dose in this setting is given by a piecewise-constant function. All methods eventually converge to zero regret, but the prescriptive approaches require more data to achieve this performance.

• Experiment 4 The optimal dose follows a piecewise-linear function. The prescriptive tree approaches have regrets above 2 for all training set sizes, significantly worse than the remaining methods (thus are not shown in the figure). The policy tree approaches have similar convergence to R&C, with the greedy policy trees performing slightly worse than the optimal approach due to the complexity of the outcome function.

In summary, we see that the policy approaches are significantly more efficient with the training data than prescriptive approaches. The optimal policy tree approach matches the R&C approach in all cases, but provides an interpretable policy in addition to performance.

Fig. 4

Results for synthetic experiments with a single continuous-dose treatment. For Experiment 4, greedy and optimal prescriptive trees have regret between 2 and 5 and are omitted from display to avoid axis distortion

4.4 Multiple continuous treatments

Our final set of experiments consider cases with multiple continuous-dose treatments. For these experiments, we define an outcome function $y(\varvec{\mathbf {x}}, t_1, t_2)$ that depends on both the features $\varvec{\mathbf {x}}$ and on two treatment doses $t_1$ and $t_2$ that are applied. We consider doses between $-4$ and 4 for both treatments, with lower outcomes more desirable. We consider two experiments as outlined in Table 7.

Table 7 Experiment design for synthetic experiments with multiple continuous treatments

We follow a similar approach to Sect. 4.3 to assign treatments in the training data. First, we randomly draw five candidate doses $(t_{k_1}, t_{k_2})$ where both $t_{k_1},t_{k_2}$ are drawn independently from $\text {Uniform}(-4, 4)$, and evaluate the outcome function $y(\varvec{\mathbf {x}}, t_{k_1}, t_{k_2})$. We then assign the treatment using softmax probabilities over these five options.

The same methods are used as in Sect. 4.3, modified appropriately to account for two treatment options. We discretize each treatment dose into six values, giving a total of 36 possible dose combinations over the two treatments.

Figure 5 shows the results. We make the following observations:

• Experiment 1 This experiment combines experiments 1 and 2 from Sect. 4.3, so the optimal doses for the treatments are linear and piecewise-constant functions, respectively. The policy trees and R&C learn this structure very quickly. The prescriptive trees learn much more slowly, due to the data being thinned across the 36 possible treatment options.

• Experiment 2 This experiment combines experiments 3 and 4 from Sect. 4.3, so the optimal doses for the treatments are piecewise-constant and piecewise-linear functions, respectively. The prescriptive tree approaches are unable to learn from this data and have regret above 8 regardless of the training set size, significantly higher than the other approaches (thus are not shown in the figure). The policy tree approaches converge similarly to R&C, with the optimal policy trees performing stronger than the greedy approach, due to the complexity of the problem structure.

In summary, the prescriptive approaches are particularly inefficient for problems of this nature, as the discretization of the treatment options thins the data and makes learning significantly more difficult. In contrast, the policy tree approaches can learn from the data equally well regardless of the number of treatment options, and match the performance of the regress-and-compare approach, with the optimal method outperforming the greedy method when the outcome function is non-trivial.

Fig. 5

Results for synthetic experiments with multiple continuous-dose treatments. For Experiment 2, greedy and optimal prescriptive trees have regret between 8 and 10 and are omitted from display to avoid axis distortion

4.5 Runtime comparison

In addition to the relative performance of each method, we are also interested in comparing their runtimes. Table 8 shows the mean runtime in seconds for each method on each of the synthetic experiments discussed earlier. These reported runtimes are for the largest instance of each problem with $n=5,000$ training points, and measure the complete time to run each method, including training, validation, and reward estimation for the policy tree methods.

Table 8 Mean runtime (in seconds) for each method on each of the synthetic experiments with $n=5,000$ training points. The methods are abbreviated as GPrT (Greedy Prescriptive Trees), OPrT (Optimal Prescriptive Trees), GPoT (Greedy Policy Trees), OPoT (Optimal Policy Trees), R&C (Regress and Compare), and CF (Causal Forest)

In the case of discrete treatments, we see that the greedy prescriptive trees are the fastest, while the greedy policy trees have times similar to R&C. This is because the greedy policy tree runtime includes the time for reward estimation, which like R&C involves training separate random forests for each treatment and dominates the runtime. As we might expect, the optimal tree methods take more time to run than their greedy variants. The runtimes for both optimal tree methods are roughly equivalent, and are typically are slower than R&C by a factor of between 1.5 and 2.5.

For the problems with continuous treatments, we see that again the greedy trees have the lowest runtimes, with greedy policy trees again having similar runtime to R&C. We see that the cost of R&C and reward estimation is much lower in the continuous treatment setting, with R&C being roughly an order of magnitude faster compared to the discrete treatments. The optimal policy trees have similar runtimes to the discrete treatment case, whereas the optimal prescriptive trees have higher runtimes. In particular, the runtimes for optimal prescriptive trees with multiple continuous treatments are much higher than for a single continuous treatment, indicating that this approach is not as suited to handling problems with so many treatment options, compared to the policy tree approach which has much lower runtimes.

In all of these cases, the optimal policy trees have runtimes on the order of minutes on these moderately-sized problems with $n=5,000$ and up to 36 treatment options, which demonstrates the scalability of this approach.

4.6 Summary of synthetic experiments

In this section we conducted a number of experiments covering both discrete and continuous dose treatments, as well as multiple treatments. The common theme seen in the results was that the policy tree approach performed similarly to the black-box regress-and-compare methods, whereas the prescriptive tree method often struggled. In the case of discrete treatments, the performance of policy trees was related to the complexity of the treatment effect alone, whereas for prescriptive trees, the performance depended on the complexity of the entire outcome function. For continuous dose treatments, the policy trees learned efficiently regardless of the number of treatment doses considered, whereas the prescriptive trees suffered if the data was spread too thinly across the doses. In both cases, the optimal policy trees approach outperformed the greedy approach when the relevant treatment function was non-trivial to learn.

5 Performance on real-world data

In this section, we consider three applications of Optimal Policy Trees in real-world applications. First, we consider the problem of pricing in a grocery store setting, where the price is a single continuous-dose treatment to optimize. Second, we consider diabetes management, where the task is to determine the optimal doses for multiple drug options. Finally, we consider the task of pricing financial instruments, where there are many existing pricing strategies that are used to construct prices based on the current market state, and we want to determine which pricing strategies work best in different conditions, thus framing the task as a prescriptive problem with multiple discrete treatment options.

5.1 Grocery pricing

In this section, we apply Optimal Policy Trees to the problem of grocery store pricing, using a publicly available dataset collated by the analytics firm Dunnhumby. The dataset has detailed transaction, household, and product information on over 200,000 shopping trips. This dataset was studied in Biggs et al. (2020) where they showed an estimated 67% increase in predicted revenue for strawberries under a greedy tree-based pricing algorithm. We treat this problem as a prescriptive problem with the price as a continuous-dose treatment, and compare the performance of Optimal Policy Trees to other methods.

We followed the same data preparation as described in Biggs et al. (2020), where each row refers to a shopping trip with detailed information on the household, the unit price of the strawberries (ranging from $1.99 to $5.00, with most of the prices in 50-cent increments), and the outcome (whether the strawberries was purchased or not). Similar to the previous analysis, if the household did not purchase any strawberries, the price was imputed using an average of previous transactions. The data was split into 50% training and 50% testing, with an independent XGBoost model estimating the rewards under each pricing scenario in the testing data.

To apply Optimal Policy Trees, we first estimated the expected revenue under each price option on the training data . To achieve this, we used XGBoost to predict the purchase probability as a function of household features and continuous price, and then for each training point and price option, we multiplied the price by the estimated purchase probability under this price to get the expected revenue. We then fit an Optimal Policy Tree on the household features and these revenue estimates. For a fair comparison to Biggs et al. (2020), we also trained a greedy policy tree on the same revenue estimates. We also compare against Optimal Prescriptive Trees, by treating each 50-cent price point as a discrete treatment and the observed revenue as the outcome. For all three methods, we used cross-validation to tune the depth of the decision trees, up to a maximum of 6.

The results are shown in Table 9, where we show the increase in revenue under each model, which is calculated as the difference between the estimated revenue under prescribed price vs. current price. We see that the Optimal Policy Trees has the best performance among the three, with over 77% improvement in revenue. The greedy policy tree approach achieved an improvement in revenue of 66%, which is similar to the result reported in Biggs et al. (2020) (where the small difference is likely attributable to a different training/testing split). The improvement of over 11% for Optimal Policy Trees over the greedy approach demonstrates the significant performance gains we can achieve by training the tree with a view to global optimality.

Table 9 Comparison of different methods in the grocery pricing example

We also observe that both policy tree approaches outperform Optimal Prescriptive Trees, which shows an estimated revenue improvement of 62%. This reinforces the results of Sect. 4.3 that separating the reward estimation and policy learning tasks provides an edge when faced with outcomes that are a complex function of a continuous dose treatment.

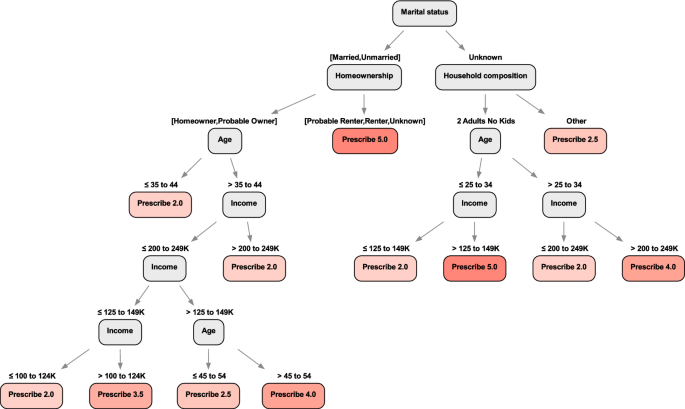
A trimmed version the Optimal Policy Tree is shown in Fig. 6 as an example. The tree splits based on marital status, home ownership, age, income level, household composition, etc., where generally it prescribes lower prices for households with lower income and vice versa. We note that we recommend the highest price of $5.00 in one of the leaves, which is defined by a younger population ($\le 34$ years old), that are two adults with no children, own their house, and have a high income level (above $125k). This is consistent with intuition that this demographic group can be price insensitive.

Note that in practice, an individual-based pricing policy may not be feasible due to regulatory and operational constraints, but this approach could be easily adapted to the store level pricing decisions based on aggregate demographic features for the region, and still deliver an improvement in revenue.

Fig. 6

Optimal Policy Tree with continuous dosing for grocery store pricing

5.2 Diabetes management

In this section, we apply our algorithms to personalized diabetes management using patient-level data from Boston Medical Center, under a multi-treatment continuous dosing setup. This dataset was first considered by Bertsimas et al. (2017), where the authors propose a k-nearest neighbors (kNN) regress-and-compare approach, and was revisited by Bertsimas et al. (2019) with Optimal Prescriptive Trees.

This dataset consists of electronic medical records for more than 1.1 million patients from 1999 to 2014. We consider more than 100,000 patient visits for patients with type 2 diabetes during this period. The features of each visit include demographic information (sex, race, gender etc.), treatment history, and diabetes progression. The goal is to recommend a treatment regimen for each patient, where a regimen is a combination of oral, insulin, and metformin drugs and their dosages.

In the previous studies, the regress-and-compare and Optimal Prescriptive Trees approaches were limited to considering discrete treatments, so the treatment options were discretized into 13 different combinations, from which the method had to prescribe one choice to the patient. This has the unfortunate side effect of removing information about the proximity of different drug combinations. For instance, the combinations “insulin + metformin” and “insulin + metformin + 1 oral” are similar prescriptions, and it is plausible we may be able to learn shared information from patients that received either of these. On the other hand, “insulin” and “metformin + 2 oral” are very unrelated and we should not expect to use the patients receiving one of these to learn about the other.

When the treatments are discretized, all treatments are completely disjoint, and the rewards are learned separately, with no ability for shared learning where appropriate. Another approach is to view this problem as multiple continuous dose treatments. In this way, the treatment decision becomes the doses of insulin, metformin and oral drugs to apply, which we can view as a vector $(z_\mathrm {insulin}, z_\mathrm {metformin}, z_\mathrm {oral})$. From this perspective, the combinations “insulin + metformin”, (1, 1, 0), and “insulin + metformin + 1 oral”, (1, 1, 1), are indeed closer than “insulin”, (1, 0, 0) and “metformin + 2 oral”, (0, 1, 2), and thus we might expect that viewing the problem in this way could lead to more efficient learning due to the ability to share information across treatments.

We consider applying Optimal Policy Trees to this problem, both with 13 discrete treatment options and also with the continuous dosing model described earlier, to examine whether this more accurate model of the treatments indeed leads to better data efficiency. We used boosting to estimate the rewards in both the discrete and continuous-dose treatment models. To ensure fairness, the continuous-dose Optimal Policy Trees were required to prescribe from the same 13 treatment options, so any difference comes from better estimation due to a more accurate model of reality.

We follow the same experimental design as in Bertsimas et al. (2017). The quality of the predictions on the testing data is evaluated using a random-forest approach to impute the counterfactuals on the test set. We use the same three metrics to evaluate the various methods: the mean HbA1c improvement relative to the standard of care; the percentage of visits for which the algorithm’s recommendations differed from the observed standard of care; and the mean HbA1c benefit relative to standard of care for patients where the algorithm’s recommendation differed from the observed care. These metrics were selected because the reduction in HbA1c is considered clinically relevant.

We varied the number of training samples between 1,000 and 50,000 (with the test set fixed) to examine the effect of the amount of training data on out-of-sample performance. In addition to both Optimal Prescriptive Trees and Optimal Policy Trees (with both discrete and continuous treatment models), we consider the performance of a baseline method that continues the current line of care, and an oracle method that prescribes the best treatment for each patient is selected according to the estimated counterfactuals on the test set.

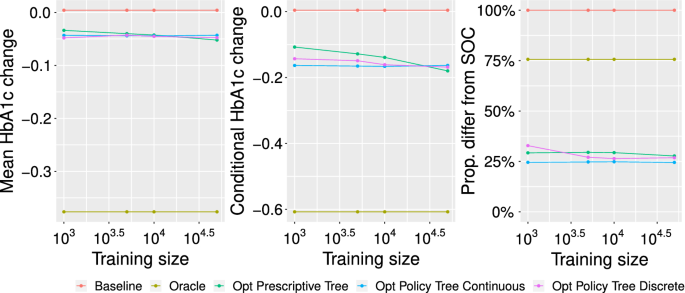
In Fig. 7, we show the performance across these methods. We observe that while all three tree methods converge to roughly the same performance as all the data is used, the Optimal Policy Trees achieve much better results when the training set is smaller. In addition, the Optimal Policy Trees based on the continuous-dose reward model outperform those based on the discrete treatment reward model. In fact, we see that the performance of the continuous-dose policy trees is roughly constant regardless of the size of the training set, indicating it is extremely efficient with the data, and only requires 1,000 samples to deliver performance equivalent to the Optimal Prescriptive Trees with 50,000 samples. This is very strong evidence that separating the counterfactual estimation and policy learning steps and permitting shared learning across treatments enable extremely efficient use of data.

Fig. 7

Comparison of methods for personalized diabetes management. The leftmost plot shows the overall mean change in HbA1c across all patients (lower is better). The center plot shows the mean change in HbA1c across only those patients whose prescription differed from the standard-of-care. The rightmost plot shows the proportion of patients whose prescription was changed from the standard-of-care

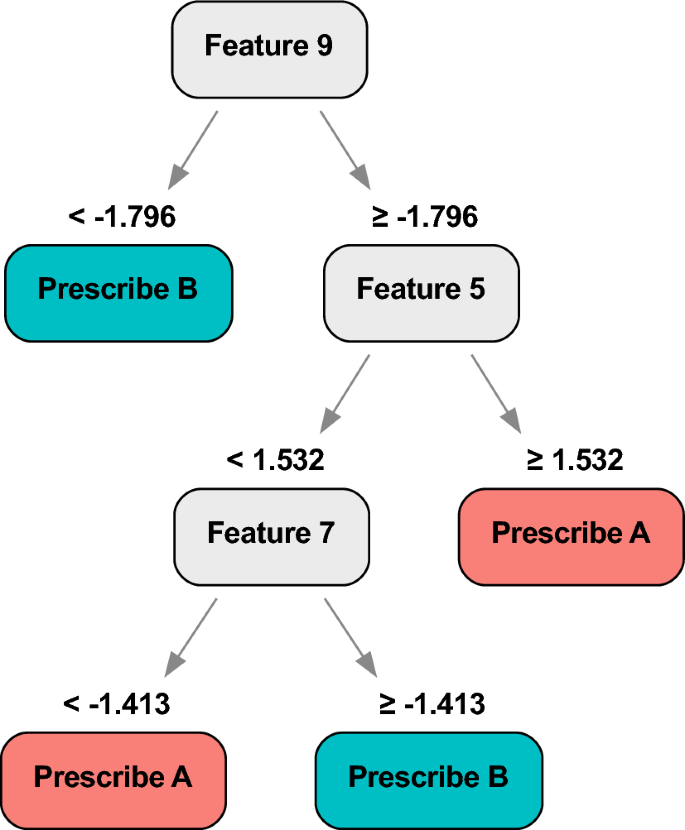
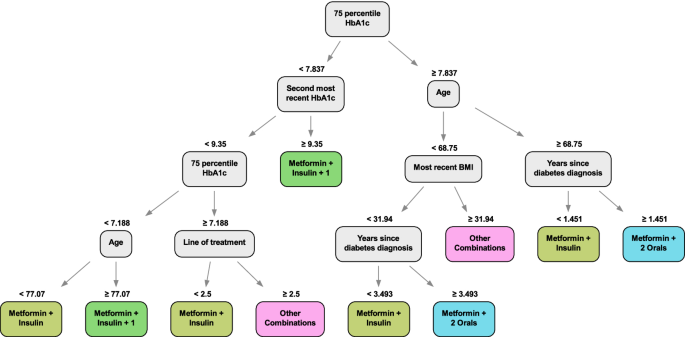
We show an example of the Optimal Policy Tree (continuous dosing) output in Fig. 8 trained with 1,000 data points. We can see that it uses the patient’s recent HbA1c history, age, current line of treatment, years since previous diagnosis, and BMI to prescribe from the variety of treatments. This tree, with 10 leaves, is significantly smaller than the best Optimal Prescriptive Tree, which had 21 leaves, with similar performance. This is strong evidence that separating the counterfactual estimation from the policy learning results in more concise trees that focus solely on the factors that affect treatment assignment. In contrast, the Optimal Prescriptive Trees are larger because the splits in the tree serve two purposes: refining the counterfactual estimation and determining the optimal treatment policy.

Fig. 8

Optimal Policy Tree with continuous dosing for personalized diabetes management

5.3 Pricing financial instruments

In this section, we apply Optimal Policy Trees to develop a new interpretable pricing methodology for exchange-traded financial instruments (e.g. stocks, bonds, etc.). For commercial sensitivity reasons, some details of the study are omitted and the tree we show is illustrative.

The problem we consider is predicting the future price of an asset at some time in the near future (on the order of minutes). The data available for prediction is the transaction history of this and other assets as well as all buy/sell orders on the market and their price points.

There are many approaches to predict future prices from this information. For instance, a common calculation is the mid-price, which is the average price of the highest “buy” (bid price) and lowest “sell” (ask price) orders. Another is the weighted mid-price, which is similar but weights the average by the size of the orders. There are many such pricing formulae that consider various aspects of the historical data (e.g. historical transaction prices, momentum prices, high-liquidity prices, etc.), and these are often highly-complex non-linear formulae that have been hand-designed based on domain expertise. In collaboration with domain experts, we identified nearly 200 such pricing formulae that are regularly used. It is known that different formulae perform well in some market conditions and poorly in others, but this is based loosely on human intuition and not directly understood in a quantitative fashion. Given the work and experience that has gone into carefully crafting these highly non-linear formulae, instead of trying to construct our own pricing formula from scratch, we decided to treat each formula as a distinct treatment option and attempt to learn which formula to apply in different market scenarios to achieve the best price predictions.

We applied Optimal Policy Trees to develop a policy for which pricing methodology is best to use under different market conditions. Mathematically, each observation i consists of market features $\varvec{\mathbf {x}}_i \in {\mathbb {R}}^p$, and we have a set of m pricing methodologies to choose from. For every observation i and every pricing methodology t, we derive the rewards $\Gamma _{it}$ by computing the absolute difference between the actual future price and the price calculated by method t given market features $\varvec{\mathbf {x}}_i$. The reward matrix $\Gamma$ is therefore fully known and does not need to be inferred. We train Optimal Policy Trees against these errors to learn which pricing strategy is most accurate in different market conditions.

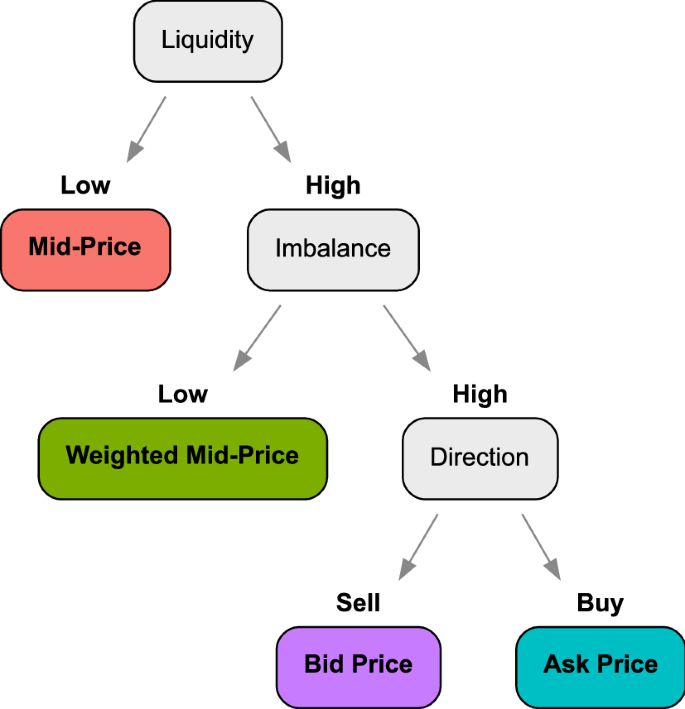
An example of the Optimal Policy Trees learned on the data is shown in Fig. 9. We observe that the tree prescribes the mid-price when liquidity is low: this is consistent with the intuition that in such conditions, most of the market signals are noisy and the best choice is to simply average the bid and ask prices. On the other hand, in high liquidity conditions, the tree then splits on order imbalance, picking the weighted mid-price as the best estimator when the number of orders on the buy and sell sides are similar and the market is balanced. On the other hand, if the sizes of buy and sell orders are highly imbalanced, the tree then splits on the direction of the disparity to either assign the ask price if the bias is towards the “buy” side, or the bid price if the bias is towards the “sell” side, mirroring the fundamental dynamics of supply and demand. Together, the splits of this tree provide a clear and understandable formalization of when each price is best that is aligned with human intuition.

Fig. 9

Example Optimal Policy Tree that prescribes the best pricing method based on market conditions

In comprehensive out-of-sample testing, the pricing approaches developed using Optimal Policy Trees consistently outperformed the existing approaches to pricing by up to 2% in terms of accuracy of future price predictions, and the interpretability and transparency of the models allow humans to derive insights and further their own understanding of the problem.

6 Conclusions

In this paper, we presented an interpretable approach for learning optimal prescription policies, combining the state-of-the-art in counterfactual estimation from the causal inference literature with the power of modern techniques for global decision tree optimization. The resulting Optimal Policy Trees are highly interpretable and scalable, and our experiments showed that they offer best-in-class performance, outperforming similar greedy approaches, and make extremely efficient use of data compared to prescriptive tree methods.

Finally, we showed in a number of real-world applications that this approach results in prescription policies of significantly higher quality when compared to existing approaches.

This framework of learning prescription policies is very general and invites many paths for potential future work. For example, one might consider multi-output scenarios where a prescription could affect several outputs at once. Another avenue could be considering constraints on which treatments can be applied to each observation depending on their features.