Abstract
Data-driven decision-making has garnered growing interest as a result of the increasing availability of data in recent years. With that growth many opportunities and challenges have sprung up in the areas of predictive and prescriptive analytics. Often, optimization can play an important role in tackling these issues. In this paper, we review some recent advances that highlight the difference that optimization can make in data-driven decision-making. We discuss some of our contributions that aim to advance both predictive and prescriptive models. First, we describe how we can optimally estimate clustered models that result in improved predictions. Next, we consider how we can optimize over objective functions that arise from tree ensemble models in order to obtain better prescriptions. Finally, we discuss how we can learn optimal solutions directly from the data allowing for prescriptions without the need for predictions. For all these new methods, we stress the need for good performance but also the scalability to large heterogeneous datasets.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Data-driven decision-making has been brought front and center in society over the recent years, particularly due to a wide variety of difficult challenges that have surfaced in many areas such as manufacturing, services, supply chains, healthcare, and sustainability. With the ever-growing availability of data as well as the increasing speed of computation, we have been able to build methods utilizing optimization, machine learning, and statistics to significantly improve decision-making. These approaches have also enabled decision-makers to make more and more granular, sometimes even personalized, decisions very quickly. The aim of data-driven analytics has been to cater to each individual’s heterogeneous preferences in real-time.
Generally, data-driven methodologies tackle real-world problems in a two phased approach. First, data is used to develop a model of the uncertainties related to the problem, e.g., estimating a customer demand model for a product. Second, this model of uncertainty is then used in solving an optimization model, e.g., solving a price optimization model for a product. While the first step is predictive, the second step is prescriptive. Naturally, the complexity of the prescriptive problem of interest directly depends on the complexity of the underlying predictive model. Simple parametric predictive models are easy to optimize over. Nevertheless, they are restricted in their predictive power and might not be as accurate in predicting uncertainties. On the other hand, complex non-parametric predictive models are very expressive and can be highly accurate in predicting uncertainties. Unfortunately, they are difficult to optimize over. Hence, there is a trade-off in modeling the predictive and prescriptive problems: generating data-driven decisions that perform well in the real-world versus keeping the models tractable with today’s computational power. This is where the importance of optimization arises, namely, to help balance this trade-off and help us understand what is possible and what is not.
In this paper, we shed some light on the power that optimization can have in molding data-driven methods. We focus on several of our own works that highlight examples where data-driven decision-making can benefit by taking an optimization perspective. These works have developed optimization tools for both predictive and prescriptive problems. In more detail, this paper discusses the following:
-
1.
We first discuss clustered predictive models and how they can be learned from data using the Cluster-while-Estimate method. Clustered models aim to address heterogeneity that exists within datasets by clustering the homogenous observations together and simultaneously predicting each observation’s outcome in the group. While this is ideal for learning from large, unstructured data, the underlying optimization problem is theoretically and computationally difficult to solve. This is where developing a new optimization-based estimation method is necessary. In this paper, we discuss the tractable Cluster-while-Estimate algorithm that is able to estimate clustered models.
-
2.
We further expand our discussion on developments in predictive tasks and optimization by discussing how ensemble trees can be optimized over in a tractable way. This task of prescription using ensemble trees has been shown to be NP-hard so we discuss several approximation algorithms that have been developed in the literature in the recent years.
-
3.
Finally, we consider the loss in quality of prescription when blindly using a prediction model as an intermediary step. Such a process can produce significantly suboptimal decisions even if the prediction loss is low. Instead, we discuss a method we developed for prescribing decisions directly from past data. This method encapsulates as a special case both a feature-based SAA (Sample Average Approximation) approach as well as robust optimization. This discussion illustrates the role optimization research plays in moving from data directly to decisions.
There is a wide range of data-driven methods that have been developed in the literature in the recent years. In this paper we will provide an overview of some of this literature. In particular, we consider three parts (i) clustered learning methods, (ii) tree-based optimization methods, and (iii) model-free optimization methods. For each part, we will review some related literature, although we mainly focus on our own related research, particularly in [1,2,3], and [4].
2 Learning clustered models
In predictive problems, we often deal with big datasets that are marked by heterogeneity across observations and high-dimensionality across features. Within the statistics and machine learning literature, there are many strong predictive models that have been developed. However, in heterogeneous settings, these models generally become weaker as they only capture the heterogeneity that can be described by the available features. Even in high-dimensional settings, we often miss some of the features that are necessary to explain heterogeneity. When these features are missing, we propose to use clustered models to describe the heterogeneous groups of observations. In the following, we discuss a clustered learning method, which uses clustering and regularization to learn homogeneous groups within the dataset and to learn which features are important to predict outcomes within that cluster. Our interest in developing these methods arose from our collaborations with industry where we encountered several operational challenges that could only be dealt with by learning predictive models from large unstructured datasets.
As an example, consider a firm introducing a new product for which it wants to forecast sales to schedule production. After the seminal paper in product diffusion [5], the new product forecasting challenge has garnered vast attention from varied fields of study [6,7,8,9]. Clearly, the major difficulty in this problem is the absence of historical data on the new product. However, there might be sales data from comparable products that were introduced previously. Still, it remains a question which products are most informative about the new product’s sales. This challenge is addressed by the clustered learning method: cluster the old products and jointly fit a model on their historical sales, then assign the new product to the right cluster and forecast its sales with the corresponding model. Instead of us specifying which product department, category, or subcategory to fit sales on and which features to use, this clustered learning method picks the most comparable products and the most predictive features by itself.
The literature has considered clustering in offline learning before we proposed novel learning and optimization methods in [1] and [2]. As an early form of incorporating clusters in learning [10], the clusterwise regression problem considers outcomes of each observation to be described by a linear regression. This framework has subsequently been applied to various application domains including market segmentation [11], income prediction [12], product lifecycles [13], rainfall prediction [14], and many others. One of the first algorithms to address this problem was also proposed by [10], which iteratively reassigned data points to different clusters if it would result in a reduction of the prediction error. Since then, improved heuristic algorithms have been proposed to solve the clusterwise regression problem. Simulated annealing is used in [15], maximum likelihood estimation and expectation-maximization in [16], and Gibbs sampling in [17]. Mathematical programming based approaches have also been proposed. For example, while [18] propose a nonlinear formulation, [19] propose a compact mixed-integer linear formulation, and [20,21,22] propose a heuristic based on column generation for an integer linear formulation. In contrast to this literature, in [1] and [2], we move beyond linear regression and propose a more general clustered learning approach that can consider logistic regression, regression trees, classification trees, and others.
Another form of incorporating clusters, is the renowned Latent Class Analysis (LCA) [23], which aims at discovering underlying latent clusters in the data, and fit different response functions inside each of these clusters. Our optimization-based approach to the problem offers more flexibility in terms of which response functions that can be fit (classical regression methods, tree-based methods, etc), which types of data that can be considered (discrete versus continuous), without needing to specify distributional assumptions on the data. These differences are further discussed in more details in [1] and [2].
2.1 General clustered model
Our clustered learning approach, the Cluster-while-Estimate method (or CWE method), was developed in [1] for regression models and extended to classification models by [2]. The aim of this approach is to cluster observations (e.g., grouping similar products) whose outcomes (e.g., sales forecasts) can be predicted through a similar model. The CWE method clusters observations based on how similar their outcomes can be predicted as a function of their features, not based on how close the observations’ features are.
This shift in perspective grants tremendous flexibility, which causes the model to be more scalable and accurate. The model is highly scalable as it can deal with big datasets where observations are not clearly linked or features might be redundant. When there are many heterogeneous observations, the method will find a model that suits each homogeneous cluster within the large dataset. When the features are high-dimensional, the algorithm will find the features within the large dataset that need to be included in each cluster’s sparse model. The model also improves predictive accuracy as clustering and fitting models jointly will eliminate harmful clusters. When just having similar features does not mean having similar outcomes, the clusters found by sequential methods have low predictive power.
For our method, we assume to have data on N observations with D features contained in the matrix \(X \in {\mathbb {R}}^{N \times D}\), and their outcomes are contained in the vector \(y \in {\mathbb {R}}^{N}\). We assume that there are L different clusters, and the matrix \(Z \in {\mathbb {R}}^{N \times L}\) indicates which observation belongs to which cluster. Finally, the model’s error of every observation is denoted by the vector \(\epsilon \in {\mathbb {R}}^{N}\). The distribution of this error varies across regression and classification models.
In a clustered model, we presume that the observations are heterogeneous. This means there are multiple clusters of observations whose outcomes are generated through different models. If the underlying data is homogeneous, our model would still be applicable by considering a single cluster. With this interpretation, we define the clustered model for any observation \(i = 1,\dots ,N\):
where \(f_{l}\) is the prediction model of each cluster. This clustered model is extremely general as each cluster can be described by any conventional regression model, or classification model if we let the above model describe the probability \({\mathbb {P}}(y_i = k)\) that \(y_i\) equals some class \(k \in \{1,\dots ,K\}\). Our interest lies in estimating the cluster assignments Z denoted by \({\widehat{Z}}\), and estimating the cluster models \(f_{l}\) denoted by \({\widehat{f}}_{l}\). We intend to estimate the cluster assignments and the cluster models jointly by solving the mixed-integer non-linear optimization formulation (2):
In this problem, we estimate our parameters by minimizing the regularized loss, which consists of two parts. The first part is the loss due to prediction error, namely the further our prediction \(\sum _{l=1}^{L} z_{il} f_l(x)\) is from the observed outcome \(y_i\) the larger the loss we incur. The second part is the loss due to the regularizer which penalizes complex models. In the case of linear regression, the loss \({\mathcal {L}}\) can be the squared error while the regularizer \({\mathcal {R}}\) can be the LASSO or Ridge regularizer. The hyperparameter \(\lambda \ge 0\) balances how much to minimize errors and penalize complexity. Clearly, we minimize the errors to make sure that our model predict accurately. However, we also penalize complexity to allow the model to expressly state which features are unimportant to a cluster.
Both theoretically and practically, the optimization problem (2) is difficult to solve. Theoretically, even in the case of linear regression, the problem is proven to be NP-hard by [24]. Practically, even though some cases of the problem can be reformulated as tractable mixed-integer optimization problems, commercial solvers are unable to solve large-scale instances.
Instead, in [1] and [2], we propose the CWE algorithm that can find an approximate solution to problem (2) within polynomial time. Notably, this algorithm can be used for any type of regression or classification model within the clusters. At its core, this algorithm initializes cluster assignments, fixes these and estimates cluster models, fixes these and estimates cluster assignments, and then repeats this process. For given data, loss \({\mathcal {L}}\), and regularization \({\mathcal {R}}\), our CWE algorithm runs along the following steps:
-
1.
Initialize the assignment of products to clusters \({\widehat{z}}_{il}^{(0)}\), either randomly, or through a clustering method like k-means or hierarchical clustering.
-
2.
Iteratively re-estimate the cluster models and cluster assignments. For iteration \(t = 1,\dots ,T\):
-
a.
Solve (2) with \(z_{il} = {\widehat{z}}_{il}^{(t-1)}\) to find \({\widehat{f}}_l^{(t)}\), i.e., estimate each cluster model given the currently assigned observations.
-
b.
Solve (2) with \(f_{l} = {\widehat{f}}_{l}^{(t)}\) to find \({\widehat{z}}_{il}^{(t)}\), i.e., assign each observation to the cluster whose model results in the least error prediction.
-
c.
Terminate with \({\widehat{z}}_{il}\) and \({\widehat{f}}_l\) if \(t = T\) or \({\widehat{z}}_{il}^{(t)} = {\widehat{z}}_{il}^{(t-1)}\), otherwise return to step 2a.
-
a.
For a large variety of cluster models, both steps 2a and 2b have tractable solution methods. In step 2a we solve L separate estimation problems for each estimated cluster, which can be done with existing algorithms from statistics and machine learning. In step 2b, observations are reassigned simply by calculating their loss within a cluster and assigning them to the one with the smallest loss. Overall, we show in Proposition 1, which is proven in [1, 2], that this CWE algorithm converges to a local optimum when the clusters do not change anymore.
Proposition 1
([1, 2]) The CWE algorithm converges to a local optimum in polynomial time.
With the CWE algorithm, we can estimate the cluster assignments and cluster models based on historical observations. To predict outcomes for new observations, we need to understand how we can assign the new observation to a cluster. Our approach uses a probabilistic model \(p_l(x)\), which provides the probability of belonging to cluster l given the observation’s features x. This model is estimated with the historical observations by fitting their previously generated cluster assignments \({\widehat{z}}_{il}\) on their features \(x_{i}\). Having estimated the cluster assignment model \({\widehat{p}}_{l}(x)\), we can use a weighted average prediction as our forecast for a new observation with features x:
2.2 Clustered linear regression model
To give an example of a regression problem, we will discuss the version of the CWE method that uses a LASSO regularized linear regression model. This version of the model is also used in [1]. In this case, the cluster models are linear regressions and the clustered model becomes:
where \(\beta _{l} \in {\mathbb {R}}^{D}\) are the linear regression coefficients for cluster l. To estimate the parameters Z and \(\beta \) of this model, we are interested in solving the joint estimation problem that was proposed earlier. In particular, we want to solve the mixed-integer non-linear optimization problem (4):
In this problem, we have two sets of decision variables. First, the binary decision variable \(z_{il} \in \{0,1\}\) indicates whether observation i belongs to cluster l, and second, the decision variable \(\beta _{lj}\) is the linear regression coefficient in cluster l of feature j. As mentioned, we want every cluster to be able to decide whether it needs to use all features, for which we add a regularizer to the model weighted by the hyperparameter \(\lambda \ge 0\).
As mentioned before, solving problem (4) is difficult, and hence, we use the CWE algorithm to estimate the parameters instead. In this case, it means that in step 2a we fit cluster models \({\widehat{f}}_l\) based on LASSO regularized linear regression, and in step 2b we assign observations to clusters \({\widehat{z}}_{il}\) that minimizes their LASSO regularized squared error. In our applications, we like to estimate a multinomial logistic regression as \({\widehat{p}}_l\) to determine cluster assignments for new observations.
To assess the strength of the overall approach, we analyze its performance both in theory and in practice. In [1], we prove that the mean squared error of our estimates shrinks as the number of observations grows, which shows that our estimates are consistent. Then, in [1], we apply our method to forecast sales for new products with data from a consumer goods manufacturer as well as a fashion clothing retailer. For new products of the consumer goods manufacturer, our CWE approach yields MAPEs between 0.21 and 0.41 and WMAPEs of 0.22 to 0.42 depending on the product category. In comparison, for a LASSO regularized linear regression, the MAPEs are on the order of 0.46 to 0.92 and WMAPEs are on the order of 0.31 to 0.83. Even in the most conservative case, our CWE approach performs substantially better than the unclustered benchmark model, improving MAPEs by at least 0.16 and WMAPES by at least 0.09. Applying our model to data from a fashion clothing retailer, we observe that our CWE method is robust. When predicting individual product sales in individual stores, the WMAPEs of our model were around 0.55 to 0.66 and were at least 0.12 lower than those from unclustered models. Also, we observed that aggregating data across their stores allowed our model to perform even better, getting WMAPEs around 0.29 to 0.37 depending on the product category. Overall, these results indicate that our model generates strong robust predictions and it outperforms traditional methods that do not utilize clustering.
2.3 Clustered multinomial logistic regression model
As an example of a classification problem, we will present the version of the CWE method that uses a multinomial logistic regression model. This is the version of the model that is described in [2]. In a multinomial logistic regression where an observation’s outcome can be one of K different classes, the clustered model becomes:
where \(\beta _{lk} \in {\mathbb {R}}^{D}\) are the multinomial logistic regression parameters for belonging to class k according to cluster l. Within our CWE framework, we estimate the parameters Z and \(\beta \) by solving the aforementioned joint estimation problem. Specifically, we reformulate to the following mixed-integer non-linear optimization problem (6):
In the formulation above, \(z_{il} \in \{0,1\}\) is a binary decision variable indicating whether observation i belongs to cluster l, \(\delta _{ik}\) is data indicating whether observation i belongs to class k, and \(p_{ikl}\) is the probability estimate that observation i belongs to class k based on the model in cluster l. Notably, we ignore how the coefficient \(\beta _l\) exactly depends on the cluster assignments Z, as we can clearly see the complexity of the problem. Additionally, we have not included any regularization in the above formulation, but this can be added as it would be for a conventional multinomial logistic regression.
Due to the complexity of solving problem (4), we apply our CWE algorithm to estimate the parameters. In step 2a of the CWE algorithm, we fit our multinomial logistic regression, while in step 2b we re-assign our observations to the best fitting cluster. With the CWE algorithm, we are able to predict outcomes for new observations, allowing us to test the accuracy of the model. In the computational experiments described in [2], we observe that our CWE approach yields accurate classifications, and is robust to a variety of settings. One particular practical finding is that the algorithm’s performance can be substantially improved by running it multiple times from different starting points.
3 Optimizing tree-based models
In prescriptive problems, we strive to always make better decisions. In doing so, we use offline learning on data to better understand uncertainties and then use optimization to improve decisions. This process of going from available data to better decisions calls on both predictive and prescriptive analytical models. Data is the input to predictive models that feed into prescriptive models which recommend good decisions. Over the last few decades, tree-based models have become increasingly popular to predict uncertainties. Based on the original classification and regression trees, machine learning and optimization has made many advances in the field of tree ensemble methods, including random forests, XGBoost, and XSTrees proposed in [25]. This section focuses on optimizing over tree ensemble methods in general.
Tree ensemble methods have a long history and are also very popular in practice. The best-performing model in KaggleFootnote 1 by number competitions won, based on predictive accuracy only, is XGBoost [26,27,28]. Inspired by the success of XGBoost, as well as the wide popularity of Random Forests [29], there has been a tremendous growth in the development of new tree ensemble methods, such as AdaBoost [30] and LightGBM [31]. Tree based ensemble methods commonly use single decision trees, often CART [32], which are called “weak learners” for predictions and then aggregate individual predictions together. Different methods use different techniques to generate individual trees. For example, Random Forests construct these single trees by sampling different subsets, both in terms of observations and features, from the data, then training CART trees on each of these subsets. XGBoost does this construction in a sequential way, by training a CART tree on the entire data, then subsequent CART trees on the residuals of the predictions of the ensemble of previously trained trees. However, while unarguably powerful, similarly to ensembles like Random Forests [29], AdaBoost [30], and LightGBM [31], XGBoost lacks both in terms of theoretical guarantees and interpretability, and sometimes needs a significant amount of data to achieve good performances. Inspired by the success of these methods, XSTrees [25] aggregates tree-based weak learners, usually single CARTs [32] which are used for all of the ensembles above, but does it in a more structured way, which allows it to train an entire distribution on the tree space, instead of an independent, finite, collection of trees. This results in more interpretability, better theoretical guarantees, and improved computational performances.
Additionally, in recent years there has been a significant increase in research on how predictive tools can be incorporated into prescriptive tasks. Specifically, researchers are interested in how machine learning models can be used as an input function in the objective when optimizing decisions. In [33], ridge regression is used to predict outcomes of clinical trials, which is then optimized along to select chemotherapy regimes for cancer. In [34], linear-log regression is used to model demand for subsequently optimizing the schedule of promotion vehicles to maximize profits in grocery stores. Additionally, in [35, 36], a ranking-based choice model is estimated which is then used to maximize revenues. There has been significant work on using neural networks as part of an objective function in mixed integer optimization [37,38,39,40,41,42]. A general framework for incorporating eventual prescriptive decisions into the evaluation of a model’s statistical validity is proposed by [43], specifically in the area of price optimization where demand is determined by a predictive model. In [44], it is shown how accounting for the downstream optimization when selecting splits for decision trees in the training process of ensemble forests improves the optimality of the end-result.
In this part of the paper, we focus on optimizing decisions based on the predictions from tree ensembles. Methods for doing so efficiently are found in [45, 46], and [3]. Specifically, these works explain how to incorporate tree structures into the mathematical optimization formulations. In this section, we will explore the relative advantages of these works. The problem that will be considered is closely related to that of [47]. They consider how to optimize prices in order to maximize revenues and prices (that correspond to decision variables in the optimization formulation) come from a discrete price ladder while demand is predicted through a random forest. The paper formulates the mixed integer optimization (MIO) by determining first the expected demand through the random forest for each item at each price point and subsequently using these values as coefficients in the objective function of the optimization formulation. In doing so, [47] avoids many of the computational challenges that come from directly encoding the random forest into the optimization formulation. However while this works well for the pricing problem considered in [47], this approach is less efficient when there are many variables that are being optimized and which the decision maker would need to forecast for all possible combinations of their realizations.
Once decision makers have learned a strong predictive model, for example through XSTrees, the question becomes how to leverage this information to make better decisions. Compared to traditional linear predictive models, ensemble tree methods have been shown to have better model representation which in turn translates into improved predictive accuracy. However, the nature of their prediction structure means there is no longer a linear relationship between the features and the outcome. As a result, new optimization methods need to be developed so that objective functions that are outcomes from ensemble tree predictive methods can then be optimized efficiently. The goal of this section is to discuss how an optimal feature vector, x, can be found to maximize an objective which is a function of the output of an ensemble tree model.
The nature of the models based on decision trees is that there is a criterion satisfaction question being asked at each branch-point of the tree (e.g. is feature \(x_i\) greater than b?). Whether the criterion is satisfied or not is binary and as a result, it can be represented in optimization formulations using binary decision variables. However, since the number of branch-points increase exponentially with the depth of the tree, there is an exponential number of binary decision variables and constraints that must be represented in the optimization formulation. As a result, the key challenge is how to approximate the optimization in a way that is scalable and yet near optimal relative to the original optimization formulation. In what follows, we will discuss three methods that propose such approximations and are based on the work in [45, 46], and [3]. The first two will formulate a version of a mixed-integer optimization. Then for scalability purposes, the papers approximate either the depth of the tree ensemble or the breath (that is, sample only a handful number of trees). The third method discussed in this paper, leverages the upper bound of the objective function on either side of a branch-point to create an algorithm which scales linearly both in terms of the tree depth and the number of trees.
3.1 Model
Consider an ensemble forest model of T trees, where each tree has weight \(w_t\). Let \(N^t\) represent the set of interior nodes in tree t and \(L^t\) represent the set of terminal or leaf nodes in tree t. At each node i in tree t, let us define \(p_i\), \(l_i\) and \(r_i\) as respectively the parent node of i, the left child node and the right child node, if they exist. For every leaf node \(i \in L^t\), there is some payoff associated with it, defined as \(S_i^t\). \(S_i^t\) is usually calculated based on averaging either the dependent variable, y, or a function on this variable f(y), of all the points that fall in the leaf.
For each interior node \(i \in N^t\), there is a linear condition of the form \((a_i^t)^\top x \ge b_i^t\). If this condition is satisfied by x, then the model would move right in the binary tree, and if it is not, then the model would move left. We represent this process using binary variable \(q_{i,j}^t\). \(q_{i,j}^t = 1\) if (and only if) j is a child-node of i and the solution to x exists in a descendant leaf of j. Each interior node i also has a depth associated with it, d(i), which represents the number of branch-points it is from the root node.
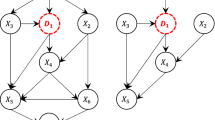
Since the notation can get dense, we present a concrete example to illustrate the different models in Fig. 1. Here we will describe a random forest of two trees, with a max depth of two built on a dataset of two features: price and discounts. The random forest is built to predict retail sales of a item. We label each node of tree by both its tree number and node number.
3.1.1 Big-M formulation
Given this we can define the optimization of how to find the values to x that maximizes the prediction value of the ensemble tree model. The first formulation is based on the work of [45].
The prediction of the ensemble tree model can be represented by \(\sum _{t = 1}^T \sum _{i \in L^t} w_t q_{p_i,i}S_i\). Here \(w_t\) is weight placed on each tree in the final prediction of the ensemble model. We are maximizing this value, so the objective function of this problem becomes:
We need constraints to enforce that \(q^t\) represents accurately the leaf of tree t which x results in. For every interior node i, we need \(q_{i,l_i}^t = 1\) and \(q_{i,r_i}^t = 0\) if \((a_i^t)^\top x \ge b_i^t\) and \(q_{i,l_i}^t = 0\) and \(q_{i,r_i}^t = 1\) if \((a_i^t)^\top x \le b_i^t\). We can enforce this using big M-constraints:
This can be paired with flow or genealogy constraints that establishes if x ends up in interior node i of tree t, meaning \(q_{p_i,i}^t = 1\), then it must end up in one of i’s children, either \(q_{i,l_i}^t =1\) or \(q_{i,r_i}^t =1\). If x does not end up in interior node i, \(q_{p_i,i}^t = 0\), then it cannot end up in either of i’s children, \(q_{i,l_i}^t = q_{i,r_i}^t = 0\). This can be represented as the following constraint:
We need to guarantee that x is represented in ending up in exactly one leaf of tree t, so we have:
Finally we account for any other business constraints which are relevant to this problem using:
Putting this together gives us Formulation (7):
To create Formulation (7) for the forest shown in Fig. 1, we assume that we are just optimizing sales, therefore \(S_i^t\) is just the sales of leaf i, and because the model is a random forest, weight on tree t is \(w_t = \frac{1}{T} = \frac{1}{2}\). We assume no additional business constraints. Given this we substitute in in the values of the tree to get the formulation:
3.1.2 Formulation with pre-processing
The second formulation we consider is based on the work of [46]. This formulation introduces a pre-processing step to streamline the optimization.
Let us consider the split criterion as before of \((a_i^t)^\top x \ge b_i^t\). If the tree has only parallel splits (as is the case in most implementations of ensemble forests), then \(a_i^t\) is a vector of all zeros except for a single one, which indicates the feature of x being considered in the split. Thus all split criteria in the tree can be simplified into \(x_{p(i)} \ge b_i^t\), where p(i) represents the feature being considered in node i, or the index of \(a_i^t\) that is 1.
This second formulation groups all split criteria in the tree by the feature being considered. Let \({\mathcal {P}}\) be the set of independent features used to create the ensemble model. For each feature \(p \in {\mathcal {P}}\), let \({\mathcal {B}}_p\) be the set of unique split points on that feature, or the set of values b such that some tree in ensemble has a split criteria \(x_p \ge b\). Let \(K_p = |{\mathcal {B}}_p |\) be the number of unique splits of feature p, so that we can denote the set of all parallel splits as \(\{c^1 , \dots , c^{K_p}\}\). And let the \(b_{p,j} \in {\mathcal {B}}_p\) be the \(j^{th}\) smallest split point of feature p, such that \(b_{p,1}< b_{p,2}< \dots < b_{p,K_p}\). We define function \(C(i) = \{j\}\) which for node i identifies the index \(j \in {1,\dots ,K_{p(i)}}\) such that that the split query of node i can be written as \(x_{p(i)} \ge b_{p(i),j}\). When we consider the sample forest from Fig. 1, we have that, \({\mathcal {P}} = \{\text {discount}, \text {price}\}\), \({\mathcal {B}}_\text {discount} = \{0.9 \}\), \({\mathcal {B}}_\text {price} = \{20,24 \}\), \(K_\text {discount} = 1\), \(K_\text {price} = 2\). Then for each of the splits we write C as: \(C(n^1_1) = 1\), \(C(n^1_2) = 1\), \(C(n^2_1) = 2\). This results in for example, the split at node \(n_1^2\) can be written as \(x_{\text {price}} \ge b_{\text {price},2} = 24\).
For every interior node in the ensemble, \(i \in \cup _{t=1}^T N_{t}\), we define left(i) as the set of leaves that are descendants of the left branch of node i and right(i) as the set of leaves that are descendants of the right branch of node i. This means that if the optimal solution x ends up in a leaf found in left(i), we know that the criteria of node i must hold and conversely if it is in a leaf of right(i), the criteria of node i must be false.
With this we can now define our decision variables for the second formulation. Before we used \(q_{p_i, i}\) to determine if a solution x ends up in some leaf i. In this formulation we will define \(y_{t,i}\) to represent if solution x ends up in leaf i of tree t. We also define z which specifies the optimal solution x, by defining which splits in the ensemble are satisfied or failed. Specifically we say that \(z_{p,j} = 1\) if \(p^{th}\) independent variable in x should be greater than or equal to the \(j^{th}\) split point in \({\mathcal {B}}_p\) and 0 otherwise.
In the second formulation, the objective function stays relatively similar to the first but we replace q with y:
Like before, the optimal solution can only end up in a single leaf of a given tree.
To enforce that the split constraints are held, we introduce the following constraints. If the constraint in node i is not satisfied, then \(z_{p(i),C(i)} = 0\) and the solution of x cannot fall into any of the leaves defined by left(i). Similarly if the constraint in node i is satisfied then \(z_{p(i),C(i)} = 1\) and the solution of x cannot fall into any of the leaves defined by right(i). Therefore we define the following constraints:
If \(z_{p,j} = 1\) this means that \(x_p \ge b_{p,j}\). It must then hold that, \(x_p \ge b_{p,j-1} \ge \dots \ge b_{p,1}\), which means for \(k \in \{1, \dots , j-1\}\), \(z_{p,k} = 1\). To enforce this, we add the following constraint:
And of course, we need z to be binary and \(y \ge 0\) (we do not need y to be explicitly bounded from above because it is already bounded by z). Putting this together we get Formulation (9):
We can again write Formulation (9) for the forest described in Fig. 1. Like before, we assume we are optimizing sales in a random forest without any additional business constraints.
We see in the example that z fully describes what leaf the solution will end up in. If \(z_{\text {discount},0} = 1\), then the discount is less than 0.9, otherwise it is greater than 0.9. Similarly if \(z_{\text {price},1} = 0\), then price is less than 20, if \(z_{\text {price},1} = 1\) and \(z_{\text {price},2} = 0\), then price is between 20 and 24 and if \(z_{\text {price},2} = 1\) then price is greater than 24.
When we compare Formulations (7) and (9), we see a few interesting differences emerge. In practice Formulation (9) has fewer binary variables than Formulation (7), as the number of binary variables in Formulation (9) are based on the number of split points of a variable rather than interior nodes. While this might not initially seem like a significant difference, ensemble trees within a model will often split a feature at the same point across trees. By comparison, Formulation (7)’s strength is in its flexibility. Formulation (7) does not require parallel splits and can also be used to optimize hyperplane trees. Furthermore it can easily account for additional business constraints.
However, while both formulations have their strengths they both have the same significant limitation. In fact Formulation (9) has been shown to be NP-hard.
Proposition 2
([46]) The tree ensemble optimization problem is NP-Hard.
Both formulations have an exponential growth in binary variables as the trees get deeper. This means that these optimization formulations will have scaling and tractability issues with larger ensemble tree models. Both [46] and [45] propose using Benders Decomposition to increase tractability, however this does not address the exponential growth of binary variables. Therefore we discuss next approximations of the optimization formulations.
3.2 Methods
In this section we will discuss three approximations to the optimization formulations. The first two will be direct extensions of Formulations (7) and (9), while the third will be a linear approximation of the optimization process.
3.2.1 Breadth-based approximation
[45] propose approximating the optimal solution using tree sampling. We can define \({\mathcal {T}}\subset \{1,\dots ,T\}\), as a randomly selected subset of the ensemble’s trees. Because all the constraints in Formulation (7), other than the business constraints, are indexed by \(t\in \{1,\dots ,T\}\), it is relatively straightforward to only consider the constraints for \(t\in {\mathcal {T}}\). Thus the Formulation (7) becomes:
For the forest described in Fig. 1, this could be thought of running the optimization only for Tree 1. The size of the sample can be set based on computational capabilities and [45] bound the suboptimality in terms of the total number of leaves in the ensemble forest, \(\cup _{t=1}^T L^t\), and the size of the sample, \(|{\mathcal {T}}|\).
3.2.2 Depth-based approximation
[46] propose approximating the optimal solution by approximating along depth. Rather than defining a sample of trees, like in [45], we subset the nodes of each tree by only consider the nodes whose depth is less than d. We can define an \(\Omega _d^t \subset N_t\) such that for any \(i \in \Omega _d^t\), \(d(i) \le d\). We now only consider constraints generated by nodes in \(\Omega _d^t\). Thus Formulation 9 becomes:
For the forest described in Fig. 1, an example would be to set \(d=0\). The optimization would only consider the split constraints induced by \(n_1^1\) and \(n_1^2\) and treat \(n_6^1\) and \(n_7^1\) as being the same leaf. Here the programmer must decide the maximum depth, d, at which to consider constraints. [46] provide computational results in order to demonstrate rates of convergence to optimality as d increases.
3.2.3 MOTEM
The final approximation method we discuss comes from [3]. This process uses the calculated upper bounds on the payoff of the best leaf in the descendants of the left and right children of a given node. Rather than optimizing the entire ensemble at once, the algorithm optimizes each level of the trees iteratively, narrowing in the optimal region with each iteration.
This algorithm, called MOTEM, or Method for Optimizing over Tree Ensemble Methods, starts at the root node of every tree in the ensemble and follows a three step process to optimize along: (1) calculate the upper bound of the left and right child of the indicated note, (2) optimize across all trees where child node is optimal based on the upper bound and feasibility constraints and (3) update optimal region feasibility constraints and move down the tree to the optimal child node. In doing this, the algorithm traces a single branch of each tree in the ensemble until it reaches a leaf. The final solution provided is a range for each independent feature that is approximately optimal given the business constraints. We explain each step of the optimization process further in the following.
1. Upper Bound Calculation
First we calculate the upper bound of each of the children of the node we are considering. Without exploring deeper in the tree it is impossible to always tell whether the left or right branch has the more optimal leaf. However we can calculate an upper bound on the payoff of the optimal leaf. For each random forest there is a pre-designated minimum leaf size, which we can designate as m. Consider that we are in node i of tree t, which has a split criterion of \((a_i^t)^\top x \ge b_i^t\). Of all the training data points that pass through node i, we can consider those that satisfy the business constraints and split criterion. Among these we can average the m points that have the highest value in terms of our objective. In other words we can average the m points with the highest values of f(y). It is impossible for the left branch of node i to have a leaf of higher value, so we call this the upper bound of the left branch’s payoff. Similarly to calculate the upper bound of the right branch, we consider all training data points that pass through i which satisfy the business constraints and fail the split criterion and average the top m. We call these left and right branch upper bounds of node i, \(u_{i,L}^t\) and \(u_{i,R}^t\) respectively. Note that \(u_{i,L}^t\) and \(u_{i,R}^t\) require no knowledge of the tree structure below the depth of node i. We show an example of what these upper bounds might look like for the Sample Random Forest in Fig. 2.
2. Optimize to Select Child Node
Next, we optimize across all trees which child node to pass to. Given \(u_{i,L}^t\) and \(u_{i,R}^t\) for all trees t in the forest we need to decide whether the optimization algorithm should focus on the left or right branch. The objective is to maximize the expected payoff as calculated through the upper bounds, rather than the final payoffs (because the algorithm doesn’t know the final payoffs). Therefore the objective function becomes:
As before q is a binary variable representing whether the optimal solution lies in the left or right branch of node i.
Similar to before we need to enforce that q accurately represents moving to the left or right child of i, so we introduce the big-M constraints.
Unlike before the optimization algorithm isn’t considering all branches of the tree at once, it is considering only one branch in which it believes the optimal solution lies. Therefore rather than needing \(q_{i,l_i} + q_{i,r_i} = q_{p_i,i}\), the algorithm assumes that the optimal solution lies in a descendent of i meaning that \(q_{p_i,i}=1\). Therefore we include the following constraint:
We have constraints on the selection of our intermediary optimal solution x. x needs to satisfy the business constraints \(Ax \le f\), so that the selection of the optimal child node is feasible in terms of business constraints. Second x needs to satisfy any previous spit criteria decided upon in the algorithm at higher levels of the tree. This is not a problem when optimizing a single tree, or when optimizing all trees in an ensemble together, however because the algorithm iteratively optimizes each level of the tree separately, we need to make sure that the solution for x doesn’t violate any of the previous split criteria. When the forest is built on parallel splits (as is the case with almost all implementations of ensemble trees), this is an easy process of remembering box constraints (higher and lower bounds of each independent variable). We will use \(x_{\min }\) and \(x_{\max }\) as vectors to represent these bounds for each feature:
Finally we need q to be binary:
Pulling this all together we get the optimization formulation for step 2:
For example, this formulation can be written for the depth 0 approximation shown in Fig. 2 as:
The key output of Formulation (13) are values for \(q_{i,l_i}^t\) and \(q_{i,r_i}^t\) which tell us for each tree t whether to go to left or right child. It also provides a sample solution x which guarantees that the selected child nodes are feasible.
3. Update Optimal Feasible Region
This brings us to the update step of each iteration. First the bounds for feasibility, \(x_{\min }\) and \(x_{\max }\). Each selected child node represents a new constraint that needs to be satisfied by the solution x. Therefore keeping the \(q_{i,l_i}^t\) and \(q_{i,r_i}^t\) constant from the output of Formulation (13), we update as follows:
The solution \({\hat{x}}\) of 15 becomes the new \(x_{\max }\). Similarly to determine the new lower bound, we solve the following:
The solution \({\hat{x}}\) of (16) becomes the new \(x_{\min }\).
The pointer for which node we are considering needs to be updated. In tree t if \(q_{i,l_i}=1\) then we move our considered node to the left child of i. If \(q_{i,r_i}=1\) then we move to the right child of i. In doing so we move one level deeper into the tree, having updated our feasibility conditions through \(x_{\min }\) and \(x_{\max }\) and we repeat the process until we reach a leaf node in all the trees. For example, if the optimal solution from Formulation 14, included \(q_{1,3}^1 = 1\), in the next iteration of the algorithm would be considering the split constraint Price \(\ge 20\), and would have as a constraint in the optimization that Discount had to be less than 0.9. For further details, we reference [3].
3.3 Approximation method comparison
Both approximation methods introduced in [46] and [45] have their merits. Formulation (11) provides a way of increasing tractability with probabilistic guarantees on sub-optimality. Formulation (12) directly tackles the issue of exponential runtime growth by cutting off the depth of trees considered. However both also have their limitations. Formulation (11) still suffers from exponential growth in runtime as depth increases and Formulation (12) does not have a clear indication of the optimal max-depth to select. If d is too large the problem remains intractable, if d is too small, the loss in sub-optimality can be significant. Without prior knowledge of actual optimality, it is unclear what depth to select.
The benefit of MOTEM is that unlike the optimization methods discussed above, this algorithm does not have an exponential number of binary variables. Rather, formulation (13) has 2T binary variables, namely, two binary variables (\(q_{i,l_i}\) and \(q_{i,r_i}\)) per tree. Furthermore, formulations (15) and (16) are pure linear optimization formulations. We will repeat this iterative process for each tree level, till at most the depth of the deepest tree. This leads us the complexity of the method ( [3] for more details):
Proposition 3
([3]) Let T be the number of trees in the ensemble and \(d_{\max }\) be the maximum depth. Then the binary variables in the optimization algorithm MOTEM grows in \({\mathcal {O}}(Td_{\max })\).
This comes from the fact that the algorithm traces only a single branch through each tree, optimizing only which child node to continue on to, rather than all branches at once.
[3] also provides bounds on the expected sub-optimality gap specifically when running MOTEM on random forests. This is done in terms of two key features of the random forest: how disparate the top leaves of the forest are and in-sample error. They show that if the random forest fits the data perfectly, then MOTEM will always find the optimal solution. However as the in-sample error grows, especially relative to the separation between the highest payoff values in the tree, then so does the sub-optimality gap. For more information on both the Proposition 3, and this bound, please see [3].
MOTEM will always scale better than either Formulation (7) or (9). MOTEM will also scale better than Formulation (11) because the formulation doesn’t address the exponentially growing with depth binary variables. Depending on where the cut off for Formulation (12), the optimization will scale similarly to MOTEM. However MOTEM provides a much clearer insight to the optimality-gap. Without running the full depth version of Formulation (9), it is hard to tell how sub-optimal the Formulation (12)’s solution is.
The quality and scalability of the MOTEM approximation can also be demonstrated numerically on a variety of datasets. For this section we will use the winequalityred dataset from [48] and the UCI Machine Learning Repository. This dataset aims to predict the quality of red Portugese wines on a scale from one to eight based on physiochemical tests such as citric acid, pH and residual sugar levels. The dataset consists of 4,898 data points and 12 features. For this dataset we built several random forests, with the number of trees ranging from 20 to 200, set the maximum tree depth to 26 and the minimum leaf size to 15. Once the random forests are built, we aim to find the “ideal” wine by using MOTEM and Formulation (9) to find the set of features which maximizes the quality of wine. We compare the objective value achieved by both Formulation (9) and MOTEM. We use the formulation from [46] because it is the faster MIO between Formulation (7) and (9). We see in Figs. 3 and 4 that MOTEM is able to capture almost all of optimality. For example, at 200 trees, MOTEM captures \(98.9\%\) of optimality. It is able to do this while scaling well as the number of trees increases, while Formulation (9) grows rapidly in the time it takes to run. For a more comprehensive numerical comparison of MOTEM, Formulation (7) and (9) as well as the approximations, please see [3].
Objective function achieved by MOTEM and Formulation (9)
Runtime required by MOTEM and Formulation (9)
4 Learning optimal decisions directly from data
So far we have discussed how to predict in an accurate, efficient, and interpretable way, and subsequently how to use these predictions to optimize prescriptive tasks. For many real world problems, prediction tasks are an intermediate goal and not the final goal. Namely, forecasts of uncertain parameters are important for a downstream optimization problem, but ultimately, only the quality of the final decision is the true measure of cost. For example, a model may be trained to forecast travel times for a transportation problem, but only the travel time of the route that we decide to travel matters. The traditional approach has been to predict independent of optimizing, which might lead to suboptimal decisions. In this section, we will discuss how to make prescriptions directly from data without performing a predictive task separately.
Recent work has focused on combining the offline learning stage (forecasting) with the downstream optimization task — investigating ways to perform gradient descent through the optimization problem itself. Some early work in the area can be found in [49], minimizing task loss for unconstrained quadratic optimization problems. The introduction of constraints naturally complicates the task of computing gradients. In [50], an explicit method has been developed that uses the KKT conditions for optimality. This is extended further by [51] to linear optimization problems by approximating the problem through adding a quadratic regularization to the objective. For linear tasks, the primary issue stems from the fact that for linear programs, the gradient of the optimal solution with respect to the cost vector is zero or undefined. This is because a small change in the cost vector either results in the same optimal solution, or a discontinuous jump to a new vertex. As an example to resolve this, [52] introduces a convex and differentiable approximation of the objective function. If the forecasting function is given by a linear model, the learning problem can be formulated by a linear optimization problem as shown for a classical newsvendor problem in [53]. This is broadly generalized in [54] to nonlinear decision rules by using reproducing kernel Hilbert spaces. For more details on different approaches, see [55,56,57] and [58] for a general survey for end-to-end combinatorial learning.
We may also view this problem of end-to-end learning through the lens of online learning and bandit problems in order to learn convex functions. For instance, [59] uses a semi-bandit setting for combinatorial problems, in which the set of possible actions is the set of decisions (e.g. paths on a graph). They aim to minimize the regret of their decisions given adversarial costs. Along these lines, [60] considers the problem of minimizing an unknown convex function given point samples. The book in [61] provides a more comprehensive review of related work to online convex optimization. However, the key difference with our work is that we also incorporate feature information.
There has been significant work within the robust optimization literature over the years (see for example, the books by [62] and by [63] and the survey paper by [64]). In robust optimization careful construction of the underlying uncertainty sets is required to ensure the models are not overly conservative. Various formulations have been constructed starting with [65,66,67]. Nevertheless, these uncertainty sets may themselves be unknown as we can only gain information about them from data (for example, because they rely on estimates of the mean and standard deviation from the available data). For example, [68] takes a data-driven robust optimization view. Furthermore, uncertainty sets could themselves vary as a function of the features, as for example in [69,70,71] as well as in the case of our work in [4].
There has also been a non-parametric stream of literature along the lines of Sample Average Approximation (SAA) [72]. However, SAA uniformly weights past data and makes no use of covariate information. To address these issues, [73] introduced a new framework that generates weights by using machine learning methods. However, these weights are still independent of the optimization problem itself. To directly target task loss, [74] uses an optimal prescriptive tree framework. Furthermore, [44] designs a paradigm to learn effective forest-based decision policies that integrate prediction and optimization. In [75] the ideas of [73] and [54] are applied specifically to a complex two-stage capacity planning problem. However, much of this work is not robust to uncertainty in the data. In the case of a feature-based newsvendor problem, [76] tackles the important problem of finding robust policies.
Nevertheless, much of the work discussed is not applicable to general optimization problems or has no mechanisms to incorporate robustness to data changes. For our setting, robustness to uncertainty and error in the data is crucial: we want to provide decisions that result in good objective values even in the face of perturbations to the data. Thus, in this paper, we will discuss an approach we have introduced in [4] that goes from the data to the prescription in robust and direct way.
4.1 Method
We consider the following optimization problem with feasible region \({\mathcal {P}}\) and convex objective function \(g_\nu (\cdot )\) parameterized by \(\nu \):
As an example, \(g_\nu (w)\) may simply be a linear function of \(\nu \), so that \(g_\nu (w) = c^Tw\) where \(\nu = c\), or a quadratic one such as \(g_{\nu }(w) = \mu ^Tw + w^T\Sigma w\) whered \(\nu = (\mu , \Sigma )\). But, the objective function itself is unknown and is a function of some features x. Crucially, for any x, the corresponding cost vector which we will denote by \(\nu _x\) is some random variable with unknown distribution dependent on x. Hence, we assume we are given training data consisting of pairs \((x^1, \nu ^1)\), \(\dots \), \((x^n, \nu ^n)\) of observed features and realized costs, respectively. For out-of-sample x, we aim to make a decision \({\hat{w}}(x)\) which incurs a low regret. Specifically, we define:
Definition 1
(Regret) The regret of a decision vector w when the realized cost is \(\nu \) is the difference between the objective value of w and the true optimal solution \(w^*(\nu )\) under the realized cost \(\nu \), namely:
Two possible goals arise. One is to make a decision which minimizes the expected regret, and the other is to produce a robust solution which minimizes the maximum regret across all possible realizations of the cost vector. We will show how our approach performs a combination of these two goals.
To build some intuition, we first briefly discuss existing approaches. For instance, a traditional two-stage method separates the learning from the optimization steps and simply learns a mapping from feature vectors to cost vectors. That is, learn some \({\hat{\nu }}(x) = \nu _{\text {2-stage}}(x)\) within some function space (such as linear functions, or neural networks) by minimizing a loss function such as the mean-squared error between the predictions and the observed costs:
Then, it would take the optimal decision \(w^*(\nu _{\text {2-stage}}(x))\) with respect to the forecast made. By contrast, an end-to-end method directly aims to learn \({\hat{\nu }}(x) = \nu _{\text {task}}(x)\) to minimize the task loss (as in for example [50, 52]):
Often, one wishes to learn such a \({\hat{\nu }}(x)\) through gradient descent. But, much of the complexity of the end-to-end approach lies in calculating the gradient of \(w^*({\hat{\nu }}(x))\). Consider instead prescribing a solution directly from the data: learn some function \({w}_{\text {task}}(x)\) that prescribes a decision minimizing task loss:
Now, the difficulty of the optimization problem is transferred into learning \({\hat{w}}_\text {task}(x)\). Additionally, this requires some way to ensure that \({w}_{\text {task}}(x)\) satisfies feasibility constraints.
Motivated by this, we propose a method that does not explicitly learn such a \({w}_\text {task}(x)\), but rather learns its actions over subsets of the feasible region. Consider choosing some fixed subsets \({\mathcal {P}}_1, \dots , {\mathcal {P}}_K\) of the feasible region. Instead of deciding a specific value for \({\hat{w}}_\text {task}(x)\), we solve the simpler problem of deciding if it should belong to each subset \({\mathcal {P}}_k\). The final decision we prescribe should belong to the intersection of the subsets we predicted the solution should belong to. See Fig. 5 for an illustration. This approach gives rise to a discretized approximation of \({w}_\text {task}\). As we introduce more and more subsets, the resulting intersections will be smaller and smaller, honing in to the correct decision. Moreover, each individual learning problem that determines if \(w^*(\nu _x)\) should belong to \({\mathcal {P}}_k\) is a much simpler classification problem.
In addition, these subsets are the key idea for robustness. In particular, suppose we have some data point \(\nu ^i\) whose corresponding solution \(w^*(\nu ^i)\) belongs to \({\mathcal {P}}_k\). Then, even under small perturbations of \(\nu ^i\), the corresponding solution will likely still belong to \({\mathcal {P}}_k\). As the subsets \({\mathcal {P}}_k\) get larger, the likelihood of this happening increases further. Hence, deciding whether a solution should belong to a subset is more robust to uncertainty in the data. This ultimately makes our decisions more robust to uncertainty as well. We see this explicitly for instance in experiments in Sect. 4.2 (Effect of cap size against noise).
We will structure our approach (see Sect. 2.3 for more details) as follows: (1) We propose a specific class of subsets \({\mathcal {P}}_i\), which we denote by \(\epsilon \)-caps. We generate these caps from the data available and as a function of the optimization problem. (2) We discuss an approach to learn how the features map into each particular \(\epsilon \)-cap. That is, how to learn if \(w^*(\nu _x) \in {\mathcal {P}}_i\). (3) For out-of-sample data points with features x, we then predict which caps the corresponding decision should belong to. We describe a method to choose a feasible solution that “best matches” these predictions by solving an optimization problem, which is of the same difficulty to solve as the nominal problem, where one knows all the information on the objective function.
4.1.1 \({\varvec{\epsilon }}\)-caps
Consider constructing one subset \({\mathcal {P}}_i\) for each datapoint \((x^i, \nu ^i)\). Ultimately, the goal is to propose decisions with low cost. Therefore, if some solution w belongs to \({\mathcal {P}}_i\), then the cost of w should be low with respect to realised cost \(\nu ^i\) associated with set \({\mathcal {P}}_i\). To quantify this, we define the notion of an \(\epsilon \)-cap. This is the set of solutions whose objective is within \(\epsilon \) of the optimal objective. That is, the set of solutions with regret at most \(\epsilon \). Below we define this notion more formally.
Definition 2
(\(\epsilon \)-cap) An \(\epsilon \)-cap \(H_\epsilon (\nu )\) is the set of points in \({\mathcal {P}}\) which produce a solution within \(\epsilon \) of optimality:
where \(G^*(\nu ) = g_\nu (w^*(\nu ))\) is the optimal objective value for cost realization \(\nu \).
Therefore, for each datapoint \((x^i, \nu ^i)\), we will take the subsets \({\mathcal {P}}_i\) to be \(H_\epsilon (\nu ^i)\).
4.1.2 Local mappings from features to decisions
Recall our goal is the following: for a given x, choose some \({\hat{w}}(x)\) that results in low regret. We aim to do so by first deciding which \(\epsilon \)-caps such a decision \({\hat{w}}(x)\) should belong to. In particular, since \(\nu _x\) is a random variable, we wish to determine the probability that \(w^*(\nu _x)\) belongs to cap \(H_\epsilon (x^j)\).
We aim to learn this information. For the training data, we can quantify this exactly since we have access to the realized costs. For point \(x^i\), the optimal decision is known to be \(w^*(\nu ^i)\). Hence, the probability that \(w^*(\nu ^i)\) belongs to cap \(H_\epsilon (x^j)\) is only a 0/1 value. We can determine this by simply calculating if the regret is at most \(\epsilon \). This allows to generate the following labelling for each datapoint \((x^j, \nu ^j)\):
where note that \(\nu ^j\) is a function of data point \(x^j\).
We wish to learn this labelling for out-of-sample points x. We can learn an approximation of this labelling through any traditional classification method (e.g., logistic regression, decision trees, neural networks among others). We denote this approximation by \({\hat{l}}^\epsilon _{\nu ^j}\). In short, \({\hat{l}}^\epsilon _{\nu ^j}\) can be viewed as the probability that the optimal solution \(w^*(\nu _x)\) should belong to \(\epsilon \)-cap \(H_\epsilon (\nu ^j)\).
4.1.3 Merging predictions
For an out-of-sample set of features x, we wish to find a solution \({\hat{w}}\) which best matches the predictions of \({\hat{l}}^\epsilon _{\nu ^j}(x)\). To do so, we devise a scoring system for feasible solutions, and construct an optimization problem to determine the solution with minimum penalty. Specifically, for each \(\nu ^i\), a solution is not assigned any penalty if it belongs to \(H_\epsilon (\nu ^i)\) and otherwise, it is penalized by \({\hat{l}}^\epsilon _{\nu ^i}(x)\) (the model’s confidence that it should have belonged to the cap) scaled by the distance from the cap. This is naturally described by the following optimization task:
We now succinctly describe the general framework.
-
1.
For the training data \(\nu ^j\), \(j=1, \ldots , n\), pre-compute the optimal solutions \(w^*(\nu ^j)\) and their corresponding objective function values \(G^*(\nu ^j)\).
-
2.
Generate the corresponding labels so that the datapoints on features, \(x^i\), have true labelling \(l^\epsilon _{\nu ^j}(x^i) = 1\), if \(w^*(\nu ^i) \in H_\epsilon (\nu ^j)\) and 0 otherwise.
-
3.
Learn function \({\hat{l}}^\epsilon _{\nu ^j}\) to approximate the labelling using any machine learning method (e.g., decision trees among others).
-
4.
For any out-of-sample data point with features x, we prescribe as near optimal solution the solution of optimization problem (24).
4.1.4 Connection to SAA and robust optimization
We now discuss the optimization formulation (24) and connect it to the Sample Average Approximation (SAA) method as well as robust optimization. First, we consider a more general formulation by allowing the cap size in the objective function to vary independently of the cap size used to train \({\hat{l}}^\epsilon \). We denote this cap size by \(\gamma \). That is, we consider the following
In [4], three cases are analyzed and interpreted:
-
1.
\(\gamma = 0\): feature-based SAA. Specifically, it is shown at \(\gamma =0\) that this approach is equivalent to
$$\begin{aligned} {\hat{w}}_{\epsilon , 0}(x) = \arg \min _{w \in {\mathcal {P}}} \sum _{j=1}^n {\hat{l}}^\epsilon _{\nu ^j}(x) \cdot g_{\nu ^j}(w). \end{aligned}$$(26)Indeed, if the values \( {\hat{l}}^\epsilon _{\nu ^j}(x) \) were uniform, then the approach is identical to SAA. In [73], another approach is taken to learn these weights by some machine learning methods. Unlike our approach, these weights are chosen independently of the optimization problem.
-
2.
\(\gamma = {\tilde{\gamma }}\): robust optimization. The goal of traditional robust optimization is to minimize the maximum regret incurred in the data. That is,
$$\begin{aligned} {\tilde{\gamma }} = \min _{w \in {\mathcal {P}}} \max _{j=1,\dots ,n} (g_{\nu ^j}(w) - G^*(\nu ^j)) \end{aligned}$$(27)If we let \({\tilde{w}}\) be the corresponding optimal solution, then by construction, \({\tilde{w}}\) belongs to the \({\tilde{\gamma }}\)-cap of each datapoint. Therefore, it incurs zero penalty according to our formulation in (25) and so the solution \(w_{\epsilon , {\tilde{\gamma }}}(x)\) is exactly this robust solution \({\tilde{\gamma }}\).
-
3.
\(0< \gamma < {\tilde{\gamma }}\): combination of SAA and robust optimization. In [4] it is shown that for any \(\gamma \) there exists some subset of costs \(V \subset \{ \nu ^1, \dots , \nu ^n \}\) so that \({\hat{w}}_{\epsilon , \gamma }(x)\) is guaranteed to have regret at most \(\gamma \) with respect to costs in V and which minimizes the expected cost with respect to costs not belonging to V. Note that this is in line with our understanding from the cases \(\gamma = 0\) and \(\gamma = {\tilde{\gamma }}\). Specifically, for \(\gamma = 0\) we can take \(V = \emptyset \), as we minimize expected cost with respect to the entire data. And for \(\gamma = {\tilde{\gamma }}\), we can take \(V = \{\nu ^1, \dots , \nu ^n \}\) as it is robust with respect to errors the entire data. As \(\gamma \) increases from 0, the resulting solution becomes robust against larger subsets of the data.
4.1.5 Stability and generalization bounds for nonlinear Lipschitz continuous objectives
It has been shown in [77] that stable learning algorithms have “good” generalization bounds. In short, a learner is stable if its prediction changes very little with the addition of one new training data-point. In our setting, we will show that given each \({\hat{l}}^\epsilon _{\nu ^j}(x)\) is stable, our solution \({\hat{w}}_{\epsilon , 0}(x)\) is also stable when \(w^*(\nu )\) is Lipschitz with respect to \(\nu \). This in turn proves generalization bounds for our algorithm. See Theorem 4 for more details.
Next, we formally define the notion of stability. Denote a training set of size n as \(S = \{(x^1, \nu ^1), \dots , (x^n, \nu ^n) \}\). For ease of notation, let \(l^S_\nu (x)\) be the labels we learn to determine if \(w^*(\nu _x) \in H_\epsilon (\nu )\) when training on dataset S.
Definition 3
A learning algorithm with single output \(l^S_\nu \) has uniform stability \(\beta \) if
where \( S^{\backslash i} \) is the same data set as S, but with \(i^{th}\) point removed.
Theorem 4
(( [4]) Generalization for Optimization Problems with Lipschitz Objective) Under the Lipschitz Assumption 1 and given that each \({\hat{l}}^{S}_{v^j}(x)\) is uniformly stable with parameter \(\beta _n = O(\frac{1}{n})\), we can bound the generalization error by the empirical error with probability \(\delta \) as follows:
Assumption 1
The optimal solution to the nominal optimization problem is Lipschitz with respect to the uncertainty \(\nu \). That is, there exists some constant \(L_1\) such that for any \(\nu ^1, \nu ^2 \in {\mathcal {V}}\), \( \left\Vert w^*(\nu ^1) - w^*(\nu ^2) \right\Vert _2 \le L_1 \left\Vert \nu ^1 - \nu ^2\right\Vert _2 \). Moreover, we assume that \(g_\nu (w)\) is \(L_2\)-Lipschitz with respect to w. That is, \(|g_\nu (w^1) - g_\nu (w^2)| \le L_2 \left\Vert w^1 - w^2\right\Vert _2\).
The theorem crucially depends on two assumptions, (1) that \(w^*(\nu )\) is Lipchitz with respect to \(\nu \) and (2) that \({\hat{l}}\) is trained by a O(1/n)-stable learning algorithm. There are many stable learning algorithms that can be applied here. For instance, support vectors machines, logistic regression, K-nearest-neighbors (see [77]), as well as certain neural networks, such as single layer graph convolutional networks (see [78]). The Lipschitz continuity assumption holds for instance for quadratic optimization problems (see [79]). Nevertheless, note that it does not hold for linear optimization problems. Indeed, in that case the optimal solution can jump discontinuously from one vertex to another given an arbitrarily small change in the cost vector.
4.2 Computational results
In this subsection, we will present numerical evidence of the advantages of our approach, showing that it is competitive in terms of average regret incurred while simultaneously providing more robust solutions in the presence of noise and uncertainty in the data.
We consider a nearly identical problem as the one used in [52]: an uncapacitated min-cost flow problem on a \(5 \times 5\) grid network, with a source at the bottom left node, and a sink at the top right node and directed edges that only move from left to right, and bottom to top. This can easily be modelled as a linear optimization problem.
In this case, the costs \(\nu \) correspond to the a vector describing the costs of each edge in the flow problem. For the data \((x^1, \nu ^1), \dots , (x^n, \nu ^n)\), each \(x^j\) is generated at random, and \(\nu ^j\) is some linear function of \(x^j\) with additional noise. The magnitude of the noise is measure by a parameter \(\delta \). For the sake of brevity, we omit the details of the data-generation process here, but they may be found in [4].
We examine and compare four different approaches—our cap approach is in red, and the labelling problem is modelled using logistic regression. The green is a two stage approach using a regression tree to predict costs, the red is a K-NN approach which falls under the framework of [73], and the orange is the smart-predict-optimize method, an end-to-end learning framework from [52]. See Fig. 6 (left). We report the average relative regret of decisions taken by each approach. In particular, given a realization \(\nu \) and the model-prescribed decisions \({\hat{w}}\), the relative regret is the percent error
We can see the SPO approach is doing particularly well. We attribute this to the fact that the underlying true distribution of the data is linear, and the hypothesis class it is learning from is also linear - so it can learn the true costs very well. Our cap approach is competitive with the others, and also does well as we increase noise in the data.
Robustness Experiment We also measure the robustness of each method against uncertainty in the data. In particular, for each out-of-sample x, we generate 1000 different random cost vectors using different samples of noise \(\delta ^i_j\). Then, we determine the solution each method produces for the given out-of-sample x and measure the maximum regret incurred on these 1000 points.
Note the comparison of the maximum regret incurred in the different approaches (Fig 6 (right)). The maximum regret of our method is much lower than it is for the other approaches, even compared to the SPO, which had a much better average regret. As we have explained, we see that as the cap size \(\gamma \) increases, the cap approach indeed becomes more robust. Note that past a certain point as \(\gamma \) increases, the maximum regret actually begins to increase as our solution becomes too conservative.
Effect of cap size against noise A crucial hyperparameter to tune is the cap size \(\epsilon \) used to learn the labelling. As \(\epsilon \) increases, the resulting regret should increase accordingly. However, when increasing the cap size, the corresponding labelling problem will be more balanced (due to the fact that the number of points labelled as 1 increases). Generally, this improves the accuracy of our labelling, hence reducing regret. Experimentally, we see that the regret of our decisions is a roughly convex function of the cap size: for very small \(\epsilon \), there are too few positive labels to learn \(l^\epsilon \) efficiently, resulting in high error; then the model accuracy improves as \(\epsilon \) increases. We can see this trade-off explicitly in Table 1 for the min-cost flow problem.
References
Baardman, L., Levin, I., Perakis, G., Singhvi, D.: Leveraging comparables for new product sales forecasting. Available at SSRN 3086237 (2019)
Perakis, G., Singhvi, D., Skali Lami, O., Borenstein, A., Lua, J.W., Mangal, A., Poninghaus, S.: Ancillary services in targeted advertising: from prediction to prescription. Manufacturing & Service Operations Management (2021)
Boroujeni, S., Panchamgam, K., Perakis, G., Thayaparan, L.: Motem: Method for optimizing over tree ensemble models. Available at SSRN 3972341 (2021)
Cristian, R., Perakis, G.: Learning near optimal decisions: From saa to robust optimization. Working Paper (2021)
Bass, F.M.: A new product growth for model consumer durables. Manage. Sci. 15(5), 215–227 (1969)
Bass, F.M.: Comments on “a new product growth for model consumer durables the bass model.” Manage. Sci. 50(12), 1833–1840 (2004)
Massiani, J., Gohs, A.: The choice of bass model coefficients to forecast diffusion for innovative products: An empirical investigation for new automotive technologies. Res. Transp. Econ. 50, 17–28 (2015)
Ford, E.W., Hesse, B.W., Huerta, T.R.: Personal health record use in the united states: Forecasting future adoption levels. J. Med. Internet Res. 18(3), 73 (2016)
Fan, Z., Che, Y., Chen, Z.: Product sales forecasting using online reviews and historical sales data: A method combining the bass model and sentiment analysis. J. Bus. Res. 74, 90–100 (2017)
Späth, H.: Algorithm 39: Clusterwise linear regression. Computing 22(4), 367–373 (1979)
Brusco, M.J., Cradit, J.D., Stahl, S.: A simulated annealing heuristic for a bicriterion partitioning problem in market segmentation. J. Mark. Res. 39(1), 99–109 (2002)
Chirico, P.: A clusterwise regression method for the prediction of the disposal income in municipalities. In: Classification and Data Mining
Hu, K., Acimovic, J., Erize, F., Thomas, D.J., Van Mieghem, J.A.: Forecasting product life cycle curves: Practical approach and empirical analysis. Manuf. Serv. Opera. Manag. 21(1), 66–85 (2019)
Bagirov, A.M., Mahmood, A., Barton, A.: Prediction of monthly rainfall in victoria, australia: Clusterwise linear regression approach. Atmos. Res. 188, 20–29 (2017)
DeSarbo, W.S., Oliver, R.L., Rangaswamy, A.: A simulated annealing methodology for clusterwise linear regression. Psychometrika 54(4), 707–736 (1989)
DeSarbo, W.S., Cron, W.L.: A maximum likelihood methodology for clusterwise linear regression. J. Classif. 5(2), 249–282 (1988)
Viele, K., Tong, B.: Modeling with mixtures of linear regressions. Stat. Comput. 12(4), 315–330 (2002)
Lau, K., Leung, P., Tse, K.: A mathematical programming approach to clusterwise regression model and its extensions. Eur. J. Oper. Res. 116(3), 640–652 (1999)
Bertsimas, D., Shioda, R.: Classification and regression via integer optimization. Oper. Res. 55(2), 252–271 (2007)
Carbonneau, R.A., Caporossi, G., Hansen, P.: Globally optimal clusterwise regression by mixed logical-quadratic programming. Eur. J. Oper. Res. 212(1), 213–222 (2011)
Carbonneau, R.A., Caporossi, G., Hansen, P.: Extensions to the repetitive branch and bound algorithm for globally optimal clusterwise regression. Computers & Operations Research 39(11), 2748–2762 (2012)
Park, Y.W., Jiang, Y., Klabjan, D., Williams, L.: Algorithms for generalized cluster wise linear regression. INFORMS J. Comput. 29(2), 301–317 (2017)
Kamakura, W.A., Russell, G.J.: A probabilistic choice model for market segmentation and elasticity structure. J. Mark. Res. 26(4), 379–390 (1989)
Megiddo, N., Tamir, A.: On the complexity of locating linear facilities in the plane. Oper. Res. Lett. 1(5), 194–197 (1982)
Perakis, G., Singhvi, D., Skali Lami, O.: Extended sampled tree ensembles for classification and regression. Available at SSRN: https://ssrn.com/abstract=3505431 (2021)
Chen, T., Guestrin, C.: Xgboost: A scalable tree boosting system. In: Proceedings of the 22nd Acm Sigkdd International Conference on Knowledge Discovery and Data Mining, pp. 785–794. ACM (2016)
Ben Taieb, S., Hyndman, R.J.: A gradient boosting approach to the kaggle load forecasting competition. Int. J. Forecast. 30(2), 382–394 (2014). https://doi.org/10.1016/j.ijforecast.2013.07.005
Bojer, C.S., Meldgaard, J.P.: Kaggle forecasting competitions: An overlooked learning opportunity. Int. J. Forecast. 37(2), 587–603 (2021)
Breiman, L.: Random forests. Mach. Learn. 45(1), 5–32 (2001)
Rätsch, G., Onoda, T., Müller, K.-R.: Soft margins for adaboost. Mach. Learn. 42(3), 287–320 (2001)
Ke, G., Meng, Q., Finley, T., Wang, T., Chen, W., Ma, W., Ye, Q., Liu, T.-Y.: Lightgbm: A highly efficient gradient boosting decision tree. Adv. Neural. Inf. Process. Syst. 30, 3146–3154 (2017)
Breiman, L., Friedman, J., Olshen, R., Stone, C.: Classification and regression trees (1984)
Bertsimas, D., O’Hair, A., Relyea, S., Silberholz, J.: An analytics approach to designing combination chemotherapy regimens for cancer. Manage. Sci. 62(5), 1511–1531 (2016)
Baardman, L., Cohen, M.C., Panchamgam, K., Perakis, G., Segev, D.: Scheduling promotion vehicles to boost profits. Manage. Sci. 65(1), 50–70 (2019)
Mišić, V.V.: Data, models and decisions for large-scale stochastic optimization problems. PhD thesis, Massachusetts Institute of Technology (2016)
Bertsimas, D., Mišić, V.V.: Exact first-choice product line optimization. Oper. Res. 67(3), 651–670 (2019)
Anderson, R., Huchette, J., Ma, W., Tjandraatmadja, C., Vielma, J.P.: Strong mixed-integer programming formulations for trained neural networks. Math. Program. 183(1), 3–39 (2020)
Bunel, R., Turkaslan, I., Torr, P.H., Kohli, P., Kumar, M.P.: A unified view of piecewise linear neural network verification. In: Proceedings of the 32nd International Conference on Neural Information Processing Systems, pp. 4795–4804 (2018)
Cheng, C.-H., Nührenberg, G., Ruess, H.: Maximum resilience of artificial neural networks. In: International Symposium on Automated Technology for Verification and Analysis, pp. 251–268. Springer (2017)
Fischetti, M., Jo, J.: Deep neural networks and mixed integer linear optimization. Constraints 23(3), 296–309 (2018)
Kumar, A., Serra, T., Ramalingam, S.: Equivalent and approximate transformations of deep neural networks. arXiv preprint arXiv:1905.11428 (2019)
Tjeng, V., Xiao, K., Tedrake, R.: Evaluating robustness of neural networks with mixed integer programming. arXiv preprint arXiv:1711.07356 (2017)
Besbes, O., Phillips, R., Zeevi, A.: Testing the validity of a demand model: An operations perspective. Manuf. Serv. Opera. Manag. 12(1), 162–183 (2010)
Kallus, N., Mao, X.: Stochastic optimization forests. ArXiv arXiv:2008.07473 (2020)
Biggs, M., Hariss, R., Perakis, G.: Optimizing objective functions determined from random forests. Available at SSRN 2986630 (2017)
Mišić, V.V.: Optimization of tree ensembles. Oper. Res. 68(5), 1605–1624 (2020)
Ferreira, K.J., Lee, B.H.A., Simchi-Levi, D.: Analytics for an online retailer: Demand forecasting and price optimization. Manuf. Serv. Opera. Manag. 18(1), 69–88 (2016)
Cortez, P.: Viticulture commission of the vinho verde region (cvrvv). University of Minho, Guimarães, Portugal. Retrieved 15, 2020 (2009)
Kao, Y.-h., Roy, B., Yan, X.: Directed regression. Advances in Neural Information Processing Systems 22 (2009)
Amos, B., Kolter, J.Z.: Optnet: Differentiable optimization as a layer in neural networks. In: International Conference on Machine Learning, pp. 136–145. PMLR (2017)
Wilder, B., Dilkina, B., Tambe, M.: Melding the data-decisions pipeline: Decision-focused learning for combinatorial optimization. In: Proceedings of the AAAI Conference on Artificial Intelligence, vol. 33, pp. 1658–1665 (2019)
Elmachtoub, A.N., Grigas, P.: Smart “predict, then optimize”. Manage. Sci. 68(1), 9–26 (2022)
Ban, G.-Y., Rudin, C.: The big data newsvendor: Practical insights from machine learning. Oper. Res. 67, 90–108 (2019)
Bertsimas, D., Koduri, N.: Data-driven optimization: A reproducing kernel hilbert space approach. Oper. Res. 70(1), 454–471 (2022)
Mandi, J., Guns, T.: Interior point solving for lp-based prediction+optimisation. Adv. Neural. Inf. Process. Syst. 33, 7272–7282 (2020). arXiv:2010.13943
Vlastelica, M.P., Paulus, A., Musil, V., Martius, G., Rolinek, M.: Differentiation of blackbox combinatorial solvers. ArXiv arXiv:1912.02175 (2020)
Berthet, Q., Blondel, M., Teboul, O., Cuturi, M., Vert, J.-P., Bach, F.: Learning with differentiable perturbed optimizers. Adv. Neural. Inf. Process. Syst. 33, 9508–9519 (2020). arXiv:2002.08676
Kotary, J., Fioretto, F., Van Hentenryck, P., Wilder, B.: End-to-end constrained optimization learning: A survey. CoRR arXiv:2103.16378 (2021)
Audibert, J.-Y., Bubeck, S., Lugosi, G.: Regret in online combinatorial optimization. Math. Oper. Res. 39(1), 31–45 (2014). https://doi.org/10.1287/moor.2013.0598
Balkanski, E., Singer, Y.: The sample complexity of optimizing a convex function. In: Conference on Learning Theory, pp. 275–301. PMLR (2017)
Hazan, E.: Introduction to online convex optimization. Found. Trends Optim. 2, 157–325 (2016)
Nemirovskiĭ, A.S., El Ghaoui, L., Ben-Tal, A.: Robust Optimization (Princeton Series in Applied Mathematics). Princeton University Press
Bertsimas, D., den Hertog, D.: Robust and adaptive optimization. Dynamic Ideas LLC 958 (2020)
Bertsimas, D., Brown, D., Caramanis, C.: Theory and applications of robust optimization. SIAM Rev. 53(3), 464–501 (2011). https://doi.org/10.1137/080734510
Soyster, A.L.: Technical note-convex programming with set-inclusive constraints and applications to inexact linear programming. Oper. Res. 21(5), 1154–1157 (1973)
Ben-Tal, A., Nemirovski, A.: Robust solutions of linear programming problems contaminated with uncertain data. Math. Program. 88(3), 411–424 (2000)
Bertsimas, D., Sim, M.: The price of robustness. Oper. Res. 52, 35–53 (2004). https://doi.org/10.1287/opre.1030.0065
Bertsimas, D., Gupta, V., Kallus, N.: Data-driven robust optimization. Math. Program. 167(2), 235–292 (2018). https://doi.org/10.1007/s10107-017-1125-8
Bertsimas, D., McCord, C., Sturt, B.: Dynamic optimization with side information. arXiv preprint arXiv:1907.07307 (2019)
Bertsimas, D., Van Parys, B.: Bootstrap robust prescriptive analytics. Mathematical Programming, 1–40 (2021)
Kannan, R., Bayraksan, G., Luedtke, J.R.: Residuals-based distributionally robust optimization with covariate information. arXiv preprint arXiv:2012.01088 (2020)
Kleywegt, A.J., Shapiro, A., Homem-de-Mello, T.: The sample average approximation method for stochastic discrete optimization. SIAM J. Optim. 12(2), 479–502 (2002)
Bertsimas, D., Kallus, N.: From predictive to prescriptive analytics. Manage. Sci. 66(3), 1025–1044 (2020)
Bertsimas, D., Dunn, J., Mundru, N.: Optimal prescriptive trees. INFORMS J. Optim. 1(2), 164–183 (2019)
Notz, P.M., Pibernik, R.: Prescriptive analytics for flexible capacity management. Manage. Sci. 68(3), 1756–1775 (2022)
Gao, R., Yang, J., Zhang, L.: Optimal robust policy for feature-based newsvendor
Bousquet, O., Elisseeff, A.: Algorithmic stability and generalization performance. Advances in Neural Information Processing Systems 13 (2000)
Verma, S., Zhang, Z.-L.: Stability and generalization of graph convolutional neural networks. In: Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, pp. 1539–1548 (2019)
Coroianu, L.: Best lipschitz constants of solutions of quadratic programs. J. Optim. Theory Appl. 170(3), 853–875 (2016). https://doi.org/10.1007/s10957-016-0966-2
Acknowledgements
The authors would like to thank the review team for their insightful comments that has helped us improve both the content and exposition of this work.
Funding
Open Access funding provided by the MIT Libraries
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Baardman, L., Cristian, R., Perakis, G. et al. The role of optimization in some recent advances in data-driven decision-making. Math. Program. 200, 1–35 (2023). https://doi.org/10.1007/s10107-022-01874-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10107-022-01874-9
Keywords
Mathematics Subject Classification
- 90B50: Management decision making including multiple objectives
- 90C11: Mixed Integer Optimization
- 90C90: Applications of mathematical programming
- 68T05: Learning and adaptive systems
- 62H30: Classification and discrimination
- cluster analysis
- 62J05: Linear regression
- 62J02: General nonlinear regression
- 62-07: Data analysis