Introduction

Retaining the functional connectivity of landscapes is a pressing issue for conservation (Goodwin and Fahrig 2002; Fahrig et al. 2011). Largely driven by urbanisation and agricultural change, increasing habitat fragmentation has implications at an individual and population level. The consequences include isolation from habitats necessary for foraging, resting or gene flow, resulting in population declines and greater vulnerability to extinction (Pulliam 1988; Beier 1993; Rossiter et al. 2000).

The identification of landscapes or habitats that provide high functional connectivity for species of conservation concern has the potential to focus resources where they can be deployed most effectively (Lawton et al. 2010). For some species, such habitats are—at least in principle—legally protected because they are vital to maintaining the integrity of key populations [e.g. landscapes connecting a network of Special Areas of Conservation of bats under the EU Habitats Directive; 92/43/EEC (EC 1992)]. However, in practical terms, trying to identify the exact locations or the extent of these habitats can be extremely challenging, with many habitat requirements being species specific (Fagan and Calabrese 2006; Fahrig 2007). For example, important corridors may offer relatively poor habitat quality in themselves, but may offer the best—or only—available route to join areas important for foraging, mating or resting.

One approach to exploring and visualising functional connectivity within a landscape is to use circuit theory (McRae 2006). In combination with random walk theory (Doyle and Snell 1984; Chandra et al. 1996), these approaches allow for all available movement possibilities to be considered and mapped using resistance surfaces. These surfaces (landscapes) are scored based on the cost incurred for an individual to move between two nodes (habitats) (Wiens 2001), with less resistance representing an increased probability of movement between nodes. Linking nodes together creates cost paths that can be represented by a cumulative resistance value or cost-weighted distance (McRae et al. 2008). Thus, the probability of movement between any two spatial locations can be measured, whilst considering all other available routes.

The application of this approach, using the software Circuitscape (McRae et al. 2008), has been successfully used to map barriers to gene flow and species movement, and to identify landscape corridors critical to the long term viability and stability of populations (Belisle 2005; Le Roux et al. 2017; e.g. Rayfield et al. 2016). However, most of this research has focused on large spatial scales (e.g. country-level), and has used direct measures of animal movement (e.g. GPS tracks). In practice, barriers to connectivity, as well as conservation actions, frequently operate at much smaller spatial scales. For example, decisions must be made about the probable effect of a single, lane major road on the ability of a local population to access parts of its habitat, and hence what, if any, mitigation is required.

Considering the cost implications and the lack of equipment to be able to GPS tag smaller bat species safely and ethically we highlight the need to be able to develop non-invasive methods for examining conservation issues surrounding landscape fragmentation at a local scale. This is of particular concern for the greater horseshoe bat (GHS; Rhinolophus ferrumequinum) which has suffered large worldwide declines and is of particular conservation concern in Britain (Jones et al. 2009). This species is highly dependent on linear features, such as hedgerows, to facilitate movement into the wider landscape (Duvergé and Jones 1994; Froidevaux et al. 2017). Using an approached detailed by Shirk et al. (2010), we use the GHS in southern Britain to test whether (i) robust, high resolution connectivity models suitable for informing conservation planning at local scales can be produced using Circuitscape, (ii) non-invasive indicators of activity can be used to populate models of functional connectivity, and (iii) the optimal connectivity model output corresponds with expert opinion ‘fly ways’.

Methods

Study area and GIS data

The study areas were defined as 3 km radii around four GHS maternity roosts in Devon, southwest England (supplementary material Fig. S1). These study areas were restricted to 3 km due to computational limitations regarding the trade-off between the extent of the area covered and the resolution of the data. As GHS are site-faithful (Rossiter et al. 2002), with limited movement of females between sites during the maternity season, the data collected from these roosts were treated as independent from each other during the modelling process. In addition, the roosts were between 13.5 and 89 km apart. The maximum distance recorded by an individual during our radio telemetry study was 9.1 km (mean: 5.4 km); this is in line with Pinaud et al. (2018), who recorded a maximum distance of 7.6 km (mean: 4.2 km). Each study area contained a mosaic of habitats and landscape features, including grazed and arable fields, broadleaved woodland, coniferous woodland, hedgerows, riparian habitats, and occasional farm buildings and residential houses (Supplementary material Fig. S2–5). Numerous single-lane roads crossed the landscape, and in two of the study areas there were two-lane highways. Immediately surrounding three of the roosts were small villages. Streetlights occurred in these villages, as well as in isolated patchy locations across the wider landscape.

One-metre resolution geographical information system (GIS) raster data were obtained for each landscape feature surrounding each of our roosts, resulting in five different environmental layers (Table 1). The Lightscape layers were created following the methodology described by Bennie et al. (2014), using streetlight position and height with Digital Terrain Models (DTM) and Digital Surface Models (DSM) to create a light irradiance GIS layer. These were used to predict the direction and intensity of streetlight at different wavelengths, modelling the night-time light environment. The Distance to Roads layers were created using ArcGIS and ranked using the most current annual average daily traffic volumes (AADT; rounded to the closest 10) (Department of Transport 2015). In this case, lower AADT meant a lower rank value. The Distance to Linear Features layers defined ‘intensively managed hedgerows’ as those typically cut annually and which have a median height < 2m; ‘sympathetically managed hedgerows’ are defined as those with a median height > 2m and which typically included mature trees, had not been cut the previous calendar year, and were managed, whether intentionally or not, in ways that benefit wildlife.

Table 1 GIS data used to model the movement of greater horseshoe bats in the study site (average annual daily traffic—AADT)
Full size table

Bat surveys

Acoustic surveys

The relative GHS activity was based on acoustic surveys for bats that were conducted as part of a citizen science project (Devon Greater Horseshoe Bat Project; June–September 2016). Acoustic data were collected at 205 survey points using full-spectrum static bat detectors (SM2 and SM2+ detectors with SMX-U1 or SMX-US ultrasonic microphones that were sensitivity-tested prior to deployment, Wildlife Acoustics, Maynard, Massachusetts, USA). Details of the acoustic detector settings are provided in Supplementary material Table S2. Microphones were placed at a height of at least 1 m above the ground and were orientated horizontally. Recordings were made for up to seven nights from 30 min before sunset to 30 min after sunrise. Bat detectors were placed as close to randomly as possible (depending on landowner permission) in all available landscape features within 3 km of each roost. During the process of univariate and multivariate model validation, no predictions within the peripheral 300 m of the survey area were used, as it is anticipated that the validity of the model would decline at its outer extremities (Koen et al. 2010).

Acoustic records were analysed using Kaleidoscope software (version 3.1.1; Bats of Europe classifier version 3.0.0; Wildlife Acoustics, Maynard, Massachusetts, USA) and were verified manually on the basis of call frequency, shape and repetition rate. Relative bat activity was assessed as the average number of bat passes per night per detector during the survey period (e.g. Jung et al. 2012; Charbonnier et al. 2014). Any bat detectors that only functioned for a single night owing to malfunction, and that did not record GHS during that night, were excluded from further analysis. GHS passes were defined as pulses of sound, as described by (Russ 2012), recorded within a single sound file. Sounds files were created by a rolling two-second window: once the detectors were triggered, recording continued until there was a two-second window without sound of sufficient amplitude to trigger recording. The average pass rates per night per detector were used to validate all models.

Radio-tracking study

During May and June 2010 and 2012, 13 female GHS were caught using mist nets and harp traps for radio-tracking at Roost 2 in southern Devon, under licence from the National Statutory Nature Conservation Organisation (Natural England). Each of the bats was weighed, and the largest parous females were selected for study. The transmitter (0.35 g) did not exceed 5% of the bat’s body weight. A small area of fur was clipped from between the scapulae, and VHS radio-transmitters (Micro-pip, Biotrack Ltd., Wareham, Dorset, UK) were attached using Torbot surgical adhesive (Torbot Group Inc., Rhode Island, USA).

The female GHS were tracked nightly for up to ten days, or until the tags dropped off or their batteries failed. Bats were followed, as closely as possible without causing a disturbance, by two teams of observers, each equipped with radio receivers (Sika, Biotrack Ltd., Wareham, Dorset, UK) connected to hand-held directional three-element Yagi antennae; to establish commuting routes and foraging grounds in situ (White and Garrott 2012), fixes were taken every 5 min. Alternatively, the general locations of the bats were identified using an omni-directional magnetic whip aerial mounted on the roof of a vehicle. Once the teams homed in on the individual GHS they switched to the hand-held equipment again, taking multiple timed bearings of the location of each bat. From these measurements, the position of the bats were then biangulated after each survey night. Using a similar approach, Pinaud et al. (2018) estimated the spatial accuracy to be approximately 100 m. To eliminate temporal correlation of our fixes, each fix was considered independent when at least 30 min separated two consecutive locations (White and Garrott 2012).

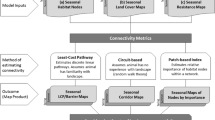
Modelling approach

An underlying premise of our approach was that relative GHS activity (in this case bat passes) are a suitable proxy for more direct indices of connectivity (e.g. genetic connectivity indices or animal movement tracks collected by GPS). Doncaster and Rondinini (2001), Braaker et al. (2014), Le Roux et al. (2017) and Pinaud et al. (2018) all demonstrate, through field observations, static bat detectors, radio-tracking and Geographical Positioning System (GPS) data, that in general species, including the GHS, spend less time in unfavourable habitats that have higher resistance values. Additionally, the same individuals are more likely to occur multiple times, and at higher activity levels, in more favourable areas of low resistance values, e.g. along commuting routes or at foraging grounds (Doncaster and Rondinini 2001). To test this, we compared the outputs of our Circuitscape models with independent data gathered using both acoustic surveys and from radio-tracking studies at our study locations.

Landscape connectivity for GHS was hypothesized to be influenced by local-scale landscape heterogeneity. To make predictions on this hypothesis, we used a similar modelling framework to that outlined by Shirk et al. (2010), and expert opinion models were created as raster resistance surfaces (spatial models) for each environmental layer. Mathematical functions that varied resistance scores and slope values were applied (see below and supplementary material Fig. S6) to the expert opinion model for each environmental layer, evaluating and identifying the peak relationship between the resistance surface parameters and the independent activity data collected around a single GHS roost (Roost 1). This process identified the optimal univariate models for each environmental layer. These optimal layers were combined into a multivariate model, which were then reanalysed to find the optimal multivariate model. In addition, we then compared the Circuitscape model output for Roost 2 against data collected through radio-tracking studies. To test the transferability of the multivariate model to other locations, we applied the same resistance values to the environmental layers at three other GHS roosts (Roosts 2–4); using independent ground truthed GHS activity data collected around each of those three roost locations to assess the utility of the models.

Expert opinion model

Based on eight expert opinions and a literature review of the movement and dispersal ability of GHS (Jones et al. 1995; Flanders and Jones 2009), 18 different landscape features were selected and ranked, within their respective environmental layer groups (Table 1), based on the likely resistance they posed to the movement of GHS. The experts were from both academic and non-governmental organizations, who specialise in, and have extensive knowledge of, GHS ecology. Each expert was sampled, via questionnaire, on the rank and potential resistance values of each landscape feature. These data were then combined to determine the initial ranks and resistance values. A rank of one indicated the least costly landscape feature for the movement of GHS, while higher ranks were associated with more costly features. If there was only one landscape feature in a given environmental layer, then no ranks were required e.g. Rivers. However, if a layer had more than one landscape feature, e.g. Roads, then the maximum rank was the total number of features—in this case four; for other layers, such as Land Cover, the maximum was eight. Those landscape features with higher ranks have greater weighting associated with them, relative to others within the same layer, and as a result, they are more resistance to species movement. Both resistance, and subsequently cost surfaces, using expert opinion data, were then created for each of the environmental layers at Roost 1, before mathematical functions (see below) were applied and analysed during the univariate modelling process.

Mathematical functions

When examining an ecological system, the relationships between environmental layers (or their resistance values) and the functional response of the species (e.g. animal movement) are rarely linear (Etherington 2016). In addition, researchers do not often account for interactions between multiple environmental layers that can occur in real landscapes. For example, a hedgerow with and without streetlights on it will influence the movement of bat species in different ways (Stone et al. 2009). To avoid these issues, and to maximise the potential accuracy of the models, we rescaled our raster data to permit a range of slope values (x; ranged from 1 to 5) relating to our resistance values. Additionally, we varied the maximum resistance value (Rmax), allowing for a range of resistance values to be considered for each layer (varied between resistance 1 and 1010; see below and Supplementary material Fig. S6).

Land cover

The eight broad land cover features were ranked based on expert opinion in order of lowest to highest resistance (Table 1). The ‘Buildings’ landscape feature was always set as the lowest permeability. Resistance surfaces for Land Cover were created using the following equation:

$$ {\text{R}} = \left( {Rank/{\text{V}}_{{{\text{max}}}} } \right)^{{\text{x}}} {\mkern 1mu} \, \times \,\,{\mkern 1mu} {\text{R}}_{{{\text{max}}}} $$

where R is the resistance for each raster pixel (each of which consist of a single Land Cover type) and Vmax is a constant that is the highest possible rank for that feature type. For example, at three of our roost locations there were seven landscape features (Orchards, Deciduous woodland, Scrub, Grassland, Coniferous woodland, Arable land, Buildings; Vmax = 7), and at one we had eight, because Lakes were only present for Roost 4 (Vmax = 8). This means that as the expert opinion ranking moves nearer to the highest resistance rank (Vmax), the overall resistance increases towards Rmax at a rate controlled by the response curve of the slope value (x) (Shirk et al. 2010).

Lightscape

The lightscape irradiance (IR) values were multiplied by the slope values and maximum resistance:

$$ {\text{R}} = \left( {IR} \right)^{{\text{x}}} {\mkern 1mu} \, \times \,{\mkern 1mu} {\text{R}}_{{{\text{max}}}} $$

Distance layers

Each of the three continuous distance layer functions were modified in different ways based on their ecological relationship with GHS bats. Euclidean distance to Rivers was calculated using the following function:

$$ {\text{R}} = \left( {{\text{D}}_{{{\text{et}}}} /{\text{V}}_{{{\text{dmax}}}} } \right)^{{\text{x}}} {\mkern 1mu} \, \times \,{\mkern 1mu} {\text{R}}_{{{\text{max}}}} $$

where Det is the nearest distance of the raster pixel to any river in the 3 km extent, and Vdmax is a constant that is defined as the maximum distance possible from Rivers within the extent of the 3 km. Based on previous literature suggesting that GHS activity occurs at close proximity to linear features, a maximum distance of 10 m was set for both the Linear Features and Rivers layers (Ransome 1996).

Distances, to Linear Features were modelled in a similar way, except as there is more than one feature; the rank order of the features were based on the resistant values chosen by the expert opinion. The lower the expert opinion resistance value the higher the rank order of the feature, meaning that those variables with higher rank order are more permeable than those with a lower rank order. Vrmax is a constant representing the highest rank value for each layer, in this case four. Both the distance to each feature and its rank carried equal weight within the function, and so were multiplied by 0.5.

$$ {\text{R}} = \left( {\left( {{\text{D}}_{{{\text{et}}}} /{\text{V}}_{{{\text{dmax}}}} } \right) \times 0.5 + 0.5 \times \left( {Rank/{\text{V}}_{{{\text{rmax}}}} } \right)} \right)^{{\text{x}}} {\mkern 1mu} \, \times \,{\mkern 1mu} {\text{R}}_{{{\text{max}}}} $$

Landscape resistance values for distance to Roads were classified using four ranks (660, 3260, 15510, 41750 AADT for each road types (Department of Transport 2015); see Table 1 for rank order). Based on examination of previous literature (Berthinussen and Altringham 2012), a maximum distance of 200 m was set for the Roads layer. As resistance was expected to decline with increasing distance to Roads (the inverse of the expectation for Linear Features), we used the following function:

$$ {\text{R}} = \left( {\left( {1 - {\mkern 1mu} \left( {{\text{D}}_{{{\text{et}}}} /{\text{V}}_{{{\text{dmax}}}} } \right)} \right) \times 0.5 + 0.5 \times \left( {Rank/{\text{V}}_{{{\text{rmax}}}} } \right)} \right)^{{\text{x}}} {\mkern 1mu} \, \times \,{\mkern 1mu} {\text{R}}_{{{\text{max}}}} $$

where Vrmax is a constant which represents the highest number of ranks within the Roads layer, set to the highest AADT (41750; rank 4).

Once each resistance surface was created, we used Circuitscape (Version 4.0.5) to create current maps (McRae et al. 2008). To identify the functional connectivity for GHS at a local scale, we used a single roost location as the source layer. Since the exact movement patterns of the bats were unknown, e.g. the locations of potential foraging grounds, we generated a layer featuring concentric circles at 100 m intervals from the roost to a maximum distance of 3 km, using this as the target or ground layer. This enabled us to model movement scenarios from 100 m to 3 km, giving equal weight to each distance and direction.

Univariate and multivariate models

The optimal univariate models for each of the five environmental layers were determined, following the method detailed by Shirk et al. (2010). For each environmental layer, the value for both parameter functions, x and Rmax, were increased or decreased (favouring the direction of increasing correlation) and revaluated after each iteration (100–161 variations per environmental layer with varying x (1–5) and Rmax (1–1010) values). This iterative process continued until an optimal model was found by examining and identifying the unimodal peak in the maximum Spearman’s rank correlation coefficient between the parameter functions (x and Rmax) output (Circuitscape current map) and the relative GHS activity data at Roost 1.

The resistance surfaces of the optimal univariate environmental layers were then combined into a multivariate model resistance surface for Roost 1. To incorporate the interactions between layers into this additive multivariate model, the parameter functions (x and Rmax) of each layer were increased or decreased independently, while keeping all other layers constant, until a unimodal peak for each layer could be identified. This started with the univariate environmental layer with the highest correlation to GHS activity. If the parameter functions of a layer with a lower correlation value changed, then the iterative process started again, beginning with the univariate environmental layer with the highest correlation value, testing each iteration against the ground-truthed GHS activity data. The same parameter functions used in the univariate optimisation were used during the multivariate optimisation, and were increased or decreased until a unimodal peak was identified. This approach was taken because analysing every single parameter variation for each variable in relation to every other variable would have required an unfeasibly large number of model tests.

The univariate and multivariate processes were undertaken twice. First they used all nightly data collected during the acoustic surveys, illustrating general GHS movement and activity around their roost, over the entire night. Then secondly, they used data specifically relating to GHS movement from their roost to their initial foraging ground at the beginning of the night, rather than movements during the entire night (activity recorded within the first hour after sunset), e.g. Pinaud et al. (2018). These two types of data sets were used to examine whether different environmental layers affected the GHS activity in different ways, depending on the bats’ behaviour.

Statistical evaluation and transferability

All statistical analysis were completed in R (version 3.3.0) (R Core Team 2016). Spearman’s rank correlations were used to examine the relationship between relative bat activity recorded at each of the detector locations and the subsequent current density produced from the Circuitscape current maps for each model. Unlike Shirk et al. (2010), Spearman’s rank correlations, rather than Mantel’s correlations, were used because our response variable (bat activity) was not a matrix of distance based metrics (e.g. genetic distance). The univariate and multivariate models were initially built using 93 bat detector locations in the study area at Roost 1 (training roost). The successful transferability of a model can be defined as the ability for it to produce accurate predictions for areas outside that used for the initial training model (Justice et al. 1999). The transferability of the optimal multivariate model from Roost 1 was tested at Roost 2–4 by examining it against independent datasets collected within 3 km of each of these respective roost (between 33 and 38 bat detector locations). Using data that were not used to train or develop the models allows for a more stringent model testing, reducing the chances of overfitting, and makes the model a more reliable predictor of new data points (Xu and Liang 2001; Urban et al. 2009).

Like Pinaud et al. (2018), we wanted to investigate the accuracy of our connectivity models further by testing whether there would be a greater likelihood of GHS radio-tracking fixes occurring in more permeable areas of higher Circuitscape current, or whether they would be more randomly located in the landscape. Following the methodology outlined in Driezen et al. (2007), z-scores were created to examine whether the cumulative sum of the cost of an individual reaching a certain location (i.e. each radio-tracking fix) was less than the mean cost of reaching all other points of equal distance from the roost (equidistant cost). For example, if the fix location was 1 km from the roost, we calculated the current value at this fix location and then compared it to the mean current value of all other locations at equal distance from the roost, i.e. all locations at 1 km from the roost. Thus, the analyses took into account the travel route and cost by each radio-tracked bat from the roost to each of their fix locations. To create the standardized z-score for each fix, we subtracted the mean equidistant cost from the Circuitscape current value at the fix location, and divided this value by the standard deviation of that mean cost. A positive value indicated that the fixes were on a route of higher functional connectivity (lower cost) than randomly selected locations. The results of the 191 fix locations were then compared with a normal distribution using a Shapiro–Wilk (W) test to examine whether they were significantly different from zero. As the radio-tracking data could have been accurate up to approximately 100 m, we resampled the final model output to a 100 m resolution and examined whether this influenced the result. The data were log transformed prior to analysis to achieve normality.

In addition, the optimal multivariate model output was compared against an expert opinion ‘fly ways’ dataset at Roost 1. This had previously been created, at the request of the Local Planning Authority and the Statutory Nature Conservation Organisation (Natural England 2010), by experts with local knowledge of bat activity in the region, who visually examined the landscape and selected areas of expected high functional connectivity for GHS. These ‘fly ways’ have been given additional protection from future developments and were designed for both local and larger scale movements. No radio-tracking data were used in the creation of the ‘fly ways’ presented in this study. To produce a comparison of the Circuitscape model and the expert opinion ‘fly ways’, we overlaid the optimal multivariate model output, and compared inside and outside the flyways that had high current (top 25%). The data were standardised by the distance of each detector to the roost. We then examined the relationship between the optimum multivariate model, produced for GHS bats, with the median data from all other bat species recorded on each bat detector at Roost 1, to try to identify whether such a modelling approach and conservation efforts for a single key species would be beneficial for the entire bat community.

Results

Multivariate connectivity models provided a better description of the environmental layers around Roost 1 compared to any univariate model. The optimal univariate model’s maximum per pixel resistance values differed from the multivariate model for three out of the five environmental layer types (Table 2). Similar results were obtained using early night, rather than all night, data, except the maximum resistance values of Land Cover and Linear Features for the multivariate model were 10,000 and 50,000, respectively (supplementary material Table S1).

Table 2 Per pixel resistance values for training roost location for both optimal univariate and multivariate models
Full size table

The optimal multivariate model of general GHS movement could be transferred from one roost location to another, with all locations showing a significant correlation (Table 3). Nevertheless, there are variation between these locations.

Table 3 Spearman’s rank correlation, the number of ground-truthed bat detector locations and model type for each of the four roost locations
Full size table

The output Circuitscape current maps demonstrate the importance of linear features for the movement of GHS and highlight the impact of streetlights, while additionally identifying ‘pinch points’ within the landscape, allowing for spatial targeting of conservation measures in order to maximise conservation value (Fig. 1). When comparing the raw data, we identify that GHS activity is 7.6% higher in the top 25% of predicted functional connectivity outside of the ‘fly ways’ compared with within them (Fig. 2).

Fig. 1
figure 1

Image depicting functional connectivity for greater horseshoe bats (GHS), pinch points, and the barrier effects of streetlights. Black triangles are streetlight locations, red indicates high, and blue indicates low functional connectivity. The inset map shows the locations of the GHS roost and area of street lighting being depicted (black square)

Full size image
Fig. 2
figure 2

Circuitscape map centred on the greater horseshoe bat (GHS) training roost location. Image illustrating the flow of current within the extent of the 3 km map boundary, with the expert opinion ‘fly way’ layer overlaid on top

Full size image

During the radio-tracking studies, 191 GHS fixes were recorded within 3 km of Roost 2 in Devon. The maximum fixes per individual was 31, with an average of 15. The results of ground-truthing the model using the 191 z-scores derived from the radio tracking data, showed a significant positive relationship with the Circuitscape current scores (mean z-score: 0.73, CI 0.69–0.78, p value: 0.016, W: 98). Similar results were obtained when the model output was resampled at a 100 m resolution (mean z-score: 1.77, CI 1.72–1.82, p-value: 0.003, W: 98).

Using GHS as an umbrella species and to explore the value of the modelling approach for the entire bat communities, we examined data for the other 10 species we recorded (Barbastella barbastellus, Myotis spp., Eptesicus serotinus, Nyctalus noctula, Pipistrellus nathusii, Pipistrellus pipistrellus, Pipistrellus pygmaeus, Plecotus auritus, and Rhinolophus hipposideros). The results of the multivariate model created (using all nightly data) for Roost 1, identified that the median number of passes for all species recorded within the top quartile (i.e. 76–100%) of the observed Circuitscape current values (i.e. high current), were at least 125% higher than any of the lower three quartiles (Table 4).

Table 4 Median number of passes of all bat species recorded per night per bat detector location at Roost 1, between 0 and 100% of observed Circuitscape current values
Full size table

Discussion

Urbanisation and agricultural intensification are well documented to be causing a loss of connectivity within our natural environment (Millennium Ecosystem Assessment 2005). In increasingly fragmented landscapes, it is vital that connecting routes, as well as habitat patches of high inherent value, are conserved. For our focal study species, the greater horseshoe bat, the results of our optimal multivariate model align with our current knowledge of its movement behaviour (Pinaud et al. 2018). We demonstrate that the characteristics in our Linear Features layer increase permeability within the landscape, whereas artificial night lighting decreases it (Duverge 1996; Stone et al. 2009; Day et al. 2015). However, the extent of the influence on functional connectivity in the landscape is unexpected. The final multivariate resistance value for the Linear Features layer indicates a dramatic decrease in the likelihood of relative GHS activity at increasing distances from the feature. The converse is true for the Lightscape layer, where streetlights were found to have a high impact on the permeability of the landscape for GHS, which is in line with current literature relating to horseshoe ecology (Stone et al. 2009, 2012; Day et al. 2015). Similar results were obtained using only early night data, except that the maximum resistance of both Land Cover and Linear Features increased compared to the general movement of GHS. This highlights that, within the first hour after sunset, the activity of light sensitive bats, such as GHS, will be more tightly constrained to hedgerows and features that are more sheltered. At a local scale, these types of considerations could play a part of the success or failure of any future conservation action plans or mitigation measures.

The ready availability of large-scale data on, for example, weather and land cover means that macro-scale models, which often are based on very course resolution data about the target species, are commonly generated. Whilst valuable, for example in identifying migration corridors or highlighting areas likely to be most appropriate for a National Park (e.g. Roever et al. 2013), effective conservation also relies on fine-resolution data relevant to local planning decisions (Lechner et al. 2015), such as that provided here. Our models are relevant for other species of conservation concern, suggesting that the outputs can be of wider general use for conservation planning if appropriate umbrella species are selected. The numbers of records for non-target bat species were at least 125% higher at areas in the top quartile of the GHS Circuitscape current values compared to any of the lower three quartiles. We also demonstrate that spatially-targeted approaches to connectivity modelling can help to identify the locations of critical ‘pinch points’ within the landscape. For example, individual streetlight placements can have a major impact on the overall functional connectivity of the study areas, with the current passing through narrow corridors of suitable dispersal habitat (e.g. Figure 1). However, one limitation of the current study was that only streetlights, but not other lights e.g. vehicle headlights or security lights, were taken into account, owing to the lack of suitable spatial data. We highlight this as an area that is a priority for future research.

We evaluated the extent to which the modelling approach taken here represented an improvement over simpler approaches for identifying key corridors in the landscape. We found that although some of the important local areas for connectivity fell within the ‘fly ways’ based on expert opinion, many of them were missed. Yet these expert-opinion ‘fly ways’ have historically been given greater protection through the Local Authority’s planning system than other regions. The model also identified some linear features as being important for functional connectivity that did not align with current ideas of optimal habitat (Duverge 1996), e.g. highly managed hedgerows surrounded by arable fields. However, while our results indicate that models can be successfully transferred from one area to another, with significant results, a precautionary approach should be taken. We therefore caution against transferring models from a ‘training’ area without any ground-truthing: where very different environmental conditions prevail, new models should be built (e.g. Roach et al. 2017). This will ensure that the resultant maps incorporate the interactions and non-linearity between predictor layers relevant to the specific locality.

This study illustrates that a relatively simple framework, and an iterative approach to connectivity modelling, permits the influence of landscape features to be visualised at a local scale. It therefore overcomes many of the difficulties encountered when trying to incorporate research into real-world decision-making by local planners (Opdam et al. 2002). Our approach has the potential to facilitate evidence-based policy and management. The resultant models can help planners and conservationists reduce human-wildlife conflicts, by applying mitigation measures strategically at locations likely to be most sensitive to species movement and future land-use change. Stakeholders can also use the modelling technique described here as a predictive tool. For example, the relative impacts of alternative scenarios, such as the positioning of new housing or lighting schemes, the creation of woodland or the restoration of hedgerows, can be assessed through this modelling process, helping to achieve evidence-based wildlife conservation.

Environmental Impact Assessments are already meant to give consideration to the landscape context of a site, including the cumulative impacts of multiple developments. In practice, most work is conducted on a site-by-site basis. The approach outlined here provides a tool to incorporate functional connectivity into decision-making.