Abstract
Context
The variation in spatial distribution between ecosystem services can be high. Hence, there is a need to spatially identify important sites for conservation planning. The term ‘ecosystem service hotspot’ has often been used for this purpose, but definitions of this term are ambiguous.
Objectives
We review and classify methods to spatially delineate hotspots. We test how spatial configuration of hotspots for a set of ecosystem services differs depending on the applied method. We compare the outcomes to a heuristic site prioritisation approach (Marxan).
Methods
The four tested hotspot methods are top richest cells, spatial clustering, intensity, and richness. In a conservation scenario we set a target of conserving 10 % of the quantity of five regulating and cultural services for the forest area of Telemark county, Norway.
Results
Spatial configuration of selected areas as retrieved by the four hotspots and Marxan differed considerably. Pairwise comparisons were at the lower end of the scale of the Kappa statistic (0.11–0.27). The outcomes also differed considerably in mean target achievement, cost-effectiveness in terms of land-area needed per unit target achievement and compactness in terms of edge-to-area ratio.
Conclusions
An ecosystem service hotspot can refer to either areas containing high values of one service or areas with multiple services. Differences in spatial configuration among hotspot methods can lead to uncertainties for decision-making. This also has consequences for analysing the spatial co-occurrence of hotspots of multiple services and of services and biodiversity.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The concept of ecosystem services (ESs) encompasses multiple contributions of ecosystems to human well-being (Haines-Young and Potschin 2010). It is increasingly being used to analyse the human-nature relationship and to inform policymaking (Carpenter et al. 2009; Larigauderie et al. 2012). An important approach to assess biophysical quantities of multiple ES has been spatial modelling and mapping (Maes et al. 2012a; Martínez-Harms and Balvanera 2012; Nemec and Raudsepp-Hearne 2013; European Commission 2014). These spatial ES assessments could be used for systematic conservation planning to ensure the long-term capacity of ecosystems to provide services (Egoh et al. 2007). Considering ESs in conservation planning is, however, a fairly new practice, which still needs to be operationalized (Chan et al. 2011; Luck et al. 2012b; Cimon-Morin et al. 2013). The advantage of this approach is that it seeks for a way to combine biodiversity conservation with the provision of ESs that originate from natural or semi-natural ecosystems.
Spatial distribution and abundance of ESs across the landscape is spatially heterogeneous and differs between ESs (Egoh et al. 2008; Raudsepp-Hearne et al. 2010; Bai et al. 2011). Different degrees of spatial overlap between ES increase the complexity of conservation planning. Hence, there is a need to identify important sites for conservation of multiple ES (Luck et al. 2012b), for instance in order to select sites for new protected areas. The term ‘ES hotspot’ is increasingly used for the purpose of informing spatial prioritisation of ES (Cimon-Morin et al. 2013). For instance, the number of studies containing the terms “ecosystem service*” and “hotspot*” in title, abstract and keywords increased from 9 in 2006 to 39 in 2013 (Scopus search, 30 October 2014). Despite this growing use of the term, ES hotspot is not clearly defined in the literature yet. While the earlier established notion of a biodiversity hotspot has been defined as an area of both high biodiversity and high level of threat (Myers 1988, 1990; Mittermeier et al. 1998; Myers et al. 2000), the use of the term ES hotspot in the literature differs from that notion. ES hotspot often refers to an area where high amounts of one particular service are present (Cimon-Morin et al. 2013), but other studies have defined hotspots as areas where multiple ESs overlap (e.g., Gos and Lavorel 2012). Spatial configuration of selected sites might differ depending on the hotspot method applied. As this could lead to inconclusive recommendations to decision makers more clarity is needed on the variety of different existing approaches and their potential advantages and shortcomings. Different hotspot methods might serve different policy purposes, which need to be clarified and discussed. Furthermore, it is unclear to what extent site prioritisation based on hotspots complies with principles of systematic conservation planning (Margules and Pressey 2000; Possingham et al. 2006), such as comprehensiveness, cost-effectiveness and compactness of the spatial arrangements of selected sites. The conservation software Marxan has been developed to select sites for conservation according to these principles and is based on a heuristic optimisation algorithm (Ball et al. 2009). Marxan prioritises sites to protect proportions of the total amount of conservation feature in an area, e.g. a species or an ES. These relative targets can refer to both presence data (e.g., a certain proportion of the habitat area of a service-providing species) and metric data (e.g., a proportion of total amount of carbon stored in an area). Marxan has recently been applied to integrate ESs in different conservation problems (Chan et al. 2006, 2011; Egoh et al. 2011; Izquierdo and Clark 2012; Reyers et al. 2012a; Schröter et al. 2014b).
A first aim of this study was to review ES hotspot definitions and methods to spatially delineate hotspots and to classify the different approaches in order to distinguish the principle differences between them. We furthermore examined whether the reviewed studies indicate which policy purpose they intended to serve. A second aim was to apply and compare the outcome of these methods. Therefore, in a subsequent step we applied a selection of four hotspot delineation methods to a hypothetical ES conservation scenario which intended to prioritise areas to conserve 10 % of the total amount of each service. For this conservation scenario we used spatial models of five ESs, which have been developed for the county of Telemark in southern Norway (Schröter et al. 2014a). In order to critically appraise the hotspot approach we compared the outcomes of the four applied hotspot methods to the site prioritisation approach of Marxan for the same set of ESs for forest areas in Telemark. We compared all five approaches in terms of characteristics of selected sites, namely difference in spatial configuration (area size, location, and shape) and mean achievement of the ES conservation target.
Review of ecosystem service hotspots
We reviewed ES hotspot definitions and delineation methods by means of a literature search. A Scopus search was performed on 22 May 2015. Search terms were adjusted until a pre-selection of studies dealing with spatial analysis of ES hotspots were all included in the search results. Title, abstract and keywords were searched for the terms “ecosystem” AND “services” AND (“hotspot*” OR “hot spot” AND “map*” OR “spatial” OR “overlap”). As earlier studies in the field did refer to ESs under the term landscape functions, a second search was done replacing the terms “ecosystem” and “services” by “landscape” and “functions”. The two searches were combined. A total of 158 studies were obtained after the initial search. Titles and abstracts were checked and only studies that performed an empirical spatial analysis on ES hotspots were selected. Some studies had done spatial analyses related to ES hotspots, but either generally defined hotspots as areas of importance for generating a service (Palomo et al. 2014), or related hotspots to spatial coincidence of landscape metrics, which were not clearly connected with ESs (Bryan et al. 2010). After excluding such studies, 23 papers were included in the review, dating from 2008 to 2015. Definitions and delineation methods were recorded, structured and classified. Through content analysis we assessed which potential policy purpose for their hotspot analysis the authors had indicated.
Review results
Two principal concepts to define hotspots were distinguished, which were each addressed by different delineation methods. Hotspots were defined in the reviewed papers either as areas with high values of one single ES or as areas containing multiple, overlapping ESs (Fig. 1).
The most common way to define an ES hotspot was in line with the definition of Egoh et al. (2008, p. 136), who defined hotspots as “areas which provide large proportions of a particular service”, where large proportion refers the upper range of service provision in an area. This approach was used in 13 of the 23 studies included in the review (Table 1). These studies often create hotspots based on a single service, but combine the different areas to define overall priority areas for conservation and management of services. While these studies used the same approach to define ES hotspots, the applied delineation methods differed. Three main delineation methods can be distinguished. First, a top richest cells (quantile) method divides high-to-low ranked grid cells with ES values into classes with an equal number of cells. According to this method the class with the highest values is chosen as a hotspot, while class definition ranged between 5 and 30 %, i.e. between the highest of 20 equally sized classes (vigintiles) and the top three deciles. Whether a top decile also accounts for exactly the top 10 % richest cells depends on ties (equal values of grid cells at the threshold between classes) (Eigenbrod et al. 2010). Second, a threshold method delineates a hotspot according to an expert-based biophysical threshold value of a particular ES, for example for the ES soil accumulation, a soil depth ≥0.8 m and ≥70 % litter cover in a specific case study (Egoh et al. 2008). This differs from the former approach as the threshold method does not consider the distribution of the ES over the grid cells. Third, cluster methods have been used to delineate hotspots with the help of Jenks natural breaks, where differences between classes are maximised according to clusters inherent in the data (Mitchell 1999). As a spatial clustering method, the G *i statistic (Getis and Ord 1992) was used, which finds spatial clusters in the data to identify hotspots or coldspots (Mitchell 2005) (further explained below).
Another principle approach of hotspot definition characterised hotspots as key areas providing more than one ES, a principle which was applied in different ways by 10 of the 23 studies. Four of these were based on aggregated ES value maps, i.e. summed and merged indices. These included an intensity approach, e.g. the highest quantile of a normalised multiple services index (“intensity”) (Willaarts et al. 2012), high point densities of multiple services (Beverly et al. 2008), summed values of multiple ES value maps where values are above average of the study area (Queiroz et al. 2015) and spatial clustering of an aggregated ES value map (Bagstad et al. 2015). Another type referred to the presence of several or all ESs included in an analysis (“richness”) (Gos and Lavorel 2012). In a particular case, Gos and Lavorel (2012) referred to ESs presence above a certain threshold. Others, however, refer to hotspots as areas that are either rich in different ESs (presence without a threshold) or show a high diversity of services (Plieninger et al. 2013). Two studies distinguished multifunctional areas as hotspots. Gimona and van der Horst (2007) delineated hotspots as areas where all considered ESs had high values. Willemen et al. (2010) delineated “multifunctional hotspots” as areas where combinations of ESs (called landscape functions) lead to a higher amount of a specific ES compared to a region’s mean of this ES.
Finally, two studies have defined hotspots in a way that specifically relates to their research interest, but all were related to the spatial congruence of two or more ES. Crossman and Bryan (2009) defined hotspots as areas with a high ratio between a multiple ES index and an index of opportunity costs of conservation. Forouzangohar et al. (2014) delineated areas as hotspots when both of the analysed services showed a positive change in a scenario analysis.
Methods
Case study area
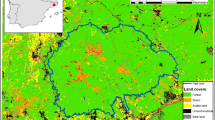
Telemark is a county in southern Norway with an area of 15,300 km2 and a population of about 170,000 (SSB 2012). The climate varies across the region with temperate conditions in the south-east (Skien, average temperature January −4.0 °C, July 16.0 °C, 855 mm annual precipitation) and alpine conditions in the north-west (Vinje, January −9.0 °C, July 11.0 °C, 1035 mm) (Meteorological Institute 2012). The forest landscape is characterized by coniferous and boreal deciduous forest (Moen 1999). A land cover map of the study area is shown in Fig. 2. As forest field mapping lacks for a small south-eastern part of the county (NFLI 2010), we excluded this area for the analysis.
Spatial models of ecosystem services
Five key ESs for Telemark, for which spatial biophysical models have been developed (Schröter et al. 2014a), were included in the analysis: carbon storage, carbon sequestration, snow slide prevention, recreational hiking and existence of wilderness-like areas. We used ES flow models for this current analysis, i.e. models reflecting the actual use of ESs. The selected ESs are conservation-compatible (Chan et al. 2011). This means that the occurrence of the service could reasonably be taken into account as an (additional) argument for conservation, and conservation would not restrict their use. Many provisioning services, such as timber production require management and (more or less intensive) extraction, and their use would normally be restricted in conservation areas, i.e. they are often not compatible with conservation. Regulating services, on the other hand, can be considered conservation-compatible if their use does not require large human interventions. Carbon sequestration and storage and snow slide prevention are examples. Cultural services can be considered conservation-compatible if their use does not conflict with conservation objectives. In the case of Norway, protected areas are often open for low-impact recreational hiking. Other cultural services, however, would conflict with conservation, such as building infrastructure for holiday cabins.
We shortly describe indicators and main inputs of the models here; detailed methods for the development of the spatial ES models can be found in Schröter et al. (2014a). Three regulating services were included (carbon storage, carbon sequestration, snow slide prevention). Carbon storage (Mg C ha−1) was based on field data on above- and belowground carbon stocks. Carbon sequestration (Mg C ha−1 year−1) was modelled as the difference between net primary production and soil respiration. Snow slide prevention by forests mediates flows in a beneficial way and reduces the risk of avalanches. This service was delineated as forest areas on snow slide release areas, whenever infrastructure was present in the respective propagation areas (indicated by presence only). The two cultural services were recreational hiking and existence value. For recreational hiking we built an index containing density of hiking paths in an area weighted by potential users in a defined surrounding. This index reflected both accessibility to hiking areas and potential use by people. Existence of wilderness-like areas was modelled as areas with a distance of more than 1 km from large infrastructure (e.g., roads, power lines) (indicated by presence only). The presence indicator for this ES merely reflects the existence of such areas, but not an active use. This service stands for the value that many people hold for the pure existence of certain ecosystems (Krutilla 1967; Noss 1991; Reyers et al. 2012b). Both the snow slide prevention model and the existence of wilderness-like area model are constructed with a presence-absence logic. While they give an indication of the spatial distribution of the ES, they do not assign different biophysical values to the site, but rather a “1” for presence and a “0” for absence.
Testing different hotspot delineation methods
We applied and compared four different hotspot delineation methods for a conservation scenario for the five ESs for forest areas of Telemark, in which we assumed a conservation target of 10 % of the biophysical amount of each ES. This target is arbitrary, but ensured comparability among the approaches as all methods were adapted so that the hotspots of each ES accounted for approximately the same biophysical amount. All spatial analyses were done in ArcMap 10 (ESRI).
We selected two hotspot delineation methods that are based on single ESs and subsequently combined the prioritised areas of each ES, and two methods that were based on multiple services. The selected delineation methods to create hotspot maps were the top richest cells approach, spatial clustering (G *i statistic), intensity and richness.
The top richest cells approach was the most commonly used approach and was thus also considered in our study. However, as two of the ES maps were presence data only (snow slide prevention, existence value), a top richest class could not be determined and these two ESs were excluded. Spatial clustering was chosen as this approach is an established method to determine hotspots in geographic information science, while it has not often been applied to ESs yet. As it is based on metric data, the presence data ESs were excluded here as well. A simple richness approach was taken that does, in contrast to the more elaborate approach in Gos and Lavorel (2012), not systematically search for thresholds first. The intensity approach was chosen as standardisation and aggregation of ES is a widespread, practical and straightforward index in studies on multiple ESs (Maes et al. 2012b; Schneiders et al. 2012; Pan et al. 2013). The threshold value approach was not applicable as expert based thresholds for ‘high’ levels of services were not available and also would not allow to pursue a specific overall target for ES conservation. The spatial delineation of top richest cells and Jenks natural breaks does not differ when a fixed amount in the top class is pursued. As the number of classes in the Jenks natural breaks approach would be adapted until the amount in the top class equals the amount in the top richest cells approach. Other approaches found in the review were either too specific in their respective purpose or not applicable to the data sets (e.g. point data based indices).
Hotspot maps
The four hotspot maps were created as follows. Data preparation steps for each method can be seen in Table 2.
Top richest cells
According to the top richest cells approach, we sorted all grid cells with descending values and iteratively adapted a top class and calculated the sum of cells in this class until the sum amounted to approximately 10 % of each ES. This iterative testing involved choosing a top quantile and when the total amount covered in this class was higher (or lower) than the 10 % target, choosing a smaller (or larger) top class. This process aimed at minimising the difference between the sum of grid cells above a threshold value and the 10 % target. In a next step, the three ES hotspot maps were merged to one single map.
Spatial clustering
Spatial clustering for finding hotspots with the help of the G *i statistic identifies high concentrations of pixels with high values within a specified distance. We followed a stepwise approach (Timilsina et al. 2013; ESRI 2014). First, for each of the three ES separately, we determined the average distance of each grid cell containing the ES to its nearest neighbour also containing the ES. We then determined the distance band from each cell that maximised spatial autocorrelation. We calculated the z-score of Global Moran’s I with the distance band equal to the average distance to the nearest neighbour, and increased this iteratively by 1 km until the z-score reached a maximum. This distance band was used for the G *i statistic in ArcMap 10 (Mitchell 2005) according to
where G * i (d) is the statistic calculated for each grid cell, d is the distance band for finding neighbours as determined in the precedent step, w ij is a binary weight (1 for cells within d, 0 for cells outside d), x j is the ES value for each of the five ES models.
We calculated a Z-score for testing the significance of the G *i statistic for each cell according to
where E(G * i ) is the expected G * i value for random distribution and n is the number of grid cells. We then ranked cells from high to low Z-scores and iteratively selected the top cells until the sum of grid values corresponded to the 10 % target. This ensured that cells within the most significant clusters were included as hotspots. Here, as well, iterative testing aimed at minimising the difference to the 10 % target. All three ES hotspot maps were merged.
Intensity
For the intensity hotspot, all spatial models of ES were standardised (0–100) by subtracting from each cell the minimum value of each ES and dividing the difference by the range of each ES, and multiplying this ratio by 100:
where x js is the standardised ES value of cell j. All five standardised maps were given equal weights and added to one ES index map (Maes et al. 2012b; Willaarts et al. 2012):
where x jI is the index value of cell j, w = 0.2, x jESi is the value of ES i (i = 1,…,5). In absence of other knowledge and for the sake of simplicity, all ES were thus assumed to be equally important. In accordance with the method used in Willaarts et al. (2012), quantiles were used to determine the top class that forms the hotspot. In contrast to the former hotspot delineation methods, the intensity method accounts for ES bundles and not for a combination of single ESs. Thus, the size of the top quantile was iteratively adapted until the mean target achievement of all five ESs approached 10 %. This iterative testing involved choosing a starting top quantile and when the total amount covered in this class was higher (lower) than the 10 % target, choosing a smaller (larger) top quantile. However, as two of the five ESs had a standard (presence) value of 1, the relative importance of those two services within the hotspot increased when the data was classified into a higher number of quantiles, while the biophysical amount of the three other ESs decreased remarkably. We thus decided to stop the iterative search process for the top quantile in order to prevent a selection bias towards two ESs and to consider all five ESs. The iterative search was stopped at 20 classes, i.e. the top quantile of 20 quantiles represented the hotspot.
Richness
For the richness method we merged the distributions of all five spatial ESs models (with a presence value of 1 for each model), which resulted in a raster grid with values of 0 (no ES present) to 5 (all five ESs present). We then analysed, which ES richness, i.e. which number of present ESs, was required to build a hotspot that most closely approached the 10 % target as a mean for target achievement for all services. Transforming metric scale data to a presence-absence logic implies a simplification of the importance of each pixel as it neglects the amount of service provided per pixel. As such, a shift of important areas could be expected. However, as we also calculated the total amount of ESs covered by each of the hotspots, comparability is given. We will discuss this in more detail in the discussion section.
Heuristic site prioritisation with Marxan
Marxan is a conservation site selection software building on an optimisation algorithm which incorporates key principles of systematic conservation planning (Margules and Sarkar 2007). These principles include comprehensiveness, i.e. reaching multiple targets, cost-effectiveness, i.e. finding solutions for the least possible cost, and compactness, which implies a low edge to area ratio (Wilson et al. 2010). Marxan (version 2.43) works with a heuristic optimisation algorithm with the help of simulated annealing (Ball et al. 2009). The software aims to minimise an objective function containing the sum of opportunity costs of conservation, represented by the costs of selected planning units and the boundary length of the reserve system. The objective function contains penalties for not meeting conservation targets as well as for breaching a given cost threshold (Game and Grantham 2008). Conservation targets are set as a proportion of the total amount of each feature in a study area. Thereby, the software allows to integrate both (binary) presence/absence data of a conservation feature and metric biophysical data of different kinds into the same decision problem. The software requires a series of inputs. Conservation targets were set at 10 % for the total amount of each ES in the study area. We divided the forest area into 241,013 quadratic planning units of 4 ha size each. This resolution was chosen as it was manageable for the software in terms of time and computing capacity (Alidina et al. 2010), while at the same time it was high enough to cover spatial heterogeneity in an adequate way. For each planning unit we calculated the amount of each ES contained in that unit. For the sake of comparability with the hotspot approach, we decided not to include site specific opportunity costs of conservation, which would have had an influence on the site selection. We therefore assigned a standard opportunity cost of 1 to each planning unit. Marxan requires a number of parameters to be set (see ESM of Appendix 1 for details). The boundary length modifier was set according to methods described in Game and Grantham (2008) in order to guide the software to select a compact, spatially coherent reserve network. A feature penalty factor was set in order to reach a high target achievement in each scenario according to the iterative procedure described in Game and Grantham (2008). Marxan was run 100 times with these parameters. The map of selected sites was produced by ranking all planning units according to the number of runs in which they have been selected (selection frequency). The selection frequency that led to a selection of sites that most closely approached the mean 10 % target for all ES was chosen. Two Marxan analyses were performed in order to compare the outcome to the different hotspot delineation methods. One analysis included the three ES measured in metric data (carbon sequestration, carbon storage and recreational hiking), and one included all five ESs.
Comparison of selected areas (hotspots, Marxan)
Each of the four hotspot delineation methods and the selected sites of the two Marxan analyses yielded a spatial prioritisation of areas. For comparison, we recorded the area size and calculated the edge-to-area ratio (where edge is the sum of the boundary lengths of all selected sites), the target achievement for each ES and the mean target achievement for all prioritized areas. We also calculated the ratio of area to mean target achievement in order to compare the different methods. Pairwise, we tested the agreement of spatial configuration between all maps with Cohen’s Kappa. For this purpose, all maps were defined as presence (1, cell selected) and absence (0, cell not selected). Each of the 787,396 cells were assigned presence and absence values for each map.
Results
Selected areas for hotspots and Marxan
Maps for the top richest cells, spatial clustering and the Marxan result for three ESs with metric data (carbon sequestration, carbon storage, recreational hiking) are presented in Fig. 3. Figure 3a shows all areas that are in the top quantile for at least one ES (top richest cells). It is inherent to the method that, because the hotspots for each ES do not completely overlap, the total selected areas for the three ESs is relatively large and dispersed, which we discuss in further detail below. The respective classes were 16 quantiles (carbon sequestration), nine quantiles (carbon storage) and 209 quantiles (recreational hiking). This large number of quantiles was due to the fact that for recreational hiking a relatively few number of cells had extraordinary high index values, representing 10 % of the total amount of the services. Figure 3b shows the spatial clustering outcome, which is also constructed as the sum of three hotspots. As this method searches for clusters within the data, the outcome appears less dispersed than the one of the top richest cells method. Figure 3c show the result of Marxan for the three ESs. A minimum selection frequency of 23 (of 100 runs) was determined as the threshold that led to an area large enough to achieve a mean of approximately 10 % of the ES target. There was an overall tendency of areas to be selected in the east and south of the county. This was mainly due to high abundance of high value cells of the recreational hiking service, which contains information about people living in proximity. Furthermore, this area contains highly productive forest, leading to relatively high abundance of cells with high carbon sequestration and storage values.
Figure 4 shows the outcomes of the hotspot delineation methods and Marxan for all five ESs. Figure 4a) shows the highest of 20 classes of the sum of the standardised ES models (intensity approach). The result is more scattered across the study area and a considerable smaller total area was selected as the method does consider multiplicity of ESs and consequently chooses areas were ESs overlap. Figure 4b shows the result of the richness approach, which depicts areas with an overlap of at least four of the five ESs. This number was required to cover approximately 10 % of each ES (see also Table 4 for statistics on conservation results). Figure 4c) shows the results of the site selection of Marxan. A minimum selection frequency of 22 (of 100 runs) was determined as the threshold that led to an area large enough to achieve a mean of approximately 10 % of the ES target. The result is several clumped areas spread over the study area.
Spatial agreement of selected areas
Spatial configurations of the results according to the four hotspot methods and Marxan differed considerably. All results for the pairwise comparisons (Table 3) are at the lower end of the scale of the Kappa statistic, of which values close to 1 would indicate almost perfect agreement (Landis and Koch 1977). Pairwise comparisons showed slight agreement for four of the six comparisons. Fair agreement was observed between Marxan and the top richest cells approach as well as between Marxan and intensity.
Comparison of aggregated target achievements and selected areas
Target achievement for single ESs differed depending on the applied method (Table 4). For instance, the intensity method exceedingly selected the ES snow slide prevention (58.7 %). This was partly due to the construction of this model as a presence-absence model (0–1 binary scale). As such, all areas containing this ES had a relatively high value, and thus a higher chance to be selected from the summed standardised intensity map. Furthermore, these areas more often overlapped with highly productive forest, which increased their chance to also have higher than average values for carbon sequestration and storage. With Marxan targets were achieved approximately even around 10 % (low standard deviation and low coefficient of variation, Table 4). Mean target achievement was also close to the 10 % target for richness. Mean target achievement was considerably higher for the top richest cells approach and spatial clustering. This was partly because these methods were first based on single ESs and were merged in a subsequent step. As the hotspots for all single ESs only partly overlapped, the total area of the combined single ES hotspot maps was larger. When an ES was present in areas that formed a hotspot of another ES, these additional selected and thus conserved ESs could be viewed as side benefits.
Table 4 summarises characteristics of the selected areas for the four hotspot methods and the two Marxan outcomes. For three ESs, the sum of selected area was smallest for Marxan, and highest for the top richest cells approach. For five ESs the area was smallest for the richness approach and highest for Marxan. Marked differences in selected areas and mean target achievements (9.6–28.7 % for 3 ESs and 7.7–18.3 % for 5 ESs) made comparison between approaches challenging. We thus calculated the ratio of area to mean target achievement as an indicator of how efficiently land is selected in order to achieve targets. This indicator was lowest for Marxan (3 ESs) and the intensity approach (5 ESs), and highest for spatial clustering (3 ESs) and Marxan (5 ESs). As expected, the intensity approach scores best in conserving relatively high amounts of ESs per land area, which leads to a low area-target achievement ratio. Spatial clustering through the G *i statistic is constructed as such that it also includes cells that have a low value, but are in the vicinity of neighbours with high values. By doing this, spatial clustering needs more area per unit target achievement, but achieves a low edge-to-area ratio. The top richest cells approach, on the other hand, selects high value cells that can, depending on the respective ES, be scattered across the landscape. This leads to a higher edge-to-area ratio. This edge-to-area-ratio is highest for the top richest cells approach (3 ESs) and the intensity approach (5 ESs).
Discussion
What is an ecosystem service hotspot?
Despite the ample use of the term hotspot within the ES literature, we observed that within the reviewed studies there was no consensus on what a hotspot is. There was, however, a tendency to characterise ES hotspots as areas of high values of single services, which is in line with the definition of one of the first studies published on that topic (Egoh et al. 2008). While 13 of the 23 reviewed studies used the same principle construction of a hotspot, a variety of methods to delineate the hotspot was observed. The lack of consensus and an exploring, occasionally pragmatic way of method development could be seen as characteristic for the current advancement in the relatively young scientific field dealing with ESs (Jacobs et al. 2013; Schröter et al. 2014c). We discuss three aspects to further develop the notion of ES hotspots in the future, namely the inclusion of threats, ES demand and a distinction of conservation-compatible ESs.
Interestingly, the definitions currently applied in ES hotspot mapping differ from the earlier established notion of a biodiversity hotspot, which has been defined as an area of both high biodiversity and high level of threat, i.e. probability of destructive ecosystem exploitation (Myers 1988, 1990; Mittermeier et al. 1998; Myers et al. 2000). Being one of the first studies to map ES hotspots, Egoh et al. (2008, p. 136) even explicitly state that they “do not include measures of threat”. Later studies also did not include threat in the definition and delineation of hotspots. One way to include threat in a future study for Telemark could be to consider accessibility of forest areas and profitability of forest exploitation as an indicator of threat (Naidoo et al. 2006). In the case of Telemark, clear-cutting can be regarded as having detrimental effects on a number of ESs and biodiversity (Schröter et al. 2014b).
Furthermore, targets for services represented within hotspots need to be formulated, i.e. a level of services that is considered particularly important from a societal point of view needs to be determined (Mastrangelo et al. 2014). Target setting of ESs for the purpose of conservation is not common practice yet (Luck et al. 2012b). New insights from research on defining demand for ESs (Wolff et al. 2015) could be integrated to formulate targets for absolute amounts of ESs. Demand could for instance relate to absolute amounts of services used in an area (Burkhard et al. 2014) or to preferences and desires regarding services (Wolff et al. 2015).
In order to meaningfully represent multiple ESs in a hotspot for the purpose of site selection for conservation, we argue that only those ESs that do not require substantial human interventions during management and harvest should be considered due to trade-offs that can occur between ESs. Many regulating and cultural ESs either show none or synergistic interactions with one another (Bennett et al. 2009) and can meaningfully be represented in a hotspot. Extractive provisioning services, such as clear-cutting timber harvest, however, impede other services such as carbon sequestration or hiking. Knowledge on effects of the use of one ES on another ES is still missing. We observed that the reviewed studies often have chosen to determine hotspots with multiple regulating and cultural ESs, which presumably have no or synergistic interactions with one another (e.g., Egoh et al. 2008; Bai et al. 2011; Locatelli et al. 2014). Such areas could meaningfully be considered as priority sites for conservation of ESs next to biodiversity. When multiple potentially conflicting ESs are considered together, for instance, timber harvest, forage or hydropower next to cultural and regulating ES (Willaarts et al. 2012; García-Nieto et al. 2013; Wu et al. 2013), the resulting areas are probably more useful to determine ‘conflict spots’ or ‘coldspots’ (sensu Willemen et al. 2010), which would require integrated management to reduce specific known trade-offs and interest conflicts.
When to choose which prioritisation method?
We found no clear link between distinct hotspot methods and specific policy purposes in our review. Most reviewed articles state generic and relatively similar purposes for applying hotspot methods, irrespective of the method used. Priority setting was most commonly stated (16 out of 23), along with informing or supporting (land) management and planning (9 out of 23) (Table 1). In principle, all hotspot methods fit these broad policy purposes, as assessing areas of high value is their core methodological purpose. Only in a few cases a specific policy purpose was stated, such as matching ES hotspots with hotspots of social value to assess synergies, trade-offs and conflicts (Bagstad et al. 2015) and informing fire risk management to focus limited resources (Beverly et al. 2008).
An important aspect to consider when choosing for either a hotspot method or a heuristic site prioritisation approach, is whether the intensity of ESs per unit land area matters for its long-term provision. From an ecological point of view, more knowledge is required on the functional traits underlying ESs as well as the spatial and temporal scales influencing ESs (Kremen 2005). From a human benefit point of view, whether intensity matters or not depends on the respective ES. For recreational hiking, one might be interested in including sites of relatively high value in a reserve and for existence of wilderness-like areas, a large, remaining area might be more valuable and preferable to include. For such ESs, hotspot methods might be more informative for decision making than an analysis with Marxan. For other ESs, however, such as carbon storage and sequestration, the total amount of conserved ES matters much more than the configuration of the selected areas. Contrary to being selected in a hotspot, such services could be spread across many connected sites containing small to medium amount of the ES. We have demonstrated that also hotspot methods can lead to considerable scattering. If ecological characteristics, such as landscape connectivity are important for the provision of services (Mitchell et al. 2015), then these hotspot methods might not be suitable for finding areas for conservation of these services. The spatial clustering hotspot method generates larger clustered areas than other hotspot methods and would therefore be most relevant if for example a single protected area or recreational area would need to be defined. Such large areas, connected throughout the landscape might be recommendable for some ESs, such as recreational hiking, which could lose a considerable part of their value if neighbouring areas are not conserved.
The principal difference between using a single or multiple ES for delineating hotspots has consequences for taking into account the concept of landscape multi-functionality (de Groot 2006; Gimona and van der Horst 2007; Mastrangelo et al. 2014), when prioritising a site for a specific policy purpose. In particular, the inclusion of cultural ESs can be regarded as a representation of different types of values. The simultaneous inclusion of different social and ethical values which are reflected by, for instance, cultural ES (Chan et al. 2012a, b; Luck et al. 2012a; Schröter et al. 2014c) might be better supported by the intensity and richness hotspot methods. To actually consider multi-functionality when applying the richness approach, only areas above a certain threshold should be included in order to prevent the inclusion of areas containing only marginal amounts of one or several ES. Such thresholds have been shown to influence the magnitude of overlap between ES (Anderson et al. 2009; Gos and Lavorel 2012). Defining and testing such thresholds before applying the richness approach was out of the scope of this study. Hotspot delineation according to methods that concentrate on one particular ES (top richest cells, thresholds, Jenks natural breaks, spatial clustering), merge areas that contain at least one ES. Such methods might in the first place prioritise areas for specific management actions towards one particular ES (O’Farrell et al. 2010; Locatelli et al. 2014). These studies, however, sometimes also consider multi-functionality by determining priority areas as overlaps between hotspots of single ES (Egoh et al. 2008; Bai et al. 2011; Wu et al. 2013).
Differences in spatial configuration of hotspots and Marxan
We found marked differences in spatial configuration of selected areas depending on the hotspot method applied for the five ESs in Telemark’s forest areas. Kappa statistics for pairwise agreement of prioritised areas showed only slight to fair agreement and were at the lower end of the scale. These findings are important to consider for future studies on the spatial synergies among ESs and between ESs and biodiversity. If even hotspot methods following the same principle differ strongly in terms of spatial configuration of prioritised areas, then results should be carefully interpreted. We have also shown that areas prioritised by hotspot methods were different in terms of spatial configuration compared to more complex spatial prioritisation methods as used in Marxan. Depending on the purpose of the area selection, the use of Marxan might have advantages compared to the use of hotspots, which we discuss below.
We also found that, when applying the different hotspot methods, the outcomes differed strongly in terms of the total amount of ES provided in these areas (Fig. 3). and studies on conservation of ESs have to rely on assumptions and expert judgements when determining targets (Chan et al. 2006; Egoh et al. 2010; Chan et al. 2011; Izquierdo and Clark 2012; Schröter et al. 2014b). The hotspot studies we reviewed did not include explicit quantitative targets for ESs, but do however, implicitly set targets for a prioritised area when choosing a top quantile of different sizes (e.g. 5–30 %). Striving for explicit targets of ESs might, however, be more consistent with the current practice in conservation planning (Carwardine et al. 2009) than spatially determining hotspots which lead, depending on the method, to differing amounts of ESs on the selected sites. The difference in total ES quantities can be attributed particularly to skewness and spatial distribution of the data. The amount of ESs held in a top quantile strongly depends on skewness. In case of a negative skew (left-skewed distribution), a fixed proportion of top richest cells would contain a high total amount of ESs, while in case of a positive skew (right skewed distribution), the top richest cells would contain a lower amount. Spatial distribution of multiple ESs and the relation to each other also has an influence of the total amount of ESs included in a hotspot. This holds, for instance, for the richness approach, where the total quantitative sum of ES in the selected areas depends very much on overlaps between different ES. Overlapping areas can contain differing amounts of ES. Similarly, when determining a top class of a standardised sum of ES, as is done in the intensity approach, the spatial distribution of each single service and the location to each other determines the amount of ES present in the selected areas. Furthermore, constructing aggregated indices as the basis for the intensity approach is subject to weighting different ESs against each other. In this study, for simplicity reasons, we have assumed equal weighting. Gimona and van der Horst (2007), however, have shown how different weights influence the location of hotspots and suggest to combine differently weighted indices for determining areas that show high values regardless of the weights they applied (multifunctional hotspots).
In our study we attempted to combine explicit targets (10 % of biophysical ES amount) with the application of hotspots and Marxan. Mean target achievements differed, ranging from underachievement (7.7 %, richness approach) to strong overachievement (28.7 %, top richest cells). Especially those methods that select hotspots of single ES resulted in a high amount of side-benefits. This strong difference in both total amounts of ESs and in selected areas restricts the comparability of the spatial configuration of the outcomes, but substantiates the observation of notable differences in the approaches. It has been shown that changing targets for ESs influences size and spatial configuration of prioritised areas (Egoh et al. 2011). An uncertainty analysis in a future study could thus test to what extent the changing targets effect the differences between spatial configuration change of hotspots and Marxan.
Criteria for site prioritisation in accordance with principles of conservation planning
The results presented here all prioritise areas for the purpose of conservation based on ES provision. Our approach should, however, be understood as a test of methods instead of as providing concrete suggestions for the location of reserves. First of all, the analysis is based on ESs only and does not include habitats of specific species or specific vegetation types which may be of high relevance for conservation. Hence, the biodiversity value of the areas is not considered in the ES-based selection approach. Biodiversity hotspots could, for instance be considered next to ES hotspots. Within the process of systematic conservation planning (Margules and Pressey 2000), site prioritisation should take into account both biodiversity and ESs, for which approaches have been tested in recent studies (Chan et al. 2011; Egoh et al. 2014; Schröter et al. 2014b). We discuss three criteria that are considered important for site prioritisation, namely comprehensiveness, compactness and cost-effectiveness (Possingham et al. 2006; Wilson et al. 2010).
The first criterion, comprehensiveness, refers to adequately meeting conservation targets (Wilson et al. 2009). Methods that are based on single ES overachieved targets when they were overlapped afterwards, as sites selected as hotspot areas for one service also provide other ESs. These methods are thus prone to selecting more areas than needed to achieve a target. In decision making, a more stringent selection of areas might still be needed if the conservation budget is not sufficient to conserve all sites. On the other hand, for methods that incorporate multiple ESs at a time, it depends on the overlap between ES and on the distribution of values whether some ESs are overrepresented Marxan contains comprehensiveness as one important factor in its objective function (Ball et al. 2009). While the software can be steered so that single solutions approximately reach the targets (Fischer et al. 2010), the approach we have taken here is based on selection frequencies, which can be considered as an indicator of how important a particular planning unit is (Possingham et al. 2010). Some ES targets were slightly overachieved, while others were slightly underachieved (Table 4). The second criterion, compactness, refers to a reserve system with a low edge-to-area ratio (Wilson et al. 2010). This indicator was lowest for the spatial clustering method, which selected compact, clustered sites including both high and low values within a certain neighbourhood. One disadvantage of this approach is that cells containing high amounts of ES are outside the selected clusters (Timilsina et al. 2013). Compactness is one of the objectives of Marxan and as such the edge-to-area ratio of the outcome of Marxan is relatively low, despite being considerably higher than that of the spatial clustering. All other approaches, in particular the intensity approach, selected many small, isolated sites. This led to a comparably high edge-to-area ratio.
The third criterion, cost-effectiveness, refers to reaching a specific conservation target for the least possible conservation cost (Naidoo et al. 2006). In this study we took the ratio of land area selected per mean target achievement as a parsimonious indicator for cost-effectiveness of selected areas. Methods that consider multiple ESs at a time (intensity and richness) need the least area per mean target achievement, followed by the outcome of Marxan. Spatial clustering, which selects cells with a low amount of ESs in proximity to cells with high amounts, showed the highest ratio of land to target achievement.
Conclusion
Currently no consensus exists on how to define an ES hotspot. We found two principally different approaches, which either consider an ES hotspot as areas with a relatively high amount of one single ES or as areas containing multiple ESs. When applied to the case of five regulating and cultural ESs for Telemark, hotspot delineation methods differed strongly in terms of spatial configuration and amount of ESs covered by these areas. We found that a recurring aim of hotspots is to inform land use decisions through site prioritisation. The marked difference in spatial configuration among hotspot methods shows, however, that there are large uncertainties involved in site prioritisation, as different methods yield different results. The difference in spatial configuration can also have consequences for studies that analyse the spatial co-occurrence of hotspots of multiple ESs and of ES hotspots and biodiversity. While determining hotspots according to one approach might lead to high degrees of spatial overlap with another ES or biodiversity, other delineation methods might lead to considerably lower degrees of overlap.
We also found that setting specific targets for ES conservation was not common in the delineation of hotspots. Defining a hotspot as the highest of several classes of a dataset for a specific ES, as is common practice, can lead to very different amounts of ESs included in a selected sites depending on the method used. In an attempt to ensure comparability between the approaches we have defined arbitrary but specific targets for ESs, but also found considerable challenges in approximately reaching these targets.
We compared outcomes of hotspot methods to outcomes of the conservation software Marxan. While some hotspot methods score better than Marxan in terms of either comprehensiveness, compactness or cost-effectiveness, Marxan is able to consider these three criteria simultaneously and thus could be preferred over hotspots to select sites for conservation. However, the sites selected by Marxan are not necessarily those that contain high amounts of ES, but those areas that fit the three criteria mentioned above. Furthermore, while determining ES hotspots with the help of a GIS is a more or less intuitive, pragmatic and easy-to-use method, Marxan requires a substantial amount of time to prepare input data.
While we did not provide a new and standardised hotspot definition and method here, we discussed that it might be useful to recall the definition of a biodiversity hotspot and thus also consider the level of threat to ES provision in the delineation of ES hotspots. This study provides an overview of currently applied hotspot methods and should be seen as a step to trigger discussion in order to harmonise methods.
References
Alidina HM, Fischer DT, Steinback C, Ferdana Z, Lombana AV, Heuttmann F (2010) Assessing and managing data. In: Ardron JA, Possingham HP, Klein CJ (eds) Marxan good practices handbook, version 2. Pacific Marine Analysis and Research Association, Victoria, pp 57–74
Anderson BJ, Armsworth PR, Eigenbrod F, Thomas CD, Gillings S, Heinemeyer A, Roy DB, Gaston KJ (2009) Spatial covariance between biodiversity and other ecosystem service priorities. J Appl Ecol 46(4):888–896
Bagstad K, Reed J, Semmens D, Sherrouse B, Troy A (2015) Linking biophysical models and public preferences for ecosystem service assessments: a case study for the Southern Rocky Mountains. Reg Environ Change:1–14
Bai Y, Zhuang C, Ouyang Z, Zheng H, Jiang B (2011) Spatial characteristics between biodiversity and ecosystem services in a human-dominated watershed. Ecol Complex 8(2):177–183
Ball IR, Possingham HP, Watts ME (2009) Marxan and relatives: software for spatial conservation prioritization. In: Molainen A, Wilson KA, Possingham HP (eds) Spatial conservation prioritization. Oxford University Press, New York, pp 185–195
Bennett EM, Peterson GD, Gordon LJ (2009) Understanding relationships among multiple ecosystem services. Ecol Lett 12(12):1394–1404
Beverly JL, Uto K, Wilkes J, Bothwell P (2008) Assessing spatial attributes of forest landscape values: an internet-based participatory mapping approach. Can J For Res 38(2):289–303
Bryan BA, Raymond CM, Crossman ND, Macdonald DH (2010) Targeting the management of ecosystem services based on social values: where, what, and how? Landsc Urban Plan 97(2):111–122
Burkhard B, Kandziora M, Hou Y, Müller F (2014) Ecosystem service potentials, flows and demand—concepts for spatial localisation, indication and quantification. Landsc Online 34:1–32
Carpenter SR, Mooney HA, Agard J, Capistrano D, DeFries RS, Díaz S, Dietz T, Duraiappah AK, Oteng-Yeboah A, Pereira HM, Perrings C, Reid WV, Sarukhan J, Scholes RJ, Whyte A (2009) Science for managing ecosystem services: beyond the Millennium Ecosystem Assessment. Proc Natl Acad Sci USA 106(5):1305–1312
Carwardine J, Klein CJ, Wilson KA, Pressey RL, Possingham HP (2009) Hitting the target and missing the point: target-based conservation planning in context. Conserv Lett 2(1):4–11
Chan KMA, Shaw MR, Cameron DR, Underwood EC, Daily GC (2006) Conservation planning for ecosystem services. PLoS Biol 4(11):e379
Chan KMA, Hoshizaki L, Klinkenberg B (2011) Ecosystem services in conservation planning: targeted benefits vs. co-benefits or costs? PLoS One 6(9):e24378
Chan KMA, Guerry AD, Balvanera P, Klain S, Satterfield T, Basurto X, Bostrom A, Chuenpagdee R, Gould R, Halpern BS, Hannahs N, Levine J, Norton B, Ruckelshaus M, Russell R, Tam J, Woodside U (2012a) Where are cultural and social in ecosystem services? A framework for constructive engagement. Bioscience 62(8):744–756
Chan KMA, Satterfield T, Goldstein J (2012b) Rethinking ecosystem services to better address and navigate cultural values. Ecol Econ 74:8–18
Cimon-Morin J, Darveau M, Poulin M (2013) Fostering synergies between ecosystem services and biodiversity in conservation planning: a review. Biol Conserv 166:144–154
Crossman ND, Bryan BA (2009) Identifying cost-effective hotspots for restoring natural capital and enhancing landscape multifunctionality. Ecol Econ 68(3):654–668
de Groot R (2006) Function-analysis and valuation as a tool to assess land use conflicts in planning for sustainable, multi-functional landscapes. Landsc Urban Plan 75(3–4):175–186
Egoh B, Rouget M, Reyers B, Knight AT, Cowling RM, van Jaarsveld AS, Welz A (2007) Integrating ecosystem services into conservation assessments: a review. Ecol Econ 63(4):714–721
Egoh B, Reyers B, Rouget M, Richardson DM, Le Maitre DC, van Jaarsveld AS (2008) Mapping ecosystem services for planning and management. Agric Ecosyst Environ 127(1–2):135–140
Egoh B, Reyers B, Rouget M, Bode M, Richardson DM (2009) Spatial congruence between biodiversity and ecosystem services in South Africa. Biol Conserv 142(3):553–562
Egoh BN, Reyers B, Carwardine J, Bode M, O'Farrell PJ, Wilson KA, Possingham HP, Rouget M, De Lange W, Richardson DM, Cowling RM (2010) Safeguarding biodiversity and ecosystem services in the little Karoo, South Africa. Conserv Biol 24(4):1021–1030
Egoh BN, Reyers B, Rouget M, Richardson DM (2011) Identifying priority areas for ecosystem service management in South African grasslands. J Environ Manag 92:1642–1650
Egoh BN, Paracchini ML, Zulian G, Schägner JP, Bidoglio G (2014) Exploring restoration options for habitats, species and ecosystem services in the European Union. J Appl Ecol 51(4):899–908
Eigenbrod F, Armsworth PR, Anderson BJ, Heinemeyer A, Gillings S, Roy DB, Thomas CD, Gaston KJ (2010) The impact of proxy-based methods on mapping the distribution of ecosystem services. J Appl Ecol 47(2):377–385
ESRI (2014) Modeling spatial relationships. http://resources.arcgis.com/en/help/main/10.2/index.html#//005p00000005000000. Accessed 17 Oct 2014
European Commission (2014) Mapping and assessment of ecosystems and their services. Technical report—2014—080. Publications office of the European Union, Luxembourg
Fischer DT, Alidina HM, Steinback C, Lombana AV, Ramirez de Arellano PI, Ferdana Z, Klein CJ (2010) Ensuring robust analysis. In: Ardron JA, Possingham HP, Klein CJ (eds) Marxan good practices handbook, version 2. Pacific Marine Analysis and Research Association, Victoria, pp 75–96
Forouzangohar M, Crossman ND, Macewan RJ, Wallace DD, Bennett LT (2014) Ecosystem services in agricultural landscapes: a spatially explicit approach to support sustainable soil management. Sci World J
Game ET, Grantham HS (2008) Marxan user manual: for Marxan version 1.8.10. University of Queensland, Pacific Marine Analysis and Research Association, St. Lucia, Queensland, Australia, Vancouver, BC, Canada
García-Nieto AP, García-Llorente M, Iniesta-Arandia I, Martín-López B (2013) Mapping forest ecosystem services: from providing units to beneficiaries. Ecosyst Serv 4:126–138
Getis A, Ord JK (1992) The analysis of spatial association by use of distance statistics. Geograph Anal 24(3):189–206
Gimona A, van der Horst D (2007) Mapping hotspots of multiple landscape functions: a case study on farmland afforestation in Scotland. Landscape Ecol 22(8):1255–1264
Gos P, Lavorel S (2012) Stakeholders’ expectations on ecosystem services affect the assessment of ecosystem services hotspots and their congruence with biodiversity. Int J Biodivers Sci Ecosyst Serv Manag 8(1–2):93–106
Haines-Young R, Potschin M (2010) Proposal for a common international classification of ecosystem goods and services (CICES) for integrated environmental and economic accounting. European Environment Agency, New York
Institute Meteorological (2012) Monthly normal values. Meteorological Institute, Oslo
Izquierdo AE, Clark ML (2012) Spatial analysis of conservation priorities based on ecosystem services in the atlantic forest region of Misiones, Argentina. Forests 3(3):764–786
Jacobs S, Keune H, Vrebos D, Beauchard O, Villa F, Meire P (2013) Ecosystem service assessments: science or pragmatism? In: Keune H, Jacobs S, Dendoncker N (eds) Ecosystem services. Elsevier, Boston, pp 157–165
Kremen C (2005) Managing ecosystem services: what do we need to know about their ecology? Ecol Lett 8(5):468–479
Krutilla JV (1967) Conservation reconsidered. Am Econ Rev 57(4):777–786
Landis JR, Koch GG (1977) The measurement of observer agreement for categorical data. Biometrics 33(1):159–174
Larigauderie A, Prieur-Richard A-H, Mace GM, Lonsdale M, Mooney HA, Brussaard L, Cooper D, Cramer W, Daszak P, Díaz S, Duraiappah A, Elmqvist T, Faith DP, Jackson LE, Krug C, Leadley PW, Le Prestre P, Matsuda H, Palmer M, Perrings C, Pulleman M, Reyers B, Rosa EA, Scholes RJ, Spehn E, Turner Ii BL, Yahara T (2012) Biodiversity and ecosystem services science for a sustainable planet: the DIVERSITAS vision for 2012–20. Curr Opin Environ Sustain 4(1):101–105
Locatelli B, Imbach P, Wunder S (2014) Synergies and trade-offs between ecosystem services in Costa Rica. Environ Conserv 41(1):27–36
Luck GW, Chan KMA, Eser U, Gómez-Baggethun E, Matzdorf B, Norton B, Potschin MB (2012a) Ethical considerations in on-ground applications of the ecosystem services concept. Bioscience 62(12):1020–1029
Luck GW, Chan KMA, Klein CJ (2012b) Identifying spatial priorities for protecting ecosystem services. http://f1000r.es/T0yHOY. F1000Research 2012, 1:17
Maes J, Egoh B, Willemen L, Liquete C, Vihervaara P, Schägner JP, Grizzetti B, Drakou EG, Notte AL, Zulian G, Bouraoui F, Luisa Paracchini M, Braat L, Bidoglio G (2012a) Mapping ecosystem services for policy support and decision making in the European Union. Ecosyst Serv 1(1):31–39
Maes J, Paracchini ML, Zulian G, Dunbar MB, Alkemade R (2012b) Synergies and trade-offs between ecosystem service supply, biodiversity, and habitat conservation status in Europe. Biol Conserv 155:1–12
Margules CR, Pressey RL (2000) Systematic conservation planning. Nature 405(6783):243–253
Margules CR, Sarkar S (2007) Systematic conservation planning. Cambridge University Press, Cambridge
Martínez-Harms MJ, Balvanera P (2012) Methods for mapping ecosystem service supply: a review. Int J Biodivers Sci Ecosyst Serv Manag 8(1–2):17–25
Mastrangelo M, Weyland F, Villarino S, Barral M, Nahuelhual L, Laterra P (2014) Concepts and methods for landscape multifunctionality and a unifying framework based on ecosystem services. Landscape Ecol 29(2):345–358
Mitchell A (1999) The ESRI guide to GIS analysis. Volume 1: geographic patterns & relationships. ESRI Press, Redlands
Mitchell A (2005) The ESRI guide to GIS analysis. Volume 2: spatial measurements & statistics. ESRI Press, Redlands
Mitchell MGE, Suarez-Castro AF, Martinez-Harms M, Maron M, McAlpine C, Gaston KJ, Johansen K, Rhodes JR (2015) Reframing landscape fragmentation’s effects on ecosystem services. Trends Ecol Evol 30(4):190–198
Mittermeier RA, Myers N, Thomsen JB, Da Fonseca GAB, Olivieri S (1998) Biodiversity hotspots and major tropical wilderness areas: approaches to setting conservation priorities. Conserv Biol 12(3):516–520
Moen A (1999) National atlas of Norway: vegetation. Norwegian Mapping Authority, Hønefoss
Myers N (1988) Threatened biotas: “hot spots” in tropical forests. Environmentalist 8(3):187–208
Myers N (1990) The biodiversity challenge: expanded hot-spots analysis. Environmentalist 10(4):243–256
Myers N, Mittermeier RA, Mittermeier CG, da Fonseca GAB, Kent J (2000) Biodiversity hotspots for conservation priorities. Nature 403(6772):853–858
Naidoo R, Balmford A, Ferraro PJ, Polasky S, Ricketts TH, Rouget M (2006) Integrating economic costs into conservation planning. Trends Ecol Evol 21(12):681–687
Nemec K, Raudsepp-Hearne C (2013) The use of geographic information systems to map and assess ecosystem services. Biodivers Conserv 22(1):1–15
NFLI (2010) Arealressurskart AR5. National Forest and Landscape Institute (NFLI, Skog og Landskap), Ås
Noss RF (1991) Sustainability and wilderness. Conserv Biol 5(1):120–122
O’Farrell PJ, Reyers B, Le Maitre DC, Milton SJ, Egoh B, Maherry A, Colvin C, Atkinson D, de Lange W, Blignaut JN, Cowling RM (2010) Multi-functional landscapes in semi arid environments: implications for biodiversity and ecosystem services. Landscape Ecol 25(8):1231–1246
Onaindia M, Fernández de Manuel B, Madariaga I, Rodríguez-Loinaz G (2013) Co-benefits and trade-offs between biodiversity, carbon storage and water flow regulation. For Ecol Manag 289:1–9
Palomo I, Martín-López B, Zorrilla-Miras P, García Del Amo D, Montes C (2014) Deliberative mapping of ecosystem services within and around Doñana National Park (SW Spain) in relation to land use change. Reg Environ Change 14(1):237–251
Pan Y, Xu Z, Wu J (2013) Spatial differences of the supply of multiple ecosystem services and the environmental and land use factors affecting them. Ecosyst Serv 5:4–10
Plieninger T, Dijks S, Oteros-Rozas E, Bieling C (2013) Assessing, mapping, and quantifying cultural ecosystem services at community level. Land Use Policy 33:118–129
Possingham HP, Wilson KA, Andelman SJ, Vynne CH (2006) Protected Areas: Goals, Limitations, and Design. In: Groom MJ, Meffe GK, Carrol CR (eds) Principles of conservation biology, 3rd edn. Sinauer, Sunderland, pp 509–551
Possingham HP, Smith JL, Royle K, Dorfman D, Martin TG (2010) Introduction. In: Ardron JA, Possingham HP, Klein CJ (eds) Marxan good practices handbook, version 2. Pacific Marine Analysis and Research Association, Victoria, pp 1–11
Queiroz C, Meacham M, Richter K, Norström AV, Andersson E, Norberg J, Peterson G (2015) Mapping bundles of ecosystem services reveals distinct types of multifunctionality within a Swedish landscape. Ambio 44(1):89–101
Raudsepp-Hearne C, Peterson GD, Bennett EM (2010) Ecosystem service bundles for analyzing tradeoffs in diverse landscapes. Proc Natl Acad Sci 107(11):5242–5247
Reyers B, O’Farrell PJ, Cowling RM, Egoh BN, le Maitre DC, Vlok JHJ (2009) Ecosystem services, land-cover change, and stakeholders: finding a sustainable foothold for a semiarid biodiversity hotspot. Ecol Soc 14(1):23
Reyers B, O’Farrell P, Nel J, Wilson K (2012a) Expanding the conservation toolbox: conservation planning of multifunctional landscapes. Landscape Ecol 27(8):1121–1134
Reyers B, Polasky S, Tallis H, Mooney HA, Larigauderie A (2012b) Finding common ground for biodiversity and ecosystem services. Bioscience 62(5):503–507
Rodríguez N, Armenteras D, Retana J (2015) National ecosystems services priorities for planning carbon and water resource management in Colombia. Land Use Policy 42:609–618
Schneiders A, Van Daele T, Van Landuyt W, Van Reeth W (2012) Biodiversity and ecosystem services: complementary approaches for ecosystem management? Ecol Indic 21:123–133
Schröter M, Barton DN, Remme RP, Hein L (2014a) Accounting for capacity and flow of ecosystem services: a conceptual model and a case study for Telemark, Norway. Ecol Indic 36:539–551
Schröter M, Rusch GM, Barton DN, Blumentrath S, Nordén B (2014b) Ecosystem services and opportunity costs shift spatial priorities for conserving forest biodiversity. PLoS One. doi:10.1371/journal.pone.0112557
Schröter M, van der Zanden EH, van Oudenhoven APE, Remme RP, Serna‐Chavez HM, Groot RS, Opdam P (2014c) Ecosystem services as a contested concept: a synthesis of critique and counter-arguments. Conserv Lett 7(6):514–523
Schulp CJE, Lautenbach S, Verburg PH (2014) Quantifying and mapping ecosystem services: demand and supply of pollination in the European Union. Ecol Indic 36:131–141
SSB (2012) Statistisk årbok 2012. SSB, Oslo
Timilsina N, Escobedo FJ, Cropper WP, Abd-Elrahman A, Brandeis TJ, Delphin S, Lambert S (2013) A framework for identifying carbon hotspots and forest management drivers. J Environ Manag 114:293–302
Willaarts BA, Volk M, Aguilera PA (2012) Assessing the ecosystem services supplied by freshwater flows in Mediterranean agroecosystems. Agric Water Manag 105:21–31
Willemen L, Hein L, van Mensvoort MEF, Verburg PH (2010) Space for people, plants, and livestock? Quantifying interactions among multiple landscape functions in a Dutch rural region. Ecol Indic 10(1):62–73
Wilson KA, Cabeza M, Klein CJ (2009) Fundamental concepts of spatial conservation prioritization. In: Molainen A, Wilson KA, Possingham HP (eds) Spatial conservation prioritization. Oxford University Press, New York, pp 16–27
Wilson KA, Possingham HP, Martin TG, Grantham HS (2010) Key concepts. In: Ardron JA, Possingham HP, Klein CJ (eds) Marxan good practices handbook, version 2. Pacific Marine Analysis and Research Association, Victoria, pp 18–23
Wolff S, Schulp CJE, Verburg PH (2015) Mapping ecosystem services demand: a review of current research and future perspectives. Ecol Indic 55:159–171
Wu J, Feng Z, Gao Y, Peng J (2013) Hotspot and relationship identification in multiple landscape services: a case study on an area with intensive human activities. Ecol Indic 29:529–537
Acknowledgments
This research was supported by the European Research Council, grant 263027 (‘Ecospace’). We thank Lars Hein and other colleagues at the Environmental Systems Analysis group for useful comments on earlier manuscript versions.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Schröter, M., Remme, R.P. Spatial prioritisation for conserving ecosystem services: comparing hotspots with heuristic optimisation. Landscape Ecol 31, 431–450 (2016). https://doi.org/10.1007/s10980-015-0258-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10980-015-0258-5