Introduction

The char + CO2 reaction is an important partial reaction of the biomass gasification processes [1, 2]. Besides, the char gasification by CO2 may be a useful way for the utilization of various biomass wastes and residues [3,4,5]. The kinetics of the char + CO2 reaction is a fast-growing field of which extensive reviews are available [6,7,8,9].

The intrinsic kinetics of the char + CO2 reaction is usually described by Eq. (1) in the kinetic regime, at a constant CO2 concentration, and a low or negligible CO concentration:

$$\text dX/\text dt = Af\left( X \right){\text{exp}}\left( { - \frac{E}{RT}} \right)$$
(1)

Here X is the reacted fraction (conversion) while A and E are the pre-exponential factor and the activation energy. The reacted fraction is typically denoted by α in the other areas of the thermal analysis [10, 11]. The f(X) function can be derived theoretically for high purity, idealistic carbons [12, 13]. Besides, other f(X) functions derived for other sorts of idealized samples are also available [10]. However, the physical and chemical structure of the real chars are usually too complex for the idealized models. Note that the wood and biomass chars are formed from feedstocks that contain different compounds, different phases, and differently bound mineral matter. Moreover, the carbonization level of the char particles is not uniform because they are formed in furnaces or reactors in which the temperature distribution is uneven or not perfectly even. Accordingly, the f(X) functions derived for ideal chars or for other idealized samples can only serve as semi-empirical or empirical models for the description of the real chars.

The kinetics of the CO2 gasification of biomass materials needs further studies because the data reported in the literature showed a huge scatter even in the last few years. Chew et al., for example, reported activation energies of 15 kJ mol−1 for the gasification of a torrefied palm kernel shell [14]. On the other hand, Sher et al. found E = 544 kJ mol−1 for the gasification of a willow char [15]. To illustrate the unreality of these E values, let us consider the definition of the activation energy by IUPAC: “an empirical parameter characterizing the exponential temperature dependence of the rate coefficient” [16]. From this point of view, an activation energy of 15 kJ mol−1 predicts nearly identical reaction rates at 800 and 900 °C while an activation energy of 544 kJ mol−1 would correspond to reaction rates that differ by a factor of 181 at the same temperatures. The large scattering of the reported activation energies raises doubts about the reliability of the corresponding f(X) functions, too.

The thermogravimetric analysis, TGA, is a suitable method to study the kinetics of the char gasification in the kinetic regime due to its high precision [7]. Usually the experiments are carried out either at isothermal or linearly increasing T(t) functions (temperature programs). The present authors emphasized the use of other sorts of temperature programs, too, to obtain more experimental information [17,18,19,20]. Besides, it is difficult to carry out true isothermal experiments in TGA. Typically, the gas is switched to CO2 or to a CO2—inert gas mixture after the heating to an isothermal temperature. Nearly, all works published in the present journal on CO2 gasification used this method as illustrated by a selection in the References [21,22,23,24,25]. However, the stabilization of the CO2 concentration in the furnace needs some time; it may take 20 min or even more [26, 27]. The increase of the CO2 concentration after the gas switch results in an increasing reaction rate that may add a false maximum to the apparent f(X) function. It is more accurate to set up the desired gas atmosphere below the gasification temperature and evaluate kinetically both the heat-up and the isothermal section. Note that suitable mathematical methods have been available for decades for the use of arbitrary T(t) functions in the evaluations [28].

In our work we follow the so-called model fitting approach and evaluate more than one experiments together by the method of least squares as we have done in our earlier investigations [17,18,19,20, 29,30,31,32,33].. In the present article the examined process is described by Eq. (1). Várhegyi proposed versatile f(X) functions for Eq. (1) in 2019 [30]. Their applicability as empirical models were extensively tested on TGA experiments from earlier studies on the thermal decomposition of biomasses [30, 31], char combustion [32], and char gasification [33]. The corresponding kinetic equation can be written as

$$\text dX/\text dt = {\text{exp}}\left[ {p(X) - \frac{E}{RT}} \right]^{ } \left( {{1} - X} \right)$$
(2)

where p(X) is a polynomial. The term (1-X) ensures that dX/dt is zero at X = 1 for any polynomial coefficients. Equation (2) can be rewritten into the form of Eq. (1) as outlined in section “Materials and methods“. Equation (2) can be solved numerically for the T(t) functions of the experiments. The polynomial coefficients of p(X) can be determined by the method of least squares ensuring that the experimental data and their counterparts calculated from the model would be close to each other [30,31,32,33].

In the present work we continued the exploration of the properties and possibilities of this type of modelling. An earlier set of experimental data of the authors [19] was reevaluated by this newer modelling tool. Two woods were examined of which chars were formed through a particularly wide range of temperature histories. These latter included torrefaction at two temperatures; slow heating till 700 °C; fast heating (ca. 1400 °C min−1) till 700 °C; and a one-hour carbonization at 750 °C. The aim was to find the common kinetic features for the gasification of these chars in the kinetic regime. Besides, the reliability of the employed methods and the obtained results was also carefully tested. This is a crucial point in all evaluations of experiments [34]. However, the methods of the mathematical statistics are not suitable for assessing the reliability of the results because the major experimental errors are neither random and nor independent in thermal analysis [18]. Accordingly, a different approach was used which is described below, in section “Tests on the reliability of the results“.

Materials and methods

About the experiments reevaluated

As mentioned in the Introduction, the present work is based on the experiments of an earlier study of the authors [19]. The detailed description of the materials and experiments can be found in that work. A summary is given here to help and orient the readers of the present work. The CO2 gasification of woods and torrefied woods was studied in a TGA apparatus. For comparison, two chars prepared at 750 °C were also included into the study. The notation of the samples refers to the type of wood (B for birch and S for spruce), followed by three digits that refer to the temperature of the torrefaction (225 and 275 °C) or carbonization (750 °C). These digits are obviously missing for the untreated woods, which are denoted by B— and S—. During the TGA experiments the samples were heated in a CO2 gas flow from room temperature till 1000 °C with a drying section at 120 °C. Three different temperature programs were employed for each sample: a linear T(t) with a heating rate of 20 °C min−1; a modulated experiment where a sine function with 5 °C peak amplitude and 200 s wavelength was added to a 5 °C min−1 linear T(t); and a constant reaction rate (CRR) T(t). In the CRR experiments, the equipment regulated the heating of the samples so that the reaction rate would remain below a preset limit. The latter was 2 µg/s in the experiments treated here. Besides, additional experiments were carried out to check how the heating rate of the devolatilization section influences the gasification of the formed chars. For this purpose, TGA experiments were carried out with a particularly slow (2 °C min−1) and a particularly fast heating rate (ca. 1400 °C min−1) until 700 °C. The sample was kept at 700 °C for 3 min in these experiments and was heated by 20 °C min−1 afterward [19]. These experiments were also included into the kinetic evaluation.

The method of least squares

As outlined in the Introduction, the evaluation is based on Eq. (2). The parameters of this empirical model were determined so that the distance between the measured and the calculated data would be minimal. The root-mean-square deviation normalized by the highest experimental value can serve as a measure of this distance for a given experiment. We shall express it as a percent of the highest experimental value:

$$reldev\left( \% \right) \, = { 1}00\left\{ {\mathop \sum \limits_{\text i = 1}^{{M_{\text j} }} \frac{{\left[ {\left( {\frac{\text dm}{{\text dt}}} \right)_{\text j}^{{{\text{obs}}}} \left( {t_{\text i} } \right) - \left( {\frac{\text dm}{{\text dt}}} \right)_{\text j}^{{{\text{calc}}}} \left( {t_{\text i} } \right)} \right]^{2} }}{{M_{\text j} h_{\text j}^{2} }}} \right\}^{{0.{5}}}$$
(3)

Here Mj is the number of points available in digital form for experiment j, m is the normalized sample mass, and hj is the highest value of the observed mass loss rate, \(- \left( {\text dm/\text dt} \right)_{\text j}^{\text {obs}}\). The fit quality of N experiments is characterized by the root-mean-square of the corresponding reldev values and is denoted by reldevN. When N experiments are evaluated together, such parameters are searched for which reldevN is minimal. This can be achieved by minimizing (reldevN)2 by the method of least squares, i.e., to use an objective function defined by Eq. (4):

$$of = \mathop \sum \limits_{\text j = 1}^{N} \mathop \sum \limits_{\text i = 1}^{{M_{\text j} }} \frac{{\left[ {\left( {\frac{\text dm}{{\text dt}}} \right)_{\text j}^{{{\text{obs}}}} \left( {t_{\text i} } \right) - \left( {\frac{\text dm}{{\text dt}}} \right)_{\text j}^{{{\text{calc}}}} \left( {t_{\text i} } \right)} \right]^{2} }}{{M_{\text j} h_{\text j}^{2} }}$$
(4)

The numerical solution of the kinetic equation, Eq. (2), provides (dX/dt)calc values which are proportional to the (-dm/dt)calc values:

$$\left( { - \text dm/\text dt} \right)^{{{\text{calc}}}} = c\left( {\text dX/\text dt} \right)^{{{\text{calc}}}}$$
(5)

Here c is a constant characteristic to the given experiment. It is equal to the total mass-loss during the gasification normalized by the initial sample mass [19]. The value of c cannot be calculated directly from the TGA data because the last part of the devolatilization overlaps with the start of the gasification, hence we do not know what the sample mass is exactly at the beginning of the gasification. Accordingly c is an unknown parameter which is determined together with the other parameters by the method of least squares [19]. One cannot assume common c values for a group of experiments because the amount of formed char depends on the temperature program in the case of biomass materials [35]. We can envisage c as a scale factor: during the evaluation the program scales the calculated (dX/dt)calc curves to the corresponding experimental (− dm/dt)obs curves for each set of kinetic parameters by calculating the best fitting c values by a simple formula shown in the Supplementary Information. Therefore, the c values are not regarded as kinetic parameters.

The description of the applied numerical methods can be found in our earlier works [30, 33]. Some aspects of the calculations are also explained in Sect. 4 of the Supplementary Information.

The model

As mentioned in the Introduction, the work is based on Eq. (2) which is a special case of Eq. (1). A simple rearrangement of Eq. (2) yields the Af(X) term [33]:

$$Af\left( X \right)^{{}} = {\text{e}}^{{\text {p(X)}}{}} \left( {{1} - X} \right)$$
(6)

Equation (6) provides a smooth function with zero at X = 1 for any polynomial coefficients. It can be factorized into an A value and an f(X) function if f(X) is normalized. A simple, straightforward normalization is to require the f(0) = 1 equality [33]. If p(X) is expressed as

$$p(X) = a_{0} + \, a_{{1}} X \, + \, a_{{2}} X^{{2}} + \, \ldots \, a_{{\text{n}}} X^{\text n}$$
(7)

then, obviously, Af(0) = \({e}^{{\text a}_{0}}\), hence the f(0) = 1 normalization results in A = \({e}^{{\text a}_{0}}\). Accordingly, the kinetic parameters to be determined are E, A, and polynomial coefficients a1, a2, … an. In the actual calculations the polynomials were represented by finite Chebyshev series to decrease the compensation effects between the polynomial coefficients during the minimization of the least squares sum [30, 32, 33, 36], and the coefficients of the Chebyshev polynomials were determined by the method of least squares. (See the explanations in section 4.2 of the Supplementary Information.)

In the present work 5th order and 7th order polynomials were tested for p(X). There were no mentionable differences between the use of 5th order and 7th order polynomials from a computational point of view. However, the reliability tests with 7th order polynomials gave more favorable results (i.e., less scatter in the obtained activation energies and f(X) functions) than the 5th order polynomials. Accordingly, the 7th order results are presented in the paper. The previous works with this type of modelling revealed that the employing of higher polynomials did not cause any problems: the unnecessary terms in the polynomials became insignificant when they were not needed [32]. This was so in the present work, too. An example is shown in section. 4.4 of the Supplementary Information.

Results and discussions

Determining an f(X) function and an activation energy value for the samples of a given feedstock

In this evaluation the experiments belonging to a given feedstock were evaluated together by the method of least squares assuming a common E and a common f(X) for the corresponding samples. The notation of the evaluations in this paper indicates the number of f(X) functions and E values for the whole set of experiments. Accordingly, the evaluation treated in this section is denoted by [2 f(X); 2 E].

It is known that the thermal pretreatments as well as the temperature programs of the experiments affect the reactivity of the char forming from biomass materials and influences the thermal deactivation (annealing) at temperatures of the gasification [35, 37, 38]. As an approximation, the corresponding changes in the reactivity can be described by the pre-exponential factors. Accordingly, the pre-exponential factors varied from experiment to experiment. We return to this point in a later section of the paper as well as in the Supplementary Information.

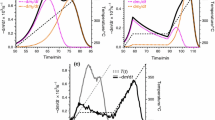
Figure 1 illustrates the obtained fit qualities: the best, the worst and a typical fit qualities are shown for the birch and the spruce samples. Circles represent the calculated curves of this evaluation.

Fig. 1
figure 1

The best, the worst and a typical fit quality for the birch and the spruce samples in evaluation [2 f(X); 2 E]. The corresponding results from evaluation [8 f(X); 2 E] are also displayed in the figure. Notation: Thick solid lines: (-dm/dt)obs; thin solid line, when present: T(t); circles and dashed lines: (−dm/dt)calc curves for evaluations [2 f(X); 2 E] and [8 f(X); 2 E], respectively

Full size image

The main characteristics of the [2 f(X); 2 E] evaluations are listed in Table 1. There are eight common kinetic parameters in this evaluation: seven polynomial coefficients for the f(X) function (as explained in section “Materials end methods”), and one activation energy. Their determination for the samples of a given feedstock was based on N experiments. As outlined above, there is a separate pre-exponential factor for each experiment. Hence the number of parameters to be determined, Npar is 7 + 1 + N. At N = 16 the number of parameters per experiment, Npar/N is 1.5.

Table 1 Evaluation of various groups of the experiments by assuming separate E values for the birch and spruce samples
Full size table

Tests on the reliability of the results

As outlined in the Introduction, the usual statistical tests can be misleading in works based on thermal analysis experiments. Instead, we checked how the evaluation of smaller numbers of experiments affect the results. For this purpose, the evaluations were also carried out on three smaller datasets which consisted of:

  1. (i)

    The modulated and the 20 °C min−1 experiments (two experiments per sample, eight experiments per least squares evaluation);

  2. (ii)

    The modulated and the CRR experiments (two experiments per sample, eight experiments per least squares evaluation);

  3. (iii)

    The modulated experiments only (one experiment per sample, four experiments per least squares evaluation).

The E, reldevN, and Npar/N values obtained in this way are listed in rows 2–4 in Table 1. The activation energies exhibit some scatter. The highest alteration from the average is the E = 293 kJ mol−1 value in the third row which is 5% higher than the corresponding mean value. This is not a considerable difference [11, 39]. The f(X) functions determined from the various subgroups of the experiments are reasonably close to each other, as shown in Fig. 2.

Fig. 2
figure 2

The f(X) functions obtained by [2 f(X); 2 E] evaluations for various subgroups of experiments

Full size image

Determining an f(X) function for each sample

In another series of evaluations, separate f(X) functions were determined for each sample. Altogether eight f(X) functions and two E values were obtained in this way, hence the corresponding notation is [8 f(X); 2 E]. The purpose of this part of the work was: (i) To obtain information on the behavior of the samples; and (ii) To continue the reliability tests outlined above. These evaluations were also carried out on different subsets of experiments by the method of least squares. The kinetic parameters determined in an evaluation consisted of one E, N pre-exponential factors, and 4 × 7 polynomial coefficients for the four f(X) functions. Table 1 contains the corresponding E, reldevN, N, and Npar/N values. The dashed lines in Fig. 1 correspond to this evaluation.

Though Npar/N varied from 1.5 to 8.3 in Table 1, only a moderate scattering of the E values was observed. The averages and standard deviations of the listed E values are also shown in Table 1. The standard deviations expressed as percent of the corresponding average are 2% for birch and 4% for spruce.

The f(X) functions determined in the [8 f(X); 2 E] evaluations are shown in Fig. 3. The f(X) functions obtained for a given sample are remarkably similar in Figs. 3a–3h, though there were some moderate differences in the middle part of the X domain in the case of sample B275. All f(X) curves in Figs. 2 and 3 start with a sharp decrease till around X = 0.15. The last phase of the pyrolysis/devolatilization may contribute to this decrease. However, the f(X) curves for samples B750 and S750 also started with a notable short decrease though these samples were prepared at 750 °C and they are not supposed to devolatilize below 750 °C. Accordingly, the rapid gasification of the most reactive parts of the samples is probably a major factor in the initial decrease of the f(X) functions. In our opinion the similarities observable in Figs. 2 and 3 affirm the reliability of the results.

Fig. 3
figure 3

The f(X) functions obtained in evaluations [8 f(X); 2 E] from different groups of experiments. (Notation: See in Fig. 3a.)

Full size image

Kinetics with common E and common f(X) for all samples

The mean activation energies of the birch and spruce samples did not differ significantly in Table 1. The f(X) functions determined for the birch and spruce samples are also similar in Figs. 2 and 3. Based on these observations an evaluation was carried out by assuming one E value and one f(X) function for all experiments on all samples. This evaluation is denoted by [1 f(X); 1 E]. The corresponding E, reldevN, and Npar/N values are listed in Table 2. The standard deviation of E is 0.8% of the corresponding average while the highest difference from the mean is 1.1% in Table 2. The f(X) functions obtained in this way are also close to each other, as Fig. 4 shows. The corresponding fit qualities are illustrated in Fig. S1 of the Supplementary Information.

Table 2 Evaluation of various groups of the experiments by assuming common E and common f(X) for all samples
Full size table
Fig. 4
figure 4

The f(X) functions obtained by [1 f(X); 1 E] evaluations for various subgroups of experiments

Full size image

The usefulness of evaluation [1 f(X); 1 E] is twofold:

  1. (i)

    The corresponding results indicate that it is possible to find common E and f(X) for different woods in a wide range of thermal pretreatments.

  2. (ii)

    The effects of the feedstock, thermal pretreatments, and heating programs on the gasification reactivity can easily be assessed by the pre-exponential factor values because everything else is common for all samples and all experiments in the [1 f(X); 1 E] evaluation.

The pre-exponential factors are listed and compared in Tables S1 and S2 of the Supplementary Information. The comparison of the pre-exponential factors gives the reactivity differences quantitatively. (Contrary to the traditional comparisons of the peak temperatures for example). For instance, a difference of 0.18 in the log10 A values in Table S1 correspond to difference by a factor of 1.5 in the reaction rates. Besides, such comparisons are applicable for nonlinear temperature programs, as well. In this way the data of Table S1 indicate that the deactivation of the chars is more expressed for the modulated temperature programs than for the roughly four times faster linear heating at 20 °C min−1. It is worth observing in Tables S1 and S2 that the spruce samples are more reactive than the birch samples, though the actual differences vary. The difference is the highest between the reactivities of samples B750 and S750. See further comparisons and explanations in the Supplementary Information.

One-by-one evaluation of the modulated experiments

As a further test, we evaluated the experiments with modulated temperature programs one-by-one by the method of least squares. The notation for this evaluation is [8 f(X); 8 E] which expresses that there is an f(X) function and an E value for each of the eight samples. It is well known that the activation energy can be determined from a single modulated experiment without any assumption on the corresponding f(X) function [40], and there is even an ASTM standard for this procedure [41]. In the present case, however, we determined nine kinetic parameters from one modulated experiment: E, A and the seven parameters of f(X). Nevertheless, we got activation energies and f(X) functions reasonably close to the ones determined by the other evaluations from the same experiments. These evaluations resulted in an average E of 271 kJ mol−1 with a standard deviation of 14 kJ mol−1. The latter value is 5% of the mean, which is only a moderate scatter in non-isothermal kinetics [11, 39]. However, this scatter is not a random noise, as will be shown later in this section.

Table 3 gives an overview on the activation energies obtained from the eight modulated experiments in the evaluations of this work. The results obtained in evaluations [8 f(X); 2 E], [2 f(X); 2 E], and [1 f(X); 1 E] are repeated here from Tables 1 and 2 while evaluations [8 f(X); 1 E] and [2 f(X); 1 E] has not yet been included into the treatment. The mean E obtained in the [8 f(X); 8 E] evaluations (271 kJ mol−1) is not far from the other E values in Table 3 which range from 264 till 270 kJ mol−1. The last row contains the averages of the E values listed in Table 3, 268 kJ mol−1. The farthest value from the average in the table is 264 kJ mol−1, its distance from the average is only 1.5%. The number of parameters per experiment, Npar/N varies from 2 to 9 in the table. A usual kinetic compensation effect [42] was observed between the E and the ln A values of the [8 f(X); 8 E] evaluation with “isoconversional temperatures” around 704 °C. However, another compensation effect was also observed between the E values and the characteristics of the obtained f(X) curves that will be outlined below.

Table 3 The activation energies determined from the eight modulated experiments
Full size table

The first three rows in Table 3 correspond to evaluations that provided separate f(X) functions the samples. These f(X) functions are compared in Fig. 5. Note that the f(X) functions determined in evaluation [8 f(X); 2 E] from the modulated experiments are shown in Fig. 2, too, hence they are represented by the same line style (by squares) in Figs. 2 and 5 to orient the readers. The activation energy values in evaluation [8 f(X); 8 E] are displayed in Fig. 5 for the easier interpretation of the results.

Fig. 5
figure 5

The f(X) functions obtained from the experiments with modulated temperature program in evaluations [8 f(X); 8 E], [8 f(X); 2 E], and [8 f(X); 1 E]. The activation energy values obtained in [8 f(X); 8 E] are indicated in the figure for each sample. (See the text for explanations.)

Full size image

The main characteristics of the f(X) functions are similar in all figures of this paper: a sharp decrease followed by a longer plateau, as it was mentioned already in the paper. The f(X) curves fit to each other well in Fig. 5a and 5b. This is due to the close activation energy values. In Fig. 5c–5h, however, a compensation effect can be observed: the plateau section is lower when E is higher and vice versa. The one-by-one evaluation of the modulated experiments provides obviously the best fit. When the assumption of an E common to several samples alters E from its best fitting value, the change of E is accompanied by a change of all other kinetic parameters, too, so that the fit between the experimental and calculated data could remain good. This might be the cause of the compensation effect observable in Fig. 5c–5h. A deeper analysis of these effects was out of the scope of the present work; we plan to return to these points in a further work. Note that the numerical finding of the best fit is more difficult when marked compensation effects exist between the parameters and requires proper parameter transformations [43]. The methods used in the computations of the present work are described in Sect. 4 of the Supplementary Information.

A closer look on the E values in Fig. 5 reveals that they depend on the thermal pretreatment of the samples. The E values of the samples torrefied at 225 °C, B225 and S225 are lower than the average: 259 and 246 kJ mol−1. On the other hand, the E values of the samples torrefied at 275 °C, B275 and S275 are higher than the average: 281 and 290 kJ mol−1. The chars prepared at 750 °C, B750 and S750 also exhibited slightly elevated activation energies, 281 and 277 kJ mol−1, respectively. Accordingly, a major part of the spread of the E values is probably not random. However, the differences between the E values in Fig. 5 are not particularly high. The lowest and the highest E values in Fig. 5 (246 and 290 kJ mol−1) differ by 9 and 7% from the average E.

Keeping the above considerations in mind, we can conclude that the one-by-one evaluation of the modulated experiments by the methods of the present work gave realistic results which are not far from the ones determined from larger groups of experiments by various assumptions.

Comparison of the results to earlier work

As mentioned in the Introduction, the literature of char gasification contains a wide range of controversial kinetic data. It is hard to make a meaningful comparison of the obtained results with the ones published in the literature. On the other hand the experiments treated in the present work have already been evaluated by similar least squares procedures earlier, though less flexible f(X) functions were employed then [19]. The spruce samples were evaluated by n-order kinetics while a two-parameter f(X) function was employed for the birch samples. Neither of those models was capable to mimic the shapes of the f(X) functions determined in the present paper. Note that the f(X) functions of the present work can follow a particularly wide range of shapes [30, 32, 33]. Table 3 in the work of Wang et al., 2014 [19] contains evaluations that were denoted as “all birch samples together” and “all spruce samples together” and aimed to determine a common f(X) function and a common activation energy for the 16 experiments belonging to a given feedstock. The corresponding reldev16 values were 5.5 and 4.5%, respectively. In the present work the [2 f(X); 2 E] evaluation of the same experiments resulted in reldev16 values of 2.6 and 2.8%, respectively, as shown in Table 1. The closer fit indicates that the calculated curves of the present work could follow better the finer details of the experimental curves. Probably the information contained in the experiments can be better exploited if the model deals with the finer details of the experimental curves, too.

Conclusions

The applicability and reliability of a modelling approach proposed in 2019 [30] were studied. Earlier experiments were reevaluated by this newer tool. Groups of experiments were evaluated together by the method of least squares. The main findings are summarized below.

  1. (1)

    Suitable models were found that described well the gasification of chars forming from woods through a wide range of temperature histories.

  2. (2)

    The reliability of the results was studied by evaluating different groups of the available experiments. Evaluations based on 4, 8, 16 and 32 experiments resulted in similar E values and f(X) functions.

  3. (3)

    The method proved to be suitable for the one-by-one evaluation of the modulated experiments by the method of least squares. It is well known that a single modulated experiment is suitable for the estimation of the activation energy without any assumption on the model function. In the present case, however, a model function, too, was determined for a modulated experiment. The results obtained in this way were similar to the results obtained from larger groups of experiments.

  4. (4)

    In other calculations common activation energy and f(X) function were found for a group of samples/experiments. In these cases, the pre-exponential factors expressed the reactivity differences that were caused by the effects of the feedstock, the pretreatments, and the temperature programs of the TGA experiments.

  5. (5)

    Besides the usual kinetic compensation effect between E and ln A, another compensation effect was also observed that connected the E values and the characteristics of the obtained f(X) curves.

  6. (6)

    The work supplied further evidence about the favorable properties, applicability, and usefulness of the examined way of modelling.