Introduction

The kinetic evaluation of non-isothermal experiments is usually based on isoconversional methods in thermal analysis. The corresponding kinetic equations have the form

$${\text{d}}\alpha /{\text{d}}t = A(\alpha )\;f(\alpha )\exp \left( { - \frac{E\left( \alpha \right)}{RT}} \right)$$
(1)

Here, α is the reacted fraction, while A(α) f(α) and E(α) are empirical functions [1, 2]. The kinetic evaluations by Eq. (2) are frequently called “model-free” methods to emphasize that no assumptions are made on the mechanism of the reactions. The literature of the “model-free” or isoconversional evaluations is huge. Around 4500 scientific articles contain the characteristic terms of these methods in the Web of Science database, of which ca. 500 appeared within a year [3]. The survey of this vast literature is out of the scope of the present work. Instead, the current state of these methods is illustrated by the best-cited works of this field from 2018 [4,5,6]. They deal with the kinetics of organic samples with highly complex chemical composition. A few recent works on similarly complex samples are also listed from the Journal of Thermal Analysis and Calorimetry [7,8,9,10,11,12,13,14]. Many further references can be found in the work of Cai et al. [6] which is an overview of the application of the isoconversional methods for biomass pyrolysis till 2017. Cai et al. [6] gave a critical summary of the available isoconversional evaluation techniques, too.

Let us have a look on the kinetic meaning of Eq. (1). It assumes one pool of reactants for which the reactivity varies as the reaction proceeds. However, most of the samples of practical interest contains more than one sort of reacting species, as it was the case in the studies [4,5,6,7,8,9,10,11,12,13,14] as well as in the nearly 100 works reviewed by Cai et al. [6]. Each species has its own reacted fraction, its own reactivity parameters, and its own concentration in the sample. See, e.g. Ref. [15] for a brief recent overview. Equation (1) can only formally describe the events taking place in a complex organic sample. On the other hand, Eq. (1) can be used to find empirical models that describe the reactions formally and predict the behaviour of the samples in reactor modelling and other tasks [16,17,18,19]. Note that Eq. (1) can easily be solved numerically if the E(α) and A(α) f(α) functions are approximated by polynomials or other smooth functions. Such approximations occur in other works, too [10, 14].

In a recent work, Várhegyi went further in this way [20]. He accepted that the aim of the isoconversional kinetic evaluation is the finding of empirical models. A good empirical model, however, should provide a good fit between the experimental and the calculated data. Besides, a dependable model should be based on a wide + range of experimental information. Accordingly, nonlinear T(t) programs were also considered, i.e. experiments with stepwise, constant reaction rate (CRR) and modulated T(t) programs were also included in the numerous evaluations and were evaluated together with constant heating rate experiments [20]. Simple, versatile E(α) and A(α) f(α) functions were proposed, and their parameters were evaluated by the method of least squares. The present paper aims at adding further considerations, explanations and examples to this work. Besides, a simple modification of the model is presented that aims at an improvement in the fit quality without increasing the number of parameters in the least-squares procedure.

About the experiments used in this work

The considerations of the present work are illustrated by evaluations on experiments that were published earlier with other sort of kinetic evaluations. For this purpose, five TGA experiments were selected from the 36 experiments in the work of Barta-Rajnai et al. [21]. The experiments had been carried out on spruce samples in a high-purity inert gas flow employing relatively low sample masses (1–4 mg).Footnote 1 The corresponding temperature programs are shown in Fig. 1.

Fig. 1
figure 1

The temperature programs of the experiments evaluated

Full size image

Evaluation by the method of least squares and characterization of the fit quality

As mentioned above, we aim at finding such empirical methods which approximate well the experimental data. This can be achieved by the method of least squares. We have a choice of using the TGA data or their derivatives. This depends on the goals of the modelling. It is well known that the DTG curves contain characteristic features which can hardly be observed on the TGA curves. If the models are supposed to reproduce such fine details, it is well worth approximating the DTG curves by the method of least squares. We shall turn back to this point later in the treatment.

In the present work, the experimental reacted fractions were defined as follows:

$$\alpha^{\text{obs}} \left( t \right)\cong\frac{{m_{{150\;{^\circ }{\text{C}}}}^{\text{obs}} - m^{\text{obs}} \left( t \right)}}{{m_{{ 1 5 0\;{^\circ }{\text{C}}}}^{\text{obs}} - m_{{ 7 0 0\;{^\circ }{\text{C}}}}^{\text{obs}} }}$$
(2)

Here, m is the sample mass normalized by the initial sample mass. 150 °C is a temperature where the drying of the samples has terminated, while the chemical reactions have not been started, while 700 °C is a convenient ending point where the TGA curves are flat enough. (Strictly speaking, the slow carbonization of the chars continues till very high temperatures. However, the char of the biomass materials frequently contains carbonates which may give disturbing side reactions above ca. 700 °C.)

The experimental dα/dt values were obtained by approximating the αobs(t) values by smoothing splines [22]. The root mean square difference between the original m(t) and the smoothing spline was typically much below 1 µg. Such small differences do not introduce considerable systematic errors into the least-squares kinetic evaluations [23].

The fitting of the αobs values is carried out by finding the model parameters which minimize the following objective function, of:

$${\text{of}} = \mathop \sum \limits_{j = 1}^{{N_{\text{exper}} }} \mathop \sum \limits_{i = 1}^{{N_{\text{j}} }} \left[ {\alpha_{\text{j}}^{\text{obs}} \left( {t_{\text{i}} } \right) - \alpha_{\text{j}}^{\text{calc}} \left( {t_{\text{i}} } \right)} \right]^{2} /N_{\text{j}}$$
(3)

Where Nexper is the number of experiments evaluated together and Nj is the number of ti time values in experiment j. When the (dα/dt)obs curves are evaluated, the objective function is

$${\text{of}} = \mathop \sum \limits_{j = 1}^{{N_{\text{exper}} }} \mathop \sum \limits_{i = 1}^{{N_{\text{j}} }} \frac{{\left[ {\left( {\frac{{{\text{d}}\alpha }}{{{\text{d}}t}}} \right)_{\text{j}}^{\text{obs}} \left( {t_{\text{i}} } \right) - \left( {\frac{{{\text{d}}\alpha }}{{{\text{d}}t}}} \right)_{\text{j}}^{\text{calc}} \left( {t_{\text{i}} } \right)} \right]^{2} }}{{N_{\text{j}} h_{\text{j}}^{2} }}$$
(4)

Where hj is the highest experimental point on the given curve:

$$h_{j} = \, \hbox{max} \left( {\frac{{{\text{d}}\alpha }}{{{\text{d}}t}}} \right)_{\text{j}}^{\text{obs}}$$
(5)

The division by hj serves for the normalization and has been used in the thermal analysis for decades [24]. It is needed because large differences may arise in the heights of the (dα/dt)obs curves. In the present work, the peak height was 14 times higher at 40 °C min−1 than at 2.5 °C min−1. Without a normalization, the 40 °C min−1 experiment would have dominated the objective function.

Note that the majority of the evaluations in work [20] were based on the least-squares evaluation of the (− dm/dt)obs. That procedure is similar to the present one except that it requested one or more additional scale factor parameters,Footnote 2 and, in this way, increased the number of unknowns in the evaluation. The evaluations by Eqs. (3) and (4) were only briefly treated. The present work is entirely based on evaluations by Eqs. (3) and (4).

The obtained fit quality can be characterized separately for each of the experiments evaluated together. For this purpose, the relative deviation (reldev, %) will be used. The root mean square (rms) difference between the observed and calculated values is expressed as the per cent of peak maximum. At the evaluation of the (dα/dt)obs curves, we get for experiment j:

$${\text{reldev}}\,\left( \% \right) \, = \, 100\left\{ {\mathop \sum \limits_{i = 1}^{{N_{\text{j}} }} \frac{{\left[ {\left( {\frac{{{\text{d}}\alpha }}{{{\text{d}}t}}} \right)_{\text{j}}^{\text{obs}} \left( {t_{\text{i}} } \right) - \left( {\frac{{{\text{d}}\alpha }}{{{\text{d}}t}}} \right)_{\text{j}}^{\text{calc}} \left( {t_{\text{i}} } \right)} \right]^{2} }}{{N_{\text{j}} h_{\text{j}}^{2} }}} \right\}^{0.5}$$
(6)

The fit quality for a given group of experiments is characterized by the root mean square of the corresponding relative deviations. For example, the root mean square reldev of five experiments is denoted by reldev5. The fit quality of the αobs evaluations can be characterized analogously.

The least-squares evaluations were carried out by simple, but safe numerical methods. The experimental temperature values were connected by linear interpolation, and Eq. (1) is solved by a Runge–Kutta method [25] for each experiment in each [ti−1, ti] interval. The minimization of the objective function was carried out by a variant of the Hooke–Jeeves method. The Hooke–Jeeves method is a slow, but simple and dependable direct search algorithm [26]. See further details in Ref. [20].

Simple, but versatile formulas for the modelling

We need parametric A(α) f(α) and E(α) functions for the least-squares evaluation. The objective function of the evaluation, Eq. (3) or (4), is minimized by the parameters of the A(α) f(α) and E(α) functions. A(α) f(α) must satisfy the following two conditions:

$$A\left( \alpha \right)f\left( \alpha \right) > 0\;{\text{at}}\;\alpha < 1$$
(7)

and

$$A\left( \alpha \right)f\left( \alpha \right) = 0\;{\text{at}}\;\alpha = 1$$
(8)

Here, Eq. (8) means that the reaction stops when dα/dt = 0. The minimization is easier if these conditions are fulfilled at any combination of the parameters. Accordingly, we shell rearrange Eq. (1) as proposed in Ref. [20].

Let us introduce the Ã(α) notation as follows:

$${\text{d}}\alpha /{\text{d}}t = \ \tilde{A}(\alpha )\exp \left( { - \frac{E\left( \alpha \right)}{RT}} \right)(1 - \alpha )$$
(9)

where Ã(α) = A(α) f(α)/(1 − α) at α < 1. Ã can have any finite positive value at α = 1 because it is multiplied by zero there. Note that the factor (1 − α) is not connected to any first-order reaction in Eq. (9); it ensures only that dα/dt = 0 at α = 1, so that we do not have to deal with the fulfilment of this condition during the least-squares curve fitting. Keeping in mind that Ã(α) is positive, Eq. (9) can be rearranged as

$${\text{d}}\alpha /{\text{d}}t = \exp \left( {\ln \ \tilde{A}\left( \alpha \right){-}\frac{E\left( \alpha \right)}{RT}} \right)\left( {1 - \alpha } \right)$$
(10)

In this equation, ln Ã(α) and \(\frac{E\left( \alpha \right)}{RT}\) have—obviously—similar magnitudes. A general and widespread way for function approximations is the use of polynomials because they have a simple form, their handling is easy, and they can approximate a wide range of functions. Accordingly, the approximation of ln Ã(α) and E(α) by polynomials is a practical way. The coefficients of the polynomials can be determined by the method of least squares so that the objective function, Eq. (3) or (4), would be minimal.

If the minimization is carried out by simple direct search methods, like in the present work, then the interrelations (i.e. the “compensation effects”) between the variables should be decreased. One step into this direction is the replacement of the ln Ã(α) polynomial by a Z(α) polynomial during the minimization:

$$Z\left( \alpha \right) = \ln \ \tilde{A}\left( \alpha \right){-}\frac{E\left( \alpha \right)}{{RT_{\text{mid}} }}$$
(11)

Where Tmid is the temperature in the middle or near to the middle of the given temperature interval. (The ln Ã(α) polynomial is obviously calculated after the least-squares minimization from Eq. (10).) This transformation was introduced in the nineties on models with constant ln A and E values [27].

The interrelationships between the coefficients within a given polynomial can also be diminished by simple transformations. The easiest way is to introduce an x = 2α − 1 variable and write the polynomials as a function of x instead of α. Note that x varies in the [− 1,1] interval. A further step in this direction is to express the E(α), ln Ã(α) and Z(α) polynomials by Chebyshev polynomials of the first kind instead of the powers of x [20, 25].

Least-squares evaluations: results and discussion

The least-squares evaluations were carried out at various orders of the E(α) polynomials. Following the advice in Ref. [20], the fifth-order polynomials were used for the ln Ã(α) functions. Table 1 gives a summary of the results.

Table 1 Least-squares evaluation of the αobs and (dα/dt)obs curves at various orders of the E(α) polynomials
Full size table

The comparison of the left-hand side and right-hand side of Table 1 shows that the evaluation of the αobs and (dα/dt)obs gives different results. The aims of the modelling should determine which way should be taken. (We shall return to this point later.) The first row in the table shows the evaluation by zero-order E(α) polynomials. In this case, E does not depend on α; all reactivity differences are described only by ln Ã(α). The corresponding curves and fit qualities are shown in the figures of the Electronic Supplementary Material belonging to this paper. The practical significance of this sort of modelling is discussed later, in a separate section. The corresponding fit quality is already suitable for every practical purpose; the relative deviations are small compared to the other sort of uncertainties in a modelling work. The number of parameters (polynomial coefficients) is seven at zero order E(α). When the evaluation is based on five experiments, the number of unknowns is 1.4 per experiment.

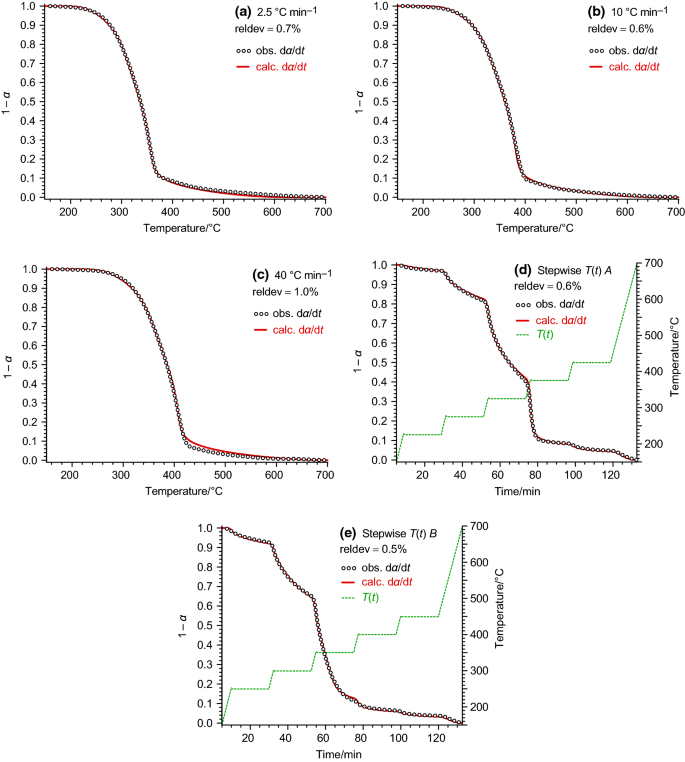
As the order of the E(α) polynomials increases, the number of parameters also increases while the relative deviation slowly decreases. There are 10 polynomial coefficients at the third-order E(α) polynomials, hence the number of unknown parameters is 2 per experiment. In the following part of this section and in the next section, the evaluations with the third-order E(α) polynomials are shown in more details. Figures 2 and 3 display the corresponding experimental and calculated curves. The reldev values (fit qualities) are also indicated in the figures.

Fig. 2
figure 2

The simultaneous evaluation of five αobs curves by the method of least squares. The order of the E(α) and ln Ã(α) polynomials was 3 and 5, respectively

Full size image
Fig. 3
figure 3

The simultaneous evaluation of five (dα/dt)obs curves by the method of least squares. The order of the E(α) and ln Ã(α) polynomials was 3 and 5, respectively

Full size image

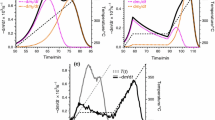
For many samples, the peak shape in the dα/dt curves contains important information about the samples and/or the reactions. In the case of biomass samples, the hemicellulose and cellulose peaks are more or less overlapping. See, e.g. the shoulders on the peaks in Fig. 3a–c, which indicate a moderate overlap of the two peaks. If we wish to have models that reflect such characteristics, we should fit the (dα/dt)obs curves, i.e. we should minimize the objective function of Eq. (4). Figure 4 indicates that the fitting of the αobs values does not necessarily reproduce well the characteristics of the (dα/dt)obs peaks.

Fig. 4
figure 4

The model obtained from the least-squares evaluation of the αobs curves cannot predict well the characteristics of the DTG curves. (Note that the least-squares evaluation of the (dα/dt)obs curves resulted in a reldev = 2.7% for this experiment, as shown in Fig. 3b.)

Full size image

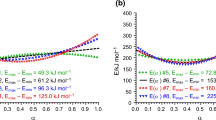
Figure 5 shows that the two sorts of evaluations provide somewhat different E(α) functions. The differences appear mainly at higher values of α. Note that the TGA curves of the biomasses, coals, and many other organic materials contain a long tailing section which corresponds to the slow carbonization of the formed chars at higher temperatures. When the αobs values are evaluated, the fit of the long tailing sections influences more the values of the objective function than the fit in the much shorter domain of the main pyrolysis reactions. On the other hand, the evaluation of the (dα/dt)obs curves by the method of least squares emphasizes the fit where the reaction rates are high.

Fig. 5
figure 5

E(α) polynomials obtained from the least-squares evaluation of the αobs curves (a) and (dα/dt)obs curves (b)

Full size image

A simple prediction test

An empirical model is supposed to predict the behaviour of the samples at such temperature programs, too, which were not used in its determination. To test these aspects, the least-squares evaluations were carried out on the constant heating rate experiments only and it was checked how the obtained models describe the two stepwise experiments. The fit qualities of the predictions are listed in Table 2. The best fit qualities were obtained at the third-order E(α) polynomials, though the difference between the second- and third-order E(α) polynomials was very small at the α-evaluations. The fit between the predicted and observed curves is shown in Fig. 6 for the model variants with the third-order E(α) polynomials. The favourable results of the present prediction tests can probably be connected to the highly different heating rates in the constant heating rate experiments. Note that the peak reaction rate, max (dα/dt)obs, proved to be 14 times higher in the 40 °C min−1 experiment than in the 2.5 °C min−1 experiment. In this way, the constant heating rate experiments represented a relatively wide range of experimental conditions. On the other hand, only 0.5 and 2 mg sample masses were employed at 40 and 10 °C min−1, respectively, to avoid the heat and mass transfer limitations [21].

Table 2 Prediction of the stepwise experiments from the evaluation of the constant heating rate experiments. reldev2/% values are listed for the α and dα/dt evaluations
Full size table
Fig. 6
figure 6

The model obtained from the evaluation of the constant heating rate experiments predicted well the stepwise experiments

Full size image

Empirical models with constant E

As mentioned above, the modelling with zero-order E(α) polynomials, i.e. with constant E parameters, gave comparable fit qualities to the fit qualities of the modelling with E(α) polynomials with orders 1–5. See, e.g. the reldev values in Tables 1 and 2. The Electronic Supplementary Material contains figures that show the fit between the observed and calculated curves in this case. With constant E, Eq. (1) is simplified to

$${\text{d}}\alpha /{\text{d}}t = A\left( \alpha \right)f(\alpha )\exp \left( { - \frac{E}{RT}} \right)$$
(12)

In Eq. (1), the A(α) f(α) function alone approximates the variation of the reactivity with α. An immediate advantage is the lower number of unknown parameters. The approximation of A(α) f(α) is carried out by a fifth-order polynomial (which describes ln Ã(α), as outlined above), hence the model has seven unknown parameters (six polynomial coefficients plus the E parameter). Accordingly, the number of parameters per experiment was only 1.4 when five experiments were evaluated (as mentioned above), and 2.3 when three experiments were evaluated. In both cases, the model parameters were mathematically well-defined by the available experimental information. Besides, the least-squares minimization itself is faster and safer at a lower number of unknowns in the evaluations.

However, the real importance of this type of models is the fast numerical solution of Eq. (12) when larger systems (e.g. reactors) are modelled.Footnote 3 Let us consider here that the variables, α and T, are separable in Eq. (12):

$$\frac{{{\text{d}}\alpha }}{A\left( \alpha \right)f\left( \alpha \right)} = \exp \left( { - \frac{E}{RT}} \right){\text{d}}t$$
(13)

Please note that the separation of a kinetic differential equation means that α occurs only at one side of the equation after the separation. If E is a function of α, then this operation cannot be carried out and the solutions based on Eq. (13) are erroneous. Accordingly, the integral isoconversional methods prior to the seminal works of Vyazovkin are mathematically erroneous [1, 2, 28, 29]. These erroneous methods include, among others, the widely used Flynn–Wall–Ozawa (FWO) and Kissinger–Akahira–Sunose (KAS) methods.Footnote 4

There are many analytic approximations for the integral of the right-hand side of Eq. (13) when the temperature–time function is linear or consists of linear sections. General quadrature formulas can be used for the other T(t) functions. There are no analytical approximations for the integration of the left-hand side. In case of larger modelling works, when the solution of Eq. (12) should be calculated many times with the same kinetic parameters, one can integrate the left-hand side with a quadrature prior to the start of the modelling itself. We can denote the integral of the left-hand side by the usual g(α) notation. The g(α) values obtained by the numerical integration can be stored in an array together with the corresponding α and A(α) f(α) values. (So that each α, A(α) f(α), and g(α) triplet occupies a row in an array containing several thousand rows.) Whenever a new value arises for the integral of the right-hand side during the work, the nearest g(α) value can easily be found in the array by a fast binary search algorithm [30] even if the array is huge. The α and A(α) f(α) values stored alongside with g(α) provide the corresponding conversion and allow the fast estimation of the reaction rate.

Please note that the numerous simple one-reaction-step models in the literature of thermal analysis cannot describe well the data shown in Figs. 2 and 3. A less-formal modelling for the pyrolysis of woods and other lignocellulosic materials should be based on three or more pseudo-components with three or more kinetic equations [15, 21].

A modification of the model

The term (1 − α) in Eq. (9) ensures mathematically that dα/dt is zero at α = 1. Obviously, other functions can also be used for this purpose. Among others, we can use a power function (1 − α)n with any n > 0 value:

$${\text{d}}\alpha /{\text{d}}t = \ \tilde{A}_{\rm{n}} (\alpha )\exp \left( { - \frac{E\left( \alpha \right)}{RT}} \right) \left( {1 - \alpha } \right)^{\rm{n}}$$
(14)

Here, n is a fixed number and Ãn(α) = A(α) f(α)/(1 − α)n at α < 1. ln Ãn(α) is approximated by polynomials in the same way as ln Ã(α) was in the treatment above. If a small n value is used, e.g. n = 0.5, then the sharp descend of (1 − α)0.5 after its maximum helps the model to mimic sharply terminating dα/dt curves. This may be useful when gasification or combustion reactions are described. On the other hand, larger n values result in (1 − α)n functions with a longer tailing and it may help the model to approximate the long, flat tailing sections of the dα/dt peaks of the biomass decomposition processes. The aim of the use of an n in eq. (14) is to achieve an improved fit quality without increasing the number of parameters in the least-squares procedure.

All calculations of the present paper were carried out by Eq. (14) at n = 0.5, 1, 2 and 3. (The results outlined in the previous sections correspond, obviously, to n = 1.) The effects of the various n values are shown in Table 3. E(α) polynomials from 0 to 5 orders were employed. In the upper part of Table 3, the results obtained at different degrees of E(α) were averaged. The average values are denoted by italics in the table. It is worth observing that the fit quality improves as n is increasing: the corresponding reldev5 values gradually decrease as n increases. The central and lower parts of Table 3 show the results at zero order and third order E(α). They show the same tendencies as the average values: the fit quality tends to improve as n increases. The best fit qualities were achieved at n = 3. The only exception was the evaluation of the αobs data with zero order E(α); then reldev5 was practically identical at n = 2 and n = 3. (Rounded to three decimals, the corresponding values were 0.764 and 0.767, respectively.) Obviously, the order of the E(α) polynomials also influenced the fit quality: a higher number of parameters (polynomial coefficients) resulted in better fit qualities. In the case of third-order E(α) polynomials, the change in n from 1 to 3 decreases reldev5 from 0.72 to 0.63 when αobs is evaluated and from 2.24 to 2.09 when (dα/dt)obs is evaluated.

Table 3 Least-squares evaluation of the αobs and (dα/dt)obs curves at various n values
Full size table

We also calculated how the parameters from the evaluation of the αobs data predict the (dα/dt)obs curves and how the parameters from the evaluation of the (dα/dt)obs data predict the αobs curves. The corresponding columns are marked by string “(test)” in Table 3. The data in column “reldev5 of dα/dt (test)” show a marked decrease as n increases. On the other hand, the values in column “reldev5 of α(t) (test)” do not exhibit a definite dependence on n. One may be interested in a model that describes well both the (dα/dt)obs and the αobs data. In the present work, we did not modify the objective function for this purpose; we just examined which of the obtained model variants is the most favourable in this respect. For a comparison, we added the best-fitting reldev5 and the test reldev5 values at each evaluation. This sum was 2.17 + 1.32 = 3.49 when (dα/dt)ob was evaluated with zero order E(α). All other model variants gave worse results in this respect. Keeping in mind that the number of the unknown parameters is only seven in this case (one E value and 6 polynomial coefficients for ln Ãn(α)), the use of this model variant is highly advisable.

Table 3 also lists the means of the E(α) polynomials, Emean. This quantity depends on whether αobs or (dα/dt)obs is evaluated, and it also depends on the order of the E(α). (See the Emean values in Table 1, too.) Nevertheless, the dependence of Emean on n proved to be negligible in those groups of evaluations which differed only in the value of n.

Conclusions

The isoconversional (or model-free) methods cannot provide meaningful kinetic description for most samples in the thermal analysis. Nevertheless, they can serve as empirical models. A usable empirical model should describe well the observed data and should be suitable for predictions, too. For this purpose, the functions in the isoconversional kinetic equation should be parametrized, and these parameters should be determined by the method of least squares. This procedure ensures that the data calculated from the model would be close to the experimental data.

The present work supplemented a preceding work of Várhegyi [20] by further considerations and evaluations. In this way, the results of the predecessor work [20] were strengthened in several points:

  • The E(α) and A(α) f(α) functions in the isoconversional kinetic equation can be well approximated by simple, versatile formulas.

  • A good fit can be obtained between the calculated and the observed data by the method of least squares.

  • The shape of the DTG peaks may contain important information about the studied reactions, and about the studied samples. If the model is wished to reflect these characteristics, the curve fitting should be carried out on the (dα/dt)obs data.

  • When the obtained empirical kinetics is intended to be used as a submodel in the modelling of larger systems, the speed of the calculations is vitally important. In such cases, model variants with constant E parameters can be used, because they allow much faster calculations. At constant E parameters, the A(α) f(α) function alone approximates the variation of the reactivity with α.

  • The prediction capabilities of the models were also tested in the present work. It was found that an evaluation based on three experiments with constant heating rates could predict well two further experiments with stepwise temperature programs.

  • A modification of the model was proposed and examined. The aim was to improve the fit quality without increasing the number of parameters in the least-squares procedure. The possibilities of this modification were examined by numerous test evaluations, and a specific model variant was proposed for the kinetic description of biomass pyrolysis.