Introduction

The reduction of iron oxides is widely studied due to the industrial importance of iron and steel [1, 2]. The powder metallurgy (PM) industry is particularly concerned with the efficient removal of oxides for three main reasons; (1) the large surface-to-volume ratio of powder particles make them susceptible to atmospheric interaction and consequently to oxidation; (2) the surface oxide layer covering the powder particles is generally considered a limiting factor for the effective creation of sinter necks; and (3) in recent decades, developments in advanced PM steels have introduced new alloying elements, such as chromium and manganese, that are prone to form thermodynamically stable oxides [3]. As a consequence, oxides in PM material systems have been studied intensively for several decades. Recent investigations on water-atomized powder grades, the work-horse of the PM industry, have utilized a range of analysis methods for this purpose, detailing the physical and chemical properties of various oxides by thermogravimetric analysis (TGA) [3,4,5], TGA coupled with mass spectrometry (MS) [6, 7], and surface analytical techniques like X-ray photoelectron spectroscopy (XPS) [5, 8,9,10,11], and Auger electron spectroscopy (AES) [5, 9, 12].

The typical water-atomized powder particle has an irregular morphology, is covered by a thin 5–7-nm iron-rich oxide layer and has a variety of thermodynamically stable, submicron oxide particulates spread on the surface. The surface coverage of particulate oxides can reach 5% for some low-alloyed steel grades while the rest of the surface is often considered a homogeneous iron oxide layer [4, 8, 9]. The stable oxides, rich in chromium, manganese and silicon, are considerably more difficult to reduce than the iron oxide layer and consequently any sintering atmosphere and temperature program that can provide adequate sintering conditions for their removal will also be able to reduce iron oxides. As a result, much of the previous work has been done to understand the nature of these oxides and the critical conditions that need to be met in order to successfully sinter advanced PM grades, particularly those alloyed with chromium and manganese [3, 6,7,8,9, 13,14,15,16]. A range of studies also detail the effects of oxide transformation events in which the less stable oxides, such as those of iron, are reduced and may act as a source of oxygen for the alloying elements that form more stable oxides [4, 7, 15, 17]. If present in developing sinter necks, the oxide residues and inclusions may then result in deterioration of mechanical properties [15]. While the majority of the previous studies on water-atomized grades have been focused on the details of the thermodynamically stable oxides, the less stable surface iron oxide layer is less studied. Despite the small thickness of the oxide layer, owing to the large specific surface area of water-atomized powder, it still accounts for accounts for 30–50% of the total oxygen content in the powder, depending on particle size distribution, alloying elements, powder manufacturing and further storage and handling [5, 8]. Consequently, a large amount of oxygen is readily available for oxygen transfer to stable oxide-forming elements if removal of oxygen released from the reduction of the iron oxide is not sufficient. Local atmospheric conditions may even become simultaneously reducing and oxidizing to the oxide layer and oxide particulates, respectively, leading to growth of the oxide particulates [7]. Conditions are expected to deteriorate further with increased levels of compaction and trapping of oxide residues and progressively become worse as sintering densifies the compacts and decreases the porosity available for outward transport of reaction products.

In the present study, thermogravimetric analysis is used for studying reduction and mass loss events relevant to iron-based PM material systems, an approach that has been proven to be effective for metal powder and compacts [3, 6, 18, 19]. Further kinetic analyses based on thermogravimetry are not uncommon with examples of the Kissinger method [20] applied to reduction of iron oxides [21, 22] and nickel oxide [23], and the Kissinger–Akahira–Sunose method [20, 24] applied to reduction of iron oxides [25, 26]. While mainly pure oxides have been investigated in these studies, analysis of more complex materials such as low-alloyed steel powder [27] is of potential interest to the PM industry. However, since the chemical composition of alloyed steels may influence the analysis by forming stable oxides, the focus of this study will be on plain water-atomized iron powder to clarify the role of iron oxide and its reduction during sintering. In this study, water-atomized iron powder of three size fractions are analyzed with respect to reduction in hydrogen atmospheres with compacted samples also analyzed to reflect the applied setting of industrial importance. Emphasis is put on the reduction of the surface iron oxide layer and high-temperature reduction of internal oxides and stable particulate oxides. For reference, pure Fe2O3 oxide powder samples are analyzed to provide a baseline for the subsequent measurements. The thermogravimetric data are then used as input for a kinetic analysis where the apparent activation energies of oxide reduction at low and high temperatures are calculated, providing information about the temperature sensitivities and mechanisms of the reduction processes. The thermogravimetric and kinetic analyses highlight both the similarities and differences between the model iron oxide and the industrially important powder material in loose and compacted form. Increasing temperatures shows the complexity of accurately describing oxide reduction and mass loss events that take place in powder metallurgy conditions.

Materials and experimental procedure

Materials

Pure iron oxide powder of Fe2O3 (99%, < 5 µm, Sigma Aldrich) was acquired and used as a reference sample for the iron oxide reduction kinetic study. Water-atomized iron powder of three different size fractions was provided by Höganäs AB, Sweden. The chemical composition of the three sieve fractions can be seen in Table 1.

Table 1 Chemical composition of the three powder fractions (mass%)
Full size table

To study the influence of initial density on the oxygen reduction and removal, the Fe75 powder was compacted using a manual hydraulic press and a small die. Small cylindrical samples of 10 mm diameter and around 3.5 mm in height with densities of approximately 7.2 g cm−3 were produced.

To obtain an overview of the initial state of the powder, the particle surfaces and fracture surfaces of compacted powder samples were analyzed using a LEO Gemini 1500 FEG-SEM. AES analysis was done using a PHI 700 instrument to depict the presence and composition of the fine particulate oxides on the powder surfaces. The accelerating voltage was 10 kV, and the beam current used was 10 nA, yielding an analytical lateral resolution of approximately 20 nm. No attempt to quantitatively assess the composition of particulate oxides was done in this study.

Thermogravimetric setup

The thermogravimetric measurements of the oxide and powder samples were done using an STA 449 F1 Jupiter® instrument from Netzsch. Reference oxide samples with mass of around 1 g, and powder and compact samples with mass of around 2 g, were put into Al2O3 crucibles and loaded into the instrument. The furnace was then evacuated (~ 3E−4 mbar) and flushed three times with high-purity argon prior to each experiment to ensure minimal contamination from the surrounding air. The temperature programs consisted of a heating stage up to 1350 °C, a hold for 30 min and a cooling stage down to room temperature at 30 °C min−1. Heating rates in the range 10–50 °C min−1 were used as the basis for the kinetic analyses. The experiments were performed in pure (99.9999%) hydrogen atmosphere to ensure a high reduction potential and enable a complete reduction of all oxides present, both on the surface and within the metal particles. The flow rate was set to 100 ml min−1 to provide sufficient supply of new gas and to transport away reaction products and therefore to provide constant reducing conditions in the furnace throughout the whole reduction processes. The supply of undiluted hydrogen and the removal of reactive gaseous products were deemed to provide conditions that would make any pressure dependence negligible [28]. In addition, the experimental setup ensured a constant pressure in the system throughout the process.

Kinetic analysis

Kinetic analyses of the reduction and deoxidation processes for all studied oxide and powder samples were done to describe the temperature influence and temperature sensitivities of the relevant reactions in order to better understand the processes that take place during sintering of metal powder.

A solid state reaction can be described by the following equation [28]:

$$\frac{{{\text{d}}\alpha }}{{{\text{d}}t}} = k\left( T \right)f\left( \alpha \right)$$
(1)

Where α is the extent of conversion of the reaction, k(T) is the temperature dependence and f(α) is the reaction model. The temperature dependent rate constant, k(T), is taken as the Arrhenius equation

$$k\left( T \right) = A\exp \left( { - \frac{{E_{\text{a}} }}{RT}} \right)$$
(2)

where A is the pre-exponential factor, Ea is the activation energy and R is the gas constant. The ICTAC Kinetics Committee recommends calling A and Ea “effective” or “apparent” kinetic parameters because of the difficulties in obtaining the true intrinsic parameters of a reaction. The non-specificity of thermal analysis measurements, process complexity and diffusion are key factors why this qualifier is advocated [28]. All upcoming references to the activation energy should thus be treated as the apparent activation energy. Non-isothermal temperature programs will be the main focus of this study so that β = dT/dt, where β is the heating rate assuming a constant value over the range of the temperature programs. The reaction model f(α) describes the conversion dependence of the process rate and can be expressed by a number of different models, the most common ones types being accelerating, decelerating and sigmoidal. While kinetic analyses based on mathematical fitting of these models to experimental data have been popular, the application can give rise to ambiguous results due to the failure to separate the conversion and temperature dependence of the reaction rate [28, 29]. With constant heating rate, and with Eqs. 1 and 2 combined, the expression for the rate of conversion becomes

$$\frac{{{\text{d}}\alpha }}{{{\text{d}}T}} = \frac{A}{\beta }\exp \left( { - \frac{{E_{\text{a}} }}{RT}} \right)f\left( \alpha \right)$$
(3)

One of the most common methods of kinetic analysis is the Kissinger [20] method, derived from Eq. 3 assuming a maximum rate of conversion where d2α/dt2= 0. With Tm as the temperature at maximum rate of conversion, the expression becomes [28]

$$\ln \left( {\frac{\beta }{{T_{\text{m}}^{2} }}} \right) = \ln \left( { - \frac{AR}{E}f^{{\prime }} \left( \alpha \right)_{\text{m}} } \right) - \frac{E}{{RT_{\text{m}} }}$$
(4)

While the use of the Kissinger method is straightforward, it is associated with limitations such as requiring f′(αm) to be independent of β [28]. Reliable values from the Kissinger analysis can be obtained if αm does not vary with β, identified by a change in peak shape [28]. Another limitation is that the Kissinger method only provides a single value of the activation energy, regardless of the kinetic complexity [28]. Relatively unknown or less studied effects, such as the influence of mechanical compaction on the reduction of oxides on metal powder, can therefore be overlooked. In the system of interest, it is believed that the reduction of oxides in the loose powder state does not necessarily represent the full picture of oxide reduction in the compacted state, as the deformation and porosity may increase the complexity of the reduction process. In this study, the Kissinger method is therefore used as a baseline providing a first quick look at the kinetics of the relevant processes. In addition, an integrated isoconversional method is used to complement the Kissinger analysis and reveal any further complexities of the processes, if present.

The integrated form of Eq. 3 can be expressed as

$$\mathop \int \limits_{0}^{\alpha } \frac{d\alpha }{f\left( \alpha \right)} = \frac{A}{\beta }\mathop \int \limits_{0}^{T} \exp \left( { - \frac{{E_{\upalpha} }}{RT}} \right){\text{d}}T$$
(5)

where an approximation [30] of the temperature integral of Eq. 5 is used, giving rise to the Kissinger–Akahira–Sunose (KAS) method [20, 24], commonly formulized as

$$\ln \left( {\frac{\beta }{{T_{\upalpha}^{2} }}} \right) = \ln \left( {\frac{{A_{\upalpha} R}}{{E_{a} g\left( \alpha \right)}}} \right) - \frac{{E_{\upalpha} }}{RT}$$
(6)

where g(a) is the integral form of Eq. 5. At a constant conversion α, the activation energy Eα can then be estimated from the slope of a plot of ln(β/T2) versus 1/T.

For the isoconversional kinetic analyses used in this paper, the conversion was calculated for each individual mass loss stage of the temperature program according to

$$\upalpha = \frac{{m_{\text{i}} - m}}{{m_{\text{i}} - m_{\text{f}} }}$$
(7)

where mi, m and mf are the initial, instantaneous and final masses of the samples. The temperature range over which the conversion was calculated varied with each sample and heating rate but was approximately 300–550 °C for the low-temperature reduction and in the range 600–1350 °C for the high-temperature mass loss.

Several limitations may be present in the current kinetic study. Thermal lag, the difference between measured and actual temperature of a sample, may be present for large samples and is accentuated by increasing heating rates. Compact samples, with poor surface-crucible contact, may be especially sensitive. The thermal lag effect is sometimes observed during pyrolysis of biomass, where even relatively small samples can give rise to thermal lag, causing an underestimation of the activation energies [31, 32]. Heat capacities and heat transfer issues were cited as possible sources of error. In the present study, the heat capacity and thermal conductivity of iron as well as the heat transfer capabilities of hydrogen gas should to some degree mitigate the thermal lag issues. A note should be made that even though thermal lag is likely present and may cause further deviation from the intrinsic kinetics of the reaction, it may also give increased insights into the applied industrial settings where very large samples of several kilograms are used.

Results and discussion

Oxide reference material

Iron oxide reference samples were used to establish a baseline for the subsequent thermogravimetric experiments and kinetic analyses of the water-atomized powder and its compacted state. The expected mass losses of these experiments can be derived from the reduction steps by means of determining the stoichiometric mass losses, see Table 2. It should be noted that the actual recorded mass losses will be a function of the heating rate of the experiment as the reduction steps show some degree of overlap and become difficult to separate as a consequence of the different activation energies of the reaction steps. The measured mass losses are therefore considered at a heating rate of 40 °C min−1 which allows for relatively accurate peak separation and resolution.

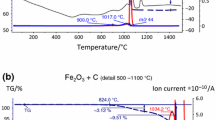
Table 2 Mass losses of reduction steps of Fe2O3 with hydrogen
Full size table

Figure 1 details the reduction of Fe(III) oxide with heating rates in the range 10–50 °C min−1, designated HR10-50, with both mass losses (a) (TG) and mass loss rates (b) (DTG). A substantial shift of the mass loss events to higher temperatures is seen when higher heating rates are used. The first clear event takes place in the range 300–500 °C, resulting in a mass loss of 3.34% which corresponds well with the theoretical mass loss of the Fe2O3 → Fe3O4 reduction step. Two subsequent mass loss events take place at higher temperatures but are not easily discernible at lower heating rates (< 30 °C min−1) which can lead to the assumption that the reduction follows Fe3O4 → Fe. Therefore, the intermediate wüstite step is not always recorded in some studies where low heating rates were used [21, 25]. However, even at 10 °C min−1 the superposition of two peaks is outlined in the first derivative curve and two peaks are clearly distinguished at higher heating rates due to the difference in activation energies between the reduction steps. Thus, it seems reasonable to expect that the intermediate Fe3O4 → FeO reduction step is indeed present in the current study but cannot be resolved at low heating rates that reflect reduction processes closer to equilibrium, especially if the reactions have vastly differing activation energies. Another important feature in Fig. 1 is the apparent temperature widening of the reduction peaks caused by the activation energy differences; complete reduction (29.98% mass loss) is reached at around 800 °C when using a heating rate of 10 °C min−1, whereas complete reduction (29.82%) is reached only at 1350 °C when using a heating rate of 40 °C min−1.

Fig. 1
figure 1

TG/DTG curves of reduction of Fe2O3 reference oxide samples

Full size image

Water-atomized iron powder

As previously explained in the introduction, iron powder is, besides a thin iron oxide layer, expected to have particulate oxides scattered on the surface. Figure 2 shows a brief surface chemical analysis of loose powder conducted by means of high lateral resolution AES. Particulate oxides scattered on the surface may exhibit a complex chemical composition of chromium, manganese and iron, as shown by the AES spectra in Fig. 2b. Consequently, the surface state of the powder can be considered a complex heterogeneous mix of different oxide particulates distributed on an iron-rich oxide layer [9]. The thickness of the iron oxide layer is typically found to be 5–7 nm as obtained by means of XPS depth profiling [5]. This value has been correlated with thermogravimetric results by estimating the thickness from the specific surface area of the powder, the oxide density and oxygen content of the oxide, and the thermogravimetric mass loss. As the average particle size becomes smaller, an increasingly large fraction of the total oxygen is bound in this oxide layer [5].

Fig. 2
figure 2

a Detailed view of metal particle surface and b AES spectrum showing composition difference between the matrix and an oxide particulate enriched in manganese

Full size image

Compacted samples

An SEM overview of a fracture surface of a compacted powder sample can be seen in Fig. 3, indicating a change in particle morphology after compaction. In parallel, the ductile matrix is easily deformed, whereby large and flat interparticle contacts are commonly observed [33]. The compaction also means that the oxide layer must be accommodated in the deformed microstructure, something that likely promotes crack formation, deformation [34] and spalling of the oxide layer, re-oxidation of the exposed metal surfaces and even presence of cold welding between metal particles [4, 35]. Furthermore, the porosity of the compact is decreased compared to loose powder. Additionally, the arrangement and geometry of the particles changes continuously during sintering because of densification through diffusion, making the real conditions highly dynamic and complex. Consequently, oxygen removal will be more difficult as there will be physical barriers that hinder the effective outflow of reaction products such as water vapor if hydrogen is the active reducing component of the sintering atmosphere. The extent of this effect was studied by subjecting compacted samples to the same sintering cycle conditions as the powder samples.

Fig. 3
figure 3

Fracture surface of compacted Fe75 powder

Full size image

Thermogravimetric analysis

Two typical thermogravimetric curves and their corresponding derivatives are shown in Fig. 4. Both a powder sample and a compact are shown to highlight the differences between them. The typical TG curve can be separated into three principal regions; (i: 300–500 °C) mass loss related to surface oxide layer reduction, (ii: 500-α → γ) mass loss in the ferrite matrix temperature range and (iii: α → γ-1350 °C) the high-temperature mass loss region. The most distinct mass loss step occurs in the oxide layer mass loss region and indicates the reduction of the thin iron oxide layer [5]. After this step, the TG signal is relatively flat but an increasing temperature enables a distinctive mass loss toward the end of the ferrite phase stability region where the iron matrix still exhibits the bcc crystal structure that allows for rapid interstitial solid state diffusion. At the onset of the α → γ transformation, the decrease in mass loss rate indicates a strong phase dependence in which the iron matrix clearly affects mass transport, see Fig. 5a. This confirms the removal of oxygen from the powder matrix, which is linked to the presence of internal oxides in untreated powder, see Fig. 5b. Above ~ 920 °C is the high-temperature mass loss region, where mass loss is believed to be connected to a combination of processes such as partial reduction of internal oxides and reduction of stable oxide particulates on the surface of the powder particles. The mass loss rate reaches a maximum in the range 1100–1150 °C, see Fig. 4, after which the rate diminishes again because of the depletion of oxygen in the samples [16]. The high temperature in region (iii) enables rapid diffusion which aids in the transport and removal of oxygen. The stable particulate oxides are expected to be reduced over a wide temperature range due to variations in chemical composition that changes their thermodynamic stabilities. The compacted sample shows a similar reduction behavior as the powder, but with three main differences; (1) the onset of the surface iron oxide reduction is at lower temperatures, whereas the completion is at higher temperatures, (2) the mass loss in the ferrite region is lower, and (3) the high-temperature mass loss is shifted to higher temperature by around 50 °C. All these changes reflect the influence of compaction on the reduction of the surface iron oxide layer, and the increased difficulties in removing reduction products due to porosity.

Fig. 4
figure 4

TG/DTG curves of Fe75 powder and Fe75 compact at 10 °C min−1

Full size image
Fig. 5
figure 5

a Phase dependence of mass loss in Fe45 powder and b particle cross section showing presence of internal oxides in Fe75 powder

Full size image

Figure 6 shows the thermogravimetric curves for Fe75 powder and Fe75 compacts at heating rates in the range 10–50 °C min−1. Identical runs were done for the Fe20 and Fe45 powder, showing the same trends, but the results are not shown here. A clear shift of the curves to higher temperatures with increased heating rates can be observed, and this forms the basis for the kinetic analyses.

Fig. 6
figure 6

TG/DTG of Fe75 powder and Fe75 compact samples at heating rates 10–50 °C min−1

Full size image

Kinetic analysis of oxide reduction and oxygen removal

Kinetic analyses are done for all thermogravimetric curves exhibiting a temperature shift with heating rate, in this case iron oxide reduction and the low and high-temperature mass losses of powder and compacts.

Low temperature

The kinetic analysis of low temperature processes is mainly concerned with the reduction of the surface iron oxide layer and the temperature range and temperature sensitivity of this process.

The kinetic analyses of oxide reduction and oxygen removal are done according to the Kissinger and Kissinger–Akahira–Sunose methodologies described previously. The analyses are done for both the pure oxide reference samples as well as on the fine water-atomized iron powder and compacted samples that represent the applied industrial setting. In this context, the reduction of iron oxides is interesting from an industrial point of view as it provides insight into events that take place during conventional press-and-sinter powder metallurgy.

Figure 7 shows the Arrhenius plots of the pure Fe2O3 reference samples. As expected, the kinetic analyses show clear linear trends when plotted according to the previously mentioned Kissinger methodology, see Eq. 4. The fitting parameters and values for the activation energies are listed in Table 3 along with similar studies of iron oxides.

Fig. 7
figure 7

Kinetic analyses of Fe2O3 and oxide layer reduction

Full size image
Table 3 Calculated Ea and other sources for the reduction of Fe2O3
Full size table

The slopes and activation energies were obtained from each reduction step separately. The results for hematite and magnetite reduction are around 100 kJ mol−1 which is in relatively good agreement with values presented in literature, see Table 3. The deviation can likely be explained by differences in starting material and experimental setup. Regarding the water-atomized iron powder, a similar kinetic analysis was done on the first reduction step at low temperatures around 400 °C, corresponding to the reduction of the surface iron oxide layer. The results can be seen in Fig. 7 and Table 3. The obtained apparent activation energy values of 85–102 kJ mol−1 correlate well with the reduction steps Fe2O3 → Fe3O4 and Fe3O4 → FeO, and it is concluded that the surface iron oxide layer is reduced in a similar way. While three oxide layers and an oxygen gradient could in theory exist in this thin surface oxide layer, the current thermogravimetric setup could not resolve this. The transient oxide states likely exist in so small amounts in the thin oxide layer that they are immediately reduced to iron when possible. The obtained apparent activation energies thus represent a compound value reflecting the overall reduction process, but may also be influenced by a particle size effect or presence of other oxides [36]. While the Fe3O4 → Fe reduction step found in literature have similar activation energy and reduction temperature as the Fe2O3 → Fe3O4 step [21], XPS analyses of untreated powder [5, 8, 9] indicate the presence of only Fe2O3. The detailed XPS analyses of the Fe 2p region in these studies show only Fe3+ ions with no observed contribution from Fe2+ or Fe0 on the powder surfaces. The information depth is estimated to be approximately equal to the thickness of the oxide layer, and it is therefore concluded that the oxide layer is based on Fe2O3 [5, 8, 9]. Further analyzing the change in ionic state of iron with oxide layer thickness can become problematic, as XPS depth profiling with Ar+ ions have been shown to reduce iron oxides, thereby introducing artifacts [39]. Should any oxygen gradient exist within the thickness of the oxide layer, it is believed to be below the detection limit of the current XPS setup. As stated previously, the presence of FeO is not always recorded in studies where low heating rates were used, leading to no relevant data for the value of the activation energy for the Fe3O4 → FeO reduction step [21, 25]. Here it is shown that reasonable peak solution is achieved mainly at heating rates of 30 °C min−1 or higher, see Fig. 1.

It can be seen from Fig. 7 that the reduction temperature increases marginally with particle size, causing an increasing deviation from the reduction of hematite. Another interesting feature is that the compacted Fe75 powder shows a slight lowering of the activation energy, which could indicate that the physical deformation of the powder particles and surface oxides facilitates an easier reduction of the oxide layer. This kind of mechanical activation has been shown previously [25] where milling facilitated reduction of iron oxide.

The Kissinger analysis was complemented by an isoconversional kinetic method based on Eq. 6 as described previously. The results can be seen in Fig. 8 detailing the conversion versus temperature (Fig. 8a) and activation energy versus conversion (Fig. 8b). It can be seen that the reduction starts and completes at low temperatures for the pure oxide. The onset of reduction is at lower temperatures for the Fe75 compact than for the Fe75 powder but completes at higher temperatures. This clearly illustrates that the reduction of the surface iron oxide layer is smeared out in temperature for compacted powder. This signifies a lower activation energy of the reduction and highlights the difficulties in removing the reaction products from a compact with complex porosity. The activation energies in Fig. 8b show a decreasing trend with conversion, something that can be explained with a nucleation and growth model where the nucleation step is associated with a higher activation energy [25]. The influence of compaction on the activation energy can also be seen in Fig. 8b where there is a significant difference between the Fe75 powder and Fe75 compact in the range 0.3 ≤ α ≤ 0.5 as well as at α = 0.9. This is believed to be attributed to the effects of the mechanical compaction causing a morphological change of the powder particles and the surface oxide, in analogy to the study of milled oxide [25]. The lowering of the activation energies of reduction was explained by the amorphization of oxides as well as development of a large number of dislocations and associated strain fields [25].

Fig. 8
figure 8

a Isoconversional analysis of Fe75 powder, Fe75 compact and the Fe2O3 → Fe3O4 reduction step and b collection of activation energies for the low-temperature reduction processes

Full size image

High temperature

At the higher temperatures, the mass loss is likely connected to oxygen removal from the cores of the powder particles, cf. Figure 5, as well as reduction of the more stable particulate oxides. The acquired values of apparent activation energies are in excess of 400 kJ mol−1 which is significantly higher than reported elsewhere, for example in the case of atomic oxygen diffusion [40]. Consequently, it is clear that the oxygen removal during the heating stage up to the final sintering temperature involves multiple processes. It must also be noted that any internal oxygen should be found almost solely in internal inclusions due to the low solubility of oxygen in any phase of solid iron [41]. The inclusions can be expected to contain stable oxide-forming elements similar to the particulate oxides found on the surface as well as less stable iron oxides. This means that the removal of internal oxygen must be viewed both as a diffusion process and a reduction process, with the corresponding kinetics governing each step.

A Kissinger analysis, based on Eq. 4, of the high temperature reduction in the austenite region can be seen in Fig. 9 with the activation energies A Kissinger analysis, and fitting parameters available in Table 4. The slopes for the loose powder and compact samples are similar, indicating that the mechanism of reduction is unchanged. However, a shift to higher temperatures with around 50 °C can be observed which likely reflects the increased difficulties in removing the reaction products from the compacted sample. Additionally, the progressive sintering and densification of the compact makes it increasingly difficult to reduce the oxides inside the compact and for the reaction products to be

Fig. 9
figure 9

Kinetic analysis of high-temperature oxygen removal transported outwards

Full size image
Table 4 Calculated Ea for high-temperature reduction
Full size table

An isoconversional kinetic analysis was done according to Eq. 6 for the high-temperature oxygen removal, see Fig. 10a-c. The conversion is calculated starting from 600 °C, where mass loss is low, up to the final sintering temperature of 1350 °C. Since all samples did not show complete conversion in this range, the conversion was normalized to the mass losses of the samples heated at 10 °C min−1. It is expected that the observed conversion represents both removal of internal oxides and thermodynamically stable particulate oxides. For this reason, a single step reduction mechanism cannot be expected and an isoconversional method may reveal the kinetic details of the processes to a greater accuracy.

Fig. 10
figure 10

Isoconversional analysis of Fe75 powder and Fe75 compact samples at high temperatures

Full size image

The conversion versus temperature plot in Fig. 10a illustrates temperature shifts with heating rate for Fe75 powder and compacts. The rate of conversion is interrupted by the α → γ transformation, again signifying the phase dependence of the mass loss. The results are plotted according to Eq. 6 for fixed conversions for Fe75 powder in Fig. 10b and a clear change in slope can be seen at the onset of the transformation. The corresponding activation energies are plotted in Fig. 10c for Fe20, Fe45 and Fe75 powder as well as for Fe75 compacts. It can be seen that the isoconversional method produces an artificially low activation energy because the transformation occurs over a range of conversions 0.25 ≤ α ≤ 0.4 for heating rates 50 and 10 °C min−1, respectively. Only at conversions α ≥ 0.4 do the activation energies increase and stabilize, albeit at different values depending on powder size fraction where the finest powder shows the lowest activation energy for reduction. A similar behavior is seen for the Fe75 compact samples, where conversions α ≤ 0.3 are discarded because of poor fit due to low mass losses in the ferrite region. As a consequence, compact samples show a larger fraction of the total conversion in the austenite region and the activation energy curve in Fig. 10c is shifted to the left. The values increase from around 200 kJ mol−1 in the beginning of the austenite region and stabilize at around 400 kJ mol−1 for high levels of conversion.

Conclusions

The reduction of oxides and removal of oxygen was studied for the industrially important water-atomized iron powder using thermogravimetric and kinetic analyses. For reference, an iron oxide (Fe2O3) was analyzed which revealed similarities between the reduction of the oxide at low temperatures and the surface oxide layer covering the water-atomized iron powder particles. At high temperatures, the reduction processes of the iron powder become more complex and reflect stable oxide reduction as well as mass transport. The main findings can be summarized as follows:

  • The TGA of pure iron oxides revealed three reduction steps, Fe2O3 → Fe3O4, Fe3O4 → FeO, and FeO → Fe, with apparent activation energies of around 102, 102 and 15 kJ mol−1 for the three steps, respectively.

  • Reduction of the surface iron oxide layer takes place at around 400 °C. Activation energies for reduction in the range 85–102 kJ mol−1 were found using both kinetic methods, correlating well with hematite and magnetite reduction. The slight decrease in activation energy for compacted samples indicate an influence of the compaction step on the reduction of the surface iron oxide.

  • Mass losses at high temperatures are believed to be dominated by removal of internal oxides in the late ferrite region 600–900 °C and by stable oxide particulates in the range 950–1350 °C.

  • Kissinger analyses yielded activation energies in excess of 400 kJ mol−1, representing a compound value for all reduction processes, whereas the isoconversional kinetic results indicate a clear phase dependence on conversion, affecting the activation energy calculations.

  • The activation energy values of compacts show good correlation between the analysis methods: 409 ± 22 kJ mol−1 and ~ 400 kJ mol−1 in the range 0.3 ≤ α ≤ 0.8.

  • For powder fractions below 20, 45 and 75 µm, the activation energy values deviate: 418 ± 30, 454 ± 12, 428 ± 19 kJ mol−1 and 150–300 kJ mol−1 in the range 0.4 ≤ α ≤ 0.8, respectively. The deviation can be partly explained by the influence of the phase transformation on the conversion, which also complicates the selection of a conversion interval.

  • It is believed that the activation energy values reflect a complex combination of breakup of internal oxides, outwards diffusion of atomic oxygen and subsequent removal of oxygen from the surface as well as reduction of stable particle oxides present on the surface. The mass transport is expected to be further complicated by compaction.