Introduction

Investigations of fluid mechanics, and heat and mass transfer in microchannel flows have drawn much attention of researchers due to the wide use of such flows in microelectromechanical and microenergy systems. The trends for future development demonstrate a demand for an increase in the capacities of these systems with their simultaneous downsizing. Mathematical modeling of microchannel flows encounters with a necessity to deal with microscales in the range of micrometers. Liquid and gaseous microflows are different from each other in that the rate of proximity and intensity of movement of the molecules in them are noticeably different. The average distance between the molecules in gases is typically larger than the molecule diameter, whereas in liquids, it lies in the range of maximum one molecule diameter. Therefore, the mechanism driving mass, momentum, and energy transfer in liquids is different from that in gases [1].

To quantify the rarefaction effects in microflows, the so-called Knudsen number (Kn) is used. The dimensionless Knudsen number is equal to the ratio between the mean free path of gas molecules (L) and the distance between the channel walls.

The authors of the works [2, 3] modeled effects of different Knudsen numbers in microflows. For the Knudsen numbers \(1 0^{ - 3} \le {\text{Kn}} \le 1 0^{ - 1}\), effects of the slippage on the walls, fluid flow can be modeled using the Navier–Stokes equations closed by the slip boundary conditions [2]. For the Knudsen numbers \(10^{ - 1} \le {\text{Kn}} \le 10\), the continuum assumption did not hold, whereas the modeling could be performed using the Monte Carlo method or Burnett equations [3].

The slippage effects are controlled by the angle of contact between the surface and the liquid, shear stress, pressure, viscous heating, the amount and nature of the gas dissolved in the liquid, electrical characteristics, and surface roughness [4]

Fluid flow in a microchannel between parallel flat plates was modeled in the work [5]. Physically, fluid slippage is attributed to the presence of a region with reduced viscosity between the fluid and the solid surface. The authors [5] demonstrated that in the channels, whose height was more than 7.5 microns, air flow was modeled using the assumption of a continuous medium. For air flows in the channels, whose height was less than 7.5 microns, one must employ the methodology based on the molecular approach.

The authors of the work [6] performed experimental and numerical studies of heat transfer in five rectangular microchannel geometries with the hydraulic diameter of 222 μm, 267 μm, 323 μm, 330 μm, and 343 μm. The Reynolds numbers varied in the range of \(2.1 \le \text{Re} \le 48\), the heat flux density lied in the range from 10 W to 100 W, the inlet fluid temperature was 29 °C, whereas the mass flow rate varied from 0.0167 kg s−1 to 0.116 kg s−1. The authors found that for a hydraulic diameter of 222 μm, the heat transfer coefficient was higher as compared to the other channels involved in the study. The agreement between the numerical modeling and experimental measurements in the work [6] was good (discrepancies of up to 5%).

An analytical solution for heat transfer and entropy generation in a microchannel flow was obtained in [7]. Three different laws for slippage on the walls were used, namely the non-linear Navier slip law, the Hatzikiriakos slip law, and the asymptotic slip law. As a result, it was demonstrated that the Nusselt number obtained by the Hatzikiriakos slip law is higher, and the average entropy generation rate is lower than that predicted by the asymptotic slip law. This difference increases together with the slip coefficient.

Peculiarities of heat transfer in flow in a wavy microchannel were simulated numerically by the finite-volume method in the work [8]. In particular, effects of slippage (Knudsen number) on the friction coefficient and on the Nusselt number were elucidated. At large Knudsen numbers, significant effects of viscous dissipation were observed. It was also pointed out that viscous dissipation causes a singular point in the Nusselt number curve.

Three-dimensional numerical modeling of the effects of the microchannel geometry on the temperature profiles, heat transfer coefficient, pressure drop, friction coefficient, and wall shear stress for the range of Reynolds numbers from 100 to 1000 was performed in [9]. The authors studied radiators, where microchannels with rectangular, trapezoidal, and triangular cross sections were used for heat removal. Each particular cross section had three different geometric dimensions. The highest coefficients of skin friction and heat transfer were obtained in microchannels with the smallest hydraulic diameter.

A numerical study of heat transfer in a microchannel of a novel design was performed in [10]. A cavity was located at the entrance to a rectangular microchannel. It was shown during the study that this cavity promotes the mixing processes in the flow, which also enhances heat transfer in the entire system.

An analytical study of forced convection in a mini/microchannel filled with microfoam was performed subject to a uniform but asymmetric wall heat flux in [11]. In particular, velocity slip, thermal slip, effects of local thermal non-equilibrium, and asymmetric heat flux were considered. As one of the results, the authors obtained relations for the velocity and temperature profiles in the solid and the liquid.

Nanofluid flow in a microchannel with a porous matrix was modeled in [12]. During the simulation, the parameters of the porous insert were varied. In addition, combined convective–radiative boundary conditions were considered. The solution of this problem made it possible to optimize the values of the slip length of the flow and the concentration of nanoparticles to minimize global entropy production, as well as an increase or a decrease in heat transfer depending on the permeability of the porous medium.

Rarefied gas flows in microelectromechanical systems (MEMS) were numerically simulated in [13] using the hybrid finite-element/finite-volume (FE/FV) method. Circular and rectangular microchannels were considered. Extended inlet boundary conditions were used for rectangular microchannels, whereas inlet boundary conditions were used for circular microchannels. It was found that the friction coefficients decreased with the increasing Knudsen number for both types of the microchannels, whereas in a rectangular microchannel, the decreasing trend was more pronounced. It was also shown that for very large Prandtl numbers and high heat transfer rates, velocity slippage prevails over the temperature jump.

The second-order velocity slip conditions considering the temperature jump for the Mach numbers \(1 \le M \le 5\) were applied to Couette stationary microflow of the Maxwell monatomic gas in the work [14]. Here, the Knudsen numbers were in the range of \({\text{Kn}} \le 1\). It was revealed that the results using Burnett equations with the second-order slip boundary conditions show much better agreement with direct simulation Monte Carlo (DSMC) data at high Kn values.

The given above analysis of the research activities on fluid flow and heat transfer in microchannels performed over the past few years indicates that studies incorporated different geometries of microchannels, namely circular, flat, rectangular, and triangular, and straight and curved, subject to different boundary and initial conditions. In the works [15,16,17,18], the lattice Boltzmann method (LBM) was successfully applied to simulate stationary and accelerated microflows in straight and curved microchannels. The simulations enabled quantifying the effects of the Rayleigh, Prandtl, and Nusselt numbers, as well as slippage on the flow development in circular, flat, and curved microchannels. A comparative analysis of the results of analytical and numerical (LBM) modeling of microflows demonstrated their good agreement (discrepancy of less than 1%) under the same boundary conditions.

An example of a numerical study of two-phase flow in a microchannel with a variable cross section using LBM is described in [19]. Also, LBM technology was successfully applied in [20] to study heat transfer characteristics of a nanofluid flow with various concentrations in a microchannel with hydrophilic and superhydrophobic walls under the influence of a transverse magnetic field.

As a rule, in analytical studies of heat transfer in microchannels, first-order boundary conditions were used. However, the use of the second-order boundary conditions [21] enables expanding the boundaries of the continuous flow regime and increasing the range of the Knudsen numbers involved in modeling.

The second-order slip boundary conditions for the velocity \(u\) and the temperature \(T\) were proposed by different researchers. In general, these conditions can be presented as [21]

$$u_{\text{w}} = A_{1} {\text{Kn}}\left( {\frac{\partial u}{\partial n}} \right)_{\text{w}} + A_{2} {\text{Kn}}^{ 2} \left( {\frac{{\partial^{2} u}}{{\partial n^{2} }}} \right)_{\text{w}} ,$$
(1)
$$T - T_{\text{w}} = A_{1} \frac{\text{Kn}}{\Pr }\left( {\frac{\partial T}{\partial n}} \right)_{\text{w}} + A_{2} \left( {\frac{\text{Kn}}{\Pr }} \right)^{2} \left( {\frac{{\partial^{2} T}}{{\partial n^{2} }}} \right)_{\text{w}} ,$$
(2)

where n is the dimensionless coordinate normal to the solid surface. The coefficient A1 is close to unity, whereas the coefficient A2 can take either positive or negative values. The positive value is A2 = 0.5, and the negative value is A2 = − 1.6875. Hence, one of the objectives of this work was to study how these boundary conditions with the positive and negative values of the coefficient A2 affect the flow pattern in the microconfusor.

Studies of fluid flow and heat transfer in microconfusors have not received enough attention yet. However, heat transfer in microconfusors represents an interesting and important phenomenon important in understanding the dynamics of flows of different nature in modern electronic equipment. In connection with the aforementioned, the main objective of this work is an analytical study of fluid flow and heat transfer in a microconfusor with the second-order boundary conditions. This analytical solution, its analysis, and interpretation represent novelty of the present work, because to the knowledge of the authors, such solution has never been published in the literature yet.

Fluid flow

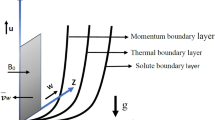
Let us consider confusor flow in a boundary layer (Fig. 1), whereas potential flow outside of the boundary layer is subject to a hyperbolic law [22]

$$U_{\infty }\left( x \right) = - \frac{{u_{1} }}{x},$$
(3)

where \(U_{\infty}\) is the velocity of the main flow and u1 is a constant. In accordance with the work [18], self-similar variables for this case are

Fig. 1
figure 1

Schematic of the flow geometry

Full size image
$$\eta = \frac{y}{x}\sqrt {\frac{{u_{1} }}{\nu }} = \frac{y}{x}\sqrt {\text{Re} } ,$$
(4)
$$u\left( {x,y} \right) = U_{\infty } f^{\prime}\left( \eta \right) = - \frac{{u_{1} }}{x}f^{\prime}\left( \eta \right).$$
(5)

The problem is considered in the parabolic approximation. This means that the complete elliptic (with respect to the coordinates) Navier–Stokes equations are replaced by the Prandtl equation of the boundary layer, as soon as one neglects the second derivatives with respect to the marching variable x.

Substituting Eqs. (4) and (5) into the equations of the boundary layer with the pressure gradient

$$\frac{\partial u}{\partial x} + \frac{{\partial {\text{v}}}}{\partial y} = 0,$$
(6)
$$u\frac{\partial u}{\partial x} + {\text{v}}\frac{\partial u}{\partial y} = U_{\infty } \frac{{dU_{\infty } }}{dx} + \nu \frac{{\partial^{2} u}}{{\partial y^{2} }}$$
(7)

yields [22]

$$f^{\prime\prime\prime} - f^{\prime 2} + 1 = 0.$$
(8)

This equation is to be solved under the following boundary conditions (A1 = 1, A2 = s)

$$f^{\prime} = {\text{Kn}}\,f^{\prime\prime} + s{\text{Kn}}^{ 2} \,f^{\prime\prime\prime}\quad {\text{at}}\,\,\eta { = 0,}$$
(9)
$$f^{\prime} = 1,\quad f^{\prime\prime} = 0\quad {\text{at}}\,\,\eta \to \infty ,$$
(10)

where Eq. (9) follows from condition (1).

Here

$${\text{Kn}} = \frac{L}{x}\sqrt {\text{Re} }$$
(11)

is the modified Knudsen number.

To solve Eq. (8), let us follow the approach [22] and multiply this equation with \(f^{\prime\prime}\) and afterward integrate, which yields as a result

$$\frac{1}{2}f^{\prime \prime 2} - \frac{1}{3}f^{\prime 2} + f^{\prime} = c_{1} .$$
(12)

Here c1 is the integration constant. With account for the boundary condition (10), one can transform Eq. (12) to

$$f^{\prime\prime} = \sqrt {\frac{2}{3}} \sqrt {2 + f^{\prime 3} - 3f^{\prime}} .$$
(13)

One can further rewrite this equation as

$$\eta = \sqrt {\frac{3}{2}} \int {\frac{{{\text{d}}f^{\prime}}}{{\sqrt {\left( {2 + f^{\prime}} \right)\left( {1 - f^{\prime}} \right)^{2} } }}} .$$
(14)

To perform the integration, let us make the following substitution

$$z^{2} = 2 + f^{\prime},\quad {\text{d}}f^{\prime} = 2z{\text{d}}z.$$
(15)

Thus, one can obtain from Eq. (14)

$$\eta + c_{2} = \sqrt {\frac{3}{2}} \int {\frac{{2z{\text{d}}z}}{{z\left( {1 - \left( {z^{2} - 2} \right)} \right)}}} = \sqrt {\frac{3}{2}} \int {\frac{{2{\text{d}}z}}{{\left( {3 - z^{2} } \right)}}} = \sqrt 2 {\text{arctanh}}\left( {\frac{\text{z}}{\sqrt 3}} \right) = \sqrt 2 {\text{arctanh}}\left( {\sqrt {\frac{{f^{\prime} + 2}}{ 3}} } \right).$$
(16)

The inverse transformation yields an equation for the velocity profile

$$\frac{u}{U} = 3{ \tanh }\left( {\frac{{\eta + c_{2} }}{\sqrt 2 }} \right) - 2.$$
(17)

Using boundary condition (9), one can obtain the following transcendental equation for the integration constant c2

$$3 {\text{sech}}^{ 2} \left( {\frac{{c_{2} }}{\sqrt 2}} \right)\left( {1 + \sqrt 2{\text{Kn}}\,{ \tanh }\left( {\frac{{c_{2} }}{\sqrt 2}} \right) + s{\text{Kn}}^{ 2} \,\left( {3{\text{sech}}^{ 2} \left( {\frac{{c_{2} }}{\sqrt 2}} \right) - 2} \right)} \right) = 1.$$
(18)

For no-slip flow, one can obtain an expression for the constant c2 from Eq. (18)

$$c_{2} = \sqrt 2 {\text{arctanh}}\left( {\sqrt {\frac{ 2}{ 3}} } \right),$$
(19)

which coincides with the respective solution obtained in [22].

Figure 2 depicts velocity profiles by Eq. (17) for different values of the Knudsen number for s = 0. As expected, an increase in the Knudsen number causes an increase in the velocity jump at the wall.

Fig. 2
figure 2

Velocity profiles as a function of the coordinate \(\eta\) at different values of the Knudsen number Kn

Full size image

At the same time, variation of the parameter s also affects the velocity jump on the wall (Fig. 3). For positive values of the parameter s, the velocity jump decreases, whereas for negative values of s, the velocity jump increases.

Fig. 3
figure 3

Velocity profiles as a function of the coordinate \(\eta\) at different values of the parameter s

Full size image

One can further determine the surface friction with the help of Eq. (17)

$$\tau_{\text{w}} = - \rho \nu \left( {\frac{\partial u}{\partial y}} \right)_{y = 0} = 3\sqrt 2 \frac{{u_{1}^{3/2} \rho \sqrt \nu }}{x}{ \tanh }\left( {\frac{{c_{2} }}{\sqrt 2 }} \right){\text{sech}}^{ 2} \left( {\frac{{c_{2} }}{\sqrt 2}} \right).$$
(20)

This yields a relation for the friction coefficient

$$c_{\text{f}} = \frac{{2\tau_{\text{w}} }}{{\rho U^{2} }} = - \rho \nu \left( {\frac{\partial u}{\partial y}} \right)_{y = 0} = \frac{6\sqrt 2 }{{\sqrt {\text{Re} } }}{ \tanh }\left( {\frac{{c_{2} }}{\sqrt 2 }} \right){\text{sech}}^{ 2} \left( {\frac{{c_{2} }}{\sqrt 2}} \right).$$
(21)

Table 1 elucidates the influence of the boundary conditions of the first and second order and the Knudsen number on the friction coefficient. With an increase in the Knudsen number, the friction coefficient decreases for all values of the parameter s, whereas for the negative value of s = − 1.6875, the trend of the decrease in the friction coefficient is more pronounced.

Table 1 Effects of the boundary conditions of the first and second order and the Knudsen number on the friction coefficient
Full size table

Heat transfer

At the first stage, a solution of the energy equation was obtained in the parabolic approximation, like it was done above during the solution of the velocity boundary layer equation. That is, the second derivative of the temperature with respect to the marching coordinate x was not considered.

The energy equation has the following form

$$c_{\text{p}} \rho \left( {u\frac{\partial T}{\partial x} + {\text{v}}\frac{\partial T}{\partial y}} \right) = k\frac{{\partial^{2} T}}{{\partial y^{2} }}.$$
(22)

For this case, the dimensionless temperature profile can be expressed as

$$\frac{{T - T_{\infty } }}{{T_{\text{w}} - T_{\infty } }} = \varTheta \left( \eta \right).$$
(23)

Substitution of Eqs. (4), (5), and (23) into Eq. (22) yields

$$\varTheta^{\prime\prime} = 0.$$
(24)

Equation (24) enables concluding that in accelerating flow in a confusor, where the potential flow follows the law (3), heat is transported by the heat conduction mechanism.

This equation is to be solved under the following boundary conditions

$$\varTheta = 1 + \frac{\text{Kn}}{\Pr }\,\varTheta^{\prime} + s\left( {\frac{\text{Kn}}{\Pr }} \right)^{2} \,\varTheta^{\prime\prime}\quad {\text{at}}\,\,\eta { = 0,}$$
(25)
$$\,\varTheta = 0,\quad {\text{at}}\quad \eta \to \infty .$$
(26)

As one can see from here, Eq. (24) has a solution in the form of a linear function. This means that it is not possible to satisfy boundary conditions (25) and (26). However, the self-similar variable (4) is a property of scaling symmetry of full Navier–Stokes and Fourier–Kirchhoff equations [23]. Therefore, the self-similar variable (4) is also valid for the elliptic energy equation

$$c_{p} \rho \left( {u\frac{\partial T}{\partial x} + {\text{v}}\frac{\partial T}{\partial y}} \right) = k\left( {\frac{{\partial^{2} T}}{{\partial y^{2} }} + \frac{{\partial^{2} T}}{{\partial x^{2} }}} \right).$$
(27)

Then, applying variable (4) to Eq. (27), one can obtain

$$\varTheta^{\prime\prime} + \frac{2\eta }{{\text{Re} + \eta^{2} }}\varTheta^{\prime} = 0.$$
(28)

The first integration brings

$$\ln \varTheta^{\prime} = - \ln \left( {\text{Re} + \eta^{2} } \right) + \ln C_{1}$$
(29)

or

$$\varTheta^{\prime} = \frac{{C_{1} }}{{\text{Re} + \eta^{2} }}.$$
(30)

The second integration yields

$$\varTheta = \frac{{C_{1} }}{{\sqrt {\text{Re} } }}\arctan \left( {\frac{\eta }{{\sqrt {\text{Re} } }}} \right) + C_{2} .$$
(31)

With the help of the boundary conditions (25) and (26), one can find the integration constants. Then, the final form of the temperature profile is

$$\varTheta = \frac{{1 - \frac{2}{\pi }\arctan \left( {\frac{\eta }{{\sqrt {\text{Re} } }}} \right)}}{{1 + \frac{2}{{\pi \sqrt {\text{Re} } }}\frac{\text{Kn}}{\Pr }}}.$$
(32)

The same result is also valid for the case s = 0, because \(\varTheta^{\prime\prime}\left( 0 \right) = 0\). Thus, the use of the second-order slip boundary conditions for accelerating flow subject to the potential flow boundary condition (3) does not affect heat transfer.

Using the Fourier law, one can derive an equation for the heat transfer coefficient

$$h = - k\left( {\frac{\partial \varTheta }{\partial y}} \right)_{\text y = 0} = \frac{2}{\pi }\frac{k}{x}\frac{1}{{1 + \frac{2}{{\pi \sqrt {\text{Re} } }}\frac{\text{Kn}}{\Pr }}}.$$
(33)

This equation can be rewritten in the dimensionless form as

$${\text{Nu}} = \frac{2}{\pi }\left( {1 + \frac{2}{{\pi \sqrt {\text{Re} } }}\frac{\text{Kn}}{\Pr }} \right)^{ - 1} = \frac{2}{\pi }\left( {1 + \frac{2}{\pi }\frac{\text{Kn*}}{\Pr }} \right)^{ - 1} ,$$
(34)

where

$${\text{Kn*}} = \frac{L}{x}.$$
(35)

One can also rewrite Eq. (34) as follows

$${\text{Nu}} = {\text{Nu}}_{ 0} \left( {1 + \frac{2}{{\pi \sqrt {\text{Re} } }}\frac{\text{Kn}}{\Pr }} \right)^{ - 1} = {\text{Nu}}_{ 0} \left( {1 + \frac{2}{\pi }\frac{\text{Kn*}}{\Pr }} \right)^{ - 1} ,$$
(36)

where \({\text{Nu}}_{ 0}\) is the Nusselt number for no-slip flow.

Equation (36) shows that for accelerating flow subject to the potential flow boundary condition (3), heat transfer rate does not depend on the Reynolds number. Moreover, for no-slip flow, heat transfer is also independent from the Prandtl number. This stands in the analogy to the circular laminar flow studied in the work [18].

Figure 4 demonstrates the effect of the Knudsen number and Prandtl number on the normalized Nusselt number.

Fig. 4
figure 4

Normalized Nusselt number depending on the Knudsen number at different values of the Prandtl number

Full size image

Figure 4 demonstrates that with an increase in the Knudsen number, the heat transfer rate decreases. This can be attributed to the weakening of the interaction of fluid flow with the channel wall due to slippage effects. In this case, the effect of slippage on heat transfer weakens with the increasing Prandtl number, which can be explained by a decrease in the temperature jump on the wall at large Prandtl numbers. The same trend was also observed at mixed convection in pure fluids in microchannels [17, 18], as well as in porous microchannels [24].

Conclusions

The paper presents the results of studies of fluid flow and heat transfer in a microconfusor with slip boundary conditions of the second order. The studies were performed based on symmetry transformations, which enabled deriving a system of equations in a self-similar form. Based on it, novel analytical solutions were obtained for the velocity and temperature profiles as well as for the friction coefficient and the Nusselt number. These solutions demonstrated a trend of the decreasing Nusselt number with an increasing Knudsen number, which is attributed to weakening of the interaction between the fluid flow and the surface. The novel analytical solutions indicate also that the account for second-order terms in the boundary conditions does not affect the heat transfer characteristics (the temperature profile and Nusselt number). At the same time, the second-order effects manifested themselves in the variation of the fluid flow characteristics (the velocity profile and the friction coefficient). It was also shown that in an accelerating flow in a confusor subject to the potential flow (3), heat is transported only by the heat conduction mechanism. Computations indicated also that with an increase in the Prandtl number, flow slippage effects on heat transfer weaken. This can be explained by a decrease in the temperature jump on the wall for large Prandtl numbers.