Introduction

Isothermal titration calorimetry (ITC) measurements are usually carried out in buffer solutions. Such an approach enables to eliminate a pH mismatch between a titrant (a syringe solution) and a titrand (a cell solution) and thus prevents a generation of an additional heat on account of a neutralization reaction (H3O+ + OH− = 2H2O) that is not connected with molecular interactions [1–4]. Furthermore, the proper maintenance of the pH is of a particular importance when studying systems of biological interest, for instance proteins (the change of pH modifies electrostatic interactions between charge functional groups of the amino acids and consequently the three-dimensional structure of the protein) [5] or processes involving enzymatic reactions that can only take place in a narrow range of pH [6]. It is also worth noticing that the choice of an appropriate buffer is of great importance as it has an impact on binding constants as well as the enthalpy of complex formation, especially for those complexes containing metal ions [5, 7–9]. If the buffer with an affinity for a metal ion is used, it affects the metal–ligand binding constant. Therefore, to obtain buffer-independent parameters (K and ΔG) the metal–buffer stability constants need to be available (or determined) and subsequently taken into account during the data analysis [10, 11]. Moreover, if a process of complex formation is accompanied with proton transfers, the equivalent number of protons is taken up or released by the buffer. It generates an additional heat that is proportional to the enthalpy of buffer ionization [12, 13]. In this case, the enthalpy measured during the ITC experiment reflects both the buffer ionization and complex formation [14].

In this article, we present the influence of the type of a buffer (the ionization enthalpy of the buffer) on the thermodynamic parameters for the binding of Cu2+ to bicine [N,N-bis(2-hydroxyethyl)glycinate] that is used in these studies as a ligand (Fig. 1). In experiments 2-(N-morpholino)ethanesulfonic acid (Mes) and dimethylarsenic acid (Caco) were used as buffer substances that differ in their ionization enthalpies (BH± = B− + H+), +3.54 and −0.72 kcal mol−1 for Mes and Caco, respectively [15].

Fig. 1
figure 1

Proposed binding mode of copper(II) ion to N,N-bis(2-hydroxyethyl)glycinate (L)

Full size image

It is also worth emphasizing that bicine is also a useful buffer standard in the range of physiological interest [16, 17] with the ionization enthalpy equal to −6.47 kcal mol−1 [15]. It has also been employed in colour photographic processes, in analytical methods, as a stabilizing agent. Bicine acts as a strong binding ligand forming a fairly stable complex with most metal ions [18]. Based on its complexation properties, the use of bicine buffer is not advisable in environmental and biological studies involving metals, unless thermodynamic parameters of the metal–bicine interaction are taken into consideration.

Experimental

Materials

All reagents, namely 2-(N-morpholino)ethanesulfonic acid hydrate (≥ 99 %) (Mes), dimethylarsenic acid (≥99 %) (Caco), Cu(NO3)2·2.5H2O (≥99.99 %) and N,N-bis(2-hydroxyethyl)glycine (≥99 %) [H(bicine)±] were purchased from Sigma-Aldrich Chemical Corp.

Isothermal titration calorimetry (ITC)

All ITC experiments were performed at 298.15 K using an AutoITC isothermal titration calorimeter (MicroCal Inc., Malvern, Northampton, USA) with a 1.4491-mL sample and the reference cells. The reference cell contained distilled water. The data, specifically the heat normalized per mole of injectant, were processed with Origin 7 from MicroCal. An initial 2 μL injection was discarded from each data set in order to remove the effect of titrant diffusion across the syringe tip during the equilibration process. All reagents were dissolved directly in the 100 mM buffer solution of Mes or Caco. The pH of the buffer solution was adjusted to 6.0 with 0.1 M HNO3. The experiment consisted of injecting 10.02 μL (29 injections, 2 μL for the first injection only) of ca 1.2 mM buffered solution of N,N-bis(2-hydroxyethyl)glycine, H(bicine), into the reaction cell which initially contained 0.07 mM buffered solution of Cu(NO3)2. A background titration, consisting of an identical titrant solution but with the buffer solution in the reaction cell only, was removed from each experimental titration to account for the heat of dilution. All the solutions were degassed prior to the titration. The titrant was injected at 5-min intervals to ensure that the titration peak returned to the baseline before the next injection. Each injection lasted 20 s. For homogeneous mixing in the cell, the stirrer speed was kept constant at 300 rpm. A calibration of the AutoITC calorimeter was carried out electrically by using electrically generated heat pulses. The CaCl2–EDTA titration was performed to check the apparatus, and the results (n—stoichiometry, K, ΔH) were compared with those obtained for the same samples (test kit) at MicroCal.

Potentiometric measurements

Potentiometric titrations were performed in the 30 mL thermostated (298.15 ± 0.10 K) cell using the Cerko Lab System microtitration unit fitted with the 0.5-mL Hamilton’s syringe, pH combined electrode (Schott–BlueLine 16 pH type) and a self-made measuring cell equipped with a magnetic stirrer. The temperature was controlled using the Lauda E100 circulation thermostat. The electrode was calibrated according to IUPAC recommendations [19]. The syringe was calibrated by a weight method. All the solutions were prepared immediately before measurements. The compositions of the titrand solutions used in the experiments were as follows: (1) H(bicine) (2.05 mM) and HNO3 (2.48 mM) and (2) Cu2+ (1.50 mM), H(bicine)± (2.05 mM) and HNO3 (2.48 mM). The solutions were potentiometrically titrated with a standardized KOH solution (25.02 mM) with the pH ranging from 2.5 to 12.0. The stability constants of the complexes were determined using the CVEQUID program [20] based on a minimization of the differences between the theoretical model and the experimental data, according to the Gauss–Newton–Marquart method for nonlinear equations (see ref [21] for more details).

Results and discussion

Bicine [N,N-bis(2-hydroxyethyl)glycinate)] acts as a tetradentate ligand and forms 1:1 metal–ligand complexes. In a solid state, one carboxylate oxygen atom, two hydroxyl oxygen atoms and one nitrogen atom participate in the copper(II) binding. In solutions an aqua ligand coordinates to the metal centre, hence completing the coordination sphere (Fig. 1).

The stability of the resulting complex (CuL, where L denotes bicine) in a solution is reflected by a value of stability constant. As far as the ITC technique is concerned, this parameter is quantified by Eq (1):

$$ K_{\text{ML}} = K_{\text{ITC}} \left( {1 + \frac{{[H^{ + } ]}}{{K_{{{\text{a}}2}} }} + \frac{{[H^{ + } ]^{2} }}{{K_{{{\text{a}}2}} \cdot K_{{{\text{a}}1}} }}} \right)(1 + K_{\text{MB}} [B]) $$
(1)

where K ML is the pH-independent and buffer-independent metal–ligand binding constant, K ITC is the Cu–L conditional stability constant obtained directly from the ITC experiment, K a is the proton dissociation constant of a ligand (here K a1 and K a2 of bicine), K MB is the stability constant for the metal–buffer complex, and [B] is the concentration of the buffer solution.

To eliminate the impact of buffer components on the thermodynamic parameters, the Mes and Caco buffers have been chosen. These buffers do not reveal an affinity towards the copper(II) ions [22–24]; therefore, they do not affect the copper(II)–ligand binding constant. For this reason, K ITC is not conditioned by the buffer competition with the ligand (bicine) for the metal (Cu2+) but it depends only on the proton competition with the metal for the ligand (Eq. 2):

$$ K_{\text{ML}} = K_{\text{ITC}} \left( {1 + \frac{{[H^{ + } ]}}{{K_{{{\text{a}}2}} }} + \frac{{[H^{ + } ]^{2} }}{{K_{{{\text{a}}2}} \cdot K_{{{\text{a}}1}} }}} \right) $$
(2)

The individual equilibria that contribute to the overall equilibrium also affect the enthalpy measured directly in the ITC experiments. In Table 1 the individual equilibria taking place in the complex formation are collected. Equilibria are written in the direction that the reaction occurs.

Table 1 Individual reactions that contribute to the overall equilibrium for the formation of the copper(II)–bicine complex in the Mes and Caco buffer solution (B)
Full size table

Taking into consideration the fact that the heat absorbed or released during ITC experiments is equal to the sum of all the energetic effects corresponding to the particular equilibria taking place in the complexation process (Table 1), the pH- and buffer-independent enthalpy of the complex formation can be calculated from the equation based on the Hess’s law (Eq. 3) [25–27]:

$$ \Delta_{\text{ITC}} {H} = n_{{{H} + }} \Delta_{\text{BH}} {H}^\circ + \, (\Delta_{\text{Cu(bicine)}} {H}^\circ {-}n_{{{H} + }} \Delta_{{{H}({\text{bicine}})}} {H}^\circ ) $$
(3)

where n H+ is the number of protons transferred during the complex formation.

The number of protons transferred was determined experimentally from potentiometric titration (PT) measurements according to the procedure described in the literature [9, 28]. Thus, the solutions containing H(bicine)± and HNO3 in the molar ratio of 1:1.21 (solution 1) and another containing Cu(II), H(bicine) and HNO3 in the molar ratio of 1:1.37:1.65 (solution 2) were titrated with a standardized NaOH solution. A relationship between the pH and the NaOH/H+ [HNO3 + H(bicine)±] molar ratio is presented in Fig. 2. The difference between the number of moles of NaOH, expended for neutralization of solutions 1 and 2 up to a pH of 6, corresponds to the number of protons (n H+) lost by H(bicine)± upon a complexation of the copper(II) ions. The number of protons determined in this way is 0.39, and this value was used for calculating ΔCu(bicine) H o based on Eq. 3.

Fig. 2
figure 2

Plot of the pH versus the NaOH/H+ [HNO3 + H(bicine)] molar ratio during the potentiometric titration of the H(bicine)–HNO3 (square) and Cu(II)–H(bicine)–HNO3 (circle) solutions with the NaOH solution

Full size image

Furthermore, the following equilibria were used to calculate the copper(II)–bicine stability constant from PT measurements:

  1. 1.

    \( {\text{HL}}^{ \pm } = {\text{H}}^{ + } + {\text{L}}^{ - } \quad pK{\text{a}}_{2} \)

  2. 2.

    \( {\text{Cu}}^{2 + } + {\text{L}}^{ - } = {\text{CuL}}^{ + } \quad \log K \)

  3. 3.

    \( {\text{CuL}}^{ + } + {\text{H}}_{2} {\text{O}} = {\text{CuL}}\left( {\text{OH}} \right) + {\text{H}}^{ + } \quad pK_{{{\text{CuL}}({\text{OH}})}} \)

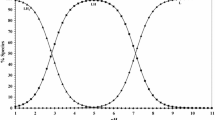
The above equilibrium model has given the best fitting of the calculated data to the experimental ones. The parameters obtained based on the assumed equilibrium model are as follows (the standard deviation in parentheses): pKa2 = 9.45 (±0.06), logK = 9.00 (±0.09) and pK CuL(OH) = 6.52 (±0.05). Species distributions as a function of pH are shown in Fig. 3. The complexation of the Cu(II) ions starts with the formation of the binary complex [Cu(bicine)]+. The complex predominates in the solution in the wide pH range (Fig. 3). Above pH 11 the stability of the complex is not favoured over the resulting hydroxo complex, CuL(OH).

Fig. 3
figure 3

Concentration distribution curves of the complexes as a function of pH calculated based on the stability constants obtained from PT measurements

Full size image

Representative binding isotherms for Cu2+–bicine interactions in the buffers (Mes, Caco) are shown in Fig. 4, whereas conditional parameters (marked by the subscript ITC) as well as pH-independent and buffer-independent parameters of the interactions are summarized in Table 2.

Fig. 4
figure 4

Calorimetric titration isotherms of the binding interaction between Cu2+ and bicine in 100 mM Mes and Caco buffers of pH 6, at 298.15 K

Full size image
Table 2 Thermodynamic parameters of copper(II) binding to bicine in buffer solutions (100 mM Mes and Caco) of pH 6, at 298.15 K
Full size table

Alternatively, the n H+ value can be calculated from the slope of the relationship described by Eq. 3 (y = ax + b). The n H+ value determined in this way (n H+ = 0.39) is in good agreement with that obtained directly from PT measurements. The numerical value of the binding enthalpy calculated based on Eq. 3 is negative (Table 2). This indicates that the endothermic effects connected with the dehydration of the [Cu(H2O)5]2+ ion are overcompensated by the exothermic effect due to the formation of new Cu2+–bicine bonds (Fig. 1).

Conclusions

Isothermal titration calorimetry (ITC) experiments supported by potentiometric titration data have successfully been applied to determine thermodynamic parameters for the complexation of the copper(II) ions with bicine. The study confirmed the fact that both Mes and Caco buffers do not bind copper(II). Thus, these buffers would be good choices for metal speciation studies within their operational pH range. It has also been presented how to include the enthalpy of proton dissociation from the ligand and the enthalpy of buffer ionization during calorimetric data analysis. These processes generate additional heat that is not connected with intermolecular interactions and should be taken into account while interpreting calorimetric data.

When a reaction involves the release (or uptake) of protons, the equation based on the Hess’s law can be applied to calculate the conditional-independent binding enthalpy ∆H. Such an approach can be used provided that the number of protons (n H+) transferred during the interaction is known. We have proved that for low molecular mass ligands this value (n H+) can be easily determined using PT measurements.