Introduction

Most of the biological and biochemical processes are proton-donor or proton-acceptor type of reaction. For this reason, biochemical experiments are usually carried out in a buffer solution [1, 2]. The same mechanism takes place during calorimetric measurements when the binding enthalpy (under isobaric conditions) is directly measured. Calorimetric methods such as the isothermal titration calorimetry (ITC) are now widely used to quantify stoichiometry, binding constants, and thermodynamics on the field of life science investigations (http://www.microcal.com/reference-center/reference-list.asp).

When a reaction involves the release (or uptake) of protons, additional heat is usually generated. This heat (thermal effect) is not connected with intermolecular interactions and should be taken into account while interpreting calorimetric data. The situation is slightly more complicated when metal ions are involved in biological processes [3–7]. In such cases, to determine condition-independent thermodynamic values (K, ΔH), the effect of buffer competition with the ligand for the metal as well as proton competition with the metal for the ligand must be taken into consideration.

2-(N-Morpholino)ethanesulfonic acid (Mes), dimethylarsenic acid (Caco), and piperazine-N,N′-bis(2-ethanesulfonic acid) (Pipes) (Fig. 1) are the buffer substances widely used in biological experiments as well as in calorimetric studies [8]. However, to the best of our knowledge, there are few reports on the interactions of such buffers with metal ions. This was, among others, the main reason that prompted us to embark on these studies.

Fig. 1
figure 1

Buffer substances used in this study

Full size image

In this article, thermodynamic parameters for complexation reactions of the Co2+ and Ni2+ ions with Mes, Pipes, and Caco buffer are presented. Metal–buffer (Mes, Pipes, Caco) formation constants were determined by potentiometric titration (PT). Then, the enthalpies of the metal–buffer interaction were determined by displacement titration using the ITC technique [9]. Nitrilotriacetic acid (H3NTA) was used in the displacement experiments as a strong-binding, competitive ligand. Finally, the effect of pH and the type of buffer on the enthalpy reaction and the stability constants of the resulting complexes were discussed.

Experimental

Materials

All reagents, namely 2-(N-morpholino)ethanesulfonic acid hydrate (≥99 %) (Mes), dimethylarsenic acid (≥99 %) (Caco), piperazine-N,N′-bis(2-ethanesulfonic acid) (≥99 %) (Pipes), Co(NO3)2·6H2O (≥99 %), Ni(NO3)2·6H2O (≥99.999 %), H3NTA (≥99 %), HClO4, and NaClO4 were purchased from Sigma-Aldrich Chemical Corp. and used as received. Double distilled water with conductivity not exceeding 0.18 μS cm−1 was used for preparation of aqueous solutions of titrant and titrand.

Isothermal titration calorimetry

All ITC experiments were performed at 298.15 K using an AutoITC isothermal titration calorimeter (MicroCal Inc. GE Healthcare, Northampton, USA) with a 1.4491 mL sample and the reference cells. The reference cell contained distilled water. The data, specifically the heat normalized per mole of injectant, were processed with Origin 7 from MicroCal. An initial 2 μL injection was discarded from each data set to remove the effect of titrant diffusion across the syringe tip during the equilibration process. All reagents were dissolved directly into 100 mM buffer solution of Mes, Caco, or Pipes. The pH of the buffer solution was adjusted to 6 with 0.1 M HClO4. The experiment consisted of injecting 10.02 μL (29 injections, 2 μL for the first injection only) of ca 5 mM buffered solution of H3NTA into the reaction cell which initially contained ca 0.25–0.5 mM buffered solution of suitable salt. A background titration, consisting of an identical titrant solution but with the buffer solution in the reaction cell only, was removed from each experimental titration to account for the heat of dilution. All the solutions were degassed prior to titration. The titrant was injected at 5-min interval to ensure that the titration peak returned to the baseline before the next injection. Each injection lasted 20 s. For homogeneous mixing in the cell, the stirrer speed was kept constant at 300 rpm. Calibration of the AutoITC calorimeter was carried out electrically by using electrically generated heat pulses. The CaCl2–EDTA titration was performed to check the apparatus and the results (n—stoichiometry, K, ΔH) were compared with those obtained for the same samples (test kit) at MicroCal.

Potentiometric measurements

PTs were performed in 30 mL thermostated (298.15 ± 0.10 K) cell using Cerko Lab System microtitration unit fitted with 0.5-mL Hamilton’s syringe, pH combined electrode (Schott – BlueLine 16 pH type) and a self-made measuring cell equipped with magnetic stirrer. The temperature was controlled using the Lauda E100 circulation thermostat. The electrode was calibrated according to IUPAC recommendations [10]. Syringe was calibrated by weight method. All the solutions were prepared immediately before measurements (ionic strength I = 100 mM NaClO4). The compositions of the titrand solutions used in the experiments were as follows: (1) Mes (18.16 mM) and HClO4 (3.11 mM), (2) Caco (10.01 mM) and HClO4 (3.10 mM), (3) Pipes (2 mM), (4) Co2+ (2.49 mM), Mes (18.16 mM), and HClO4 (3.11 mM), (5) Ni2+ (2.46 mM), Mes (18.16 mM), and HClO4 (3.11 mM), (6) Co2+ (1.97 mM), Caco (10.01 mM), and HClO4 (3.10 mM), (7) Ni2+ (1.95 mM), Caco (10.01 mM), and HClO4 (3.10 mM), (8) Co2+ (1.68 mM), Pipes (2 mM), (9) Ni2+ (1.69 mM), Pipes (2.00 mM), and (10) H3NTA (2.01 mM). The solutions were potentiometrically titrated with a standardized KOH solution (100.43 mM) with pH ranging from 2.5 to 12.0. The stability constants of the complexes were determined using CVEQUID program [11] by minimization of the differences between the theoretical model and the experimental data, according to Gauss–Newton–Marquart for nonlinear equations (see Ref. [12] for more details). The original CVEQUID algorithm was combined with CerkoLab software. After titration the acquired data was processed and the equilibria model was symbolically described by set of equations. The formalism used to define a “pK model” was based on a simplified way customary used to describe equilibrium state in the mixture. To further simplify the preparation of data required for numerical procedures the “pK model” included statements describing the composition of titrant, titrand, electrode parameters, and solvent. The stoichiometric matrix required for the procedure was automatically generated from the model.

Results and discussion

The conditions under which ITC experiments are carried out influence both the binding constants (K) and the enthalpies (ΔH) of the reaction. To compare ITC thermodynamic values with other methods one should take into account the pH, temperature as well as the kind of buffer solution in which the measurements are done. In systems where metal ions (M) are involved, metal–buffer complex formation must also be considered during ITC data analysis.

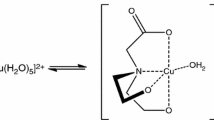
To determine thermodynamic values (K, ΔH) of metal–buffer interactions, displacement ITC experiments were carried out. Thus, a weak ligand (buffer Mes, Caco, or Pipes) was replaced by a strong one in the coordination sphere of the central ion. H3NTA was used in our study as the strong-binding, competitive ligand. The nitrilotriacetate ions (NTA3−) act as tetradentate ligands and form 1:1 metal–ligand complexes (ML) with most ions [13, 14]. Oxygen atoms of three carboxylic groups and a central nitrogen atom participate in the metal binding (Fig. 2). Moreover, the acid–base dissociation constants of H3NTA, the enthalpies of proton-ligand dissociation as well as the enthalpies of complexation of cobalt(II) and nickel(II) ions with H3NTA are known [15]. These values are required to determine the thermodynamic values of metal–buffer interactions by a displacement ITC experiment [9].

Fig. 2
figure 2

The coordination mode of metal(II) ion to nitrilotriacetate anion (NTA3−)

Full size image

H3NTA is a weak triprotonated acid which dissociates in three steps presented by Eqs. 1–3:

$$ {\text{H}}_{ 3} {\text{NTA}} = {\text{H}}_{ 2} {\text{NTA}}^{ - } + {\text{H}}^{ + } \quad K_{\text{a1}} = \frac{{ [ {\text{H}}_{ 2} {\text{NTA}}^{ - } ] [ {\text{H}}^{ + } ]}}{{ [ {\text{H}}_{ 3} {\text{NTA]}}}} $$
(1)
$$ {\text{H}}_{ 2} {\text{NTA}}^{ - } = {\text{HNTA}}^{ 2- } + {\text{H}}^{ + } \quad K_{\text{a2}} = \frac{{ [ {\text{HNTA}}^{{ 2 { - }}} ] [ {\text{H}}^{ + } ]}}{{ [ {\text{H}}_{ 2} {\text{NTA}}^{ - } ]}} $$
(2)
$$ {\text{HNTA}}^{ 2- } = {\text{NTA}}^{ 3- } + {\text{H}}^{ + } \quad K_{\text{a3}} = \frac{{ [ {\text{NTA}}^{{ 3 { - }}} ] [ {\text{H}}^{ + } ]}}{{ [ {\text{HNTA}}^{{ 2 { - }}} ]}} $$
(3)

At 298.15 K equilibrium constants pK a1, pK a2, and pK a3 are 1.68–2.08, 2.67–2.95, and 9.49–9.95, respectively [15]. For calculations, we used the pK a1, pK a2, and pK a3 values obtained in our laboratory. They are as follows: pK a1 = 2.28 (±0.17), pK a2 = 2.88 (±0.19), and pK a3 = 9.55 (±0.07).

The concentration of H3NTA is equal to the sum of the concentrations of all the particular components involved in equilibrium (Eq. 4). The concentration of these chemical species depends on the pH of a solution.

$$ c_{{{\text{H}}_{ 3} {\text{NTA}}}} = \left[ {{\text{NTA}}^{ 3- } } \right] + \left[ {{\text{HNTA}}^{ 2- } } \right] + \left[ {{\text{H}}_{ 2} {\text{NTA}}^{ - } } \right] + \left[ {{\text{H}}_{ 3} {\text{NTA}}} \right]. $$
(4)

Knowing the pK a values of H3NTA and using appropriate formulas (Eqs. 5a–5c) one can find an expression that describes the relationship between the pH of a solution and the stability constant (Eq. 6).

$$ c_{{{\text{H}}_{3} {\text{NTA}}}} = [{\text{NTA}}^{3 - } ] + [{\text{HNTA}}^{2 - } ] + [{\text{H}}_{2} {\text{NTA}}^{ - } ] + [{\text{H}}_{3} {\text{NTA}}] = [{\text{NTA}}^{3 - } ]\left( {1 + \frac{{[{\text{H}}^{ + } ]}}{{K_{{{\text{a}}3}} }} + \frac{{[{\text{H}}^{ + } ]^{2} }}{{K_{{{\text{a}}3}} \cdot K_{{{\text{a}}2}} }} + \frac{{[{\text{H}}^{ + } ]^{3} }}{{K_{{{\text{a}}3}} \cdot K_{{{\text{a}}2}} \cdot K_{{{\text{a}}1}} }}} \right) $$
(5a)
$$ \alpha_{{\text{proton}}} = 1 + \frac{{[{\text{H}}^{ + } ]}}{{K_{{{\text{a}}3}} }} + \frac{{[{\text{H}}^{ + } ]^{2} }}{{K_{{{\text{a}}3}} \cdot K_{{{\text{a}}2}} }} + \frac{{[{\text{H}}^{ + } ]^{3} }}{{K_{{{\text{a}}3}} \cdot K_{{{\text{a}}2}} \cdot K_{{{\text{a}}1}} }} $$
(5b)
$$ c_{{{\text{H}}_{3} {\text{NTA}}}} = [{\text{NTA}}^{3 - } ] \cdot \alpha_{{\text{proton}}} $$
(5c)
$$ K_{{\text{ITC}}} = \frac{[{\text{MNTA}}]}{{[{\text{M}}] \cdot c_{{{\text{H}}_{3} {\text{NTA}}}} }} = \frac{[{\text{MNTA}}]}{[{\text{M}}][{\text{NTA}}]} \cdot \frac{1}{{\alpha_{{\text{proton}}} }} = K_{{\text{MNTA}}} \cdot \frac{1}{{\alpha_{{\text{proton}}} }} $$
(6)

where M denotes metal ion, K ITC is the conditional (observed) binding constant obtained directly from the ITC experiment. K ITC depends on the pH of a solution and the pK a values of a ligand (as well as ionic strength and temperature), α proton is the function of pH and pK a’s, K MNTA is the pH-independent metal (M2+)–ligand (NTA3−) binding constant (M2+ + NTA3− = MNTA−) and can be compared to K values obtained by other methods. It can also be extrapolated to different conditions.

The situation is slightly more complicated when metal ions are involved in the system under study. If one assumes that the metal ions (M) with buffer type of H n B form complexes having a molar metal to ligand ratio of 1:1 (MB) the following equations should be used during calorimetric data analysis (Eqs. 7a–7c):

$$ {\text{M}} + {\text{B}} = {\text{MB}}\quad K_{\text{MB}} = \frac{{ [ {\text{MB]}}}}{{ [ {\text{M][B]}}}} $$
(7a)
$$ \left[ {\text{M}} \right]_{\text{ITC}} = \left[ {\text{M}} \right] + \left[ {\text{MB}} \right] = \left[ {\text{M}} \right] + K_{\text{MB}} \left[ {\text{M}} \right]\left[ {\text{B}} \right] = \, \left[ {\text{M}} \right]\left( { 1 { } + K_{\text{MB}} \left[ {\text{B}} \right]} \right) $$
(7b)
$$ \left[ {\text{M}} \right]_{\text{ITC}} = \left[ {\text{M}} \right] \cdot \alpha_{\text{buffer}} $$
(7c)

where [M]ITC indicates the concentration of the metal species not involved in the MB complex, K MB indicates the stability constant for the metal–buffer complex (MB), [B] indicates the concentration of a buffer solution, α buffer = 1 + K MB[B] is a function of the K MB and [B].

In such a case, to determine the pH and buffer-independent stability constant K MNTA the following equation must be applied (Eq. 8):

$$ K_{\text{ITC}} = \frac{{ [ {\text{ML]}}}}{{ [ {\text{M]}}_{\text{ITC}} c_{{{\text{H}}_{ 3} {\text{NTA}}}} }} = \frac{{ [ {\text{ML]}}}}{{ [ {\text{M][L]}}}} \cdot \frac{ 1}{{\alpha_{\text{proton}} \cdot \alpha_{\text{buffer}} }} = \frac{{K_{\text{MNTA}} }}{{\alpha_{\text{proton}} \cdot \alpha_{\text{buffer}} }} $$
(8)

which finally leads to an expression (Eq. 9) for the condition-independent K MNTA:

$$ K_{\text{MNTA}} = K_{\text{ITC}} \cdot \alpha_{\text{proton}} \cdot \alpha_{\text{buffer}} $$
(9)

The assumption that in the systems under study, 1:1 metal–buffer complexes (MB) are formed, was verified by PT. The following equilibria were assumed and used to calculate the metal–buffer stability constants.

Equilibrium models for interactions of the metal ions (M) with the Mes or Caco buffers (HB):

$$ \begin{aligned} {\text{HB}} & = {\text{B}}^{ - } + {\text{H}}^{ + } \quad \quad \quad {\text{p}}K_{\text{a}} \\ {\text{M}}^{ 2+ } + {\text{B}}^{ - } & = {\text{MB}}^{ + } \quad \quad \quad \quad { \log }K_{\text{MB}} \\ {\text{MB}}^{ + } + 2 {\text{OH}}^{ - } & = {\text{MB}}\left( {\text{OH}} \right)_{ 2}^{ - } \quad { \log }K_{{{\text{MB}}\left( {\text{OH}} \right)_{ 2} }} \\ {\text{H}}_{ 2} {\text{O}} & = {\text{H}}^{ + } + {\text{ OH}}^{ - } \quad {\text{p}}K_{\text{w}} \\ \end{aligned} $$

Equilibrium models for interactions of the metal ions (M) with the Pipes buffer (H2B):

$$ \begin{aligned} {\text{H}}_{ 2} {\text{B}} & = {\text{BH}}^{ - } + {\text{H}}^{ + } \quad \quad {\text{p}}K_{\text{a1}} \\ {\text{BH}}^{ - } & = {\text{B}}^{ 2- } + {\text{ H}}^{ + } \quad \quad {\text{p}}K_{\text{a2}} \\ {\text{M}}^{ 2+ } + {\text{B}}^{ 2- } & = {\text{MB}}\quad \quad \quad \quad { \log }K_{\text{MB}} \\ {\text{MB}} + 2 {\text{OH}}^{ - } & = {\text{MB}}\left( {\text{OH}} \right)_{ 2}^{ 2- } \quad { \log }K_{{{\text{MB}}\left( {\text{OH}} \right)_{ 2} }} \\ {\text{H}}_{ 2} {\text{O}} & = {\text{H}}^{ + } + {\text{OH}}^{ - } \quad \quad {\text{p}}K_{\text{w}} \\ \end{aligned} $$

The pK and logK values of the individual equilibria that contribute to the experimental equilibrium involving a metal (M) binding to a buffer (B), together with their standard deviations, are summarized in Table 1. The K MB values obtained from PTs are the pH-independent stability constants and can be extrapolated to the conditions, under which the calorimetric measurements were carried out. The metal–buffer conditional stability constants K′MB at pH 6 (I = 0.100 M NaClO4) were calculated using Eq. 10.

$$ K_{\text{MB}}^{ '} = \frac{{ [ {\text{MB]}}}}{{ [ {\text{M]}} \cdot c_{\text{B}} }} = \frac{{ [ {\text{MB]}}}}{{ [ {\text{M][B]}}}} \cdot \frac{ 1}{{\alpha_{\text{proton}} }} = K_{\text{MB}} \cdot \frac{ 1}{{\alpha_{\text{proton}} }}, $$
(10)

where c B is the concentration of buffer (B) and equals c B = [HB] + [B] for the Mes and Caco buffer or c B = [H2B] + [HB] + [B] for the Pipes buffer.

Table 1 pK and logK values (standard deviation in parentheses) for the metal–buffer interactions in water at T = 298.15 K (ionic strength I = 0.100 M NaClO4) obtained by adapting the equilibrium model to PT data
Full size table

To find α proton (Eq. 5b), the values of the acid-based dissociation constants of the buffers were taken from Table 1. The logarithms of the K′MB value equal to 1.68, 1.95, and 2.03 for the Co–Mes, Co–Caco, and Co–Pipes complex, respectively, and 1.69, 1.96, and 2.03 for the Ni–Mes, Ni–Caco, and Ni–Pipes complex, respectively. Then, the K′MB constants were used to determine the enthalpies of the metal–buffer interaction. Assuming, based on potentiometric data, that the Co2+ and Ni2+ ions form 1:1 complexes with buffer (B) as well as taking into account four protonation states of H3NTA ligand (Eq. 4), the individual equilibria that contribute to the overall equilibrium, as well as the coefficients that indicate the percentage of the particular chemical species in solution under experimental conditions are presented in Table 2. The overall reaction for the formation of metal–H3NTA complex is given by general equation 11.

$$ \begin{aligned} ( 1-\alpha_{\text{MB}} ){\text{M}} + \alpha_{\text{MB}} {\text{MB}} + ( 1- \alpha_{\text{HNTA}} - \alpha_{{{\text{H}}_{ 2} {\text{NTA}}}} - \alpha_{{{\text{H}}_{ 3} {\text{NTA}}}} ){\text{NTA}} + \alpha_{\text{HNTA}} {\text{HNTA}} + \alpha_{{{\text{H}}_{ 2} {\text{NTA}}}} {\text{H}}_{ 2} {\text{NTA}} + \alpha_{{{\text{H}}_{ 3} {\text{NTA}}}} {\text{H}}_{ 3} {\text{NTA}} + (\alpha_{\text{HNTA}} + 2\alpha_{{{\text{H}}_{ 2} {\text{NTA}}}} + 3\alpha_{{{\text{H}}_{ 3} {\text{NTA}}}} ){\text{B}} = {\text{MNTA}} + (\alpha_{\text{HNTA}} + 2\alpha_{{{\text{H}}_{ 2} {\text{NTA}}}} + 3\alpha_{{{\text{H}}_{ 3} {\text{NTA}}}} ){\text{BH}} \end{aligned} $$
(11)
Table 2 Individual equilibria that contribute to the overall equilibrium for the formation of metal–H3NTA complex in the Mes, Caco, or Pipes buffer solution (B) (the charges of ions are omitted for the sake of clarity)
Full size table

In Eq. 11, the sum \( (\alpha_{\text{HNTA}} + 2\alpha_{{{\text{H}}_{ 2} {\text{NTA}}}} + 3\alpha_{{{\text{H}}_{ 3} {\text{NTA}}}} ) \) corresponds to the number of protons transferred. The coefficients in Table 2 indicate the percentage of the metal and ligands in solution under experimental conditions and are defined as follows (Eqs. 12–15):

$$ \alpha_{\text{MB}} = \frac{{K_{\text{MB}}^{ '} [ {\text{B]}}}}{{ 1+ K_{\text{MB}}^{ '} [ {\text{B]}}}} $$
(12)
$$ \alpha_{\text{HNTA}} = \frac{{ [ {\text{HNTA}}^{ 2- } ]}}{{c_{{{\text{H}}_{ 3} {\text{NTA}}}} }} \, = \frac{{ [ {\text{H}}_{ 3} {\text{O}}^{ + } ]}}{{K_{\text{a3}} \cdot \alpha_{\text{proton}} }} $$
(13)
$$ \alpha_{{{\text{H}}_{ 2} {\text{NTA}}}} = \frac{{ [ {\text{H}}_{ 2} {\text{NTA}}^{ - } ]}}{{c_{{{\text{H}}_{ 3} {\text{NTA}}}} }} = \frac{{ [ {\text{H}}_{ 3} {\text{O}}^{ + } ]^{ 2} }}{{K_{\text{a3}} \cdot K_{\text{a2}} \cdot \alpha_{\text{proton}} }} $$
(14)
$$ \alpha_{{{\text{H}}_{ 3} {\text{NTA}}}} = \frac{{ [ {\text{H}}_{ 3} {\text{NTA]}}}}{{c_{{{\text{H}}_{ 3} {\text{NTA}}}} }} = \frac{{ [ {\text{H}}_{ 3} {\text{O}}^{ + } ]^{ 3} }}{{K_{\text{a3}} \cdot K_{\text{a2}} \cdot K_{\text{a1}} \cdot \alpha_{\text{proton}} }} $$
(15)

In pH 6, the \( (\alpha_{\text{HNTA}} + 2\alpha_{{{\text{H}}_{ 2} {\text{NTA}}}} + 3\alpha_{{{\text{H}}_{ 3} {\text{NTA}}}} ) \) calculated according to Eqs. 13–15, equals 1. This means that during the experiment the number of moles of the protons released by 1 mol of H3NTA during complexation of the Co2+ or Ni2+ ions equals to 1.

When a proton is released from a ligand during complexation a new, additional energy is generated. It is connected with the transfer of the proton from the ligand to the buffer. Carrying out the ITC measurements in buffer solutions of equal pH but different enthalpies of proton association of its components (Mes, Caco, Pipes), ΔH BH, made it possible to determine the enthalpy of complex formation, independent of the nature of the buffer used [16–18]. Moreover, when the enthalpy of the metal–ligand (strong ligand) reaction is known, ΔH oMNTA , the metal–buffer (weak ligand) enthalpy can be calculated, ΔH oMB . The observed enthalpy of binding, ΔH ITC, obtained from ITC titration, can be expressed by Eq. 16, which is based on Hess’s law [19]:

$$ \begin{aligned} \Updelta H_{\text{ITC}} = & - \alpha_{\text{MB}} \Updelta H_{\text{MB}}^{\text{o}} - \alpha_{\text{HNTA}} \Updelta H_{\text{HNTA}}^{\text{o}} - \alpha_{{{\text{H}}_{ 2} {\text{NTA}}}} \Updelta H_{{{\text{H}}_{ 2} {\text{NTA}}}}^{\text{o}} - \alpha_{{{\text{H}}_{ 3} {\text{NTA}}}} \Updelta H_{{{\text{H}}_{ 3} {\text{NTA}}}}^{\text{o}} \\ & + (\alpha_{\text{HNTA}} + 2\alpha_{{{\text{H}}_{ 2} {\text{NTA}}}} + 3\alpha_{{{\text{H}}_{ 3} {\text{NTA}}}} )\Updelta H_{\text{BH}} + \Updelta H_{\text{MNTA}}^{ \circ } \\ \end{aligned} $$
(16)

Finally, the metal–buffer enthalpy, ΔH oMB , can be found by transformation of Eq. 16:

$$ \begin{aligned} \Updelta H_{\text{MB}}^{ \circ } & = [ - \Updelta H_{\text{ITC}} - \alpha_{\text{HNTA}} \Updelta H_{\text{HNTA}}^{ \circ } - \alpha_{{{\text{H}}_{ 2} {\text{NTA}}}} \Updelta {\text{H}}_{{{\text{H}}_{ 2} {\text{NTA}}}}^{ \circ } - \alpha_{{{\text{H}}_{ 3} {\text{NTA}}}} \Updelta H_{{{\text{H}}_{ 3} {\text{NTA}}}}^{ \circ } \\ & + (\alpha_{\text{HNTA}} + 2\alpha_{{{\text{H}}_{ 2} {\text{NTA}}}} + 3\alpha_{{{\text{H}}_{ 3} {\text{NTA}}}} )\Updelta H_{\text{BH}} + \Updelta H_{\text{MNTA}}^{ \circ } ]/\alpha_{\text{MB}} \\ \end{aligned} $$
(17)

To do this, the ΔH ITC of Co2+–H3NTA and Ni2+–H3NTA interactions were measured in Mes, Caco, and Pipes buffered solutions. The obtained results (logK ITC, ΔH ITC) as well as the ΔH oMB values calculated from Eq. 17 are listed in Table 3. Representative binding isotherms for Ni–H3NTA interactions are shown in Fig. 3. Calorimetric titration isotherms of the binding interaction between Co2+ and H3NTA are presented in the Supplementary Material (Fig. S1). The proton-association enthalpies of buffers, ΔH BH (H+ + B− = HB±), used in this study are +0.71, −2.68, and −3.54 kcal mol−1 for Caco, Pipes, and Mes, respectively [20]. The metal–H3NTA formation constants, the enthalpies of metal–H3NTA interactions, ΔH oMNTA , as well as the enthalpies of the proton association to the ligand used in the calculations were taken from literature [15, 21]. They are listed below:

$$ \begin{aligned} {\text{Log}}K_{\text{CoNTA}} \left( {{\text{Co}}^{ 2+ } + {\text{ NTA}}^{ 3- } = {\text{CoNTA}}^{ - } } \right) = 10. 5 {\text{Log}}K_{\text{NiNTA}} \left( {{\text{Ni}}^{ 2+ } + {\text{NTA}}^{ 3- } = {\text{NiNTA}}^{ - } } \right) = 1 1. 4 \Updelta H_{\text{CoNTA}}^{^\circ } \left( {{\text{Co}}^{ 2+ } + {\text{NTA}}^{ 3- } = {\text{CoNTA}}^{ - } } \right) = - 0.0 7\;{\text{kcal}}\;{\text{mol}}^{ - 1} \Updelta H_{\text{NiNTA}}^{^\circ } \left( {{\text{Ni}}^{ 2+ } + {\text{NTA}}^{ 3- } = {\text{NiNTA}}^{ - } } \right) = - 2. 5 3\;{\text{kcal}}\;{\text{mol}}^{ - 1} \Updelta H_{\text{HNTA}}^{^\circ } \left( {{\text{NTA}}^{ 3- } + {\text{H}}^{ + } = {\text{HNTA}}^{ 2- } } \right) = - 4. 90\;{\text{kcal}}\;{\text{mol}}^{ - 1} \Updelta H_{{{\text{H}}_{ 2} {\text{NTA}}}}^{^\circ } \left( {{\text{HNTA}}^{ 2- } + {\text{H}}^{ + } = {\text{H}}_{ 2} {\text{NTA}}^{ - } } \right) = + 0. 80\;{\text{kcal}}\;{\text{mol}}^{ - 1} \Updelta H_{{{\text{H}}_{ 3} {\text{NTA}}}}^{^\circ } \left( {{\text{H}}_{ 2} {\text{NTA}}^{ - } + {\text{H}}^{ + } = {\text{H}}_{ 3} {\text{NTA}}} \right) = + 0. 7 5\;{\text{kcal}}\;{\text{mol}}^{ - 1} \end{aligned} $$
Table 3 Thermodynamic parameters (logK ITC, ΔH ITC) of the Co2+ and Ni2+ ions binding to H3NTA and the ΔH MB values of the metal–buffer (Mes, Caco, and Pipes) interactions in solutions of pH 6, at 298.15 K
Full size table
Fig. 3
figure 3

Calorimetric titration isotherms of the binding interaction between Ni2+ and H3NTA in buffers with different ionization enthalpies (Mes, Pipes, Caco, 100 mM each) of pH 6, at 298.15 K

Full size image

The ΔH ITC determined from the ITC experiment depends on the nature of the buffer solution in which the measurement was carried out (Table 3). The drop of the ΔH ITC value with decreasing buffer association enthalpy, ΔH BH, shows that during complexation of the metal ions, the protons are transferred from the ligand to the buffer. For this reason, energetic effects due to metal–ligand interaction in buffer solutions of negative association enthalpies (Mes, Pipes) are reduced by the energy (heat) released during proton binding to a buffer component. With the Caco buffer of positive association enthalpy (+0.71 kcal mol−1), the proton transfer during complexation of the metal ions results in an increase in ΔH ITC. It is especially seen in the case of Ni2+–H3NTA interactions, where ΔH ITC is negative when titration is carried out in the Mes and Pipes buffer solutions, then changes to positive in the Caco buffer (Table 3; Fig. 3).

Equation 16 can be transformed to the linear relationship y = a + bx (Eq. 18) as seen below:

$$ \begin{aligned} \Updelta H_{\text{ITC}} + \alpha_{\text{MB}} \Updelta H_{\text{MB}}^{^\circ } & = (\alpha_{\text{HNTA}} + 2\alpha_{{{\text{H}}_{ 2} {\text{NTA}}}} + 3\alpha_{{{\text{H}}_{ 3} {\text{NTA}}}} )\Updelta H_{\text{BH}}^{^\circ } + \Updelta H_{\text{MNTA}}^{^\circ } - \alpha_{\text{HNTA}} \Updelta H_{\text{HNTA}}^{^\circ } \\ & - \alpha_{{{\text{H}}_{ 2} {\text{NTA}}}} \Updelta_{{{\text{H}}_{ 2} {\text{NTA}}}}^{^\circ } - \alpha_{{{\text{H}}_{ 3} {\text{NTA}}}} \Updelta H_{{{\text{H}}_{ 3} {\text{NTA}}}}^{^\circ } \\ \end{aligned} $$
(18)

where y = ΔH ITC + α MBΔH oMB , \( a = \Updelta H_{\text{MNTA}}^{{\text{o}}} - \alpha_{\text{HNTA}} \Updelta H_{\text{HNTA}}^{{\text{o}}} - \alpha_{{{\text{H}}_{2} {\text{NTA}}}} \Updelta H_{{{\text{H}}_{2} {\text{NTA}}}}^{{\text{o}}} - \alpha_{{{\text{H}}_{3} {\text{NTA}}}} \Updelta H_{{{\text{H}}_{3} {\text{NTA}}}}^{{\text{o}}} \), \( b = \alpha_{\text{HNTA}} + 2\alpha_{{{\text{H}}_{2} {\text{NTA}}}} + 3\alpha_{{{\text{H}}_{3} {\text{NTA}}}} \)—the number of proton transferred, and x = ΔH oBH —the proton-association enthalpy of buffer.

The plots of (ΔH ITC + α MBΔH oMB ) versus ΔH oBH for the Co2+ and the Ni2+ complexes are shown in Fig. 4. From a slope of the relationship described by Eq. 18, the number of protons transferred was determined and equaled 0.999 (±0.001) for both the Co2+ and the Ni2+–H3NTA complexes. These values agree with those calculated using Eqs. 13–15.

Fig. 4
figure 4

Plot of (ΔH ITC + α MBΔH oMB ) versus ΔH oBH for the Co2+ and Ni2+–H3NTA interactions in 100 mM Mes, Caco, and Pipes at pH 6, 298.15 K

Full size image

When the enthalpy of metal (M)–ligand (L) interaction is unknown, ΔH oML , it can be determined, for triprotonated ligand (H3L), using the value at the point of interception of the plot presented in Fig. 4, \( \Updelta H_{\text{ML}}^{\text{o}} - \alpha_{\text{HL}} \Updelta H_{\text{HL}}^{\text{o}} - \alpha_{{{\text{H}}_{ 2} {\text{L}}}} \Updelta H_{{{\text{H}}_{ 2} {\text{L}}}}^{\text{o}} - \alpha_{{{\text{H}}_{ 3} {\text{L}}}} \Updelta H_{{{\text{H}}_{ 3} {\text{L}}}}^{\text{o}} \).

Conclusions

ITC and PT methods have successfully been applied to determine thermodynamic parameters (K MB, ΔH MB) for complexation reactions of Co2+ and Ni2+ ions with buffer substances Mes, Caco, and Pipes. The metal–buffer formation constants K MB were determined by PTs. The stability of the examined complexes increased in the following directions: CoMes (logK CoMes = 2.04) < CoCaco (logK CoCaco = 2.30) < CoPipes (logK CoPipes = 3.12) and NiMes (logK NiMes = 2.06) < NiCaco (logK NiCaco = 2.33) < NiPipes (logK NiPipes = 3.20). Furthermore, these values were extrapolated to the conditions under study (pH 6) and used for calculation of the enthalpies of metal–buffer interactions ΔH MB. The enthalpies, ΔH MB, were determined indirectly by ITC displacement titration using H3NTA as a strong-binding, competitive ligand. Based on Hess’s law the following values were obtained: ΔH CoMes = 0.29 kcal mol−1, ΔH CoPipes = 0.58 kcal mol−1, ΔH CoCaco = 1.25 kcal mol−1, ΔH NiMes = 0.40 kcal mol−1, ΔH NiPipes = 0.63 kcal mol−1, and ΔH NiCaco = 1.18 kcal mol−1.

The ITC method is a useful tool for investigation of the metal–ligand interactions in solution. It can be used as a supportive or alternative technique for other methods. However, the determination of thermodynamic parameters is not always easy, especially when metal ions are involved in the systems under study. During analysis of calorimetric data the experimental conditions must be taken into consideration. The most important energetic effects that are not connected with the metal–ligand interactions are the enthalpy of proton dissociation from the ligand, the enthalpy of buffer ionization as well as the enthalpy formation, and the stability constant of metal–buffer complex. In this article, it has been presented how to include these factors during calorimetric data analysis.