Introduction

According to a series of recent white papers on nuclear data [1,2,3], improved knowledge on inelastic scattering of fast neutrons i.e. (n,n´γ)-reactions are required for various applications in nuclear science and technology such as chemical analysis with neutron interrogation systems, design of fast neutron reactors and radiation protection. Fast-neutron-induced reactions, (n,n´γ)- or (n,p)-, (n,α)- and (n,2n)-reactions can be investigated with the instrument FaNGaS (Fast Neutron induced Gamma Spectrometry) [4,5,6] installed at MLZ to perform elemental analysis of large samples by measurement of prompt and delayed gamma rays from interaction with fast neutrons. The latter are produced by a highly enriched-uranium (93% 235U) convertor plate plunged into the reactor pool and extracted through a beam port and a set of collimators into an experimental bunker used for medical application (MEDAPP). Neutron-induced gamma radiation is detected with a well-shielded high-purity germanium detector mounted perpendicular to the neutron beam axis. Beside further development of FaNGaS to increase the sensitivity of prompt gamma-ray detection we aim to develop a modern comprehensive catalogue on (n,n´γ)-reactions by verifying and extending the only available database in this field: the “Atlas of Gamma-rays from the Inelastic Scattering of Reactor Fast Neutrons” published in 1978 by Demidov et al. [7]. From this Atlas a relational database of inelastic neutron scattering (n,n´γ) data has been recently developed [8]. The suitability of FaNGaS to provide reliable and accurate data for (n,n´γ)-reactions was demonstrated first by measuring prompt gamma rays generated by inelastic scattering of fast neutrons on natural iron [6]. Thanks to the modern design of the FaNGaS instrument, it was possible to identify 33 additional and 11 falsely identified compared to Demidov catalogue. In the present work, we report on the measurement of prompt and delayed gamma rays produced by capture of epithermal and fast neutrons and by inelastic scattering of fast neutrons on indium. Gamma-ray intensities and, partial and neutron spectrum-averaged reaction cross sections for indium isotopes are determined and compared with literature data.

Theory

Prompt gamma rays of indium are induced mainly from neutron capture via the 115In(n, γ)116In reaction and from inelastic scattering of fast neutrons via the 115In(n,n´)115In and113In(n,n´)113In reactions. Delayed gamma rays are emitted from the decay of 116m2In (T1/2 = 2.18 s) and 116mIn (T1/2 = 54.29 m) formed by neutron capture (116m2In decays to 100% into 116mIn) and from the decay of 115mIn (T1/2 = 4.49 h) generated by inelastic scattering of fast neutrons (115mIn decays to 95% into 115In by isomeric conversion and to 5% into 115Sn by beta decay). The reaction rates \(R\) (atom−1 s−1) and the effective cross sections \(\sigma\) (cm2) for the aforementioned reactions and for the In(n,tot) reaction may be estimated as follows:

$$R = \mathop \sum \limits_{i} \sigma \left( {E_{i} } \right) \cdot \Phi \left( {E_{i} } \right){ }$$
(1)

and

$$\sigma = \frac{R}{{\mathop \sum \nolimits_{i} \Phi \left( {E_{i} } \right)}}$$
(2)

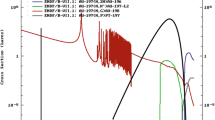
where \(\Phi \left( {E_{i} } \right)\) is the neutron flux in the neutron energy bin i and \(\sigma \left( {E_{i} } \right)\) the reaction cross section averaged over the neutron energy bin i. The neutron energy spectrum at sample position measured in our previous work [6] by means of the foil activation technique is shown in Fig. 1. It may be divided into three components designated as thermal (10–10 MeV < \(E_{i}\) < 1.42 10–7 MeV), epithermal (1.42 10–7 MeV < \(E_{i}\) < 0.06 MeV) and fast (0.06 MeV < \(E_{i}\) < 20 MeV) neutron energy regions with the respective neutron fluxes, (9.4 ± 2.8) × 102 cm−2 s−1, (1.85 ± 0.09) × 106 cm−2 s−1 and (1.40 ± 0.05) × 108 cm−2 s−1. The integral neutron flux is (1.42 ± 0.05) × 108 cm−2 s−1. The average energy of the neutron spectrum is 2.30 MeV. The values of \(\sigma \left( {E_{i} } \right)\) were produced with the GROUPR module of the NJOY Nuclear Data Processing System [9] from the Evaluated Nuclear Data File databases ENDF/B-VIII.0 [10] for the 115In(n, γ)116In, and 115In(n,n´)115In and 113In(n,n´)113In reactions and ENDF/B-VI.8 [11] for the In(n,tot)-reaction. Their neutron energy dependence is shown together with the neutron energy spectrum in Fig. 1. The reaction rates \(R\) and the effective cross sections \(\sigma\) determined by means of Eqs. (1) and (2), respectively, for the epithermal and fast region of the neutron spectrum are given Table 1. Due to the low thermal neutron flux, the reaction rate of 115In(n,γ)116In induced by thermal neutrons was neglected. The rates produced by capture of epithermal and fast neutrons represent 74% and 26% of the total reaction rate, respectively. The reaction rates of 115In(n,n´)115In and 113In(n,n´)113In are about two times higher than the total reaction rate of 115In(n, γ)116In. The effective cross sections \(\langle\sigma_{epi}\rangle\) estimated for capture of epithermal neutrons are 31 ± 2 b for 115In(n, γ)116In and 38 ± 3 b for the In(n,tot) reaction. It should be mentioned here that these values are not comparable to the resonance integrals obtained for a reactor spectrum since our spectrum does not follow 1/E dependence in the epithermal region. The effective cross sections \(\langle\sigma_{fast}\rangle\) determined for capture and for inelastic scattering of fast neutrons agree well with the values given in JANIS (Java-based Nuclear Data Information System) Book of neutron induced cross section [12] (see Table 1). The neutron spectrum-averaged cross sections \(\langle\sigma_{int}\rangle\) are given in the last column of Table 1.

Fig. 1
figure 1

Neutron energy spectra of FaNGaS at sample position (right scale of y-axis) and neutron energy dependence of the cross section \({\varvec{\sigma}}\left( {{\varvec{E}}_{{\varvec{i}}} } \right)\) averaged over the neutron energy bin i for the 115In(n,γ)116In, 115In(n,n´)115In, 113In(n,n´)113In and In(n,tot) reactions (left scale of y axis)

Full size image
Table 1 Reaction rates R and effective cross sections < σ > for the reactions 115In(n, γ)116In, 115In(n,n´)115In, 113In(n,n´)113In and In(n,tot) calculated by mean of Eq. (1) and Eq. (2), respectively and neutron self-shielding factors fn calculated by means of Eq. (7), for the considered neutron-energy ranges
Full size table

Experimental

Prompt and delayed gamma radiation generated by irradiation of a high-purity indium foil of natural composition (mass: 1.334 g, surface: 2.7 × 2.7 cm2, thickness: 0.025 cm) with epithermal and fast neutrons was investigated with the FaNGaS instrument described in [6]. The shape of the neutron beam was quadratic with a cross sectional area of 6 × 6 cm2 at sample position. The neutron spectrum at sample position is given in Fig. 1. The gamma-ray spectrum was recorded during neutron irradiation with the FaNGaS spectrometer composed of a well-shielded electromechanically cooled HPGe-detector with a relative efficiency of 50% and a resolution (FWHM) of 2.1 keV at 1.33 MeV [4]. The measurement was performed at an angle of 90° between neutron beam direction and detector. The sample-to-detector distance was 67 cm. The foil was irradiated for 9.91 h with it surface perpendicular to the neutron beam and counted for 7.46 h (live time). The spectrum was analyzed with the software HYPERMET-PC [13]. The analysis of the beam background carried out in a previous work [6] was used to facilitate the identification of gamma lines. The spectra of indium and beam background are shown together for various energy ranges in Figs. 2 and 3. In comparison to the beam background, the count rates of background lines in the indium spectrum were higher by a mean factor 1.11 ± 0.02 due to the scattering of fast neutrons towards the spectrometer. The identification of capture gamma rays of 115In was performed using the PGAA (Prompt Gamma Activation Analysis) database [14]. The prompt gamma rays arising from inelastic neutron scattering were assigned to 115In or 113In using the database NutDat 2.8 [15] and nuclear data provided in [16].

Fig. 2
figure 2

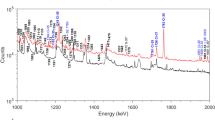
Gamma ray spectra in the energy range 0–2000 keV acquired during 26,850 s for the indium foil (red) and during 46,454 s for the beam background (black). Prompt and delayed gamma rays induced by capture of resonance and fission neutrons are labelled with asterisks. Prompt gamma rays issued from inelastic scattering of fission neutrons are written in bold

Full size image
Fig. 3
figure 3

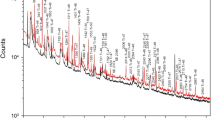
Gamma ray spectra in the energy range 2000–6000 keV acquired during 26,850 s for the indium foil (red) and during 46,454 s for the beam background (black). Prompt and delayed gamma rays induced by capture of resonance and fission neutrons are labelled with asterisks. Prompt gamma rays issued from inelastic scattering of fission neutrons are written in bold

Full size image

Method

The net peak area of a prompt gamma ray of energy Eγ induced by neutron capture or by inelastic neutron scattering, \(P_{E\gamma }\), may be expressed by the following relation:

$$P_{E\gamma } = { }\frac{m}{M} \cdot N_{A} \cdot h \cdot \varepsilon_{E\gamma } \cdot \langle\sigma_{E\gamma }\rangle \cdot \Phi \cdot t_{c} \cdot f_{n} \cdot f_{E\gamma }$$
(3)

where m (g) is the amount of element, M (g mol−1) the molar mass of the element, NA the Avogadro number, h the abundance of the isotope considered, \(\varepsilon_{E\gamma }\) the full energy peak efficiency, \(\langle\sigma_{E\gamma }\rangle\) (cm2) the neutron spectrum averaged isotopic cross section for gamma ray production, \(\Phi\) (cm−2 s−1) the corresponding integral neutron flux, \(t_{c}\) (s) the counting (live) time, \(f_{n}\) a factor for neutron self-shielding and \(f_{E\gamma }\) a factor for gamma-ray self-absorption. In the case of (n,n´γ)-reactions, the gamma emission is anisotropic and therefore \(\langle\sigma_{E\gamma }\rangle\) depends on the measurement angle i.e. the angle between the neutron beam direction and the detector.

The net peak area of a delayed gamma ray of energy Eγ measured during irradiation may be given by:

$$P_{E\gamma } = { }\frac{m}{M} \cdot N_{A} \cdot h \cdot \varepsilon_{E\gamma } \cdot \langle \sigma_{E\gamma } \rangle \cdot \Phi \cdot f_{n} \cdot f_{E\gamma } \cdot g\left( {t_{b} ,t_{c} ,t_{1/2} } \right)$$
(4)

with

$$g\left( {t_{b} ,t_{c} ,t_{1/2} } \right) = \frac{{t_{c} }}{{t_{b} }} \cdot \mathop \smallint \limits_{0}^{{t_{b} }} \left( {1 - e^{{ - \frac{ln2 \cdot t}{{t_{1/2} }}}} } \right)dt = \left[ {t_{c} - \frac{{t_{c} \cdot t_{1/2} }}{{t_{b} \cdot ln2}} \cdot \left( {1 - e^{{ - \frac{{ln2 \cdot t_{b} }}{{t_{1/2} }}}} } \right)} \right]$$
(5)

where \(t_{b}\) is the irradiation (real) time, \(t_{c}\) the counting (live) time and \(t_{1/2}\) the half-live of activation product. In both relations (3) and (4), the averaged isotopic cross section for gamma-ray production \(\langle\sigma_{E\gamma }\rangle\) is linked to the effective cross section \(\langle\sigma\rangle\) of the considered reaction through the intensity of the gamma ray \(I_{E\gamma }\) as

$$\langle\sigma_{E\gamma }\rangle = I_{E\gamma } \cdot \langle\sigma\rangle$$
(6)

The gamma ray intensity contains the contribution of internal conversion. The neutron self-shielding factor \(f_{n}\) for a pure element foil in a neutron beam may be calculated as follows [17]:

$$f_{n} = \frac{{1 - e^{{ - \langle\sigma_{ }\rangle \cdot \rho_{a} \cdot d}} }}{{\langle\sigma_{ }\rangle \cdot \rho_{a} \cdot d}}\user2{ }$$
(7)

with \(\langle\sigma_{ }\rangle\) the effective elemental cross section for the (n,tot)-reaction, \(\rho_{a}\) the atomic density (atoms/cm3) and \(d\) the foil thickness (cm). The \(f_{n}\)-values for the indium foil (\(\rho_{a}\) = 3.83 1022 atoms/cm3, \(d\) = 0.025 cm) calculated by means of (7) for different neutron energy regions using the corresponding estimated effective cross sections for the In(n,tot)-reaction, are given in the last row of Table 1. As expected, the neutron-shielding factors are close to unity since the foil is very thin. Thus, corrections for neutron absorption and multiple scattering may be neglected.

The gamma-ray self-absorption of the indium foil was determined numerically using the Monte Carlo transport simulation code PHITS (Particle and Heavy Ion Transport code System) Version 3.02 [18]. Several mono-energetic photons of energies ranging from 50 keV to 5 MeV were considered and generated homogeneously over the indium foil volume. A spherical detector surrounding the foil was used to count the outgoing photons at the same single energy bin as for the primary photons and thus, to deduce the self-attenuation ratio. The dependence of the gamma-ray self-absorption \(f_{E\gamma }\) on the gamma energy Eγ is shown on Fig. 4 and can be approximated with the following semi-empirical function:

$$f_{E\gamma } = a_{0} + a_{1} \cdot \left( {1 - e^{{ - a_{2} \cdot E_{\gamma } }} } \right) + a_{3} \left( {1 - e^{{ - a_{4} \cdot E_{\gamma } }} } \right)$$
(8)

with \(a_{0}\) = − 0.9403, \(a_{1}\) = 0.0556, \(a_{2}\) = 3.301·10–3, \(a_{3}\) = 1.8712, \(a_{4}\) = 0.0201 and Eγ in keV.

Fig. 4
figure 4

Dependence of the gamma self-absorption \(\user2{ f}_{{{E\gamma }}}\) on the gamma energy Eγ The solid line represent the fit of the data with Eq. (8)

Full size image

Gamma rays from neutron capture

42 capture gamma rays and 10 delayed gamma rays (9 for 116mIn and 1 for 116m2In) were observed in the spectrum. They are given in Table 2 and 3, together with their respective isotopic cross sections for gamma-ray production \(\langle\sigma_{E\gamma }\rangle\) calculated by means of Eq. (3) and Eq. (4), respectively with an integral neutron flux of (1.42 ± 0.05) × 108 cm−2 s−1. The intensities of the prompt gamma rays \(I_{E\gamma }\) calculated by means of Eq. (6) using the integral cross section \(\langle\sigma_{int}\rangle\) = 0.55 ± 0.04 b determined for the 115In(n,γ)116In reaction (see Table 1) are given in column 4 of Table 2. For comparison, the isotopic cross sections for production of the prompt and delayed gamma rays by thermal neutron capture \(\sigma_{E\gamma ,th}\) deduced from the PGAA (Prompt Gamma Activation Analysis) database [14] are also given Table 2 and 3 and the intensities of the prompt gamma rays \(I_{E\gamma ,th}\) calculated from the adopted thermal neutron cross section 202 ± 2 b [19] given in column 6 of Table 2. The intensities of the delayed gamma rays of 116mIn and 116m2In are taken from the WWW Table of Radioactive Isotopes [20] and given in column 3 of Table 3. Concerning the prompt gamma rays, the intensities of the two data sets are comparable within their uncertainties, except for the lines at 60.9, 94.04 + 94.06 and 5891.9 keV which show large deviations. The average value of the \(I_{E\gamma }\)/\(I_{E\gamma ,th}\)-ratios is 0.95 ± 0.11 and the average value of the \(\langle\sigma_{E\gamma }\rangle /\sigma_{E\gamma ,th}\)-ratios, (2.58 ± 0.32) × 10–3 fit well the ratio of the neutron capture reaction cross sections, (2.72 ± 0.20) × 10–3. The overall relationship between \(I_{E\gamma }\) and \(I_{E\gamma ,th}\) is shown in Fig. 5 and can be expressed by:

$$I_{E\gamma } = a \cdot \left( {I_{E\gamma ,th} } \right)^{b}$$
(9)
Table 2 Prompt gamma rays of 115In induced by neutron capture
Full size table
Table 3 Delayed gamma rays induced by neutron capture
Full size table
Fig. 5
figure 5

Relationship between the absolute intensities \({\varvec{I}}_{{{E\gamma }}}\) of prompt gamma rays issued from the capture of resonance and fast neutrons by 115In and the absolute intensities \({\varvec{I}}_{{{E\gamma },{\varvec{th}}}}\) of same prompt gamma rays induced by thermal neutron capture The solide line represents the fit of the data with Eq. (9)

Full size image

with \(a\) = 0.92 ± 0.03 and \(b\) = 0.98 ± 0.03. Further investigations must be carried out to understand the large differences observed for the aforementioned prompt gamma lines.

The isotope cross sections of delayed gamma rays are used to determine the integral cross sections of the reactions 115In(n, γ)116mIn and 115In(n, γ)116m2In by means of Eq. (6). The \(\langle\sigma_{int}\rangle\)-values obtained for the 115In(n, γ)116mIn reaction from the various gamma rays of 116mIn agree well with each other (see column 5 in Table 4) providing a mean value of 508 ± 20 mb. This value in conjugation with the average value of the \(\langle\sigma_{E\gamma }\rangle /\sigma_{E\gamma ,th}\)-ratios, (3.13 ± 0.14) × 10–3, leads to a thermal cross section of 163 ± 9 b which is in good agreement with the adopted value, 162.3 ± 0.7 b [19]. The \(\langle\sigma_{int}\rangle\)-value obtained for the 115In(n, γ)116m2In reaction is 201 ± 10 mb and leads with a \(\langle\sigma_{E\gamma }\rangle /\sigma_{E\gamma ,th}\)-ratio of (4.54 ± 0.30) × 10–3 to a thermal cross section of 44 ± 4 b which disagrees with literature data, 81 ± 8 b [19, 21], 83 ± 8 b [22] and 92 ± 14 [23]. Therefore, the thermal cross section of the 115In(n, γ)116m2In reaction must be reevaluated.

Table 4 Prompt gamma rays of 115In induced by inelastic scattering of fast neutrons
Full size table

Gamma rays from neutron inelastic scattering

A total of 94 prompt gamma lines issued from the inelastic scattering of fast neutrons were identified, 69 associated to 115In and 25 to 113In (see Tables 2 and 3). Interferences from capture gamma lines were corrected determining their contributions by means of Eqs. (3), (6) and (9). All indium lines reported in the work of Demidov et al. [7] were observed and additional lines were also detected (13 for 115In and 2 for 113In). Some lines given in the Demidov Atlas are not mentioned in the database NuDat 2.8. The gamma lines listed at energies 149.7, 284.7, 288.7, 293.6, 306.1, 376.2 and 633.8 keV are probably capture gamma lines of 115In as the delayed gamma rays of 116mIn and 116m2In are visible in the indium spectrum given in the Demidov Atlas. The line at 312 keV can be assigned to the decay of 114m2In (T1/2 = 43.1 ms, Eγ = 311.7 keV, Iγ = 86.6%) formed by neutron capture. From our measurement we derive by means of Eq. (4) a neutron spectrum averaged cross section of 288 ± 13 mb for the 113In(n, γ)114m2In reaction. The line at 336 keV can be related to the decay of 115mIn (T1/2 = 4.486 h, Eγ = 336.2 keV, Iγ = 45.8%) produced by fast neutrons including also the capture gamma ray of 115In at 335.4 keV as interference. The latter represents in our case 36 ± 4% of the measured count rate of the 336-keV line. After correction of this interference we obtain by means of Eq. (5) a fast neutron averaged cross section of 194 ± 18 mb for the 115In(n,n´)115mIn reaction which agrees well with the values of 188 ± 11 mb [26] and 162.6 ± 13 mb [27]. Therefore, the 336-keV line cannot be considered as a prompt gamma line arising from the inelastic scattering of neutrons as given in Demidov Atlas. The line at 391 keV can be associated to the decay of 113mIn (T1/2 = 1.658 h, Eγ = 391.7 keV, Iγ = 64.2%) induced by fast neutrons. From our measurement we determine by means of Eq. (5) a fast neutron averaged cross section of 143 ± 22 mb for the 113In(n,n´)113mIn reaction which agrees with the value of 133.7 ± 10.7 mb [27].

The intensity of the prompt gamma rays (\(I_{R}\)) were calculated relative to the 933-keV line of 115In (100%), and they are given with the values (\(I_{RD}\)) determined in [7] in Tables 4 and 5. The relationship between the relative intensities is given in Fig. 6. The values were fitted with semi-empirical function:

$$I_{R} = a \cdot \left( {I_{RD} } \right)^{b}$$
(10)
Table 5 Prompt gamma rays of 113In induced by inelastic scattering of fast neutrons
Full size table

with \(a\) = 1.21 ± 0.06 and \(b\) = 0.94 ± 0.03. The consistency between the two sets of data is shown in Fig. 7 in the form of a histogram of the residuals in unit of standard deviation [σ] calculated as

$$R = \frac{{I_{R} - I_{RD} }}{{\sqrt {\left( {s_{{I_{R} }} } \right)^{2} + \left( {s_{{I_{RD} }} } \right)^{2} } }}$$
(11)
Fig. 6
figure 6

Relationship between the relative intensities \(I_{R}\) of the prompt gamma rays induced by fast neutron inelastic scattering on indium measured in this work and the relative intensities \({I}_{RD}\) tabulated in Demidov Atlas [7]. The solide line represents the fit of the data with Eq. (10)

Full size image
Fig. 7
figure 7

Comparison of the relative intensities of the prompt gamma rays induced by fast neutron inelastic scattering on indium obtained in this work with the data tabulated in Demidov Atlas [7] in the form of a histogramm of the residuals R in unit of standard deviation [σ] calculated with Eq. (11). The values of R are given in Tables 4 and 5. The solid line represents the fit of the data with a Gaussian

Full size image

The fit of the histogram with a Gaussian shows an agreement between the data at the 1.6σ level, implying a reasonable consistency. The shift of the Gaussian centroid to a value of 0.68 indicates a probable systematic effect. The fast neutron spectrum averaged isotopic cross sections for gamma ray production calculated by means of Eq. (3) with a neutron flux of (1.40 ± 0.05) × 108 cm−2 s−1 are given in column 4 of Tables 4 and 5.

Conclusions

Prompt gamma ray emission induced by capture of epithermal and fast neutrons as well as by inelastic scattering of fast neutrons on indium was measured with the FaNGaS instrument operated at FRM II. The measurement was carried out at an angle of 90° between the fast neutron beam and the detector with an integral neutron flux of 1.42 × 108 cm−2 s−1 and a epithermal flux of 1.85 × 106 cm−2 s−1 at sample position. A total of 42 neutron capture gamma lines issued from the 115In(n,γ)116In reaction were detected. Their absolute intensities were calculated with a spectrum-averaged reaction cross section of 0.55 b and found to be comparable to the absolute intensities of the corresponding thermal neutron capture lines derived from PGAA database [14]. From the delayed gamma rays of 116mIn and 116m2In, spectrum-averaged cross sections of 508 ± 24 mb and 201 ± 10 mb were determined for the 115In(n, γ)116mIn and 115In(n,γ)116m2In reactions, respectively. Additionally, we show the necessity to reevaluate the thermal cross section of the 115In(n, γ)116m2In reaction. A total of 94 prompt gamma lines arising from 115In(n,n´)115In and 113In(n,n´)113In reactions were observed and their relative intensities (using the 933 keV gamma ray of 115In as reference) and spectrum-averaged production cross sections were determined. Compared to the work of Demidov et al. [7], 15 gamma lines were detected additionally. Several lines mentioned in the Demidov Atlas were identified as neutron capture gamma lines or decay gamma lines of 113mIn, 114m2In and 115mIn. For the reactions 113In(n,n´)113mIn, 113In(n, γ)114m2In and 115In(n,n´)115mIn we determine spectrum-averaged cross sections of 143 ± 22, 288 ± 13 and 194 ± 18 mb, respectively. The relative intensities of the prompt gamma lines measured in our work agree reasonably well (1.6σ level) with the values given in the Demidov Atlas.