Introduction

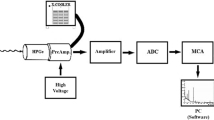
FaNGaS (Fast Neutron induced Gamma-ray Spectrometry) is a unique instrument which uses the intense fission neutron beam delivered by the SR10 channel (Strahlrohr 10) of the research reactor FRM II (Forschungs-Neutronenquelle Heinz Maier-Leibnitz) to investigate fast-neutron induced prompt gamma-ray emission [1, 2]. FaNGaS offers new possibilities for the chemical analysis of large or small samples as a complementary method to conventional thermal- or cold-neutron based PGAA (Prompt Gamma Activation Analysis). Furthermore, it has an ultimate goal to create a modern and comprehensive data catalogue on (n,n´γ)-reactions. Fast neutrons are generated by thermal neutron fission of 235U in uranium silicide converter plates immersed in the reactor pool. The fast neutron beam is extracted through a beam port and a set of collimators into an irradiation room. The detection of neutron-induced gamma radiation is performed with a well shielded high-purity germanium detector positioned perpendicular to the neutron beam axis. In previous works we reported on the prompt gamma-rays induced by fast neutrons on iron [3] and on the prompt and delayed gamma rays produced by epithermal and fast neutrons on indium [4]. In this work, the results from the measurement of aluminum, titanium and copper are presented and compared to the data provided in the “Atlas of Gamma-rays from the Inelastic Scattering of Reactor Fast Neutrons” published in 1978 by Demidov et al. [5]. Additionally, the detection limits of the elements investigated in this work as well as of iron and indium were determined.

Experimental

Prompt gamma radiation induced by inelastic scattering of fast neutrons on pure aluminum (m = 0.343 g, S = 2.3 × 2.3 cm2), titanium (m = 0.772 g, S = 2.6 × 2.6 cm2) and copper (m = 0.583 g, S = 1.6 × 1.6 cm2) foils of natural composition, respectively, was studied with the FaNGaS set-up described in [3]. The foils with a thickness of 0.025 cm were irradiated with their surface perpendicular to the neutron beam of quadratic shape (6 × 6 cm2). The fast neutron flux at sample position was (1.40 ± 0.05) × 108 cm−2 s−1 and the average neutron energy 2.30 MeV. The irradiation time was 9.7 h for aluminum, 8.2 h for titanium and 11.8 h for copper. The gamma-ray spectra were collected during neutron irradiation for 8.0, 6.5 and 9.5 h (live times), respectively. The measurement was performed at an angle of 90° between neutron beam axis and spectrometer at a sample-to-detector distance of 67 cm. The spectra were analyzed with the software HYPERMET-PC [6]. Previous beam background analysis [3] was taken into account for gamma lines identification and correction of possible interferences. Part of the spectra and beam background in the energy range 750–3050 keV, are shown in Fig. 1. The scattering of fast neutrons towards the detector leads to an increase of the count rates of background lines by mean factors of 1.10 ± 0.05 for aluminum, 1.27 ± 0.09 for titanium and 1.22 ± 0.08 for copper. These factors were used for correcting possible background interferences. The assignment of the gamma rays to the corresponding isotopes was carried out using the database NutDat 3.0 [7] and nuclear data provided in [8,9,10,11,12,13,14,15].

Fig.1
figure 1

Gamma ray spectra of the a aluminium, b titanium and c copper foils (red) in the energy range 750–3050 keV recorded during 28,776 s, 29,553 s and 34,319 s, respectively and of the beam background (black) recorded for 46,454 s

Full size image

Method

The net peak area \({P}_{E\gamma }\) of a gamma ray of energy Eγ may be expressed by the following relation:

$$P_{E\gamma } = \frac{m}{M} N_{A} h \varepsilon_{E\gamma } \sigma_{E\gamma } \Phi f_{n} f_{E\gamma } g\left( {t_{b} ,t_{c} ,t_{1/2} } \right)$$
(1)

where m (g) is the amount of element, M (g mol−1) the molar mass of the element, NA the Avogadro number, h the abundance of the isotope considered, \({\varepsilon }_{E\gamma }\) the full energy peak efficiency, \(\langle {\sigma }_{E\gamma }\rangle\) (cm2) the fast neutron spectrum averaged isotopic cross section for gamma-ray production, \(\Phi\) (cm−2 s−1) the fast neutron flux, \({f}_{n}\) a factor for neutron self-shielding and \({f}_{E\gamma }\) a factor for gamma-ray self-absorption. For prompt gamma rays the term \(g\left({t}_{b},{t}_{c},{t}_{1/2}\right)\) reduces to \({t}_{c}\) the counting (live) time. For delayed gamma rays emitted from the decay of activation products it may be expressed by:

$$g\left( {t_{b} ,t_{c} ,t_{1/2} } \right) = t_{c} - \frac{{t_{c} t_{1/2} }}{{t_{b} ln2}} \cdot \left( {1 - e^{{ - \frac{{{\text{ln}}2 \cdot t_{b} }}{{t_{1/2} }}}} } \right)$$
(2)

where \({t}_{b}\) is the irradiation (real) time, and \({t}_{1/2}\) the half-life of activation product.

The value of \(\langle {\sigma }_{E\gamma }\rangle\) is connected to the effective cross section \(\langle \sigma \rangle\) of the considered reaction through the absolute intensity of the gamma ray \({I}_{E\gamma }\), including the contribution of internal conversion, as:

$$\sigma_{E\gamma } = I_{E\gamma } \sigma$$
(3)

In the case of (n,n´γ)-reactions \(\langle {\sigma }_{E\gamma }\rangle\) depends on the measurement angle, i.e. the angle between the neutron beam direction and the detector owing to the anisotropy of the gamma emission.

As the foils are very thin, the corrections for neutron absorption and multiple scattering can be neglected, i.e. \({f}_{n}\)≈1. The gamma-ray self-absorption of the foils was determined numerically using the Monte Carlo transport simulation code PHITS (Particle and Heavy Ion Transport code System) Version 3.02 [16] as described in [4]. The dependence of the factor for gamma-ray self-absorption \({{\varvec{f}}}_{{\varvec{E}}{\varvec{\gamma}}}\) on the gamma energy Eγ is shown on Fig. 2 and was approximated with the following semi-empirical function:

$$f_{E\gamma } = a_{0} + a_{1} \cdot \left( {1 - e^{{ - a_{2} \cdot E_{\gamma } }} } \right) + a_{3} \left( {1 - e^{{ - a_{4} \cdot E_{\gamma } }} } \right)$$
(4)
Fig. 2
figure 2

Dependence of the gamma-ray self-absorption \({f}_{E\gamma }\) on the gamma energy Eγ for the aluminum, titanium and copper foils. The solid lines represent the fit of the data with Eq. (4)

Full size image

The parameters \({a}_{i}\) obtained from the fit of the data with relation (4) are given in Table 1.

Table 1 Fit parameters of Eq. (4) for determination of the gamma-ray self-absorption factor \({f}_{E\gamma }\)
Full size table

The intensity of the gamma rays of aluminum, titanium and copper, respectively, were calculated relative to the element-specific reference gamma line used in [5]. The relationship between the measured intensities (\({I}_{R}\)) and the intensities (\({I}_{RD}\)) determined in [5] was analyzed with the following semi-empirical function:

$$I_{R} = a \cdot \left( {I_{RD} } \right)^{b}$$
(5)

with \(a\) and \(b\) the coefficients returned by the fit of the data. Additionally, the consistency between the sets of data was derived from the distribution of the residuals in unit of standard deviation [σ], calculated, as:

$$R = \frac{{I_{R} - I_{RD} }}{{\sqrt {\left( {s_{{I_{R} }} } \right)^{2} + \left( {s_{{I_{RD} }} } \right)^{2} } }}$$
(6)

Possible interferences from delayed gamma rays of activation products induced by (n,p) and (n,α) reactions were evaluated by means of Eq. (1) and (2) using the reaction cross sections for a fission spectrum given in [17] and in the case of aluminum and titanium those determined in [3].

Gamma rays of aluminum

Twenty two prompt gamma lines due to inelastic scattering of fast neutrons on aluminum were measured (see Table 2). In comparison with the work of Demidov et al. [5] one additional gamma line at 3395.6 keV was detected. The gamma lines listed at energies 2371.7, 2664.5 and 2940.6 keV in [5] are not observed in our measurement. However, they are reported in the database NuDat 3.0 at similar energies, 2368.7, 2665.8 and 2942.1 keV deexciting the same levels assigned by Demidov. The fact that the strongest gamma from each level is also observed by Demidov makes their assignments plausible. The 4307-keV line given in [5] is neither mentioned in NuDat 3.0 and nor observed in our spectrum. The 843.7-keV (\({I}_{E\gamma }\) = 71.8%) ray of 27 Mg (T1/2 = 9.46 min) induced by the 27Al(n,p)27 Mg reaction and the 1368.6-keV (\({I}_{E\gamma }\) = 100%) and 2754.0-keV (\({I}_{E\gamma }\) = 99.94%) rays of 24Na (T1/2 = 14.96 h) induced by the 27Al(n,α)24Na reaction were found to interfere significantly with the prompt gamma lines of same energy. Their contributions to the net count rates were estimated to 4.0 ± 0.2%, 39 ± 3% and 54 ± 4%, respectively. The intensities of the corresponding aluminum gamma rays were corrected accordingly. The intensities of the gamma rays were calculated relative to the 1014-keV line (100%), and they are given with the values determined in [5] in Table 2. The relationship between the relative intensities is shown in Fig. 3a and is expressed by Eq. (5) with \(a\) =0.94 ± 0.05 and \(b\) =1.01 ± 0.03. The histogram of the residuals \(R\) calculated from Eq. (6) is given in Fig. 4a. Its fit with a Gaussian shows an agreement between the data at the 0.7σ level, indicating a good consistency. The \(\langle {\sigma }_{E\gamma }\rangle\)-values calculated by means of Eq. (1) are given in column 4 of Table 2.

Table 2 Prompt gamma rays of 27Al induced by inelastic scattering of fast neutrons
Full size table
Fig. 3
figure 3

Relationship between the relative intensities \({I}_{R}\) of the prompt gamma rays induced by fast neutron inelastic scattering on a aluminum, b titanium and c copper measured in this work and the relative intensities \({I}_{RD}\) tabulated in Demidov Atlas [5]. The solide line represents the fit of the data with Eq. (5)

Full size image
Fig. 4
figure 4

Comparison of the relative intensities of the prompt gamma rays induced by fast neutron inelastic scattering on a aluminum, b titanium and c cooper obtained in this work with the data tabulated in Demidov Atlas [5] in the form of a histogramm of the residuals R in unit of standard deviation [σ] calculated with Eq. (6). The values of R are given in Tables 1, 2, 3, 4, 5, 6 and 7. The solid line represents the fit of the data with a Gaussian

Full size image

Gamma rays of titanium

A total of 72 prompt gamma lines of titanium were identified, 11 related to 46Ti, 18 to 47Ti, 35 to 48Ti, 7 to 49Ti and 1 to 50Ti (see Tables 3,4,5 and 6). Most of the gamma lines given in [5] were measured and additional lines were detected: 2683.3, 2954.2 and 3904.5 keV for 46Ti, 243.5, 2245.2, 2460.4, 2679.0, 2799.4 and 3738.2 keV for 47Ti and 972.2, 1195.6, 1486.4, 2084.7, 3360.3, 3402.8, 3596.9, 3738.2, 3807.8 and 4310.3 keV for 48Ti. Gamma lines listed at energies 134.8, 708.2, 962.8, 1613.6, 1911.2, 1932.6, 2088.2, 2140.5, 2575.1 and 3287 keV in [5] were not observed. These lines are not mentioned in the database NuDat 3.0 except the 1614-keV line whose placement in the level scheme of 48Ti is uncertain. It should be mentioned here that the unobserved lines other than the 138.4-keV line were earlier reported as tentative assignments by Demidov and were not placed in any titanium decay scheme. The fact that they are not observed in our measurement helps provide support that they do not belong to titanium. The 138.4-keV gamma was assigned to the 3358.9-keV 3− level in 48Ti by Demidov. However, no similar energy gamma from the corresponding level is reported in NuDat 3.0, even though it is conceivable that a gamma of this energy could be associated with an electric-dipole (E1) transition from this 3− level to the 3224-keV 3+ level. Such a transition was not observed in our measurement which agrees with NuDat 3.0 but is at odds with Demidov´s findings. Interferences from delayed gamma rays of activation products induced by (n,p) and (n,α) reactions were found to be negligible. The intensities of the gamma rays calculated relative to the 983.5-keV line of 48Ti (100%) are given with the values determined in [5] in Tables 3, 4, 5 and 6. The relationship between the values is expressed by relation Eq. (5) with \(a\) =0.98 ± 0.04 and \(b\) =1.06 ± 0.03 as shown in Fig. 3b. The fit of the histogram of the residuals \(R\) with a Gaussian shows an agreement between the data at the 0.8σ level, indicating a good consistency (Fig. 4b). The \(\langle {\sigma }_{E\gamma }\rangle\)-values are given in Tables 3, 4, 5 and 6.

Table 3 Prompt gamma rays of 46Ti induced by inelastic scattering of fast neutrons
Full size table
Table 4 Prompt gamma rays of 47Ti induced by inelastic scattering of fast neutrons
Full size table
Table 5 Prompt gamma rays of 48Ti induced by inelastic scattering of fast neutrons
Full size table
Table 6 Prompt gamma rays of 49Ti and 50Ti induced by inelastic scattering of fast neutrons
Full size table

Gamma rays of copper

A total of 120 prompt gamma lines induced by inelastic scattering of fast neutrons on copper were identified, 82 associated to 63Cu and 38 to 65Cu. (see Tables 7 and 8). Further, the 156-keV prompt gamma line of 63Ni produced by the 63Cu(n,p)63Ni reaction was also observed. On the other hand, the 525-keV line assigned in [5] to 63Ni was not observed. This line is also not reported in the database NuDat 3.0. Most likely it was a background line that was observed during the Demidov´s measurement, thus, it is not expected to be observed in the absence of interference. Most of the gamma lines of copper given in [5] were measured and additional lines were detected: 954.8, 971.3, 1051.3, 1118.3, 1123.2, 1150.0, 1169.1, 1196.5, 1219.7, 1289.8, 1533.1, 1902.7, 1972.2, 2421.2, 2581.7, 2648.0, 2719.6, 2834.2, 2842.5, 3456.6, 3474.3 and 3565.9 keV for 63Cu and 255.3, 311.1, 315.1, 343.2, 381.7, 487.8, 1025.8, 1156.7, 1174.5, 1187.1, 1260.2, 1270.5, 1871.5, 1894.4 and 3354.4 keV for 65Cu. Both the 1013.5- and 1955.4-keV gamma rays in Demidov´Atlas are reported as tentative assignments and are unplaced in the copper decay schemes. The lines are not mentioned in NuDat 3.0 and were not observed in our measurement confirming the fact that they do not belong to copper. It was not possible to identify the lines at 1099.9 and 1357.9 keV due to the interference of the Doppler-broadened 1356.5-keV line of 19F produced by the interaction of fast neutrons with the sample holder made of Teflon and of the 1101.3-keV line of 74Ge induced by fast neutrons with the germanium crystal, respectively. The 2095.0-keV line of 65Cu (reported at 2094.3 keV in NuDat 3.0) could not be uniquely identified due to the interference of the 2093.7-keV line of 207Pb induced by fast neutron on the lead shielding of the detector which also forms a doublet with the 2092.6-keV line of 63Cu. Interferences from delayed gamma rays of activation products induced by (n,p) and (n,α) reactions were found to be negligible. The intensities of the gamma rays calculated relative to the 962.0-keV line of 63Cu (100%) are given with the values determined in [5] in Tables 7 and 8. The relationship between the values is expressed by Eq. (5) with \(a\) =0.95 ± 0.03 and \(b\) =1.02 ± 0.03 as shown in Fig. 3c. The fit of the histogram of the residuals \(R\) with a Gaussian shows an agreement between the data at the 0.7σ level, indicating a good consistency (Fig. 4c). The \(\langle {\sigma }_{E\gamma }\rangle\)-values are given in Tables 7 and 8.

Table 7 Prompt gamma rays of 63Cu induced by inelastic scattering of fast neutrons
Full size table
Table 8 Prompt gamma rays of 65Cu induced by inelastic scattering of fast neutrons
Full size table

Detection limit

Neglecting any neutron and absorption effects, the detection limit (DL) representing here the smallest amount of pure element that can be detected was calculated by means of Eq. (1) from the minimum peak area \({P}_{E\gamma }(\mathrm{c})\) which can be expressed according to [18] by

$$P_{E\gamma } \left( c \right) = \frac{{\sqrt {2 \cdot B_{E\gamma } } }}{c}$$
(7)

with \({B}_{E\gamma }\) the area of the background below the gamma line of interest and c a predefined value for the relative uncertainty of the peak area. In the case of the presence of an interfering line \({P}_{E\gamma }(\mathrm{c})\) can be given by

$$P_{E\gamma } \left( c \right) = \frac{{\sqrt {2 \cdot \left( {P_{{\text{int}}} + 2 \cdot B_{E\gamma } } \right)} }}{c}$$
(8)

where \({P}_{int}\) is the net area of the interfering peak.

The detection limits of the elements investigated in this work as well as those of iron and indium were determined from their most intense gamma lines for a counting time of 12 h and for c = 0.5 corresponding to a peak area uncertainty of 50% using the beam background spectrum. The fast neutron flux is 1.40 108 cm−2 s−1 and the sample-to-detector distance 67 cm. In this case, the smallest amount of pure element that can be detected is 0.4 mg for titanium (48Ti, Eγ = 982.9 keV, \(\langle {\sigma }_{E\gamma }\rangle\) = 627 mb), 0.5 mg for iron (56Fe, Eγ = 846.9 keV, \(\langle {\sigma }_{E\gamma }\rangle\) = 586 mb), 0.9 mg for copper (63Cu, Eγ = 961.5 keV, \(\langle {{\varvec{\sigma}}}_{{\varvec{E}}{\varvec{\gamma}}}\rangle\) = 410 mb), 1.0 mg for aluminum (27Al, Eγ = 1013.9 keV, \(\langle {\sigma }_{E\gamma }\rangle\)= 136 mb) and 1.3 mg for indium (115In, Eγ = 933.1 keV, \(\langle {\sigma }_{E\gamma }\rangle\)= 222 mb).

Conclusions

The measurement of prompt gamma rays induced by inelastic scattering of fast neutrons on aluminum, titanium and copper was conducted with the FaNGaS instrument operated at FRM II. The fast neutron flux at sample position was 1.40 108 cm−2 s−1. The detection of gamma rays was performed at an angle of 90° between the neutron beam and the spectrometer. A total of 22, 72 and 120 prompt gamma lines were observed for aluminum, titanium and copper, respectively, and their relative intensities and spectrum-averaged production cross sections were determined. In comparison with the work of Demidov et al. [5], 57 gamma lines were detected additionally (1 for aluminum, 19 for titanium and 37 for copper). We also found that 18 lines (1 for aluminum, 10 for titanium and 4 for copper) were incorrectly assigned in [5]. These lines are not specified in the database NuDat 3.0. The relative intensities of the prompt gamma lines measured in our work are in good agreement (0.7σ level) with the values given [5]. The detection limits of aluminum, titanium, iron, copper and indium are around 1 mg for a counting time of 12 h which is acceptable in view of the chemical analysis of large samples with the FaNGaS instrument.