Introduction

At Heinz Maier-Leibnitz Zentrum (MLZ), Prompt Gamma Neutron Activation Analysis (PGNAA) [1,2,3] with cold and thermal neutrons is routinely used to determine non-destructively the elemental composition of small samples [4,5,6,7,8]. The FaNGaS (Fast Neutron-induced Gamma-ray Spectrometry) instrument was installed at MLZ in 2014 [9,10,11,12,13,14] and upgraded in 2020 [15, 16] to enable chemical analysis of large or small objects with fission neutrons, whose advantages were already demonstrated several decades ago [17,18,19,20,21]. The latter ones are produced with a converter made of uranium, which is highly-enriched (93% of 235U) and plunged into the heavy water moderator of the research reactor FRM II (Forschungs-Neutronenquelle Heinz Maier-Leibnitz). Beamtube SR10 (Strahlrohr 10) is used to extract the neutron beam from the outer core region into the experimental room of the MEDAPP (Medical Application) instrument [22] by means of various collimators and filters. The detection of the gamma radiation induced by fast-neutron interactions within the sample is performed with a high-purity germanium (HPGe) detector that is well-shielded and positioned at an angle of 90° relative to the axis of the incident neutron beam. In contrast to PGNAA, which is based on radiative neutron capture processes, prompt gammas induced by inelastic scattering of fast neutrons, i.e. (n,nʹγ) reactions, are mainly measured with FaNGaS. We call this method here “Prompt Gamma Analysis based on Inelastic Neutron Scattering” (PGAINS), even if in some cases gammas from other fast-neutron reactions such as (n,pγ)- or (n,αγ)-reactions can be detected [15, 16].

The development of a comprehensive data catalogue on (n,nʹγ) reactions is a primary objective of FaNGaS, aside from experimental and numerical optimization studies aiming for a higher peak-to-background ratio. Since the need for precise information on (n,nʹγ) reactions is observed to be continuously increasing in both the industrial and scientific community of nuclear technology and science [23,24,25], the aforementioned data is expected to meet this demand. Furthermore, it complements the”Atlas of Gamma-rays from the Inelastic Scattering of Reactor Fast Neutrons”, which was published by Demidov et al. in 1978 [26] and basically represents the only available database of inelastic neutron scattering. Although the data derived from measurements at FRM II generally is in reasonable agreement with the data from Demidov et al. [12,13,14,15,16], we pointed out the need for a cautious reevaluation of the data given in [26]. In addition, the FRM II measurements make new gamma-ray data available for the nuclear data community since they are performed with a mean energy of the incident neutron beam (2.30 MeV) that is closer to the expectation value of a classical fission spectrum on the one hand and much higher than in the work of Demidov et al. (0.63 MeV [27]) on the other hand.

In this work, nuclear data derived from the measurement of the prompt gamma rays of terbium induced by inelastic scattering of fast neutrons on a terbium(III) chloride hexahydrate (TbCl3·6H2O) sample is presented. The thermal and epithermal neutron flux within the sample was experimentally determined in order to correct interferences from radiative capture lines. Numerical simulations of the sample flux were also performed to determine the moderation of the neutrons due to the water of crystallization and the neutron self-shielding factors as well as to investigate a possible increase of the incident thermal and epithermal neutron flux due to the installation of the new multi-leaf collimator (MLC) as presumed in our previous work [15]. We present relative intensities and fast-neutron spectrum averaged partial cross sections of the terbium gamma lines inlcuding comparisons with available literature data. Additionally, cross sections measured for the oxygen and chlorine lines are compared with the values obtained in [15, 16]. Furthermore, we give the elemental detection limit for terbium.

Experimental

Prompt gamma radiation generated by interactions of a fission neutron beam with a TbCl3·6H2O powder sample (mass: 2.05 g, Tb: 0.87 g, Cl: 0.58 g, O: 0.53 g) was examined with the FaNGaS instrument. Technical specifications of the latter one can be found in [15]. During measurement, the powder was contained in a small bag of PTFE (Polytetrafluorethylene), whose maximum thickness was estimated as 6 mm. Attached to a thin PTFE rod, the sample was tilted by an angle of 45° with respect to the incident beam direction. In front of the sample, the magnitude of the fast-neutron flux was (1.13 ± 0.04) × 108 cm−2 s−1 with an average neutron energy of 2.30 MeV. The sample was irradiated for 9.7 h and counted for 7.7 h (live time). The gamma rays were measured at a sample-to-detector distance of 67 cm and perpendicular to the neutron beam direction, i.e. at an angle of 90°. The analysis of the recorded spectrum was carried out using the HYPERMET-PC software [28] and it is depicted in Figs. 1 and 2. Prompt gamma rays associated to fast-neutron reactions were identified using the NuDat 3.0 database [29] as well as related nuclear data from different evaluations for all nuclides covered in this work [30,31,32,33]. Gamma rays from radiative capture reactions were identified with the PGNAA database [34].

Fig. 1
figure 1

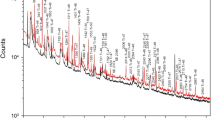
Measured gamma-ray spectra in the energy range from 0 to 3000 keV. The spectrum of the TbCl3·6H2O sample (red) was obtained during 27,879 s counting live time and the spectrum of the beam background (black) during 51,506 s. Prompt gamma rays that are written in black with an asterisk belong to either (n,pγ) reactions (S-35) and (n,αγ) reactions (P-32) on Cl-35 or represent X-rays from terbium. Prompt gamma rays marked in black and bold are issued from (n,nʹγ) inelastic scattering of fast neutrons on terbium. Prompt gamma rays from (n,γ) radiative capture reactions in terbium are written in black. Gamma rays written in bold blue are induced by inelastic scattering reactions on chlorine. Radiative capture gamma rays from Cl-35 are marked with light blue. Single and double escape peaks are indicated by the abbreviations SE and DE, respectively. Our former publications [10, 12] provide information on the origin of relevant background lines

Full size image
Fig. 2
figure 2

Measured gamma-ray spectra in the energy range from 3000 to 8000 keV. The spectrum of the TbCl3·6H2O sample (red) was obtained during 27,879 s counting live time and the spectrum of the beam background (black) during 51,506 s. Prompt gamma rays marked in black and bold are issued from (n,nʹγ) inelastic scattering of fast neutrons on terbium. Gamma rays written in bold blue are induced by inelastic scattering reactions on chlorine. Radiative capture gamma rays from Cl-35 are marked with light blue. Single and double escape peaks are indicated by the abbreviations SE and DE, respectively. Our former publications [10,11,12] provide information on the origin of relevant background lines

Full size image

Since a small fraction of neutrons scatter towards the detector the count rate of background lines was found to be increased by a mean factor of 1.53 ± 0.32. This factor was used in the interference corrections of background lines. Relevant interferences arising from escape peaks (denoted as SE and DE for a single or double escape peak, respectively) were found for two lines and corrected with the correction curves given in [16].

Method

For a prompt gamma ray of energy Eγ and produced by neutron capture or inelastic neutron scattering the net peak area, i.e. PEγ, can be described as [1, 12,13,14,15,16]:

$${P}_{E\gamma }= \frac{m}{M}{ \cdot N}_{{\text{A}}}\cdot h\cdot {\varepsilon }_{E\gamma }\cdot \langle {\sigma }_{E\gamma }\rangle \cdot \langle \Phi \rangle \cdot {t}_{c}{ \cdot f}_{n}{\cdot {f}_{mod}\cdot f}_{E\gamma }$$
(1)

where m (g) represents the mass of the considered element, M (g mol−1) equals the molar mass of the element, NA is the Avogadro number, h the abundance of the considered isotope, εEγ the full-energy-peak (FEP) efficiency, < σEγ > (cm2) the spectrum-averaged isotopic cross section for gamma-ray production, < Φ > (cm−2 s−1) the integral neutron flux in the considered energy range, tc (s) the counting live time, fn the neutron self-shielding factor and fEγ the gamma-ray self-absorption factor. The factor fmod accounts for possible moderation effects in samples that contain water.

The gamma-ray self-absorption factor fEγ was calculated analytically according to the following equation [1, 35]:

$${f}_{E\gamma }=\frac{1-{e}^{-\frac{\mu }{\rho }\cdot \rho \cdot l}}{\frac{\mu }{\rho }\cdot \rho \cdot l}$$
(2)

where l = 0.85 cm is the effective thickness of the sample, μ/ρ (cm2 g−1) represents the mass attenuation coefficient and ρ = 4.35 g cm−3 is the sample density. Including coherent scattering, the value of μ/ρ was obtained from the NIST (National Institute of Standards and Technology) photon cross sections database XCOM [36, 37]. For several discrete energies ranging between 100 and 5000 keV the corresponding fEγ values were calculated using Eq. (2). The variation of the gamma-ray self-absorption factors fEγ as a function of the gamma-ray energy Eγ is depicted in Fig. 3. Individual data points were fitted with a semi-empirical function that is given as:

$$f={a}_{0}+{a}_{1}\cdot \left(1-{e}^{-{a}_{2}\cdot {E}_{\gamma }}\right)+{a}_{3}\cdot \left(1-{e}^{-{a}_{4}\cdot {E}_{\gamma }}\right)$$
(3)

with a0 = −0.8829 ± 0.0528, a1 = 0.1558 ± 0.0187, a2 = 0.0011 ± 0.0002, a3 = 1.6665 ± 0.0416 and a4 = 0.0098 ± 0.0004.

Fig. 3
figure 3

Variation of the gamma-ray self-absorption factor fEγ as a function of the gamma-ray energy Eγ. The data points were obtained from NIST XCOM [36, 37] and the fit of the data after Eq. (3) is shown by the solid line

Full size image

The value of < σEγ > in Eq. (1) is coupled with the effective cross section < σ > (cm2) of a certain reaction via the absolute gamma-ray intensity IEγ, including the contribution of internal conversion, as:

$$\langle {\sigma }_{E\gamma }\rangle ={I}_{E\gamma } \cdot \langle \sigma \rangle$$
(4)

The effective cross section < σ > can be expressed as follows:

$$\langle \sigma \rangle = \frac{\sum_{i=m}^{n}\sigma \left({E}_{i}\right)\bullet \Phi \left({E}_{i}\right)}{\sum_{i=m}^{n}\Phi \left({E}_{i}\right)}$$
(5)

where Φ(Ei) denotes the neutron flux in the neutron energy bin i and σ(Ei) the neutron-bin averaged reaction cross section. The value of i = m corresponds to the first and i = n to the last neutron-energy bin in the considered neutron-energy ranges. The term \(\sum_{i=m}^{n}\sigma \left({E}_{i}\right)\bullet \Phi \left({E}_{i}\right)\) gives the rate of the reaction in units of atom−1 s−1.

With respect to the irradiation geometry of the previous FaNGaS set-up [12] we showed in [15] that the fast-neutron flux at irradiation position was reduced by about 20% due to an increase of the sample-to-neutron-source distance related to the installation of the new MLC of the MEDAPP facility. The same reduction is simply assumed here for the thermal and epithermal neutron flux and the resulting neutron energy spectrum at sample position is shown in Fig. 4. It can be split into three energy ranges designated as thermal (10−10 MeV < Ei < 1.42 × 10−7 MeV, m = 1, n = 7), epithermal (1.42 × 10−7 MeV < Ei < 0.06 MeV, m = 8, n = 49) and fast (0.06 MeV < Ei < 20 MeV, m = 50, n = 100), with the respective neutron fluxes of (7.63 ± 2.27) × 102 cm−2 s−1, (1.50 ± 0.07) × 106 cm−2 s−1 and (1.13 ± 0.04) × 108 cm−2 s−1. The integral neutron flux, covering all three aforementioned energy regions, is (1.15 ± 0.04) × 108 cm−2 s−1. The values of σ(Ei) were produced with the RECONR, BROADR and GROUPR modules of the NJOY Nuclear Data Processing System (Version 2016) [38, 39] using ENDF/B-VIII.0 [40] nuclear data library for the 35Cl(n,nʹγ)35Cl, 35Cl(n,pγ)35S, 35Cl(n,αγ)32P, 37Cl(n,nʹγ)37Cl, 159Tb(n,γ)160Tb and 159Tb(n,nʹγ)159Tb reactions. In the case of 35Cl(n,γ)36Cl, the nuclear data from ENDF-B-VIII.0 [40], JENDL4.0 [41], JEFF-3.3 [42] and TENDL-2019 [43] were considered due to considerable deviations between these libraries.

Fig. 4
figure 4

Neutron energy spectrum of FaNGaS as assumed in [15, 16] incident on the sample (right scale of y-axis) and variation of the NJOY grouped microscopic cross sections σi(E) averaged over the neutron energy bin i as a function of the neutron energy (left scale of y-axis) for total (n,tot), fast-neutron inelastic scattering (n,nʹγ), (n,pγ) and (n,αγ) reactions for terbium and oxygen (top side) and chlorine (bottom side). The values of the (n,tot) reaction for oxygen and chlorine are elemental and they were calculated as the sum of isotopic cross sections in each energy bin multiplied with the corresponding isotopic abundance

Full size image

The effective cross sections < σ > determined by means of Eqs. (4) and (5), respectively, are given in Table 1 for the aforementioned neutron-energy ranges and observed reactions. The neutron-energy dependence of the NJOY grouped cross sections is depicted along with the neutron energy spectrum in Fig. 4. Due to large uncertainties of the flux in the thermal neutron-energy range, cross sections given in JANIS (Java-based nuclear information software) [44] were preferred.

Table 1 Effective cross sections < σ > for (n,γ), (n,nʹγ), (n,pγ) and (n,αγ) reactions observed from the irradiation of the TbCl3·6H2O sample calculated with Eq. (5) and neutron self-shielding factors fn for all three neutron-energy ranges considered determined with MCNP6 [45, 46]. Data for the total (n,tot) reaction is given elementary
Full size table

Sample neutron flux

Many radiative-capture lines of 159Tb were found to interfere with lines from the 159Tb(n,nʹγ)159Tb reaction and their corrections require knowledge on the thermal and epithermal neutron flux within the sample. The latter contains 29 wt% water of crystallization, which could moderate the epithermal neutrons of the incident beam.

The sample neutron flux was determined in a first step by means of numerical simulation performed with the Monte Carlo N-Particle (MCNP, version 6.1) [45, 46] code. Use of ENDF/B-VIII.0 data [40] was enabled by means of the Lib80x library [47]. The neutron-energy distribution of the incident spectrum given in Fig. 4 was used to simulate the irradiation of a 6 mm thick TbCl3·6H2O slab with a mass corresponding to the one of our experiment and tilted by an angle of 45°. The sample neutron flux, derived with the F4 Tally, is depicted in Fig. 5. It shows a non-negligible increase of the flux below a neutron energy of 1 eV resulting from water moderation. The flux in the three neutron energy regions is (8.3 ± 2.5) × 103 cm−2 s−1 for thermal neutrons, (3.2 ± 0.4) × 106 cm−2 s−1 for epithermal neutrons and (1.15 ± 0.09) × 108 cm−2 s−1 for fast neutrons. In order to determine the neutron self-shielding (fn), irradiation of the sample with each component of the incident flux (thermal, epithermal and fast) was simulated separately with 108 primary neutrons. The neutron self-shielding factor was calculated as the ratio of the neutron flux within the sample (F4 tally) to the neutron flux within a diluted sample of 10−6 the density [48,49,50], i.e. in void in practice. In fact, this is equivalent to the ratio of the sample flux (F4 tally) to the incident neutron flux (F2 tally). The value of fn = 0.991 for fast neutrons implies that the self-shielding effect is negligible, whereas values of fn = 0.772 for thermal and fn = 0.976 for epithermal neutrons must be considered. The simulations to determine the moderation (fmod) factors comprised also three simulations (thermal, epithermal, integral) and the number of primary particles was chosen here to yield statistical uncertainties of the same order of magnitude in each simulation. The moderation factors were calculated as the ratio of the thermal and epithermal sample neutron flux obtained from the simulations with the part of the incident neutron-energy distribution of interest (i.e. thermal and epithermal) to the simulation with the whole incident neutron-energy distribution (flux values given above). The resulting moderation factors are fmod = 14 ± 6 for thermal neutrons and fmod = 2.1 ± 0.4 for epithermal neutrons. Dividing the sample fluxes by the corresponding shielding and moderation factors reproduces well the incident flux values at sample position as given above.

Fig. 5
figure 5

Neutron energy spectrum of FaNGaS assumed in our previous works [15, 16] (blue curve), reconstructed in this work (red) and the volume-averaged sample flux derived with MCNP6 (dark green)

Full size image

The thermal and epithermal neutron flux within the sample were also determined experimentally from the net counts of the interference-free capture lines of 159Tb (193, 243, 339, 357, 451, 464 and 525 keV) and 35Cl (1164, 1951 and 1959 keV) using Eq. (1) with fn = 1 and fmod = 1 and Eqs. (4) and (5). The intensities of the gamma rays Iγ were deduced from the partial elemental capture cross sections and the associated isotopic cross sections for thermal neutrons as given in [34]. The counts of the 159Tb and 35Cl lines were corrected first for the contribution of the fast neutrons with a flux of 1.13 × 108 cm−2 s−1 and the cross sections given in column 5 of Table 1. The epithermal neutron flux was then determined directly from the lines of 159Tb as the rate of the 159Tb(n,γ)160Tb reaction induced by thermal neutrons is negligible (the effective cross sections for thermal and epithermal neutrons are approximately the same (see Table 1) and the thermal neutron flux is about four orders of magnitude less than the epithermal neutron flux). The value obtained for the latter is (6.1 ± 1.6) × 106 cm−2 s−1. The thermal neutron flux, obtained from the lines of 35Cl after correction of the contribution of epithermal neutrons, is (3.4 ± 1.4) × 104 cm−2 s−1. The experimentally determined sample fluxes are significantly higher than the values obtained by simulation, indicating a possible increase of the incident thermal and epithermal neutron flux owing to the MLC. Correcting the experimental flux with the corresponding shielding and moderation factors provides a thermal and epithermal flux of (3.2 ± 1.3) × 103 cm−2 s−1 and (2.9 ± 0.8) × 106 cm−2 s−1, respectively, at sample position. The ratio of these flux values to the previously assumed values yields scaling factors of 4.1 ± 2.1 and 2.0 ± 0.5, respectively, which are used to rescale the flux in each energy bin of the thermal and epithermal region, respectively. The proposed new neutron energy spectrum at sample position is shown in Fig. 5.

Gamma rays from inelastic neutron scattering in terbium

A total of 124 prompt gamma lines assigned to the 159Tb(n,nʹγ)159Tb reaction were measured. Aforementioned gamma rays are marked accordingly in Figs. 1 and 2 and their corresponding data is provided in Table 2. Interferences with lines arising from the 159Tb(n,γ)160Tb and 35Cl(n,γ)36Cl reaction are corrected with the intensities taken from [34] by means of Eqs. (1), (4) and (5). Four lines were corrected for the contribution of delayed lines of 160Tb as described in [13] with intensities taken from [52]. With respect to [34] and [52] 23 radiative capture lines from 159Tb and 5 lines from 35Cl were found to interfere significantly with (n,nʹγ) lines with contributions ranging between 2 and 53%. Doppler broadening [53, 54] was only observed for gamma lines from chlorine. The composition of the TbCl3·6H2O sample was checked using the measurement of the PVC foil performed in our previous work on CeCl3 [16]. The interference-free (with respect to data on [29, 30]) lines at 1185, 1763, 2645, 2694, 3002, 3085, 3103 and 3163 keV (see Figs. 1 and 2) from chlorine were used to calculate an average chlorine mass of (0.58 ± 0.01) g, which agrees well with the value from the stoichiometry of the sample.

Table 2 Prompt gamma rays of 159Tba induced by inelastic scattering of fast neutrons
Full size table

Gamma-ray intensities were determined relative to the 331-keV line. They are presented together with the values determined in [26] in columns 3 and 6 of Table 2. We have detected 54 of the 60 lines listed in the Demidov Atlas. The lines listed at energies of 154.0, 194.1, 272.9, 282.7, 339.2, 451.3, and 464.6 keV are either partly unassigned or partly assigned to radiative capture lines of 159Tb. Based on [34] we found that all of those lines belong to the neutron capture reaction in terbium except the 272.9-keV line, which belongs to the 159Tb(n,nʹγ)159Tb reaction as specified in [29, 30]. Gamma rays with energies of 260.9, 274.8, 596.4, 608.2, 617.5 and 1003.0 keV given in [26] have not been observed in our work. From the aforementioned lines, only the lines at 274.8 and 617.5 keV were assigned to fast-neutron inelastic scattering by Demidov. These assignments seem to be reasonable with respect to [29, 30], but it is surprising that our spectrometer with a better energy resolution did not distinguish the 617.5-keV line from a close-lying line at 615.4 [26], also observed in our spectrum. However, a relative intensity of (36 ± 2)% for our line at 615.6 keV agrees well with the sum of the intensities of the two lines given in [26], (34 ± 10)%. For the lines at 596.4 and 608.2 keV, assigned to (n,γ) reaction and unassigned, respectively, in [26], no suitable transition is proposed in [30]. In our measurement these lines are interfered by background lines of 74Ge and 73Ge [10, 12], respectively. As both lines also appear in the background analysis in the Demidov Atlas we assume an erroneous identification. Absence of the unassigned lines at 260.9 and 1003.0 keV in our measurement and missing data on [29, 30] helps providing support that they do not belong to terbium.

On the other hand, compared to [26] we have identified 76 new gamma lines. The identification of new lines is mainly associated to the better energy resolution of our spectrometer and our higher mean neutron energy (2.30 MeV vs. 0.63 MeV [27]). In contrast to [26] we were able to resolve doublets in the lines listed at energies of 184.2, 305.2, 947.0, 1094.1, 1195.1 and 1276.7 keV in [26]. It is worth to mention that from all 124 observed gamma lines 76 are not specified in [29, 30]. Of those, 16 are listed in the Demidov Atlas, confirming that they originate from fast-neutron inelastic scattering. The other 60 lines detected in our measurement are unambiguously associated to the 159Tb(n,nʹγ)159Tb reaction. All these new lines may help to extend the decay scheme of terbium.

The relationship between the relative intensities derived from our work and those listed in [26] is shown in Fig. 6. The values have been fitted with the following semi-empirical function:

$${I}_{R}=a\cdot {\left({I}_{RD}\right)}^{b}$$
(6)

with a = 1.27 ± 0.17 and b = 0.92 ± 0.06.

Fig. 6
figure 6

Correlation between the relative intensities IR of the prompt gamma rays issued from fast-neutron inelastic scattering (n,nʹγ) reactions on terbium measured in this work and the relative intensities IRD listed in the Demidov Atlas [26]. The fit of the data according to Eq. (6) is shown by the solid line

Full size image

The two measurements show a good agreement as the average value of the intensity ratio, i.e. IR/IRD, is 1.16 ± 0.39. In order to assess the consistency further, the two data sets are shown in Fig. 7 as a histogram of the residuals R in units of standard deviation [σ], determined as:

Fig. 7
figure 7

Histogram plot of the residuals R, calculated with Eq. (7) in units of standard deviation [σ], demonstrating the agreement between the relative intensities of prompt gamma rays from the 159Tb(n,nʹγ)159Tb reaction derived in this work with the data listed in [26]. The data was fitted with a Gaussian, which is shown by the solid line

Full size image
$$R=\frac{{I}_{R}-{I}_{RD}}{\sqrt{{\left({s}_{{I}_{R}}\right)}^{2}+{\left({s}_{{I}_{RD}}\right)}^{2}}}$$
(7)

The data is fitted with a Gaussian and it agrees at the 1.6σ level with the Gaussian centroid being aligned at R = 0.00 ± 0.26, indicating no relevant systematic effect. One should be aware, however, that Demidov et al. mention the presence of capture lines in their spectra, but no reliable information is given according to their treatment of interferences.

The partial cross sections for the production of identified gamma-rays, averaged over the fast-neutron spectrum and calculated by means of Eq. (1) with a flux of (1.13 ± 0.04) × 108 cm−2 s−1, are given in column 4 of Table 2.

Prompt gamma rays of oxygen and chlorine

The prompt gamma lines induced by interaction of fast neutrons on oxygen and chlorine were also analyzed and the corresponding partial cross sections determined by means of Eq. (1). The values obtained for the 1981-keV line from 18O(n,nʹγ)18O, 213 ± 40 mb, and for the 6129-keV line from 16O(n,nʹγ)16O, 2.22 ± 0.31 mb, agree well with the values achieved in our work on CaCO3 [15], i.e. 201 ± 28 mb and 2.20 ± 0.37 mb, respectively. The 1981-keV line was corrected for the interference with the DE from the 3002-keV line of 35Cl, with a contribution to the net counts of (39.4 ± 6.6)%.

In the case of chlorine, 28 lines were observed, 15 associated to 35Cl(n,nʹγ)35Cl, 9 to 37Cl(n,nʹγ)37Cl and 4 to 35Cl(n,pγ)35S. The 78.0-keV line from 35Cl(n,αγ)32P observed in [16] was not considered uniquely due to the strong interference of the 79-keV line from the 159Tb(n,nʹγ)159Tb reaction. The ratios of measured partial cross sections to the values obtained in our work on CeCl3 [16] are shown in Fig. 8. Taking the corresponding uncertainties into account, the data of both measurements is observed to agree well with each other.

Fig. 8
figure 8

Ratio of gamma-ray production cross sections < σEγ(90°) > in mb for chlorine lines from (n,nʹγ) and (n,pγ) reactions obtained in this work compared to these obtained in our previous work [16]. The solid line represents the mean value of the ratios, i.e. 1.00 ± 0.27, while the dash-dotted lines represent the error margins corresponding to one standard deviation

Full size image

Detection limit

The smallest amount of a pure element that is related to the measurement of a net signal above the background with a certain standard deviation σ obtained by the irradiation over a certain time corresponds to the detection limit (DL). Neglecting neutron self-shielding and gamma-ray self-absorption, i.e. fn = 1 and fEγ = 1, respectively, the value of the DL can be determined with Eq. (1) from the minimum peak area PEγ(c) that could be expressed according to [55] as:

$${P}_{E\gamma }\left(c\right)=\frac{\sqrt{2\cdot {B}_{E\gamma }}}{c}$$
(8)

where BEγ represents the area of the background below the gamma line of interest and c equals a predefined value for the relative uncertainty of the peak area.

The DL of terbium was calculated for the most intense gamma line by means of Eqs. (1) and (8) assuming a counting live time of 12 h. The HYPERMET-PC [28] software was used to determine the value of BEγ from the beam background. For a peak area uncertainty of 50%, i.e. a value of c = 0.5 in Eq. (8), the smallest amount of pure element that can be detected is 1 mg for terbium (159Tb, Eγ = 57.9 keV, < σEγ(90°) >  = 445 mb).

Conclusions

The emission of prompt gamma rays in terbium induced by (n,nʹγ) reactions was examined with the FaNGaS instrument by irradiating a TbCl3·6H2O sample with fission neutrons. To correct for interferences of radiative-capture lines of terbium and chlorine the thermal and epithermal neutron flux within the sample were determined from the interference-free (n,γ)-lines of terbium and chlorine. Simulations performed with the MCNP code show a significant increase of the neutron flux below a neutron energy of 1 eV, which is related to the moderation of neutrons by water of crystallization. Comparison of the experimental and simulated sample-flux values indicates an increase of the incident thermal and epithermal neutron flux by a factor of 4 and 2, respectively; the fast-neutron flux being unchanged. We associate the increase of the flux in the thermal and epithermal regions to the MLC made of materials enabling neutron moderation.

In total, we identified 124 prompt gamma lines from the 159Tb(n,nʹγ)159Tb reaction. Relative intensities as well as fast-neutron spectrum-averaged partial gamma-ray production cross sections were measured. Compared to the work of Demidov et al. [26] we were able to detect 76 additional gamma lines, which is mainly attributed to the better energy resolution of our detector and a higher mean neutron energy. Since the majority of observed lines is unreported in [29, 30], we consider this work as an important contribution to the expansion of terbium level and decay schemes. Our relative intensities are in reasonable agreement (1.6σ level) with the values listed in [26]. The detection limit of terbium was determined as 1 mg assuming a counting time of 12 h. Furthermore, the partial production cross sections for prompt gamma lines of oxygen and chlorine were found to agree well with the values from previous works [15, 16].