Molecular dynamics simulation of polypropylene: diffusion and sorption of H₂O, H₂O₂, H₂, O₂ and determination of the glass transition temperature

Abstract

Molecular dynamics (MD) simulations in the canonical (NVT) and the isothermal-isobaric (NPT) ensemble using COMPASS III molecular force fields were performed to study the penetrant diffusion of water (H₂O), hydrogen peroxide (H₂O₂) and oxygen (O₂) in isotactic polypropylene (iPP) and hydrogen (H₂) in iPP and atactic polypropylene (aPP) for time intervals up to 11 ns and in the case of H₂O₂ up to 22 ns. We found robust cluster formation in the case of H₂O and H₂O₂. Further, the diffusion coefficients for all these systems were estimated by mean-square displacement analysis. Our results are consistent with previously published experimental and computational data except for the diffusion of H₂ in polypropylene where our results are one and two orders of magnitude higher, respectively. Grand Canonical Monte Carlo (GCMC) simulations were used to determine the sorption loading and saturation concentration of H₂O, O₂ and H₂ in iPP, where we find good agreement for H₂O with experimental results. By means of MD simulation the glass transition temperature (T_g) of iPP was estimated to 273.66 ± 4.21 K which is consistent with previously published experimental results.

Introduction

The world’s demand for the polymeric material polypropylene (PP) is the second largest, after polyethylene (PE), and it grows from year to year. In 2018 the global production volume amounted to 56 million tons and by 2026, it is forecasted that the production volume will reach 88 million tons [1]. In terms of sustainability, the goal must be to reduce this output significantly and to force the recycling and reuse of material. However, this requires the design of high quality and robust PP-based products that maintain their integrity over long times. Especially when used in moisture environments, e.g. for food packaging or as part of household appliances like washing machines, polymeric materials show aging and degradation behaviour that can significantly reduce their quality and lifetime. Responsible for this behaviour are catalytic reactions and autoxidation processes induced by oxygen (O₂) or reactive oxygen species (ROS) such as hydrogen peroxide (H₂O₂) producing molecules like water (H₂O) and hydrogen (H₂) as reaction products. When used in washing machines, H₂O as a molecule is even more important, since it serves as a carrier medium for laundry detergents and bleaching agents [2, 3]. In order to study such interactions on an atomistic level Molecular dynamics (MD) and Monte Carlo (MC) simulations have proven to be powerful computational tools. With increasing hardware specs and more advanced digital analysing methods, computational approaches play an important role in the process of guiding experimental developments and studying the complex interaction and behaviour of molecules in different polymer systems.

In 1989 and 1990 Trohalaki et al., Takeuchi and Okazaki, Takeuchi as well as Madkour et al. in 1992 performed pioneering studies of the penetrant diffusion of carbon dioxide and O₂ in polyethylene (PE) by means of MD [4,5,6,7,8]. Until 1994 Boyd et al. and Müller-Plathe provided results on methane as a penetrant in PE [9,10,11,12,13], in polyisobutene (PIB) [9, 10, 12] and atactical polypropylene (aPP) [12, 14]. Furthermore, Müller-Plathe et al. studied the behaviour of O₂ and H₂ as diffusive penetrants in aPP and PIB [14,15,16] as well as helium in PIB [16].

The experimental determination of diffusive properties of H₂O and other polar penetrants in polyolefins is difficult due to the small solubility that is caused by the hydrophobic character of the polymeric host material. In contrast to this, MD and MC simulation methods provide excellent tools to study diffusive properties theoretically on an atomic scale. The first computational investigation of H₂O in PE was carried out by Tamai et al. in 1994 and 1995 [17, 18]. However, they modelled only a single H₂O molecule in a PE membrane. Tamai et al. further investigated the diffusion of five H₂O molecules in poly(dimethylsiloxane) (PDMS) and found an aggregation of these molecules due to the formation of hydrogen bonds between them. Moreover, it has been found that the diffusion coefficients of aggregated H₂O molecules compared to a single H₂O molecule in PDMS are smaller by a factor of 50 [17].

Further investigations of H₂O as a penetrant were carried out by Fukuda and Kuwajima in 1997 with one, three and ten H₂O molecules in PE. They found H₂O molecules aggregating and forming clusters of various sizes and the obtained diffusion coefficients were reduced by one order of magnitude compared to that of a single H₂O molecule [19]. Fukuda and Kuwajima extended their study of H₂O as a penetrant in aPP and isotactical polypropylene (iPP). Again, they found a clustering of the H₂O molecules in both systems. For iPP they found that the clustered structure is robust and maintained over several nanoseconds [20].

More recently in 2009 Chang-Gui et al. and in 2010 Rong et al. calculated the diffusion coefficient of O₂ in PP [21], PE, iPP and poly(vinyl chloride) (PVC) [22] by means of MD. Furthermore, by using a Grand canonical Monte Carlo (GCMC) approach they were able to determine the number of O₂ molecules absorbed in PP [21] and PE [22]. In 2013 Börjesson et al. calculated the solubility, diffusion coefficients, and the permeation of O₂ and H₂O in PE using an MD and MC approach [23]. In 2019 Sun et al. studied the diffusion behaviour of five different flavor organic molecules in low density polyethylene (LDPE) as well as the effects of the presence of these flavors on the diffusion of O₂ and H₂O by combined experimental and MD simulation studies. They found out that the presence of these flavors hinders the diffusion of O₂ and H₂O because of the smaller available free volume and negative interaction energies between O₂ and H₂O with the flavor molecules [24].

Due to its high chemical reactivity H₂O₂ plays an important role in many biological processes as well as in cleaning and pharmaceutical applications, e.g. as protection against microbes, as a bleaching agent and as a decontamination agent. Technical applications in these areas typically use polymers since they are cheap, reliable, and light weighted as compared to other materials. However, exposed to H₂O₂ polymers suffer from degradation of the surface and the bulk [25,26,27]. Thus, understanding the interaction of H₂O₂ with a polymer matrix is important for the development of robust and inert polymer materials. The experimental analysis of such interaction is difficult since there are superimposing effects, e.g. one cannot disentangle desorption from diffusion effects. On the other hand, a computational analysis allows to disentangle such superimposing effects by studying the interactions of H₂O₂ within a polymer matrix solely.

There is little experimental results on the diffusivity of H₂O₂ in polymers available: In 1959, Dietrick and Meeks studied the permeability of H₂O₂ diluted in LDPE, PVC, polyester and polyvinylidene chloride [28]. In 2011, Radl et al. determined the diffusion coefficient and the saturation of H₂O₂ in PP, LDPE, PVC and glass. For PP they determined D = 5.50 · 10^–9 cm²/s for T = 298 K and D = 2.00 · 10^–8 cm²/s at T = 308 K, respectively. The results differ by a remarkably large factor of 3.6 [29]. In 2018, Tjell and Almdal studied the permeability of H₂O₂ in different commercially available water-swelled polyurethanes [25]. Recently, Yabuta et al. determined the diffusion coefficients in the range of D ~ 10^–8 cm²/s for H₂O₂ in PE, chlorosulfonated PE, PVC, silicone and polyoxymethylene (POM) at 298 K in aeration experiments [26].

In this paper we provide molecular dynamics simulation results for small molecules in PP. Since commercially used PP is usually isotactic, the focus of our investigation is on iPP. We study the clustering behaviour of H₂O and for the first time of H₂O₂ using one and ten molecules within an iPP matrix for different time scales up to 11 ns and in the case of ten H₂O₂ molecules in iPP for up to 22 ns. The latter is necessary due to the observation of subdiffusive behaviour at short times. In addition, we calculate and compare the diffusion coefficients for H₂O, H₂O₂, O₂ and H₂ in iPP and for H₂ also in aPP. With respect to the glassy and rubbery state of PP and an expected strong temperature dependency of the diffusion coefficients, we calculated and compared the diffusion coefficient of O₂ for different temperatures. By means of GCMC sorption loadings and saturations of H₂O, O₂ and H₂ in iPP are estimated. Furthermore, we determined the glass transition temperature of iPP by means of MD simulations.

Simulation models and methodology

We used Materials Studio version 20.1 [30] for our simulation studies, including its pre-processing and post-processing capabilities. Constant temperature MD simulations have been carried out in the canonical ensemble (NVT) and in the isothermal-isobaric ensemble (NPT). Furthermore, we used the Grand canonical Monte Carlo (GCMC) approach to determine the sorption loading of H₂O, O₂ and H₂ in isotactic polypropylene (iPP).

For the MD simulations the proper choice of the force field is crucial to obtain accurate results. The Condensed-phase Optimized Molecular Potentials for Atomistic Simulation Studies (COMPASS) force field [31] and the Polymer Consistent Forcefield (PCFF) [32, 33] are improvements of the Consistent Force Field (CFF) developed in the 1990’s by Maple et al. [34,35,36]. These force fields are recommended for studies of soft materials like polymers or carbon-based systems [37,38,39]. In a direct comparison of COMPASS and PCFF, several authors report that COMPASS provides a better agreement with experimental results [40], is less erroneous, more reliable, delivers more uniform results [41], determines the steady-state density closer to the correct density and delivers smaller volatility in the calculation of mechanical properties [42].

The COMPASS force field was further improved to produce more reliable results and to be applicable to different materials systems [31, 43,44,45,46]. Thus, for our study we used the latest version COMPASS III [47].

Preparation of the polypropylene model system

For the construction of the iPP model systems and one aPP model system we used the Build Polymers tool of Materials Studio. After geometry optimization, a three-dimensional box with periodic boundary conditions is created via the Amorphous Cell module. The polymer chains are added into the box segment by segment while every new segment takes the interaction with previously placed atoms into account. Using this technique an amorphous polymer structure with a realistic conformation can be constructed, while minimizing the number of close contacts [40, 48]. In a final step we performed another geometry optimization of the simulation cell to avoid numerical instabilities.

We employ a nomenclature for our model systems similar to Fukuda and Kuwajima [19, 20]. A three-dimensional cell consisting of four isotactic polypropylene chains and each chain containing 50 monomers is referred to as iPP50(4). If the model contains additional small molecules, e.g. five O₂-molecules it is referred to as iPP50(4-5o). Table 1 shows the abbreviations used in the nomenclature for this study. Table 2 shows the different model systems that have been created and studied in this work.

Table 1 List of abbreviations used in the nomenclature for the studied simulation cells

Table 2 Systems and studies performed in this work

Simulation details

All MD and GCMC simulations have been carried out using the Forcite Plus module of Materials Studio based on the COMPASS III force field. We obtained the best numerical stability using a time step length of 1 fs. To reduce the computational effort of the MD simulations, we used the group based electrostatic and van der Waals calculation approach as implemented in the Materials Studio software with a cut-off radius of 15.5 Å [30]. The temperature is controlled by a Nosé-Hoover thermostat with the default value for Q of 0.01. The maximum energy deviation between successive steps is set to the default value of 50,000 kcal/mol. In all GCMC simulations the electrostatic interactions were calculated using the Ewald summation method and a cut-off radius of 12.5 Å.

Equilibration

After construction the polypropylene chains do not uniformly occupy the space in the simulation cell and therefore the total energy of the system is far from equilibrium. To equilibrate the system, we performed MD simulations for 100 ps in the NVT ensemble at temperatures given in Table 2.

The iPP240(4) and iPP60(4) cells undergo an additional annealing procedure consisting of five heating and cooling cycles for further relaxation of internal stresses in the NPT ensemble at a pressure of 0 GPa. Each cycle consists of three heating and cooling stages over ΔT = 50 K of which each stage has a duration of 100 fs.

Diffusion studies

In order to determine the diffusion coefficients of the different penetrants in the PP50 cells we have been performed 10 simulations per system in the NPT ensemble, each starting with random initial velocities and temperatures given in Table 2. The pressure was set to 10^–4 GPa and the total simulation time was set to 11 ns except for iPP50(3-10hp) where it was set to 22 ns. Just like in the NVT ensemble, the temperature is controlled by a Nosé-Hoover thermostat, the pressure is controlled by a Berendsen barostat with a decay constant of 0.1 ps.

The diffusion coefficients D of the different penetrants in the polypropylene matrix are determined by the mean-square displacement (MSD) of the centre of mass:

$$MSD\left(t\right)=\langle {\left|{r}_{i}\left(t\right)-{r}_{i}(0)\right|}^{2}\rangle ,$$

(1)

where ${r}_{i}(0)$ is the i-th initial position and ${r}_{i}\left(t\right)$ is the position of the same molecule after a time t and $\langle \dots \rangle$ denotes the ensemble average. For long enough times the Einstein relation [49] predicts a linear slope of the MSD vs. time for regular Brownian diffusion. Therefore, D can be determined by taking the slope of a linear fit to MSD(t) vs. t according to

$$D=\frac{1}{6}\sum_{i=1}^{N}\frac{\Delta MSD\left(\Delta t\right)}{\Delta t}$$

(2)

However, for short times one can observe local mobility followed by an anomalous diffusion behaviour where MSD(t) is proportional to tⁿ with n < 1 [50]. In order to simulate sufficiently long times this behaviour must be taken into account.

Sorption studies

After equilibration of the iPP60(4) cells by the above-described procedure, the Sorption Module of Materials Studio is used to carry out GCMC simulations. Within our simulation protocol the first 50,000 equilibration steps are used to adjust the fugacities and the temperature in the PP matrix followed by 150,000 production steps. The fugacities and the temperature in the PP matrix are kept constant as if the system was in open contact with an infinite sorbate reservoir at a fixed pressure of 101.325 kPa. During a production step a sorbate exchange with the reservoir as well as translation, rotation or torsion change of existing sorbate molecules are allowed to happen. The tool specific sample spacing is set to 25 steps and the grid spacing to 0.25 Å. For each system five simulations have been performed. With M_pp and M_s being the molecular weights of a polypropylene chain and one small-molecule sorbate, respectively, one can calculate the saturation content s in wt.% of the averaged penetrant loading l over all simulation steps. The factor n denotes the number of polypropylene chains within the simulation cell, i.e. for iPP60(4) n = 4.

$$s\ (wt.\%)=\frac{{l\cdot M}_{s}}{{n\cdot M}_{pp}}\cdot 100\%$$

(3)

Determination of the glass transition temperature

A common approach to determine one of the most important properties of amorphous polymers, the glass transition temperature, is to analyse the change in density or specific volume as a function of temperature [51]. While the volume increases linearly with increasing temperature due to the increasing molecular vibration, in amorphous or semi-crystalline materials one can find a change in that linear slope at the so-called glass transition temperature T_g distinguishing the glassy state (below T_g) from the rubbery state (above T_g). In the rubbery state the polymer chains can wiggle around causing the whole system to be more elastic. Using ten iPP240(4) model systems equilibrated at T = 303 K we determined the glass transition temperature according to the following procedure: We decreased the temperature from T = 303 K to T = 243 K in steps of ΔT = 5 K. At T = 303 K we used random initial velocities, while for every following temperature the configurations and velocities of the previous simulation were used as initial conditions. The first 150 ps of every simulation were discarded for equilibration purposes, followed by 50 ps for determining the relation of the specific volume and temperature.

Results and discussion

Clustering of H₂O and H₂O₂

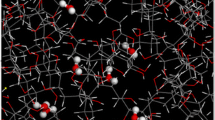
Fukuda and Kuwajima discovered and described the clustering of H₂O molecules in PP [20]. Here, we show that their results are reproducible within out setup. Furthermore, we performed simulations with H₂O₂ and obtain very similar results. Figure 1 shows snapshots of an iPP50(3-10w) cell in its initial configuration, after a 100 ps relaxation in the NVT ensemble and after 11 ns production-run in the NPT ensemble. Figure 2 shows snapshots at the same times for iPP50(3-10hp). After the production-run the formation of a compact cluster can be observed in the case of H₂O and H₂O₂, respectively. Interestingly, already after relaxation sub clusters of different sizes appear. For iPP50(3-10w) we find three sub clusters containing five, three and two H₂O molecules and for iPP50(3-10hp) we find sub clusters of four, four and two H₂O₂ molecules, respectively. While each of the 11 ns production-runs results in compact clusters, the intermediate configurations after relaxation differ in the amount and size of the sub clusters formed. To prevent these random pre-clustering during the relaxation we set up a series of iPP50(3-10w) simulation cells in which the H₂O molecules were fixed in their position during relaxation. We refer to this model system as iPP50(3-10w)_fixed. During the NPT production-runs this constraint is lifted. Figure 3 shows snapshots of an NPT simulation of iPP50(3-10w)_fixed in its initial configuration, after 100 ps, after 1 ns and in its final configuration. After 1 ns there is a single fully clustered configuration that persists until the end of the simulation at 11 ns. The same fast clustering after 1 ns we found for our other production-runs as well. However, we have to emphasize that this is not a general result but occurs due to the high H₂O concentration in our model system. For a larger simulation cell with a smaller concentration of H₂O we expect a longer formation time due to larger initial distances of the H₂O molecules. However, our results show that once the cluster is formed, it moves through the free volume in the iPP as an entity. For our analysis of diffusion coefficients, we have to distinguish between the motion of a single molecule not being influenced by the cluster forming process and the motion of a cluster of molecules which we will do in the following section.

Fig. 1

Typical snapshots of the iPP50(3-10w) study, a in its initial configuration: The H₂O molecules are randomly distributed within the simulation box, b after a 100 ps NVT relaxation: The H₂O molecules form sub clusters containing five, three and two molecules, c after an 11 ns NPT production-run: A single compact cluster containing all ten H₂O molecules is formed

Fig. 2

Typical snapshots of the iPP50(3-10hp) study, a in its initial configuration: The H₂O₂ molecules are randomly distributed within the simulation box, b after a 100 ps NVT relaxing-run: The H₂O₂ molecules form sub clusters containing four, four and two molecules, c after an 11 ns NPT production-run: A single cluster containing all ten H₂O₂ molecules is formed

Fig. 3

Typical snapshots of the iPP50(3-10w)_fixed study: During the NVT relaxation the H₂O molecules are fixed in their positions while the iPP chains could relax, a the initial configuration for the 11 ns NPT production-run, b after 100 ps showing three sub clusters containing four, three and three H₂O molecules, c after 1 ns showing a single cluster containing all ten H₂O molecules, d final configuration after the 11 ns showing a single cluster

Determination of diffusion coefficients

We found 11 ns for the molecules H₂O, O₂ and H₂ and 22 ns for H₂O₂ to be sufficiently long enough times to apply the Einstein relation [49] to determine the diffusion coefficients by a linear fit of the MSD(t) curve (Eq. 2). As shown in Figs. 4, 5, 6 and 7 for non-polar penetrants such as O₂ and H₂ the linear fit works very well with R² > 0.94. In contrast to that, the fit to the MSD curves for the polar molecules H₂O and H₂O₂ (Figs. 4, 5, 6 and 7) yields R² values of less than 0.9 showing clear deviations from the linear behaviour, i.e. Brownian diffusion dynamics. This is caused by the interactions of the hydrophobic iPP with the polar penetrants as well as the interaction of the polar molecules among each other.

Fig. 4

MSD curve for the diffusion of O₂ in the system iPP50(3-10o) at 298 K

Fig. 5

MSD curve for the diffusion of H₂ in the system iPP50(3-10h) at 298 K

Fig. 6

MSD curve for the diffusion of H₂O in the system iPP50(3-10w) at 298 K

Fig. 7

MSD curve for the diffusion of H₂O₂ in the system iPP50(3-10hp) at 298 K

As described above, for our investigation of the polar molecules H₂O and H₂O₂ we want to distinguish between the diffusive behaviour of a single molecule and a cluster of molecules. Fukuda and Kuwajima [20] compared the systems aPP500(3-1w) with aPP500(3-3w) at 298 K where their calculated diffusion coefficient for the H₂O cluster of three molecules was one order of magnitude smaller than that for a single H₂O molecule. They also compared iPP500(3-10w) with aPP500(3-10w). For one H₂O molecule in aPP their diffusion coefficients lie in the order of 10^–6 cm²/s which is in good agreement with our results for iPP. Their results for ten H₂O molecules forming a cluster and moving in iPP are of the order of 10^–7 cm²/s which is also in agreement with our results (see Table 3).

Table 3 Comparison of the calculated diffusion coefficients for different time intervals for H₂O in iPP at 298 K

Just as Fukuda and Kuwajima [20], we determined diffusion coefficients for the time intervals 0–6, 6–11 and 0–11 ns. Furthermore, we used the time interval of 0–1 ns in order to investigate the influence of the cluster formation process, and in addition, we have determined the D values for one H₂O molecule in iPP as well. Note that determining D for a specified time interval does not include any data of other time intervals, i.e. determining D in the time interval 6–11 ns is based on the evaluation of a 5 ns long run with initial coordinates and velocities at t = 6 ns. In Table 3 we show a comparison of the different simulations for H₂O in iPP and the derived diffusion coefficients. The D values are averaged over ten MD runs. Figures 8, 9, and 10 shows the associated averaged D values of the ten runs together with their standard deviations.

Fig. 8

Average diffusion coefficients with standard deviations from ten NPT-MD simulations of iPP50(3-1w) calculated from the MSD for different time intervals at 298 K

Fig. 9

Average diffusion coefficients with standard deviations from ten NPT-MD simulations of iPP50(3-10w) calculated from the MSD for different time intervals at 298 K

Fig. 10

Average diffusion coefficients with standard deviations from ten NPT-MD simulations of iPP50(3-10w)_fixed calculated from the MSD for different time intervals at 298 K

The averaged diffusion coefficient for a single H₂O molecule (iPP50(3-1w)) ranges from 2.9 · 10^–6 to 5.8 · 10^–6 cm²/s which is one order of magnitude higher than the average value for ten H₂O molecules (iPP50(3-10w)) which ranges from 1.0 · 10^–7 to 3.0 · 10^–7 cm²/s. There are no significant differences between D of iPP50(3-10w) and iPP50(3-10w)_fixed, where for the latter we find values ranging from 2.4 · 10^–7 to 3.9 · 10^–7 cm²/s. Because of the very fast cluster formation process, even for the first ns in iPP50(3-10w)_fixed there is no measurable influence on D compared to 6 or 11 ns.

A possible solution to to distinguish between the diffusion of single H₂O molecules during the cluster formation and the diffusion of an H₂O cluster as an entity in a single simulation, is a study of much larger simulation cells with a smaller concentration of H₂O so that the cluster formation takes longer and thus the diffusion coefficients can be calculated during the cluster forming process more precisely.

For iPP50(3-1w) and for iPP50(3-10w)_fixed there are no significant differences of the standard deviations for the D values across different simulations observable. However, for iPP50(3-10w) the standard deviation is smaller at smaller times, i.e. 1 ns and 6 ns compared to larger times, i.e. 6–11 ns and 11 ns. For iPP50(3-10w)_fixed we expected more volatility at shorter times since the H₂O molecules are excluded from the equilibration process. When comparing the two equilibrated systems containing one and ten H₂O molecules, we find a smaller standard deviation at shorter times in iPP50(3-10w) which is due to the better statistics when averaging over ten (independent) H₂O molecules instead of one. For larger times this effect vanishes because of the correlated motion of the clustered H₂O molecules as an entity.

For H₂O₂ we find diffusion coefficients in the range of 10^–6 for a single and 10^–8 cm²/s for ten H₂O₂ molecules. The results for the two systems are shown in Table 4 and Figs. 11 and 12. For a single H₂O₂ molecule the diffusion coefficient ranges from 3.4 to 6.8 · 10^–6 cm²/s. The standard deviation of the longer time intervals 6–11 and 0–11 ns are very large compared to the results of ten H₂O₂ molecules and even compared to the result of a single H₂O molecule. This is consistent with the expected stronger interactions of the hydrophobic PP chains with the more polar penetrant H₂O₂ as compared to H₂O [52, 53]. For ten H₂O₂ molecules D ranges between 2.3 and 8.6 · 10^–8 cm²/s and the standard deviations are much smaller due to the better statistics just like in the case of ten H₂O molecules. The only experimental value we can compare our result with was published by Radl et al. [29]. They determined the diffusion coefficient of H₂O₂ in PP at 298 K and found D = 5.50 · 10^–9 cm²/s which is one order of magnitude smaller than our value. We attribute this discrepancy to the difference of our simulation procedure to the experimental procedure they used. Radl et al. used fully saturated strips of PP in an aqueous 30% (w/w) H₂O₂ solution and determined the diffusion coefficient by measuring the desorption of H₂O₂ over time. In contrast to this our MD simulations are idealized in the sense that we only consider motion of H₂O₂ within the surrounding polymer matrix. Further, we calculated the motion of the H₂O₂ molecules within the polymer matrix only for several ns while the diffusion coefficient in the experimental approach was measured by desorption for which the H₂O₂ molecules must overcome the surface energy barrier before they get measured. This process could lead to a significantly lower diffusion rate as compared to the diffusion rate in the bulk material. Nevertheless, our computationally determined diffusion coefficients for H₂O₂ in PP are useful as a reference for future theoretical and experimental studies.

Table 4 Comparison of the calculated diffusion coefficients for different time intervals for H₂O₂ in iPP at 298 K

Fig. 11

Average diffusion coefficients with standard deviations from ten NPT-MD simulations of iPP50(3-1hp)_fixed calculated from the MSD for different time intervals at 298 K

Fig. 12

Average diffusion coefficients with standard deviations from ten NPT-MD simulations of iPP50(3-10hp)_fixed calculated from the MSD for different time intervals at 298 K

Due to its reactive character O₂ generally plays an important role in damaging and aging processes of polymers. Apart from chemical reactions it is vital to know the temperature dependent transport properties of the molecule within a polymer matrix. In case of iPP we expect an increase of the transport properties at higher temperatures where the material is getting softer. Therefore, we did a temperature-dependant study at 268 K where iPP is more rigid, at room temperature, i.e. 298 K, and at 328 K where iPP is softer. We picked room temperature as a reference temperature because at this temperature we can compare our results to previously published simulational and experimental results. In Table 5 we show our results for the diffusion coefficients for the different simulation runs for the non-polar penetrant O₂ in iPP. Figures 13, 14, and 15 shows the statistical evaluation of the determined D values. For iPP50(3-10o) at 298 K our averaged D values range from 5.7 · 10^–6 to 8,2 · 10^–6 cm²/s and show a significantly smaller standard deviation compared to H₂O and H₂O₂. This is in good agreement with previously analysed O₂ diffusion in polypropylene by MD and experimentally. For atactical PP Müller-Plathe calculated D values for O₂ via MD simulations. Referring to our nomenclature he studied the system aPP76(1-8o) at T = 300 K and finds D = 4.04 · 10^–6 cm²/s [14]. Rong et al. determined a value of D = 3.688 · 10^–6 cm²/s for iPP60(4-2o) at T = 298 K [22]. Experimental values for D of the order of 10^–7 cm²/s at T = 298 K have been obtained by Kiryushkin and Gromov, and Eken et al. [54, 55].

Table 5 Diffusion coefficient results of iPP50(3-10o) at 268 K, 298 K, and 328 K

Fig. 13

Average diffusion coefficients with standard deviations from ten NPT-MD simulations of iPP50(3-10o) at 268 K calculated from the MSD for different time intervals

Fig. 14

Average diffusion coefficients with standard deviations from ten NPT-MD simulations of iPP50(3-10o) at 298 K calculated from the MSD for different time intervals

Fig. 15

Average diffusion coefficients with standard deviations from ten NPT-MD simulations of iPP50(3-10o) at 328 K calculated from the MSD for different time intervals

We have determined the average O₂ diffusion coefficient for T = 268 K in the range of 2.0 · 10^–6 to 2.4 · 10^–6 cm²/s. In comparison, for higher temperatures, i.e. 298 K and 328 K, one can clearly see that D is increased by a factor of three for T = 298 K and further increased by a factor of seven at T = 328 K. This is consistent with the expected higher mobility of the penetrants when iPP becomes softer and with the finding of Chang-Gui et al. that D increases for O₂ in PP with increasing temperature [21].

Comparing the widths of the standard deviations for the different temperatures shows the smallest at 268 K which indicates that the more rigid state also leads to more uniform results.

As pointed out in the beginning, H₂ appears as a reaction product of chemical reactions when H₂O₂ is involved. We therefore investigated its mobility in iPP at 298 K as well (see Table 6 and Figs. 16 and 17). For aPP76(1-8h) at 300 K Müller-Plathe determined a value of 4.35 · 10-5 cm²/s by means of MD simulations [14] using the class I force field GROMOS [56]. In comparison, we obtained our results by using the class II force field COMPASS and find a D value which is larger by factor of six in the range of 2.4 · 10^–4 to 2.7 · 10^–4 cm²/s. In order to find out whether the tacticity of PP could cause such a difference we did another calculation using an aPP50(3-10 h) simulation cell. Here, we find D in the range of 2.0 · 10^–4 to 2.4 · 10^–4 cm²/s which shows that the tacticity alone cannot explain the discrepancies. We therefore conclude that the deviation is caused by the choice of the force fields. The only experimental result obtained by Jeschke and Stuart is 6.6 · 10^–6 cm²/s for H₂ diffusion in aPP and 3.0 · 10^–6 cm²/s in iPP, both at 293 K. Their experimental setup comprised two gas compartments separated by a thin PP foil. While one chamber is vacuumed, the other is filled with H₂-gas and the change in pressure was used to determine the diffusion coefficient [57]. In comparison our results are two orders of magnitude larger. We attribute this discrepancy to the idealized setup in our MD simulation. Like our previous results on H₂O₂, we only take the interaction effects of H₂ within the polymer matrix into account while the experimental setup additionally took sorption and desorption of the H₂ molecules into account which decreases the measured diffusion coefficient.

Table 6 Comparison of the calculated diffusion coefficients for different time intervals for H₂ in iPP at 298 K

Fig. 16

Average diffusion coefficients with standard deviations from ten NPT-MD simulations of iPP50(3-10h) calculated from the MSD for different time intervals at 298 K

Fig. 17

Average diffusion coefficients with standard deviations from ten NPT-MD simulations of aPP50(3-10h) calculated from the MSD for different time intervals at 298 K

Sorption loading analysis

An important property that characterizes the durability of the surface and bulk of polymeric materials is the absorption of and saturation with small molecules. We performed GCMC simulations comparing the free energy of a molecule in a gas reservoir with the state of it being in the polymer matrix. Figures 18, 19, and 20 shows the average loadings and their standard deviations obtained by performing five GCMC simulations for H₂O, O₂ and H₂ in iPP60(4), respectively. We used 150,000 MC samples per temperature. Table 7 shows the average number of absorbed molecules and the resulting saturation calculated by Eq. 3.

Fig. 18

The calculated loadings of H₂O molecules in iPP60(4) for five GCMC-runs

Fig. 19

The calculated loadings of O₂ molecules in iPP60(4) for five GCMC-runs

Fig. 20

The calculated loadings of H₂ molecules in iPP60(4) for five GCMC-runs

Table 7 Averaged number of absorbed H₂O, O₂ and H₂ molecules over five GCMC runs in iPP60(4) and resulting saturation values

As for PP being a highly hydrophobic material often used in the packaging industry to preserve food from getting in contact with moisture, the absorption of H₂O in PP is very small. Therefore, the exact determination of the saturation is challenging on the one hand but provides useful information for industrial applications on the other hand. The average loading of H₂O molecules in our iPP system ranges between 0.037 and 0.140 which corresponds to a saturation between 0.007 and 0.025 wt.% over all simulated temperatures from 263 to 303 K. There are only a few experimental results in the literature to compare with. Kahraman and Abu-Sharkh, Deng et al. and Mat-Shayuti et al. immersed polypropylene samples in distilled water for several months at room temperature [58], for one month at 296 K [59] as well as for 49 days at 296 K and for 7 days at 373 K [60]. Karahman and Abu-Sharkh reported that the moisture uptake was negligible and not significant enough to be published. For 296 K Deng et al. found a saturation of 0.03 wt.% and Mat-Shayuti et al. of 0.064 wt.%. At 373 K Mat-Shayuti et al. found a saturation of 0.571 wt.%. Our simulated results are consistent with the experimental results and show very limited H₂O uptake and no significant change with increasing or decreasing temperatures at and around room temperature.

Experimental sorption studies of O₂ in polymers are generally difficult because of autoxidation processes taking place as soon as O₂ diffuses into a polymer like PP. Except for T = 268 K, the loading and saturation values obtained by GCMC simulations for O₂ in iPP show a decreasing trend with increasing temperature. This is consistent with the findings of Chang-Gui et al. and Rong et al. for O₂ sorption in PP [21] and PE [22]. The interaction and therefore the binding forces between the polymer and O₂ decreases with increasing temperature. We find an averaged saturation of O₂ of 0.186 wt.% at 263 K and 0.079 wt.% at 303 K, however with a large standard deviation.

In contrast to that, the loading values and the standard deviations for H₂ are smaller. This is expected because the interaction force between iPP and O₂ is much larger since more valence electrons are involved. Here, again a decreasing trend of loading and saturation with increasing temperature is visible, except for the value at 293 K where we find the highest saturation value of 0.00110 wt.%. The saturation of H₂ is 0.00096 wt.% at 263 K and 0.00077 wt.% at 303 K.

Determination of the glass transition temperature

For different types of polypropylene Cowie found experimentally an asymptotic increase of T_g with the molecular weight saturating at weights of 10⁴ and above [61] which is equivalent to a degree of polymerisation of ≈ 238. By means of MD simulations Yu et al. found for chain lengths longer than ~200 units that the glass transition temperature is insensitive to further increasing the chain length [62]. Given this we performed simulations using a model system with a chain length of 240.

In Fig. 21 we show a plot of the density per cell of iPP240(4) for a 200 ps simulation at 303 K. In total, we performed 10 simulation runs with different initial configurations (see Ch. 2.1) and the average density and the specific volume V_spec were calculated using the last 50 ps of each run at each temperature. Figure 22 shows the averaged specific volumes including standard deviations vs. temperature with R² = 0.997. To obtain a value for T_g we fitted the data simultaneously to two piecewise linear functions using a least square fitting routine [63]. As a result, we find the intersection at T_g = 273.66 ± 4.21 K which is in good agreement with the experimental findings shown in Table 8. Two of the published simulational results differ by over 100 K, namely T_g = 248 K [62] and T_g = 364 K [64], respectively. One can argue that the standard deviation for our results is quite large. However, none of the referenced experimental and simulational results provided any standard deviation at all.

Fig. 21

Density of iPP240(4) over a 200 ps NPT simulation at 303 K

Fig. 22

Determination of T_g using a simultaneous least-square fit of two piecewise linear functions to the averaged specific volume of ten runs per temperature for iPP240(4)

Table 8 Literature data and our result for the glass transition temperature T_g of polypropylene

Conclusions

We have studied the behaviour and interaction of different penetrants within polypropylene by means of molecular dynamics (MD) and Grand Canonical Monte Carlo (GCMC) simulations by considering isotactic polypropylene (iPP) and in one case atactic polypropylene (aPP) as well. For the polar penetrant water (H₂O) we find clusters forming and persisting over the whole simulation time length of 11 ns. This is consistent with previous results [19, 20]. Furthermore, for the first time we have also studied the diffusion of hydrogen peroxide (H₂O₂) in PP over a simulation time length of 22 ns which shows similar robust clustering as H₂O.

Diffusion coefficients for H₂O and oxygen (O₂) in iPP as well as for hydrogen (H₂) in iPP and aPP have been estimated by mean-square displacement (MSD) analysis of different time intervals up to 11 ns and for H₂O₂ in iPP for up to 22 ns. The MSD curves of polar penetrants are more volatile compared to the non-polar penetrants which imposes a larger uncertainty of the obtained results. For the case of oxygen, we first determined the glass transition temperature of iPP and further studied the influence of the glassy state and rubbery state of iPP on the diffusion coefficient as well. Our results are consistent with previously published experimental and computational data except for H₂ in polypropylene where our results are up to two orders of magnitude larger than other computational [14] and experimental results [57], respectively.

Sorption loading analysis on H₂O, O₂ and H₂ for iPP were performed and saturations were calculated. For H₂O our results are consistent with experimental results [59, 60]. However, due to different hindering effects like the polarity of H₂O, autoxidation for O₂ and the small size of H₂ molecules these systems are difficult to study experimentally which may explain the observed differences.