New Interior-Point Approach for One- and Two-Class Linear Support Vector Machines Using Multiple Variable Splitting

Abstract

Multiple variable splitting is a general technique for decomposing problems by using copies of variables and additional linking constraints that equate their values. The resulting large optimization problem can be solved with a specialized interior-point method that exploits the problem structure and computes the Newton direction with a combination of direct and iterative solvers (i.e. Cholesky factorizations and preconditioned conjugate gradients for linear systems related to, respectively, subproblems and new linking constraints). The present work applies this method to solving real-world binary classification and novelty (or outlier) detection problems by means of, respectively, two-class and one-class linear support vector machines (SVMs). Unlike previous interior-point approaches for SVMs, which were practical only with low-dimensional points, the new proposal can also deal with high-dimensional data. The new method is compared with state-of-the-art solvers for SVMs that are based on either interior-point algorithms (such as SVM-OOPS) or specific algorithms developed by the machine learning community (such as LIBSVM and LIBLINEAR). The computational results show that, for two-class SVMs, the new proposal is competitive not only against previous interior-point methods—and much more efficient than they are with high-dimensional data—but also against LIBSVM, whereas LIBLINEAR generally outperformed the proposal. For one-class SVMs, the new method consistently outperformed all other approaches, in terms of either solution time or solution quality.

1 Introduction

Machine learning applications require the solution of a—usually large—optimization problem [2]. In the case of support vector machines (SVM, one of the preferred tools in machine learning), the optimization problem to be solved is convex and quadratic [10]. SVMs can be used for either binary classification or novelty detection. When used for binary classification, they are referred to as a support vector classifier or two-class SVM [9]; for novelty (or outlier) detection, they are called one-class SVM [8, 20]. Although in recent years they have been replaced by neural networks in some applications (e.g. for image detection and classification), SVMs are still one of the preferred techniques for text classification [2].

In this work, we present a new approach for solving real-world two-class and one-class SVMs. It is based on reformulating the SVM problem by decomposing it into smaller SVMs and using linking constraints to equate the values of the split variables. The resulting optimization problem has a primal block-angular structure which can be efficiently solved using the specialized interior-point method (IPM) of [3,4,5,6]. The extensive computational experience in Sect. 4 shows that the new approach can be competitive against state-of-the-art methods for two-class SVM and that it outperformed all of them for one-class SVM.

Briefly, SVMs attempt to find a hyperplane separating two classes of multidimensional points (two-class SVM), or points with some distribution from a set of outliers (one-class SVM). For either one-class or two-class SVMs, we are given a set of p d-dimensional points $a_i \in \mathbb {R}^d$, $i=1,\dots ,p$. Each point could be related to some item, and the d components of the point would be related to variables (named features in machine learning jargon) for that item. In two-class SVMs, we also have a vector $y\in \mathbb {R}^p$ of labels $y_i\in \{+1,-1\}$, $i=1,\dots ,p$, indicating whether point i belongs to class “$+1$” or class “$-1$”. In some applications, points $a_i$ need to be previously transformed by function $\phi :\mathbb {R}^d \rightarrow \mathbb {R}^{d'}$, especially if the two classes of points cannot be correctly separated by a hyperplane. When dimension d is high, such a transformation is usually not needed, since a good separation hyperplane can be found. That is, $\phi (x)=x$, and we refer to this problem as the linear SVM. In this work, we focus on linear SVMs.

1.1 The Two-Class SVM Optimization Problem

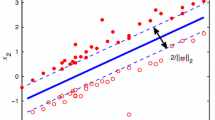
For the two-class SVM (or support vector classifier), we compute a plane $w^{\top }x + \gamma =0$, $w\in \mathbb {R}^d$, $\gamma \in \mathbb {R}$, such that points $a_i$ with $y_i=+1$ should be in the half-plane $w^{\top }x +\gamma \ge 1$, and those points with label $y_i=-1$ should be in the half-plane $w^{\top }x +\gamma \le -1$. Slack variables $s\in \mathbb {R}^p$ are introduced to account for possible misclassification errors if the data points are not linearly separable. At the same time, we also attempt to maximize the distance between the parallel planes $w^{\top }x +\gamma = 1$ and $w^{\top }x +\gamma = -1$, such that the two classes of points are far enough from each other. This distance, named separation margin, is $2/\Vert w\Vert$ [10]. Using $A\in \mathbb {R}^{p\times d}$ to define the matrix storing row-wise the p d-dimensional points $a_i, i=1,\dots ,p$, and $Y=\text{ diag }(y)$ to define the diagonal matrix made from the vector of labels y, the primal formulation of the two-class SVM problem is

$$\begin{aligned} \displaystyle \min _{ w, \gamma ,s} \quad&\displaystyle \frac{1}{2}w^{\top }w +\nu e^{\top }s \end{aligned}$$

(1a)

$$\begin{aligned} \text{ subject } \text{ to }\quad&Y(Aw+\gamma e) + s \ge e \end{aligned}$$

(1b)

$$\begin{aligned}&s\ge 0, \end{aligned}$$

(1c)

where $e\in \mathbb {R}^p$ is a vector of 1s, and $\nu$ is a fixed parameter to balance the two opposite terms of the objective function: the first quadratic term maximizes the separation margin, and the second term minimizes the misclassification errors.

Defining the vectors of Lagrange multipliers $\lambda \in \mathbb {R}^p$ and $\mu \in \mathbb {R}^p$, respectively, for constraints (1b) and (1c), the Lagrangian function of (1) is

$$\begin{aligned} L(w,\gamma ,s,\lambda ,\mu )= \frac{1}{2}w^{\top }w + \nu e^{\top }s - \lambda ^{\top }(Y(Aw+\gamma e) + s - e) -\mu ^{\top }s, \end{aligned}$$

(2)

and the Wolfe dual of (1) becomes

$$\begin{aligned} \displaystyle \max _{w,\gamma ,s,\lambda ,\mu } \quad&L(w,\gamma ,s,\lambda ,\mu ) \end{aligned}$$

(3a)

$$\begin{aligned} {\hbox {subject to}}\quad&\nabla _{w} L(\cdot )= w -(\lambda ^{\top }YA)^{\top }=0 \end{aligned}$$

(3b)

$$\begin{aligned}&\nabla _{\gamma } L(\cdot )= \lambda ^{\top }y =0 \end{aligned}$$

(3c)

$$\begin{aligned}&\nabla _{s} L(\cdot )= \nu e -\lambda -\mu =0 \end{aligned}$$

(3d)

$$\begin{aligned}&\lambda \ge 0,~~ \mu \ge 0. \end{aligned}$$

(3e)

Using relations (3b)–(3e) in (3a), we obtain the dual problem (in minimization form)

$$\begin{aligned} \displaystyle \min _{\lambda } \quad&\frac{1}{2} \lambda ^{\top }Y AA^{\top }Y \lambda - \lambda ^{\top }e \end{aligned}$$

(4a)

$$\begin{aligned} \text{ subject } \text{ to } \quad&\lambda ^{\top }y = 0 \end{aligned}$$

(4b)

$$\begin{aligned}&0 \le \lambda \le \nu e. \end{aligned}$$

(4c)

The dual (4) is a convex quadratic optimization problem with only one linear constraint and simple bounds. The linear constraint (4b) comes from $\nabla _\gamma L(\cdot )$. Therefore, if a linear (instead of an affine) separation plane $w^{\top }x = 0$ is considered in the primal formulation (that is, without the $\gamma$ term), the dual is only defined by (4a) and (4c). Such a problem can be effectively dealt with by gradient and coordinate descent methods [23]. This fact is exploited by some of the most popular and efficient packages in machine learning (such as LIBLINEAR [11]). We note, however, that both problems are slightly different, since they compute either a linear or an affine separation plane.

1.2 The One-Class SVM Optimization Problem

The purpose of the one-class SVM problem (introduced in [20]) is to find a hyperplane $w^{\top }x - \gamma =0$, $w\in \mathbb {R}^d$, $\gamma \in \mathbb {R}$, such that points in the half-plane $w^{\top }x - \gamma \ge 0$ are considered as belonging to the same distribution, and the separation margin with respect to the origin is maximized. Points that are not in the previous half-plane are considered outliers. Defining, as in the two-class SVM problem, the matrix $A\in \mathbb {R}^{p\times d}$ whose row i contains point $a_i$, $i=1,\dots ,p$, the primal formulation of the one-class SVM problem is

$$\begin{aligned} \displaystyle \min _{ w, \gamma ,s} \quad&\frac{1}{2}w^{\top }w - \gamma +\frac{1}{\nu p} e^{\top }s \end{aligned}$$

(5a)

$$\begin{aligned} \text{ subject } \text{ to } \quad&A w -\gamma e + s \ge 0 \end{aligned}$$

(5b)

$$\begin{aligned}&s \ge 0, \end{aligned}$$

(5c)

where the positive components of s in the optimal solution would be associated with outliers, and $\nu \in [0,1]$ is a fixed parameter. It was shown in [20] that $\nu$ is an upper bound on the fraction of detected outliers in the optimal solution.

As in the two-class SVM problem, we can use Wolfe duality to compute the dual of (5), thereby obtaining:

$$\begin{aligned} \displaystyle \min _\lambda \quad&\frac{1}{2} \lambda ^{\top }AA^{\top }\lambda \end{aligned}$$

(6a)

$$\begin{aligned} \text{ subject } \text{ to } \quad&\lambda ^{\top }e = 1 \end{aligned}$$

(6b)

$$\begin{aligned}&0 \le \lambda \le \frac{1}{\nu p}e. \end{aligned}$$

(6c)

One significant difference with respect to the two-class SVM problem is that the linear constraint (6b) cannot be avoided by removing $\gamma$ from the primal formulation (5) (that is, by computing a linear instead of an affine plane): if $\gamma$ was removed, problem (5) would have the trivial and useless solution $w^*=0$, $s^*=0$. As will be shown in the computational results of Sect. 4, this fact has far reaching implications for methods that solve (6) by means of coordinate gradient descent [8], as they may provide a poor quality solution that is far from the optimal one.

1.3 Alternative Approaches for SVMs

Several approaches have been developed for solving the two-class SVM problem by using either (1) or (4). We will avoid giving an extensive list and will focus instead on only those based on IPMs (like ours) and those implemented in the current state-of-the-art packages for SVMs that will be used in the computational results of this work.

Since (1) and (4) are convex quadratic linearly constrained optimization problems, they can be solved by a general solver implementing an IPM. However, when using either the primal or dual formulation, computing the Newton direction would mean solving a linear system involving matrix $A\Theta A^{\top }\in \mathbb {R}^{p\times p}$ (where $\Theta$ is some diagonal scaling matrix that is different for each IPM iteration). For datasets with a large number of points p, the Cholesky factorization can be prohibitive because matrices A are usually quite dense. However, for low-rank matrices A which involve many points and just a few variables (that is, $p\gg d$), a few very efficient approaches have been devised. The first one was that of [12], who considered the dual problem (4) and solved the Newton system by applying the Sherman–Morrison–Woodbury (SMW) formula. In [12], the authors solved problems with millions of points but only $d=35$ features. A similar approach was used in [13] for the solution of smaller (up to 68,000 points, and less than 1000 features) but realistic datasets. The product form Cholesky factorization introduced in [14] for IPMs with dense columns was applied in [15] for solving the dual SVM formulation. This approach was shown to have a better numerical performance than those based on the SMW formula, but no results for real SVM instances were reported in [15]. State-of-the-art IPM solvers including efficient strategies for dealing with dense columns (such as CPLEX) can also be used for solving the primal formulation (1). Indeed, the computational results of Sect. 4 will show that CPLEX 20.1 is competitive against specialized packages for both one-class and two-class SVMs when d is small.

More recently, [21] suggested a separable reformulation of (4) by introducing the extra free variables u. The resulting problem

$$\begin{aligned} \begin{array}{ll} \displaystyle \min _{\lambda } &{} \frac{1}{2} u^{\top }u -\lambda ^{\top }e \\ &{} \lambda ^{\top }y = 0 \\ &{} A^{\top }Y \lambda = u \\ &{} 0 \le \lambda \le \nu e, \quad u \hbox { free}, \end{array} \end{aligned}$$

was efficiently solved when A is low-rank. This approach was implemented in the SVM-OOPS package, and [21] extensively tested it against state-of-the-art machine learning packages for SVMs, showing competitive results (but only for problems with a few features). SVM-OOPS can be considered one of the most efficient specialized IPM approaches for linear SVMs when d is small, and it will be one of the packages considered in Sect. 4 for the computational results (but only for classification, since it does not deal with one-class SVMs).

The two likely best packages for SVMs in the machine learning community are LIBSVM [7] and LIBLINEAR [11]. Both will be used for comparison purposes in the computational results of Sect. 4. LIBSVM solves the duals (4) and (6) (and can thus be used for both two-class and one-class SVMs) without removing the linear constraint (that is, it considers the $\gamma$ term of the primal formulation). It applies a gradient descent approach combined with a special active set constraint technique named sequential minimal optimization (SMO) [19], where all but two components of $\lambda$ are fixed, and each iteration deals only with a two-dimensional subproblem. Each iteration of SMO is very fast, but convergence can be slow. As will be shown in Sect. 4, LIBSVM is generally not competitive against the other methods. On the other hand, it is the only one that can efficiently deal with nonlinear SVMs—that is, when $\phi (x)$ is a general transformation function.

LIBLINEAR [11] is considered the fastest package for linear SVMs. For two-class SVMs, it solves either the primal or the dual formulation without the $\gamma$ variable. For the primal formulation, it considers the following approximate unconstrained reformulation:

$$\begin{aligned} \min _{w} \frac{1}{2}w^{\top }w + \nu \sum _{i=1}^p \max (0,1- y_i w^{\top }a_i)^2. \end{aligned}$$

The nondifferentiable $\max ()$ term (known as hinge loss function in the machine learning field) must be squared to avoid differentiability issues with the first derivative (this term, however, has no second derivative at 0). This unconstrained problem is solved by a trust-region Newton method based on conjugate gradients while further using a Hessian perturbation to deal with the second derivatives at 0. Due to the lack of $\gamma$, LIBLINEAR solves the dual formulation (4) without the linear constraint:

$$\begin{aligned} \begin{array}{ll} \displaystyle \min _{\lambda } &{} \frac{1}{2} \lambda ^{\top }Y AA^{\top }Y \lambda - \lambda ^{\top }e\\ &{} 0 \le \lambda \le \nu e. \end{array} \end{aligned}$$

(7)

This problem is solved using a coordinate gradient descent algorithm. For one-class SVM, LIBLINEAR solves only the exact dual (6) (which includes the linear constraint) by means of a coordinate descent algorithm [8]. Alternative approaches also considered nondifferentiable formulations [1], but resulted less efficient than that implemented in LIBLINEAR.

The rest of the paper is organized as follows: Section 2 introduces the multiple variable splitting reformulation considered in this work for linear SVMs. Section 3 presents the specialized IPM that will be used for the efficient solution of the multiple variable splitting reformulation of the SVM problem. Finally, computational results for one-class and two-class SVMs using real datasets will be provided in Sect. 4, showing the efficiency and competitiveness of this new approach.

2 Multiple Variable Splitting Reformulation of Linear SVMs

The approach introduced in this work consists of partitioning the dataset of p points into k subsets of, respectively, $p_i$, $i=1,\dots ,k$, points (where $\sum _{i=1}^k p_i=p$). The points in each subset and their labels are assumed to be stored, respectively, row-wise in matrices $A^i\in \mathbb {R}^{p_i \times d}$ and diagonally in matrices $Y^i\in \mathbb {R}^{p_i \times p_i}$, $i=1,\dots ,k$. Considering k smaller SVMs, each with its own variables $(w^i,\gamma ^i,s^i), i=1,\dots ,k$ (where $w^i\in \mathbb {R}^d$, $\gamma ^i\in \mathbb {R}$ and $s^i\in \mathbb {R}^{p_i}$), problem (1) is equivalent to the following multiple variable splitting formulation with linking constraints:

$$\begin{aligned} \displaystyle \min _{ (w^i, \gamma ^i,s^i)}\quad&\frac{1}{2}\left( \sum _{i=1}^k {w^i}^{\top }w^i\right) /k + \nu \sum _{i=1}^k {e^i}^{\top }s^i \end{aligned}$$

(8a)

$$\begin{aligned} \text{ subject } \text{ to } \quad&Y^i(A^i w^i+\gamma ^i e^i) +s^i \ge e^i&i=1,\dots ,k \end{aligned}$$

(8b)

$$\begin{aligned}&s^i\ge 0&i=1,\dots ,k \end{aligned}$$

(8c)

$$\begin{aligned}&w^i = w^{i+1},\quad \gamma ^i=\gamma ^{i+1}&i=1,\dots ,k-1, \end{aligned}$$

(8d)

where $e^i\in \mathbb {R}^{p_i}$ is a vector of ones. Linking constraints (8d) impose the same hyperplanes for the k SVMs. Slacks $s^i$ represent the potential misclassification errors, so they are particular to the points of each subset and do not have to be included in the linking constraints.

Similarly, the one-class SVM problem (5) can be reformulated as

$$\begin{aligned} \displaystyle \min _{ (w^i, \gamma ^i,s^i)}\quad&\frac{1}{2}\left( \sum _{i=1}^k {w^i}^{\top }w^i -\gamma ^i\right) /k + \frac{1}{\nu p} \sum _{i=1}^k {e^i}^{\top }s^i \end{aligned}$$

(9a)

$$\begin{aligned} \text{ subject } \text{ to } \quad&A^i w^i-\gamma ^i e^i +s^i \ge 0&i=1,\dots ,k \end{aligned}$$

(9b)

$$\begin{aligned}&s^i\ge 0&i=1,\dots ,k \end{aligned}$$

(9c)

$$\begin{aligned}&w^i = w^{i+1},\quad \gamma ^i=\gamma ^{i+1}&i=1,\dots ,k-1. \end{aligned}$$

(9d)

The constraints of problems (8) and (9) exhibit a primal block-angular structure. Putting aside the linking constraints (8d) and (9d), the solution of either (8) or (9) with an IPM requires k Cholesky factorizations involving $A^i\Theta ^i {A^i}^{\top }\in \mathbb {R}^{p_i\times p_i}$, $i=1,\dots ,k$, at each IPM iteration ($\Theta ^i$ being a diagonal scaling matrix that depends on the particular iteration). If each subset has the same number of points, that is $p_i= p/k$, the complexity of the k Cholesky factorizations is

$$\begin{aligned} O\left( k \left( \frac{p}{k}\right) ^3\right) = O\left( \frac{p^3}{k^2}\right) \ll O\left( p^3\right) , \end{aligned}$$

(10)

where $O\left( p^3\right)$ is the complexity of the Cholesky factorizations of the original formulations (1) and (5). Of course, to benefit from (10), we need an IPM that can efficiently deal with the linking constraints of primal block-angular optimization problems. Such an approach is summarized in the next section.

3 The IPM for the Multiple Variable Splitting Reformulation of SVMs

After transforming (8b) and (9b) into equality constraints by adding extra nonnegative variables $\xi ^i\in \mathbb {R}^{p_i}$,

$$\begin{aligned} Y^i(A^i w^i+\gamma ^i e^i) +s^i -\xi ^i = e^i,&\quad \xi ^i \ge 0,&\quad i=1,\dots ,k \\ A^i w^i-\gamma ^i e^i +s^i -\xi ^i = 0 ,&\quad \xi ^i \ge 0,&\quad i=1,\dots ,k, \end{aligned}$$

problems (8) and (9) match the following general formulation of primal block-angular optimization problems:

$$\begin{aligned} \min&\quad \displaystyle \sum _{i=0}^{k} f_i(x^i) \end{aligned}$$

(11a)

$$\begin{aligned} {\hbox {subject to}}&\begin{array}{l} \left[ \begin{array}{ccccc} M_1 &{} &{} &{} &{} \\ &{} M_2 &{} &{} &{} \\ &{} &{} \ddots &{} &{} \\ &{} &{} &{} M_k &{} \\ L_1 &{} L_2 &{} \ldots &{} L_k &{} I\\ \end{array} \right] \left[ \begin{array}{c} x^1 \\ x^2 \\ \vdots \\ x^k \\ x^{0} \\ \end{array} \right] = \left[ \begin{array}{c} b^1 \\ b^2 \\ \vdots \\ b^k \\ b^{0} \\ \end{array} \right] \end{array} \end{aligned}$$

(11b)

$$\begin{aligned}&0 \le x^i_j \le u^i_j ~~ j\not \in {{\mathcal {F}}}^i,\quad x^i_j \text{ free } ~ j\in {{\mathcal {F}}}^i,\quad i = 0,\ldots , k. \end{aligned}$$

(11c)

Vectors $x^i=({w^i}^{\top }\; {\gamma ^i}^{\top }\; {s^i}^{\top }\; {\xi ^i}^{\top })^{\top }\in \mathbb {R}^{n_i=d+1+2p_i}$, $i=1,\dots ,k$, contain all the variables for the i-th SVM; and ${{\mathcal {C}}}^2 \ni f_i:\mathbb {R}^{n_i}\rightarrow \mathbb {R}$, $i=0,\dots ,k$, are convex separable functions. For SVM problems, they are quadratic functions:

$$\begin{aligned} f_i(x^i)= {c^i}^{\top }x^i + \frac{1}{2}{x^i}^{\top }Q_i x^i, \quad Q_i\succeq 0 \text{ and } \text{ diagonal, } \qquad i=1,\dots ,k, \end{aligned}$$

(12)

whereas for $i=0$ we have $f_0(x^0)= 0$. Matrices $M_i \in \mathbb {R}^{m_i \times n_i}$ and $L_i \in \mathbb {R}^{l \times n_i}$, $i= 1,\dots ,k$, respectively, define the block-diagonal and linking constraints, where $m_i=p_i$ (the number of points in the i-th SVM) and $l= (d+1)(k-1)$ is the number of linking constraints defined in either (8d) or (9d). Vector $b^i \in \mathbb {R}^{m_i}, i=1,\dots ,k$, is the right-hand side for each block of constraints, whereas $b^{0} \in \mathbb {R}^l$ is for the linking constraints. In our case $b^i=e^i$ for two-class SVM and $b^i=0$ for one-class SVM, $i=1,\dots ,k$, whereas $b^0= 0$ in both problems. $x^{0} \in \mathbb {R}^l$ are the slacks of the linking constraints. The sets ${{\mathcal {F}}}^i$ contain the indices of the free variables for each block (corresponding to $w^i$ and $\gamma ^i$). The upper bounds for each group of variables are $u^i\in \mathbb {R}^{n_i}, i=0,\dots ,k$; these upper bounds apply only to the components of $x^i$ that are not in ${{\mathcal {F}}}^i$ (that is, they apply only to $s^i$ and $\xi ^i$), and in our problem $u^i= +\infty$ for all $i=1,\dots ,k$. For the linking constraints, we have ${{\mathcal {F}}}^0= \emptyset$, that is, slacks $x^0$ are bounded—otherwise the linking constraints could be removed. For problems with equality linking constraints, as in our case, $u^0$ can be set to a very small (close to 0) value.

The total numbers of constraints and variables in (11) are thus, respectively, $m= l+\sum _{i=1}^k m_i$ and $n= l+\sum _{i=1}^k n_i$. Formulation (11) is a very general model which accommodates to many block-angular problems. In this work, problem (11) is solved by the specialized infeasible long-step primal-dual path-following IPM, which was initially introduced in [3] for multicommodity network flows and later extended to general primal block-angular problems [4, 6]. For the solution of SVM problems, we extended the implementation of this algorithm in order to deal with free variables, as described in [5].

For completeness, we will outline the path-following IPM used in this work, in order to derive the particular structure of the systems of equations to be solved. A detailed description of primal-dual path-following IPMs can be found in the monograph [22]. Problem (11) can be recast in general form as

$$\begin{aligned} \begin{array}{rl} \min &{} \quad \displaystyle c^{\top }x + \frac{1}{2}x^{\top }Q x \\ \hbox {subject to} &{} \quad M x= b\\ &{} \quad 0\le x_i \le u_i~ i \not \in {{\mathcal {F}}}, \quad x_i \text{ free } ~ i\in {{\mathcal {F}}}, \end{array} \end{aligned}$$

(13)

where $c\in \mathbb {R}^n$, $Q\in \mathbb {R}^{n\times n}$, $b\in \mathbb {R}^m$, $M\in \mathbb {R}^{m \times n}$, and ${\mathcal {F}}$ denote the set of indices of free variables. Matrix Q is diagonal with nonnegative entries for SVM problems. Let $\zeta \in \mathbb {R}^m$, $\upsilon \in \mathbb {R}^{n-|{{\mathcal {F}}}|}$ and $\omega \in \mathbb {R}^{n-|{{\mathcal {F}}}|}$ be the vectors of Lagrange multipliers of, respectively, equality constraints, lower bounds, and upper bounds. To simplify the notation, given any vector $z\in \mathbb {R}^{n-|{{\mathcal {F}}}|}$, the vector ${\tilde{z}}\in \mathbb {R}^n$ will be defined as

$$\begin{aligned} {\tilde{z}}_i= \left\{ \begin{array}{ll} z_i &{} \hbox { for } i\not \in {{\mathcal {F}}} \\ 0 &{} \hbox { for } i\in {{\mathcal {F}}} \end{array}\right. ; \end{aligned}$$

and given any vector $z\in \mathbb {R}^n$, the matrix $Z\in \mathbb {R}^{n\times n}$ will be $Z= \text{ diag }(z)$.

For any $\mu \in \mathbb {R}_{+}$, the central path can be derived as a solution of the $\mu$-perturbed Karush–Kuhn–Tucker optimality conditions of (13):

$$\begin{aligned} r_b \quad&\equiv \quad b - M x&= 0, \end{aligned}$$

(14)

$$\begin{aligned} r_c \quad&\equiv \quad Qx+c - M^{\top }\zeta - \tilde{\upsilon }+ \tilde{\omega }&= 0 , \end{aligned}$$

(15)

$$\begin{aligned} r_{x\upsilon } \quad&\equiv \quad \mu {\tilde{e}} - X\tilde{\Upsilon }{\tilde{e}}&= 0, \end{aligned}$$

(16)

$$\begin{aligned} r_{x\omega } \quad&\equiv \quad \mu {\tilde{e}} - ({\tilde{U}}-X) \tilde{\Omega }{\tilde{e}}&= 0, \end{aligned}$$

(17)

$$\begin{aligned}&\qquad (x,\upsilon ,\omega )&\ge 0, \end{aligned}$$

(18)

The primal-dual path-following method consists in solving the nonlinear system (14)–(18) by a sequence of damped Newton’s directions (with step-length reduction to preserve the nonnegativity of variables), decreasing the value of $\mu$ at each iteration. On the left-hand side of (14)–(18), we have explicitly defined the residuals of the current iterate $r_b$, $r_c$, $r_{x\upsilon }$ and $r_{x\omega }$.

By performing a linear approximation of (14)–(18) around the current point, we obtain the Newton system in variables $\Delta x$, $\Delta \zeta$, $\Delta \upsilon$ and $\Delta \omega$. Applying Gaussian elimination the Newton system can be reduced to the normal equations form (see, for instance, [22] for details)

$$\begin{aligned} M\Theta M^{\top }\Delta {\zeta }= g, \end{aligned}$$

(19)

where

$$\begin{aligned} g&= r_b + M\Theta (r_c+({\tilde{U}}-X)^{-1} r_{x\omega } - X^{-1} r_{x\upsilon }) ~ \in ~ \mathbb {R}^m ,\nonumber \\ \Theta&= (Q+\tilde{\Omega }({\tilde{U}}-X)^{-1} + \tilde{\Upsilon }X^{-1})^{-1} ~ \in ~ \mathbb {R}^n, \end{aligned}$$

(20)

The values of $\Delta x$, $\Delta \upsilon$ and $\Delta \omega$ can be easily computed once $\Delta \zeta$ is known. Note that $\Theta$ is a diagonal matrix since Q is diagonal.

Free variables in ${{\mathcal {F}}}$ do not have associated Lagrange multipliers in $\omega$ and $\upsilon$, and then, according to (20), $\Theta _{{\mathcal {F}}}= Q_{{\mathcal {F}}}^{-1}$ (where $\Theta _{{\mathcal {F}}}$ and $Q_{{\mathcal {F}}}$ are the submatrices of $\Theta$ and Q associated with free variables). For the variables $w^i$ that define the normal vector of the SVM hyperplane, this is not an issue, since those variables have a nonzero entry in matrix Q of the quadratic costs. However, the intercept $\gamma ^i$ of the SVM hyperplane has neither a multiplier in $\omega$ and $\upsilon$ nor a quadratic entry in Q; thus, its associated entry in the scaling matrix $\Theta$ is 0, making it singular. This can be fixed by using the regularization strategy for free variables described in [17]. A derivation and additional details about the normal equations can be found in [22].

Exploiting the block structure of M and $\Theta$ we have:

$$\begin{aligned} \begin{array}{rcl} M\Theta M^{\top }\Delta {\zeta } &{} = &{} \left[ \begin{array}{cccc|c} M_1 \Theta _1 M^{\top }_1 &{} &{} &{}&{} M_1 \Theta _1 L_1^{\top }\\ &{} \ddots &{} &{}&{} \vdots \\ &{} &{} M_k \Theta _k M^{\top }_k &{}&{} M_k \Theta _k L_k^{\top }\\ &{} &{} &{} &{} \\ \hline &{} &{} &{} &{} \\ L_1 \Theta _1 M^{\top }_1 &{} \ldots &{} L_k\Theta _k M^{\top }_k &{}&{} \Theta _0+ \sum _{i=1}^k L_i\Theta _i L_i^{\top }\end{array} \right] \Delta {\zeta } \\ \\ &{} = &{} \left[ \begin{array}{c c} B &{} C \\ C^{\top }&{} D \end{array} \right] \left[ \begin{array}{c} \Delta {\zeta _1}\\ \Delta {\zeta _2}\end{array}\right] = \left[ \begin{array}{c} g_1\\ g_2\end{array}\right] , \end{array} \end{aligned}$$

(21)

where $\Delta {\zeta _1}\in \mathbb {R}^{\sum _{i=1}^k m_i}$ and $\Delta {\zeta _2}\in \mathbb {R}^l$ are the components of $\Delta {\zeta }$ associated with, respectively, block and linking constraints; $\Theta _i = (Q_i+\tilde{\Omega }_i ({\tilde{U}}_i-X_i)^{-1} + \tilde{\Upsilon }_i X_i^{-1})^{-1}$, $i=0,\dots ,k$, are the blocks of $\Theta$; and $g=(g_1^{\top }g_2^{\top })^{\top }$ is the corresponding partition of the right-hand side g. We note that matrix B is comprised of k diagonal blocks $M_i\Theta _i M_i^{\top }$ for $i=1,\dots ,k$, each of them associated with one of the subsets in which the dataset of points was partitioned. By eliminating $\Delta {\zeta _1}$ from the first group of equations of (21), we obtain

$$\begin{aligned} (D-C^{\top }B^{-1}C)\Delta {\zeta _2}= & {} (g_{2} - C^{\top }B^{-1} g_{1}) \end{aligned}$$

(22a)

$$\begin{aligned} B\Delta {\zeta _1}= & {} (g_{1} - C\Delta {y_2}). \end{aligned}$$

(22b)

The specialized IPM for this class of problems solves (22) by performing k Cholesky factorizations for the k diagonal blocks of B and by using a preconditioned conjugate gradient (PCG) for (22a). System (22a) can be solved by PCG because matrix $D-C^{\top }B^{-1}C \in \mathbb {R}^{l \times l}$ of (22a) (whose dimension is the number of linking constraints) is symmetric and positive definite, since it is the Schur complement of the normal equations (21), which are symmetric and positive definite. A good preconditioner is, however, instrumental. We use the one introduced in [3], which is based on the P-regular splitting theorem [18]. $D-C^{\top }B^{-1}C$ is a P-regular splitting, i.e. it is symmetric and positive definite; D is nonsingular; and $D+C^{\top }B^{-1}C$ is positive definite. Therefore, the P-regular splitting theorem guarantees that

$$\begin{aligned} 0< {\rho (D^{-1}(C^{\top }B^{-1} C)) < 1}, \end{aligned}$$

(23)

where $\rho (\cdot )$ denotes the spectral radius of a matrix (i.e. the maximum absolute eigenvalue). This allows us to compute the inverse of $D-C^{\top }B^{-1}C$ as the following infinite power series (see [3, Prop. 4] for a proof).

$$\begin{aligned} (D-C^{\top }B^{-1} C)^{-1}= \left( \sum _{i=0}^\infty (D^{-1}(C^{\top }B^{-1} C))^i \right) D^{-1}. \end{aligned}$$

(24)

The preconditioner is thus obtained by truncating the infinite power series (24) at some term. In theory, the more terms that are considered, the fewer PCG iterations that are required, although at the expense of increasing the cost of each PCG iteration. Including only the first, and only the first and second terms of (24), the resulting preconditioners are, respectively, $D^{-1}$ and $(I+D^{-1}(C^{\top }B^{-1} C)) D^{-1}$. As observed in [5], $D^{-1}$ generally provided the best results for most applications, and it will be our choice for solving SVM problems.

Although its performance is problem dependent, the effectiveness of the preconditioner obtained by truncating the infinite power series (24) most often depends on two criteria:

• First, the quality of the preconditioner relies on the spectral radius $\rho (D^{-1} (C^{\top }B^{-1}C))$, which is always in (0, 1): the farther from 1, the better the preconditioner [6]. The value of the spectral radius strongly depends on the particular problem (even instance) being solved. Therefore, it is difficult to know a priori if the approach will be efficient for some particular application. However, there are a few results that justify its application for solving SVMs: Theorem 1 and Proposition 2 of [6] state that the preconditioner is more efficient for quadratic problems (such as SVMs) than for purely linear optimization problems.

• Secondly, the structure of matrix $D=\Theta _0+ \sum _{i=1}^k L_i\Theta _i L_i^{\top }$, since systems with this matrix have to be solved at each PCG iteration. Therefore, D has to be easily formed and factorized. We show in the next subsection that building and factorizing the matrices D that arise in SVMs are computationally fast operations.

3.1 The Structure of the Preconditioner D

According to (21), the preconditioner D is defined as

$$\begin{aligned} \mathbb {R}^{l \times l} \ni D=\Theta _0+ \sum _{i=1}^k L_i\Theta _i L_i^{\top }\end{aligned}$$

(25)

where, from (8d) and (9d), the structure of $\begin{bmatrix} L_1&\dots&L_k \end{bmatrix}$ is

(26)

From (26) by block multiplication we get

$$\begin{aligned} \sum _{i=1}^k L_i\Theta _i L_i^{\top }= \left[ \begin{array}{ccccc} \Theta _1 + \Theta _2 &{} -\Theta _2 &{} &{} &{} \\ -\Theta _2 &{} \Theta _2+\Theta _3 &{} -\Theta _3 &{} &{} \\ &{} \ddots &{} \ddots &{} \ddots &{} \\ &{} &{} -\Theta _{k-2} &{} \Theta _{k-2}+ \Theta _{k-1}&{} -\Theta _{k-1} \\ &{} &{} &{} -\Theta _{k-1}&{} \Theta _{k-1}+ \Theta _k \\ \end{array} \right] . \end{aligned}$$

(27)

Therefore, from (25), the preconditioner D is a t-shifted (symmetric and positive definite) tridiagonal matrix, where t is the number of split variables (in the SVM problem, $t= d+1$ is the number of components in $(w,\gamma )$ defining the separation hyperplane). A t-shifted tridiagonal matrix is a generalization of a tridiagonal matrix where the superdiagonal (nonzero diagonal above the main diagonal) and subdiagonal (nonzero diagonal below the main diagonal) are shifted t positions from the main diagonal, i.e. elements (i, j) are non-zero only if $|i-j|$ is either 0 or t. Matrices with such a structure can be efficiently factorized with zero fill-in by extending a standard factorization for tridiagonal matrices. The algorithm in Fig. 1 shows the efficient factorization of matrix (27).

Fig. 1

Algorithm for efficiently computing the factorization of matrix (27)

The above discussion is summarized in the following result:

Proposition 1

For any two-class or one-class SVM problem based, respectively, on the splitting formulations (8) and (9), the preconditioner D defined in (25) is a $(d+1)$-shifted tridiagonal matrix of dimension $(d+1)(k-1)$, where $d+1$ is the number of components in $(w,\gamma )$ and k is the number of subsets in which the points of the SVM were partitioned.

Proof

From (25), D is the sum of the diagonal matrix $\Theta _0$ and $\sum _{i=1}^k L_i\Theta _i L_i^{\top }$. Using the structure of $[L_1 \dots L_k]$ in (25), by block multiplication we get that $\sum _{i=1}^k L_i\Theta _i L_i^{\top }$ is the tridiagonal matrix (27), where each diagonal matrix $\Theta _i$, $i=1,\dots ,k$ has dimension $d+1$. Therefore, D is a $(d+1)$-shifted tridiagonal matrix. $\square$

4 Computational Results

The specialized algorithm for SVMs detailed in Sect. 3 has been coded in C++ using the BlockIP package [5], which is an implementation of the IPM for block-angular problems. The resulting code will be referred to as SVM-BlockIP. SVM-BlockIP solves both the two-class and one-class SVM models (8) and (9). The executable file of SVM-BlockIP can be downloaded at http://www-eio.upc.edu/~jcastro/SVM-BlockIP.html.

SVM-BlockIP is compared with the following solvers:

• The standard primal-dual barrier algorithm in CPLEX 20.1. In general this interior-point variant is faster than the homogeneous-self-dual one, especially when a loose optimality tolerance is considered (which is our case, as discussed below). For a fair comparison, both the original compact SVM models (1) and (5) as well as the new splitting ones (8) and (9) will be solved with CPLEX 20.1.

• SVM-OOPS [21] is a very efficient IPM based on a separable reformulation of the dual of the two-class SVM compact model (4). SVM-OOPS does not solve one-class SVM problems.

• LIBSVM [7] solves the dual compact models (4) and (6), so it can be used for both two-class and one-class SVMs. It is based on a specialized algorithm developed in the machine learning community for SVMs, which is called sequential minimal optimization [19].

• LIBLINEAR [11] solves the compact models of two-class and one-class SVMs. For two-class SVMs, it can solve either the dual or the primal model, but without the $\gamma$ variable (so the models solved by LIBLINEAR are a bit different—and simpler—than those considered by the other solvers). For one-class SVMs, it solves the dual (6) with a coordinate descent algorithm.

The same parameters (e.g. optimality tolerance) were used for all the solvers.

It is in general not desirable (and indeed, not recommended) to compute an optimal solution to an SVM optimization problem using a tight optimality tolerance because, otherwise, the plane $(w^*,\gamma ^*)$ may excessively fit to the dataset of points $a_i$, $i=1,\dots ,p$ (named the training dataset), and it might not be able to properly classify a new and different set of points (named the testing dataset). This phenomenon is named overfitting in the data science community [10]. For this reason, SVM-BlockIP and the rest of solvers will be executed with an optimality tolerance of $10^{-1}$. It is worth noting that loose optimality tolerances are more advantageous for SVM-BlockIP than for the other interior-point solvers that rely only on Cholesky factorizations (CPLEX 20.1 and SVM-OOPS), namely because it has been observed [3,4,5,6] that SVM-BlockIP needs a greater number of PCG iterations for computing the Newton direction when approaching the optimal solution. A loose tolerance thus avoids SVM-BlockIP’s last and most expensive interior-point iterations.

A loose optimality tolerance also allows using loose tolerances for solving PCG systems. Indeed, the requested PCG tolerance is one of the parameters that most influence the efficiency of the specialized IPM. The PCG tolerance in the BlockIP solver is dynamically updated at each interior-point iteration i as $\epsilon _i = \max \{\beta \epsilon _{i-1}, \min _\epsilon \}$, where $\epsilon _0$ is the initial tolerance, $\min _\epsilon$ is the minimum allowed tolerance, and $\beta \in [0,1]$ is a tolerance reduction factor at each interior-point iteration. For SVM-BlockIP, we used $\epsilon _0= 10^{-2}$ and $\beta = 1$, that is, a tolerance of $10^{-2}$ was used for all the interior-point iterations. It is known that the resulting inexact Newton direction does not seriously affect the convergence properties of IPMs [16].

Table 1 Dimensions of SVM instances

For the computational results, we considered a set of 19 standard SVM instances. Their dimensions are reported in Table 1. Columns p and d show the number of points and features, respectively. The instances are divided into two groups according to their number of features, since previous interior-point approaches for SVM could handle only instances with a few features. Column k is the number of subsets of points considered, and each instance was tested with different values. Rows with $k=1$ (that is, without splitting) refer to the compact formulations (1) and (5), while for $k>1$ the row is associated with the splitting models (8) and (9). The cases with $k=1$ (compact model) were solved with CPLEX, SVM-OOPS, LIBSVM and LIBLINEAR; when $k>1$, only CPLEX and SVM-BlockIP can be used. Since very dense matrices $A^i{A^i}^{\top }$ in the interior-point method may be provided by submatrices $A^i$ (which are related to the splitting model’s i-th subset of $p_i$ points), the value of $k>1$ was selected so that p/k ($\approx p_i$) was always less than 1000 (we observed that the dense factorization of $A^i{A^i}^{\top }$ was too expensive for dimensions greater than 1000). For instances with a large number of points, two values of k were tested (one being ten times greater than the other); increasing k reduces the dimensions of systems $A^i{A^i}^{\top }$ at the expense of increasing the number of variables and linking constraints of the splitting formulation. As a rule of thumb, as as will be shown below, the best results with the splitting formulation are obtained with the greatest k when d is small, and with the smallest k when d is large. Finally columns “n.vars.”, “n.cons.” and l give, respectively, the numbers of variables, constraints (excluding linking constraints) and linking constraints, which are computed, also respectively, as $(d+1)k+2p$, p, and $(d+1)(k-1)$. This set of SVM instances includes the full version of the four largest (out of the five) cases tested in [21]. It is worth noting that SVM-BlockIP was extended with dense matrix operations (in addition to the default sparse ones in the BlockIP IPM package) in order to handle problems with very dense matrices of points $A^i$. Executions with both sparse and dense matrices were considered only for four of the instances in Table 1 (namely, “gisette”, “madelon”, “sensit”, and “usps”).

The instances tested are in the format used by the standard SVM packages LIBSVM [7] and LIBLINEAR [11], and they were retrieved from https://www.csie.ntu.edu.tw/~cjlin/libsvmtools/datasets/. Points $a_i \in \mathbb {R}^d$, $i=1,\dots ,p$ in those instances were properly scaled by the authors of LIBSVM and LIBLINEAR, such that most features are in the range of $[-1,1]$. In those instances, for two-class SVM, the value of parameter $\nu$ was 1 for all the solvers; for one-class SVM, $\nu = 0.1$ was used.

From the previous original instances, we generated a second set of cases by applying an alternative (linear) scaling to the original features. In most cases of the new linear scaling, features were concentrated within the interval [0, 0.001]. This second set of instances has the same dimensions as those in Table 1. As a result of the new scaling, the optimal normal vector $w^*$ will take larger values, so the quadratic term in the objective function will be larger. To compensate for this fact, a value of $\nu = 1000$ was used for two-class SVM. For one-class SVM, we used the same value of $\nu =0.1$ that was used for the original instances, since $\nu$ is related to the upper bound on the fraction of detected outliers in the one-class SVM problem. The increase in the quadratic term due to the new scaling turned out to be very advantageous for SVM-BlockIP, since (as was proven in [6, Prop. 2]) the quadratic terms in the objective function of (11) reduce the spectral radius (23), thus making the preconditioner more efficient. The set of scaled instances can be retrieved from the SVM-BlockIP webpage http://www-eio.upc.edu/~jcastro/SVM-BlockIP.html.

The next two subsections show the computational results for, respectively, two-class SVM and one-class SVM, using both the original datasets, and those with the new scaling. All the computational experiments in this work were carried out on a DELL PowerEdge R7525 server with two 2.4 GHz AMD EPYC 7532 CPUs (128 total cores) and 768 Gigabytes of RAM, running on a GNU/Linux operating system (openSuse 15.3), without exploitation of multithreading capabilities.

4.1 Results for Two-Class SVM Instances

Tables 2 and 3 show the results obtained for two-class SVM with, respectively, the original and scaled instances. For all the solvers (namely, SVM-BlockIP, CPLEX 20.1, LIBSVM, and LIBLINEAR), the tables provide: the number of iterations (columns “it”), solution time (columns “CPU”), objective function achieved (columns “obj”), and accuracy of the solution provided (columns “acc%”). The accuracy is the percentage of correctly classified points (of the testing dataset) using the hyperplane provided by the optimal solution (which was computed with the training dataset); that is, the accuracy is related to the the optimal solution’s usefulness for classification purposes. For SVM-BlockIP, the tables also provide the overall number of PCG iterations (columns “PCGit”). The CPU time of the fastest execution for each instance is marked in boldface, excluding the LIBLINEAR time, since it solved the simpler problem (7) whereas the other solvers dealt with (1) or (4).

Table 2 Results for two-class SVM original instances (in boldface the CPU of fastest execution for each instance)

Table 3 Results for two-class SVM scaled instances (in boldface the CPU of fastest execution for each instance)

SVM-BlockIP allows computing both the Newton direction (19) and the predictor-corrector direction [22], both of which were tried for solving SVM problems. Although, in general, predictor-corrector directions are not competitive for PCG-based IPMs because they force using twice the PCG at each interior-point iteration, in some cases they provided the fastest solution. Those cases are marked with an “$^*$” in their “CPU” columns.

From Table 2, it is observed that SVM-BlockIP was not competitive against the other solvers for instances with a small number of features (first rows in the table). In general, SVM-OOPS provided the fastest executions in six of these instances, CPLEX in four, and LIBSVM in three. All solvers converged to solutions of similar objective functions for all the instances but three (namely “covtype”, “madelon”, and “mushrooms”), in which LIBLINEAR and LIBSVM (after a large number of iterations) stopped at non-optimal points. However, it is worth noting that the accuracy of LIBLINEAR and LIBSVM in two of these three instances was still good. Furthermore, when the number of features increase (last rows of Table 2 ), SVM-OOPS was unable to solve five out of the six instances; LIBSVM was the fastest approach in three of these instances; and CPLEX in two (but in those two, SVM-BlockIP reported a similar time). In two cases (namely “rcv1” and “real-sim”), SVM-BlockIP obtained the fastest solutions in 23.5 and 524.9 seconds while CPLEX needed 2086.1 and 91,482.1 seconds. The fastest solution times—for any k—with SVM-BlockIP, CPLEX, SVM-OOPS and LIBSVM, are summarized in plot (a) of Fig. 2. LIBLINEAR was excluded from the comparison because it solved the slightly different problem (7). CPU times are in log scale. Note that there is no information for SVM-OOPS and the five rightmost instances, since, due to their large number of features, it could not solve them. Similarly, plot (a) of Fig. 3 shows the accuracy of the solutions obtained with SVM-BlockIP, LIBLINEAR (whose accuracies are similar to those of LIBSVM), and SVM-OOPS. It is evident that, in general, all methods provided similar accuracies (unlike for “covtype” and “mushrooms”, where SVM-BlockIP underperformed the other solvers).

Fig. 2

CPU seconds (in log scale) required by SVM-BlockIP, CPLEX, SVM-OOPS and LIBSVM for two-class SVM, with the original instances in Table 2 (plot a) and the scaled instances in Table 3 (plot b)

Fig. 3

Accuracies (in %) provided by solutions with SVM-BlockIP, LIBLINEAR and SVM-OOPS for two-class SVM, with the original instances in Table 2 (plot a) and the scaled instances in Table 3 (plot b)

The results in Table 3 show a different behaviour of the solvers in the scaled dataset. For the instances with a few features, CPLEX, SVM-OOPS and LIBSVM were not significantly affected; for the instances with large d (last rows in the table), the CPU times increased notably for CPLEX and LIBSVM, whereas SVM-OOPS was once again unable to solve most of the problems. The coordinate gradient descent algorithm of LIBLINEAR significantly increased the CPU time for all the instances, independently of the number of features. However, the CPU times for SVM-BlockIP dropped drastically, thereby allowing it to solve the scaled dataset in a fraction of the times it required for the original dataset, which are reported in Table 2. SVM-BlockIP was the most efficient approach (including LIBLINEAR) in most cases, especially when the number of features was large. For example, for the instances “rcv1” and “real-sim”, SVM-BlockIP required, respectively, 7.9 and 14.4 seconds whereas CPLEX needed, respectively, 1236.7 and 40,484.8 seconds for $k=1$, and 3223.8 and 320,107.0 seconds for the same $k>1$ used with SVM-BlockIP. This fact can be explained by the higher importance of the quadratic term in the objective function due to the scaling (which is reflected in the larger objective values in Table 3 as compared to those in Table 2). Plot (b) of Fig. 2 shows the best CPU time, for any value of k, of SVM-BlockIP, CPLEX, SVM-OOPS and LIBSVM for the scaled dataset. LIBLINEAR is again excluded because it solves the simpler problem (7). Comparing plots (a) and (b) of Fig. 2 is clearly observed that the solution times with SVM-BlockIP significantly dropped for the scaled dataset. The downside of the scaling was that the accuracy decreased slightly in several instances (although it increased in a few, such as for problem “leu”), as can be observed in plot (b) of Fig. 3.

4.2 Results for One-Class SVM Instances

Tables 4 and 5 give the results of one-class SVM for, respectively, the original and scaled instances. SVM-OOPS does not solve the one-class SVM problem, so it is excluded from the comparison in those tables. The meaning of the columns is the same as in the previous Tables 2 and 3. For one-class SVM, the accuracy is measured as the percentage of dataset points that are not considered novelty or outliers; that is, 100 minus the accuracy is the percentage of detected outliers or novelty points. Since a value of $\nu =0.1$ was used for one-class SVM (which is an upper bound on the fraction of detected outliers), accuracies should theoretically be greater than or equal to $90\%$.

Table 4 Results for one-class SVM original instances (in boldface the CPU of fastest execution for each instance)

Table 5 Results for one-class SVM scaled instances (in boldface the CPU of fastest execution for each instance)

Looking at Tables 4 and 5, it is clearly observed that LIBSVM and LIBLINEAR could not solve any instance, and their objective values were very different from those reported by CPLEX and SVM-BlockIP (which, in addition, were similar). Indeed, the solutions reported by LIBSVM and LIBLINEAR had very poor accuracy, usually around 50%, which means that the reported hyperplane is not useful for outlier or novelty detection. Such a different behaviour of LIBSVM and LIBLINEAR between two-class (where they provided high-quality hyperplanes) and one-class SVM is likely explained by the existence of constraint (6b), which complicates solving (6) by means of a coordinate gradient algorithm.

Unlike LIBSVM and LIBLINEAR, SVM-BlockIP was able to compute a fast and good solution for all the instances. For the original datasets in Table 4, SVM-BlockIP and CPLEX had similar performance for the instances with few features. However, for the instances with a large number of features (last rows in Table 4), SVM-BlockIP was generally much more efficient than CPLEX. For example, for the cases “gisette”, “news20”, “rcv1”, and “real-sim” the best SVM-BlockIP times were, respectively, 40.5, 109.8, 7.4 and 22.2 seconds, whereas CPLEX required, respectively, 1104.9, 3141.7, 2624.1 and 71,227.9 seconds. This difference in performance between SVM-BlockIP and CPLEX slightly increased even for the scaled instances in Table 5. The fastest executions—for any value of k—with SVM-BlockIP and CPLEX are shown in plots (a) (for the original instances) and (b) (for the scaled instances) of Fig. 4. The CPU times for LIBSVM and LIBLINEAR are not given since they did not solve the optimization problem. It is clearly observed that SVM-BlockIP is much more efficient than CPLEX for the (rightmost) instances with a large number of features.

As for the accuracies, it can be observed in plot (a) of Fig. 5 that SVM-BlockIP generally provided values of around 90% (as expected by theory) for the runs in Table 4, except for the instances “madelon” and “colon-cancer” (in the latter it was outperformed even by LIBSVM and LIBLINEAR). For the scaled instances in Table 5, SVM-BlockIP accuracies were even higher, about 100% in most cases, as shown in plot (b) of Fig. 5. Whether or not hyperplanes with such high accuracies are useful in practice for outlier or novelty detection is a question beyond the scope of this work, which focuses on the efficient solution of the resulting SVM optimization problems.

Fig. 4

CPU seconds (in log scale) required by SVM-BlockIP and CPLEX for one-class SVM, with the original instances in Table 4 (plot a) and the scaled instances in Table 5 (plot b)

Fig. 5

Accuracies (in %) provided by solutions with SVM-BlockIP, LIBLINEAR and LIBSVM for one-class SVM, with the original instances in Table 4 (plot a) and the scaled instances in Table 5 (plot b)

5 Conclusions

For large-scale optimization problems arising from data science and machine learning applications, first-order coordinate descent algorithms are traditionally considered to be superior to second-order methods (in particular, to interior-point methods). For the particular case of two-class and one-class SVMs, we have shown in this work that a specialized interior-point method for an appropriate multiple variable splitting reformulation of the SVM problem can provide decent results when compared to the best machine learning tools (i.e. LIBLINEAR). More importantly, when the optimization problem involves at least a single linear constraint (as in the dual of the one-class SVM problem), we have shown that the second-order interior-point method is very efficient and provides high-quality solutions, whereas the (far from optimal) solutions obtained by first-order algorithms (i.e. LIBSVM and LIBLINEAR) are not useful in practice. In addition, when working with high-dimensional data, the new approach presented in this work outperformed to a large degree the best interior-point methods for SVM (namely, CPLEX 20.1 and SVM-OOPS).