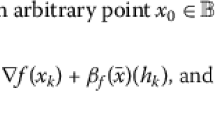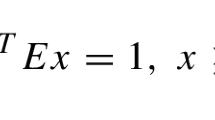First- and Second-Order Optimality Conditions for Quadratically Constrained Quadratic Programming Problems

Abstract

We consider a quadratic programming problem with quadratic cone constraints and an additional geometric constraint. Under suitable assumptions, we establish necessary and sufficient conditions for optimality of a KKT point and, in particular, we characterize optimality by using strong duality as a regularity condition. We consider in details the case where the feasible set is defined by two quadratic equality constraints and, finally, we analyse simultaneous diagonalizable quadratic problems, where the Hessian matrices of the involved quadratic functions are all diagonalizable by means of the same orthonormal matrix.

1 Introduction

We analyse a quadratic programming problem with general quadratic cone constraints and an additional geometric constraint. This problem has received attention in the literature in the last decades (see, e.g. [5, 7, 18, 20]) since it contains as a particular case several classic optimization problems as trust region problems, the standard quadratic problem and the max cut problem; moreover, it has many applications in robust optimization under matrix norm data uncertainty and in the field of biology and economics [12].

In this paper, we are interested in establishing necessary or sufficient global optimality conditions for a point that fulfils the Karush–Kuhn–Tucker (KKT) conditions or under the assumption of strong duality on the given problem. The general formulation of the considered quadratic programming problem allows us to treat simultaneously quadratic problems with one or more quadratic equality or inequality constraints and possibly additional constraints that can be included in the geometric one, which makes the analysis of the given problem very general, particularly as regards the possibility of providing equivalent formulations and associating a dual problem with the given one. Our approach allows to recover or generalize several known results in the literature [13, 14, 20].

The paper is organized as follows. In Sect. 2 we recall the main definitions and preliminary results that will be used throughout the paper. In Sect. 3, we characterize global optimality for a KKT point or in the presence of the property of strong duality on the given problem and in Sect. 4, we consider in details the case where the feasible set is defined by two quadratic equality constraints. In Sect. 5 we analyse a simultaneous diagonalizable quadratic problem (SDQP), where the Hessian matrices of the involved quadratic functions are all diagonalizable by means of the same orthonormal matrix S. The analysis previously developed allows us to provide suitable conditions that guarantee the existence of a convex reformulation of SDQP improving some results stated in [15] in the presence of two quadratic inequality constraints.

2 Preliminary Results

Let us recall the basic notations and preliminary results that will be used throughout the paper. Given $C\subseteq \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n$, $\mathrm{co}~C$, $\mathrm{int}~ C$, $\mathrm{ri}~ C$, $\mathrm{cl}~{C}$, $\mathrm{span}~{C}$, denote the convex hull of C, the topological interior of C, the relative interior, the closure of C and the smallest vector linear subspace containing C, respectively. C is said to be a cone if $tC\subseteq C$, $\forall ~t\ge 0$. A convex cone C is called pointed if $C\cap (-C)=\{0\}$. We define $\mathrm {cone}~ C:=\bigcup _{t\ge 0}tC$.

We set $\mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^m_+:= \{x\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^m:x\ge 0\}$. If C is a convex set and $x\in C$, the normal cone to C at ${\bar{x}}\in C$ is defined by $N_C({\bar{x}}):=\{\xi \in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n:\langle \xi ,x-\bar{x}\rangle \le 0,~~\forall ~x\in C\}$.

The positive polar of a set $C\subseteq \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n$ is defined by $C^*:=\{y^*\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n:\langle y^*,x\rangle \ge 0, \ \forall x\in C\}.$ It is well known that

$$\begin{aligned}&C^*=(\mathrm{cl}~{C})^*=(\mathrm{co}~C)^*=(\mathrm{cone}~C)^*,~~ \mathrm{cl}~{\mathrm{co}}(\mathrm{cone}~C)\nonumber \\&\quad =\mathrm{cl}~{\mathrm{cone}}(\mathrm{co}~C)=C^{**}:=(C^*)^*. \end{aligned}$$

(1)

$C^\perp :=\{v\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n:~v^\top x=0,~\forall ~x\in C\}$ is the orthogonal subspace to the set C.

The contingent cone $T(C;\bar{x})$ of C at $\bar{x}\in C$ is the set of all $v \in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n$ such that there exist sequences $(x_k,t_k)\in C\times \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits _+$ with $x_k\rightarrow \bar{x}$ and $t_k(x_k-\bar{x})\rightarrow v$.

Let $P\subseteq \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^m$ be a convex cone and $C\subseteq \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n$ a convex set. A function $f:\mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n\rightarrow \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^m$ is said P-convex on C if for every $x_1,x_2\in C$ and for every $\lambda \in [0,1]$,

$$\begin{aligned} \lambda f(x_1) +(1-\lambda )f(x_2) - f(\lambda x_1 +(1-\lambda )x_2)\in P. \end{aligned}$$

For $m=1$ and $P=\mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits _+$, we recover the classic definition of a convex function. It is known that if f is P-convex on C, then the set $f(C)+P$ is convex.

In the paper we will use the following preliminary results.

Let $C:=\{x\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n:g(x)=0\}$, where $g:\mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n\rightarrow \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits$. Then, we get [6]

$$\begin{aligned} T(C;\bar{x})=\{v\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n:~\nabla g(\bar{x})^\top v=0\}= \nabla g(\bar{x})^\perp ~~\text{ if }~\nabla g(\bar{x})\ne 0, \end{aligned}$$

(2)

and so $[T(C;\bar{x})]^*=\mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits \nabla g(\bar{x})$; whereas if $g(x)\doteq \dfrac{1}{2}x^\top Bx+b^\top x+\beta$ is a quadratic function, with B being a real symmetric matrix of order n, $b\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n$ and $\beta \in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits$, then

$$\begin{aligned} T(C;\bar{x})=\{v\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n:~v^\top B v=0\}~~\text{ if }~\nabla g(\bar{x})=0. \end{aligned}$$

(3)

A symmetric matrix B is positive semidefinite on C, if $x^\top Bx\ge 0,~\forall ~x\in C.$

Lemma 2.1

( [18, Lemma 3.10]) Assume that B is an indefinite real symmetric matrix and set $Z:=\{v\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n:~v^\top Bv=0\}$. Then

$$\begin{aligned} \mathrm{co}~Z=\mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n=\mathrm{span}~Z. \end{aligned}$$

3 The General Case with Cone Quadratic Constraints

Let us consider the problem

$$\begin{aligned} \mu :=\inf \{f(x):~g(x)\in -P, \ x\in C\}, \end{aligned}$$

(4)

where P is a convex cone in $\mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^m$, $g(x):= ( g_1(x),\ldots ,g_m(x))$ and $f,g_i:\mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n\rightarrow \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ,~i=1,\ldots ,m$ are quadratic functions, $C\subseteq \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n$,

$$\begin{aligned} f(x):=\dfrac{1}{2}x^\top Ax+a^\top x+\alpha ,~g_i(x):=\dfrac{1}{2}x^\top B_ix+b_i^\top x+\beta _i,~i=1,\ldots ,m, \end{aligned}$$

(5)

with $A,~B_i$ being real symmetric matrices; $a,~b_i$ being vectors in $\mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n$ and $\alpha ,~\beta _i\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits$ for $i=1,\ldots ,m$. $K:= \{x\in C:~g(x)\in -P\}$ is the feasible set of (4). We associate with (4) the Lagrangian function $L(\lambda , x)\doteq f(x)+\displaystyle \sum _{i=1}^m\lambda _ig_i(x)$ and its dual problem

$$\begin{aligned} \nu :=\sup _{\lambda \in P^*}\inf _{x\in C}\ L(\lambda ,x). \end{aligned}$$

(6)

We say that strong duality holds for (4), if there exists $\lambda ^*\in P^*$ such that

$$\begin{aligned} \inf _{x\in K}f(x)=\inf _{x\in C}L(\lambda ^*,x). \end{aligned}$$

In case (4) admits an optimal solution ${\bar{x}}\in K$, then the previous condition is equivalent to

$$\begin{aligned} L(\lambda ^*,{\bar{x}})\le L(\lambda ^*,x),\ \forall x\in C, \qquad \langle \lambda ^*,g({\bar{x}})\rangle =0, \qquad g({\bar{x}})\in -P, \qquad {\bar{x}}\in C. \end{aligned}$$

(7)

Under suitable assumptions on the cone $T(C;{\bar{x}})$, we first establish three general results: the first and the second consider the case where ${\bar{x}}$ is a KKT point and provide a sufficient optimality condition and a characterization of its optimality in the case where $P=\{0\}^m$, respectively, while the third one characterizes optimality under the assumption of strong duality.

Proposition 3.1

Let f, $g_1,\ldots ,g_m$ be quadratic functions as above. Assume that ${\bar{x}}\in K$ is a KKT point for (4), i.e. there exists $\lambda ^*\in P^*$ such that

$$\begin{aligned} \nabla _xL(\lambda ^*,{\bar{x}})\in [T(C;\bar{x})]^*,\quad \langle \lambda ^*,g({\bar{x}})\rangle =0, \end{aligned}$$

(8)

and, additionally, $(K-{\bar{x}})\subseteq \mathrm{cl}~\mathrm{co}~T(C;{\bar{x}})$. Then the following assertion holds.

If $\nabla _x^2L(\lambda ^*,\bar{x})$ is positive semidefinite on $K-\bar{x}$, then $\bar{x}$ is a (global) optimal solution for problem (4).

Proof

By (8), $\nabla _xL(\lambda ^*,{\bar{x}})^\top v\ge 0$, for every $v\in T(C;{\bar{x}})$, and by (1) we obtain

$$\begin{aligned} \nabla _xL(\lambda ^*,{\bar{x}})^\top v\ge 0, \forall v\in \mathrm{cl}~\mathrm{co}~T(C;{\bar{x}}). \end{aligned}$$

The assumptions imply that

$$\begin{aligned} \nabla _x L(\lambda ^*,{\bar{x}})^\top v \ge 0, \quad \forall v\in (K-{\bar{x}}). \end{aligned}$$

(9)

We note that, since the involved functions are quadratic, then, the following equality holds:

$$\begin{aligned}&L(\lambda ^*,x)-L(\lambda ^*,{\bar{x}})= \nabla _xL(\lambda ^*,\bar{x})^\top (x-\bar{x})+\dfrac{1}{2}(x-\bar{x})^\top \nabla _x^2L(\lambda ^*,\bar{x})(x-\bar{x}),\nonumber \\&\quad \forall x\in {\mathbb {R}}^n. \end{aligned}$$

(10)

Exploiting (10) and (9), for every $x\in K$, we get

$$\begin{aligned}&f(x)-f(\bar{x})\ge f(x)+\sum _{i=1}^m\lambda ^*_ig_i(x)-f(\bar{x}) =L(\lambda ^*,x)-L(\lambda ^*,{\bar{x}})\\&\quad \ge \dfrac{1}{2}(x-\bar{x})^\top \nabla _x^2L(\lambda ^*,\bar{x})(x-\bar{x}). \end{aligned}$$

By the previous inequalities, the assertion follows. $\square$

Remark 3.2

Proposition 3.1 is related to Theorem 2.1 in [4] when applied to a quadratic problem. Indeed, Theorem 2.1 in [4] requires that K is a convex set and $C:=\mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n$, which guarantees that the condition $(K-{\bar{x}})\subseteq \mathrm{cl}~\mathrm{co}~T(C;{\bar{x}})$ is fulfilled.

Proposition 3.3

Let f, $g_1,\ldots ,g_m$ be quadratic functions as above, let $P:=\{0\}^m$ and ${\bar{x}}\in K$. Assume that

$$\begin{aligned} (K-{\bar{x}})\subseteq \mathrm{cl}~\mathrm{co}~T(C;{\bar{x}})\subseteq -\mathrm{cl}~\mathrm{co}~T(C;{\bar{x}}), \end{aligned}$$

(11)

and that ${\bar{x}}$ is a KKT point for (4), i.e. there exists $\lambda ^*\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^m$ such that

$$\begin{aligned} \nabla _xL(\lambda ^*,{\bar{x}})\in [T(C;{\bar{x}})]^*. \end{aligned}$$

(12)

Then the following conditions are equivalent:

(a):

$\bar{x}$ is an optimal solution for the problem (4);

(b):

$\nabla _x^2L(\lambda ^*,\bar{x})$ is positive semidefinite on $K-\bar{x}$ and so on cl cone$(K-{\bar{x}})$.

Proof

By (12), $\nabla _xL(\lambda ^*,{\bar{x}})^\top v\ge 0$, for every $v\in T(C;{\bar{x}})$ and by (1) we get,

$$\begin{aligned} \nabla _xL(\lambda ^*,{\bar{x}})^\top v\ge 0, \forall v\in \mathrm{cl}~\mathrm{co}~T(C;{\bar{x}}). \end{aligned}$$

The second inclusion in (11) implies that

$$\begin{aligned} \nabla _x L(\lambda ^*,{\bar{x}})^\top v= 0, \quad \forall v\in \mathrm{cl}~\mathrm{co}~T(C;{\bar{x}}), \end{aligned}$$

(13)

and, by the first inclusion in (11), $\nabla _x L(\lambda ^*,{\bar{x}})^\top v = 0$, for every $v\in (K-{\bar{x}})$.

By (10) and (13), for every $x\in K$, we get

$$\begin{aligned}&f(x)-f(\bar{x})=f(x)+\sum _{i=1}^m\lambda ^*_ig_i(x)-f(\bar{x}) =L(\lambda ^*,x)-L(\lambda ^*,{\bar{x}})\nonumber \\&\quad =\dfrac{1}{2}(x-\bar{x})^\top \nabla _x^2L(\lambda ^*,{\bar{x}})(x-\bar{x}). \end{aligned}$$

(14)

By the previous equalities, the equivalence between (a) and (b) follows. $\square$

Remark 3.4

Note that the second inclusion in assumption (11) is not needed for proving that (b) implies (a), as shown by Proposition 3.1.

In the following proposition we characterize optimality under the strong duality property that can be considered as a regularity condition in view of the fulfilment of the KKT conditions.

Proposition 3.5

Let f, $g_1,\ldots ,g_m$ be quadratic functions as above, let ${\bar{x}}\in K$, and assume that

$$\begin{aligned} (C-{\bar{x}})\subseteq \mathrm{cl}~\mathrm{co}~T(C;{\bar{x}})\subseteq -\mathrm{cl}~\mathrm{co}~T(C;{\bar{x}}). \end{aligned}$$

(15)

Then the following assertions are equivalent:

(a):

$\bar{x}$ is an optimal solution for the problem (4) and strong duality holds;

(b):

there exists $\lambda ^*\in P^*$ such that (8) is fulfilled and $\nabla _x^2L(\lambda ^*,\bar{x})$ is positive semidefinite on $C-\bar{x}$.

Proof

Assume that (a) holds, or equivalently there exists $\lambda ^*\in P^*$ such that (7) is fulfilled. Then,

$L(\lambda ^*,{\bar{x}})\le L(\lambda ^*, x)$, for every $x\in C$, implies that $\nabla _xL(\lambda ^*,{\bar{x}})^\top v\ge 0$, for every $v\in T(C;{\bar{x}})$ and, consequently,

$$\begin{aligned} \nabla _xL(\lambda ^*,{\bar{x}})^\top v\ge 0, \forall v\in \mathrm{cl}~\mathrm{co}~T(C;{\bar{x}}). \end{aligned}$$

(16)

The assumption (15) yields $\nabla _x L(\lambda ^*,{\bar{x}})^\top v= 0$, for every $v\in \mathrm{cl}~\mathrm{co}~T(C;{\bar{x}})$ and, in turn,

$$\begin{aligned} \nabla _x L(\lambda ^*,{\bar{x}})^\top v = 0, \quad \forall v\in (C-{\bar{x}}). \end{aligned}$$

(17)

From (10) we have

$$\begin{aligned} 0\le L(\lambda ^*,x)-L(\lambda ^*,{\bar{x}})=\dfrac{1}{2}(x-\bar{x})^\top \nabla _x^2L(\lambda ^*,{\bar{x}})(x-\bar{x}),\quad \forall x\in C, \end{aligned}$$

and (b) follows.

Conversely if (b) holds then (8) implies (16) and, consequently, (17).

From (10) we have

$$\begin{aligned} L(\lambda ^*,x)-L(\lambda ^*,{\bar{x}})=\dfrac{1}{2}(x-\bar{x})^\top \nabla _x^2L(\lambda ^*,{\bar{x}})(x-\bar{x})\ge 0,\quad \forall x\in C, \end{aligned}$$

and, taking into account that $\langle \lambda ^*,g({\bar{x}})\rangle =0$, (a) follows. $\square$

Remark 3.6

We note that, for the implication $(b)\Rightarrow (a)$ in Proposition 3.5, the second inclusion in (15) is not needed: indeed, by (8) we have $\nabla _x L(\lambda ^*,{\bar{x}})^\top (x-{\bar{x}}) \ge 0, \ \forall x\in C$ and $\langle \lambda ^*,g({\bar{x}})\rangle =0$, so that (10) allows us to prove (a).

Remark 3.7

Condition (15) is fulfilled under the following circumstances:

(i):

${\bar{x}}\in \mathrm{int}\,C$;

(ii):

C is defined by linear equalities, i.e. $C:=\{x\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n:H x=d\}$, $H\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^{p\times n}$, $d\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^p$;

(iii):

$C:=\{x\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n:h(x)=0\}$, where h is a quadratic function with $\nabla h({\bar{x}})=0$ and $H:=\nabla ^2 h({\bar{x}})$ is indefinite. In this case $T(C;{\bar{x}})=C-{\bar{x}}=\{v\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n:~v^\top Hv=0\}$, this is a consequence of Lemma 3.1 proved in what follows. By Lemma 2.1, cl co $T(C;{\bar{x}})=\mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n$.

Lemma 3.1

Let $g_i$ be defined as in (5), for $i=1,\ldots ,m$. Assume that $\bar{x}\in A:=\{x\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n:g_i(x)=0, i=1,\ldots ,m\}$ and set $Z_i(\bar{x}):=\{v\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n:~\nabla g_i(\bar{x})^\top v + \dfrac{1}{2}v^\top B_iv=0\}$, for $i=1,\ldots ,m$. Then,

$$\begin{aligned} Z({\bar{x}}):=\bigcap _{i=1}^mZ_i(\bar{x})=A-\bar{x}. \end{aligned}$$

(18)

Proof

Let $i\in [1,..,m]$. Let $v\in Z_i(\bar{x})$, then $g_i(v+\bar{x})=g_i(\bar{x})+\nabla g_i(\bar{x})^\top v+\dfrac{1}{2}v^\top B_iv=0$, proving that $v+\bar{x}\in \{x\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n:g_i(x)=0\}$. Therefore, $\bigcap _{i=1}^mZ_i(\bar{x})\subseteq A-{\bar{x}}$.

For the other inclusion, take any $x\in A$. Then

$$\begin{aligned} 0=g_i(x)-g_i({\bar{x}})=\nabla g_i(\bar{x})^\top (x-\bar{x})+ \dfrac{1}{2}(x-\bar{x})^\top B_i(x-\bar{x}),\ i=1,\ldots ,m,\nonumber \\ \end{aligned}$$

(19)

which implies $x-{\bar{x}}\in \bigcap _{i=1}^mZ_i(\bar{x})$ . $\square$

Remark 3.6 leads to the following result.

Corollary 3.8

Let f, $g_1,\ldots ,g_m$ be quadratic functions as above, let ${\bar{x}}\in K$, and assume that $C:=\{x\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n:g_i(x)\le 0, i=m+1,\ldots ,p\}$,where $g_i$ are convex functions, for $i=m+1,\ldots ,p$.

If there exists $\lambda ^*\in P^*$ such that (8) is fulfilled and $\nabla _x^2L(\lambda ^*,\bar{x})$ is positive semidefinite on $C-\bar{x}$, then $\bar{x}$ is an optimal solution for the problem (4) and strong duality holds.

Proof

By Proposition 3.5 and taking into account Remark 3.6, it is enough to prove that $(C- {\bar{x}})\subseteq \mathrm{cl}~\mathrm{co}~T(C;{\bar{x}})$. The convexity of the functions $g_i$, $i=m+1,\ldots ,p$, yields that C is convex.

Since C is convex then $T(C;{\bar{x}})=\mathrm{cl}~\mathrm{cone}(C-{\bar{x}})$ which implies $(C- {\bar{x}})\subseteq \mathrm{cl}~\mathrm{co}~T(C;{\bar{x}})$ (see, e.g. [2]). $\square$

All the results so far obtained generalize optimality conditions for classical quadratic programming to a quadratic problem with cone constraints and a geometric constraint set. We now present suitable particular cases where our results allow to recover and generalize known optimality conditions.

We first consider the quadratic programming problem with bivalent constraints (QP1) defined by

$$\begin{aligned} \inf _{x\in K} \ f(x):= x^\top Ax+2a^\top x+\alpha , \end{aligned}$$

where $K:= \{x\in C: g_i(x):= x^\top B_ix+2b_i^\top x+\beta _i =0,~i=1,\ldots ,m, \ g_{m+j}(x):= x^\top E_{m+j}x -1 =0,~j=1,\ldots ,n\}$, $E_{m+j}=\mathrm{diag}(e_j)$ and $e_j$ is a vector in $\mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n$ whose $j$ $th$ element is equal to 1 and all the other entries are equal to 0.

Let $L(\lambda ,\gamma ,x):= f(x)+\sum _{i=1}^m\lambda _ig_i(x)+\sum _{j=1}^n\gamma _jg_{m+j}(x),$ be the Lagrangian function associated with (QP1).

By Proposition 3.3 and Lemma 3.1 we recover Lemma 3.1 of [14] which can be stated as follows.

Proposition 3.9

Let $C:=\mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n$ and ${\bar{x}}\in K$. Assume that there exist $\lambda \in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^m$ and $\gamma \in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n$ such that $\nabla _xL(\lambda ,\gamma ,\bar{x})=0$ . Then ${\bar{x}}$ is an optimal solution for (QP1) if and only if $\nabla _x^2L(\lambda ,\gamma ,\bar{x})$ is positive semidefinite on $Z({\bar{x}})$ defined by (18).

Proof

It is enough to notice that since $C=\mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n$, then, by Lemma 3.1, $Z({\bar{x}})= K-{\bar{x}}$ and, moreover, (11) is fulfilled. Proposition 3.3 allows us to complete the proof. $\square$

By Proposition 3.5 we obtain the following result.

Next result is inspired by Theorem 3.1 of [14] and provides a characterization and a sufficient condition for strong duality for (QP1).

Proposition 3.10

Let ${\bar{x}}\in K$ with $C:=\mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n$. Consider the following assertions:

(a):

$\bar{x}$ is an optimal solution for (QP1) and strong duality holds;

(b):

there exist $\lambda \in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^m$ and $\gamma \in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n$ such that $\nabla _xL(\lambda ,\gamma ,\bar{x})=0$ and $\nabla _x^2L(\lambda ,\gamma ,\bar{x})$ is positive semidefinite;

(c):

$A-\mathrm{diag}({\bar{X}}A{\bar{x}} +{\bar{X}}a)$ is positive semidefinite, where ${\bar{X}}:= \mathrm{diag}({\bar{x}}_1,\ldots ,{\bar{x}}_n)$.

Then $(c)\Rightarrow (b)\Leftrightarrow (a)$.

Proof

$(b)\Leftrightarrow (a)$; it follows from Proposition 3.5 with $C:=\mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n$, $K:=\{x\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n:g_i(x)=0, i=1,..,m+n\}$, $P:=\{0\}^{m+n}$.

$(c)\Rightarrow (b)$; in the proof of Theorem 3.1 of [14] it is shown that, for any feasible point ${\bar{x}}$, the condition $\nabla _xL(\lambda ,\gamma ,\bar{x})=0$ is fulfilled with $\lambda := (0,\ldots ,0)^\top$ and $\gamma := ({\bar{X}}A{\bar{x}} +{\bar{X}}a)$ and, moreover, for such $\lambda$ and $\gamma$, $\nabla _x^2L(\lambda ,\gamma ,\bar{x})=A-\mathrm{diag}(\bar{X}A{\bar{x}} +{\bar{X}}a)$. Therefore, if (c) holds, then (b) is fulfilled and so is (a), by the previous part of the proof. $\square$

Conditions (11) and (15) in general are not fulfilled for a problem with bivalent constraints.

Example 3.11

Let $C:=\{x\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^2:x_1^2=1\}$, $K:=\{x\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^2:x_1^2=1, x_2^2=1\}$, ${\bar{x}}=(1,1)\in K$. Then, $T(C,{\bar{x}})= \{x\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^2:x_1=0\}= \mathrm{cl\, co}~T(C;\bar{x})$,

$$\begin{aligned} K- {\bar{x}}=\{(0,0),(0,-2),(-2,-2),(0,-2)\} \not \subseteq \mathrm{cl \, co}~T(C;{\bar{x}}). \end{aligned}$$

This also implies that $C-{\bar{x}} \not \subseteq \mathrm{cl}~\mathrm{co}~T(C;{\bar{x}})$ so that Propositions 3.3 and 3.5 in general cannot be applied to problem (QP1).

Let us make some further comparison with the literature; until the end of this section we assume that $f,g_i,~i=1,\ldots ,m,$ are quadratic functions defined as in (5). According to Remark 3.7, the following results are all particular cases of Proposition 3.5.

Corollary 3.12

([13] Theorem 2.1, [20] Theorem 1) Consider the problem

$$\begin{aligned} \mu :=\inf \{f(x):~g_1(x)\le 0,\ldots ,g_m(x)\le 0,~x\in C\}, \end{aligned}$$

(20)

where $C:=\{x\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n: H x=d\}$, H is a $(p\times n)$ matrix , and let ${\bar{x}}$ be feasible for (20).

The following assertions are equivalent:

(a):

${\bar{x}}$ is an optimal solution and strong duality holds for (20);

(b):

there exists $\lambda ^*\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^m_+$ such that $\nabla _x L(\bar{x},\lambda ^*)\in H^\top (\mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^p)$, $\lambda ^*_ig_i(\bar{x})=0,~i=1,\ldots ,m$, and $\nabla ^2_x L(\bar{x},\lambda ^*)$ is positive semidefinite on $\mathrm{Ker}~H$.

Consequently, when $C:= \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n$, then (b) reduces to the following:

$(b')$:

there exists $\lambda ^*\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^m_+$ such that $\nabla _x L(\bar{x},\lambda ^*)=0$, $\lambda ^*_i g_i(\bar{x})=0,~i=1,\ldots ,m$ and $\nabla ^2_x L(\bar{x},\lambda ^*)$ is positive semidefinite.

4 The Case with Two Quadratic Equality Constraints

In this section we analyse in details a quadratic problem with two quadratic equality constraints defined by

$$\begin{aligned} \mu :=\inf \{f(x):~g_1(x)=0,~g_2(x)=0\}, \end{aligned}$$

(21)

where $f,g_i,~i=1,2$ are quadratic functions defined as in (5).

Let $K:=\{x\in {\mathbb {R}}^n:~g_1(x)=0, ~g_2(x)=0\}$.

The standard Lagrangian associated with (21) $L_S:\mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^2\times \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n\longmapsto {\mathbb {R}}$ is given by

$$\begin{aligned} L_S(\lambda _1,\lambda _2,x):= f(x)+\lambda _1g_1(x)+\lambda _2g_2(x). \end{aligned}$$

The following result is a consequence of Proposition 3.3.

Proposition 4.1

Let f, $g_1,g_2$ be defined as above, let ${\bar{x}}\in K$ be a KKT point for (21), i.e. there exists $\lambda _1, \lambda _2\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits$ such that $\nabla f({\bar{x}}) +\lambda _1\nabla g_1({\bar{x}}) + \lambda _2\nabla g_2 ({\bar{x}}) =0.$

Then the following conditions are equivalent:

(a):

$\bar{x}$ is an optimal solution for (21);

(b):

$A+\lambda _1B_1 +\lambda _2B_2$ is positive semidefinite on $K-\bar{x}$.

If, additionally, $\nabla g_2({\bar{x}})=0$ then (b) is equivalent to:

(b1):

$A+\lambda _1B_1$ is positive semidefinite on $K-\bar{x}$.

Proof

The equivalence between (a) and (b) follows from Proposition 3.3 where we set $C:={\mathbb {R}}^n$. Assume now that $\nabla g_2({\bar{x}})=0$. The equality $g_2(x)-g_2({\bar{x}})= \nabla g_2({\bar{x}})(x-{\bar{x}})+ \dfrac{1}{2}(x-\bar{x})^\top \nabla ^2 g_2({\bar{x}})(x-\bar{x})$ yields $(x-\bar{x})^\top B_2(x-\bar{x})=0$, $\forall x\in K$. Therefore, $\nabla _x^2L_S(\lambda _1,\lambda _2,\bar{x})=A+\lambda _1B_1+\lambda _2B_2$ is positive semidefinite on $K-\bar{x}$ if and only if (b1) holds. $\square$

In the following we set $C:=\{x\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n:~g_2(x)=0\}$, so that $K=\{x\in C:~g_1(x)=0\}$. The dual problem and the standard dual problem associated with (21) are, respectively, defined by:

$$\begin{aligned}&\nu :=\sup _{\lambda _1\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits }\inf _{x\in C}\{L(\lambda _1,x)\}; \end{aligned}$$

(22)

$$\begin{aligned}&\nu _S:=\sup _{\lambda _1,\lambda _2\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits } \inf _{x\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n}\{L_S(\lambda _1,\lambda _2,x)\}. \end{aligned}$$

(23)

We say that standard strong duality (SSD) holds for problem (21) if $\mu =\nu _S$ and problem (23) admits solution. It easy to check that $\nu _S\le \nu \le \mu .$

Theorem 4.1

Let $\bar{x}\in K$ be feasible for (21) and suppose that $\mu \in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits$.

(a):

Assume that $\nabla g_2(\bar{x})\ne 0$. Then the following assertions are equivalent

(a1):

$\bar{x}$ is an optimal solution and strong duality holds for problem (21);

(a2):

$\exists ~\lambda _1,~\lambda _2\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits$ such that $\nabla _x L_S(\lambda _1,\lambda _2,{\bar{x}})=0$ and $A+\lambda _1B_1 +\lambda _2B_2$ is positive semidefinite on $C-\bar{x}$ (and so on $\mathrm{cl \, cone}(C-{\bar{x}})$).

(b):

Assume that $\nabla g_2(\bar{x})=0$, and $B_2$ positive (or negative) semidefinite. Then, (a1) is equivalent to

(b1):

$\exists ~ \lambda _1\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits$ and $\exists y\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n$ s.t. $\nabla f({\bar{x}})+\lambda _1\nabla g_1({\bar{x}})+B_2y=0$ and $A+\lambda _1B_1$ is positive semidefinite on $\mathrm{ker}~B_2$.

(c):

Assume that $\nabla g_2(\bar{x})=0$, and $B_2$ indefinite. Then, (a1) is equivalent to

(c1):

$\exists ~ \lambda _1\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits$ s.t. $\nabla f({\bar{x}})+\lambda _1\nabla g_1({\bar{x}})=0$ and $A+\lambda _1B_1$ is positive semidefinite on $C-{\bar{x}}$ (and so on $\mathrm{cl \, cone}(C-{\bar{x}})$).

Proof

(a): $(a1)\Rightarrow (a2)$. By assumption there exists $\lambda _1\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits$ such that

$$\begin{aligned} f(x)+\lambda _1g_1(x)\ge f(\bar{x})=f(\bar{x})+\lambda _1g_1(\bar{x}),~ \forall ~x\in C. \end{aligned}$$

(24)

Thus, $\nabla f(\bar{x})+\lambda _1\nabla g_1(\bar{x})\in [T(C,\bar{x})]^*$. Since $\nabla g_2({\bar{x}})\not =0$, by (2) we get, $[T(C;{\bar{x}})]^*=\mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits \nabla g_2({\bar{x}})$. Hence, there exists $\lambda _2\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits$ satisfying $\nabla _xL_S(\lambda _1,\lambda _2,{\bar{x}})=0$. Then, for every $x\in C$,

$$\begin{aligned} \begin{array}{ll} 0&{}\le f(x)+\lambda _1g_1(x)-f({\bar{x}})=L_S(\lambda _1,\lambda _2,x)- L_S(\lambda _1,\lambda _2,{\bar{x}})\\ &{}\\ &{}=\nabla _xL_S(\lambda _1,\lambda _2,{\bar{x}})^\top (x-\bar{x})+ \dfrac{1}{2}(x-\bar{x})^\top \nabla ^2_xL_S(\lambda _1,\lambda _2,{\bar{x}})(x-\bar{x})\\ &{}\\ &{}=\dfrac{1}{2}(x-\bar{x})^\top \nabla ^2_xL_S(\lambda _1,\lambda _2,\bar{x})(x-\bar{x}). \end{array} \end{aligned}$$

This proves our claim. The previous equalities also show $(a2)\Rightarrow (a1)$. (b): $(a1)\Rightarrow (b1)$. By assumption there exists $\lambda _1\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits$ such that (24) holds. Thus, $\nabla f(\bar{x})+\lambda _1\nabla g_1(\bar{x})\in [T(C,\bar{x})]^*$. Since $\nabla g_2({\bar{x}})=0$, then (3) yields $T(C;\bar{x})=\{v\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n:~v^\top B_2v=0\}$ and, since $B_2$ is positive or negative semidefinite, then $T(C;{\bar{x}})=\mathrm{ker}~B_2=Z_2({\bar{x}})=C-\bar{x}$, where the last equality is due to Lemma 3.1. Thus we can choose $y\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n$ such that

$$\begin{aligned} \nabla f(\bar{x})+\lambda _1\nabla g_1(\bar{x})+B_2y=0. \end{aligned}$$

Then, from (24) and for all $x\in C$ (which means $g_2(x)=0$), it follows that

$$\begin{aligned} 0\le & {} L(\lambda _1,x)-L(\lambda _1,\bar{x})\nonumber \\= & {} \nabla _x L(\lambda _1,\bar{x})^\top (x-\bar{x})+ \dfrac{1}{2}(x-\bar{x})^\top \nabla ^2_xL(\lambda _1,\bar{x})(x-\bar{x}) \nonumber \\= & {} -(B_2y)^\top (x-{\bar{x}})+ \lambda _1(x-\bar{x})^\top A_1(x-\bar{x})\nonumber \\= & {} \lambda _1(x-\bar{x})^\top A_1(x-\bar{x}). \end{aligned}$$

(25)

Notice that $(B_2y)^\top (x-{\bar{x}})=0$, since $\mathrm{ker}~B_2=C-\bar{x}$. These chains of equalities also show that $(b1)\Rightarrow (a1)$. (c): $(a1)\Rightarrow (c1)$. By the above discussion, $T(C;\bar{x})=Z_2({\bar{x}})$. Lemma 2.1 yields $[T(C;{\bar{x}})]^*=(\mathrm{co}~Z_2({\bar{x}}))^* =\{0\}$, which implies that $\nabla f(\bar{x})+\lambda _1\nabla g_1(\bar{x})=0$. By using the relation (25), one concludes that $A+\lambda _1B_1$ is positive semidefinite on $C-{\bar{x}}$. The same relation allows us to prove that $(c1)\Rightarrow (a1)$. $\square$

Necessary or sufficient optimality conditions for a quadratic problem with two quadratic inequality constraints have been obtained in [1, 18]. To the best of our knowledge, Theorem 4.1 is a new characterization of strong duality for a quadratic problem with two quadratic equality constraints.

5 Simultaneously Diagonalizable Quadratic Problems

In this section we characterize strong duality for a simultaneously diagonalizable quadratic problem with quadratic cone constraints, providing conditions that guarantee the existence of a convex reformulation. Our results generalize those obtained in [15] where two quadratic inequality constraints are considered under the assumption that the classic Slater condition is fulfilled.

Consider problem (4) and assume that the matrices A and $B_i$, $i=1,..,m$ are simultaneously diagonalizable, i.e. there exists an orthonormal matrix S order n, such that $S^\top AS=D_0$, $S^\top B_iS=D_i$, $S^\top S=I$, where $D_i$ are diagonal; we set $D_i=\mathrm{diag}(\gamma _i)$, $\gamma _i:=(\gamma _{i1},\ldots ,\gamma _{in})^\top$, $i=0,1,\ldots ,m$.

We refer to [3] for an extensive description of the applications of this problem.

Setting $y=S^\top x$, then (4) can be written as follows:

$$\begin{aligned} \tau :=\inf {\tilde{f}}(y) \quad s.t.\quad y\in K:= \{y\in C:~{\tilde{g}}(y)\in -P\}, \end{aligned}$$

(26)

where P is a closed and convex cone in $\mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^m$, $\tilde{g}(y):= ({\tilde{g}}_1(y),\ldots ,{\tilde{g}}_m(y))$ and $\tilde{f},{\tilde{g}}_i:\mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n\rightarrow \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ,~i=1,\ldots ,m$ are quadratic functions,

$$\begin{aligned} {\tilde{f}}(y):=\dfrac{1}{2}y^\top D_0y+a^\top S y+\alpha ,~{\tilde{g}}_i(y):=\dfrac{1}{2}y^\top D_iy+b_i^\top Sy+\beta _i,~i=1,\ldots ,m. \end{aligned}$$

We assume that $\alpha =0$ and $C=\mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n$. Now, set $\dfrac{1}{2}y_i^2=z_i$, $i=1,\ldots ,n$, then $\dfrac{1}{2}y^\top D_iy=\gamma _i^\top z$ and (26) can be rewritten as follows:

$$\begin{aligned} \inf \left\{ \gamma _0^\top z+a^\top Sy \ : \ {\hat{g}}(y,z)\in -P , \ \frac{1}{2}y_i^2=z_i,\ i=1,\ldots ,n, \right\} \end{aligned}$$

(27)

where ${\hat{g}}_i(y,z):= \gamma _i^\top z +b_i^\top Sy+\beta _i,~i=1,\ldots ,m.$

Replacing the last n equality constraints with the corresponding inequalities, we obtain the following relaxation of (27) (and therefore of (26)):

$$\begin{aligned} \tau _R:= \inf \left\{ \gamma _0^\top z+a^\top Sy \ : \ {\hat{g}}(y,z)\in -P , \ \frac{1}{2}y_i^2\le z_i,\ i=1,\ldots ,n \right\} . \end{aligned}$$

(28)

Let $L:{\mathbb {R}}^m\times {\mathbb {R}}^n \rightarrow {\mathbb {R}}$ be defined by $L(\lambda ,y):= \dfrac{1}{2}y^\top D_0y+a^\top Sy +\sum _{i=1}^m\lambda _i{\tilde{g}}_i(y)$ as the Lagrangian function associated with (26) and let $\sup _{\lambda \in P^*}\inf _{y\in C} L(\lambda ,y)$ be the related dual problem. Similarly, let $L_R:{\mathbb {R}}^m\times {\mathbb {R}}^n \times {\mathbb {R}}^n \times {\mathbb {R}}^n \rightarrow {\mathbb {R}}$ be defined by

$$\begin{aligned} L_R(\lambda ,\mu ,y,z):= \gamma _0^\top z+a^\top Sy +\sum _{i=1}^m\lambda _i{\hat{g}}_i(y,z) +\sum _{i=1}^n\mu _i (\frac{1}{2}y_i^2 - z_i) \end{aligned}$$

as the Lagrangian function associated with (28) and let

$$\begin{aligned} \sup _{\begin{array}{c} \lambda \in P^*\\ \mu \in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n_+ \end{array}}\inf _{\begin{array}{c} y\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n \\ z\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n \end{array}} L_R(\lambda ,\mu ,y,z), \end{aligned}$$

be the corresponding dual problem.

Proposition 5.1

The dual problems associated with (26) and (28) are equivalent, i.e.

$$\begin{aligned} \sup _{\lambda \in P^*}\inf _{y\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n} L(\lambda ,y)=\sup _{\begin{array}{c} \lambda \in P^*\\ \mu \in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n_+ \end{array}}\inf _{\begin{array}{c} y\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n \\ z\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n \end{array}} L_R(\lambda ,\mu ,y,z). \end{aligned}$$

(29)

Moreover, if the supremum in the right-hand side of (29) is attained at $(\lambda ^*,\mu ^*)$, then the supremum in the left-hand side is attained at $\lambda ^*$.

Proof

Let us compute $\psi (\lambda ,\mu ):= \displaystyle \inf _{\begin{array}{c} y\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n \\ z\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n \end{array}} L_R(\lambda ,\mu ,y,z)$. Note that

$$\begin{aligned}&L_R(\lambda ,\mu ,y,z)= \gamma _0^\top z+a^\top Sy +\sum _{i=1}^m\lambda _i(\gamma _i^\top z +b_i^\top Sy+\beta _i ) +\sum _{j=1}^n\mu _j (\frac{1}{2}y_j^2 - z_j) \\&\quad =\sum _{j=1}^n \gamma _{0j} z_j + a^\top Sy +\sum _{i=1}^m\lambda _i(\sum _{j=1}^n \gamma _{ij} z_j + b_i^\top Sy+\beta _i) +\sum _{j=1}^n\mu _j (\frac{1}{2}y_j^2 - z_j) \\&\quad =a^\top Sy +\sum _{i=1}^m\lambda _i(b_i^\top Sy+\beta _i ) +\sum _{j=1}^n \frac{1}{2}\mu _j y_j^2 + \sum _{j=1}^n[ \sum _{i=1}^m\lambda _i\gamma _{ij}+\gamma _{0j}-\mu _j]z_j. \end{aligned}$$

Then, $\psi (\lambda ,\mu )= \inf _{y\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n}[a^\top Sy +\sum _{i=1}^m\lambda _i(b_i^\top Sy+\beta _i ) +\sum _{j=1}^n \frac{1}{2}\mu _j y_j^2],$

$$\begin{aligned} \text {if } \ \sum _{i=1}^m\lambda _i\gamma _{ij}+\gamma _{0j}-\mu _j=0, j=1,\ldots ,n, \qquad \psi (\lambda ,\mu )= -\infty , \ \text { otherwise}. \end{aligned}$$

By eliminating the variables $\mu _j$, we obtain:

$$\begin{aligned}&\psi (\lambda ,\mu )= \inf _{y\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n}[a^\top Sy +\sum _{i=1}^m\lambda _i(b_i^\top Sy+\beta _i ) +\sum _{j=1}^n \frac{1}{2}( \sum _{i=1}^m\lambda _i\gamma _{ij}+\gamma _{0j} )y_j^2], \ \\&\text {if } \sum _{i=1}^m\lambda _i\gamma _{ij}+\gamma _{0j}=\mu _j\ge 0, j=1,\ldots , n,\quad \psi (\lambda ,\mu ) = -\infty , \ \text { otherwise}. \end{aligned}$$

Now, observe that $L(\lambda ,y)= \dfrac{1}{2}y^\top D_0y+a^\top Sy +\sum _{i=1}^m\lambda _i[ \frac{1}{2}y^\top D_i y+b_i^\top Sy+\beta _i ]$

$$\begin{aligned}&= \dfrac{1}{2}\sum _{j=1}^n \gamma _{0j}y^2_j +a^\top Sy +\sum _{i=1}^m\lambda _i[ \dfrac{1}{2}\sum _{j=1}^n \gamma _{ij}y_j^2 +b_i^\top Sy+\beta _i ] \\&= a^\top Sy +\sum _{i=1}^m\lambda _i[b_i^\top Sy+\beta _i ] +\sum _{j=1}^n \frac{1}{2}(\sum _{i=1}^m \lambda _i\gamma _{ij} +\gamma _{0j} )y_j^2. \end{aligned}$$

Therefore,

$$\begin{aligned} \psi (\lambda ,\mu )={\left\{ \begin{array}{ll} \inf _{y\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n} L(\lambda ,y), \ \text {if } \sum _{i=1}^m\lambda _i\gamma _{ij}+\gamma _{0j}\ge 0, j=1,\ldots ,n, \\ -\infty ,\qquad \text { otherwise } \end{array}\right. } \end{aligned}$$

(30)

and

$$\begin{aligned} \sup _{\lambda \in P^*}\inf _{y\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n} L(\lambda ,y)=\sup _{\begin{array}{c} \lambda \in P^*\\ \mu \in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n_+ \end{array}}\inf _{\begin{array}{c} y\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n \\ z\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n \end{array}} L_R(y,z,\lambda ,\mu ) \end{aligned}$$

provided that

$$\begin{aligned} \sum _{i=1}^m\lambda _i\gamma _{ij}+\gamma _{0j}\ge 0, \ j=1,\ldots ,n, \text { for some } \lambda \in P^*. \end{aligned}$$

(31)

Notice that, if (31) does not hold, then $\sup _{\lambda \in P^*}\inf _{y\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n} L(\lambda ,y)=-\infty ,$ which yields (29).

The final assertion follows from (30). $\square$

Consider problem (28) and let

$$\begin{aligned}&{\hat{f}}(y,z):= \gamma _0^\top z+a^\top Sy, {\hat{h}}(y,z):= (\frac{1}{2}y_1^2 - z_1,...,\frac{1}{2}y_n^2 - z_n), \\&\quad G:=({\hat{g}},{\hat{h}}), \ F:= ({\hat{f}},{\hat{g}},{\hat{h}}). \end{aligned}$$

Assuming that $\tau _R\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits$, following the image space approach introduced by Giannessi [10, 11], we define the extended image associated with (28) by:

$$\begin{aligned} \mathcal{E}:= {F(\mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n\times \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n)-\tau _R(1,0,0)+(\mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits _+\times P\times \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n_+)}. \end{aligned}$$

It is possible to show that since ${\hat{f}}$ and ${\hat{g}}$ are linear and ${\hat{h}}$ is convex, then $\mathcal{E}$ is a convex set, in fact F turns out to be a $(\mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits _+\times P\times \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n_+)$-convex function. Many remarkable properties of a constrained extremum problem can be characterized (see [11]) by means of the set $\mathcal{E}$, as in the next result.

Proposition 5.2

Assume that $\tau _R\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits$ and

$$\begin{aligned} \mathrm{cl}\mathcal{( E})\cap -(\mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits {_+}\times \{0\}\times \{0\})=\emptyset . \end{aligned}$$

(32)

Then, $\tau =\tau _R$ if and only if $\tau =\sup _{\lambda \in P^*}\inf _{y\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n} L(\lambda ,y)$, i.e. the duality gap is zero for (26).

Proof

It is known that condition (32) is equivalent to the fact that the duality gap is zero for (28) (see [17] Theorem 4.2, for a proof where it is assumed that the infimum $\tau _R$ of (28) is attained, we notice that it is still valid if merely $\tau _R\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits$). Then, by Proposition 5.1, the following relations hold:

$$\begin{aligned} \tau \ge \sup _{\lambda \in P^*}\inf _{y\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n} L(\lambda ,y)=\sup _{\begin{array}{c} \lambda \in P^*\\ \mu \in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n_+ \end{array}}\inf _{\begin{array}{c} y\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n \\ z\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n \end{array}} L_R(\lambda ,\mu ,y,z)=\tau _R. \end{aligned}$$

(33)

The proof is now straightforward. $\square$

Condition (32) is not easy to check: next result, based on a well-known constraints qualification, provides the connections with strong duality for (26).

Proposition 5.3

Assume that $\tau _R\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits$ and that the following condition holds for (28):

$$\begin{aligned} 0\in \mathrm{ri }(G(\mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n\times \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n)+(P\times \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n_+)). \end{aligned}$$

(34)

Then, $\tau =\tau _R$ if and only if strong duality holds for (26).

Proof

We first prove that (34) implies that strong duality holds for (28): to this aim we will apply Theorem 3.6 of [8] where (34) is requested as one of the assumptions. The other one is given by the following condition:

$$\begin{aligned} 0\not \in \text { ri }[\text {co}(\mathcal{E} \cup \{0\})], \end{aligned}$$

(35)

where $\mathcal{E}$ is the extended image associated with (28). We now prove that (35) is fulfilled.

We have already observed that $\mathcal{E}$ is a convex set; we claim that

$$\begin{aligned} \text { ri }\mathcal{E}= \text { ri }[\text {co}(\mathcal{E} \cup \{0\})]. \end{aligned}$$

Let us prove our claim. Notice that, since F is a continuous function then $0\in \mathrm{cl}~{\mathcal{E}}$ and since $\mathcal{E}$ is convex so is $\mathrm{cl}~{\mathcal{E}}$, so that

$$\begin{aligned} \mathrm{cl}~{\text {co}}({\mathcal{E} \cup \{0\})}\subseteq \mathrm{cl}~{\mathcal{E}}. \end{aligned}$$

The reverse inclusion is obvious, so that cl co$(\mathcal{E} \cup \{0\})= \mathrm{cl}~{\mathcal{E}};$ by Theorem 6.3 of [19] we prove our claim. Now, since $\tau _R\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits$, by Proposition 3.1 of [8] we have

$$\begin{aligned} \mathcal{E} \cap -(\mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits _+\times P\times \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n_+)=\emptyset , \end{aligned}$$

which implies

$$\begin{aligned} \text { ri }\mathcal{E} \cap - \text { ri }(\mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits _+\times P\times \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n_+)=\emptyset , \end{aligned}$$

or, equivalently,

$$\begin{aligned} 0\not \in \text { ri }[ \mathcal{E} +(\mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits _+\times P\times \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n_+)]=\text { ri }\mathcal{E}. \end{aligned}$$

This proves that (35) is fulfilled and that strong duality holds for (28).

Finally, Proposition 5.1 leads to the following relations:

$$\begin{aligned} \tau \ge \sup _{\lambda \in P^*}\inf _{y\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n} L(\lambda ,y)=\max _{\begin{array}{c} \lambda \in P^*\\ \mu \in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n_+ \end{array}}\inf _{\begin{array}{c} y\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n \\ z\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n \end{array}} L_R(\lambda ,\mu ,y,z)=\tau _R. \end{aligned}$$

(36)

Assume that $\tau =\tau _R$; then the first inequality in (36) is fulfilled as equality and because of the second equality, the supremum is attained (see Proposition 5.1), i.e. strong duality holds for (26).

Conversely, if strong duality holds for (26), then $\tau = \max _{\lambda \in P^*}\inf _{y\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n} L(\lambda ,y)$ and (36) yields $\tau =\tau _R$. $\square$

We note that, when int$\,P\ne \emptyset$ the (34) collapses to the classic Slater condition.

Corollary 5.4

Assume that $\tau _R\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits$, (34) holds and ${\bar{y}}$ is an optimal solution of (26). Then $\tau =\tau _R$ if and only if there exist $\lambda ^*_i\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits _+$, $i=1,..,m$, such that:

• (i) $D_0 {\bar{y}}+Sa+\displaystyle \sum _{i=1}^m\lambda ^*_i(Sb_i+D_i {\bar{y}})=0$;

• (ii) $D_0+\displaystyle \sum _{i=1}^m\lambda ^*_iD_i$ is positive semidefinite.

Proof

It is a direct consequence of Proposition 5.3 and Proposition 3.5. $\square$

Proposition 5.5

Assume that $({\bar{y}},{\bar{z}})$ is a KKT point for (28) with $({\bar{\lambda }},{\bar{\mu }})$ the associated multipliers. If ${\bar{\mu }} >0$, then ${\bar{y}}$ is an optimal solution and strong duality holds for (26).

Proof

We first note that, since (28) is a convex problem, then the KKT conditions guarantee the optimality of $({\bar{y}},{\bar{z}})$ and $({\bar{\lambda }},{\bar{\mu }},{\bar{y}},{\bar{z}})$ is a saddle point of the Lagrangian function $L_R$. Moreover, if ${\bar{\mu }}>0$, then the constraints $\frac{1}{2}y_j^2 - z_j\le 0$ are active for $j=1,..,n$, which yields that ${\bar{y}}$ is feasible for (27) and therefore for (26), which proves that $\tau =\tau _R$ and ${\bar{y}}$ is a global optimal solution for (26).

By Proposition 5.1 the following relations hold:

$$\begin{aligned} \tau \ge \sup _{\lambda \in P^*}\inf _{y\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n} L(\lambda ,y)=\sup _{\begin{array}{c} \lambda \in P^*\\ \mu \in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n_+ \end{array}}\inf _{\begin{array}{c} y\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n \\ z\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n \end{array}} L_R(\lambda ,\mu ,y,z)= L_R({\bar{\lambda }},{\bar{\mu }},{\bar{y}},{\bar{z}})=\tau _R, \end{aligned}$$

(37)

where the last two equalities follow from the fact that $({\bar{\lambda }},{\bar{\mu }},{\bar{y}},{\bar{z}})$ is a saddle point of $L_R$. Since $\tau =\tau _R$ then

$$\begin{aligned} \tau = \sup _{\lambda \in P^*}\inf _{y\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n} L(\lambda ,y)=\inf _{y\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n} L({\bar{\lambda }},y), \end{aligned}$$

where the last equality is due to Proposition 5.1, which proves that strong duality holds for (26). $\square$

We provide a sufficient condition for (34) to be fulfilled.

Proposition 5.6

Assume that

• (i) $\mathrm{cl~cone}({\hat{g}}(\mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n\times \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n)+P)=\mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^m$;

• (ii) There exists $({\hat{y}},{\hat{z}})$ such that ${\hat{g}}({\hat{y}},{\hat{z}})\in -P$ and $\displaystyle \frac{1}{2}{\hat{y}}_j^2 - {\hat{z}}_j < 0$, $j=1,..,n$.

Then (34) is fulfilled.

Proof

Assume that (34) does not hold, i.e. $0\not \in \mathrm{ri }(G(\mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n\times \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n)+(P\times \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n_+)).$

Since $G(\mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n\times \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n)+(P\times \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n_+)$ is a convex set, by the separation theorem for convex sets (see, e.g. [19]), there exists $(\lambda ^*,\mu ^*)\in (\mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^m\times \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n)\setminus \{(0,0)\}$ such that

$$\begin{aligned}&\langle \lambda ^*,{\hat{g}}(y,z)+v\rangle + \sum _{j=1}^n \mu ^*_j(\frac{1}{2} y_j^2 - z_j+w_j) \le 0,\nonumber \\&\quad \forall (y,z)\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n\times \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n, \forall v\in P, \forall w\ge 0, \end{aligned}$$

(38)

where $w:=(w_1,..,w_n)$.

Note that, since (38) must be fulfilled for every $v\in P$ and $w\ge 0$, it follows that $\lambda ^*\in -P^*$ and $\mu ^*\le 0$. Moreover, by condition (i), we can easily prove that $\mu ^*\ne 0$. Indeed, if $\mu ^*=0$, then $\lambda ^*\ne 0$ and (38) becomes

$$\begin{aligned} \langle \lambda ^*,{\hat{g}}(y,z)+v\rangle \le 0,\quad \forall (y,z)\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n\times \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n, \forall v\in P, \end{aligned}$$

which implies

$$\begin{aligned} \langle \lambda ^*, t({\hat{g}}(y,z)+v)\rangle \le 0,\quad \forall t\ge 0, \ \forall (y,z)\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n\times \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n, \forall v\in P, \end{aligned}$$

i.e.

$$\begin{aligned} \langle \lambda ^*, v\rangle \le 0,\quad \forall t\ge 0, \ \forall v\in \mathrm{cl~cone}({\hat{g}}(\mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n\times \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n)+P), \end{aligned}$$

but the previous inequality cannot hold, since $\mathrm{cl~cone}({\hat{g}}(\mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n\times \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n)+P)=\mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^m$.

Finally, because of condition (ii), setting $y:={\hat{y}}$, $z:={\hat{z}}$, $v:=0$, $w:=0$ in (38), yields

$$\begin{aligned} 0< \langle \lambda ^*,{\hat{g}}({\hat{y}},{\hat{z}})\rangle + \sum _{j=1}^n \mu ^*_j(\frac{ 1}{2} {\hat{y}}_j^2 - {\hat{z}}_j) \le 0, \end{aligned}$$

a contradiction, which completes the proof. $\square$

In the particular case where the feasible set of (28) is defined by explicit equality and inequality constraints, i.e. $P:=\{0\}_s\times \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^{m-s}_+$, for $0\le s\le m$, we obtain a refinement of Proposition 5.3.

Proposition 5.7

Let $P:=\{0\}_s\times \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^{m-s}_+$, let $({\bar{y}},{\bar{z}})$ be an optimal solution of (28), $I({\bar{y}},{\bar{z}}):=\{i\in [s+1,..,m]:{\hat{g}}_i({\bar{y}},{\bar{z}})=0\}$, $J({\bar{y}},{\bar{z}})\doteq \{i\in [1,..,n]:{\hat{h}}_i({\bar{y}},{\bar{z}})=0\}$.

Assume that there exists $d\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^{n}\times \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n$ such that

• (i) $\nabla {\hat{g}}_i({\bar{y}},{\bar{z}})^\top d=0, i=1,..,s$, $\nabla {\hat{g}}_i({\bar{y}},{\bar{z}})^\top d\le 0, i\in I({\bar{y}},{\bar{z}})$ ;

• (ii) $\nabla {\hat{h}}_i({\bar{y}},{\bar{z}})^\top d < 0, i\in J({\bar{y}},{\bar{z}})$.

Then, $\tau =\tau _R$ if and only if strong duality holds for (26).

Proof

We first prove that there exist $(\lambda ^*,\mu ^*)\in P^*\times \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n_+$ such that

$$\begin{aligned} L_R(\lambda ^*,\mu ^*,y,z)\ge L_R(\lambda ^*,\mu ^*,{\bar{y}},\bar{z}),\quad \forall (y,z)\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n\times \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n. \end{aligned}$$

(39)

Denote by Q the feasible set of (28) and set $w:= (y,z)$. Since ${\bar{w}}= ({\bar{y}},{\bar{z}})$ is an optimal solution of (28), then $\langle c,d\rangle \ge 0,\ \forall d\in T(Q;{\bar{w}}),$ where $c^\top := \nabla {\hat{f}}({\bar{y}},\bar{z})=(a^\top S,\gamma _0^\top )$. Consider the set

$$\begin{aligned}&\varGamma :=\{d\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n\times \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n: \nabla {\hat{g}}_i({\bar{w}})^\top d=0, i=1,\ldots ,s, \nabla {\hat{g}}_i({\bar{w}})^\top d\le 0, i\in I({\bar{w}} ),\\&\quad \nabla {\hat{h}}_i({\bar{w}})^\top d < 0, i\in J({\bar{w}})\}. \end{aligned}$$

Note that, since $\varGamma \ne \emptyset$, then

$$\begin{aligned}&\mathrm{cl}~\varGamma = \{d\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n\times \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n: \nabla {\hat{g}}_i({\bar{w}})^\top d=0, i=1,\ldots ,s, \nabla \hat{g}_i({\bar{w}})^\top d\le 0, i\in I({\bar{w}} ), \\&\quad \nabla \hat{h}_i({\bar{w}})^\top d \le 0, i\in J({\bar{w}})\}. \end{aligned}$$

We show that $\mathrm{cl}~\varGamma =T(Q;\bar{w})$. We first prove that $\varGamma \subseteq T(Q;{\bar{w}})$. Let $d\in \varGamma$, $\{\alpha _k\} >0, \ \alpha _k \downarrow 0$, then

$$\begin{aligned}&{\hat{g}}_i({\bar{w}}+\alpha _kd)= {\hat{g}}_i({\bar{w}})+\alpha _k\nabla {\hat{g}}_i({\bar{w}})^\top d=0, \ i=1,\ldots ,s \\&{\hat{g}}_i({\bar{w}}+\alpha _kd)= {\hat{g}}_i({\bar{w}})+\alpha _k\nabla {\hat{g}}_i({\bar{w}})^\top d \le 0, \ i\in I({\bar{w}}), \\&{\hat{h}}_i({\bar{w}}+\alpha _kd)= {\hat{h}}_i({\bar{w}})+\alpha _k\nabla {\hat{h}}_i({\bar{w}})^\top d +o(\alpha _k d), \ i\in J({\bar{w}}). \end{aligned}$$

The third relation may be written as

$$\begin{aligned} \frac{1}{\alpha _k}[{\hat{h}}_i({\bar{w}}+\alpha _kd)]= \nabla {\hat{h}}_i({\bar{w}})^\top d +\frac{o(\alpha _k d)}{\alpha _k}, \ i\in J({\bar{w}}). \end{aligned}$$

Since $\nabla {\hat{h}}_i({\bar{w}})^\top d < 0, i\in J({\bar{w}})$, then ${\hat{h}}_i({\bar{w}}+\alpha _kd)<0$, for k sufficiently large. Therefore, $w_k:= {\bar{w}}+\alpha _kd\in Q$, for k sufficiently large, $w_k\rightarrow {\bar{w}}$ and $\frac{1}{\alpha _k}[w_k-{\bar{w}}]=d, \forall k$, which implies that $d\in T(Q;{\bar{w}})$. Since $T(Q;{\bar{w}})$ is closed, then $\mathrm{cl}~\varGamma \subseteq T(Q;{\bar{w}})$. We now prove that $T(Q;\bar{w})\subseteq \mathrm{cl}~\varGamma$. Let $d\in T(Q;{\bar{w}})$, then $\exists \alpha _k >0$, $\exists w_k\in Q$, $w_k\rightarrow {\bar{w}}$, $\alpha _k(w_k -{\bar{w}})\rightarrow d$. Then, recalling that ${\hat{g}}$ is linear, we have

$$\begin{aligned}&0={\hat{g}}_i(w_k)= \nabla {\hat{g}}_i({\bar{w}})^\top [w_k-{\bar{w}}], \ i=1,\ldots ,s \\&0\ge {\hat{g}}_i(w_k)= \nabla {\hat{g}}_i({\bar{w}})^\top [w_k-{\bar{w}}] , \ i\in I({\bar{w}}), \\&0\ge {\hat{h}}_i(w_k)\ge \nabla {\hat{h}}_i({\bar{w}})^\top [w_k-{\bar{w}}] \ i\in J({\bar{w}}), \end{aligned}$$

where the last inequality is due to the convexity of ${\hat{h}}$. Multiplying the previous relations by $\alpha _k$ and taking the limit for $k\rightarrow \infty$ yields $d\in \mathrm{cl}~\varGamma$, which proves that $T(Q;{\bar{w}})\subseteq \mathrm{cl}~\varGamma$. Since $T(Q;\bar{w})=\mathrm{cl}~\varGamma$ and ${\bar{w}}$ is an optimal solution of (28), then the following system is impossible:

$$\begin{aligned}&\langle c,d\rangle < 0 \nonumber \\&\nabla {\hat{g}}_i({\bar{w}})^\top d=0, i=1,\ldots ,s, \nonumber \\&\nabla {\hat{g}}_i({\bar{w}})^\top d\le 0, i\in I({\bar{w}}), \nonumber \\&\nabla {\hat{h}}_i({\bar{w}})^\top d \le 0, i\in J({\bar{w}}). \end{aligned}$$

(40)

Applying the Motzkin’s alternative theorem (see, e.g. [16]), we obtain that there exists a solution $(\lambda ^*,\mu ^*)\in P^*\times \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n_+$ of the following system:

$$\begin{aligned}&c+ \sum _{i=1}^m \lambda ^*_i \nabla {\hat{g}}_i({\bar{w}}) + \sum _{i=1}^n \mu ^*\nabla {\tilde{h}}_i({\bar{w}}) =0\nonumber \\&\langle \lambda ^*,{\hat{g}}({\bar{w}})\rangle =0, \ \langle \mu ^*,{\hat{h}}({\bar{w}})\rangle =0. \end{aligned}$$

(41)

Finally, note that $L_R(\lambda ^*,\mu ^*,y,z)$ is a convex function such that $\nabla L_R(\lambda ^*,\mu ^*,{\bar{y}}, \bar{z})=0$, because of (41), where, we recall ${\bar{w}}=(\bar{y},{\bar{z}})$. This implies that $({\bar{y}},{\bar{z}})$ is a global minimum point of $L_R(\lambda ^*,\mu ^*,y,z)$ on $\mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n\times \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n$, which proves (39).

Since (39) and the complementarity conditions in (41) are fulfilled, then strong duality holds for (28). With the same arguments used in Proposition 5.5, we have that Proposition 5.1 leads to the relations:

$$\begin{aligned} \tau \ge \sup _{\lambda \in P^*}\inf _{y\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n} L(\lambda ,y)= \sup _{\begin{array}{c} \lambda \in P^*\\ \mu \in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n_+ \end{array}}\inf _{\begin{array}{c} y\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n \\ z\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n \end{array}} L_R(\lambda ,\mu ,y,z)=\inf _{\begin{array}{c} y\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n \\ z\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n \end{array}} L_R(\lambda ^*,\mu ^*,y,z)=\tau _R.\nonumber \\ \end{aligned}$$

(42)

Assume that $\tau =\tau _R$; then, the first inequality in (42) is fulfilled as equality and because of the second equality, the supremum is attained at $\lambda ^*$ (see Proposition 5.1), i.e. strong duality holds for (26).

Conversely, if strong duality holds for (26), then

$$\begin{aligned} \tau = \max _{\lambda \in P^*}\inf _{y\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n} L(\lambda ,y)= \sup _{\begin{array}{c} \lambda \in P^*\\ \mu \in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n_+ \end{array}}\inf _{\begin{array}{c} y\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n \\ z\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n \end{array}} L_R(\lambda ,\mu ,y,z)=\tau _R. \end{aligned}$$

$\square$

The proof is complete.

Remark 5.8

Computing explicitly the gradients of ${\hat{g}}$ and ${\hat{h}}$, then (i) and (ii) of Proposition 5.7 can be written as

• (i’) $(b_i^\top S,\gamma _i^\top ) d=0, i=1,\ldots ,s$, $(b_i^\top S,\gamma _i^\top ) d\le 0, i\in I({\bar{y}},{\bar{z}})$ ;

• (ii’) $({{\bar{y}}}_ie^\top _i, -e_i^\top ) d < 0, i\in J({\bar{y}},{\bar{z}})$, where $e_i$ denotes the i-th unit vector in $\mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n$.

Next result relates condition (ii) of Proposition 5.6 with the assumptions of the previous proposition.

Proposition 5.9

Let $P:=\{0\}_s\times {\mathbb {R}}^{m-s}_+$. If there exists $({\hat{y}},{\hat{z}})\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n\times \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^n$ such that ${\hat{g}}({\hat{y}},{\hat{z}})\in -P$ and ${\hat{h}}({\hat{y}},{\hat{z}})<0$, then the assumptions (i) and (ii) of Proposition 5.7 are fulfilled.

Proof

Set $d\doteq ({\hat{y}},{\hat{z}})-({\bar{y}},{\bar{z}})$. Since ${\hat{g}}$ is an affine function then

$$\begin{aligned} \nabla {\hat{g}}_i({\bar{y}},{\bar{z}})^\top d={\hat{g}}_i({\hat{y}},{\hat{z}})-{\hat{g}}_i({\bar{y}},{\bar{z}}),\quad i=1,\ldots ,m, \end{aligned}$$

which yields (i), because ${\hat{g}}({\hat{y}},{\hat{z}})\in -P$. Moreover, since ${\hat{h}}_i$ is convex, then

$$\begin{aligned} 0>{\hat{h}}_i({\hat{y}},{\hat{z}})-{\hat{h}}_i({\bar{y}},{\bar{z}})\ge \nabla {\hat{h}}_i({\bar{y}},{\bar{z}})^\top d,\quad \forall i\in J({\bar{y}},{\bar{z}}), \end{aligned}$$

and (ii) follows. $\square$

Next example shows that the conditions of the previous proposition are weaker than (34).

Example 5.10

Set $n:= 1$, $P:=\mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^2_+$, ${\hat{g}}_1(y,z):= -y-z$, ${\hat{g}}_2(y,z):= y+z$, ${\hat{h}}(y,z):= \frac{1}{2}y^2-z$. Then,

$G(\mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits \times \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits )+\mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^3_+= \{(u,v,w)\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^3:u\ge -y-z, \ v\ge y+z, \ w\ge \frac{1}{2}y^2-z, (y,z)\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^2\}$

$$\begin{aligned} \subseteq \{(u,v,w)\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^3:u+v\ge 0\}. \end{aligned}$$

This implies that $(0,0,0)\not \in \mathrm{int}[G(\mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits \times \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits )+\mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^3_+]$, i.e. (34) is not fulfilled.

Nevertheless, the assumptions of Proposition 5.9 are fulfilled. Indeed, $(y^*,z^*):= (-1,1)$ fulfils the inequalities:

$$\begin{aligned} {\hat{g}}_i(-1,1)\le 0, \ i=1,2,\quad {\hat{h}}(-1,1) < 0. \end{aligned}$$

We note that in [15] the Slater-type condition (34) has been considered as a blanket assumption. Finally, we provide a refinement of Corollary 5.4.

Corollary 5.11

Let $P:=\{0\}_s\times \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits ^{m-s}_+$, let ${\bar{y}}$ be an optimal solution of (26), ${\bar{z}}:=(\frac{1}{2}{\bar{y}}_1^2,\ldots ,\frac{1}{2}{\bar{y}}_n^2)$ and assume that the assumptions (i) and (ii) of Proposition 5.7 hold. Then $\tau =\tau _R$ if and only if there exist $\lambda ^*_i\in \mathop {{\mathrm{I}}{\mathrm{R}}}\nolimits _+$, $i=1,\ldots ,m$, such that:

• (i) $D_0{\bar{y}}+Sa+\displaystyle \sum _{i=1}^m\lambda ^*_i(Sb_i+D_i{\bar{y}})=0$;

• (ii) $D_0+\displaystyle \sum _{i=1}^m\lambda ^*_iD_i$ is positive semidefinite.

Proof

Assume that $\tau =\tau _R$. Let us prove that $({\bar{y}},{\bar{z}})$ is an optimal solution of (28). Indeed, ${\tilde{f}}({\bar{y}})=\tau =\tau _R$ and $({\bar{y}},\bar{z})$ is an optimal solution of (27). Since $({\bar{y}},\bar{z})$ is feasible for (28) and $\gamma _0^\top {\bar{z}}+a^\top S{\bar{y}}=\tau =\tau _R$, then $(\bar{y},{\bar{z}})$ is an optimal solution of (28). By Proposition 5.7, strong duality holds for (26). Conversely, if strong duality holds for (26), then $\tau =\tau _R$, as proved in Proposition 5.3. Recalling that here $C={\mathbb {R}}^n$, applying Proposition 3.5 we complete the proof. $\square$

6 Conclusions

We have considered a quadratic programming problem with general quadratic cone constraints and an additional geometric constraint. We have established necessary and sufficient conditions for global optimality for a KKT point or in the presence of the property of strong duality, considering in details the case where the feasible set is defined by two quadratic equality constraints. As a further application, we have obtained conditions that guarantee the existence of a convex reformulation of a simultaneous diagonalizable quadratic problem.