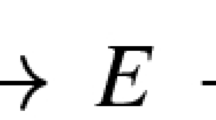Limit Theorems and Fluctuations for Point Vortices of Generalized Euler Equations

Abstract

We prove a mean field limit, a law of large numbers and a central limit theorem for a system of point vortices on the 2D torus at equilibrium with positive temperature. The point vortices are formal solutions of a class of equations generalising the Euler equations, and are also known in the literature as generalised inviscid SQG. The mean-field limit is a steady solution of the equations, the CLT limit is a stationary distribution of the equations.

1 Introduction

The paper analyses the mean-field limit and the corresponding fluctuations for the point vortex dynamics, at equilibrium with positive temperature, arising from a class of equations generalising the Euler equations. Consider the family of models

$$\begin{aligned} \partial _t\theta + u\cdot \nabla \theta = 0, \end{aligned}$$

on the two dimensional torus ${{\mathbb {T}}_2}$ with periodic boundary conditions and zero spatial average. Here $u=\nabla ^\perp (-\Delta )^{-\frac{m}{2}}\theta$ is the velocity, and m is a parameter. When $m=2$, the model corresponds to the Euler equations, and when $m=1$ it corresponds to the inviscid surface quasi-geostrophic (SQG) equation.

One route to understand the behaviour of a turbulent flow is to study invariant measures for the above equations. Onsager [43] proposed to do this via a finite dimensional system, called vortex model. In this model, we consider a vorticity field which is a linear combination of $\delta$-functions concentrated in points in physical space, in formula

$$\begin{aligned} \sum _{j=1}^N \gamma _j\delta _{X_j(t)}, \end{aligned}$$

where $X_1,X_2,\dots ,X_N$ are vortex positions and $\gamma _1,\gamma _2,\dots ,\gamma _N$ are vortex intensities. Positions evolve according to

$$\begin{aligned} {\dot{X}}_j = \sum _{k\ne j}\gamma _k\nabla ^\perp G_m(X_j,X_k), \end{aligned}$$

where $G_m$ is the Green function for the fractional Laplacian, and intensities are constant by a generalized version of Kelvin’s theorem. This evolution is Hamiltonian, with Hamiltonian

$$\begin{aligned} H_N = \frac{1}{2}\sum _{j\ne k}\gamma _j\gamma _k G_m(X_j,X_k), \end{aligned}$$

and has a family of Gibbsian invariant distributions indexed by a parameter $\beta$, which reads

$$\begin{aligned} \frac{1}{Z_\beta ^N}{\text {e}}^{-\beta H_N}. \end{aligned}$$

The Gibbs measures associated to such a system can be considered as invariant measures for the flow.

The investigation of the limit as $N \rightarrow \infty$ of the point vortex model was initiated by Onsager, as described in the review of Eyink and Srinivasan [15], and developed by many scholars. In order not to overburden this introduction with notation, we postpone the account of existing results and challenges to Sects. 2.3.1 and 2.4, where we describe also our own contribution.

In this work we investigate the mean-field limit and characterize its (Gaussian) fluctuations around the limit measure in the case $m < 2$ and random vortex intensities. The investigation of such fluctuations dates back to Messer and Spohn [39] for bounded interactions and Ben Arous and Brunaud [2] for smooth interaction and positive intensities. Central limit theorems are also contained in the work of Bodineau and Guionnet [3] on Euler vortices (the case $m=2$ in the language of the present paper), or the recent series of results with Coulomb potential and constant charges, see Serfaty and coauthors [33,34,35, 49] and references therein.

In the case $m<2$ and intensities of arbitrary sign, the situation is more complex than in the case $m=2$: the invariant distributions do not make sense since the Green function $G_m$ of the fractional Laplacian $(-\Delta )^{\frac{m}{2}}$ has a singularity which is non-integrable.

We therefore introduce in Sect. 2.3 a regularization of the Green function with a regularization parameter $\epsilon$ that goes to 0 as the number of vortices N increases to $\infty$. In this way we recover the original problem, as well as the intrinsic singularity of the potential, in the limit of infinite vortices. The regularization parameter $\epsilon$ is a ultraviolet cutoff in the potential that controls when vortices are too close to each other, and inhibits an uncontrolled growth of the energy of the system.

Our problem is fundamentally different from the case of a smooth potential: We prove in section Sect. 4.1 a uniform (in $\epsilon$) control of the main quantities of the problem, such as the partition function, which is slowly relaxed as the number of vortices increase. To ensure the validity of our result, the speed of convergence of $\epsilon =\epsilon (N)$ must be at least logarithmically slow in terms of N.

Under the conditions $\beta \ge 0$ and $m<2$, and when $\epsilon (N)\downarrow 0$, we prove propagation of chaos, namely vortices decorrelate and are independent in the limit, via a variational principle associated to the energy-entropy functional. Notice that in the mean field limit of both the regularized systems and the singular system the overall distribution of pseudo-vorticity $\theta$ is uniform, due to the fact that on the torus the total pseudo-vorticity is zero (see Remark 3.7 for comments). But this by itself does not provide a meaningful conclusion. Our proof rigorously links the particle systems to the variational problem and proves convergence of free energies. The mean field limit result on the singular system is then a by-product.

We prove a law of large numbers and, in terms of $\theta$, that the limit is a stationary solution of the original equation. In Sect. 3.2 we prove a central limit theorem. The limit Gaussian distribution for the $\theta$ variable turns out to be a statistically stationary solution of the equations. The fluctuations result holds due to a higher order expansion analysis of the partition function, similar to [21], where the same statement for Euler vortices has been recently proved.

1.1 Possible Extensions and Future Work

This paper covers the basic case of uniform distribution of total pseudo-vorticity on the simplest geometry. Our results should hold as well on every compact Riemann surface without boundary and zero mean pseudo-vorticity, although we do not dwell upon this line. Extensions to bounded domains with boundary and to non–uniform limit distributions of total pseudo-vorticity are on-going works, see Remark 3.7 for further details.

The case of negative temperature, which is considered the most interesting, is far from being understood. While Kiessling [27] has proved, for the Euler case $m=2$, that there is only one minimiser of the free energy for small negative values of $\beta$, the energy profile for $\beta <0$ and $m<2$ is much more involved. Indeed, we prove that in this case the free energy functional is unbounded from below. New and deep ideas are needed to consider this case. We have included a short discussion in Sect. 2.4.

1.2 Structure of the Paper

The paper is organized as follows: in Sect. 2 we introduce the model with full details, we give some preliminary results and we prepare the framework to state the main results. Section 3 contains the main results, as well as some consequences and additional remarks. Finally, Sect. 4 is devoted to the proof of the main results.

2 The Model

2.1 General Notation

We denote by ${{\mathbb {T}}_2}$ the two dimensional torus, and by $\ell$ the normalized Lebesgue measure on ${{\mathbb {T}}_2}$. Given a metric space E, we shall denote by C(E) the space of continuous functions on E, and by ${\mathcal {P}}(E)$ the set of probability measures on E. If $x\in E$, then $\delta _x$ is the Dirac measure on x. Given a measure $\mu$ on E, we will denote by $\mu (F)=\langle F,\mu \rangle =\int F(x)\,\mu (dx)$ the integral of a function F with respect to $\mu$. Sometimes we will also use the notation ${\mathbb {E}}_\mu [F]$. We will use the operator $\otimes$ to denote the product between measures. We shall denote by $\lambda _1,\lambda _2,\dots$ the eigenvalues in non-decreasing order, and by $e_1,e_2,\dots$ the corresponding orthonormal basis of eigenvectors of $-\Delta$, where $\Delta$ is the Laplace operator on ${{\mathbb {T}}_2}$ with periodic boundary conditions and zero spatial average. With these positions, if $\phi =\sum _k \phi _k e_k$, then the fractional Laplacian is defined as

$$\begin{aligned} (-\Delta )^{\frac{m}{2}}\phi = \sum _{k=1}^\infty \lambda _k^{\frac{m}{2}}\phi _k e_k. \end{aligned}$$

2.2 General Setup

Consider the family of models,

$$\begin{aligned} \partial _t\theta + u\cdot \nabla \theta = 0, \end{aligned}$$

(2.1)

on the torus with periodic boundary conditions and zero spatial average, where the velocity $u=\nabla ^\perp \psi$, and the stream function $\psi$ is solution to the following problem,

$$\begin{aligned} (-\Delta )^{\frac{m}{2}}\psi = \theta , \end{aligned}$$

with periodic boundary conditions and zero spatial average. As above, $m\in (0,2]$ denotes the order of the fractional Laplacian. The case $m=2$ corresponds to the Euler equation in vorticity formulation, $m=1$ is the inviscid surface quasi-geostrophic equation (briefly, SQG), and for a general value is sometimes known in the literature as the inviscid generalized surface quasi-geostrophic equation. Here we will consider values $m<2$ of the parameter.

2.3 Generalities on the Model

We start by giving a short introduction to the main features of the model (2.1).

2.3.1 Existence and Uniqueness of Solution

The inviscid SQG has been derived in meteorology to model frontogenesis, namely the production of fronts due to tightening of temperature gradients. It has become an active subject of research since the first mathematical and geophysical studies about strong fronts [13, 23, 24], see also [8, 45]. The generalized version of the equations bridges the cases of Euler and SQG and it is studied to understand the mathematical differences between the two cases.

Regarding the existence, uniqueness and regularity of solutions to (generalized) SQG equations, a local existence result is known, namely data with sufficient smoothness give local in time unique solutions with the same regularity of the initial condition, see for instance [5]. Unlike the Euler equation, it is not known if the inviscid SQG (as well as its generalized version) has a global solution. There is numerical evidence [7] of emergence of singularities in the generalized SQG, for $m\in [1,2)$. On the other hand see [10] for classes of global solutions. Finally, [6] presents a regularity criterion for classical solutions.

The picture for weak solutions is different: existence of weak solutions is known since [44], see also [36]. For existence of weak solution for the generalized SQG model one can see [5]. Global flows of weak solution with a invariant measure (corresponding to the measure in (2.2) with $\beta =0$) as initial condition has been provided in [42].

2.3.2 Invariant Quantities

As in the case of Euler equations, equation (2.1) can be solved by means of characteristics, in the sense that if $\theta$ is solution of (2.1) and $u=\nabla ^\perp \theta$,

$$\begin{aligned} {\left\{ \begin{array}{ll} {\dot{X}} = u(t,X_t),\\ X(0) = x, \end{array}\right. } \end{aligned}$$

then, at least formally,

$$\begin{aligned} \frac{d}{dt}\theta (t,X_t) = \partial _t \theta (t, X_t) + {\dot{X}}_t \cdot \nabla \theta (t, X_t) = (\partial _t \theta + u \cdot \nabla \theta )(t, X_t) = 0, \end{aligned}$$

therefore $\theta (t, X_t) = \theta (0, x)$. This formally ensures conservation of the sign and of the magnitude ($L^\infty$ norm) of $\theta$.

Equation (2.1) admits an infinite number of conserved quantities, for instance of $L^p$ norms of $\theta$. We are especially interested in the quantity

$$\begin{aligned} \Vert \theta (t)\Vert _{L^2}^2 = \int _{{\mathbb {T}}_2}|\theta (t,x)|^2\,\ell (dx), \end{aligned}$$

which is, for $m=2$, the enstrophy. Another important conserved quantity is

$$\begin{aligned} \int _{{\mathbb {T}}_2}\theta (t,x)\psi (t,x)\,\ell (dx) = \Vert (-\Delta )^{-\frac{m}{4}}\theta \Vert _{L^2(\ell )}^2. \end{aligned}$$

which is, however, unlike the case $m=2$, not the kinetic energy. Formally, corresponding to these conserved quantities, in analogy with the invariant measures of the Euler equations [1], one can consider the invariant measures

$$\begin{aligned} \mu _{\beta ,\alpha }(d\theta ) = \frac{1}{Z_{\beta ,\alpha }}{\text {e}}^{-\beta \Vert (-\Delta )^{-\frac{m}{4}}\theta \Vert ^2 -\alpha \Vert \theta (t)\Vert _{L^2}^2}\,d\theta , \end{aligned}$$

(2.2)

with $\alpha >0$ a consant connected to the variance of the intensities. The invariant measures (2.2) are classically interpreted as Gaussian measures with suitable covariance (see Remark 3.5).

2.4 The Point Vortex Motion

The central topic of this paper is to give results about the mean-field limit of a system of point vortices governed by (2.1). Mathematical results about the general dynamics of point vortices [38] and about the connection with the Euler equations [48] are classical, we refer to the general survey on point vortices [19] for an overview.

Consider now a configuration of N point vortices located at $x_1,x_2,\dots ,x_N$, with respective intensities $\gamma _1,\gamma _2,\dots ,\gamma _N$, that is the measure

$$\begin{aligned} \theta (0) = \sum _{j=1}^N \gamma _j\delta _{X_j} \end{aligned}$$

as the initial condition of (2.1), one can check that, at least in the sense given in Remark 2.1, the solution evolves as a measure of the same kind, where the “intensities” $\gamma _j$ remain constant (a generalized version of Kelvin’s theorem about the conservation of circulation), and where the vortex positions evolve according to the system of equations

$$\begin{aligned} {\left\{ \begin{array}{ll} {\dot{X}}_j = \sum _{k\ne j}\gamma _k\nabla ^\perp G_m(X_j,X_k),\\ X_j(0) = x_j, \end{array}\right. } \qquad j=1,2,\dots ,N, \end{aligned}$$

(2.3)

where $G_m$ is the Green function of the operator $(-\Delta )^{\frac{m}{2}}$ on the torus with periodic boundary conditions and zero spatial average. The effective connection between the equations and the point vortex dynamics has been discussed in [20, 46], see also [9, 17, 18]. In particular, when $m>1$, there are no collisions, and the solution of (2.3) is global outside of a set of initial conditions of Lebesgue measure zero, see [19, 46] for a proof on the plane, and [17] for a proof on the torus.

Remark 2.1

(Notion of solution) We wish to explain in which sense a combination of point vortices $\sum _j \gamma _j\delta _{X_j}$ can be understood as a solution of (2.1), at least when $m>1$. In principle the weak formulation of (2.1) for a combination of point vortices $\theta$,

$$\begin{aligned} \frac{d}{dt}\int _{{\mathbb {T}}_2}\phi (x)\,\theta _t(dx) = \int _{{\mathbb {T}}_2}u(t,x)\cdot \nabla \phi (x)\,\theta _t(dx), \end{aligned}$$

is not well defined, due to the self-interaction term appearing on the right hand side. Indeed, if $\theta _t=\sum _j \gamma _j\delta _{X_j(t)}$, then $u(t,x)=\sum _j \gamma _j\nabla ^\perp G_m(x,X_j(t))$, and

$$\begin{aligned} \int _{{\mathbb {T}}_2}u(t,x)\cdot \nabla \phi (x)\,\theta _t(dx), = \sum _{j,k}\gamma _j\gamma _k\nabla ^\perp G_m(X_j,X_k)\cdot \nabla \phi (X_j), \end{aligned}$$

which is singular when $j=k$.

If on the other hand we define $K_m(x,y)=\nabla ^\perp G_m(x,y)$ when $x\ne y$, and 0 on the diagonal, and define the dynamics (2.3) as

$$\begin{aligned} {\dot{X}}_j = \sum _{k=1}^N \gamma _k K_m(X_j,X_k), \qquad j=1,2,\dots ,N, \end{aligned}$$

by the non-collisions results in [17, 19] it follows that outside a set of initial conditions of Lebesgue measure zero, the dynamics defined through $K_m$ and the one defined in (2.3) are the same. If then we neglect the self-interaction term in the transport velocity u, in other terms if we set

$$\begin{aligned} u(t,x) =\sum _{j=1}^N \gamma _j K_m(x,X_j(t)), \end{aligned}$$

then the weak formulation above is well defined and a superposition of point vortices is a solution of equation (2.1).

The motion of vortices is described by the Hamiltonian

$$\begin{aligned} H_N(\gamma ^N,X^N) = \frac{1}{2}\sum _{j\ne k}\gamma _j\gamma _k G_m(X_j,X_k), \end{aligned}$$

(2.4)

where $X^N=(X_1,X_2,\dots ,X_N)$ and $\gamma ^N=(\gamma _1,\gamma _2,\dots ,\gamma _N)$.

A natural invariant distribution for the Hamiltonian dynamics (2.3) should be the measure

$$\begin{aligned} \mu _\beta ^N(dX^N) = \frac{1}{Z_\beta ^N} {\text {e}}^{-\beta H_N(X^N,\gamma ^N)}\ell ^{\otimes N}(dX^N), \end{aligned}$$

(2.5)

where here and throughout the paper we denote by $\ell$ the normalized Lebesgue measure on ${{\mathbb {T}}_2}$. Due to the singularity of the Green function on the diagonal, which diverges like $G_m(x,y)\sim |x-y|^{m-2}$, the density above is not integrable and thus the measure $\mu ^N_\beta$ does not make sense (unless intensities are all positive).

To overcome this difficulty, we consider a regularization of the Green function, which we will introduce in detail in the forthcoming Sect. 2.3, which gives us a regularized Hamiltonian dynamics (2.7). Before explaining the details, we finish the setup of our model: In terms of invariant distributions, we want to consider a problem slightly more general and consider vortices with random intensities.¹

For this, let $\nu$ be a probability measure on the real line with support on a compact set $K_\nu \subset {\mathbb {R}}$. The measure $\nu$ will be the prior distribution on vortex intensities. A natural invariant distribution for the regularized Hamiltonian dynamics (2.7) with random intensities is

$$\begin{aligned} \mu _{\beta ,\epsilon }^N(d\gamma ^N,dX^N) = \frac{1}{Z_{\beta ,\epsilon }^N} {\text {e}}^{-\frac{\beta }{N} H_N^\epsilon (\gamma ^N,X^N)} \,\ell ^{\otimes N}(dX^N)\,\nu ^{\otimes N}(d\gamma ^N), \end{aligned}$$

(2.6)

where $\ell$ is the normalized Lebesgue measure on ${{\mathbb {T}}_2}$ and $Z_{\beta ,\epsilon }^N$ is the normalization factor.

Note that in the above formula for the measure we have scaled the parameter $\beta$ by $N^{-1}$, which corresponds to the mean-field limit scaling. There are several different scaling limits for the N point vortex model, and their respective limits as $N \longrightarrow \infty$ give insight into different phenomena:

In his pioneering work [43] , Onsager studied the microcanonical ensemble and predicted the occurrence of negative temperature states when the energy of the system exceeds a critical value, which was further investigated by Joyce and Montgomery [37]. Their claim that negative temperatures would exist in the usual thermodynamic limit was invalidated by Fröhlich and Ruelle [16] in the case of a neutral point vortex Hamiltonian.

The study and comparison of different scaling limits continued, in special cases, with contributions of Lundgren and Pointin [31, 32] and many others, see e.g. the survey [19]. Specifically for the Euler case $m=2$, the inhomogeneous mean-field thermodynamical limit was investigated by Lions and coauthors [11, 12, 30] and by Kiessling and coauthors [26, 28]. Their results build upon the work of Messer and Spohn [39] on Lipschitz continuous interactions, which was extended by Eyink-Spohn [14] to the (quasi)-microcanonical setting, working with a regularized Dirac measure on configuration space.

Mean-field limit results of point vortices with random intensities can be found in [29, 40, 41]. The analysis of fluctuations can be found in [3, 4] and in the recent [21].

2.5 The Regularized System

As pointed out, a difficulty for mean-field limit results is posed by the singular interaction among vortices. In fact, the techniques developed in [39] for bounded interaction fail to control the partition of the invariant distributions as $N \longrightarrow \infty$. To overcome this difficulty, we consider a regularization of the Green function. To define it, notice that we can represent the Green function for the fractional Laplacian through the eigenvectors,

$$\begin{aligned} G_m(x,y) = \sum _{k=1}^\infty \lambda _k^{-\frac{m}{2}}e_k(x)e_k(y). \end{aligned}$$

Given $\epsilon >0$, consider the following regularization of the Green function,

$$\begin{aligned} G_{m,\epsilon }(x,y) = \sum _{k=1}^\infty \lambda _k^{-\frac{m}{2}}{\text {e}}^{-\epsilon \lambda _k}e_k(x)e_k(y). \end{aligned}$$

Here, we have regularized the fractional Laplacian so that the new operator $D_{m,\epsilon }$ reads $D_{m,\epsilon }=(-\Delta )^{m/2}{\text {e}}^{-\epsilon \Delta }$ and the eigenvalues change from $\lambda ^{m/2}$ to $\lambda ^{m/2}{\text {e}}^{\epsilon \lambda }$. We remark that, as long as $G_{m,\epsilon }$ is translation invariant and non-singular on the diagonal, the exact form of the regularization is not essential for our main results.

If we replace $G_m$ by $G_{m,\epsilon }$ in (2.3), the motion is still Hamiltonian with Hamiltonian $H_N^\epsilon$ given by (2.4), with $G_m$ replaced by $G_{m,\epsilon }$, namely

$$\begin{aligned} H_N^\epsilon (\gamma ^N,X^N) = \frac{1}{2}\sum _{j\ne k}\gamma _j\gamma _k G_m^\epsilon (X_j,X_k). \end{aligned}$$

(2.7)

2.5.1 Mean-Field Limit of the Regularized System

At fixed $\epsilon$, the interaction among particles is bounded, and it has been shown already by Messer and Spohn [39] that $(\mu _{\beta ,\epsilon }^N)_{N\ge 1}$ has limit points. To characterize the limit, consider the free energy functional on measures on $(K_\nu \times {{\mathbb {T}}_2})^N$,

$$\begin{aligned} {\mathcal {F}}_N^\epsilon (\mu )= {\mathcal {E}}(\mu |\nu ^{\otimes N}\otimes \ell ^{\otimes N}) + \frac{\beta }{N}{\mathcal {K}}^\epsilon _N(\mu ), \end{aligned}$$

(2.8)

where ${\mathcal {E}}$ is the relative entropy and

$$\begin{aligned} {\mathcal {K}}_N^\epsilon (\mu ) = \iint \dots \iint H_N^\epsilon \,\mu (d\gamma _1,\dots ,d\gamma _N,dx_1,\dots ,dx_N). \end{aligned}$$

(2.9)

is the potential energy. One can see that $\mu _{\beta ,\epsilon }^N$ is the unique minimiser of the free energy, and this can be carried to the limit.

Given an exchangeable measure $\mu$ on $(K_\nu \times {{\mathbb {T}}_2})^{{\mathbb {N}}_\star }$ with absolutely continuous (with respect to powers of $\nu \otimes \ell$) marginals and with corresponding bounded densities, by convexity and subadditivity we can define the entropy ${\mathcal {E}}_\infty$ and thus the limit free energy functional,

$$\begin{aligned} {\mathcal {F}}_\infty ^\epsilon (\mu ) = {\mathcal {E}}_\infty (\mu ) + \frac{1}{2}\beta \iint H_2^\epsilon (\gamma _1,\gamma _2,x_1,x_2) \,\pi _2\mu (d\gamma _1,d\gamma _2,dx_1,dx_2), \end{aligned}$$

(2.10)

where $\pi _2\mu$ is the two dimensional marginal of $\mu$.

As in [40, Theorem 11], all limit points of $(\mu _{\beta ,\epsilon }^N)_{N\ge 1}$ are minima of ${\mathcal {F}}_\infty ^\epsilon$, and if ${\mathcal {F}}_\infty ^\epsilon$ has a unique minimum, then the limit is a product measure.

The mean-field equation, or, in other words, the Euler-Lagrange equation for ${\mathcal {F}}_\infty ^\epsilon$, reads

$$\begin{aligned} \rho (\gamma ,x) = \frac{1}{Z}{\text {e}}^{-\beta \gamma \psi _\rho (x)}, \end{aligned}$$

(2.11)

where Z is the normalization constant, and $\psi _\rho$ is the averaged stream function, that is $\psi _\rho (x)=\int \gamma G_{m,\epsilon }(x,y)\rho (\gamma ,y)\,\nu (d\gamma )\,\ell (dx)$. Moreover, the function $\rho _0=1$ is a solution, with stream function $\psi _{\rho _0}=0$. If $\mu _0=(\rho _0\nu \otimes \ell )^{\mathbb {N}}$ is the product measure corresponding to $\rho _0$, it follows that ${\mathcal {F}}_\infty ^\epsilon (\mu _0)=0$. If $\beta \ge 0$, i.e. the inverse temperature is positive, then limit free energy ${\mathcal {F}}_\infty ^\epsilon$ is non-negative, and $\mu _0$ is the unique minimum.

2.6 Negative Temperatures

In the case $m=2$ (Euler’s equation), Kiessling [27] has proved that there is only one minimiser for small negative values of $\beta$, and thus propagation of chaos also holds.

Here the energy profile when $\beta <0$ is much more involved. Indeed, when $\beta <0$ and $m<2$, the relative entropy fails to control the potential energy term (as in the case $m=2$) and the free energy functional is unbounded from below. Moreover, the infimum of the regularized functionals converges (consistently) to $-\infty$. If we turn to our solution $\nu \otimes \ell$ for negative $\beta$, we can see that, at least when $\beta$ is sufficiently negative, this is not even a local minimum.

To be more precise, consider the functional

$$\begin{aligned} \begin{aligned} {{\tilde{{\mathcal {F}}}}}_\infty ^\epsilon (\mu )&={\mathcal {E}}(\mu |\nu \otimes \ell ) \\&\quad + \frac{1}{2}\beta \iint \iint H_2^\epsilon (\gamma ^2,x^2) \rho (\gamma _1,x_1)\rho (\gamma _2,x_2) \,\nu ^{\otimes 2}(d\gamma _1d\gamma _2) \,\ell ^{\otimes 2}(dx_1dx_2), \end{aligned} \end{aligned}$$

where $\mu$ is a probability measure on $K_\nu \times {{\mathbb {T}}_2}$, and ${\mathcal {E}}$ is the relative entropy. Define ${\tilde{{\mathcal {F}}}}^0_\infty$ similarly, with the original Hamiltonian (2.4) that replaces the regularized Hamiltonian. The variational principle for ${\mathcal {F}}_\infty ^\epsilon$ can be read on product measures as a variational principle for the “one point vortex” marginal $\rho$ with respect to the above defined functional ${\tilde{{\mathcal {F}}}}^\epsilon _\infty$, for $\epsilon >0$. The functional ${\tilde{{\mathcal {F}}}}_\infty ^0$ plays a similar role for the unregularized problem.

Proposition 2.2

If $m<2$ and $\beta <0$,

$$\begin{aligned} \inf {\tilde{{\mathcal {F}}}}_\infty ^0(\mu ) = -\infty . \end{aligned}$$

Moreover, $\inf {\tilde{{\mathcal {F}}}}_\infty ^\epsilon (\mu )\downarrow -\infty$.

Proof

The idea is to construct a measure $\mu =\omega (x)\nu \otimes \ell (d\gamma dx)$, with $\omega$ a non-negative function, with mass one, such that $\omega \in L^p({{\mathbb {T}}_2})$ for some $p>1$, and $\omega \not \in H^{-m/2}({{\mathbb {T}}_2})$. The condition $\omega \in L^p({{\mathbb {T}}_2})$ ensures that the relative entropy ${\mathcal {E}}(\mu |\nu \otimes \ell )$ is finite, while,

$$\begin{aligned} \iint \iint \gamma _1\gamma _2 G_m(x_1,x_2)\,\mu (d\gamma _1 x_1)\mu (d\gamma _2 x_2) = \Bigg (\int \gamma \,\nu (d\gamma )\Bigg )^2\Vert \omega \Vert _{H^{-\frac{m}{2}}}^2 = +\infty . \end{aligned}$$

This proves that $\inf {\tilde{{\mathcal {F}}}}_\infty ^0(\mu )=-\infty$. If $\int \gamma \,\nu (d\gamma )=0$, it is sufficient to modify $\mu =\varrho (\gamma )\omega (x)\nu \otimes \ell (d\gamma dx)$ with a density on the $\gamma$ component so that $\int \gamma \varrho (\gamma )\,\nu (d\gamma )\ne 0$. If the infimum is taken only over smooth (in the x component) densities, it is sufficient to consider a sequence $\mu _n=\omega _n(x)\nu \otimes \ell (d\gamma dx)$, with $\omega _n$ smooth and convergent to $\omega$ in $L^p$. Finally, by monotone convergence, ${\tilde{{\mathcal {F}}}}_\infty ^\epsilon (\mu )\downarrow {\tilde{{\mathcal {F}}}}_\infty ^0(\mu )$.

It remains to construct a suitable function $\omega$. For $m<2$, by Sobolev’s embeddings we know that $L^p({{\mathbb {T}}_2})$ is not embedded in $H^{-m/2}({{\mathbb {T}}_2})$ for all $p\in [1,\tfrac{4}{m+2})$. Indeed, there exists infinitely many non-zero $u\in L^p\setminus H^{-m/2}$, with $p\in (1,\tfrac{4}{m+2})$. Consider one such function u. If $u\ge 0$, then we take u (normalized to have mass 1) as $\omega$. Otherwise, consider the positive and negative part $u_+$, $u_-$ of u. Both are in $L^p$, and at least one, say $u_+$, cannot be in $H^{-m/2}$. We take $u_+$ (normalized to have mass one) as $\omega$. $\square$

We then prove that, at least for $\beta$ negative enough, the measure $\nu \otimes \ell$ is not even a local minimum. Notice that we still have ${\tilde{{\mathcal {F}}}}_\infty ^\epsilon (\nu \otimes \ell )=0$ for all $\epsilon \ge 0$. The computation below is similar to [30, section 5.3].

Lemma 2.3

Let $\epsilon \ge 0$ and $\beta <0$. Then $\mu _0=\nu \otimes \ell$ is not a local minimum of ${\tilde{{\mathcal {F}}}}_\infty ^\epsilon$ (as well as of (2.10)) for $\beta <\beta _0$, where

$$\begin{aligned} \beta _0 :=- \lambda _1^{\frac{m}{2}}{\text {e}}^{\epsilon \lambda _1} \Bigg (\int \gamma ^2\,\nu (d\gamma )\Bigg )^{-1}. \end{aligned}$$

Proof

Let $\varphi$ be bounded and with zero average with respect to $\nu \otimes \ell$, and set $\rho _t=1+t\varphi$, so that $\rho _t\nu \otimes \ell$ is a perturbation of $\mu _0$ for t small. We have

$$\begin{aligned} {\tilde{{\mathcal {F}}}}_\infty ^\epsilon (\rho _t) = \int \rho _t\log \rho _t\,\nu (d\gamma )\,\ell (dx) + \frac{1}{2}\beta t^2\Vert (-\Delta )^{-\frac{m}{4}} {\text {e}}^{\frac{1}{2}\epsilon \Delta }{\bar{\varphi }}\Vert _{L^2(\ell )}^2, \end{aligned}$$

where ${\bar{\varphi }}(x)=\int \gamma \varphi (\gamma ,x)\,\nu (d\gamma )$. Expand the entropy around $t=0$ and choose $\varphi =\gamma e_1$, to get

$$\begin{aligned} {\tilde{{\mathcal {F}}}}_\infty ^\epsilon (\rho _t) = {\tilde{{\mathcal {F}}}}_\infty ^\epsilon (\rho _0) + \frac{1}{2}t^2\Bigg (1+\beta /\beta _0\Bigg ) + o(t^2). \end{aligned}$$

Thus $\mu _0$ cannot be a local minimum. $\square$

Remark 2.4

As a final remark of this section, we wish to emphasize that the result of Proposition 2.2 shows that two different divergences characterize the problem under consideration in the paper. The first is the divergence of the configurational canonical partition function (and in turn of the problem in the definition of (2.5)). This is induced both by the power law singularity of the Green function, and the fact that vortex intensities can have different signs. Nevertheless, when $\beta >0$, the free energy functional is bounded from below and our approach allows to capture the mean equilibrium of vortices through a vanishing regularization of the interaction.

The second divergence, the one of Proposition 2.2 of the free energy functional, emerges when $\beta <0$ and basically originates again from the power law singularity of the Green function (but not from the choice of signs in the intensities). Indeed the construction of Proposition 2.2 shows that, when $m<2$, entropy fails to control potential energy, unlike what happens in the borderline case $m=2$.

3 Main Results

In this section we illustrate our main results, that is convergence of distributions of a finite number of vortices and propagation of chaos, and a central limit theorem for the point vortex system under the assumption of positive temperature $\beta >0$. Our results are asymptotic both in the number of vortices and the regularization parameter $\epsilon$, and thus they capture the behaviour of the original system (2.1). The results hold, though, only if the regularization parameter is allowed to go to zero with a speed, with respect to the number of vortices, which is at least logarithmically slow.

3.1 Propagation of Chaos

We know from Sect. 2.3.1 that, at finite $\epsilon$, propagation of chaos holds and the limit distribution of a pair (position, intensity) is the measure $\nu \otimes \ell$. This is also the candidate limit when $\epsilon ,N$ converge jointly to 0 and $\infty$.

Our first main result is convergence of distributions of position and intensities of vortices in the mean-field limit. The proof is based on identification and minimization of the limiting energy.

Before stating the main result of the section, we start with the definition of some relevant quantities. Set

$$\begin{aligned} {\mathscr {D}}_N = \{\rho \in L^1((K_\nu \times {{\mathbb {T}}_2})^N):\rho \log \rho \in L^1((K_\nu \times {{\mathbb {T}}_2})^N)\}. \end{aligned}$$

Clearly $\mu _{\beta ,\epsilon }^N$, as a density, is in ${\mathscr {D}}_N$. Define also the (relative) entropy ${\mathcal {E}}_N$ on ${\mathscr {D}}_N$ as

$$\begin{aligned} {\mathcal {E}}_N(\rho ) = \iint \dots \iint \rho (\gamma ^N,x^N) \log \rho (\gamma ^N,x^N) \,\nu ^{\otimes N}(d\gamma ^N)\,\ell ^{\otimes N}(dx^N), \end{aligned}$$

where we recall that $\gamma ^N=(\gamma _1,\dots ,\gamma _N)$ and $x^N=(x_1,\dots ,x_N)$.

If $N\ge 2$ and $\mu \in {\mathcal {P}}((K_\nu \times D)^N)$, define the potential energy for the non-regularized system (compare with (2.9)) as

$$\begin{aligned} {\mathcal {K}}_N(\mu ) = \iint \dots \iint H_N(\gamma ^N,x^N)\,\mu (d\gamma ^N,dx^N). \end{aligned}$$

where $H_N$ has been given in (2.4). Set finally for $\rho \in {\mathscr {D}}_N$, in analogy with (2.8),

$$\begin{aligned} {\mathcal {F}}_N(\rho ) = {\mathcal {E}}_N(\rho ) + \frac{\beta }{N} {\mathcal {K}}_N(\rho ). \end{aligned}$$

Notice that ${\mathcal {F}}_N^\epsilon$, ${\mathcal {F}}_N$ are convex, since ${\mathcal {E}}_N$ is convex and the potential energies are linear. We readily verify that ${\mathcal {F}}_N^\epsilon$ is lower semi-continuous for the weak topology of $L^1$, therefore $\mu _{\beta ,\epsilon }^N$ is the unique minimizer of the problem

$$\begin{aligned} \min \Bigg \{{\mathcal {F}}_N^\epsilon (\rho ): \rho \in {\mathscr {D}}_N, \int \rho (\gamma ^N,x^N)\,\nu ^{\otimes N}(d\gamma ^N)\,\ell ^{\otimes N}(dx^N)=1\Bigg \}. \end{aligned}$$

Let us define the following sets,

$$\begin{aligned} \begin{aligned} {\mathscr {E}}_\infty&= \{\mu \in {\mathcal {P}}((K_\nu \times {{\mathbb {T}}_2})^{{\mathbb {N}}_\star }):\mu \text { exchangeable}\},\\ {\mathscr {D}}_\infty&= \{\mu \in {\mathscr {E}}_\infty : \pi _N\mu \text { absolutely continuous wrt }(\nu \otimes \ell )^{\otimes N} \text { for all }N\ge 1\}, \end{aligned} \end{aligned}$$

where ${\mathbb {N}}_\star$ is the set of positive integers. Set moreover, for $\mu \in {\mathscr {D}}_\infty$,

$$\begin{aligned} {\mathcal {E}}_\infty (\mu ) = \lim _{N\rightarrow \infty }\frac{1}{N} {\mathcal {E}}_N(\pi _N \mu ), \end{aligned}$$

where $\pi _N$ is the projection onto the first N components (or any N different components, by exchangeability). The limit, possibly infinite but non-negative by the Gibbs inequality, exists by a standard super-additivity argument.

Define for $\mu \in {\mathscr {E}}_\infty$,

$$\begin{aligned} {\mathcal {K}}_\infty ^\epsilon (\mu ) :=\frac{1}{2}\iint \iint \gamma _1\gamma _2 G_{m,\epsilon }(x_1,x_2) \pi _2\mu (d\gamma _1,dx_1,d\gamma _2,dx_2), \end{aligned}$$

and likewise ${\mathcal {K}}_\infty$ in terms of $G_m$. Finally, set

$$\begin{aligned} {\mathcal {F}}_\infty ^\epsilon = {\mathcal {E}}_\infty + \beta {\mathcal {K}}_\infty ^\epsilon , \qquad {\mathcal {F}}_\infty = {\mathcal {E}}_\infty + \beta {\mathcal {K}}_\infty . \end{aligned}$$

Theorem 3.1

Assume $m<2$ and $\beta >0$, and fix a sequence $\epsilon =\epsilon (N)$. Assume there is $C>0$ large enough (depending on $\nu$ and $\beta$) such that

$$\begin{aligned} \epsilon (N) \downarrow 0 \quad \text {as}\quad N\uparrow \infty ,\qquad \epsilon (N)\ge C(\log N)^{-\frac{2}{2-m}}. \end{aligned}$$

(3.1)

Then $(\mu _{\beta ,\epsilon _N}^N)_{N\ge 2}$ converges, in the sense of finite dimensional distributions, to the unique solution of the following variational problem,

$$\begin{aligned} \min _{R\in {\mathscr {D}}_\infty } {\mathcal {F}}_\infty (R) = \min _{R\in {\mathscr {E}}_\infty } {\mathcal {F}}_\infty (R). \end{aligned}$$

The unique solution is $(\nu \otimes \ell )^{\otimes {\mathbb {N}}_\star }$, and propagation of chaos holds.

We remark again that, even though we work on the simple geometry of the torus (thus with uniform total distribution), the previous result is highly nontrivial because it proves convergence of the variational problems (and not the trivial convergence of minima).

The proof of convergence of finite dimensional distribution will be given in Sect. 4.2.

Corollary 3.2

Under the same assumptions of the previous theorem, if we are given $(\Gamma _1^N,X_1^N,\dots ,\Gamma _N^N,X_N^N)$ random variables on $({\mathbb {R}}\times {{\mathbb {T}}_2})^N$ with distribution $\mu _{\beta ,\epsilon _N}^N$, then

$$\begin{aligned} \eta _N :=\frac{1}{N}\sum _{k=1}^N\delta _{(\Gamma _K^N,X_k^N)} \end{aligned}$$

converges in probability to $\nu \otimes \ell$, as $N\uparrow 0$.

Proof

Let $g\in C(K_\nu \times {{\mathbb {T}}_2})$. The previous theorem and symmetry of vortices ensure that

$$\begin{aligned} \begin{gathered} {\mathbb {E}}[g(\Gamma _k^N,X_k^N)] = {\mathbb {E}}[g(\Gamma _1^N,X_1^N)] \longrightarrow \iint g(\gamma ,x)\,\nu (d\gamma )\,\ell (dx),\\ {\mathbb {E}}[g(\Gamma _h^N,X_h^N)g(\Gamma _k^N,X_k^N)] = {\mathbb {E}}[g(\Gamma _1^N,X_1^N)g(\Gamma _2^N,X_2^N)] \longrightarrow \Bigg (\iint g(\gamma ,x)\,\nu (d\gamma )\,\ell (dx)\Bigg )^2, \end{gathered} \end{aligned}$$

therefore

$$\begin{aligned} \begin{aligned}&{\mathbb {E}}\Bigg [\Bigg (\frac{1}{N}\sum _{k=1}^N g(\Gamma _K^N,X_k^N) - \iint g(\gamma ,x)\,\nu (d\gamma )\,\ell (dx)\Bigg )^2\Bigg ]^2 \\&\quad = \frac{1}{N}{\mathbb {E}}[g(\Gamma _1^N,X_1^N)^2] + \frac{N-1}{N}{\mathbb {E}}[g(\Gamma _1^N,X_1^N)g(\Gamma _2^N,X_2^N)]\\&\qquad - 2{\mathbb {E}}[g(\Gamma _1^N,X_1^N)]\iint g(\gamma ,x)\,\nu (d\gamma )\,\ell (dx) + \Bigg (\iint g(\gamma ,x)\,\nu (d\gamma )\,\ell (dx)\Bigg )^2\\&\quad \longrightarrow 0, \end{aligned} \end{aligned}$$

and in particular convergence in probability holds. $\square$

Remark 3.3

It is elementary to verify that convergence in the Corollary above implies immediately convergence of the empirical pseudo-vorticity,

$$\begin{aligned} \theta _N =\frac{1}{N}\sum _{j=1}^N\gamma _j^N\delta _{X_j^N} \end{aligned}$$

to $\nu (\gamma )\ell$, with $\nu (\gamma )=\int \gamma \,\nu (d\gamma )$. This yields a law of large numbers for the empirical pseudo-vorticity.

3.2 Fluctuations

Finally, we can analyze fluctuations with respect to the limit stated in the previous theorem, namely the limit of the measures

$$\begin{aligned} \zeta _N = \sqrt{N}(\eta _N - \nu \otimes \ell ) \end{aligned}$$

to a Gaussian distribution. To this end define the operators ${\mathscr {E}}$, ${\mathscr {G}}$ as

$$\begin{aligned} \begin{gathered} {\mathscr {G}}\phi (x) :=\int _{{\mathbb {T}}_2}G_m(x,y)\phi (y)\,\ell (dy),\\ {\mathscr {E}}\phi (\gamma ,x) :=\gamma \int _{K_\nu }\int _{{\mathbb {T}}_2}\gamma 'G_m(x,y)\phi (\gamma ',y)\,\nu (d\gamma ')\ell (dy). \end{gathered} \end{aligned}$$

The operator ${\mathscr {G}}$ provides the solution to the problem $(-\Delta )^{\frac{m}{2}}\Phi =\phi$ with periodic boundary conditions and zero spatial average, and extends naturally to functions depending on both variables $\gamma$, x by acting on the spatial variable only. The proof of the following theorem will be the subject of Sect. 4.3.

Theorem 3.4

(Central limit theorem) Assume $m<2$ and $\beta >0$, and choose $\epsilon =\epsilon (N)$ as in (3.1). Then $(\zeta _N)_{N\ge 1}$ converges, as $N\uparrow \infty$, to a Gaussian distribution with covariance $I - \beta (I+\beta \Gamma _\infty {\mathscr {G}})^{-1}{\mathscr {E}}$, in the sense that for every test function $\psi \in L^2(\nu \otimes \ell )$, $\langle \psi ,\zeta _N \rangle$ converges in law to a real centred Gaussian random variable with variance

$$\begin{aligned} \sigma _\infty (\psi )^2 :=\langle I - \beta (I+\beta \Gamma _\infty {\mathscr {G}})^{-1}{\mathscr {E}}(\psi -{\bar{\psi }}), (\psi -{\bar{\psi }}) \rangle , \end{aligned}$$

where

$$\begin{aligned} \Gamma _\infty :=\int \gamma ^2\,\nu (d\gamma ),\qquad {\bar{\psi }} :=\int \psi (\gamma ,x)\nu (d\gamma )\,\ell (dx). \end{aligned}$$

(3.2)

Remark 3.5

As in Remark 3.3, we can derive a central limit theorem for the empirical pseudo-vorticity $\theta _N$. Indeed, $\sqrt{N}(\theta _N-\nu (\gamma )\ell )$ converges to a Gaussian distribution with covariance $\Gamma _\infty (I+\beta \Gamma _\infty {\mathscr {G}})^{-1}$, in the sense that for every test function $\psi \in L^2(\ell )$, $\langle \sqrt{N}(\theta _N-\nu (\gamma )\ell ),\psi \rangle$ converges in law to a real centred Gaussian random variable with variance

$$\begin{aligned} {\tilde{\sigma }}_\infty (\psi )^2 = \Gamma _\infty \langle (I+\beta \Gamma _\infty {\mathscr {G}})^{-1} (\psi -{\bar{\psi }}),(\psi -{\bar{\psi }}) \rangle . \end{aligned}$$

The Gaussian measure obtained corresponds to the invariant measure (2.2) of the original system (2.1), when one takes $\alpha =1/\Gamma _\infty$.

Remark 3.6

(Quenched results) The above results hold also in a “quenched” version, namely if intensities are non-random but given at every N. For instance, consider the result about convergence of finite dimensional distributions of vortices and propagation of chaos (Theorem 3.1) For every N, fix a family $\Gamma _N^q:=(\gamma _j^N)_{j=1,2,\dots ,N}$ and consider the quenched version of (2.6),

$$\begin{aligned} \mu _{\beta ,\epsilon }^{\Gamma _N^q,N}(dx^N) = \frac{1}{Z_{\beta ,\epsilon }^{\Gamma _N^q,N}} {\text {e}}^{-\frac{\beta }{N} H_N^\epsilon (\gamma _1^N,\dots ,\gamma _N^N,x^N)} \,\ell ^{\otimes N}(dx^N). \end{aligned}$$

If there is a measure $\nu _\star$ such that

$$\begin{aligned} \frac{1}{N}\sum _{j=1}^N\delta _{\gamma _j^N} \rightharpoonup \nu _\star , \qquad N\uparrow \infty , \end{aligned}$$

(3.3)

and, due to our singular setting (in view of Lemma 4.3), if

$$\begin{aligned} \Bigg |\frac{1}{N}\sum _{j=1}^N (\gamma _j^N)^2 - \int \gamma ^2\,\nu _\star (d\gamma )\Bigg | G_{m,\epsilon _N}(0,0) \longrightarrow 0 \qquad N\uparrow \infty , \end{aligned}$$

then the k-dimensional marginals of $\mu _{\beta ,\epsilon }^{\Gamma _N^q,N}$ converge to $(\nu _\star \otimes \ell )^{\otimes k}$, for all $k\ge 1$. Under the same assumptions, the law of large numbers also holds. To obtain the central limit theorem, one needs to assume some concentration condition on the convergence (3.3).

Remark 3.7

(Extensions to non-trivial geometries and distributions) At this stage it is possible to illustrate the difficulties related to the extension of the resulted presented here to non-trivial geometries (manifolds with boundary) and to non-trivial limit distributions.

In a general planar domain we expect that the boundary, as in the case of Euler vortices [38], has an effect on the motion (2.3) of vortices and thus on the Hamiltonian (2.4). Namely we expect the Hamiltonian acquires an additional term,

$$\begin{aligned} H = \frac{1}{2}\sum _{j\ne k}\gamma _j\gamma _k G_m(X_j,X_k) + \frac{1}{2}\sum _j \gamma _j^2 g_m(X_j,X_j). \end{aligned}$$

where $G_m-g_m$ is the free Green function of the fractional Laplacian on the plane. To carry over the results given here on the torus, several properties of $G_m,g_m$ amd of the corresponding regularized version are needed and are subject of a work in progress. We believe that this should be possible under the condition of neutrality of vortices, namely ${\mathbb {E}}_\nu [\gamma ] = 0$, where $\nu$ is the prior on intensities. Without neutrality, again, the cornerstone of our techniques, Lemma 4.2, becomes ineffective and the control on the partition function will result much weaker.

4 Proofs of the Main Results

Prior to the proof of our main results we state some preliminary results that will be useful in the rest of the section.

Lemma 4.1

Let $f\in L^3({{\mathbb {T}}_2})$ with zero average on ${{\mathbb {T}}_2}$, then

$$\begin{aligned} \Bigg |\int _{{\mathbb {T}}_2}{\text {e}}^{\mathrm {i}f(x)}\,\ell (dx) - {\text {e}}^{-\frac{1}{2}\Vert f\Vert _{L^2}^2}\Bigg | \le \Vert f\Vert _{L^3}^3. \end{aligned}$$

Here the norms $\Vert \cdot \Vert _{L^2}$ and $\Vert \cdot \Vert _{L^3}$ are computed with respect to the normalized Lebesgue measure $\ell$ on ${{\mathbb {T}}_2}$.

Proof

Using the well-known inequalities

$$\begin{aligned} \begin{gathered} |{\text {e}}^{\mathrm {i}x} - (1+\mathrm {i}x-\tfrac{1}{2} x^2)| \le |x|^3,\\ |{\text {e}}^{-\frac{1}{2} x^2} - (1 - \tfrac{1}{2} x^2)| \le |x|^3, \end{gathered} \end{aligned}$$

the proof is elementary. $\square$

In the proof of our limit theorems we will streamline and adapt to our setting an idea from [4]. The key point is to give a representation of the equilibrium measure density in terms of a Gaussian random field. Here the condition $\beta >0$ is crucial.

Lemma 4.2

Let $(x_1,x_2,\dots ,x_N)\in {{\mathbb {T}}_2}^N$ be N distinct points, and let $\gamma _1,\gamma _2,\dots ,\gamma _N\in K_\nu$. Then

$$\begin{aligned} {\text {e}}^{-\frac{\beta }{N}H_N^\epsilon (x^N,\gamma ^N)} = {\mathbb {E}}_{U_{\beta ,\epsilon }}\Bigg [{\text {e}}^{\frac{\mathrm {i}}{\sqrt{N}} \sum _{j=1}^N\gamma _j U_{\beta ,\epsilon }(x_j)}\Bigg ] {\text {e}}^{\frac{1}{2N}\beta G_{m,\epsilon }(0,0) \sum _{j=1}^N \gamma _j^2}, \end{aligned}$$

where $U_{\beta ,\epsilon }$ is the periodic mean zero Gaussian random field on the torus with covariance $\beta G_{m,\epsilon }$, and ${\mathbb {E}}_{U_{\beta ,\epsilon }}$ denotes expectation with respect to the probability framework on which $U_{\beta ,\epsilon }$ is defined.

Proof

The proof is elementary, since by definition of the random field $U_{\beta ,\epsilon }$, the random vector $(U_{\beta ,\epsilon }(x_1), U_{\beta ,\epsilon }(x_2),\dots ,U_{\beta ,\epsilon }(x_N))$ is centred Gaussian with covariance matrix $(\beta G_{m,\epsilon }(x_j,x_k))_{j,k=1,2,\dots ,N}$. Notice finally that by translation invariance, $G_{m,\epsilon }(x,x)=G_{m,\epsilon }(0,0)$. $\square$

Lemma 4.3

Assume there are a sequence of i. i. d. real random variables $(X_k)_{k\ge 1}$ such that there is $M>0$ with $0\le X_k\le M$ for all k, and a sequence of complex random variables $(Y_k)_{k\ge 1}$ such that ${\mathbb {E}}Y_k\rightarrow L$, a. s. and $|Y_k|\le M$ for all k. Set $S_n=\frac{1}{n}\sum _{k=1}^n X_k$, $S={\mathbb {E}}[X_1]$.

If $F_n:[-S,M]\rightarrow {\mathbb {R}}$ is a sequence of functions such that there is $\alpha <\frac{1}{4}$ with

• $F_N(0)=1$ and $|F_n(y)|\le {\text {e}}^{c_0 n^{2\alpha }}$ for all $y\in [-S,M]$,

• ${\mathcal {B}}_\delta :=\sup _{|y|\le \delta ,n\ge 1} |F_n(n^{-\alpha }y)-1| \longrightarrow 0$ as $\delta \rightarrow 0$,

then

$$\begin{aligned} {\mathbb {E}}[F_n(S_n-S)Y_n] \longrightarrow L, \end{aligned}$$

as $n\rightarrow \infty$.

Proof

Choose $\beta$ such that $\alpha \le \beta <\frac{1}{2}(1-2\alpha )$, fix $\delta >0$ and set

$$\begin{aligned} A_n :=\{n^\beta |S_n-S|\le \delta \}. \end{aligned}$$

By the Bernstein inequality there is $c_1>0$ such that

$$\begin{aligned} {\mathbb {P}}[A_n^c] \le {\text {e}}^{-c_1 n^{1-2\beta }}. \end{aligned}$$

(4.1)

In particular, $n^\beta (S_n-S)\rightarrow 0$ a. s.. Now,

First, using the first assumption on $F_n$ and (4.1),

by the choice of $\beta$. For the other term, let $\theta _\delta (y)=(y\wedge \delta )\vee (-\delta )$, then (recall that $\alpha \le \beta$),

By (4.1), ${\mathbb {E}}[Y_n\mathbb {1}_{A_n^c}]\rightarrow L$, moreover,

$$\begin{aligned} \Bigg |{\mathbb {E}}\Bigg [\Bigg (F_n(n^{-\alpha }\theta _\delta (n^\alpha (S_n-S)))-1\Bigg ) Y_n\mathbb {1}_{A_n}\Bigg ]\Bigg | \le M {\mathcal {B}}_\delta , \end{aligned}$$

and ${\mathcal {B}}_\delta \rightarrow 0$ as $\delta \rightarrow 0$ by the second assumption. The conclusion follows by first taking the limit in n, and then the limit in $\delta$. $\square$

4.1 Bounds on the Partition Function

We preliminarily prove upper and lower bounds on the partition function.

Lemma 4.4

If $\beta \in {\mathbb {R}}$ and $m<2$, then $Z_{\beta ,\epsilon }^N\ge 1$.

Proof

By the Jensen inequality,

$$\begin{aligned} Z_{\beta ,\epsilon }^N \ge \exp \Bigg (-\frac{\beta }{2N} \iint \dots \iint \sum _{i\ne j}\gamma _i\gamma _j G_{m,\epsilon }(x_i,x_j) \,\nu ^{\otimes N}(d\gamma ^N)\ell ^{\otimes N}(dx^N)\Bigg ) = 1, \end{aligned}$$

since the Green function has zero average. $\square$

Lemma 4.5

Let $\beta \ge 0$. If $m<2$ and if $(\epsilon _N)_{N\ge 1}$ satisfies (3.1), then

$$\begin{aligned} \sup _{N\ge 2}\frac{1}{N}\log Z_{m,\epsilon _N}^N <\infty . \end{aligned}$$

Proof

By Lemma 4.2,

$$\begin{aligned} \begin{aligned} Z_{\beta ,\epsilon }^N&= \int \dots \int {\text {e}}^{\frac{1}{2}\beta \Gamma _N G_{m,\epsilon }(0)} {\mathbb {E}}_{U_{\beta ,\epsilon }}\Bigg [\prod _{i=1}^N\int _{{\mathbb {T}}_2}{\text {e}}^{\frac{\mathrm {i}}{\sqrt{N}}\gamma _j U_{\beta ,\epsilon }(x_j)}\,\ell (dx_j)\Bigg ] \nu ^{\otimes N}(d\gamma ^N)\\&={\text {e}}^{\frac{1}{2}\beta \Gamma _\infty G_{m,\epsilon }(0)}{\mathcal {Z}}^N_\epsilon , \end{aligned} \end{aligned}$$

where $\Gamma _\infty$ has been defined in (3.2),

$$\begin{aligned} \Gamma _N :=\frac{1}{N}\sum _{j=1}^N \gamma _j^2, \end{aligned}$$

(4.2)

and

$$\begin{aligned} \begin{aligned} {\mathcal {Z}}^N_\epsilon&= \int \dots \int {\text {e}}^{\frac{1}{2}\beta (\Gamma _N-\Gamma _\infty ) G_{m,\epsilon }(0)} {\mathbb {E}}_{U_{\beta ,\epsilon }}\Bigg [\prod _{i=1}^N\int _{{\mathbb {T}}_2}{\text {e}}^{\frac{\mathrm {i}}{\sqrt{N}}\gamma _j U_{\beta ,\epsilon }(x_j)}\,\ell (dx_j)\Bigg ] \,\nu ^{\otimes N}(d\gamma ^N)\\&\le \int \dots \int {\text {e}}^{\frac{1}{2}\beta (\Gamma _N-\Gamma _\infty ) G_{m,\epsilon }(0)} \,\nu ^{\otimes N}(d\gamma ^N). \end{aligned} \end{aligned}$$

By Lemma 4.3 it follows that the integral on the right hand side in the displayed formula above converges to 1. Indeed, if we set $F_N(x)=\exp \Bigg (\frac{1}{2}\beta G_{m,\epsilon }(0)x\Bigg )$, in order to meet the assumptions of Lemma 4.3, it is sufficient to find $\alpha \in (0,\tfrac{1}{4})$ such that $G_{m,\epsilon }(0)N^{-\alpha }\lesssim O(1)$. It is elementary to see that

$$\begin{aligned} G_{m,\epsilon }(0,0) = \sum _{k=1}^\infty g^\epsilon _k = \sum _{k=1} \lambda _k^{-\frac{m}{2}}{\text {e}}^{-\epsilon \lambda _k} \approx \epsilon ^{-\frac{1}{2}(2-m)}, \end{aligned}$$

(4.3)

since $\lambda _k\sim k$, therefore our assumption ensures that $\sup _{N\ge 2}{\mathcal {Z}}_{\epsilon _N}^N\in (0,\infty )$.

To conclude the proof it is sufficient to notice that

$$\begin{aligned} \frac{1}{N}\log Z_{m,\epsilon }^N \le \frac{\beta }{2N}\Gamma _\infty G_{m,\epsilon }(0) + \log \sup _{N\ge 2}{\mathcal {Z}}_{\epsilon _N}^N \lesssim N^{-\alpha }G_{m,\epsilon }(0) + \log \sup _{N\ge 2}{\mathcal {Z}}_{\epsilon _N}^N, \end{aligned}$$

and by the choice of the sequence $(\epsilon _N)_{N\ge 1}$, the right hand side is uniformly bounded in N.

$\square$

4.2 Proof of Theorem 3.1

This section contains the proof of convergence of finite dimensional distributions of the equilibrium measure (2.6). The key point is the following lemma, which unfortunately, being based on the Sine-Gordon transformation of Lemma 4.2, only holds for $\beta \ge 0$.

Lemma 4.6

If $\beta >0$, under the same assumptions of Theorem 3.1, for every $k\ge 1$,

$$\begin{aligned} \iint \iint \gamma _1\gamma _2 e_k(x_1)e_k(x_2) \pi _2\mu _{\beta ,\epsilon _N}^N(d\gamma _1d\gamma _2 dx_1 dx_2) \longrightarrow 0, \end{aligned}$$

where $\pi _2\mu _{\beta ,\epsilon _N}^N$ is the “two point vortices” marginal of $\mu _{\beta ,\epsilon _N}^N$. In particular,

$$\begin{aligned} \frac{1}{N} {\mathcal {K}}_N^{\epsilon _N}(\mu _{\beta ,\epsilon _N}^N) \longrightarrow 0, \qquad \text {and}\qquad \frac{1}{N} {\mathcal {K}}_N(\mu _{\beta ,\epsilon _N}^N) \longrightarrow 0. \end{aligned}$$

Proof

We prove the statement for ${\mathcal {K}}_N$. The proof of the same statement for ${\mathcal {K}}_N^{\epsilon _N}$ follows likewise. We have that

$$\begin{aligned} \begin{aligned} \frac{1}{N} {\mathcal {K}}_N(\mu _{\beta ,\epsilon }^N)&= \frac{1}{N^2}\iint \dots \iint H_N(\gamma ^N,x^N)\,\mu _{\beta ,\epsilon }^N(d\gamma ^N,dx^N)\\&= \frac{N-1}{2N}\iint \dots \iint \gamma _1\gamma _2 G_m(x_1,x_2)\,\mu _{\beta ,\epsilon }^N(d\gamma ^N,dx^N)\\&= \sum _{k=1}^\infty \lambda _k^{-\frac{m}{2}} \iint \dots \iint \gamma _1\gamma _2 e_k(x_1)e_k(x_2)\,\mu _{\beta ,\epsilon }^N(d\gamma ^N,dx^N). \end{aligned} \end{aligned}$$

Set

$$\begin{aligned} {\mathcal {I}}_k^N :=\iint \dots \iint \gamma _1\gamma _2 e_k(x_1)e_k(x_2)\,\mu _{\beta ,\epsilon }^N(d\gamma ^N,dx^N), \end{aligned}$$

then, by Lemma 4.2,

$$\begin{aligned} Z_{\beta ,\epsilon }^N{\mathcal {I}}_k^N= & {} \iint \dots \iint \gamma _1\gamma _2e_k(x_1)e_k(x_2) {\text {e}}^{\frac{1}{2}\beta \Gamma _N G_{m,\epsilon }(0)} \\&{\mathbb {E}}\Bigg [\prod _{j=1}^N {\text {e}}^{\frac{\mathrm {i}}{\sqrt{N}}\gamma _j U_{\beta ,\epsilon }(x_j)}\Bigg ] \,\nu ^{\otimes N}(d\gamma ^N)\,\ell ^{\otimes N}(dx^N). \end{aligned}$$

A simple Taylor expansion yields, since $e_k$ has zero average,

$$\begin{aligned} \int _{{\mathbb {T}}_2}e_k(x_1) {\text {e}}^{\frac{\mathrm {i}}{\sqrt{N}}\gamma _1 U_{\beta ,\epsilon }(x_1)}\,\ell (dx_1) = O\Bigg (\tfrac{1}{\sqrt{N}}\Vert U_{\beta ,\epsilon }\Vert _{L^1}\Bigg ), \end{aligned}$$

and, since $Z_{m,\epsilon }^N\ge 1$ by Lemma 4.4, we have that

$$\begin{aligned} |{\mathcal {I}}_k^N| \le Z_{\beta ,\epsilon }^N|{\mathcal {I}}_k| \lesssim \frac{1}{N}{\text {e}}^{\frac{1}{2}\beta \Gamma _\infty G_{m,\epsilon }(0)} \int \dots \int {\text {e}}^{\frac{1}{2}\beta (\Gamma _N-\Gamma _\infty ) G_{m,\epsilon }(0)} {\mathbb {E}}[\Vert U_{\beta ,\epsilon }\Vert _{L^2}^2] \,\nu ^{\otimes N}(d\gamma ^N). \end{aligned}$$

If $\epsilon =\epsilon _N$, by Lemma 4.3 it follows that ${\mathcal {I}}_k^N\rightarrow 0$.

To prove that the whole energy converges to 0 it is sufficient to prove that there is $\delta >0$ (small) such that

$$\begin{aligned} \sum _{k=1}^N\lambda _k^{-\frac{m}{2}+\delta }|{\mathcal {I}}_k^N| \end{aligned}$$

is bounded uniformly in N. To this end, let M be a constant such that $|\gamma |\le M$, $\nu$–a. s., then

$$\begin{aligned} \begin{aligned} \Bigg |\int _{{\mathbb {T}}_2}e_k(x){\text {e}}^{\frac{\mathrm {i}}{\sqrt{N}}\gamma U_{\beta ,\epsilon }(x)}\,\ell (dx)\Bigg |&=\Bigg |\sum _{p=0}^\infty \int _{{\mathbb {T}}_2}e_k(x) \frac{(\mathrm {i}\gamma )^p}{p!N^{p/2}}U_{\beta ,\epsilon }(x)^p\,\ell (dx)\Bigg |\\&\le \sum _{p=1}^\infty \frac{M^p}{p! N^{p/2}}|U_k^p|, \end{aligned} \end{aligned}$$

where $U_k^p$ is the Fourier coefficient of $U_{\beta ,\epsilon }^p$ corresponding to $e_k$. Therefore

$$\begin{aligned} \begin{aligned} |{\mathcal {I}}_k^N|&=\Bigg |\iint \dots \iint \gamma _1\gamma _2 e_k(x_1)e_k(x_2) {\text {e}}^{\frac{1}{2}\beta \Gamma _N G_{m,\epsilon }(0)} \\&\quad {\mathbb {E}}\Bigg [\prod _{j=1}^N{\text {e}}^{\frac{\mathrm {i}}{\sqrt{N}}\gamma _j U_{\beta ,\epsilon }(x_j)}\Bigg ] \,\nu ^{\otimes N}(d\gamma ^N)\ell ^{\otimes N}(dx^N)\Bigg |\\&\le M^2{\text {e}}^{\frac{1}{2}\beta \Gamma _\infty G_{m,\epsilon }(0)}\\&\quad {\mathbb {E}}\Bigg [\Bigg (\sum _{p=1}^\infty \frac{M^p}{p! N^{p/2}}|U_k^p|\Bigg )^2\Bigg ] \int \dots \int {\text {e}}^{\frac{1}{2}\beta (\Gamma _N-\Gamma _\infty )G_{m,\epsilon }(0)} \,\nu ^{\otimes N}(d\gamma ^N). \end{aligned} \end{aligned}$$

The integral in the formula above converges to 1 by Lemma 4.3 and is independent from k. We can safely ignore it and we will do so for simplicity. The first term (the exponential in the formula above) diverges and will be controlled by the choice of the sequence $\epsilon _N$. We focus on the relevant term,

$$\begin{aligned} \sum _{k=1}^\infty \lambda _k^{\delta -m/2} {\mathbb {E}}\Bigg [\Bigg (\sum _{p=1}^\infty \frac{M^p}{p! N^{p/2}}|U_k^p|\Bigg )^2\Bigg ] \le \Bigg (\sum _{p=1}^\infty \frac{M^p}{p! N^{p/2}} {\mathbb {E}}[\Vert U_{\beta ,\epsilon }^p\Vert _{H^{\delta _0}}^2]^{\frac{1}{2}}\Bigg )^2, \end{aligned}$$

where $\delta _0=(\delta -m/2)_+$. Since the field $U_{\beta ,\epsilon }$ is Gaussian, with covariance $\beta G_{m,\epsilon }$, we claim that there is $c>0$ such that

$$\begin{aligned} {\mathbb {E}}[\Vert U_{\beta ,\epsilon }^p\Vert _{H^{\delta _0}}^2] \le c^{2p}p^{3\delta _0}\epsilon ^{\frac{1}{2}(m-2)p-\delta _0}(2p-1)!!. \end{aligned}$$

(4.4)

Set

$$\begin{aligned} \phi (x) = \sum _{p=1}^\infty p^{\frac{3}{2}\delta _0}\frac{\sqrt{(2p-1)!!}}{p!}x^p, \end{aligned}$$

then $\phi$ is an entire function over ${\mathbb {R}}$ and

$$\begin{aligned} \sum _{k=1}^\infty \lambda _k^{\delta -m/2}|{\mathcal {I}}_k^N| \lesssim \epsilon ^{-\frac{1}{2}\delta _0} {\text {e}}^{\frac{1}{2}\beta \Gamma _\infty G_{m,\epsilon }(0)} \phi (u_\epsilon ^N)^2, \end{aligned}$$

where $u_\epsilon ^N = c M N^{-\frac{1}{2}}\epsilon ^{\frac{1}{4}(m-2)}$. By the choice of $\epsilon _N$, $u_{\epsilon _N}^N\rightarrow 0$ as $N\uparrow \infty$, therefore there is $c'>0$ (independent from N) such that $|\phi (u_{\epsilon _N}^N)|\le c'|u_{\epsilon _N}^N|$, and

$$\begin{aligned} \sum _{k=1}^\infty \lambda _k^{\delta -m/2}|{\mathcal {I}}_k^N| \lesssim \frac{1}{N} \epsilon _N^{\frac{1}{2}(m-2-\delta _0)} {\text {e}}^{\frac{1}{2}\beta \Gamma _\infty G_{m,\epsilon _N}(0)} \lesssim O(1), \end{aligned}$$

by our assumption (3.1).

It remains to prove (4.4). It suffices to prove the claim on $H^n$ for non-negative integers n, and by the Poincaré inequality,

$$\begin{aligned} \Vert U_{\beta ,\epsilon }^p\Vert _{H^n}^2 = \sum _{|\alpha |=n}\Vert D^\alpha U_{\beta ,\epsilon }^p\Vert _{L^2}^2. \end{aligned}$$

Fix a multi-index $\alpha =(\alpha _1,\alpha _2)$, then

$$\begin{aligned} \begin{aligned} D^\alpha U_{\beta ,\epsilon }^p(x)&= \sum _{\begin{array}{c} h_1+\dots +h_p=\alpha _1\\ k_1+\dots +k_p=\alpha _2 \end{array}} \left( {\begin{array}{c}\alpha _1\\ h_1\dots h_p\end{array}}\right) \left( {\begin{array}{c}\alpha _2\\ k_1\dots k_p\end{array}}\right) \\&\quad (D^{h_1}_{x_1}D^{k_1}_{x_2}U_{\beta ,\epsilon })(x)\dots (D^{h_p}_{x_1}D^{k_p}_{x_2}U_{\beta ,\epsilon })(x). \end{aligned} \end{aligned}$$

Therefore, since the cardinality of non-negative integers $h_1,\dots ,h_p$ such that $h_1+\dots +h_p=\alpha _1$ is $\left( {\begin{array}{c}\alpha _1+p\\ p\end{array}}\right) \le (p+n)^{\alpha _1}/\alpha _1!$ (same for the term in $\alpha _2$), by the Hölder inequality,

$$\begin{aligned} \begin{aligned} {\mathbb {E}}[\Vert D^\alpha U_{\beta ,\epsilon }^p\Vert _{L^2}^2]&\le \frac{(p+n)^n}{\alpha _1!\alpha _2!} \sum _{\begin{array}{c} h_1+\dots +h_p=\alpha _1\\ k_1+\dots +k_p=\alpha _2 \end{array}} \left( {\begin{array}{c}\alpha _1\\ h_1\dots h_p\end{array}}\right) ^2\left( {\begin{array}{c}\alpha _2\\ k_1\dots k_p\end{array}}\right) ^2\\&\quad {\mathbb {E}}[\Vert D^{h_1}_{x_1}D^{k_1}_{x_2}U_{\beta ,\epsilon }\Vert _{L^{2p}}^{2p}]^{\frac{1}{p}}\dots {\mathbb {E}}[\Vert D^{h_p}_{x_1}D^{k_p}_{x_2}U_{\beta ,\epsilon }\Vert _{L^{2p}}^{2p}]^{\frac{1}{p}} \end{aligned} \end{aligned}$$

Notice that $D^{h}_{x_1}D^{k}_{x_2}U_{\beta ,\epsilon }$ is a centred Gaussian random field with covariance $\beta D^{2h}_{x_1}D^{2k}_{x_2}G_{m,\epsilon }$, therefore,

$$\begin{aligned} \begin{aligned} {\mathbb {E}}[\Vert D^{h_1}_{x_1}D^{k_1}_{x_2}U_{\beta ,\epsilon }\Vert _{L^{2p}}^{2p}]&= \int _{{\mathbb {T}}_2}{\mathbb {E}}[|D^{h_1}_{x_1}D^{k_1}_{x_2}U_{\beta ,\epsilon }(x)|^{2p}]\,\ell (dx)\\&= (2p-1)!!\int _{{\mathbb {T}}_2}{\mathbb {E}}[|D^{h_1}_{x_1}D^{k_1}_{x_2}U_{\beta ,\epsilon }(x)|^2]^p\,\ell (dx)\\&= (2p-1)!!\int _{{\mathbb {T}}_2}\beta (D^{2h}_{x_1}D^{2k}_{x_2}G_{m,\epsilon })(x,x)\,\ell (dx)\\&\le c^p\epsilon ^{\frac{1}{2}(m-2)p-(h+k)p}(2p-1)!! \end{aligned} \end{aligned}$$

We additionally notice that

$$\begin{aligned} \sum _{\begin{array}{c} h_1+\dots +h_p=\alpha _1\\ k_1+\dots +k_p=\alpha _2 \end{array}} \left( {\begin{array}{c}\alpha _1\\ h_1\dots h_p\end{array}}\right) ^2\left( {\begin{array}{c}\alpha _2\\ k_1\dots k_p\end{array}}\right) ^2 \le p^{2n}, \end{aligned}$$

and that

$$\begin{aligned} \sum _{|\alpha |=n}\frac{(p+n)^n}{\alpha _1!\alpha _2!} = \frac{2^n}{n!}(p+n)^n \lesssim p^n. \end{aligned}$$

Claim (4.4) now follows by putting all the above inequalities together. $\square$

If $R\in {\mathscr {E}}_\infty$, by Hewitt-Savage’s theorem [25], there is a measure $\pi \in {\mathcal {P}}({\mathcal {P}}(K_\nu \otimes \ell ))$ such that

$$\begin{aligned} R = \int \mu ^{\otimes {\mathbb {N}}_\star }\,\pi (d\mu ), \end{aligned}$$

(4.5)

and if $R\in {\mathscr {D}}_\infty$, the same representation hold for a probability measure $\pi$ on the cone of non-negative, mass one functions in $L^1(K_\nu \times {{\mathbb {T}}_2},\nu \otimes \ell )$.

We notice the following facts:

• If $R\in {\mathscr {D}}_\infty$, then

  $$\begin{aligned} \begin{aligned} {\mathcal {K}}_N^\epsilon (\pi _N R)&=\frac{1}{2N}\sum _{i\ne j}\iint \gamma _i\gamma _j G_{m,\epsilon }(x_i,x_j) \pi _2R(d\gamma _i,d\gamma _j,dx_i,dx_j)\\&=(N-1){\mathcal {K}}_\infty ^\epsilon (R), \end{aligned} \end{aligned}$$

  and likewise for ${\mathcal {K}}_N$ in terms of ${\mathcal {K}}_\infty$.

• ${\mathcal {E}}_N$ is lower semi-continuous for the weak topology of $L^1(K_\nu \times D)$.

• If $R\in {\mathscr {E}}_\infty$, then $R\in {\mathscr {D}}_\infty$ if and only if ${\mathcal {E}}_\infty (R)<\infty$ (see for instance [47]).

• If $R\in {\mathscr {E}}_\infty$ and $\epsilon _N\downarrow 0$, then

  $$\begin{aligned} \frac{1}{N} {\mathcal {K}}_N^{\epsilon _N}(\pi _N R) \uparrow {\mathcal {K}}_\infty (R). \end{aligned}$$

  (4.6)

Proof of Theorem 3.1

Fix a sequence $\epsilon _N\downarrow 0$ as in the statement of the theorem and set $\nu _N=\mu _{\beta ,\epsilon _N}^N$.

Step 1: existence of limit points Existence of limit points is trivial, since $K_\nu \times {{\mathbb {T}}_2}$ is compact. For the rest of the proof we consider a limit point $\nu _\infty$ of $(\nu _N)_{N\ge 1}$, and a sequence $(N_j)_{j\ge 0}$ such that $\nu _{N_j}\rightharpoonup \nu _\infty$ in the sense of convergence of finite dimensional distributions

Step 2: convergence of entropy We have that

$$\begin{aligned} {\mathcal {E}}_\infty (\nu _\infty ) \le \liminf _{j\rightarrow \infty }\frac{1}{N_j}{\mathcal {E}}_{N_j}(\nu _{N_j}) \end{aligned}$$

(4.7)

Indeed, fix $k\ge 1$, then by super-additivity of the entropy, if $N_j=a_jk+b_j$, with $0\le b_j\le k-1$, then

$$\begin{aligned} \frac{a_j}{N_j}{\mathcal {E}}_k(\pi _k\nu _{N_j}) \le \frac{a_j}{N_j}{\mathcal {E}}_k(\pi _k\nu _{N_j}) + \frac{1}{N_j}{\mathcal {E}}_{b_j}(\pi _{b_j}\nu _{N_j}) \le \frac{1}{N_j}{\mathcal {E}}_{N_j}(\nu _{N_j}). \end{aligned}$$

since by the Gibbs inequality entropy is non-negative. By first taking the limit $j\rightarrow \infty$, we have that $\tfrac{a_j}{N}\rightarrow \tfrac{1}{k}$ and, by semi-continuity,

$$\begin{aligned} \frac{1}{k}{\mathcal {E}}_k(\pi _k\nu _\infty ) \le \liminf _{j\rightarrow \infty }\frac{1}{N_j} {\mathcal {E}}_k(\pi _k\nu _{N_j}). \end{aligned}$$

By taking the limit as $k\rightarrow \infty$ and the definition of ${\mathcal {E}}_\infty$, one gets (4.7).

Step 3: $\nu _\infty \in {\mathscr {D}}_\infty$. To this end it is sufficient to prove that ${\mathcal {E}}(\nu _\infty )<\infty$. Indeed, by (4.7) and Lemma 4.6,

$$\begin{aligned} {\mathcal {E}}_\infty (\nu _\infty ) \le \liminf _{j\rightarrow \infty }\frac{1}{N_j}{\mathcal {E}}_{N_j}(\nu _{N_j}) = \liminf _{j\rightarrow \infty }\frac{1}{N_j}{\mathcal {F}}_{N_j}^{\epsilon _{N_j}}(\nu _{N_j}) <\infty . \end{aligned}$$

Step 4: ${\mathcal {K}}_\infty (\nu _\infty )=0$. By exchangeability, if $R\in {\mathscr {E}}_\infty$ has the representation (4.5),

$$\begin{aligned} \begin{aligned} {\mathcal {K}}_\infty (\nu _\infty )&= \frac{1}{2}\sum _{k=1}^\infty \lambda _k^{-\frac{m}{2}} \iint \iint \gamma _1\gamma _2e_k(x_1)e_k(x_2) \,\pi _2R(d\gamma _1,d\gamma _2,dx_1,dx_2)\\&= \frac{1}{2}\sum _{k=1}^\infty \lambda _k^{-\frac{m}{2}} \int \Bigg (\iint \gamma e_k(x)\,\mu (d\gamma ,dx)\Bigg )^2\,\pi (d\mu ). \end{aligned} \end{aligned}$$

(4.8)

By Lemma 4.6,

$$\begin{aligned} \iint \iint \gamma _1\gamma _2e_k(x_1)e_k(x_2) \,\pi _2\nu _\infty (d\gamma _1,d\gamma _2,dx_1,dx_2) = 0, \end{aligned}$$

thus ${\mathcal {K}}_\infty (\nu _\infty )=0$.

Step 5: $\nu _\infty$ is a minimizer of ${\mathcal {F}}_\infty$ in ${\mathscr {D}}_\infty$ (as well in ${\mathscr {E}}_\infty$). Let $R\in {\mathscr {E}}_\infty$. If $R\not \in {\mathscr {D}}_\infty$, then by (4.8) ${\mathcal {K}}_\infty (R)\ge 0$, therefore $\infty ={\mathcal {E}}_\infty (R)\le {\mathcal {F}}_\infty (R)$ and R cannot minimise. Let then $R\in {\mathscr {D}}_\infty$. By steps 4 and 2 and since $\nu _N$ is the unique minimiser of ${\mathcal {F}}_{N_j}^{\epsilon _{N_j}}$,

$$\begin{aligned} {\mathcal {F}}_\infty (\nu _\infty ) = {\mathcal {E}}_\infty (\nu _\infty ) \le \liminf _{j\rightarrow \infty }\frac{1}{N_j}{\mathcal {F}}_{N_j}^{\epsilon _{N_j}}(\nu _{N_j}) \le \liminf _{j\rightarrow \infty }\frac{1}{N_j}{\mathcal {F}}_{N_j}^{\epsilon _{N_j}}(\pi _{N_j}R). \end{aligned}$$

Finally, by the definition of ${\mathcal {E}}_\infty (R)$ and (4.6), the $\liminf$ on the right hand side in the formula above is equal to ${\mathcal {F}}_\infty (R)$. In conclusion ${\mathcal {F}}_\infty (\nu _\infty )\le {\mathcal {F}}_\infty (R)$.

Step 6: conclusion The functional ${\mathcal {F}}_\infty$ is convex, non-negative, and ${\mathcal {F}}_\infty (\mu )=0$ only for $\mu =\nu \otimes \ell$. Therefore each limit point $\nu _\infty$ is equal to $\nu \otimes \ell$. $\square$

4.3 Central Limit Theorem

We finally turn to the proof of Theorem 3.4 on the fluctuations of point vortices. First of all we notice that it suffices to prove convergence of the characteristic functions over test functions $\psi$, with $\psi \in C^1(K_\nu \times {{\mathbb {T}}_2})$, namely to prove that

$$\begin{aligned} {\mathbb {E}}_{\mu _{\beta ,\epsilon }^N}[{\text {e}}^{\mathrm {i}\langle \psi ,\zeta _N \rangle }] \longrightarrow {\text {e}}^{-\frac{1}{2}\sigma _\infty (\psi )^2}. \end{aligned}$$

This is because random measures can be interpreted as random distributions (see for instance [22] for more details on the argument). To this end fix $\psi \in C^1(K_\nu \times {{\mathbb {T}}_2})$, set for brevity $\ell _\psi (\gamma ):=\int \psi (\gamma ,x)\,\ell (dx)$ and $\phi :=\psi -\ell _\psi$. For a function $a\in C(K_\nu )$, define

$$\begin{aligned} M_N(a) = \frac{1}{N}\sum _{j=1}^N a(\gamma _j). \end{aligned}$$

Let $(\phi _k)_{k\ge 1}$ and $(G_{m,k})_{k\ge 1}$ be the Fourier coefficients of $\phi$ and $G_m$ with respect to the basis of eigenvectors $e_1,e_2,\dots$. Straightforward computation yields

$$\begin{aligned} \sigma _\infty (\psi )^2 = \int \ell _\psi (\gamma )^2\,\nu (d\gamma ) - {{\bar{\gamma }}} + \Vert \phi \Vert _{L^2(\nu \otimes \ell )}^2 -\beta \sum _{k=1}^\infty \frac{G_{m,k}\nu (\gamma \phi _k)^2}{1+\beta \Gamma _\infty G_{m,k}}. \end{aligned}$$

(4.9)

where ${{\bar{\gamma }}}$ has been defined in (3.2). By using Lemma 4.2,

$$\begin{aligned} \begin{aligned} {\mathbb {E}}_{\mu _{\beta ,\epsilon }^N}[{\text {e}}^{\mathrm {i}\langle \psi ,\zeta _N \rangle }]&= \frac{1}{Z_{\beta ,\epsilon }^N}\int \ldots \int {\text {e}}^{\mathrm {i}\sqrt{N}(M_N(\ell _\psi )-{{\bar{\psi }}})} {\text {e}}^{\frac{1}{2}\beta \Gamma _N G_{m,\epsilon }(0,0)} \\&\quad \cdot {\mathbb {E}}_{U_{\beta ,\epsilon }^N}\Bigg [ {\text {e}}^{\frac{\mathrm {i}}{\sqrt{N}}\sum _{j=1}^N \phi (\gamma _j,x_j) + \gamma _j U_{\beta ,\epsilon }(x_j)}\Bigg ] \,\nu ^{\otimes N}(d\gamma ^N)\,\ell ^{\otimes N}(dx^N), \end{aligned} \end{aligned}$$

where $\Gamma _N$ has been defined in (4.2). With the positions

$$\begin{aligned} \begin{aligned} A_{\epsilon j}^N(\phi )&:=\int _{{\mathbb {T}}_2}{\text {e}}^{\frac{\mathrm {i}}{\sqrt{N}} \Bigg (\phi (\gamma _j,x_j) +\gamma _j U_{\beta \epsilon }(x_j)\Bigg )}\,\ell (dx_j),\\ B_{\epsilon j}^N(\phi )&:={\text {e}}^{-\frac{1}{2N}\Bigg \Vert \phi (\gamma _j,\cdot ) +\gamma _j U_{\beta \epsilon }\Bigg \Vert _{L^2(\ell )}^2},\\ D_{\epsilon j}^N(\phi )&:=A_{\epsilon j}^N(\phi ) - B_{\epsilon j}^N(\phi ). \end{aligned} \end{aligned}$$

we have the following expansion,

$$\begin{aligned} \prod _{j=1}^N A_{\epsilon j}^N(\phi ) = \prod _{j=1}^N B_{\epsilon j}^N(\phi ) + \sum _{k=1}^N\Bigg (\prod _{j=1}^{k-1} A_{\epsilon j}^N(\phi )\Bigg ) \cdot D_{\epsilon j}^N(\phi )\cdot \Bigg (\prod _{j=k+1}^N B_{\epsilon j}^N(\phi )\Bigg ). \end{aligned}$$

Set also

$$\begin{aligned} \begin{gathered} E_N(\psi ) = {\text {e}}^{\mathrm {i}\sqrt{N}(M_N(\ell _\psi )-{{\bar{\psi }}})},\\ {\mathcal {L}}(\psi ) :=\int \dots \int {\text {e}}^{\frac{1}{2}\beta (\Gamma _N-\Gamma _\infty )G_{m,\epsilon }(0,0)} E_N(\psi ) {\mathbb {E}}_{U_{\beta \epsilon }}\Bigg [\prod _{j=1}^N B_{\epsilon j}^N(\phi )\Bigg ] \,\nu ^{\otimes N}(d\gamma ^N), \end{gathered} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} {\mathcal {G}}(\psi )&:=\int \dots \int {\text {e}}^{\frac{1}{2}\beta (\Gamma _N-\Gamma _\infty )G_{m,\epsilon }(0,0)} E_N(\psi ) \\&\quad \cdot {\mathbb {E}}_{U_{\beta \epsilon }}\Bigg [ \sum _{k=1}^N\Bigg (\prod _{j=1}^{k-1} A_{\epsilon j}^N(\phi )\Bigg ) D_{\epsilon k}^N(\phi ) \Bigg (\prod _{j=k+1}^N B_{\epsilon j}^N(\phi )\Bigg ) \Bigg ] \,\nu ^{\otimes N}(d\gamma ^N), \end{aligned} \end{aligned}$$

then we have that

$$\begin{aligned} {\mathbb {E}}_{\mu _{\beta ,\epsilon }^N}[{\text {e}}^{\mathrm {i}\langle \psi ,\eta _N \rangle }] = \frac{1}{Z_{\beta \epsilon }^N} {\text {e}}^{\frac{1}{2}\beta \Gamma _\infty G_{m,\epsilon }(0,0)} \Bigg ({\mathcal {L}}(\psi ) + {\mathcal {G}}(\psi )\Bigg ). \end{aligned}$$

A similar formula can be obtained for $Z_{\beta \epsilon }^N$, therefore

$$\begin{aligned} {\mathbb {E}}_{\mu _{\beta ,\epsilon }^N}[{\text {e}}^{\mathrm {i}\langle \psi ,\eta _N \rangle }] =\frac{{\mathcal {L}}(\psi ) + {\mathcal {G}}(\psi )}{{\mathcal {L}}(0) + {\mathcal {G}}(0)}, \end{aligned}$$

and it is sufficient now to prove that

$$\begin{aligned} \frac{{\mathcal {L}}(\psi )}{{\mathcal {L}}(0)} \longrightarrow {\text {e}}^{-\frac{1}{2}\sigma _\infty (\psi )^2} \qquad \text {and}\qquad \frac{{\mathcal {G}}(\psi )}{{\mathcal {L}}(0)} \longrightarrow 0, \end{aligned}$$

as $N\uparrow \infty$, $\epsilon =\epsilon (N)\downarrow 0$, for all $\psi$.

We first prove the convergence of the ratio ${\mathcal {L}}(\psi )/{\mathcal {L}}(0)$. Let $(U_{\beta ,\epsilon ,k})_{k\ge 1}$ and $(\phi _k)_{k\ge 1}$ be the components of $U_{\beta ,\epsilon }$ and $\phi$ with respect to the eigenvectors $e_1,e_2,\dots$, and set $g^\epsilon _k:=\lambda _k^{-m/2}{\text {e}}^{-\epsilon \lambda _k}$. By Plancherel, independence, and Gaussian integration,

$$\begin{aligned} \begin{aligned} {\mathbb {E}}_{U_{\beta \epsilon }}\Bigg [\prod _{j=1}^N B_{\epsilon j}^N(\phi )\Bigg ]&={\mathbb {E}}_{U_{\beta \epsilon }}\Bigg [{\text {e}}^{-\frac{1}{2N}\sum _{j=1}^N \Vert \phi (\gamma _j,\cdot )+\gamma _j U_{\beta ,\epsilon }\Vert _{L^2(\ell )}^2} \Bigg ]\\&={\text {e}}^{-\frac{1}{2} M_N(\Vert \phi \Vert _{L^2(\ell )}^2)} \prod _{k=1}^\infty {\mathbb {E}}_{U_{\beta ,\epsilon }}\Bigg [ {\text {e}}^{-\frac{1}{2}(\Gamma _N U_{\beta ,\epsilon ,k}^2 + 2M_N(\gamma \phi _k) U_{\beta ,\epsilon ,k})} \Bigg ]\\&={\text {e}}^{-\frac{1}{2} M_N(\Vert \phi \Vert _{L^2(\ell )}^2)} \prod _{k=1}^\infty \Bigg (\frac{1}{(1+\beta \Gamma _N g^\epsilon _k)^{\frac{1}{2}}} {\text {e}}^{\frac{\beta g^\epsilon _k M_N(\gamma \phi _k)^2}{2(1+\beta \Gamma _N g^\epsilon _k)}}\Bigg ). \end{aligned} \end{aligned}$$

Thus we have

$$\begin{aligned} {\mathcal {L}}(\psi ) = \Bigg (\prod _{k=1}^\infty \frac{1}{\sqrt{1+\beta \Gamma _\infty g^\epsilon _k}}\Bigg ) {\mathcal {L}}_0(\psi ), \end{aligned}$$

(4.10)

with

$$\begin{aligned} \begin{aligned} {\mathcal {L}}_0(\psi )&:=\int \dots \int F_N(\Gamma _N-\Gamma _\infty ) E_N(\psi ) \\&\quad \cdot {\text {e}}^{-\frac{1}{2} M_N(\Vert \phi \Vert _{L^2(\ell )}^2)} {\text {e}}^{\frac{1}{2}\beta \sum _{k=1}^\infty \frac{g^\epsilon _k M_N(\gamma \phi _k)^2}{1+\beta \Gamma _N g^\epsilon _k}} \,\nu ^{\otimes N}(d\gamma ^N), \end{aligned} \end{aligned}$$

and where $F_N$ is defined by

$$\begin{aligned} F_N(X) = {\text {e}}^{\frac{1}{2}\beta X G_{m,\epsilon }(0,0)} \prod _{k=1}^\infty \Bigg (1 + \frac{\beta g^\epsilon _k}{1+\beta g^\epsilon _k\Gamma _\infty }X\Bigg )^{-\frac{1}{2}}. \end{aligned}$$

At this stage it suffices to prove that ${\mathcal {L}}_0(\psi )\rightarrow {\text {e}}^{-\frac{1}{2}\sigma _\infty (\psi )^2}$ as $N\uparrow \infty$ and $\epsilon =\epsilon (N)\downarrow 0$, for all $\psi$.

We preliminarily prove that $F_N$ meets the assumptions of Lemma 4.3. Indeed, set

$$\begin{aligned} c_k = \frac{\beta g^\epsilon _k}{1+\beta g^\epsilon _k\Gamma _\infty }, \end{aligned}$$

then, by using the elementary inequality $\log (1+x)\ge x-\frac{1}{2}x^2$,

$$\begin{aligned} \begin{aligned} 2\log F_N(x)&= \beta G_{m,\epsilon }(0,0)x - \sum _{k=1}^\infty \log (1+c_k x)\\&\le \Bigg (\beta G_{m,\epsilon }(0,0) - \sum _{k=1}^\infty c_k\Bigg )x + \frac{1}{2} \Bigg (\sum _{k=1}^\infty c_k^2\Bigg )x^2\\&\le \Bigg (\beta G_{m,\epsilon }(0,0) - \sum _{k=1}^\infty c_k\Bigg )x + \frac{1}{2} \Bigg (\sum _{k=1}^\infty c_k\Bigg )^2 x^2. \end{aligned} \end{aligned}$$

Since

$$\begin{aligned} 0 \le \sum _k c_k < \beta \sum _k g^\epsilon _k = \beta G_{m,\epsilon }(0,0), \end{aligned}$$

both assumptions of the lemma hold if there is $\alpha <\frac{1}{4}$ such that $G_{m,\epsilon }(0,0)\lesssim N^\alpha$. By (4.3), it is immediate to see that our choice of $\epsilon =\epsilon (N)$ is sufficient to ensure the assumptions of Lemma 4.3 for $F_N$.

To conclude the proof of convergence of ${\mathcal {L}}_0(\psi )$, it is sufficient to prove convergence in expectation of the other terms in ${\mathcal {L}}_0(\psi )$. First,

$$\begin{aligned} {\text {e}}^{-\frac{1}{2} M_N(\Vert \phi \Vert _{L^2(\ell )}^2)} \longrightarrow {\text {e}}^{-\frac{1}{2}\Vert \phi \Vert _{L^2(\nu \otimes \ell )}^2}, \end{aligned}$$

and

$$\begin{aligned} {\text {e}}^{\frac{1}{2}\beta \sum _{k=1}^\infty \frac{g^\epsilon _k M_N(\gamma \phi _k)^2}{1+\beta \Gamma _N g^\epsilon _k}} \longrightarrow {\text {e}}^{\frac{1}{2}\beta \sum _{k=1}^\infty \frac{G_{m,k}\nu (\gamma \phi _k)^2}{1+\beta \Gamma _\infty G_{m,k}}} \end{aligned}$$

converge a. s. and in $L^1$ by the strong law of large numbers. The first term is obviously bounded, the second is bounded since $M_N(\gamma \phi _k)^2\le \Gamma _NM_N(\phi _k^2)$ and

$$\begin{aligned} \sum _{k=1}^\infty \frac{\beta M_N(\gamma \phi _k)^2 g^\epsilon _k}{1+\beta \Gamma _N g^\epsilon _k} \le \sum _{k=1}^\infty M_N(\phi _k^2) = M_N(\Vert \phi \Vert _{L^2(\ell )}^2). \end{aligned}$$

Using the smoothness of $\phi$, we can pass to the limit in the sum. Finally, by the Central Limit Theorem for i. i. d. random variables,

$$\begin{aligned} E_N(\psi ) \longrightarrow \exp \Bigg (-\frac{1}{2}\int \ell _\psi (\gamma )^2\,\nu (d\gamma ) - {{\bar{\psi }}}^2\Bigg ). \end{aligned}$$

By recalling the explicit form of $\sigma _\infty (\psi )$ given in (4.9), we conclude that ${\mathcal {L}}_0(\psi )$ converges to ${\text {e}}^{-\frac{1}{2}\sigma _\infty (\psi )^2}$.

We turn to the analysis of ${\mathcal {G}}(\psi )/{\mathcal {L}}(0)$. By Lemma 4.1,

$$\begin{aligned} \begin{aligned} {\mathbb {E}}_{U_{\beta \epsilon }}[|D_{\epsilon j}^N(\phi )|]&\lesssim \frac{1}{N^{3/2}}{\mathbb {E}}_{U_{\beta \epsilon }}\Bigg [\Bigg \Vert \phi (\gamma _j,\cdot ) + \gamma _j U_{\beta \epsilon } \Bigg \Vert _{L^3(\ell )}^3\Bigg ]\\&\lesssim \frac{1}{N^{3/2}}\Bigg (1 + {\mathbb {E}}_{U_{\beta ,\epsilon }} [\Vert U_{\beta ,\epsilon }\Vert _{L^4(\ell )}^4]\Bigg )^\frac{3}{4}\\&\lesssim \frac{1}{N^{3/2}}(1 + G_{m,\epsilon }(0,0)^{\frac{3}{2}}), \end{aligned} \end{aligned}$$

since

$$\begin{aligned} \begin{aligned} {\mathbb {E}}_{U_{\beta ,\epsilon }}[\Vert U_{\beta ,\epsilon }\Vert _{L^4(\ell )}^4]&= \int _{{\mathbb {T}}_2}{\mathbb {E}}[U_{\beta ,\epsilon }(x)^4]\,\ell (dx) \\&= \int _{{\mathbb {T}}_2}3\beta ^2 G_{m,\epsilon }(x,x)^2\,\ell (dx) = 3\beta ^2 G_{m,\epsilon }(0,0)^2. \end{aligned} \end{aligned}$$

Therefore,

$$\begin{aligned} \begin{aligned} {\mathcal {G}}(\psi )&\le \int \dots \int {\text {e}}^{\frac{1}{2}\beta (\Gamma _N-\Gamma _\infty )G_{m,\epsilon }(0,0)} \sum _{k=1}^N {\mathbb {E}}_{U_{\beta \epsilon }}[|D_{\epsilon k}^N(b)|] \,\nu ^{\otimes N}(d\gamma ^N)\\&\lesssim \frac{1}{\sqrt{N}}(1+G_{m,\epsilon }(0,0)^{\frac{3}{2}}){\mathcal {G}}_0, \end{aligned} \end{aligned}$$

where we have set for brevity

$$\begin{aligned} {\mathcal {G}}_0 :=\int \dots \int {\text {e}}^{\frac{1}{2}\beta (\Gamma _N-\Gamma _\infty )G_{m,\epsilon }(0,0)} \,\nu ^{\otimes N}(d\gamma ^N). \end{aligned}$$

It is easy to see that by Lemma 4.3, ${\mathcal {G}}_0\rightarrow 1$. Moreover, since

$$\begin{aligned} \prod _{k=1}^\infty \frac{1}{1+\beta \Gamma _\infty g^\epsilon _k} = {\text {e}}^{-\sum _k \log (1+\beta \Gamma _\infty g^\epsilon _k)} \ge {\text {e}}^{-\sum _k \beta \Gamma _\infty g^\epsilon _k} = {\text {e}}^{-\beta \Gamma _\infty G_{m,\epsilon }(0,0)}, \end{aligned}$$

and by (4.10) we finally have that

$$\begin{aligned} \frac{{\mathcal {G}}(\psi )}{{\mathcal {L}}(0)} \lesssim \frac{1}{\sqrt{N}}(1 + G_{m,\epsilon }(0,0)^{\frac{3}{2}}) {\text {e}}^{\beta \Gamma _\infty G_{m,\epsilon }(0,0)} \frac{{\mathcal {G}}_0}{{\mathcal {L}}_0(0)}. \end{aligned}$$

So it is sufficient to choose $\epsilon =\epsilon (N)$ so that

$$\begin{aligned} \frac{1}{\sqrt{N}}(1 + G_{m,\epsilon }(0,0)^{\frac{3}{2}}) {\text {e}}^{\beta \Gamma _\infty G_{m,\epsilon }(0,0)} \longrightarrow 0. \end{aligned}$$

Using (4.3), we see immediately that it suffices to choose $\epsilon ^{-\frac{1}{2}(2-m)}\le c\log N$, with c small enough.